1 引言
合成孔径雷达(Synthetic Aperture Radar)图像分类是遥感图像分类的不可或缺的一部分,是PolSAR图像解译的重要研究内容[1]。SAR图像区别于光学图像,难以直观解译,PolSAR图像包含了丰富的地物信息,如地物的几何形状、结构等[2]。目前PolSAR图像数据逐渐递增,对海量数据进行快速的解译,利用卫星遥感数据进行地物分类的课题成为近些年来的研究热点[3]。
目标极化特征研究是目标极化分解、分类的基础[4]。最先利用极化SAR数据对地物进行分类的是Jin-Au Kong教授[5],之后,Van Zyl运用特征值分解对地物的极化信息分解为单一的散射信息[6],但由于其存在应用局限、运算量偏大等诸多问题,对处理实时的图像数据并不适用。Cloude, Pottier[7]从极化信息中提取了极化散射熵和极化散射参数进行分类,是目前最为合理的分解方法,但在计算极化散射熵和散射参数的同时,需要提取目标相干矩阵的特征值和特征向量,因此使得对于数据量大的极化SAR数据,不利于高效得到地物信息。许多研究者开始寻找能解决这些问题的其他方法,其中比较有代表性的是散射相似性理论[8-11]。与目标极化分解不同,散射相似性是通过将目标散射与典型散射相比较得来的,度量的是目标散射与典型散射的相似程度,然而由于只利用到相干矩阵的部分极化信息,且设置的区域边界存在任意性,分类结果有时不尽如人意。因此需要在通过散射相似性理论分类后,然后将初始分类结果输入Wishart分类器[12-13],得到最终的分类结果。
本文提出了一种结合散射相似性和统计模型分类器的非监督分类方法。该方法运用了基于归一化相干矩阵组成的平面代替了H/α平面避免了特征值和特征向量的提取,结合Wishart统计模型分类器分类,进一步分出地物类型,最后结合Radarsat-2卫星获取的黄河冰凌的极化数据分析对比分析了H/α分类方法和本文方法。
本文结构如下:第2节提出了归一化相干矩阵并得到了散射相似性系数,第3节结合散射相似性和Wishart统计模型对地物进行分类,第4节进行分类和对比,第5节做出了总结。
2 目标散射相似性度量
2.1 归一化相干矩阵
为便于目标极化散射特性分析,雷达极化中常采用Pauli基矩阵将Sinclair矩阵矢量化为![]() 即
即
(1)
式中,![]() 为Pauli基特征矢量,其中trace(S)为矩阵迹运算,矩阵右上角T为矩阵的转置;
为Pauli基特征矢量,其中trace(S)为矩阵迹运算,矩阵右上角T为矩阵的转置;
利用目标散射矢量![]() 得到目标相干矩阵定义为:
得到目标相干矩阵定义为:
(2)
式中上标*为矢量共轭转置运算。
为了得到数据的极化特征,对相干矩阵进行特征值分解,得到特征值Λ和特征向量U,公式(3)所示得到极化散射熵H和极化散射参数α的计算公式:
det(T-ΛI)=0
(T-ΛiI)Ui=0
U=[ui1,ui2,ui3]T
(3)
式中,ui1为归一化特征向量U中的元素,pi为对应特征值Λ获得的伪概率;极化散射熵H可以表示散射机制随机性的度量,极化散射参数α表示平均散射机制的类型。
由于提取极化散射熵H和平均极化散射参数α涉及到计算复杂的矩阵特征值和特征矢量分解,不利于图像实时处理;而特征值和矩阵的相似不变量相关,如公式(4)所示,将目标相干矩阵进行归一化处理,得到归一化目标相干矩阵NT。
(4)
式中,![]() 为目标散射矢量,其中上标* 表示矢量共轭转置运算,trace(T)表示对相干矩阵求迹。
为目标散射矢量,其中上标* 表示矢量共轭转置运算,trace(T)表示对相干矩阵求迹。
2.2 散射相似性系数
归一化后的相干矩阵NT和目标相干矩阵T有共同的特征矢量,而且特征矢量对应的特征值分别为Λi,i=1,2,3。归一化后的目标相干矩阵NT和目标相干矩阵T同样也为Hermitian矩阵,因此有
trace(NT)=Λ1+Λ2+Λ3
(5)
(6)
考虑到归一化目标相干矩阵NT的迹恒等于1,特征值为多项式方程(7)的根,即
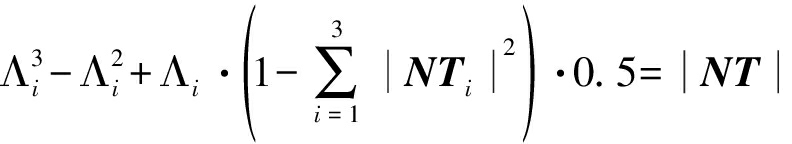
(7)
然后通过计算归一化目标相干矩阵NT的行列式和归一化目标相干矩阵NT元素的平方和求和以及对角线元素的和得到特征值;可以看出目标相干矩阵NT的特征值Λ1、Λ2、Λ3可表示不变特征量函数,这样极化散射熵H可表示为矩阵行列式与元素的平方和的函数,因此该函数为非线性函数;但是归一化相干矩阵NT元素的平方和与极化散射熵H包含信息非常相似,且当极化散射熵最大时即H=1时,归一化目标相干矩阵NT元素的平方和Q最小等于1/3;当极化散射熵最小时即H=0时,归一化目标相干矩阵NT元素的平方和Q最大等于1。
另一个分类参数表征平均散射机制参数α不是相干矩阵的相似不变量,通过分析目标相干矩阵特征矢量参数化形式,归一化目标相干矩阵NT的第一个元素NT1可表示为:
(8)
比较NT1与平均极化散射参数α的表达式(3)和(8)两式,都为pi和αi的函数,说明它们包含了相同的目标信息。
3 结合散射相似性和统计模型的分类方法
本文基于散射相似性,提出了将散射相似性分类方法与威沙特分类器相结合的分类方法。该分类方法首先根据输入的极化SAR数据获取图像的相干矩阵,由相干矩阵计算出散射相似性系数,对极化SAR图像进行初始聚类,然后将获取的初始化聚类结果输入威沙特分类器,对要处理的SAR图像中的像素进行迭代Wishart分类,当满足迭代终止条件后,得到最终的分类结果。这种分类方法的详细流程图如图1所示。
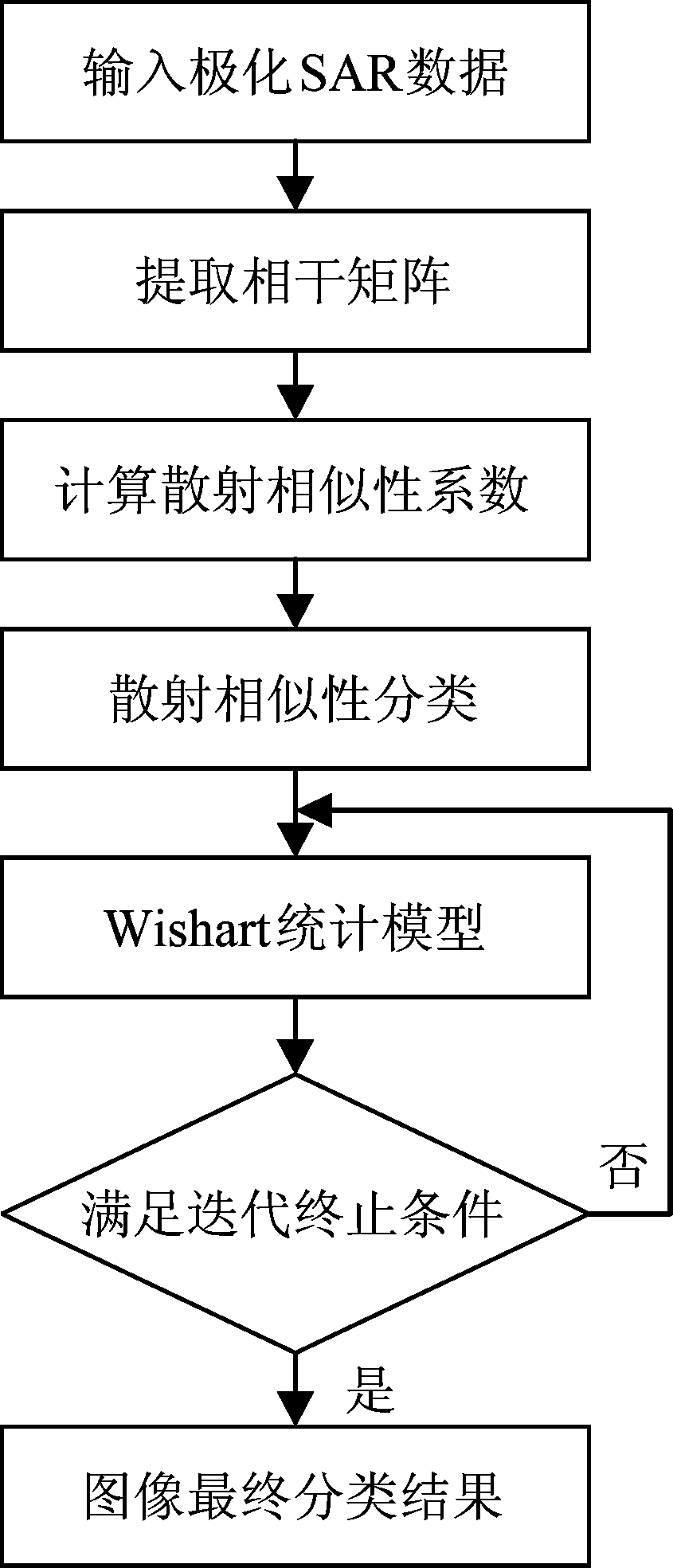
图1 地物分类流程图
Fig.1 Flow chart for classification of Terrain
3.1 基于散射相似性的初始聚类
结合归一化目标相干矩阵NT的第一个元素NT1的分类法类似于H/α分类法,但是每一类对应的空间有一定的不确定性,这是由平方和函数Q与熵H之间的关系以及NT1与平均散射机制参数α都取决两个归一化特征值引起的。
如式(9)所示为归一化目标相干矩阵NT元素的平方和Q与归一化相干矩阵NT的第一个元素NT1的关系:
(9)
当H=1时,Q=0.33,H=0时,Q=1,H=0.5时,Q=0.4,H=0.9时,Q=0.7;先将Q/NT1平面分为三种情形;
当目标极化散射熵H的取值范围[0.9,1],此时Q的取值范围[0.33,0.4),目标为高随机散射情况;
当目标极化散射熵H的取值范围[0.5,0.9),此时Q的取值范围[0.4,0.7),目标为中随机散射情况;
当目标极化散射熵H的取值范围[0,0.5),此时Q的取值范围[0.7,1],目标为低随机散射情况;
由此可形成与H/α分类方案相似的分类方案,对照H/α分类平面形成Q/NT1分类平面。如表1所示给出了α角边界值和NT1边界值的关系。
表1 α角边界值和NT1边界值
Tab.1 α boundary value and NT1 boundary estimate

α0°40°42.5°47.5°50°55°90°NT110.590.480.5550.4250.3550
图2所示为Q/NT1和H/α平面对比图,八种不同的散射机制划分类比图2(a)所示H/α平面划分区域,如图2(b)所示为本算法分类平面和根据Q/NT1平面分类边界将Q/NT1平面进行分类, 分别用Z1到Z8来表示。
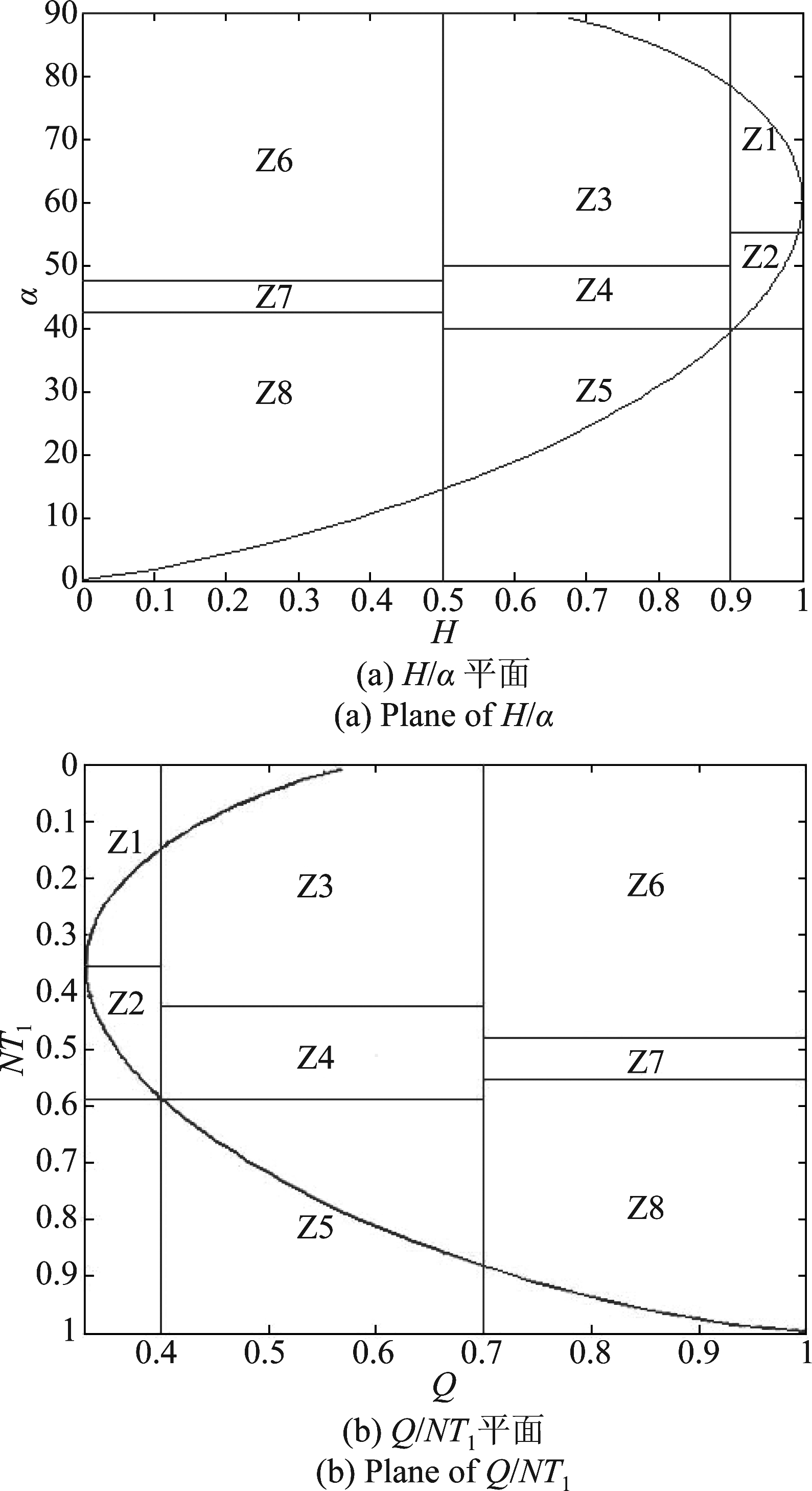
图2 Q/NT1和H/α平面对比图
Fig.2 Collation map of Q/NT1 and H/α
通过图2的仿真结果对比可知,Q/NT1平面的边界值和H/α的平面的边界值一一对应,在对极化SAR图像初始聚类时,散射相似性分类方法是根据提取的相干矩阵求解出散射相似性系数,与H/α分类方法不同的是避免了提取特征值和特征矢量这一步骤,从而减小了运算量。
当目标为高散射情况时,若归一化目标相干矩阵NT的第一个元素NT1的取值范围为[0,0.355)时,该区域记为Z1,对应高熵多次散射;若NT1的取值范围为[0.355,0.59)时,该区域记为Z2,对应高熵植被散射。
当目标为中散射情况时,若归一化目标相干矩阵NT的第一个元素NT1的取值范围为[0,0.425)时,该区域记为Z3,对应中等极化熵的二面角散射;若NT1的取值范围为[0.425,0.59)时,该区域记为Z4,对应中熵植被散射;若NT1的取值范围为[0.59,1)时,该区域记为Z5,对应中熵表面散射。
当目标为低散射情况时,若归一化目标相干矩阵NT的第一个元素NT1的取值范围为[0,0.48)时,该区域记为Z6,对应低熵二次散射或偶次散射;若散射相似性系数NT1的取值范围为[0.48,0.555)时,该区域记为Z7,对应低熵偶极子散射;若散射相似性系数NT1的取值范围为[0.555,1)时,该区域记为Z8,对应低熵表面散射。
3.2 结合散射相似性和统计模型的分类方法
本文算法同时利用相干矩阵的极化信息和统计信息,使得Q/NT1区域边界的设置较为固定,有利于得到理想的分类结果。该方法有效的避免了由于只利用相干矩阵的极化信息造成的某些聚类出现在Q/NT1区域边界附近,或者没有聚类在一个单独的Q/NT1区域内部和多个类同时聚类在同一区域的情况。首先利用散射相似性对极化SAR图像进行初始聚类,然后用这些初始的聚类结果输入Wishart分类器,最后得到极化SAR图像的分类结果。根据极化SAR数据得到的散射相似性系数Q和NT1,将其划分在Q/NT1平面的8个区域得到初始化的聚类结果。
由初始的聚类图得到极化8个聚类中心的相干矩阵:
(10)
式中ni为聚类ωi中所占像素的个数。然后对极化SAR图像中每个像素计算相干矩阵到聚类中心的Wishart距离,然后得到新的分类结果:
(11)
然后再利用公式(10)对新的分类结果计算其中心聚类,再代入公式(11)重新聚类,重复上述过程直到收敛。
4 实验数据与分析
为了验证本文的分类方案,研究区选择在内蒙古自治区鄂尔多斯和包头交界的黄河冰凌区,研究区具体位置为:115°49′~116°12′ E,42°32′~42°50′ N,这里选取由Radarsat-2卫星于2018年2月获取的极化SAR数据,包含四种极化工作方式。如图3(a)为原始PolSAR图像的切片图,图像尺寸为1500*1600,如图3(b)所示,是本次研究区对应的光学图像。

图3 研究区数据
Fig.3 Research area data
4.1 分类效果对比
分别使用H/α和Q/NT1的分类方案对研究区极化数据进行分类,图4(a)、(b)所示为两种分类结果图,两种分类方法分类后的结果具有一致性,在视觉感官上难以区分,然后利用散射机制刻画参数α或NT1将三种散射随机情况进一步细分为八种不同的散射类别,而且参数NT1和参数α存在对应关系,因此构建的Q/NT1分类方案与H/α分类方案存在一致性,同时也保证了分类结果上有一致性。

图4 分类结果对比
Fig.4 Research area data
为了定量化评估两种分类方案的一致性,基于黄河冰凌区的分类结果,分别计算Q/NT1分类结果中的类别Zi(i=[1,8]),H/α分类结果中的类别Ci(i=[1,8])间的重叠率,经计算两种分类方法在此数据上的整体一致性比率高达0.9010。
4.2 运算效率分析
虽然验证了两种方法分类结果具有高度一致性,但在H/α分类方法中,首先要计算参数H和α,其次为了形成分类,还需要对所有像素的目标相干矩阵进行特征分解,这样就产生了额外的运算量,而本文分类方法可完全避免,参数Q和NT1可通过公式由相干矩阵直接获得,所以计算效率很高。
为了量化两种分类算法的计算效率,分别分析H/α和Q/NT1的运算量,H/α的计算方法如公式(3)所示,对于每个像素来说,求解H和α首先需要计算相干矩阵T的特征值Λ和特征向量U,求解特征值需要计算一个一元三次方程,不仅用到了乘法和加法运算,另外在算法中还要计算反余弦和对数等非线性运算,Q/NT1的计算方法如公式(4)和(9)所示,只用到了加法和乘法运算,记O(f(n),n为函数的规模)为算法的时间复杂度,则H/α的算法复杂度为O(n2)+O(nlog2n)+O(n)+O(acos(n)),Q/NT1的算法复杂度为O(n2)+O(n),假设加法和乘法运算量相当,则本文算法省去了计算非线性运算的耗时,从而提高了运算效率。
为了验证理论分析结果,在环境相同的情况下,对大小为1500*1600的极化SAR图像,采用未优化的本文算法和H/α分类方法,分别执行两种算法各十次,计算两种方法运算时间的平均值。通过仿真计算,如图5所示,横坐标为分类方法,纵坐标为运算时间(单位为s)。
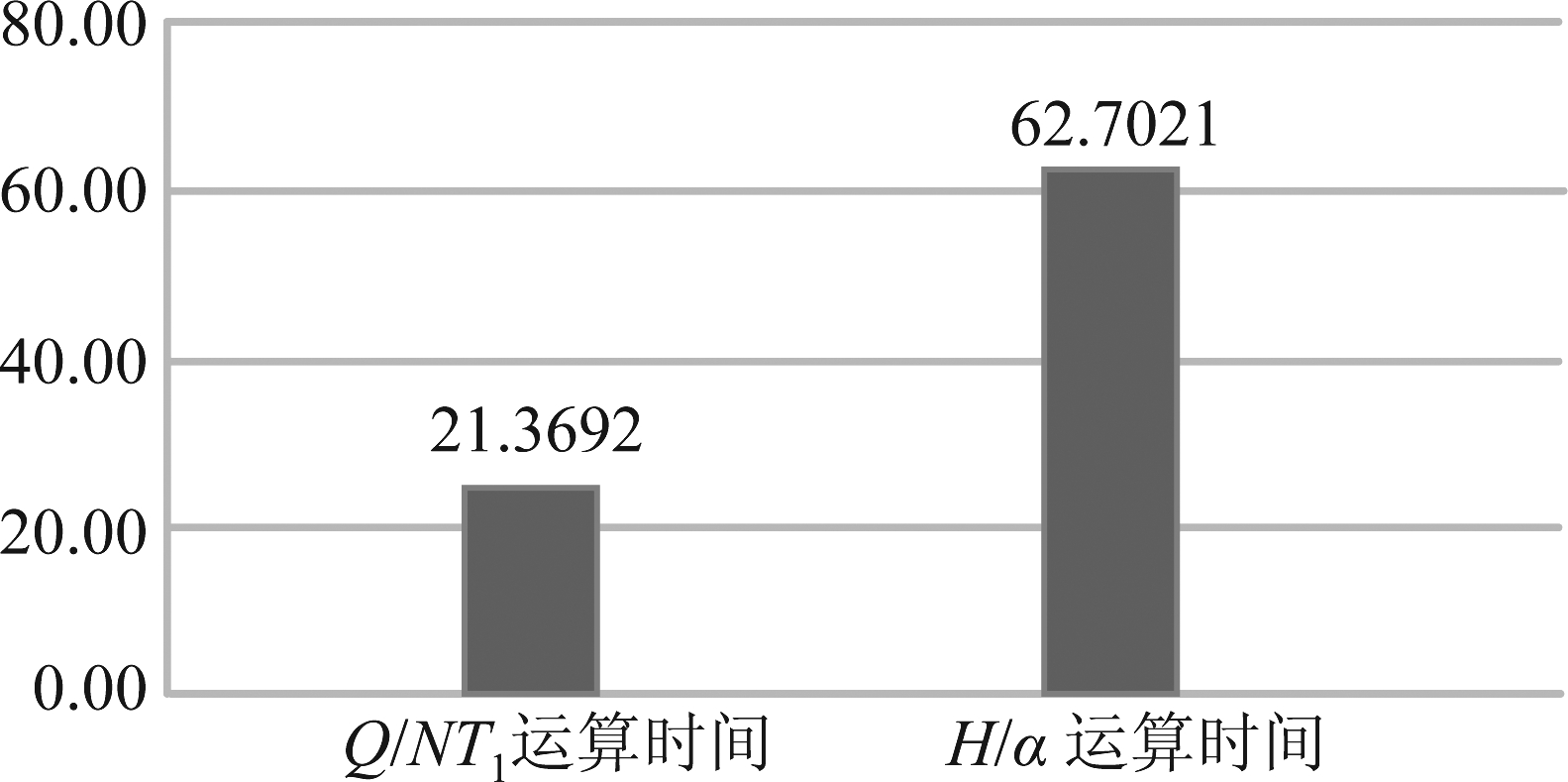
图5 运算时间对比
Fig.5 Comparison of running time
通过图5发现在黄河冰凌区,Q/NT1分类方法平均耗时为H/α分类方法平均耗时的1/3,这与前文分析是一致的。
4.3 最终分类结果
通过初步分类结果分析可知,仅通过散射相似性分类区分不出明显的地物类型,因此需进一步聚类分出地物类别,结合Wishart统计模型非监督分类,分类结果如图6所示,聚类后分为8类,而从分类结果中可以得到7种明显的地物类型。
为了验证本文地物分类方法的精确性,进行了实地考察并对实验基地拍摄取样。如图7(a)~(e)分别为部分地物拍摄图,图7(a)为冰面对应分类结果的1类,图7(b)为冰水边界对应分类结果的2类,图7(c)为树林对应分类结果的3类,图7(d)为黄河边农田对应分类结果4类,图7(e)为黄河边的芦苇丛对应分类结果6类,分类结果的5类是道路,7类是乡镇,最终和分类图能一一对应。

图6 分类结果
Fig.6 The collation map of Classification

图7 地物实拍图
Fig.7 Photographs of ground objects
5 结论
本文首先针对H/α分类方法运算量偏大的缺点进行了改进,在黄河冰凌地物分类方面提出了基于散射相似性和统计模型的分类方法,用归一化相干矩阵NT元素的平方和Q与归一化目标相干矩阵NT的第一个元素NT1组成的平面代替了H/α平面,并结合了Wishart分类器的优势。本文算法有以下优势:第一,相较于H/α分类方法简化了运算量,处理数据时间减少,这一点对于大场景图像和批量化处理来说相对比较重要;第二,在基于散射相似性的基础上加入了Wishart距离度量特征,使得地物分类效果更明显。
[1] 周晓光, 匡纲要, 万建伟. 极化SAR图像分类综述[J]. 信号处理, 2008, 24(5): 806- 812.
Zhou Xiaoguang, Kuang Gangyao, Wan Jianwei. A Review of Polarimetric SAR Image Classification[J]. Signal Processing, 2008, 24(5): 806- 812.(in Chinese)
[2] 徐丰, 王海鹏, 金亚秋. 深度学习在SAR目标识别与地物分类中的应用[J]. 雷达学报, 2017, 6(2): 136-148.
Xu Feng, Wang Haipeng, Jin Yaqiu. Deep Learning as Applied in SAR Target Recognition and Terrain Classification[J]. Journal of Radars, 2017, 6(2): 136-148.(in Chinese)
[3] 陈强, 蒋咏梅, 匡纲要. 基于球面散射相似性的POLSAR图像分类方法[J]. 信号处理, 2010, 26(5): 659- 664.
Chen Qiang, Jiang Yongmei, Kuang Gangyao. Classification for POLSAR Images Based on Surface Scattering Similarity[J]. Signal Processing, 2010, 26(5): 659- 664.(in Chinese)
[4] 刘妍. 极化SAR特征量分析与分类研究[D]. 西安: 西安电子科技大学, 2014.
Liu Yan. Research on Polarimetric SAR Signature Analysis and Classification[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2014.(in Chinese)
[5] Kong J A, Swartz A A, Yueh H A, et al. Identification of Terrain Cover Using the Optimum Polarimetric Classifier[J]. Journal of Electromagnetic Waves & Applications, 1988, 2(2): 171-194.
[6] Zyl J J V. Unsupervised classification of scattering behavior using radar polarimetry data[J]. IEEE Trans. Geosci. Remote Sens, 1989, 27(1): 36- 45.
[7] Cloude S R, Pottier E. A Review of Target Decomposition Theorems in Radar Polarimetry[J]. IEEE Transactions on Geoscience & Remote Sensing, 1996, 34(2): 498-518.
[8] Praks J, Hallikainen M. Entropy-Alpha Classification Alternative for Polarimetric SAR Image[C]∥Applications of Sar Polarimetry & Polarimetric Interferometry. Applications of SAR Polarimetry and Polarimetric Interferometry, 2003.
[9] 李洪忠, 陈劲松, 王超, 等. 基于相似性的POLSAR占优散射归类及非监督聚类[J]. 电子与信息学报, 2012, 34(6): 1501-1505.
Li Hongzhong, Chen Jinsong, Wang Chao, et al. POLSAR Dominant Scattering Mechanism Clustering and Unsupervised Classification Based on Similarity[J]. Journal of Electronics & Information Technology, 2012, 34(6): 1501-1505.(in Chinese)
[10] Yang J, Peng Y N, Lin S M. Similarity between two scattering matrices[J]. Electronics Letters, 2002, 37(3): 193-194.
[11] Praks J, Koeniguer E C, Hallikainen M T. Alternatives to Target Entropy and Alpha Angle in SAR Polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 2262-2274.
[12] 韩萍, 季静敏, 石庆研. 散射模型与Wishart分类相结合的极化SAR图像分类[J]. 信号处理, 2015, 31(11): 1497-1503.
Han Ping, Ji Jingmin, Shi Qingyan. Classification of Polarimetric SAR Images with Scattering Model and Wishart Classifier[J]. Journal of Signal Processing, 2015, 31(11): 1497-1503.(in Chinese)
[13] Guo S, Tian Y, Li Y, et al. Unsupervised classification based on H/alpha decomposition and Wishart classifier for compact polarimetric SAR[C]∥Geoscience & Remote Sensing Symposium. IEEE, 2015.




