1 引言
调制样式识别(Modulation Type Recognition,MTR)是非协作通信过程中重要环节,是完成解调进而获取信息前提,常用于电子侦察、电子干扰、非法频谱监管等。近年来深度学习[1](Deep Learning,DL)方法由于其优异的性能广泛用于计算机视觉、自然语言处理以及数据挖掘等领域。DL能逼近任意线性、非线性函数,能自动从信号中提取具有区分度的特征,DL在MTR应用引起研究人员关注。文献[2]利用信号眼图和卷积神经网络(Convolution Neural Network,CNN)识别DPSK等四种信号,Li J等[3]利用循环谱和深度自编码器识别FSK、PSK、 ASK、QAM 和MSK 5种调制信号,文献[4]利用星座图和CNN识别三种QAM信号,Zhao Z J等[5]利用信号的高阶累积量特征和三阶受限玻尔兹曼机识别2ASK、4ASK、QPSK、8PSK,2FSK,16QAM等六种信号,周龙梅[6]利用短时傅里叶变换和受限玻尔兹曼机识别GFSK、16QAM、2ASK、4ASK、2FSK、OQPSK六种调制样式,文献[7]利用高阶累积量和自编码器对BPSK、QPSK、8PSK、16QAM、32QAM、16APSK、32APSK 七种信号进行识别,G. J. Mendis等[8]利用谱相关函数和深度信念网络(Deep Belief Network, DBN)识别4FSK、16QAM、BPSK、QPSK和OFDM等五种信号,Byeoungdo Kim等[9]提取21种信号特征参数,利用深度神经网络(Deep neural network)完成了BPSK、QPSK、8PSK、16QAM、64QAM五种调制信号识别。但是文献[3-9]算法需对信号进行预处理,可扩展性受限。文献[10]和[11]直接利用正交解调的I、Q信号和卷积神经网络进行信号识别,文献[12]应用单层、堆栈长短期记忆网络(Long Short-team Memory,LSTM)网络和原始信号数据识别BASK、4ASK、BFSK、4FSK、BPSK、QPSK和16QAM 等七种信号。上述研究主要利用单种网络,卷积神经网络具有良好的空间特征学习提取能力,长短期记忆网络[13]具有很强的时间序列处理能力。文献[14]采用两层卷积层后级联一层长短期记忆层结构,在-4 dB信噪比时,对8PSK, AM-DSB, AM-SSB, BPSK, CPFSK, GFSK, PAM4, QAM16, QAM64, QPSK, WBFM 平均识别率能达到90%。但是时间信号经过卷积层后会丢失部分时序特征,且使用两层卷积层提取空域特征会大大增加模型的复杂度,导致训练时间增长。对此,本文提出一种CNN-LSTM并联的MTR算法(简记为CLP算法)。将信号的同向分量(I(t))和正交分量(Q(t))并行输入CNN网络和LSTM网络,经过CNN提取输入信号的空间特征,由LSTM网络获取信号时域特征,将两路输出特征融合再送入输出层,完成MTK。对BPSK、QPSK、8PSK、16QAM、32QAM、16APSK、32APSK 等7种信号识别的仿真实验结果表明:本文算法无需人为设计特征,低信噪比(Signal To Noise Ratio,SNR)下对相位调制和幅相调制信号的识别率较高。
2 CNN-LSTM并联网络模型及参数更新
在接收端,经过符号速率估计、载波估计、下变频得到复基带信号R(t),其实部、虚部分别为同向分量I(t)和正交分量Q(t)。将I路和Q路原始数据的2×N维矩阵作为网络输入,所提出的CLS算法网络如图1所示,由四部分组成,第一部分为网络输入部分,其次是并联层,第三部分为特征融合部分,第四部分为输出层(包括全连接层和分类器)。
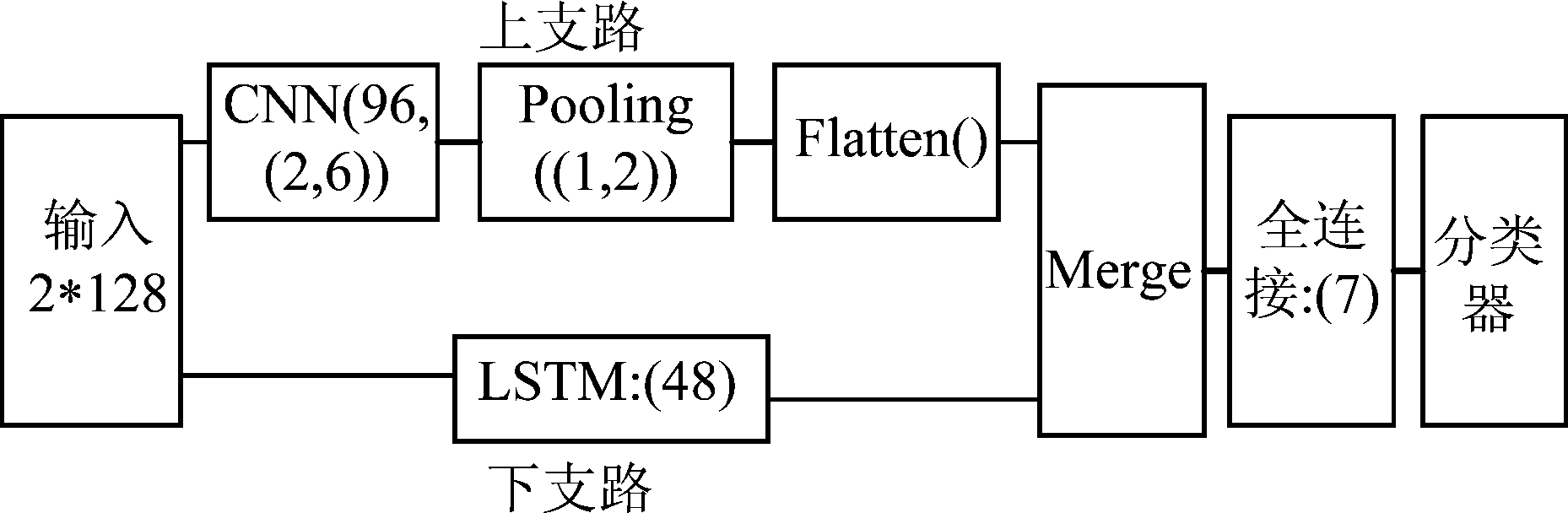
图1 CLP网络模型图
Fig.1 CLP network model diagram
输入层主要完成输入数据信息的收集。每个输入样本为2*128大小的矩阵,128代表I路、Q路的采样点个数,用I2,128表示,I2,128中元素用I(i, j)表示。
第二部分由CNN与单层LSTM并联构成。上支路为卷积层、池化层(平均池化)构成的CNN网络,主要实现对原始输入信号样本的空间特征提取,与输入层之间采取局部连接。卷积层使用96个大小为2*6的卷积核(以下简称核)与输入进行卷积操作,得到卷积层输出:
(1)
其中
为第m个卷积核与输入进行卷积操作后的第j个神经元输出,
为卷积层第m个尺寸为2*6的核,
为卷积层的第m个偏置;f()是激活函数(Activation Function,AF),卷积层使用Relu函数作为AF, Relu函数如式(2)所示:
(2)
输入经二维卷积操作变成一维矢量形式的特征图,输入池化层。池化操作能减少全连层中的参数数量,加快计算速度且能防止陷入过拟合。本文使用的池化窗大小为1*2,步长设置为4。输入特征图经过池化后输出为:
(3)
池化输出经过Flatten层处理后,输入下一层。
下支路为单层LSTM网络,用于提取信号的时序特征。 LSTM的网络拓扑图如图2所示。
图2 LSTM网络拓扑图
Fig.2 LSTM network topology
LSTM网络由一个记忆单元(Memory Cell,以下简称Cell)和三个控制单元组成,即忘记门(Forget Gate, FG)、输入门(Input Gate, IG)、输出门(Output Gate, OG),每个控制单元都是大小一样的两层全连接网络。FG决定是否从Cell状态中保留历史信息,IG通过对输入乘上[0,1]之间的记忆因子决定当前输入数据对Cell状态的影响程度,OG决定输出信息[15]。图2中,LSTM在当前t时刻将接收信号xt、t-1时刻输出ht-1作为输入,经过FG得到忘记因子ft:
ft=δ(Wf[ht-1,xt]+bf)
(4)
其中,Wf为输入与FG之间连接权重矩阵,bf为连接偏置,δ为“sigmoid”函数,表达式为:
(5)
当ft为0时,完全忘记Cell里面的历史信息;当ft为1时,记住全部历史信息。然后,IG根据输入和Cell历史信息进行状态更新如下:
it=δ(Wi·[ht-1,xt]+bi)
(6)
(7)
(8)
其中,Wi、Wc分别为IG连接权值与tanh层权值,bi、bc为对应偏置,
为tanh层产生的候选值,参与Cell信息
的更新过程。由OG得到输出控制因子Ot如式(9)所示,其决定是否输出Cell信息,即得到t时刻输出ht,如式子(10)所示:
Ot=δ(Wo[ht-1,xt]+bo)
(9)
ht=Ot*tanh(Ct)
(10)
其中,Wo为输入与OG之间连接矩阵,bo为偏置,Ot为输出控制因子,其控制机理同FG。
第三部分为特征融合层,将上支路卷积网络提取的信号空间信息与下支路单层LSTM提取的时序信息融合,两路特征串接成新的特征,送入到下一部分。
第四部分为softmax分类输出层,利用融合层融合的两支路特征进行分类输出,该层为普通全连接层,节点设置为7,以7维概率向量形式输出,最大值对应的索引号为对应的分类结果。
将式(4)、(6)、(7)、和(9)中的
和
都统一分别表示为参数集W和b。上述模型的优化目标函数为实际输出标签和真实标签值之间的交叉熵函数,如式(11)所示,其中
和y分别是实际输出标签和真实标签值。W和b更新包括信息前向、反向两个传播过程,使用梯度下降法对参数W和b按式(12)和(13)所示进行更新[6]。
(11)
(12)
(13)
为了保证网络能够有效训练和收敛,对网络各层的权值W用服从N(0,1)分布的随机数初始化,偏置b初始化为0。
3 算法仿真及性能分析
3.1 仿真数据集及环境
待识别信号集包括BPSK、QPSK、8PSK、16QAM、32QAM、16APSK和32APSK。信号参数设置为:载波速率为24 kHz,采样速率为60 kHz;16APSK信号半径为R1=1、R2=2.7,32APSK信号半径为R1=1、R2=2.70、R3=5.71。仿真使用高斯白噪声,SNR从-4 dB至18 dB,间隔2 dB,信号样本采样点数为128,采用一个7×1向量表示样本标记,根据1出现的不同位置标识不同的信号调制样式。
本文使用matlab编程语言完成信号预处理等过程,生成实验数据集,在Ubuntu 16.04 64位操作系统上完成算法仿真。使用python、keras框架完成网络的搭建、训练、测试等整个过程,涉及的依赖库主要是CUDA、cudnn等加速库。实验硬件使用华硕主板,配备四核Intel 酷睿i7 7700 CPU,搭载Nvidia GTX1080 8G显存的显卡,配置了8G运行内存和480G固态存储硬盘。
3.2 算法性能分析
实验1 训练迭代次数Epoch对识别性能影响。
Epoch参数对识别性能起关键作用,Epoch过多或过少模型都难达到最优。Epoch过少,模型没有充分学习到信号的特征,导致误差函数偏大,从而识别性能差;Epoch过多不仅导致网络训练时间(Network Training Time,简记为Time)过长而且容易陷入过拟合,从而使得识别性能下降。本文用不同的训练迭代次数训练网络,然后进行信号调制样式识别测试,得到7种信号平均正确识别率(Average Correct Recognition Accuracy,简记为Acc)和Time分别如图3和图4所示。从图3可以看出,当Epoch小于50时,信号平均正确识别率近似呈分段线性增长,当Epoch为50时达到最大值,此后增加Epoch,Acc稍有减小,说明当网络训练到一定程度时单纯增加Epoch并不能提升识别性能,甚至会产生过拟合,使得识别性能下降。由图4可见,随着Epoch的增加Time几乎呈现线性增长,说明Epoch是影响训练快慢的重要因素。综合考虑Acc和Time,下文仿真均选取Epoch为50。
图3 不同Epoch对Acc影响
Fig.3 Average recognition accuracy of different epoch
图4 不同Epoch对Time影响
Fig.4 Network training time of different epoch
实验2 上支路卷积层数对识别性能影响。
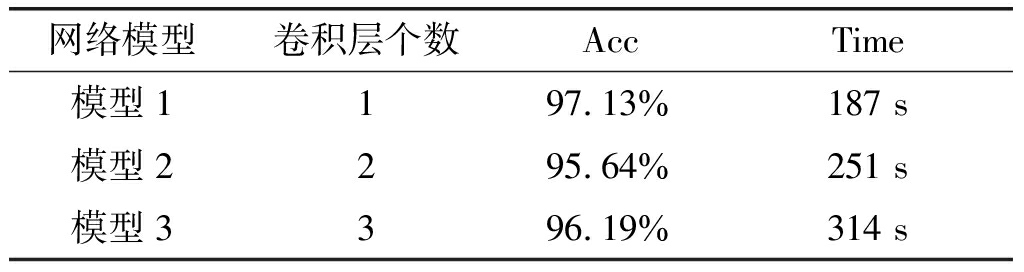
为了分析上支路卷积层层数对调制样式识别性能的影响,固定并联网络其他结构不变,只改变卷积层的个数,只对最后一个卷积层输出加池化层,且由于经第一层卷积之后,信号变成一维向量,故对卷积层数大于2的卷积核尺寸都采用1×3,在训练样本相同、训练迭代次数相同情况下,得到不同网络模型的7种信号Acc和Time如表1所示。由表1可以看出:当采用一层卷积层和一层池化层时网络有最高的识别精度和最短的训练时间;当增加卷积层后,网络性能下降,说明当网络采用一层卷积层时,卷积层提取的特征已经可以很好的反映调制样式信息,继续增加卷积层数只会提取一些冗余特征,使模型变得复杂,泛化性能下降。故上支路选择一层卷积层和一层池化层
表1 上支路不同卷积层数对Acc及Time影响
Tab.1 Average recognition accuracy and network training time of different convolutional layer signals in the upper branch
网络模型卷积层个数AccTime模型11 97.13%187 s模型22 95.64%251 s模型3396.19%314 s
实验3 上支路核尺寸与池化窗大小对识别性能的影响
CNN的卷积核尺寸大小决定输入信号的识别粒度,卷积核尺寸过大会造成信号的一些细节信息丢失,尺寸过小又会使得卷积操作转化特征能力降低,不能很好提取特征。池化层的作用是对卷积操作后的特征图进行去冗余处理,如窗口太大会使得重要信息丢失,若窗口太小则达不到去冗余的效果。在实验1和2基础上,改变卷积核和池化窗口的大小,CLP算法对本文7种信号的平均正确识别率和模型训练时间如表2所示。
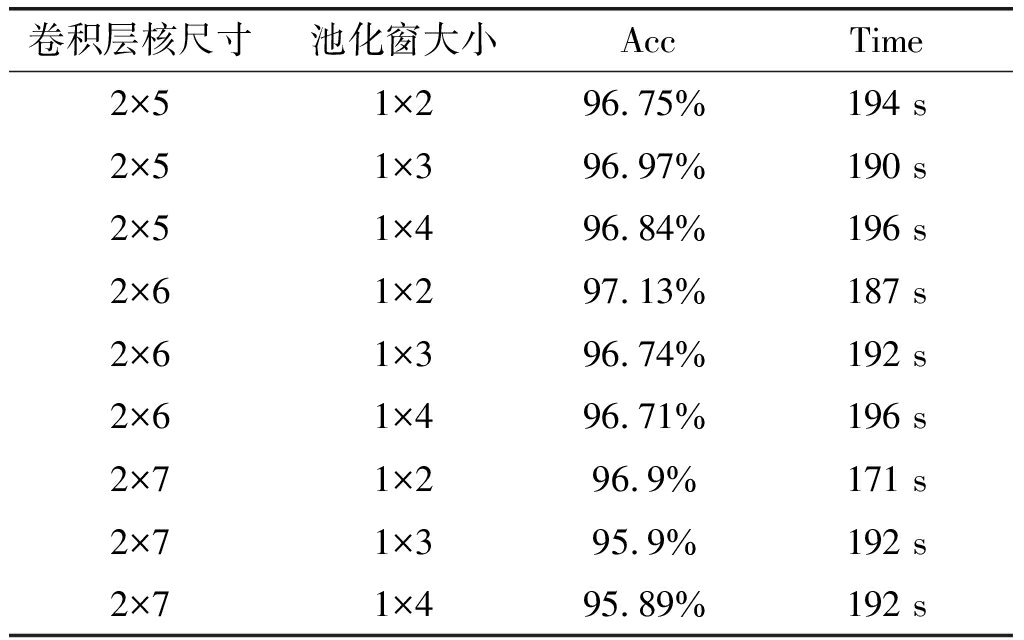
由于本文算法的输入数据的维度为2*128,因此本文卷积层的卷积核尺寸都为2*。从表2平均正确识别率数据可以看出,在网络其他参数相同时,随着卷积核尺寸增加信号平均正确识别率先增加后减少,所以核太大和太小都不利于网络模型的学习,故核大小选为2*6。当确定核大小时,可以看出,池化窗口选择为1*2时网络有最好的Acc,且Time最少。故下文仿真中选取卷积层核尺寸为2*6、池化窗口设置为1*2。
表2 不同核尺寸网络的Acc和Time
Tab.2 Average recognition accuracy and model training time for different kernel size networks
卷积层核尺寸池化窗大小AccTime2×51×296.75%194 s2×51×396.97%190 s2×51×496.84%196 s2×61×297.13%187 s2×61×396.74%192 s2×61×496.71%196 s2×71×296.9%171 s2×71×395.9%192 s2×71×495.89%192 s
实验4 下支路LSTM层数对识别性能的影响
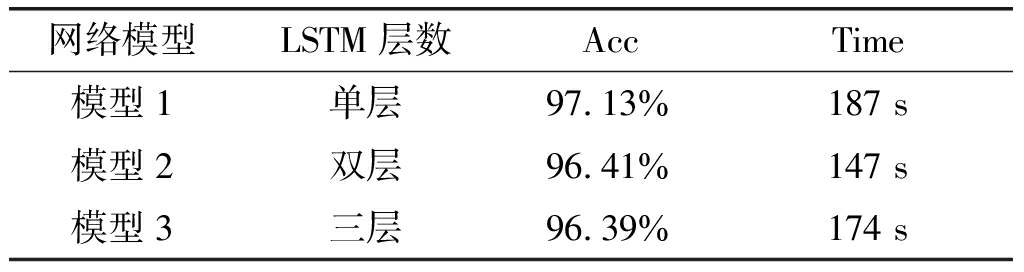
第一层LSTM提取的初步时序特征为输入后,多层LSTM网络进一步提取时序特征。LSTM层数过少可能特征提取不完全,从而识别结果较差;过多则会达到一个饱和状态,继续增加层数只会造成网络臃肿,性能难以提升。本实验设置下支路第一层LSTM控制门大小为48,当层数大于1时设置为24。下支路采用不同层数LSTM网络对7种信号的平均正确识别率和模型训练时间如表3所示。
表3 下支路不同LSTM层数网络对Acc及Time影响
Tab.3 Average recognition accuracy and model training
time of different LSTM layer networks in the lower branch
网络模型LSTM层数AccTime模型1单层97.13%187 s模型2双层96.41%147 s模型3三层96.39%174 s
由表3可以看出,下支路采用一层LSTM网络时,平均正确识别率最高,当层数增加时,Acc下降。说明下支路仅仅采用一层LSTM,就能充分提取信号的时序信息,故本文在其他实验中下支路采用一层LSTM网络。
实验5 不同算法性能分析
图5 四种算法Acc比较
Fig.5 Comparison of four algorithm average recognition accuracy
本实验分析比较本文CLP算法、文献[14]应用级联形式网络(CNN+CNN+LSTM)的CLS算法、文献[11]应用CNN网络的CNN算法和文献[12]应用LSTM网络的LSTM算法;CLS算法第一卷积层使用128个大小为1*3的核,第二卷积层使用32个大小为2*3的核,LSTM控制门大小选取128;其他算法参照图1所示参数选取。四种算法对7种信号的Acc如图5所示,四种算法在整个测试集上的平均正确识别率如表4所示,四种算法所需训练参数个数及时间如表5所示。由图5可见,本文CLP算法识别性能最好,其次是CLS算法, LSTM算法相对较差。当SNR为-4 dB时,CLP、CLS、CNN和LSTM算法的Acc分别达到87%、85%、82%和75%;随着SNR增大,CLP、CLS、CNN和LSTM算法的Acc分别稳定在98%、97%、96.5%、86%;从表4可以看出,CLP算法在整个测试集上的平均正确识别率最高,比CNN算法高1.48个百分点。这是由于不同信号具有不同幅度、相位和星座图特征,因此具有不同的空间特征和时序特征;并联CNN-LSTM网络能提取信号的时间和空间特征;级联网络中,信号经过卷积操作后,已丢失了原始信号时序特性;CNN网络和LSTM网络特征提取不如前二者。
由表5可以看出,本文提出的CLP算法训练时间远远低于文献[14]提出的CLS算法,四种算法中,LSTM 算法训练时间最短,CLP算法次之,CNN算法最长,但LSTM算法的Acc相对其他三种算法最低,识别性能最差。
表4 四种算法平均正确识别率比较
Tab.4 Average accuracy comparison of four algorithms
算法CLPCLSCNNLSTM平均正确识别率/%97.1396.0895.7485.02
表5 四种算法所需训练参数个数及时间
Tab.5 Comparison of training parameters and time of four algorithms
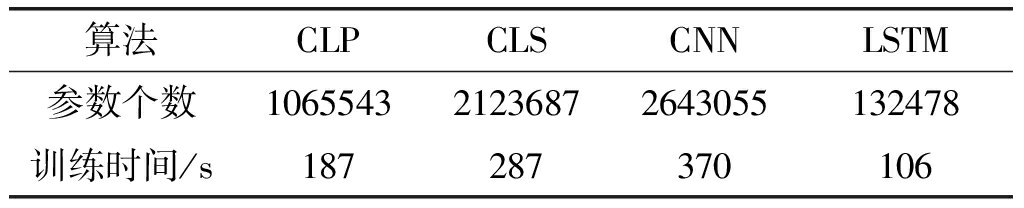
算法CLPCLSCNNLSTM参数个数106554321236872643055132478训练时间/s187287370106
实验6 CLP算法识别性能分析
当SNR为-4 dB至18 dB时,四种算法对七种信号的正确识别率分别如图6、图7、图8和图9所示。对比四幅图可以看出,SNR大于2 dB时,CLP 算法对7种信号的正确识别率在90%以上,CLS算法在85%以上,CNN算法在70%以上,LSTM算法最差。
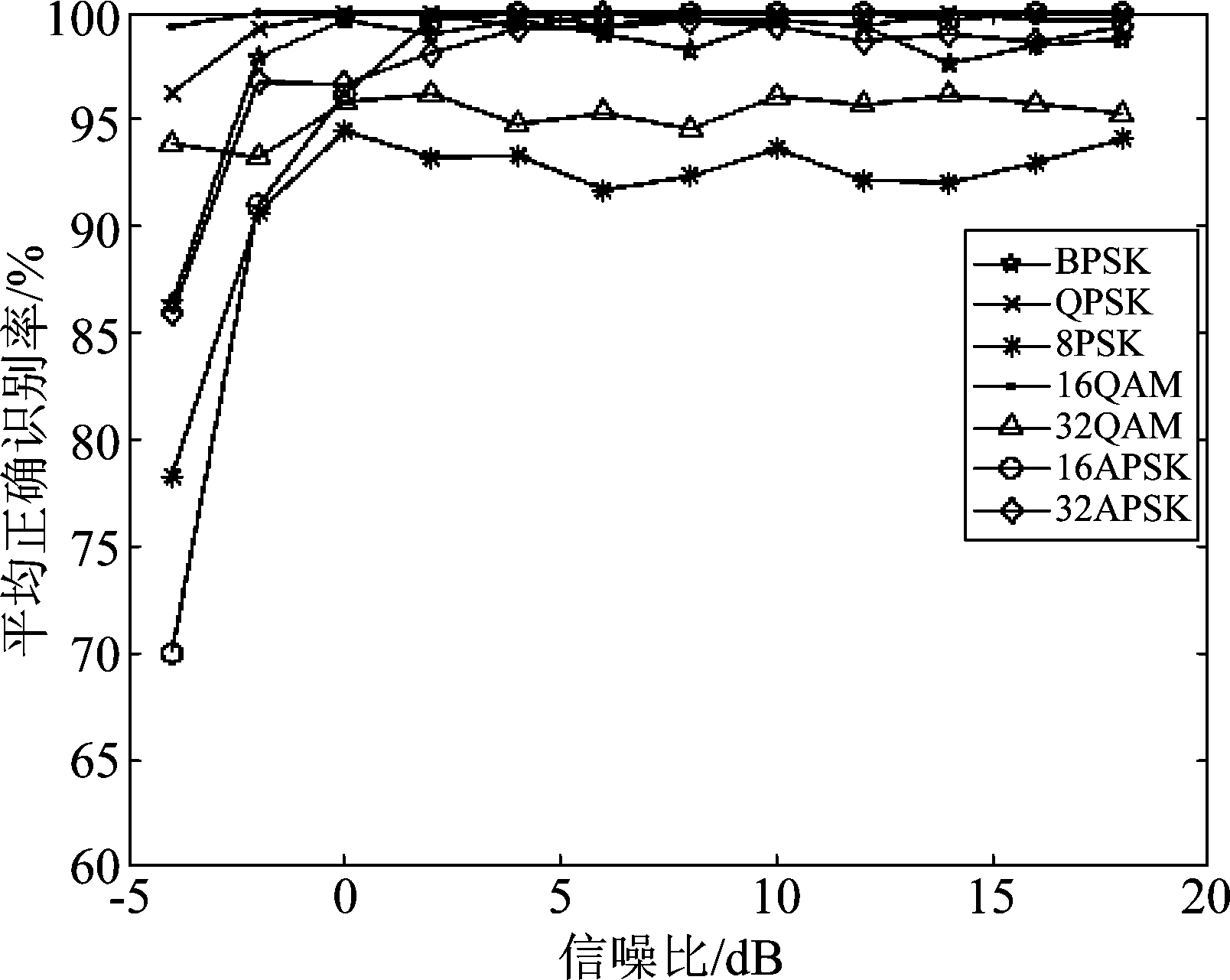
图6 CLP算法单个信号正确识别率曲线
Fig.6 Single signal Acc curve of CLP
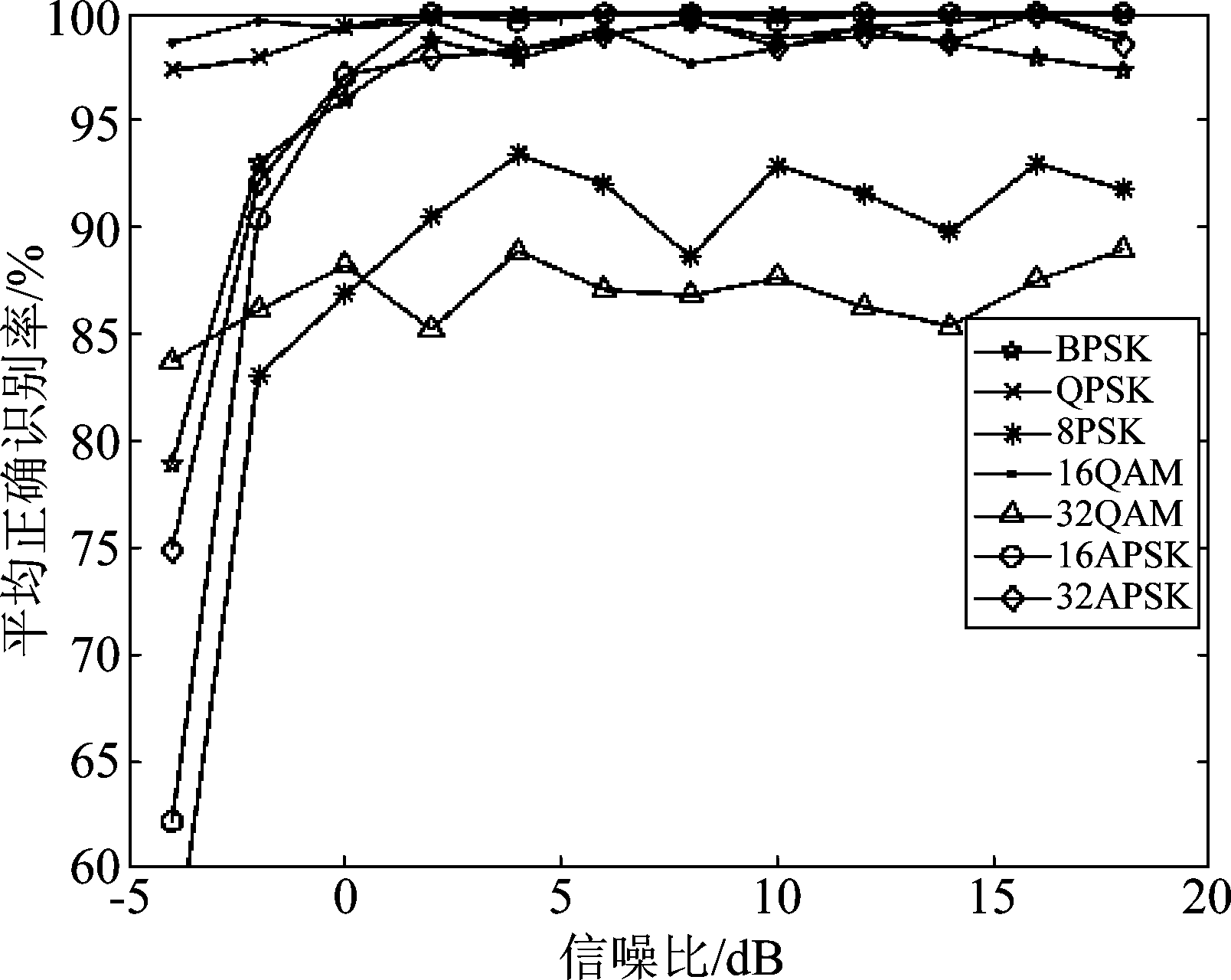
图7 CLS算法单个信号正确识别率曲线
Fig.7 Single signal Acc curve of CLS
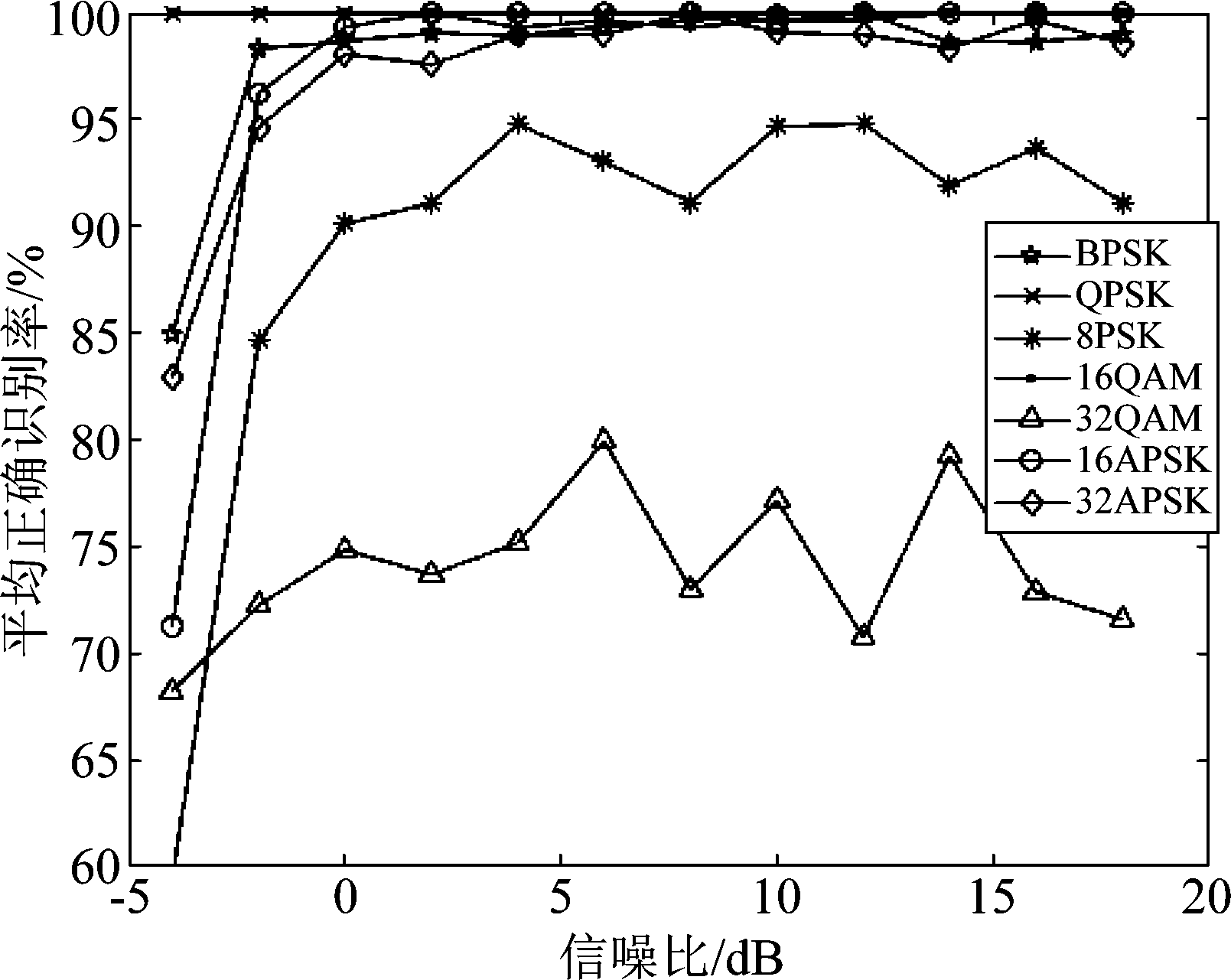
图8 CNN算法单个信号正确识别率曲线
Fig.8 Single signal Acc curve of CNN
图9 LSTM算法单个信号正确识别率曲线
Fig.9 Single signal Acc curve of LSTM
除LSTM算法外,CLP 算法、CLS算法和CNN算法对BPSK、QPSK、16QAM、32APSK和16APSK识别性能相当,单个信号正确识别率基本都达到97%以上。CLP算法对32QAM和8PSK信号的正确识别率达到90以上,优于其他算法,且相对其他算法曲线波动小。
4 结论
针对人工提取信号特征复杂及识别性能受特征参数影响大的问题,本文提出一种基于信号数据的CLP调制样式识别算法。将接收信号的同向分量和正交分量构造数据集,利用CNN、LSTM并行提取信号的空间特征、时间特征,进而完成信号识别。计算机仿真结果验证了算法的有效性,该算法具有实际应用价值。
[1] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-509.
[2] Wang D, Zhang M, Li Z, et al. Modulation format recognition and OSNR estimation using CNN based deep learning[J]. IEEE Photonics Technology Letters, 2017, 29(19): 1667-1670.
[3] Li J, Qi L, Lin Y. Research on modulation identification of digital signals based on deep learning[C]∥2016 IEEE International Conference on Electronic Information & Communication Technology. IEEE, 2016.
[4] 彭超然, 刁伟鹤, 杜振宇. 基于深度卷积神经网络的数字调制方式识别[J]. 计算机测量与控制, 2018, 26(8): 222-226.
Peng Chaoran, Yan Weihe, Du Zhenyu. Digital Modulation Recognition Based on Deep Convolution Neural Network[J]. Computer Measurement & Control, 2018, 26(8): 222-226.(in Chinese)
[5] Zhao Zhijin, Gu Jiawei. Recognition of digital modulation signals based on hybrid three-order restricted Boltzmann machine[C]∥IEEE 16th International Conference on Communication Technology(ICCT). IEEE, 2016.
[6] 周龙梅. 基于深度学习的通信信号识别技术研究[D]. 北京: 北京邮电大学, 2018.
Zhou Longmei. Research on Communication Signal Recognition Technology Based on Deep Learning[D]. Beijing: Beijing University of Posts and Telecommunications, 2018.(in Chinese)
[7] 杨安锋, 赵知劲, 陈颖. 利用稀疏自编码器的调制样式识别算法[J]. 信号处理, 2018, 34(7): 833- 842.
Yang Anfeng, Zhao Zhijin, Chen Ying. Modulation Pattern Recognition Algorithm Using Sparse Self-Encoder[J]. Journal of Signal Processing, 2018, 34(7): 833- 842.(in Chinese)
[8] Gihan J, Mendis, Jin Wei, Arjuna Madanayake. Deep learning-based automated modulation classification for cognitive radio[C]∥2016 IEEE International Conference on Comunication Systems(ICCS). IEEE 2016.
[9] Byeoungdo Kim, Jaekyum Kim, Hyunmin Chae, et al. Deep neural network-based automatic modulation classification technique[C]∥2016 International Conference on Information and Communication Technology Convergence(ICTC). IEEE, 2016.
[10] Karra K, Kuzdeba S, Petersen J. Modulation recognition using hierarchical deep neural networks[C]∥IEEE International Symposium on Dynamic Spectrum Access Networks, 2017.
[11] O’Shea T J, Corgan J, Clancy T C. Convolutional Radio Modulation Recognition Networks[J]. Engineering Applications of Neural Networks, 2016, 6(29): 213-226.
[12] 周江. 基于神经网络的通信信号调制识别研究及实现[D]. 成都: 电子科技大学, 2018.
Zhou Jiang. Research and implementation of communication signal modulation recognition based on neural network[D]. Chengdu: University of Electronic Science and Technology, 2018.(in Chinese)
[13] Felix A. Gers, Nicol N. Schraudolph, Jürgen Schmidhuber. Learning precise timing with LSTM recurrent network[J]. Journal of Machine Learning Research, 2002, 3(1): 115-143.
[14] Wu Y, Li X, Fang J. A Deep learning approach for modulation recognition via exploiting temporal correlations[C]∥2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications(SPAWC). IEEE, 2018.
[15] 黄婷婷, 余磊. SDAE-LSTM模型在金融时间序列预测中的应用[J]. 计算机工程与应用, 2019, 55(1): 142-148.
Huang Tingting, Yu Lei. Application of SDAE-LSTM model in financial time series prediction[J]. Computer Engineering and Applications, 2019, 55(1): 142-148.(in Chinese)
