1 引言
阵列下视三维合成孔径雷达(Three-dimensional SAR,3D-SAR)[1-3]在垂直于雷达平台运动方向和信号收发方向的跨航向上布置阵列天线,通过阵列收发获得跨航向的合成孔径,结合高程向的带宽信号和载机运动形成的航迹向合成孔径,对机底区域三维成像[4-5]。
阵列下视3D-SAR成像在军事侦察和军事目标判读、复杂地形测绘、城区建筑物提取、灾难救援等领域具有广泛应用潜力。然而在实际应用中仍存在一些技术难点,一方面,阵列下视3D-SAR跨航向需要较大的阵元数目,造成系统复杂度较高,另一方面雷达数据需要三个维度采样数据量大,给数据存储以及快速高效成像带来困难。为了解决上述问题,2007年,Baraniuk将压缩感知理论引入雷达成像[6]。2010年,A. Budillon等人将压缩感知应用到层析SAR中,在高程向采用压缩感知算法进行重构,提升了高程向分辨率。2012年,X.X.Zhu、Bamler等人提出了基于压缩感知l1范数最小化的SLIMMER算法,利用TerraSAR-X数据实现了建筑物的高分辨率三维重构。2017年,L Ferro-Famil等人提出了一种基于小波的稀疏断层估计方法,用于三维成像和辨别叶下物体[7- 8]。
国内在稀疏天线阵列3D-SAR成像方面的研究从近些年才开始,2012年,中科院电子所的研究人员构造了跨航向稀疏的下视阵列天线构型的多发多收机载3D-SAR,提出了适用于该模型的三维成像算法;同年,成都电子科技大学的学者利用压缩感知方法获得了分辨率增强的三维成像结果;2014年,中科院电子所的研究员提出一种基于压缩感知的连续场景稀疏阵列SAR三维成像方法;2016年,有学者结合了伪极坐标变换和稀疏正则化方法,提出了一种能够有效重构跨航向稀疏阵列的改进阵列下视3D-SAR成像算法;2017年,有研究人员提出一种直接在距离频域稀疏采样条件下对目标场景进行下视三维成像的方法[9-13]。
由上述内容可以看出,国内外对于压缩感知的应用大多数集中在常规成像,由压缩感知的重构算法增强常规SAR的分辨率,而对于稀疏成像,大多集中在某一维度的稀疏,对于两维稀疏却很少有学者涉及,因此,本文提出了一种应用压缩感知重构算法对跨航向和航迹向两个维度进行稀疏重构的算法。
本文提出了一种在跨航向和航迹向两个维度稀疏的3D-SAR算法。与常规3D-SAR算法相比,该算法在跨航向和航迹向两个维度进行稀疏,在跨航向随机稀疏地布置天线阵元以减少阵元数目,在航迹向随机稀疏采样以减少回波数目,利用正交匹配追踪算法对两个维度的数据进行重构。在保证成像质量的情况下,节约了成本、降低了系统的复杂度、减少了对硬件存储能力的依赖。。
本文结构如下:第2节介绍正交匹配追踪算法的基本原理;第3节分析信号的稀疏性及稀疏成像的信号模型,并对两维稀疏成像算法进行详细分析;第4节通过仿真实验对算法的有效性进行验证;第5节对文章内容进行了总结。
2 正交匹配追踪算法原理
运用稀疏信号处理方法的前提是信号本身具有稀疏性或者信号可以被某个稀疏基稀疏表示,假设有信号x∈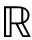
N,则x需满足:
x=Ψα
(1)
其中Ψ为稀疏基,α为系数向量,α中只有K个非0(或绝对值较大)的系数,其余N-K个系数为0(或绝对值很小)。对于稀疏信号x,可用测量矩阵Φ∈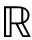M*N对其进行降维观测,得到测量信号[12]:
y=Φx
(2)
将公式(1)代入公式(2),可以得到:
y=Φx=ΦΨα=Θα
(3)
其中,Θ∈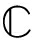
M×N为传感矩阵。压缩感知重构的过程即为寻找最稀疏解的过程,正交匹配追踪算法正是借用了l0范数的概念,正交匹配追踪算法是为了解决l0范数最小化问题:
(4)
该算法的基本思想是:从传感矩阵中选择一个与测试信号最匹配的原子(也就是某列),对选择的原子进行正交化处理后,构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,原始信号可以由这些原子再加上最后的残差值来表示。
3 成像方法
3.1 观测场景划分
以雷达波束照射区域地平面和垂直于该地平面向上的单位向量所构成的空间直角坐标作为线阵SAR的观测场景目标空间Ω,将观测场景划分为大小相等的分辨单元,场景目标空间的总单元个数为M,m表示观测场景中的第m个单元。
3.2 信号的稀疏性及信号模型
雷达对地面物体进行三维成像时,通常在每个俯仰向和跨航向二维方向上仅能探测到一个距离雷达最近的散射源,这个散射源会遮挡其他的散射源,而三维成像仅仅是由雷达探测到的散射源进行成像,这些散射源相对于三维空间是稀疏的。若在三维空间的每个维度上都进行采样,运算量十分巨大,对系统要求太高,因此在一至两个方向上稀疏采样是最佳的选择。
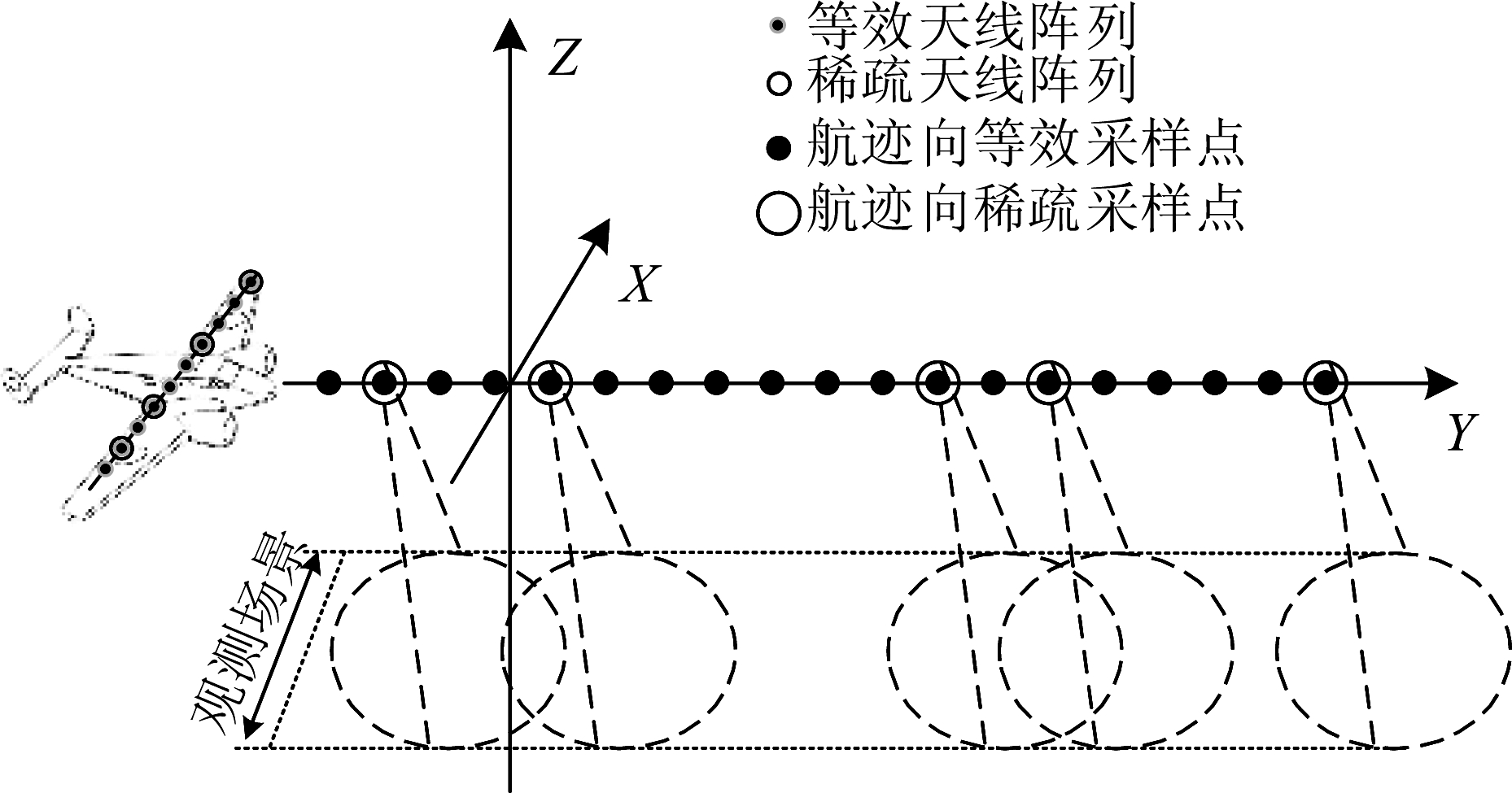
图1 几何模型
Fig.1 Geometry model
两维稀疏的下视阵列3D-SAR的几何模型如图1所示,将x轴、y轴、z轴分别定义为跨航向、航迹向、高程向。雷达平台沿y轴飞行,飞行速度恒为Vr。我们假设平台的相邻沿航迹向采样位置之间的采样间隔是随机的。阵列天线为收发共置,沿跨航向随机稀疏分布,观测场景位于平台正下方。
天线阵列的第ξ个阵元的坐标为(xξ,yη,H),yη是随着平台的移动而变化的航迹向坐标,H是天线阵列的高度,假定H随着平台的移动而不变。假设观测场景中第m个单元的坐标为(xm,ym,zm),则第ξ个阵元到观测场景第m个单元的距离历程由下式给出:
(5)
本文使用的发射信号为调频连续波,在航迹向时间η时刻阵列天线的等效采样点Pξ,η接收到观测场景第m个单元的回波信号Sm(t,η,ξ)为:
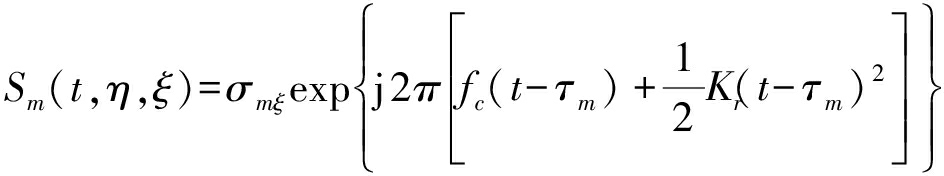
(6)
其中,τm是观测场景第m个单元到等效采样点Pξ,η的电磁波传播时间,
(7)
其中利用泰勒展开可得Rξm(ξ,η,m)的近似表达式:
(8)
将接收信号与发射信号做混频,得到中频信号Sm0(t,η,ξ)为:
(9)
公式(10)的相位最后一项
为残余视频相位(RVP)项。对于测场景第m个单元,解斜后信号改变为频率Krτm的单频信号,解斜处理的过程很大程度上降低信号带宽,而且降低离散采样的频率要求,也降低了后续处理的复杂程度,直接对采样后的中频信号做IFFT即可达到高程向压缩的效果。
整个观测场景总的回波信号可以表示为:
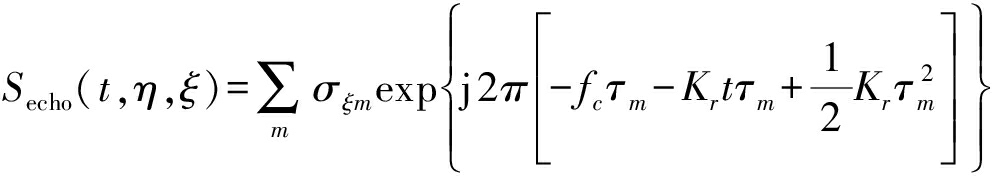
(10)
由于相对于整个观测场景,目标的个数较少,即σξm中大部分数值为0或绝对值很小,因此回波信号可以进行稀疏表示。
3.3 成像算法推导
基于跨航向和航迹向两维稀疏的3D-SAR算法流程图如图2所示。该算法的第一步高程向IFFT与常规3D-SAR算法的第一步相同,高程向IFFT后即可得到高程向压缩之后的信号。在合成孔径过程中,雷达与目标之间的斜距变化可能会超过一个距离分辨单元,使得来自同一目标的回波信号在高程向分布于不同的距离单元内,造成了信号在航迹向和高程向的耦合。因此,在对航迹向信号进行数据重建之前先进行距离徙动校正。对经过航迹向距离徙动校正之后的信号运用正交匹配追踪算法进行航迹向数据重构,由此可以得到高程向-航迹向聚焦之后的信号。与航迹向相似,跨航向进行距离徙动校正之后,运用正交匹配追踪算法进行跨航向数据重建,由此可以得到所需的三维聚焦之后的图像。下面就每个步骤做详细介绍。
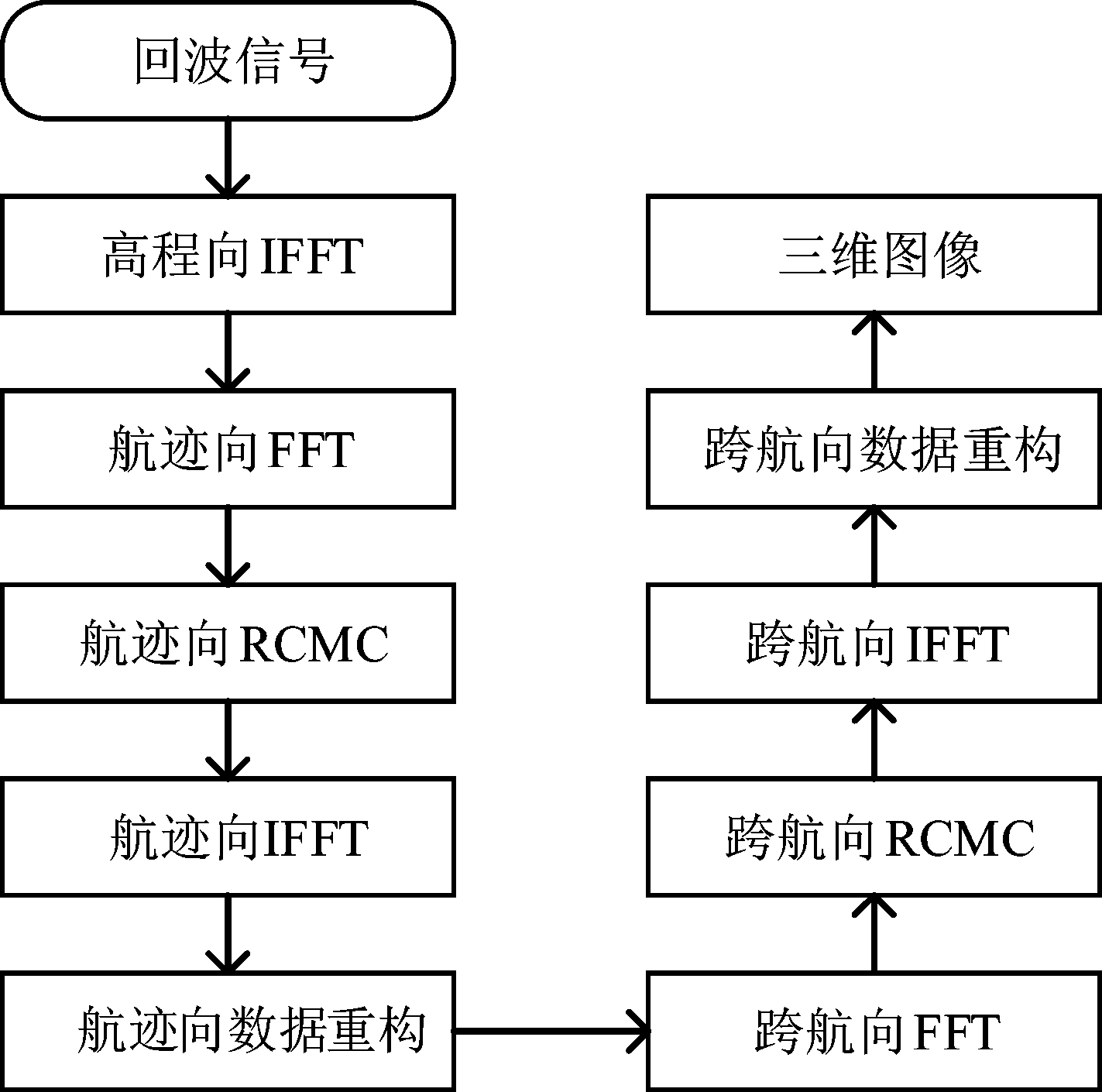
图2 算法流程图
Fig.2 Algorithm flowchart
3.3.1 高程向压缩
阵列天线获得的回波信号为Secho(t,η,ξ),对其进行数据预处理,获得阵列成像数据,然后通过成像处理,获得观测场景的微波幅度图像。
由于Secho(t,η,ξ)可以看成ft=Krt的频率信号,所以对Secho(t,η,ξ)沿高程向进行逆傅里叶变换,即可获得高程向压缩后的信号SIFFT_ele_RVP(t,η,ξ):
SIFFT_ele_RVP(t,η,ξ)=IFFTt{Secho(t,η,ξ)}
(11)
其中,IFFTt表示沿高程向t进行逆傅里叶变换。
对SIFFT_ele_RVP(t,η,ξ)进行去斜、剩余视频相位补偿,补偿函数为:
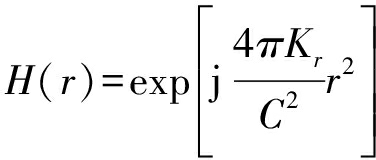
(12)
其中,r为天线采集信号起始和终止时刻对应的观测场景距离变量;经过去斜及剩余视频相位补偿的信号SIFFT_ele(t,η,ξ)为:
SIFFT_ele(t,η,ξ)=SIFFT_ele_RVP(t,η,ξ)×H(r)
(13)
3.3.2 航迹向距离徙动校正
首先对SIFFT_ele(t,η,ξ)进行航迹向傅里叶变换,在航迹向频域采用sin c函数插值的方法对信号进行航迹向距离徙动校正,然后进行航迹向逆傅里叶变换,得到变换后的时域信号SIFFT_alo(t,η,ξ):
SIFFT_alo(t,η,ξ)=
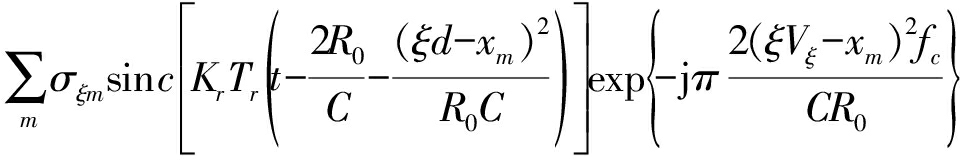
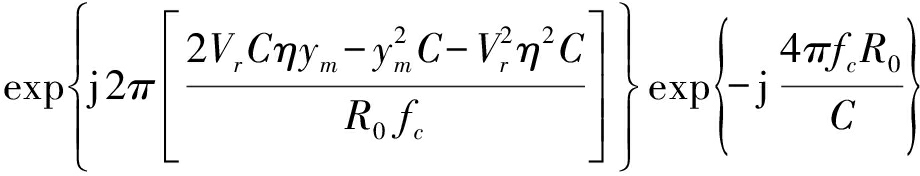
(14)
进行航迹向数据重构之前对信号进行高程向切片处理,假设:
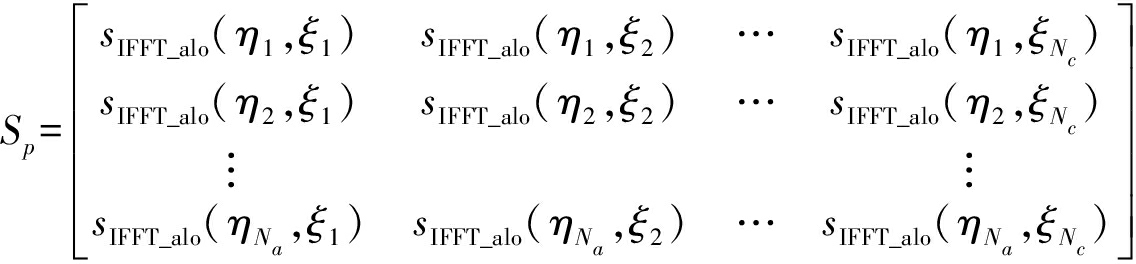
(15)
Sp为第p个脉冲信号下高程向的切片信号。
3.3.3 航迹向传感矩阵的构造
对航迹向和跨航向信号进行数据重构之前要构造传感矩阵,根据第2节压缩感知基础可知,信号确定之后,稀疏基Ψ即可确定,再选取合适的测量矩阵Φ,即可得到所需传感矩阵Θ。
测量矩阵Φ需满足约束等距特性(RIP),RIP等价于测量矩阵Φ与稀疏基Ψ不相关,当测量矩阵Φ为随机矩阵时,RIP特性即相关性很容易满足,因此,本文选用随机矩阵作为测量矩阵。随机选取单位矩阵的部分行,得到航迹向测量矩阵Φa。
依据匹配滤波参考函数来确定航迹向稀疏基ψa,
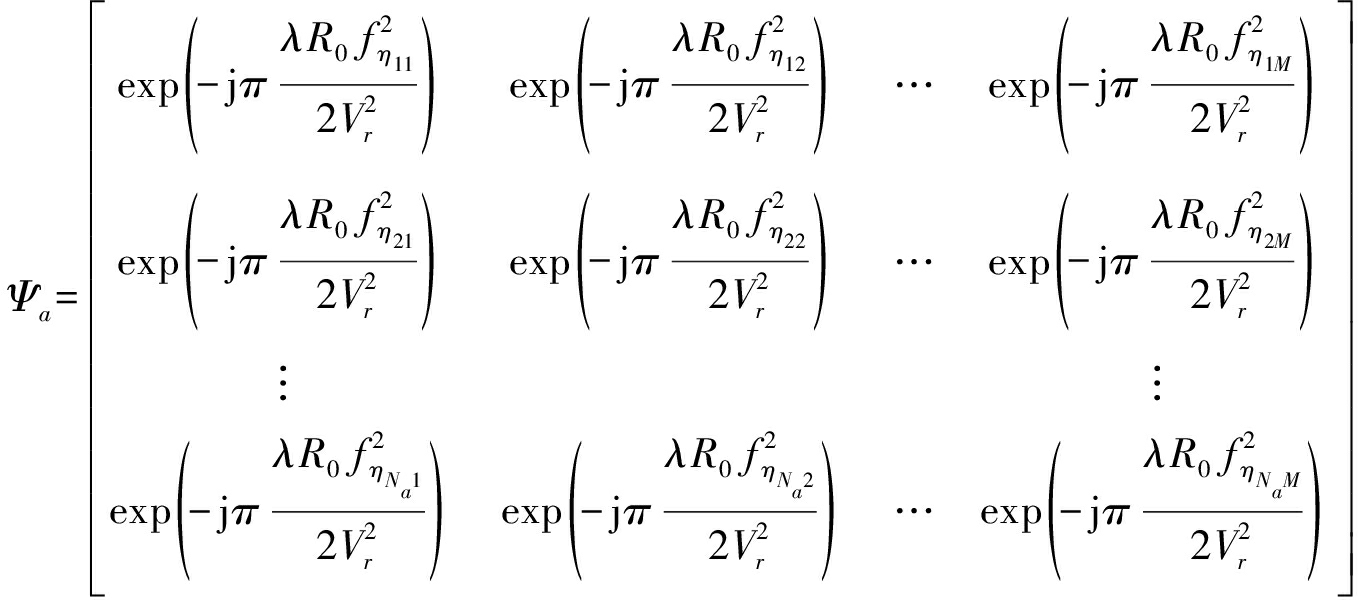
(16)
因此,可以得到航迹向传感矩阵Θa:
Θa=ΦaΨa
(17)
3.3.4 航迹向数据重构
本节采用运算复杂度较低的正交匹配追踪算法对航迹向信号进行数据重构,具体步骤如下:
1)设置正交匹配追踪算法的初始参数:预设一个稀疏度K作为正交匹配追踪算法的迭代终止条件。k表示第k次迭代,k∈{1,2,…,K};b表示传感矩阵与残差内积的脚标,B表示脚标b的集合;r表示残差,r的初始值为r0,表示原始信号;y是测量向量。
2)计算传感矩阵和残差的最大相干项:依据公式bk=arg maxj=1…N|〈rk-1,θj〉|,计算出残差r和传感矩阵的列θj内积的最大值,并记录该内积的脚标。其中,θj为传感矩阵Θa的第j列。|〈·〉|表示内积的绝对值。
3)更新索引集:根据公式Bk=Bk-1∪{bk},更新当前的索引集,并记录找到的传感矩阵中的重建原子集合Θak=[Θak-1,θabk]。其中,符号∪表示集合并运算,Bk-1表示前k-1迭代所选中的传感矩阵的列向量脚标集合,bk表示本次迭代所选取的传感矩阵列向量的脚标。Θak-1表示前k-1迭代所选中的传感矩阵的列向量集合,θbk表示本次迭代所选取的恢复矩阵列向量,Θak表示下次迭代时不再选取Θak中的元素,避免重复迭代。
4)散射系数向量重构:根据公式
其中,
表示本次迭代的散射系数向量估计值,‖·‖2表示l2范数。
5)根据公式
更新本次迭代的残差值。
6)判断是否终止迭代,令k=k+1,即迭代次数加一,并判断是否满足终止迭代条件。若k=K,则终止迭代;若k<K,则继续迭代。
7)根据公式
进行信号重构,其中,为正交匹配追踪算法重构得到的散射系数估计值。
由以上步骤可以得到航迹向重构之后的信号。
3.3.5 跨航向数据重构
跨航向重构之前要先对信号进行跨航向距离徙动校正,本次校正采用sin c插值的方法来进行校正,对校正之后的信号进行跨航向数据重构,步骤与航迹向重构大体相同。
首先,构造跨航向传感矩阵。随机选取单位矩阵的部分列,得到跨航向测量矩阵Φc。
依据匹配滤波参考函数来确定跨航向稀疏基ψc,
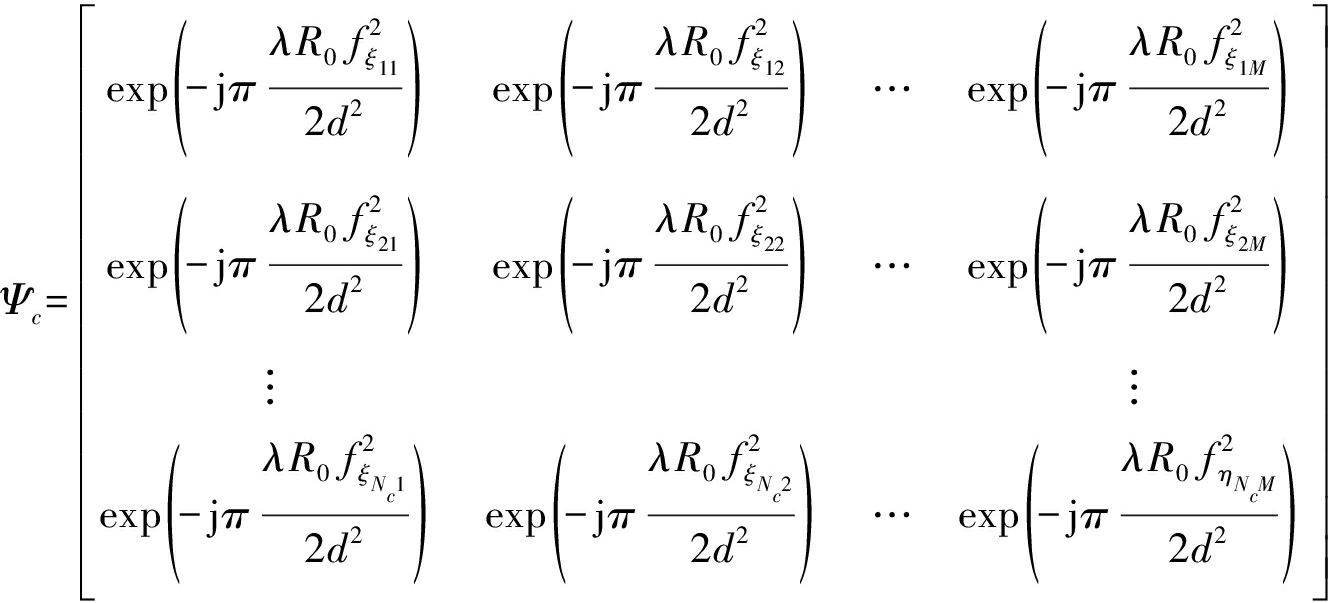
(18)
因此,可以得到跨航向传感矩阵Θc:
Θc=ΦcΨc
(19)
得到重构之后的信号为:
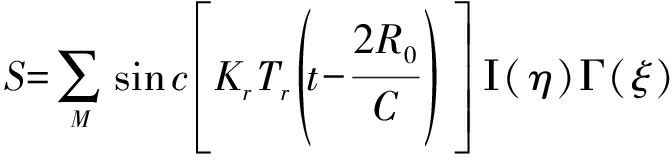
(20)
其中,Ι(η)为航迹向重构之后的结果,Γ(ξ)为跨航向重构之后的结果。
4 仿真分析
为了验证以上分析的准确性和算法的有效性并且与常规算法进行比较,本文运用两维稀疏的3D-SAR算法和常规3D-SAR分别进行了8个点目标的仿真分析,点目标的位置如表1所示。阵列天线为收发共置,两维稀疏的3D-SAR沿跨航向随机稀疏分布,航迹向随机稀疏采样,常规3D-SAR跨航向和航迹向均满采样,系统工作在下视成像模式,仿真参数如表2所示,等效采样即为满采样。
表1 点目标位置
Tab.1 Point target position
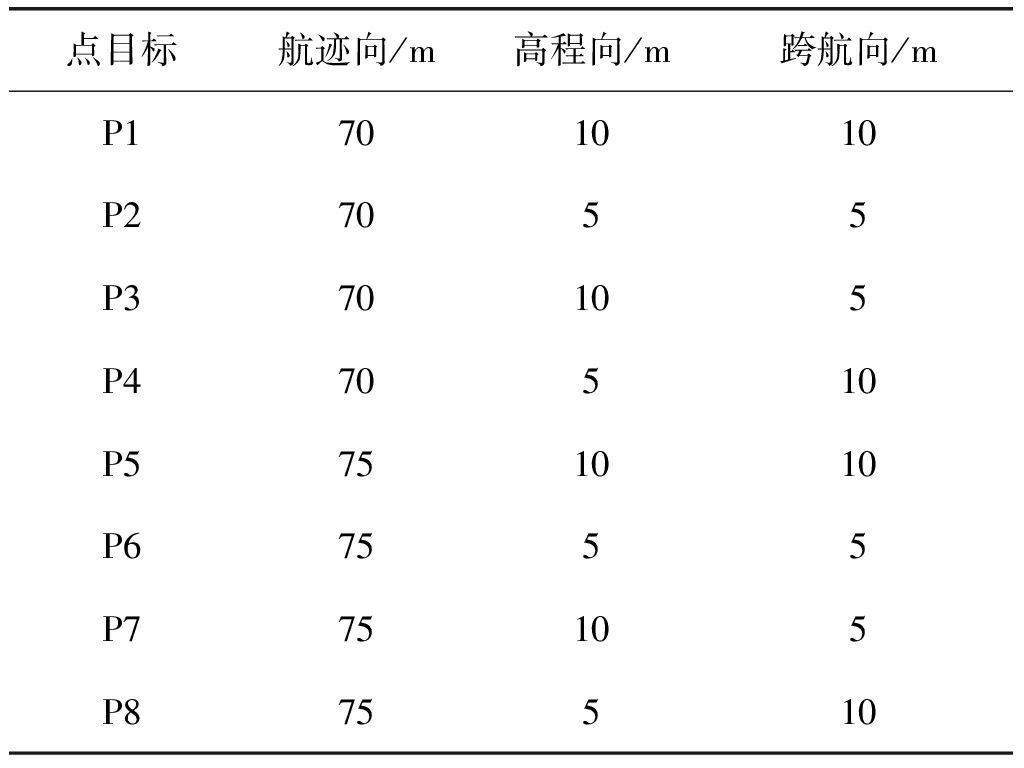
点目标航迹向/m高程向/m跨航向/mP1701010P27055P370105P470510P5751010P67555P775105P875510
表2 仿真参数
Tab.2 Simulation parameter
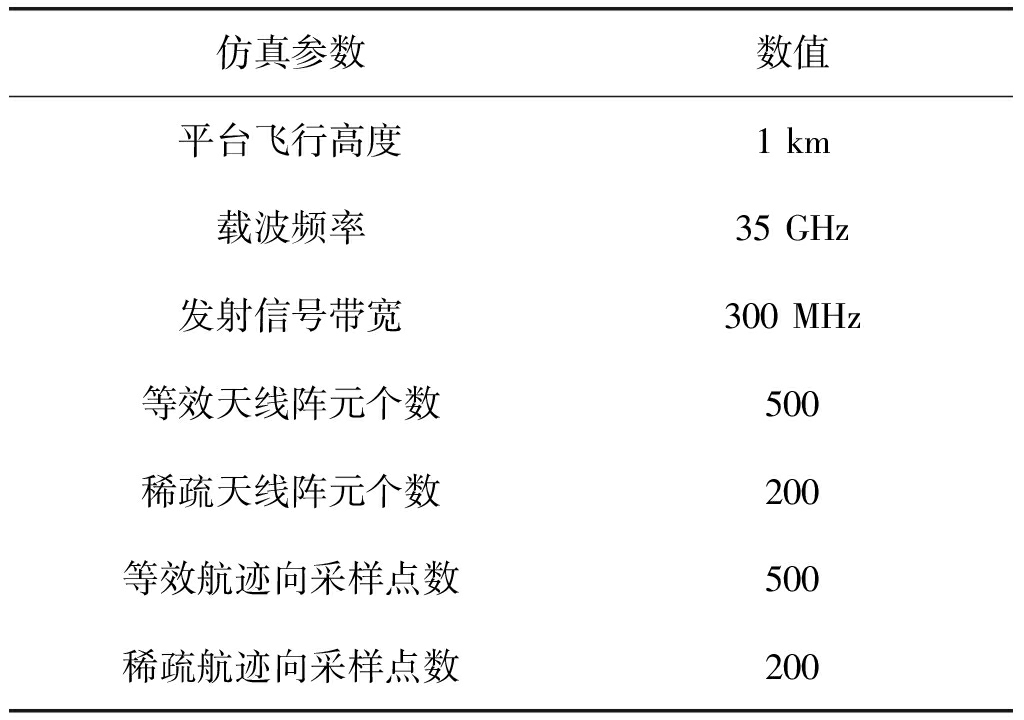
仿真参数数值平台飞行高度1 km载波频率35 GHz发射信号带宽300 MHz等效天线阵元个数500稀疏天线阵元个数200等效航迹向采样点数500稀疏航迹向采样点数200
最终获取观测场景点目标的三维SAR成像仿真图,如图3所示。其中图(a)为两维稀疏3D-SAR的仿真结果,图(b)为常规3D-SAR仿真结果,由图3可以看出两种算法重建得到的目标位置与仿真设定的位置均一致,这说明了本文提出的算法与常规3D-SAR的重建效果效果相同。
为了验证算法的成像性能,对常规3D-SAR算法仿真结果和两维稀疏3D-SAR算法仿真结果分别取出位于对角线上的两个点目标P1、P6单独分析,进行成像分析,主要包括航迹向、跨航向两个维度上的截面图及响应函数。图4和图5分别为两维稀疏3D-SAR算法仿真结果中点目标P1和P6的跨航向-航迹向截面图及两个维度的响应函数,图6和图7分别为常规3D-SAR算法仿真结果中点目标P1和P6的跨航向-航迹向截面图及两个维度的响应函数。
图6和图7中点目标的跨航向与航迹向的响应函数为标准的sin c函数,图4与图5中点目标的航迹向与跨航向的响应函数类似冲激函数,由此可得两维稀疏算法的仿真结果与常规算法相比,航迹向与跨航向旁瓣得到明显抑制,表3中给了两种算法的理论分辨率与仿真分辨率,航迹向的理论分辨率由公式(21)给出:
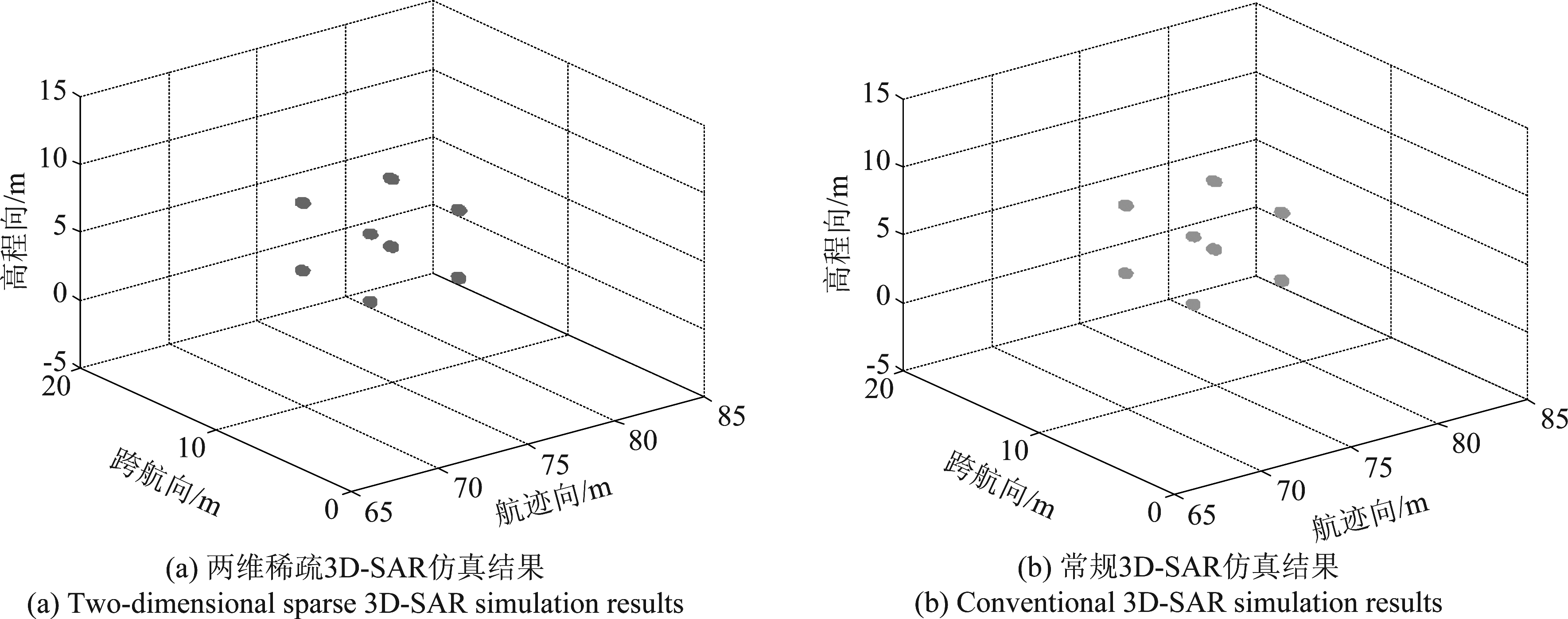
图3 点目标轮廓图
Fig.3 Point target contour map
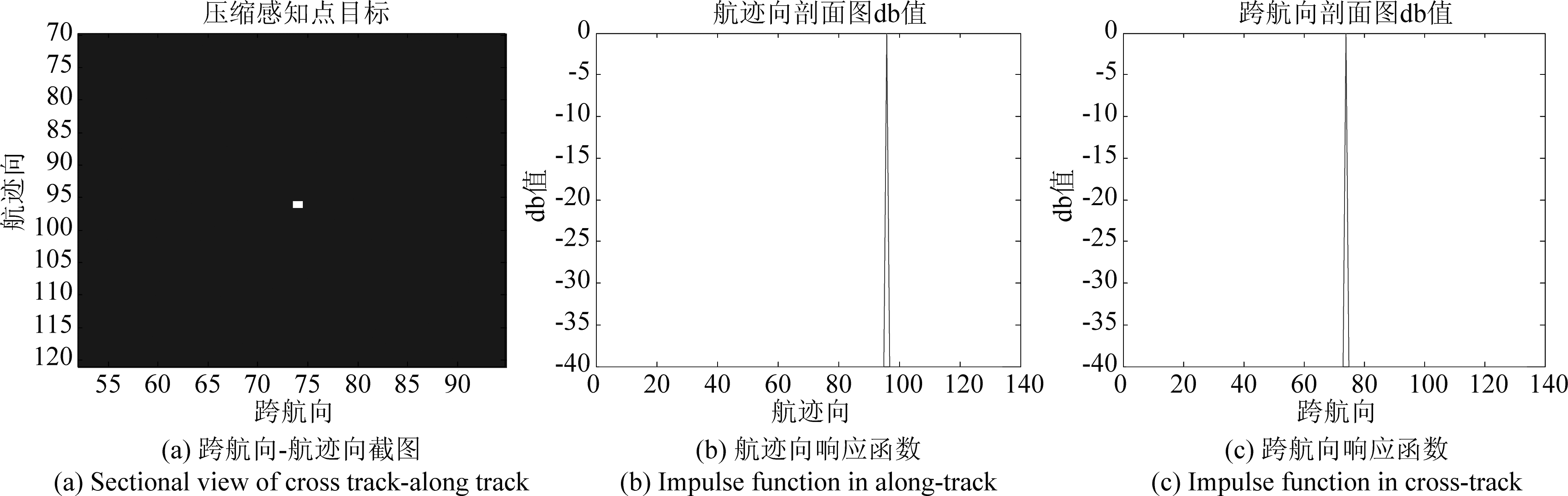
图4 稀疏算法点目标P1截面图与响应函数
Fig.4 Sparse algorithm point target P1 cross-section and response function
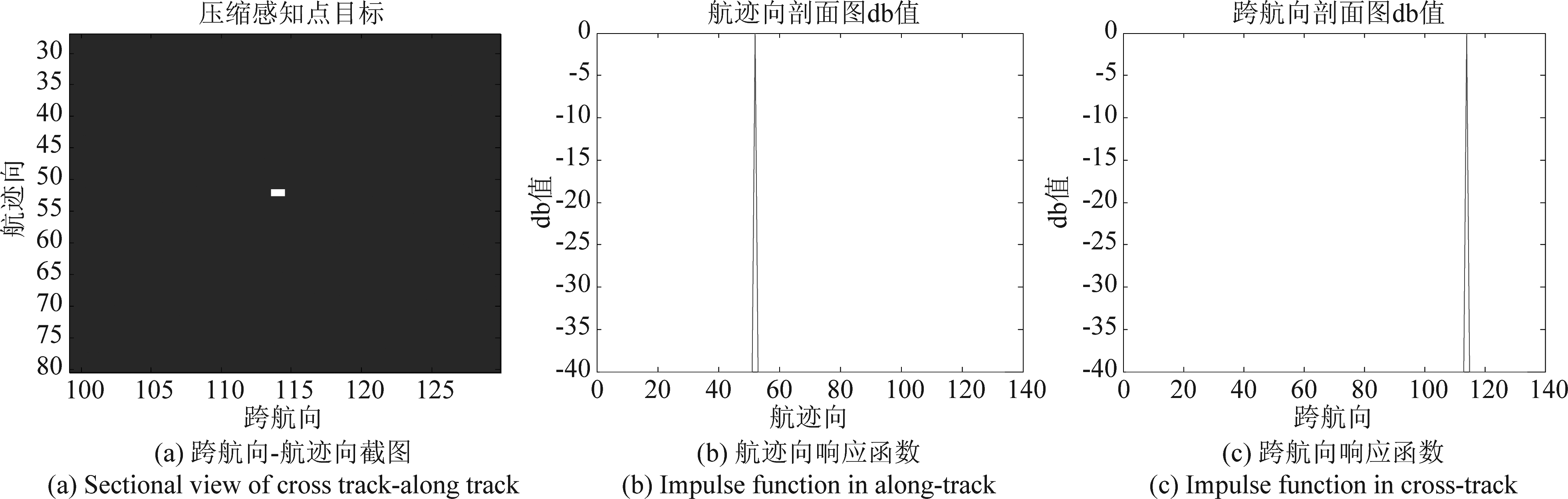
图5 稀疏算法点目标P6截面图与响应函数
Fig.5 Sectional view and impulse function of point target P6
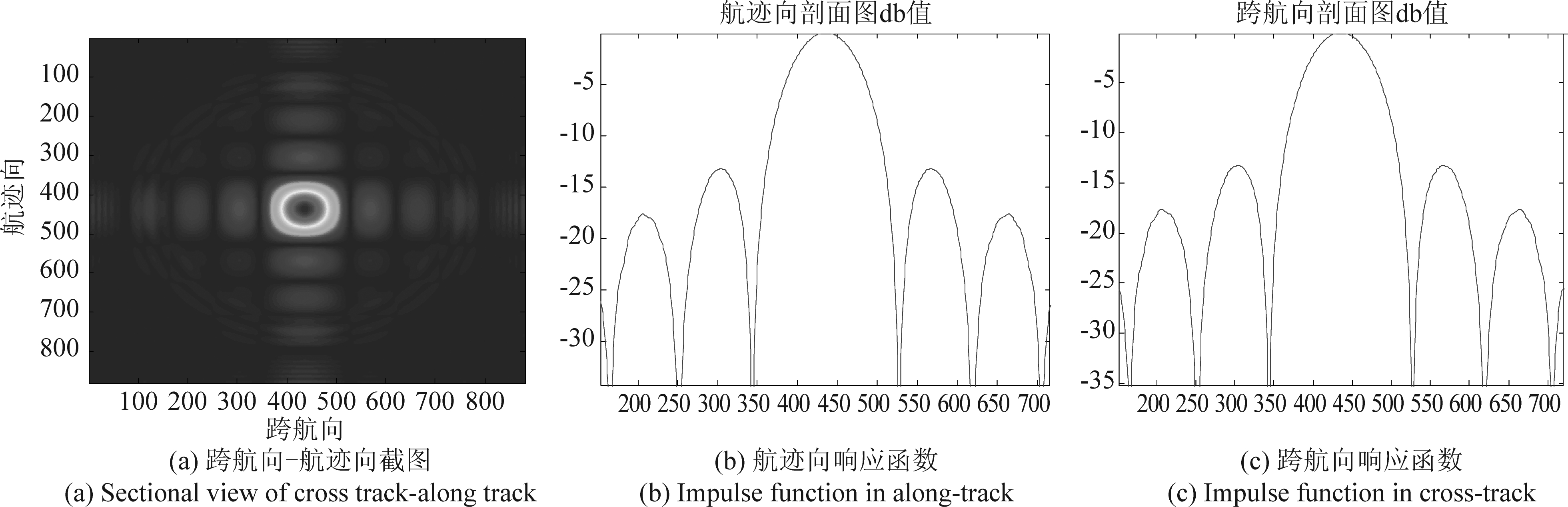
图6 常规算法点目标P1截面图与响应函数
Fig.6 Conventional algorithm point target P1 cross-section and response function
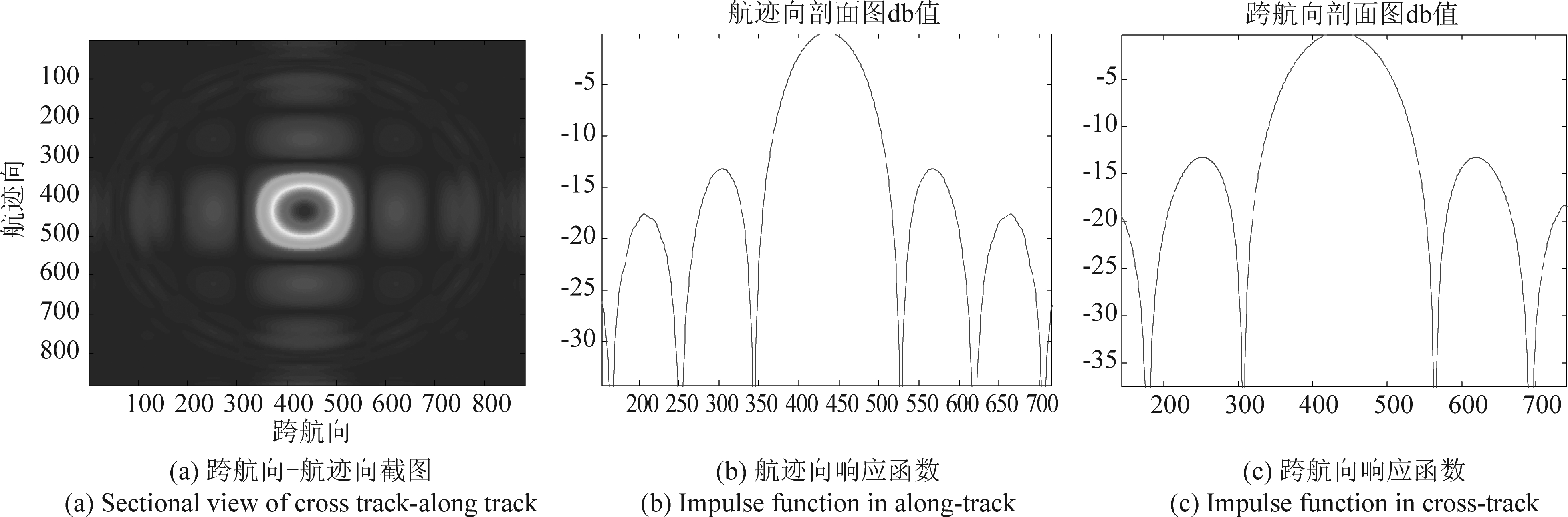
图7 常规算法点目标P6截面图与响应函数
Fig.7 Conventional algorithm point target P6 cross-section and response function
表3 成像分辨率
Tab.3 Imaging resolution
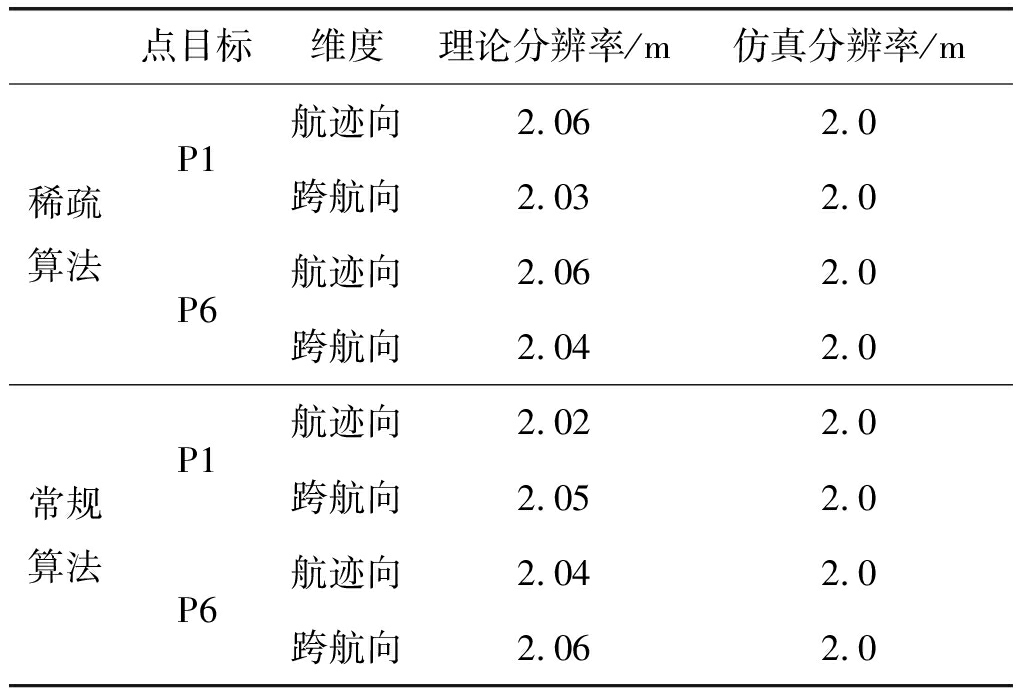
点目标维度理论分辨率/m仿真分辨率/m稀疏算法P1P6航迹向2.062.0跨航向2.032.0航迹向2.062.0跨航向2.042.0常规算法P1P6航迹向2.022.0跨航向2.052.0航迹向2.042.0跨航向2.062.0
(21)
航迹向的分辨率与天线阵列在航迹向上的尺寸有关。本次仿真中航迹向的天线尺寸为4,因此航迹向的分辨率为2 m。跨航向的理论分辨率由公式(22)给出:
(22)
本次仿真中假设平台飞行高度为1 km,等效天线阵列的数目为500,等效阵元的间距为d=λ/2,则根据公式可以算出跨航向的分辨率为2 m。
由表3可以看出两种算法的仿真分辨率与理论分辨率整体一致。
本次仿真实验中,常规算法航迹向的采样点数为500,跨航向的天线数目为500,两维稀疏算法的航迹向采样点数为200,跨航向的天线数目为200,与常规算法相比,两维稀疏算法的航迹向与跨航向的采样数减少了60%。结合仿真结果的分析,与常规算法相比,两维稀疏算法在保证了成像分辨率的情况下,将跨航向和航迹向的数据量减少了60%并且明显抑制了旁瓣,提高了成像质量。然而数据量的大幅度降低牺牲了一定的运算量,在上述仿真实验中,两维稀疏算法与上述常规算法相比,运算时间提高了近10倍。
5 结论
本文将压缩感知理论应用到3D-SAR成像的航迹向和跨航向,大幅度降低了3D-SAR系统复杂度和数据量。在跨航向上,对天线阵列进行随机布局,数据量减少了60%;在航迹向上,进行随机稀疏采样,数据量减少了60%。根据跨航向和航迹向两维稀疏的雷达回波信号模型,本文提出了一种两维稀疏的3D-SAR成像算法,详细推导了算法的重要步骤;最后,通过比较常规算法仿真与两维稀疏算法的仿真,验证了文中提出的两维稀疏的3-D SAR成像算法的有效性。
[1] Liu X, Zhang J, Li X, et al. The sparse sampling and compressed sensing imaging for forward-looking array SAR[C]∥Cie International Conference on Radar. IEEE, 2017.
[2] 李伟华, 张晓玲. 一种基于多发多收的虚拟阵列的三维SAR成像模型[C]∥全国雷达学术年会, 2008.
Li Weihua, Zhao xiaoling. An 3-D SAR Imaging Model Baced on Virtual Linear Array Composed MIMO Antenna[C]∥National Radar Academic Annual Meeting, 2008.(in Chinese)
[3] Tian H, Li D. Sparse Flight Array SAR Downward-Looking 3-D Imaging Based on Compressed Sensing[J]. IEEE Geoscience & Remote Sensing Letters, 2016, 13(10): 1395-1399.
[4] 刘向阳, 孟进, 刘许刚, 等. 一种前视阵列SAR系统的天线设计和分析方法[J]. 红外与毫米波学报, 2018, 37(1): 66-71.
Liu Xiangyang, Meng Jin, Liu Xugang, et al. A method of antenna design and analysis for forward-looking array SAR system[J]. Infrared Millim. Waves, 2018, 37(1): 66-71.(in Chinese)
[5] 张清娟, 李道京, 李烈辰. 连续场景的稀疏阵列SAR侧视三维成像研究[J]. 电子与信息学报, 2013, 35(5): 1097-1102.
Zhang Qingjuan, Li Daojing, Li Liechen. Research on Continuous Scene Side-looking 3D Imaging Based on Sparse Array[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1097-1102.(in Chinese)
[6] 刘记红, 徐少坤, 高勋章, 等. 压缩感知雷达成像技术综述[J]. 信号处理, 2011, 27(2): 251-260.
Liu Jihong, Xu Shaokun, Gao Xunzhang, et al. A Review of Radar Imaging Technique based on Compressed Sensing[J]. Signal Processing, 2011, 27(2): 251-260.(in Chinese)
[7] Wu Y R. Concept of Multidimensional Space Joint-observation SAR[J]. Journal of Radars, 2013, 2(2): 135-142.
[8] Liu X, Yu J, Zhao H, et al. An along-track sparse imaging method for forward-looking array SAR[C]∥Radar Conference 2015, IET International. IET, 2016.
[9] Liu X Y, Zeng C, Mao Z J, et al. A Three-Dimensional Imaging Method Based on High Resolution Signal Source Estimation for Airborne Forward-Looking Array Radar[J]. Acta Electronica Sinica, 2013, 41(6): 1048-1055.
[10] Zhang S, Kuang G, Zhu Y, et al. Compressive sensing algorithm for downward-looking sparse array 3-D SAR imaging[C]∥Radar Conference 2015, IET International. IET, 2016: 5-5.
[11] 蒋成龙, 赵曜, 张柘, 等. 基于相关准则的稀疏微波成像方位向采样优化方法[J]. 电子与信息学报, 2015, 37(3): 580-586.
Jiang Chenglong, Zhao Yao, Zhang Zhe, et al. Azimuth Sampling Optimization Scheme for Sparse Microwave Imaging Based on Mutual Coherence Criterion[J]. Journal of Electronics & Information Technology, 2015, 37(3): 580-586.(in Chinese)
[12] Wei S J, Zhang X L. Linear array SAR 3-D imaging based on compressed sensing[J]. Journal of Astronautics, 2011, 32(11): 2403-2409.
[13] 李学仕, 孙光才, 徐刚, 等. 基于压缩感知的下视三维SAR成像新方法[J]. 电子与信息学报, 2012, 34(5): 1017-1023.
Li Xueshi, Sun Guangcai, Xu gang, et al. A New Method of Downward-looking 3D-SAR Based on Compressed Sensing[J]. Journal of Electronics & Information Technology, 2012, 34(5): 1017-1023.(in Chinese)
