1 引言
债券是一类有价证券[1-2],能够给持有人在未来特定的时间带来稳定的现金流回报[3]。影响债券的因素包括微观主体和宏观环境[4]。债券按照发行主体划分可以分为国债、政策性银行金融债、企业债、公司债等[5]。国债是以国家信用为基础发行的债券,由中央政府向投资者出具的、承诺在一定时期支付利息和到期偿还本金的债券,具有最高信用度。由于国债的特殊发行主体,国债常常作为其他各类债券的定价基准。实际中,决定债券价值的关键要素主要有发行主体、面额、票面利息、偿还方式、偿还年限及收益率等。利息一般指贷出资金方在一定期限内收到的补偿,而一定期限内的利息与贷出额度之比便是利率,也就是资金的收益率。本文研究对象为国债收益率,因为其他债券利率的定价规则都是在相同年限的国债收益率上加上奉献溢价。
国债利率期限结构是指在某一个时间点上,国债到期期限与相应利率之间的关系。对国债利率期限结构的深入研究有利于制定更为有效的利率风险策略、防范金融市场上的整体利率风险,是利率市场化所亟待解决的问题。国债利率期限结构按期限长短可分为以下4种情况:(1)短期限利率小于长期限利率;(2)短期限利率大于长期限利率;(3)短期限利率等于长期限利率;(4)短期限利率和长期限利率处于一个波动当中,并无明确的大小关系。研究利率期限结构主要涉及三种理论:预期理论、市场分割理论和偏好利率结构理论[6]。
对利率期限结构的估计方法主要有两种:一类是静态拟合[7-9];一类是动态拟合[10-13]。这两种方法在应用中都存在一定的局限性。静态拟合的主要缺点为:(1)模型的稳定性较差,自变量发生细微的变化会导致参数波动激烈,对结果产生严重的影响;(2)不同期限的国债衍生品的流动性差异特别大,比较容易受偶然性因素的影响。动态拟合的主要缺点为:(1)单因子模型过于简单,利率期限结构的多样性得不到解释,实用性较差;(2)多因子模型能够较好的模拟数据,但是模型过于复杂,预测能力不够强。有些学者也利用国债衍生品来进行估计利率。用国债衍生品估计会让模型更加精确,但由于不同期限的国债衍生品的流动性差异特别大,也比较容易存在一定的偶然性。
高斯过程混合模型作为一种有效的统计学习工具[14],具有强大的学习或拟合能力,被广泛的应用在机器学习和模式识别中[15]。高斯过程混合模型能够描述多模态数据[16],可有效地反映出数据的波动性。从生成过程角度看,高斯过程混合模型可以分成两类:生成模型和判别模型;从混合方式角度看,高斯过程混合模型可以分为时间域上的混合,称之为MGP模型,和从输出空间上的混合,称之为mix-GP模型。
本文采用MGP模型对国债利率期限结构数据进行建模和分析。国债收益率数据是“时间流动”形成的数据,各数据点与相邻的数据点是相关的,而这个相关性可以用MGP模型的协方差矩阵表示出来。由于各时间点上的政策等因素的影响,在不同的时间段内,国债收益率数据产生波动性差异,这种具有差异的波动性可以用MGP模型的各个GP分量分别表示,即让这些GP分量分别进行局部描述,联合起这些GP分量,使得MGP模型更好的描述整体数据的变化规律。实际中,金融环境中的影响或作用因子(即驱动或输入变量)对期限利率收益率的预测至关重要。本文筛选的关键影响或作用因子为CPI(居民消费价格指数)、IP(工业增加值)以及银行间7天质押回购利率,大大增加模型的完整性和精准性。
本文结构安排如下:第2节介绍高斯过程模型和MGP模型;第3节建立了MGP模型的参数学习算法;第4节给出了MGP模型及其对比方法的实验结果;第5节为总结。
2 高斯过程混合模型
2.1 高斯过程(GP)模型
在数学上,Y(X)被称为是一个高斯过程如果对于任意给定的N和X=(x1,…,xN),相应的Y=(y1,…,yN)服从高斯分布,即Y～N(m(X),K(X,X′)),其中,m(X)是均值函数,K(X,X)是协方差函数。在数学上,高斯过程可以表示为:
Y(X)～GP(m(X),K(X,X′))
(1)
在一般问题中,通常假设m(X)=0。本文采用平方指数(Squared Exponential, SE)协方差函数:
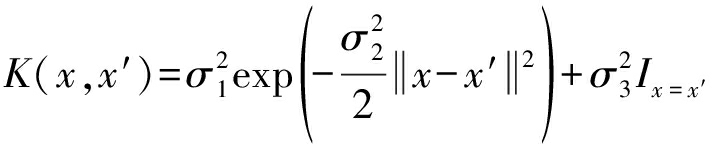
(2)
为了方便表示,令参数为
采用极大似然估计算法有效地完成GP模型的参数学习。
2.2 MGP模型
本文采用生成模型形式的MGP模型,其中各GP分量是相互独立的。假设高斯混合模型包括有C个高斯分量,每个GP模型表示为GPc。高斯过程混合模型产生样本数据集D={(xn,yn)|n=1,…,N}的规则如下:
(1)首先,引入隐变量
用来描述样本与GP分量的归属关系,并服从如下分布:
(3)
其中
(2)在
的条件下,样本输入xn服从均值为μc,协方差为
的正态分布:
(4)
(3)定义
分别为第c个GP分量的样本标号、输入和输出。定义第c个GP如下:
Yc～GP(0,K(Xc,Xc|θc))
(5)
由上面三个步骤可以看出,MGP模型的信息流动方向为“z→x→y”,这种数据生成方式符合国债收益率的特点,与MGP模型的应用场景相符合。基于数据集D,容易推导出MGP的如下对数似然函数:
log p(Θ,Ψ|X,Y,Z)=
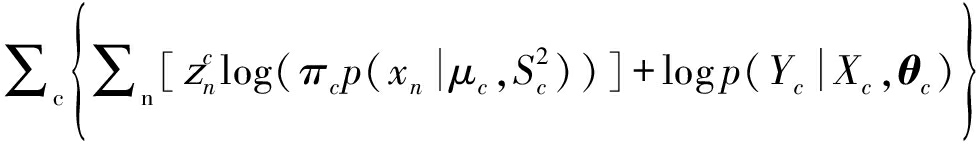
(6)
其中Θ={θc|c=1,…,C}和
分别表示MGP模型中的超参数和参数。
3 算法设计
本文采用EM算法学习超参数Θ={θc|c=1,…,C}和参数
实际中,MGP模型的参数学习算法主要有MCMC算法、变分贝叶斯(VB)算法以及EM算法。虽然MCMC算法一般能够获得较精确的估计结果,但是算法需要大量的采用,效率很低,结果也不稳定。而在VB算法中,我们需要假设模型中参数和隐变量都是相互独立的,这常常导致其估计的结果偏离真实值,学习效果较差。EM算法则是一种有效的混合模型的参数学习算法,但在MGP模型中必须引入简化或近似计算策略以解决涉及指数级隐变量的计算,硬分类(hard-cut)处理便是有效的简化计算策略。
硬分类(Hard-cut)EM算法的核心思想是利用最大后验概率准则将样本的后验分布转换成0-1二项分布,然后将样本分配到后验概率p=1的模型分量中。由于数据的分布特点,绝大多数样本的后验概率呈现0-1分布,在这些样本上,hard-cut策略的误差很小;在各模型分量边缘的样本上,hard-cut策略会产生较大的误差,但由于样本数量少,产生的误差总量也很小。另一方面,Hard-cut EM算法大大简化了EM算法中Q函数的计算,提升了算法速度。Hard-cut EM算法用如下步骤描述:
(1)初始化:使用k-means算法将样本D分成C类,并初始化超参数(Θ,Ψ );
(2)M步:分三个步骤学习参数:
1)更新后验概率
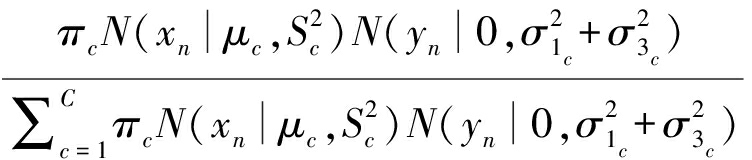
(7)
2)更新模型参数
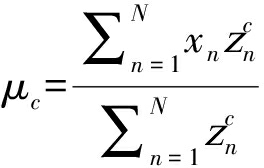
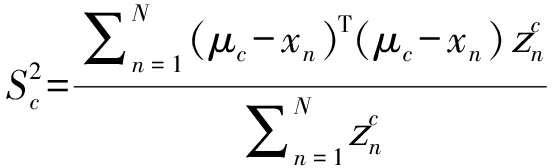
(8)
3)更新超参数Θ={θc|c=1,…,C}。使用极大似然估计算法独立地学习各个GP分量的超参数θc。
(3)E步:按照最大后验概率原则更新样本的类别信息:
(9)
如果c*=arg max1≪c≪C{πcN(xn)N(yn)}。
(4)如果两次迭代中的变化率小于阈值γ或者达到最大迭代次数,则终止算法;否则返回M步。
4 实验结果与分析
在实验中,我们首先采用10年国债收益率与5年国债收益率之差进行了建模分析,记作“10-5”;其次,对5年国债收益率与1年国债收益率之差进行了建模分析,记作“5-1”;最后,对10年国债收益率进行了建模分析,记作“10”。图1展示了“10-5”、CPI、IP以及银行间7天质押回购利率的变化曲线。由于国家统计局每月更新一次CPI、IP,为了保持一致,通过线性插值法将CPI、IP变为每日更新值。根据数据的形式,分别在上述三个数据上进行了两组实验:第一组实验,将CPI、IP、7天回购利率当成输入,5-1、10-5、10年国债收益率分别作为输出;第二组实验,将5-1、10-5、10年国债收益率分别作为时间序列,并按照不同的回归(或递推)阶数和采样间隔对数据进行重组。本文选择了Linear(线性回归)、RBF[18]、Kernel[19]、SVM[20] 等模型与方法进行对比分析。
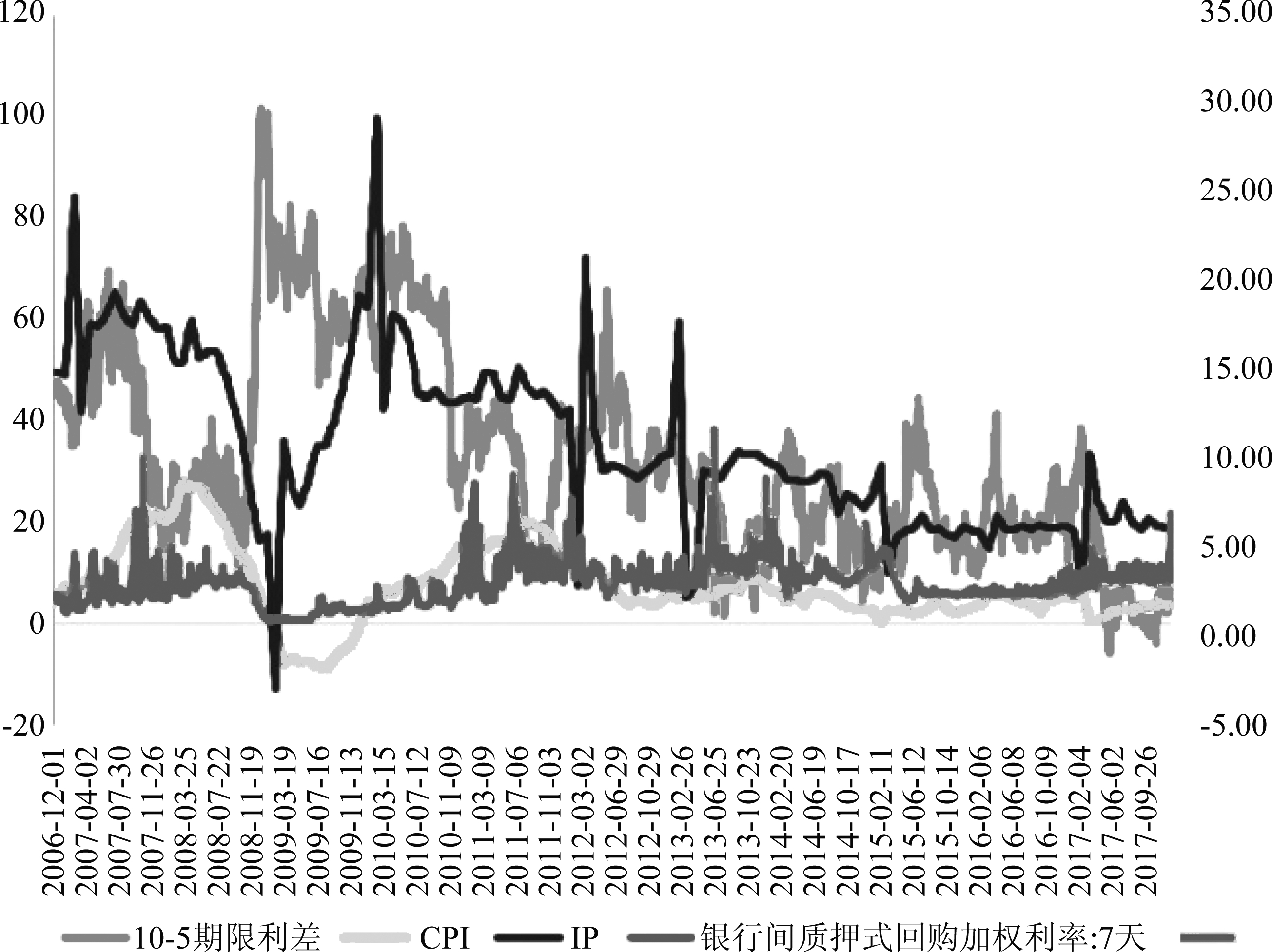
图1 期限利差10-5、CPI、IP、7天回购利率变化曲线
Fig.1 The change curves of term spread 10-5、CPI、IP、interest rate of 7-day repurchase
4.1 第一组实验
本小节的实验数据是以下三个数据:CPI、IP、7天回购利率作为输入,分别将5-1、10-5、10年国债收益率分别作为输出,每种情况都随机选取三分之二作为训练数据,另外三分之一作为测试样本。将高斯过程混合模型与Linear、SVM、RBF、Kernel应用在三个数据上分别重复20次,并得出各个算法的测试样本均方根误差(RMSE)以及运行时间TIME,其中RMSE的定义为
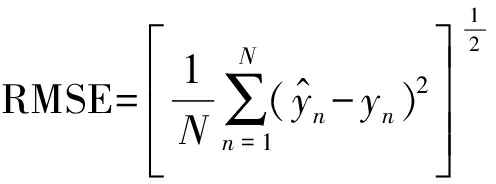
其中
表示模型的预测值,yn表示样本输出真实值。通过RMSE值,能够清楚地反映出模型的平均预测精度或确信的区间,即RMSE值越小,模型对未来值的预测越准确,也越稳定。由于这是在测试集上的平均误差,总体上已经反映了预测的精度,而高斯过程混合模型的预测涉及到后验概率、均值估计及融合等复杂的数学问题,造成单点预测的确信度很难计算,故这里不再考虑预测的确信度的计算和比较。
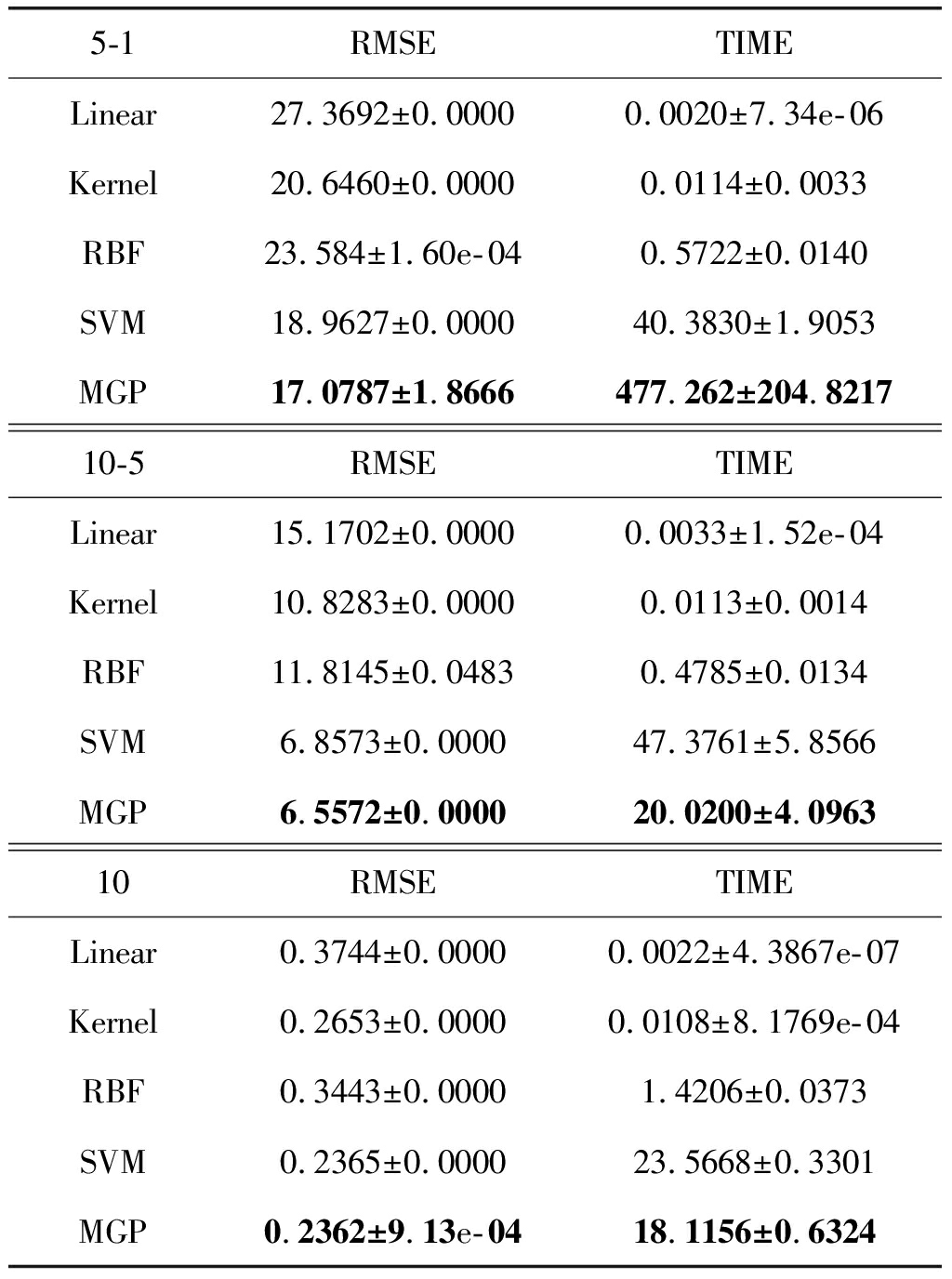
表1展示了各算法在三组数据上的实验结果。从表1可以看出,在预测精度RMSE上,MGP模型在期限利差10-5、期限利差5-1、以及10年国债收益率等三个数据的RMSE都是最小的,说明MGP模型的预测精度是最高的,最有效地刻画了国债利率期限结构。
主要是因为两个原因:第一,这是因为相比于其他对比机器学习算法,MGP模型将国债收益率样本集按照波动性差异分组,每组样本集服从一个GP模型分量,每个GP分量的样本独立学习相关参数。同时,GP分量内样本的协方差函数保证了学习的有效性,能够有效的拟合数据。通过门限函数将各个GP模型分量联合起来,从而有效的在整个数据集上学习参数。第二,使用硬分类预测方法。Hard-cut EM算法记录了样本的类别信息,按照最大后验概率准则将测试样本分配到相应的GP分量,基于单个GP模型分量的预测规则即得预测结果。通常情况下,该预测方法是更准确的。同理,MGP模型在第二组实验上获得较好实验结果。
但在算法的运行时间上,MGP模型是特别耗时的,尤其是在期限利差5-1数据上,比对比算法大一个数量级,这是达到高精度需要付出的代价。但我们也发现了导致高计算复杂度的原因有:(1)MGP模型的学习算法需要求解协方差矩阵的逆,这是一个高计算复杂度的过程;(2)MGP模型在数据上需要多次迭代才能收敛。因此,未来有两个很有前景的改进方向:第一,是对实际数据作预处理,使之更加适用于GP或MGP模型,使MGP模型能够以较少的迭代次数收敛;第二,对模型进行稀疏化操作,通过提取样本的特征,选择出来代表样本集,从而减少训练样本的个数,达到降低计算量的目的。
表1 各算法在三组数据上的预测结果
Tab.1 Prediction results of each algorithm on three datasets
5-1RMSETIMELinear27.3692±0.00000.0020±7.34e-06Kernel20.6460±0.00000.0114±0.0033RBF23.584±1.60e-040.5722±0.0140SVM18.9627±0.000040.3830±1.9053MGP17.0787±1.8666477.262±204.821710-5RMSETIMELinear15.1702±0.00000.0033±1.52e-04Kernel10.8283±0.00000.0113±0.0014RBF11.8145±0.04830.4785±0.0134SVM6.8573±0.000047.3761±5.8566MGP6.5572±0.000020.0200±4.096310RMSETIMELinear0.3744±0.00000.0022±4.3867e-07Kernel0.2653±0.00000.0108±8.1769e-04RBF0.3443±0.00001.4206±0.0373SVM0.2365±0.000023.5668±0.3301MGP0.2362±9.13e-0418.1156±0.6324
4.2 第二组实验
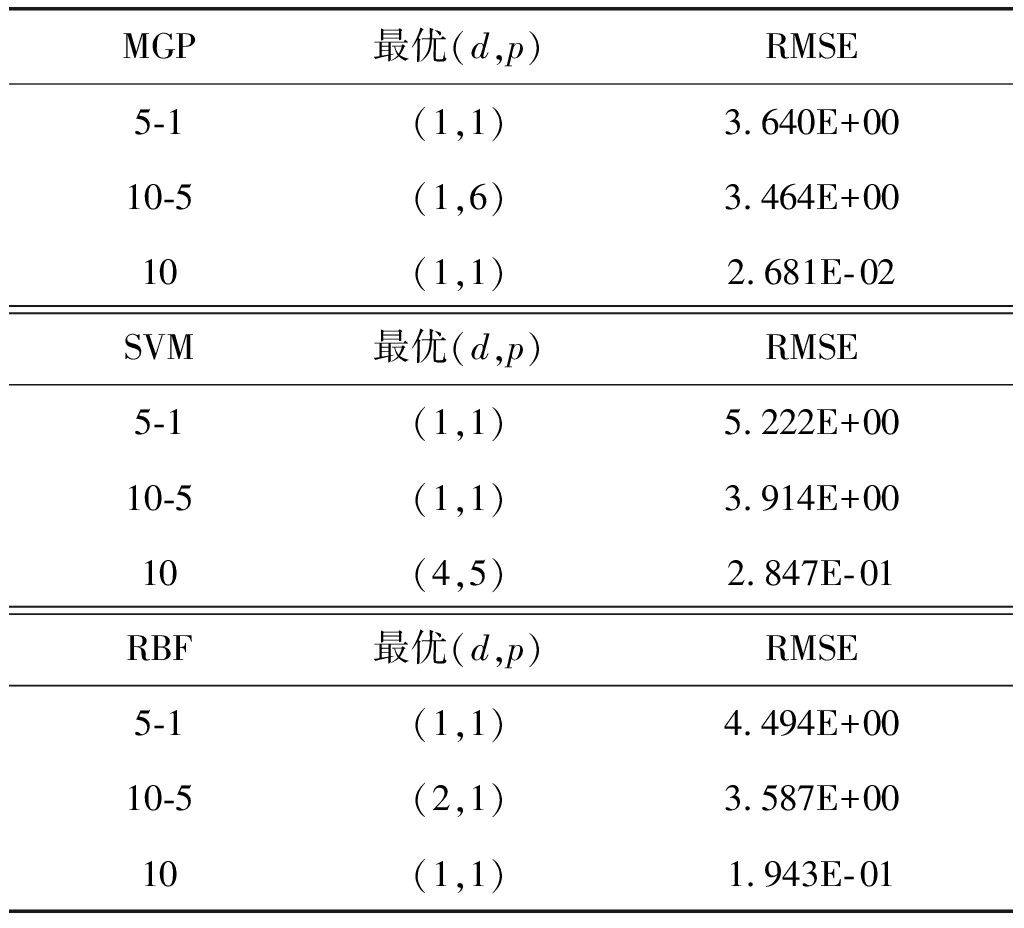
进一步,我们分别将期限利差5-1、期限利差10-5、10年国债收益率作为时间序列数据集。首先,采用不同的回归(或递推)阶数和采样间隔分别对上述时间序列数据重组,其中重组之后的输入和输出分别为Xti=(Xti-d,Xti-2d,…,Xti-pd),Yti=Xti,其中p是回归(或递推)阶数,d是采样间隔;其次,将高斯过程混合模型与RBF模型、SVM回归模型应用在三个数据集上。在实验中,我们分别选取了p=1,…,6,d=1,…,8,一共进行了48组实验。表2中展示了各算法在48组实验中获得最好实验结果以及相应的p和d。
在三个数据的重组数据上,从48组实验中选择出各算法的最优实验结果。从表2中可以看出,MGP模型在三个数据的重组数据上都获得了最好的预测误差RMSE。同时,我们还可以观测到,在不同的数据上,获得最好预测误差的重组数据的p和d不同。而这在实际应用中,想要获得最优的p和d也是困难的。未来通过模型选择算法获得最优的p和d是一个有前景的研究方向。在运行时间上, MGP模型的时间仍然是最长的,这一点和第一组实验的结果是一致的。
表2 各算法在三组重组数据上的回归分析结果
Tab.2 Regression analysis results of each algorithm on three reconstructed datasets
MGP最优(d,p)RMSE5-1(1,1)3.640E+0010-5(1,6)3.464E+0010(1,1)2.681E-02SVM最优(d,p)RMSE5-1(1,1)5.222E+0010-5(1,1)3.914E+0010(4,5)2.847E-01RBF最优(d,p)RMSE5-1(1,1)4.494E+0010-5(2,1)3.587E+0010(1,1)1.943E-01
5 结论
由于国债利率期限结构对于国债利率分析和市场投资具有极大的价值,其发现与研究已经吸引了大批学者和投资者,并成为金融工程中的重要课题。本文首先分析了国内外处理利率期限结构的方法,并发现它们仅限于从已知的市场行为去挖掘利率期限结构的特点。本文突破先有研究框架,通过对大量历史数据的分析,提取出三个影响国债利率期限结构的关键因子:通货膨胀指数CPI、工业增加值增速IP和衡量市场资金面的一个重要因子,即银行间7天质押回购利率。本文进一步跳出学术界传统的思考框架,从市场参与者的角度出发,在尊重市场的历史变化同时,利用高斯过程混合模型来对未来行为进行有效的预测。实验结果表明相比于其他机器学习算法,MGP模型获得了更精确的预测结果,相比于市场传统的线性回归算法有明显的优势。
[1] Choudhry M. Corporate Bond Markets: Instruments and Applications[M]. Corporate Bond Markets: Instruments and Applications. J. Wiley & Sons(Asia), 2011.
[2] Bao J, Pan J, Wang J. The Illiquidity of Corporate Bonds[J]. The Journal of Finance, 2011, 66(3): 911-946.
[3] Kang J, Pflueger C E. Inflation Risk in Corporate Bonds[J]. The Journal of Finance, 2015, 70(1): 115-162.
[4] Nikolaenko S A, Lohbauer U, Roggendorf M, et al. Influence of c-Factor and Layering Technique on Microtensile Bond Strength to Dentin[J]. Dental Materials, 2004, 20(6): 579-585.
[5] Bollerslev T, Cai J, Song F M. Intraday Periodicity, Long Memory Volatility, and Macroeconomic Announcement Effects in the US Treasury Bond Market[J]. Journal of Empirical Finance, 2000, 7(1): 37-55.
[6] Okou C, Jacquier É. Horizon Effect in the Term Structure of Long-Run Risk-Return Trade-Offs[J]. Computational Statistics and Data Analysis, 2016, 100: 445- 466.
[7] Levant J, Ma J. Investigating United Kingdom’s Monetary Policy with Macro-Factor Augmented Dynamic Nelson-Siegel Models[J]. Journal of Empirical Finance, 2016, 37: 117-127.
[8] Laurini M P, Caldeira J F. A macro-finance term structure model with multivariate stochastic volatility[J]. International Review of Economics and Finance, 2016, 44: 68-90.
[9] Dubecq S, Monfort A, Renne J P, et al. Credit and Liquidity in Interbank Rates: A Quadratic Approach. Journal of Banking and Finance, 2016, 68: 29- 46.
[10] Gong P, Dai J. Pricing Real Estate Index Options Under Stochastic Interest Rates[J]. Physica A: Statistical Mechanics and its Applications, 2017, 479: 309-323.
[11] Favero C A, Gozluklu A E, Yang H. Demographics and the Behavior of Interest Rates[J]. IMF Economic Review, 2016, 64(4): 732-776.
[12] Maciel L, Gomide F, Ballini R. A Differential Evolution Algorithm for Yield Curve Estimation[J]. Mathematics and Computers in Simulation, 2016, 129: 10-30.
[13] Vieira F, Fernandes M, Chague F. Forecasting the Brazilian Yield Curve using Forward-Looking Variables[J]. International Journal of Forecasting, 2017, 33(1): 121-131.
[14] Murphy K. Machine Learning a Probabilistic Perspective[J]. Chance, 2014, 27(2): 62- 63.
[15] Kou P, Gao F, Guan X. Sparse Online Warped Gaussian Process for Wind Power Probabilistic Forecasting[J]. Applied Energy, 2013, 108: 410- 428.
[16] Tresp V. Mixtures of Gaussian processes[C]∥Advances in Neural Information Processing Systems(NIPS), 2001: 654- 660.
[17] Chen Z, Ma J, Zhou Y. A precise hard-cut EM algorithm for mixtures of Gaussian processes[C]∥International Conference on Intelligent Computing. Springer, Cham, 2014: 68-75.
[18] Gutmann H M. A Radial Basis Function Method for Global Optimization[J]. Journal of Global Optimization, 2001, 19(3): 201-227.
[19] Tresp V. Scaling Kernel-Based Systems to Large Data Sets[J]. Data Mining and Knowledge Discovery, 2001, 5(3): 197-211.
[20] Shevade S K, Keerthi S S, Bhattacharyya C, et al. Improvements to the SMO Algorithm for SVM Regression[J]. IEEE Transactions on Neural Networks, 2000, 11(5): 1188-1193.
