1 引言
传统的线性阵列雷达只能对阵列单元前方区域进行单一视角观测,而不能对大视角大场景区域进行感知,近年来针对其在广域观测中的不足,相关学者提出了一种基于弧形阵列天线的SAR成像系统[1- 4]。与线性阵列成像方式相比[5-9],弧形阵列SAR具有大视角的观测能力。弧形阵列SAR通过沿圆弧向布置一系列天线单元形成一个弧形孔径,通过合成孔径理论实现角度向的分辨。
与线性阵列SAR的等间隔采样不同,弧形阵列SAR在方位向上采用的是等角度采样,因此常规的用于线性阵列的成像方法不再适用于弧形阵列。而且在成像算法的设计过程中,由场景几何可得其斜距公式的根号下包含三角函数,这对于推导信号二维频谱带来困难。文献[10]采用了一种在方位采样点所在圆弧半径远小于目标最短斜距情况下对斜距进行Taylor展开并保留一阶项的远场近似方法,文献[11]对斜距模型进行了二阶的Taylor展开,但是以上两种方法所引入的误差较大,会对成像结果产生影响。本文对目标斜距展开到了四阶项,有效的保证了成像质量的要求。
在推导信号的二维频谱中会有一个解一元三次方程的过程,通常情况下对于解一元三次方程分别有卡尔丹公式法与盛金公式法,这两种解决方法都比较复杂。本文采用了一种级数反演[12-13]的方法来推导信号的二维频谱。然后在二维频域对回波信号进行处理,最终得到聚焦图像。
本文第2节首先介绍弧形阵列SAR的成像几何与原理,并分析了基于该成像几何的回波信号模型;第3节给出了一种基于斜距高阶近似的弧形阵列SAR成像处理方法;第4节通过点目标的成像仿真实验来验证方法的有效性。
2 弧形阵列SAR工作原理
2.1 成像几何
弧形阵列SAR作为一种新型的机载阵列SAR观测系统,它采用了一种广域圆环的波束扫描方式,拥有更大的观测区域,加快了雷达获取场景信息的速度。弧形阵列SAR的成像场景几何如图1的坐标系所示。在距离向上,通过发射带宽信号实现距离向分辨;在方位向上,通过沿圆弧向布置的天线阵元形成弧形孔径实现方位向分辨。其中,弧形阵列等效采样点Papc在高度为H的平面上,其坐标为(θ,Rarc,H),θ为等效采样点所对应的水平角度值,Rarc为等效采样点的半径;O为观测场景中心点,P(φn,rn,hn)为场景中目标的位置坐标,φn为目标所对应的水平角度值,rn为目标距场景中心的水平半径,hn为目标的高度。
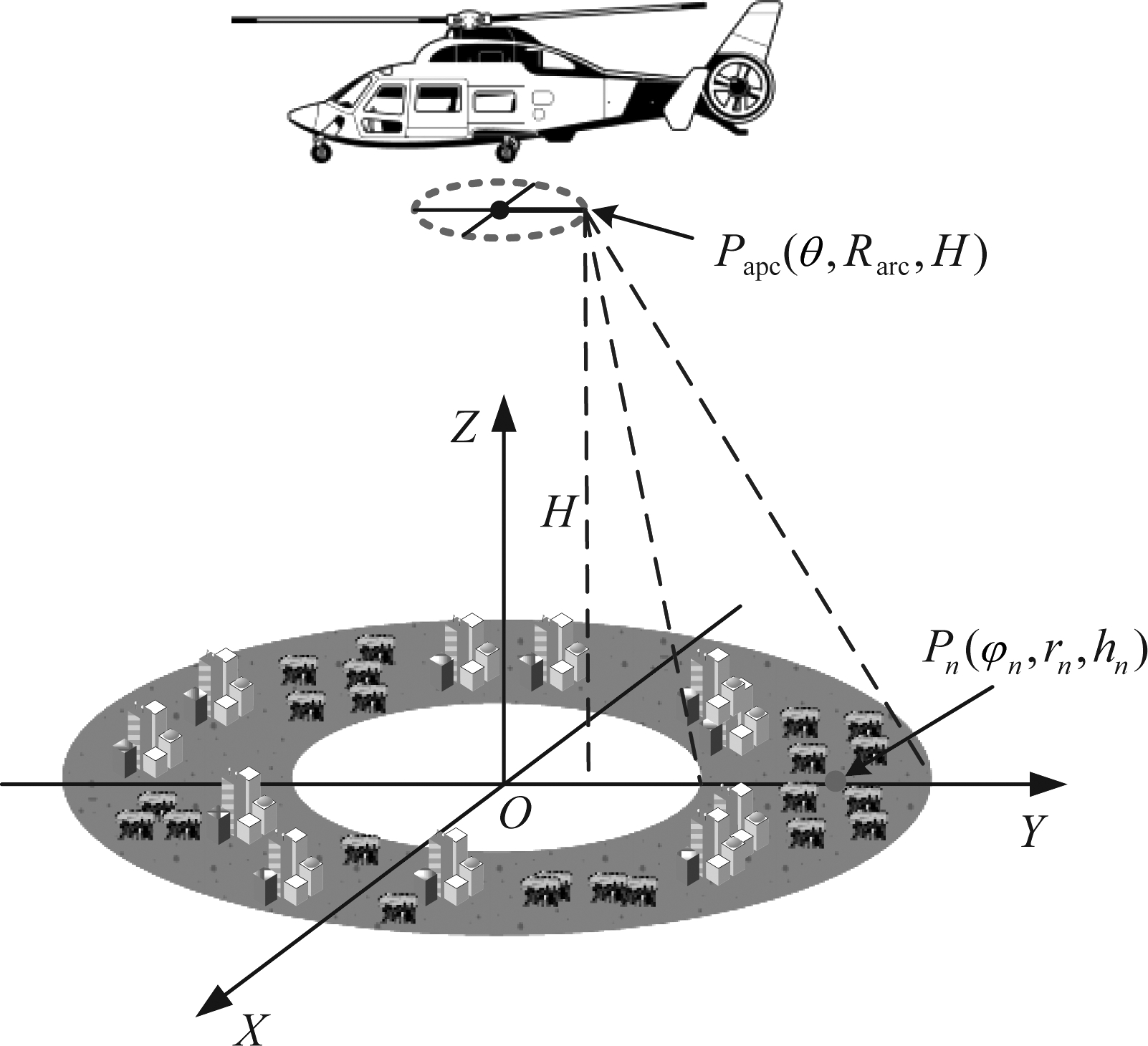
图1 弧形阵列SAR成像场景几何
Fig.1 The imaging scene of arc array SAR
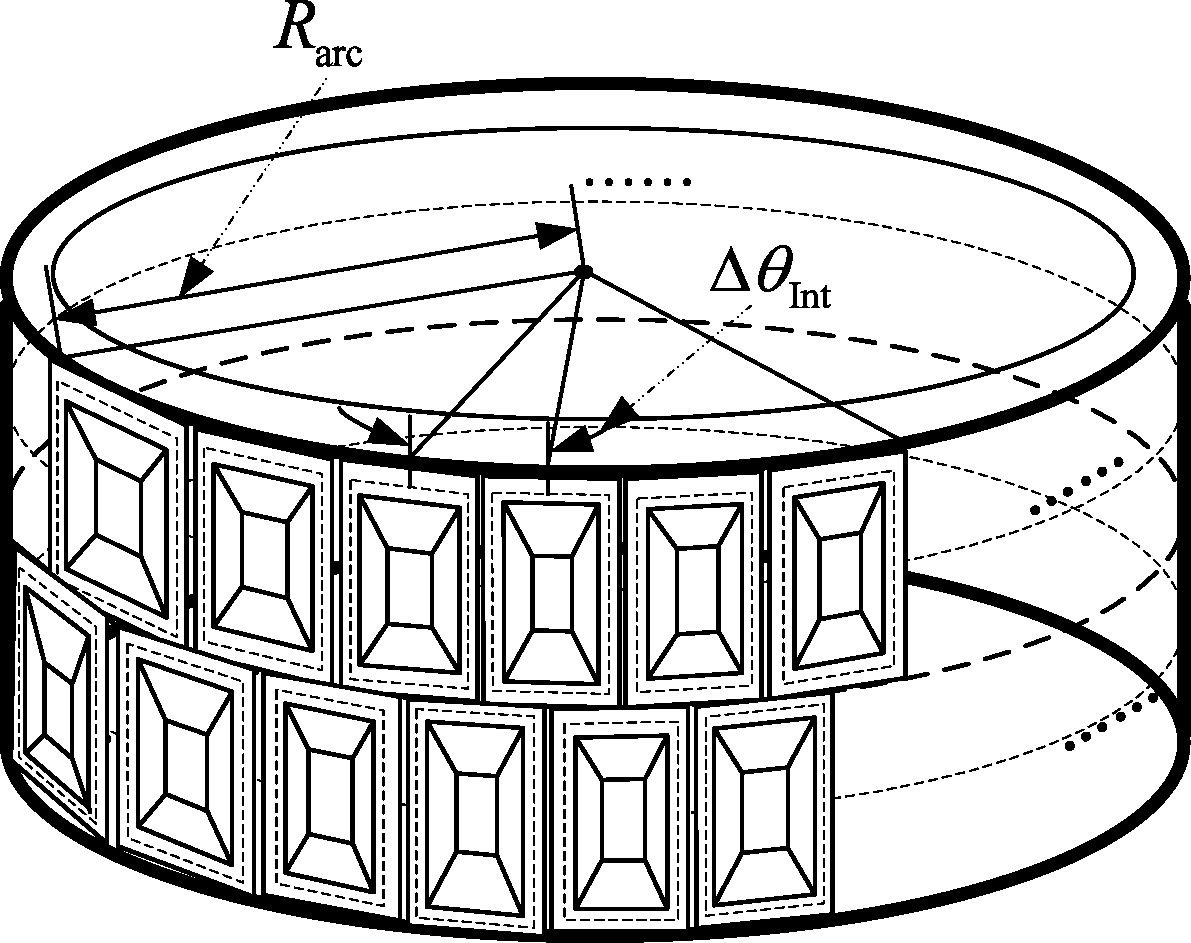
图2 弧形阵列天线结构
Fig.2 Configuration of arc array antenna
弧形阵列SAR成像系统采用调频连续波(FMCW)体制的工作方式,该系统的优点是体积小、重量轻。其中,弧形阵列天线的结构如图2所示,天线单元沿圆弧向均匀分布,采用收发分置的布局方式,发射天线和接收天线分开排列,通过微波开关实现天线的发射和接收。通常情况下将弧形阵列天线安装在直升机平台上对周围场景进行大视角的快速感知观测。
弧形阵列等效采样点与点目标位置的瞬时斜距为:
R(θ)=
(1)
上式中![]() 其中Δθ为相邻等效采样点之间的角度间隔,Nr为方位向的等效采样点数。
其中Δθ为相邻等效采样点之间的角度间隔,Nr为方位向的等效采样点数。
由上面的公式可以看出,目标的瞬时斜距存在根号下的三角函数,当推导回波的二维频谱表达式时会产生困难,所以需要对斜距进行近似展开再设计成像方法。一般情况下我们可以认为,当斜距R(θ)的近似模型所带来的相位误差4πΔR/λ小于π/4时,其对成像结果产生的影响可以忽略[12-13]。而文献[10]对斜距进行了远场近似,文献[11]对于斜距展开到了二阶项,舍弃了高阶项的信息,这两种方法所引入的误差较大,会影响成像的质量。而在本文中将斜距Taylor展开到四阶项,提高了近似的精度。下面为斜距展开式:
(2)
其中,
(3)
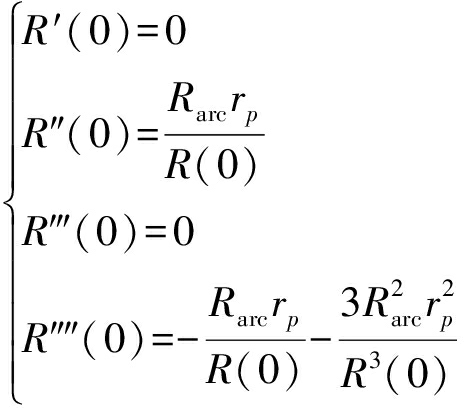
(4)
为了便于表达令![]() 则斜距方程可以重新整理为:
则斜距方程可以重新整理为:
R(θ)≈R(0)+Q2θ2+Q4θ4
(5)
在图3中分别对斜距的远场近似、泰勒二阶近似及四阶近似时的误差进行了对比分析。其中仿真参数如下:平台高度H为1000 m,弧形阵列半径为0.6 m,中心频率为35 GHz,参考目标的坐标为(0,1000,0)。从图中可知,对斜距进行远场近似及二阶泰勒近似时的相位误差都比较大,而当斜距进行四阶泰勒级数展开时相位误差远小于π/4。
2.2 信号模型
如前所述,弧形阵列SAR成像系统采用调频连续波(FMCW)体制,其相应的发射信号str(t)为:

(6)
式中, fc为系统工作频率,t为距离向时间变量,Tr为信号持续时间,Kr为发射信号的线性调频率,信号带宽为Br=KrTr。
阵列天线上某一个等效采样点Papc接收到点目标Pn经混频处理之后的回波信号可以表示为:
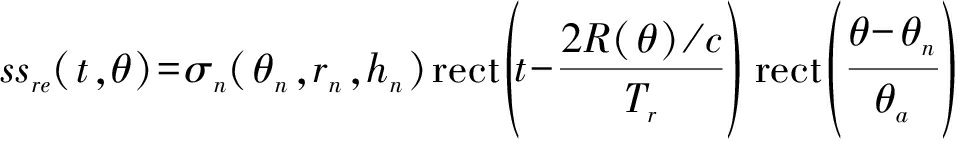
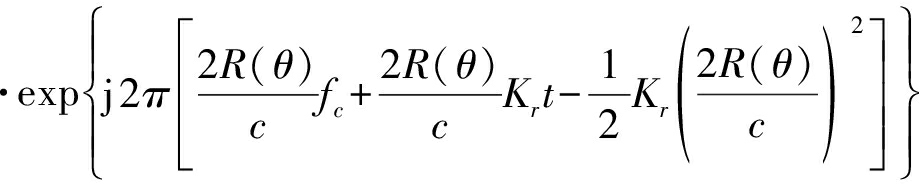
(7)
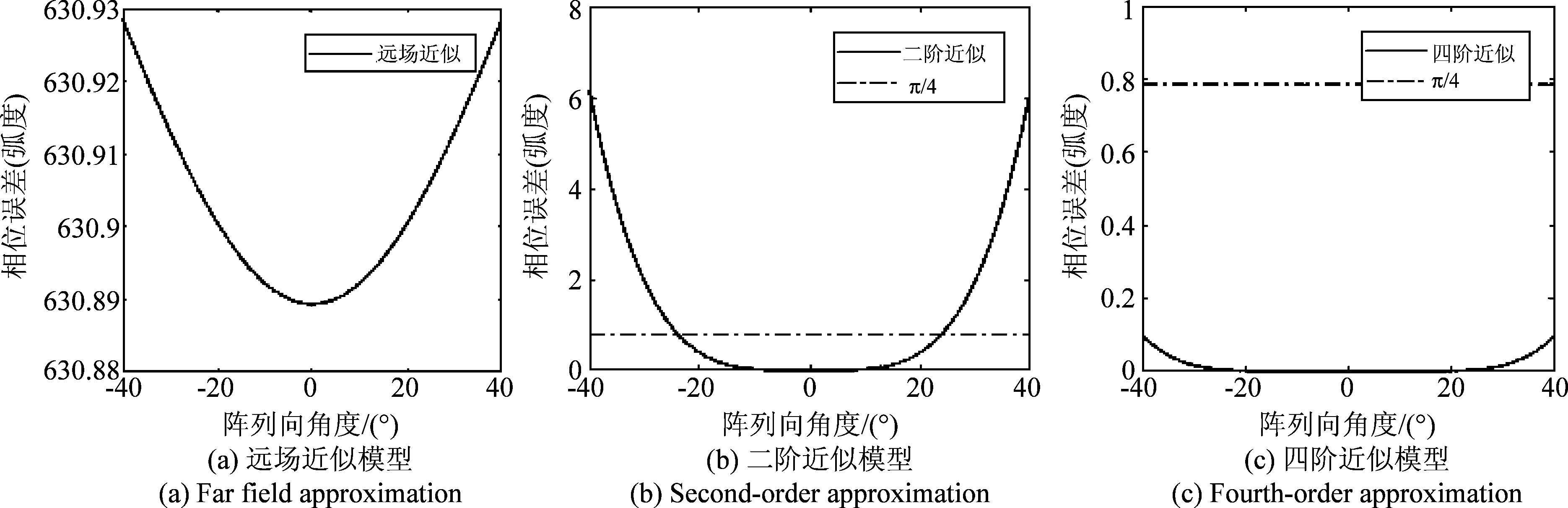
图3 斜距近似误差分析
Fig.3 Error analysis of slant range approximation
式中,σn(θn,rn,hn)表示目标的散射系数,θa为水平方向的波束宽度,第三个相位项jπKr[2R(θ)/c]2为残余视频相位项(RVP),需要对其补偿,则RVP补偿后的信号回波表达式为:
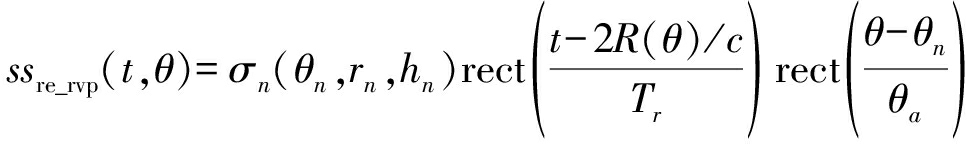
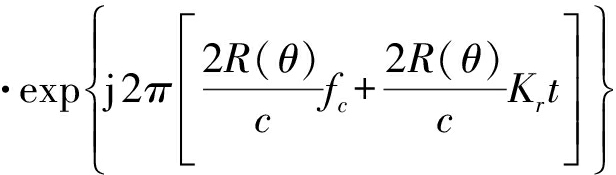
(8)
3 成像方法
3.1 二维频谱的推导
在这里令fr=Krt,对式(8)进行时频替换,则其可以重新整理为式(9):
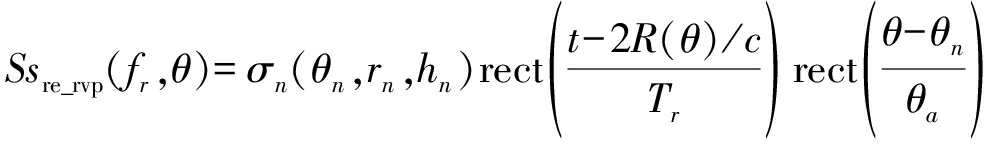
(9)
之后,对式(9)做阵列向的傅里叶变换,将回波信号变换到二维频域对其进行成像处理,其傅里叶变换的方程如下式所示:
SS(fr, fθ)=![]() Ssre_rvp(fr,θ)·exp{-j 2πfθθ}dθ
Ssre_rvp(fr,θ)·exp{-j 2πfθθ}dθ
(10)
在这里我们利用级数反演[12-13]的思想推导其二维频谱表达式,首先对上式中被积的相位进行求导,并令导数为零,则可得其驻相点θt的方程为:
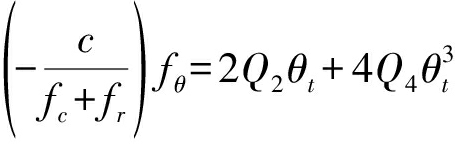
(11)
然后利用级数反演的方法解得驻相点为:
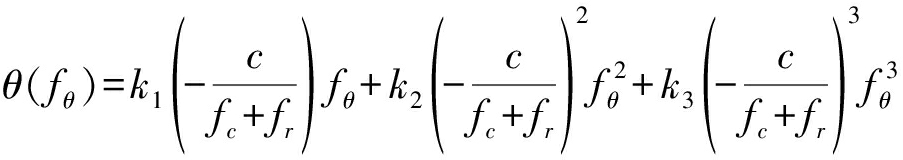
(12)
其中,![]() 为阵列向的多普勒频率。然后我们可得点目标的二维频域表达式为:
为阵列向的多普勒频率。然后我们可得点目标的二维频域表达式为:
SS(fr, fθ)=σn(θn,rn,hn)·exp{jΦ(fr, fθ)}
(13)
式中的相位表示如下:
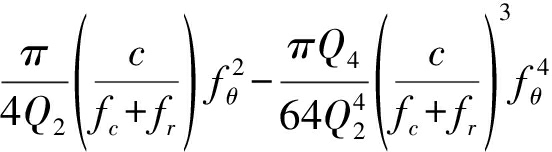
(14)
3.2 二维频域处理
由上式推导的二维频谱可知距离向的频率fr和方位向的多普勒频率fθ之间存在耦合,对于下一步的成像处理带来不便,所以首先要消除距离方位之间的耦合,在这里将式(14)进行展开[13],整理后可以得到如下的表达式:
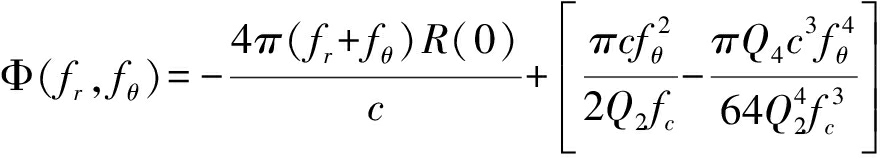
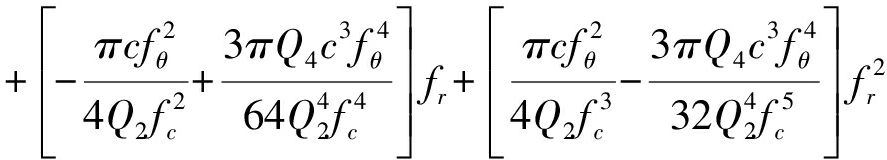
(15)
为了便于表达,在这里令:
(16)
(17)
(18)
其中φaz(fθ)为方位调制项,该项将在距离多普勒域完成方位向的脉压;φrcm(fθ)为fr的一次项,称为距离徙动项,需在二维频域对其校正;φsrc(fθ)为二次距离压缩项,该项体现了目标的距离调频率,需要在二维频域对其补偿。

图4 成像算法流程图
Fig.4 The process of imaging algorithm
通过对上述表达式的分析,在二维频域中补偿距离徙动、距离方位的耦合,其补偿函数可以表达为:
(19)
完成了在二维频域的处理之后,对回波信号做距离向IFFT,在距离多普勒域完成方位向的匹配滤波,其方位向滤波函数为:
Haz(fr, fθ)=exp{-jφaz(fθ)}
(20)
方位向压缩后,再做方位向IFFT,最终得到目标的聚焦图像。上述算法的完整流程如图4所示。
4 仿真分析
4.1 参数设置
为了验证本文用于弧形阵列SAR成像方法的有效性,进行了点目标的仿真试验。其中弧形阵列SAR系统仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters

参数符号参数定义参数值fc中心频率/GHz35.5Br 信号带宽/MHz1000Tr 扫频时间/ms0.1H平台高度/m1000Rarc弧形阵列半径/m0.6θinc入射角/(°)25θr俯仰向波束宽度/(°)30θa 阵列向波束宽度/(°)60
在仿真中设置一个点阵目标场景,其位置如图5所示,三个点目标的坐标分别为P1(10°,300,0)、P2(0°,500,0)、P3(-10°,700,0)。采用本文的成像处理算法对点目标回波进行仿真验证,其聚焦图像如图6所示,图7分别给出目标区域中3个点目标P1、P2和P3成像结果的等高线图,从中可以看出,不同距离和角度处的3个点目标都得到了很好的聚焦效果;点目标所对应的阵列向与距离向响应函数如图8所示。
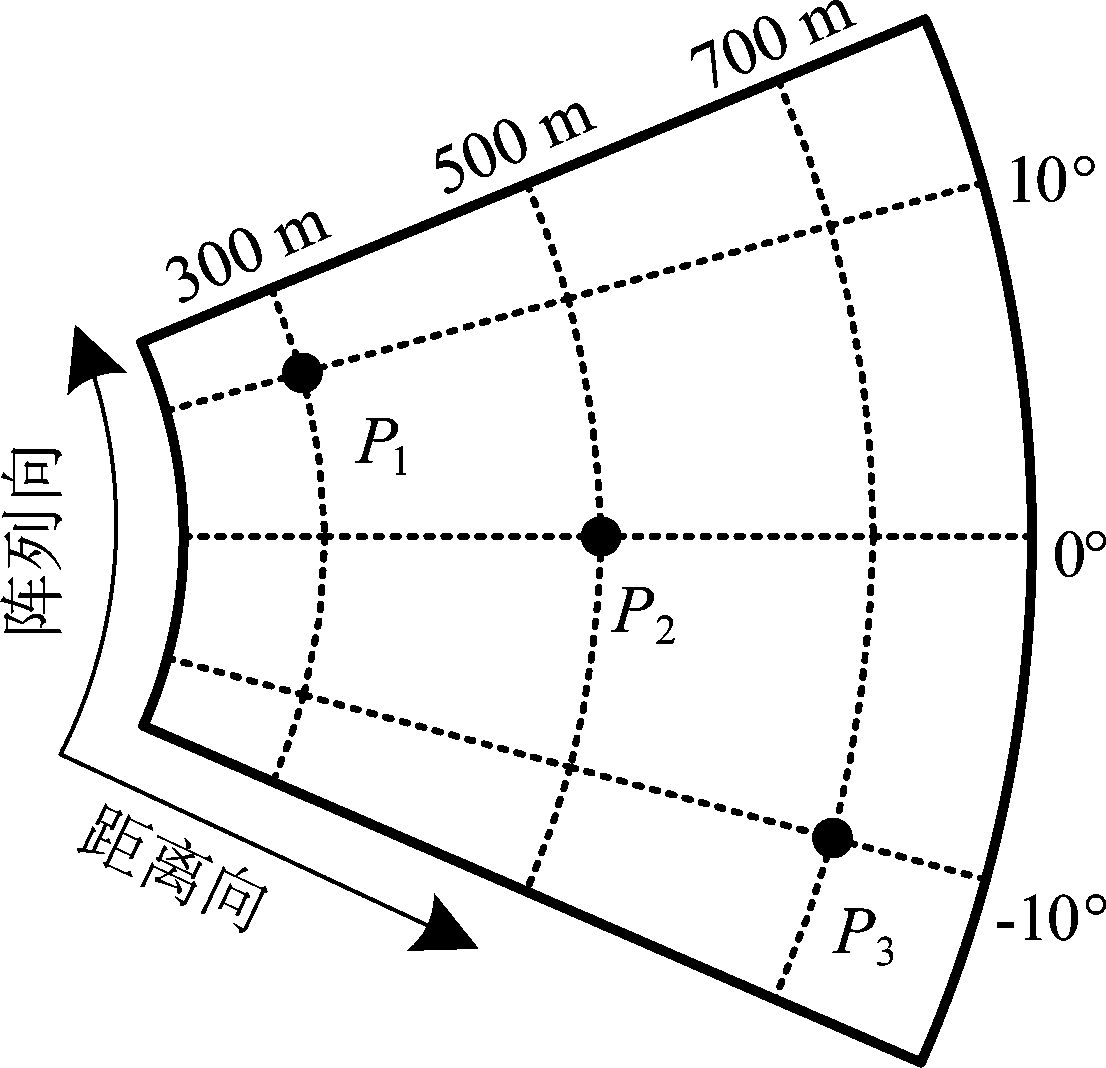
图5 点目标位置分布
Fig.5 The positions of point target
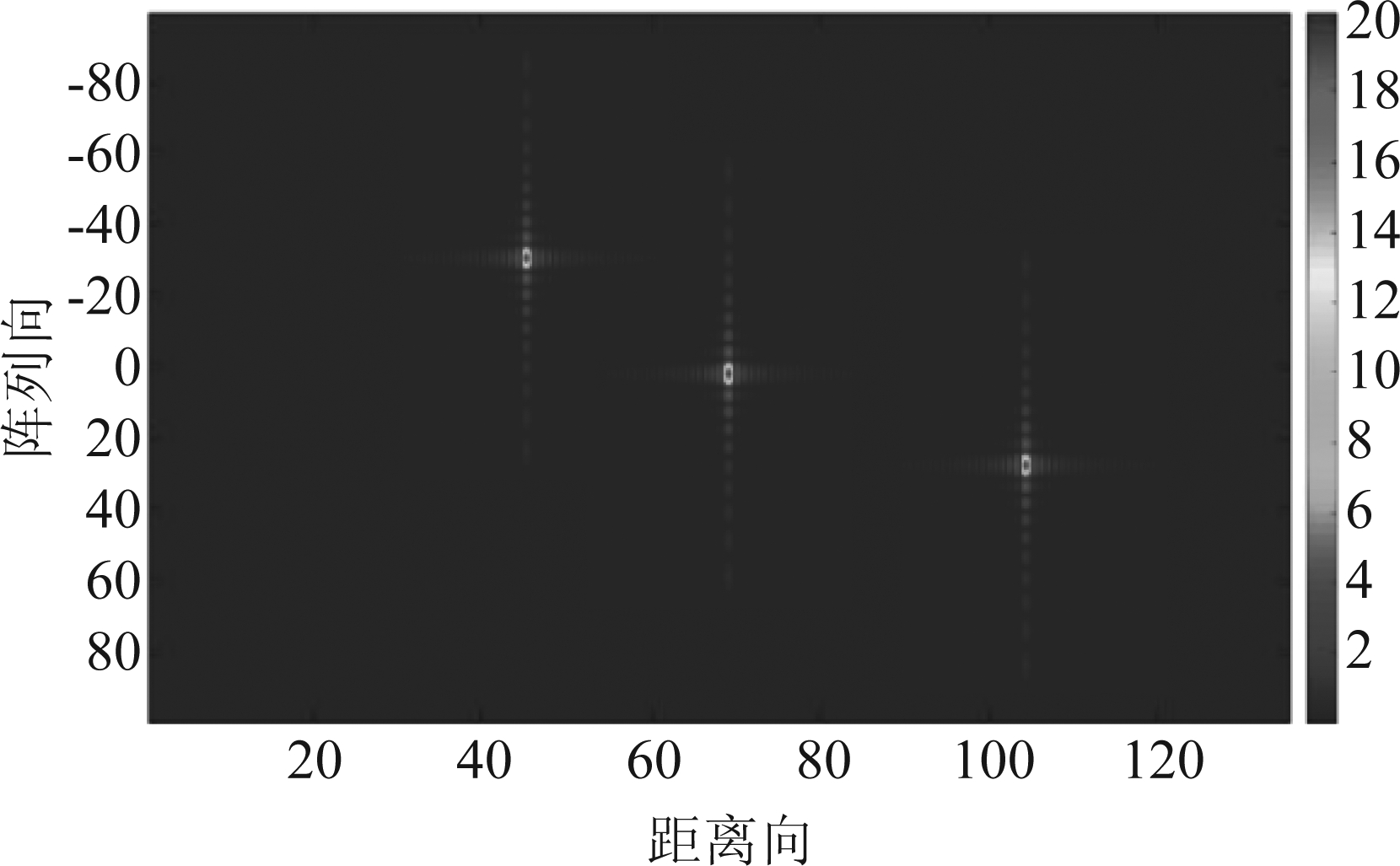
图6 点目标聚焦图像
Fig.6 Focus image of point target
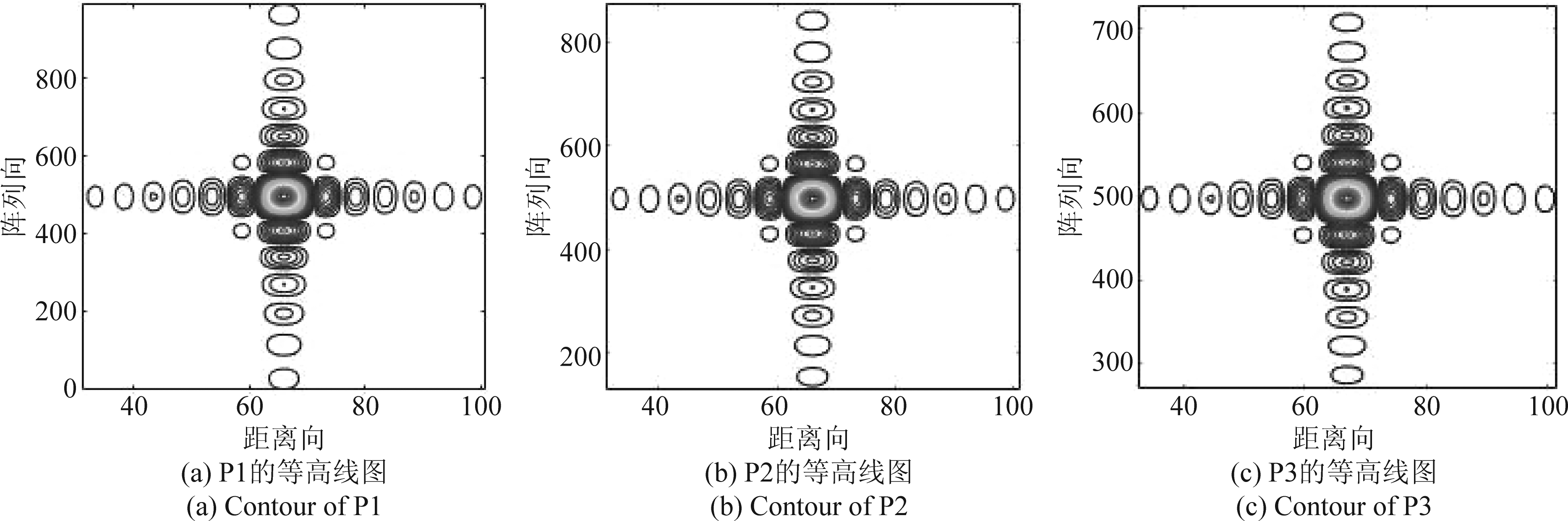
图7 不同位置的点目标等高线图
Fig.7 Contour of targets at different positions
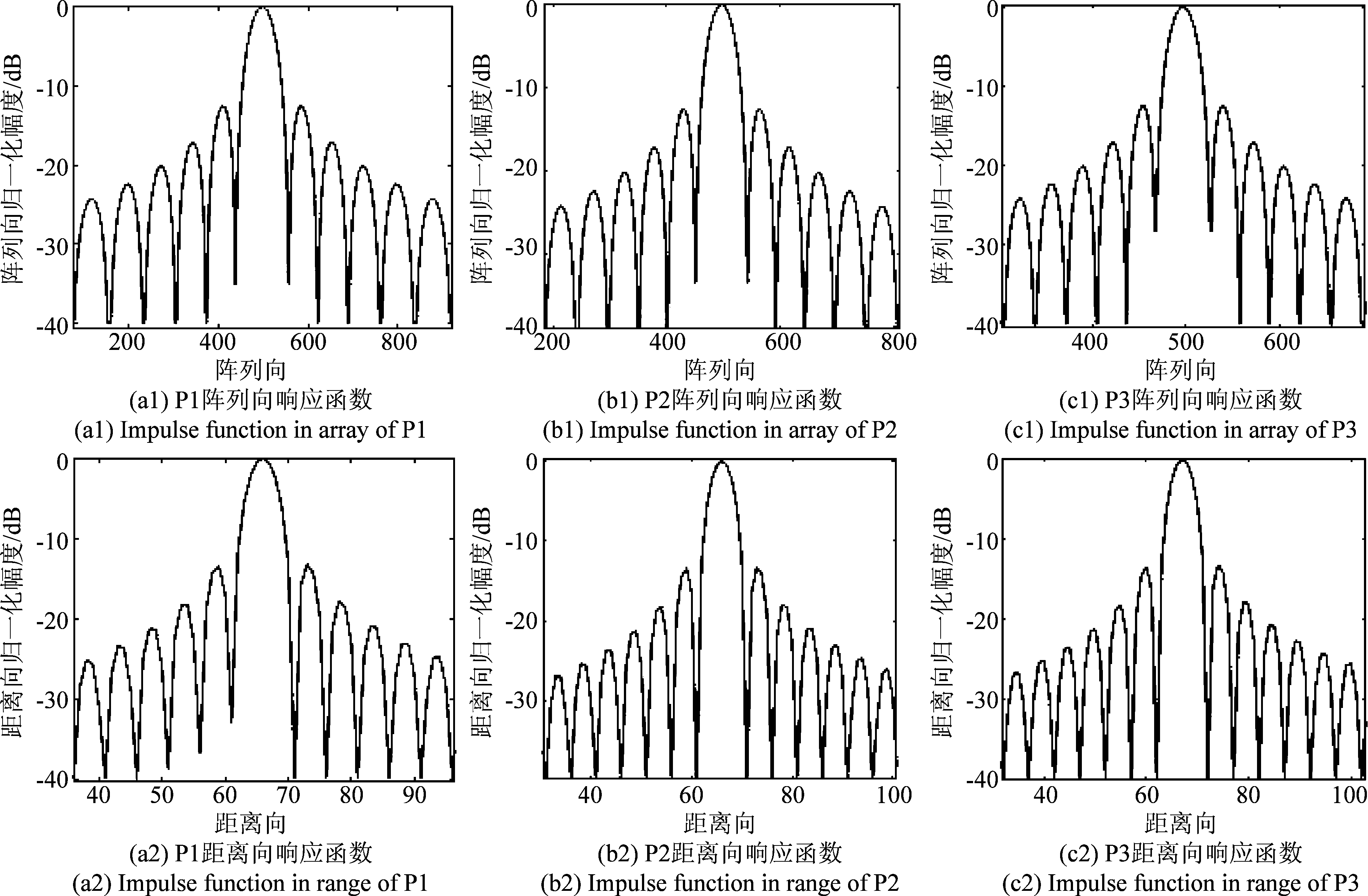
图8 不同位置点目标的响应函数
Fig.8 Impulse function of target at different positions
为了进一步对成像结果分析,由表2给出了点目标P1、P2和P3的具体成像性能指标,其中,PSLR和ISLR分别表示峰值旁瓣比和积分旁瓣比。P1、P2和P3距离向分辨率的理论值分别为0.561 m、0.362 m和0.285 m,阵列向分辨率的理论值分别为1.404°、0.902°和0.703°,对比表中的数据可以看出,各点成像结果性能指标与理论分析基本相符,从而验证了本文提出的基于弧形阵列的二维频域算法的有效性。
表2 点目标成像性能分析
Tab.2 The imaging performance analysis for point
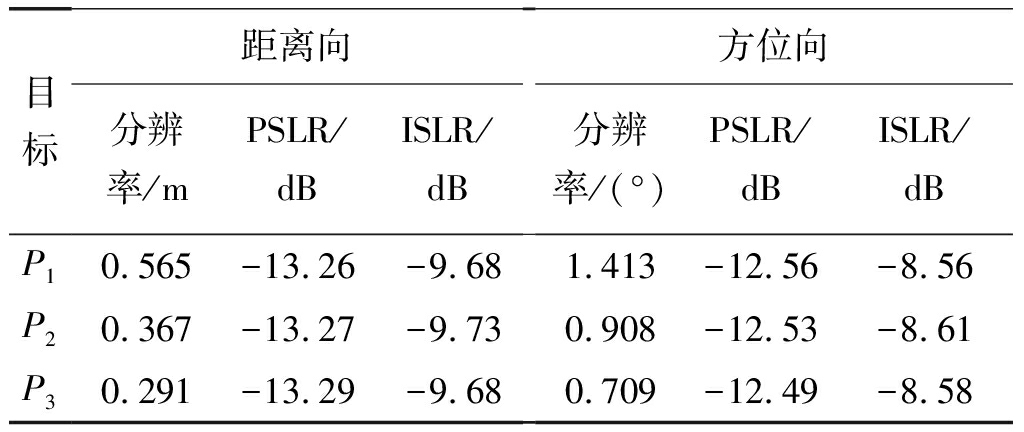
目标距离向分辨率/mPSLR/dBISLR/dB方位向分辨率/(°)PSLR/dBISLR/dBP10.565-13.26-9.681.413-12.56-8.56P2 0.367-13.27-9.730.908-12.53-8.61P3 0.291-13.29-9.680.709-12.49-8.58
5 结论
本文首提出了一种基于斜距高阶近似的弧形阵列SAR成像算法。该算法使用高阶逼近来近似弧形阵列SAR的斜距模型,然后推导其二维频谱表达式,根据得到的近似两维频谱再进行成像处理。该成像算法中只涉及到距离向和方位向的傅里叶变换和相位的复乘操作,相比于已有的时域投影算法大幅度提高了运算效率。
[1] 黄平平. 弧形阵列MIMO-SAR成像算法研究[C]∥高分辨率对地观测学术年会分会, 2014.
Huang P P. Research on Imaging Algorithm with MIMO-SAR based on Arc Antenna Array[C]∥High Resolution Earth Observation Conference, 2014.(in Chinese)
[2] Huang P P, Tan W X, Su Y. MIMO-SAR imaging technology for helicopter-borne based on ARC antenna array[C]∥IEEE Geoscience and Remote Sensing Symposium, 2015: 1801-1804.
[3] 黄平平, 谭维贤, 苏莹, 等. 直升机载弧形阵列MIMO微波成像技术研究[J]. 雷达学报, 2015, 4(1): 11-19.
Huang P P, Tan W X, Su Y, et al. Research on Helicopter-borne MIMO Microwave Imaging Technology Based on Arc Antenna Array[J]. Journal of Radars, 2015, 4(1): 11-19.(in Chinese)
[4] 黄平平, 谭维贤, 洪文. 用于MIMO-SAR成像的微波信号收发系统、方法及成像系统[P]. 中国: ZL 2014105617313, 2016.03.02.
Huang P P, Tan W X, Hong W. Microwave signal transceiving system, method and imaging system for MIMO-SAR imaging[P]. China: ZL 2014105617313, 2016.03.02.(in Chinese)
[5] 黄平平, 邓云凯, 徐伟. 基于CS算法的MIMO-SAR成像研究[J]. 电子科大学报, 2012, 41(2): 222-226.
Huang P P, Deng Y K, Xu W. Research on Multiple-Input and Multiple-Output SAR Imaging Based on CS Algorithm[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(2): 222-226.(in Chinese)
[6] Huang P P, Li H C, Feng F, et al. The waveform analysis and signal processing for space-borne MIMO-SAR[C]∥European Conference on Synthetic Aperture Radar. VDE, 2012: 579-582.
[7] 谭维贤. 合成孔径雷达三维成像理论与方法研究[D]. 北京: 中国科学院研究生院, 2009.
Tan W X. Study on Theory and Algorithms for Three-Dimensional Synthetic Aperture Radar Imaging[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2009.(in Chinese)
[8] 师君. 双基地SAR与线阵SAR原理及成像技术研究[D]. 成都: 电子科技大学, 2009.
Shi J. Research on Principles and Imaging Techniques of Bistatic SAR and linear array SAR[D]. Chengdu: University of Electronic Science and Technology of China, 2009.(in Chinese)
[9] 杜磊. 阵列天线下视合成孔径雷达三维成像模型、方法与实验研究[D]. 北京: 中国科学院研究生院, 2010.
Du L. Study on Model, Algorithm and Experiment for Downward-Looking Synthetic Aperture Radar Three-Dimensional Imaging Based on Linear Array Antennas[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2010.(in Chinese)
[10] Luo Y H, Song H J, Wang Y, et al. Signal Processing of Arc FMCW SAR[C]∥APSAR 2013, 2013: 412- 415.
[11] 孙兵, 周荫清, 陈杰, 等. 广域观测圆轨迹环扫SAR成像模式研究[J]. 电子与信息学报, 2008, 30(12): 2805-2808.
Sun B, Zhou Y Q, Chen J, et al. Operation Mode of Circular Trace Scanning SAR for Wide Observation[J]. Journal of Electronics and Information Technology, 2008, 30(12): 2805-2808.(in Chinese)
[12] Liao Y. An Imaging Algorithm for Airborne Circular Scanning SAR Based on the Method of Series Reversion[J]. Journal of Electronics and Information Technology, 2012, 34(11): 2587-2593.
[13] 李东, 廖桂生, 徐青, 等. 高分辨直升机载旋转合成孔径雷达成像算法[J]. 系统工程与电子技术, 2013, 35(7): 1389-1395.
Li D, Liao G S, Xu Q, et al. High resolution imaging algorithm for helicopter-borne rotating synthetic aperture radar[J]. Systems Engineering and Electronics, 2013, 35(7): 1389-1395.(in Chinese)





