1 引言
波达方向估计(Direction of Arrival, DOA)问题一直是阵列信号处理研究的热点问题。传统的DOA算法通常假设接收信号来自远场点源,然而在诸如无线定位、雷达和移动通信等实际环境中,传输的信号经常被建筑物、车辆和树木等遮挡或被粗糙表面反射,造成信号的多径传播,并由此产生角度扩展效应。在多径条件下,点信源DOA估计算法不再适用。针对此问题,引入了分布式信源模型[1]。根据信道的相干时间和观察周期之间的关系,来自不同方向的信号分量表现出不同程度的相关性,由此,分布式信源可以分为相干分布(Coherently Distributed, CD)源和非相干分布式源[2]。
S.Valaee等人[3]系统阐述了分布式信源模型,提出了DSPE(Distributed Signal Parameter Estimator,DSPE)算法来估计分布式信源的角度参数,该算法需要进行频谱峰值搜索,计算复杂度较高。文献[4]介绍了一种基于TLS-ESPRIT[5]的分布式信源参数估计算法。ESPRIT类算法无需进行谱峰搜索,大大降低了计算复杂度。文献[6]提出了用于估计二维CD源的酉-ESPRIT算法,该方法基于酉变换,计算复杂度较低,但是估计精度不理想。上述经典算法都是基于圆信号特性的假设,没有考虑信号的非圆特性,而在实际应用中非圆信号大量存在。例如二进制相移键控(Binary Phase Shift Keying, BPSK)信号和幅度调制(Amplitude Modulation,AM)信号。非圆信号的伪协方差矩阵不为零,可以改善DOA的估计性能[7]。文献[8]首次将信号的非圆性引入到二维CD模型中估计中心方位角和中心俯仰角,提出CDNC-ESPRIT算法。文献[9]结合信号的非圆特性提出了两种用于估计CD源的MUSIC(Multiple Signal Classification,MUSIC)类算法,可以在圆信号和非圆信号同时入射时实现DOA估计,提升了估计性能。上述分布式信源参数估计方法都是基于高斯噪声假设的,实际上在一些复杂的多径散射环境中可能存在脉冲噪声,如大气环境噪声、雷达反向散射回波及城市移动无线电信道中的电磁噪声,此时用Alpha稳定分布[10]描述噪声更合适。由Alpha稳定分布理论可知,在脉冲噪声下,其二阶或以上阶统计量都是不存在的[10-11]。文献[12]将分数低阶统计量应用于脉冲噪声环境下的点源非圆信号DOA估计问题,结合ESPRIT技术提出EXC-NC-ESPRIT算法,但分数低阶理论依赖于Alpha稳定分布α参数的先验知识,在实际应用中受到限制。
本文提出一种新的非线性相似性度量,即广义复相关熵(Generalized Complex Correntropy,GCC)。GCC克服了分数低阶统计量对噪声先验知识的依赖,具有更好的鲁棒性。本文以受脉冲噪声干扰的相干分布式非圆信号为研究对象,利用信号的非圆性构造扩展阵列输出矩阵,结合广义复相关熵对ESPRIT算法进行改进,进而提出NC-ESPRIT-GCC算法,实现在脉冲噪声条件下更好的DOA估计性能。
2 信号模型
假设有P个相互独立的窄带相干分布式信号入射到M个阵元组成的均匀线阵中,阵列输出矢量可表示为
(1)
式中,a(θ)为点信源的方向矢量,si(θ,t;ψi)为第i个信源的角信号密度函数,ψi为第i个相干分布源的位置参数矢量,θi和σθi分别为第i个信源的中心波达方向角和扩散角,n(t)为阵列噪声矢量。
对于相干分布式信源,其角信号密度函数可以表示为
si(θ,t;ψi)=si(t)ρ(θ;ψi)
(2)
其中,si(t)表示第i个发射信源,ρ(θ;ψi)表示确定性角度信号密度函数,通常为高斯分布或均匀分布。当相干分布式信源服从高斯分布时有
当相干分布式信源服从均匀分布时
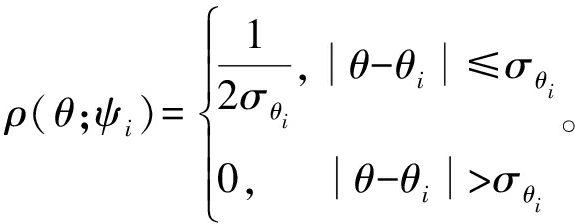将式(2)代入式(1)可以提取相干分布源的方向矢量为
b(ψi)=
a(θ)ρ(θ;ψi)dθ
(3)
令B=[b(ψ1),…,b(ψP)]为相干分布源的阵列导向矩阵,s(t)=[s1(t),s2(t),…,sP(t)]T为信源矢量,整理上式可得
x(t)=Bs(t)+n(t)
(4)
对于非圆信号,非圆率δ取决于发射信号的调制方式,本文考虑最大非圆率信号,即满足非圆率δ=1的信号,此时非圆信号[13]可表示为s=Φ1/2s0,其中s0∈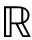
为实值矢量,Φ1/2=diag{ejφ1/2,…,ejφP/2}∈CP×P,其对角线元素表示每个信号的复相移。
3 基于广义复相关熵的DOA估计算法
3.1 复相关熵和广义复相关熵
相关熵[14]与相关函数类似,是一种相似性度量概念,其特点是可以有效抑制脉冲噪声。复相关熵将相关熵的定义域从实数域扩展到复数域,可以适用于实值信号和复值信号两种情况。假设有两个复随机变量C1和C2,C1与C2的复相关熵统计量[15]定义为
V(C1,C2)=E[Gυ(C1,C2)]
(5)
其中,高斯核
式中υ为核长。复相关熵包含随机变量C1-C2所有的偶阶矩
该式由高斯核函数的泰勒展开而得。hυ6(C1-C2)表示变量C1和C2的所有高阶矩信息,并随着核长υ的增加逐渐趋于零,此时二阶矩E[(C1-C2)(C1-C2)*]成为主成分。
本文为了解决脉冲噪声下相干分布式非圆信号DOA估计问题,引入了一种基于复相关熵的新算子,即广义复相关熵(GCC),它可以在各种脉冲噪声环境下结合ESPRIT算法使用。其定义为
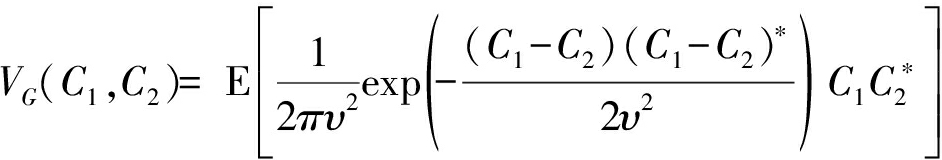
(6)
如上式,GCC是复相关熵与复相关函数的结合,利用高斯核函数将随机变量从线性空间映射到非线性空间,在非线性空间内受到核函数约束的样本对相似性度量结果有直接影响,选取合适的核长便可抑制噪声野点[16]。因此在信号含有异常值即野点时,新算子GCC具有有效反映两个复随机变量相关性的优势。在含有脉冲噪声的实际应用中,用GCC替换传统的相关函数可以实现更为准确的DOA估计。
3.2 算法描述
利用非圆特性的优势,对式(4)进行扩展得到扩展阵列输出
(7)
由最大非圆率信号的性质s=Φ1/2s0,可将上式整理如下:
(8)
其中,Φ=diag{ejφ1,…,ejφP}为非圆相位矩阵。令
为相干分布式非圆信号的扩展阵列导向矩阵。
式(7)为数据增强模型[13],CDNC-ESPRIT算法[8]利用的信号子空间信息由该模型的协方差矩阵分解而得。高斯噪声下,xnc(t)的协方差矩阵为
然而对于0<α<2的Alpha稳定分布信号,当处理算法的统计矩阶数p与信号的特征指数α满足p≥α时,有E[|X|p]=+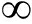
,即二阶或以上阶统计量不再有界。故在脉冲噪声条件下,x(t)不存在有限的二阶统计量,即Rnc不存在。文献[12]针对此问题,提出使用共变矩阵来代替传统二阶统计量。但是以共变理论为代表的分数低阶理论具有两个局限性:一是只能应用在噪声特征指数1<α<2的范围;二是算法严重依赖噪声先验知识α,而该参数在现实中难于获得。GCC统计量抑制脉冲噪声的机理与分数低阶统计量不同。GCC得益于核函数的约束,可以抑制脉冲噪声且不需要噪声先验知识,同时在噪声特征指数0<α<2的范围内均有效。本文采用GCC替换传统的二阶统计量,对EXC-NC-ESPRIT算法[12]进行改进。
xnc(t)的广义复相关熵矩阵表示为
Vnc=VG(xnc(t),xnc(t))
(9)
已知信号与噪声相互独立,可将Vnc分解为Vnc=Vsnc+Vnnc,其中
和Un分别为矩阵Vnc的信号子空间和噪声子空间,κn=VG(n(t),n(t))为噪声的GCC矩阵。事实上因熵函数不呈现均匀的矩特性,分离Vnc非常复杂。但因GCC算子表现稳健的统计特性且包含随机变量的所有高阶矩信息,可以对GCC矩阵进行矩阵分解。脉冲噪声下的GCC矩阵Vnc与高斯噪声下的协方差矩阵Rnc具有相同的子空间特性,故信号子空间Us与阵列流型张成的子空间为同一个空间,即span{Us}=span{Bnc}。存在唯一的非奇异矩阵T,满足Us=BncT。
定理1 若相干分布源的阵列流型矩阵B具有旋转不变性,则Bnc也具有旋转不变特性,且满足下式
J1BncΛ=J2Bnc
(10)
其中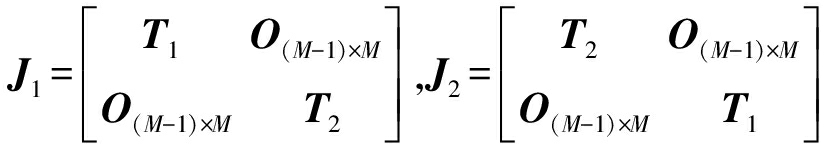
分别为两个选择矩阵,且T1=[I(M-1)×(M-1) 0(M-1)×1],T2=[0(M-1)×1 I(M-1)×(M-1)]。Λ=diag{ej2π(d/λ)sin θ1,ej2π(d/λ)sin θ2,…,ej2π(d/λ)sin θP}是旋转矩阵,λ是载波波长,d为相邻两阵元的间隔,θ1,θ2,…,θP是信源的中心波达方向角。定理1在附录中给出证明。
定理1反映了两个信号子空间的旋转不变特性,利用该特性可以应用诸如LS-ESPRIT或TLS-ESPRIT的ESPRIT类型算法来估计信源的中心波达方向角。将Us=BncT其代入式(10)得整理得J2Us=J1UsTΛT-1。令Q=TΛT-1,用最小二乘准则(LS)有
Q=(J1Us)+(J2Us)
(11)
其中,(·)+表示求矩阵的伪逆。由矩阵的相似性可知,矩阵Q与矩阵Λ具有相同的特征值。通过Q的特征值
求解下式来估计出分布源的中心波达方向角度。
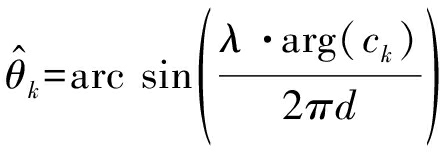
(12)
式中,arg表示求复数相角,
为相干分布式非圆信号的中心波达角估计值。
4 计算机仿真
在本节中仿真验证算法性能,采用提出的NC-ESPRIT-GCC算法进行DOA估计,设定5个阵元组成均匀线阵,阵元间距为半个波长。仿真中假设两个窄带相干分布式信源BPSK信号,角度密度函数均服从高斯分布,信源1中心波达方向角为15°,扩散角为1°,信源2中心波达方向角为17°,扩散角为2°,显然两个相干分布源在空间上有重叠。加性噪声为服从SαS分布的脉冲噪声(即Alpha稳定分布的对称参数β=0)[10]。每个仿真均独立进行200次蒙特卡罗实验。由于SαS随机过程不存在有限的二阶矩,故采用广义信噪比(Generalized signal-to-noise ratio, GSNR)对信号和噪声能量之比进行度量,其定义式为GSNR=10log(E[|s(t)2|/γ]),其中γ为SαS随机过程的分散系数。采用可分辨概率和均方根误差来评价算法性能,并与TLS-ESPRIT[4]、CDNC-ESPRIT[8]、EXC-NC-ESPRIT[12]算法进行对比分析。若满足
则表示一次成功分辨,其中,
和θk分别表示中心波达方向估计值及真值。若L次蒙特卡罗实验的成功次数为Ls,可分辨概率为Ls/L。均方根误差定义为
其中,
表示第n次蒙特卡罗实验的DOA估计值。
实验1 广义信噪比GSNR的影响。设定SαS分布噪声特征指数α=1.2,阵元快拍次数为300。图1给出了几种算法随GSNR变化时的可分辨概率和估计均方根误差结果。从图1可以看出,所有算法均随着GSNR的降低出现性能退化,本文提出的NC-ESPRIT-GCC算法表现出最好的估计性能。NC-ESPRIT-GCC算法利用信号非圆性的优势扩展了阵列输出数据,带来了阵列孔径的增加,故性能优于仅利用阵列输出数据的TLS-ESPRIT算法。CDNC-ESPRIT算法使用了只适于高斯噪声的扩展阵列输出的协方差矩阵,因此在低GSNR条件下性能退化严重。EXC-NC-ESPRIT算法尽管表现出了对脉冲噪声的适应性,性能仍劣于NC-ESPRIT-GCC算法。这是因为NC-ESPRIT-GCC算法在扩展了阵列输出的同时,构造了GCC矩阵,利用高斯核能够更好地抑制脉冲噪声中的野点。
实验2 特征指数α的影响。GSNR设定为0 dB,图2给出了几种算法随α变化时的性能对比。从图中可以看出,当特征指数α越小,即信号的脉冲特性增强时,所有算法的估计性能均有所下降。EXC-NC-ESPRIT算法采用分数低阶统计量来抑制脉冲噪声的影响,但因其受噪声特征指数影响较大的缺点,性能不如NC-ESPRIT-GCC算法。而GCC不依赖于脉冲噪声的先验知识,NC-ESPRIT-GCC算法表现出较好的性能。
实验3 快拍数的影响。设定特征指数α为1.2且GSNR为0 dB的脉冲噪声,图3给出了几种算法随快拍数N变化时的算法性能对比。图3表明,NC-ESPRIT-GCC算法在低快拍数的情况下性能依旧良好,这是因为本文算法利用了信号非圆性构造扩展阵列输出,利用了更多的数据信息从而提高了估计性能。同时由于受到脉冲噪声环境的影响,TLS-ESPRIT算法与CDNC-ESPRIT算法性能下降。
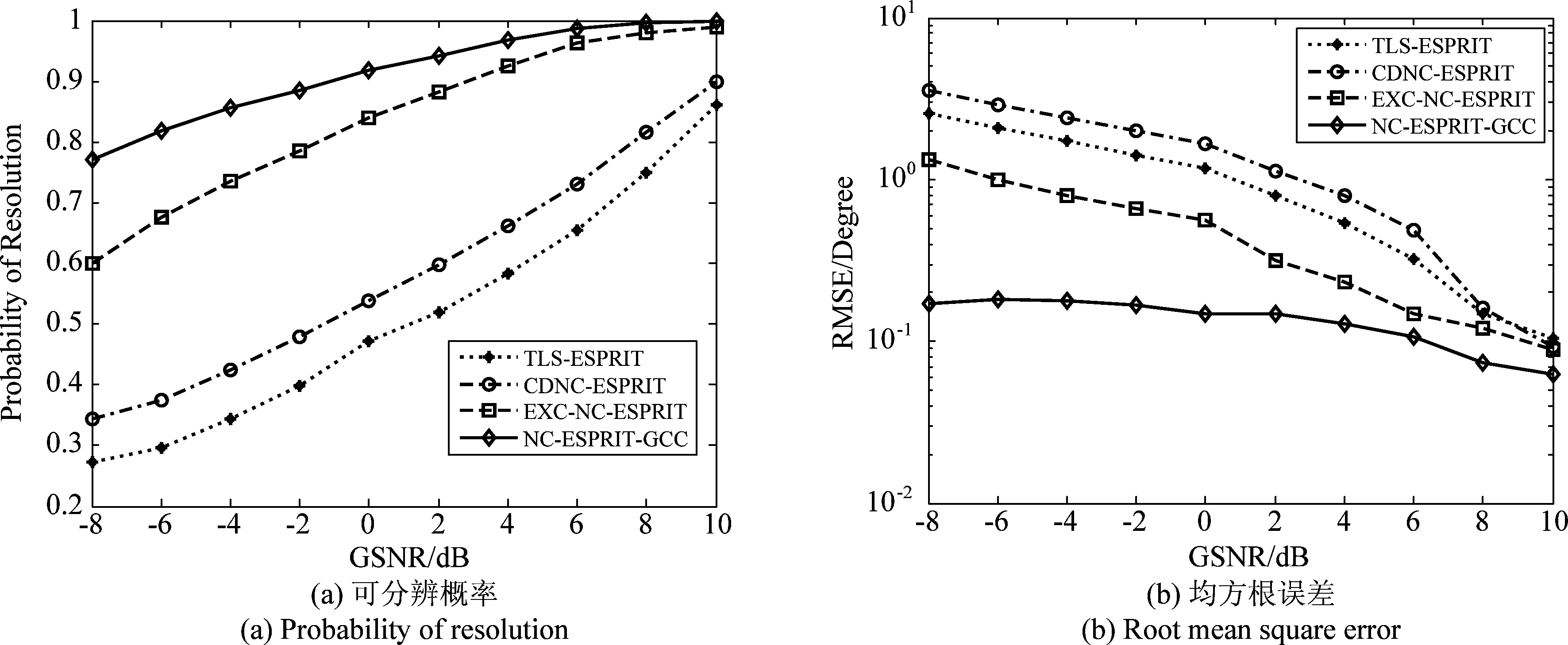
图1 算法性能随GSNR的变化
Fig.1 The performance of the algorithms versus GSNR
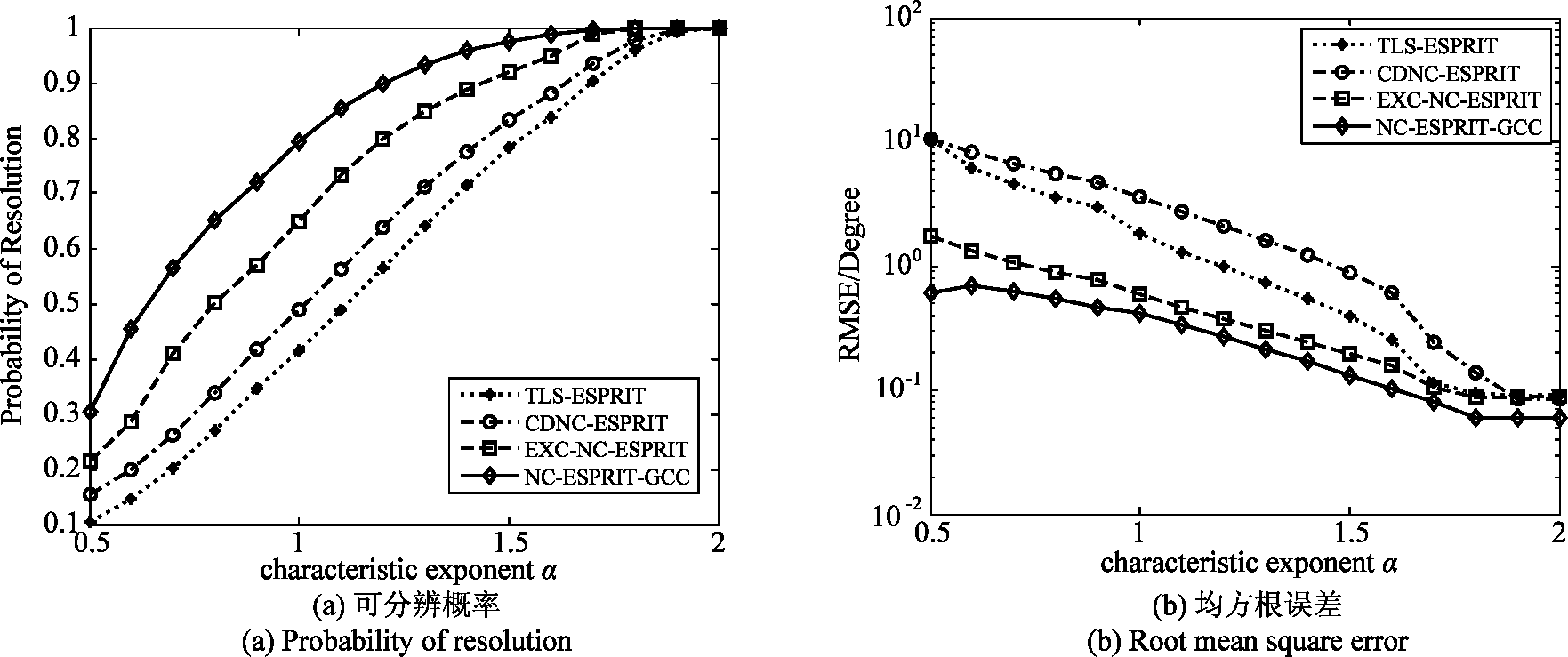
图2 算法性能随特征指数的变化
Fig.2 The performance of the algorithms versus characteristic exponent
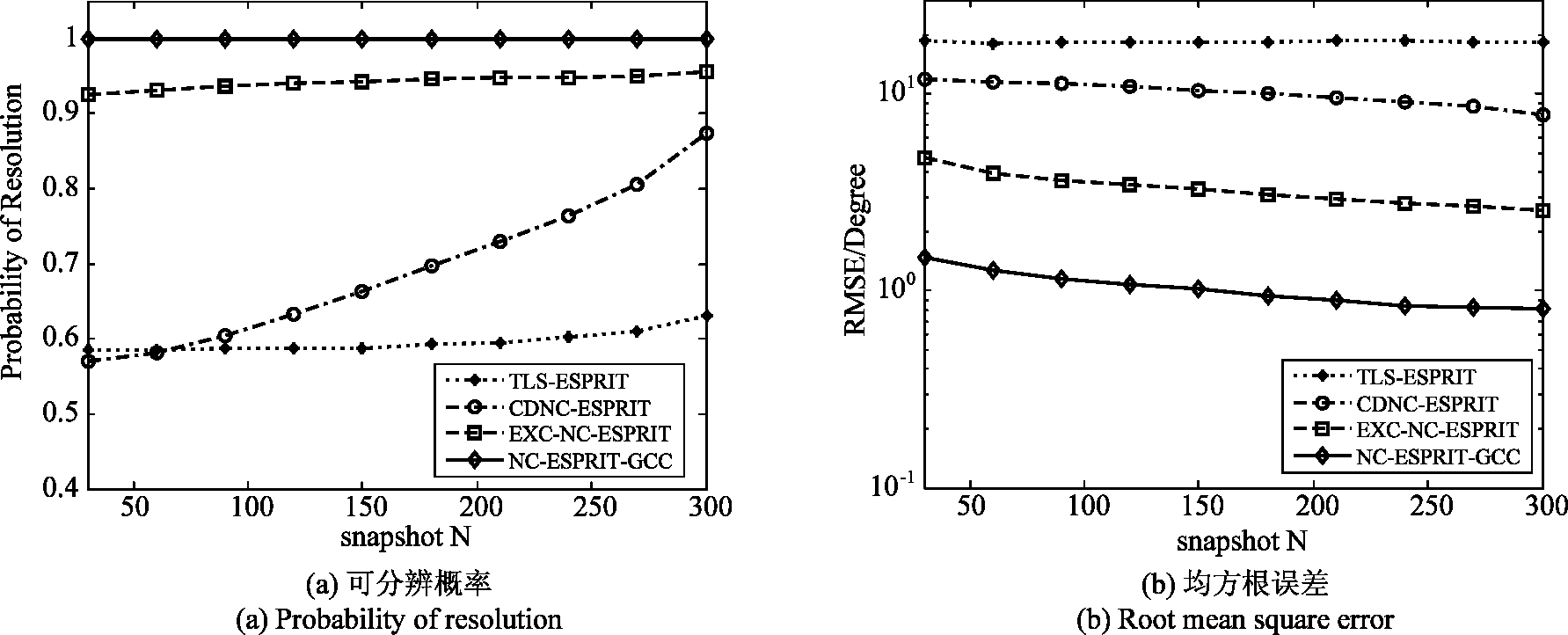
图3 算法性能随快拍数的变化
Fig.3 The performance of the algorithms versus number of snapshots
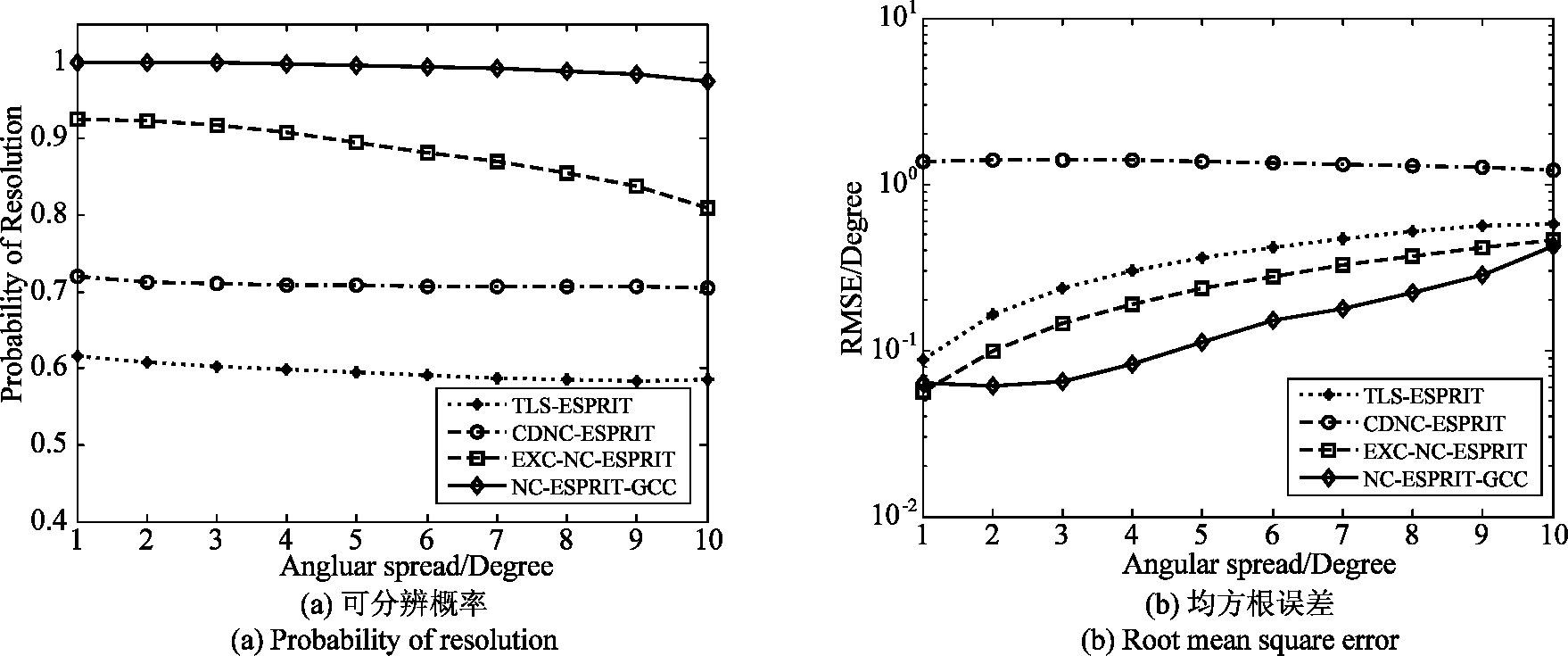
图4 算法性能随扩散角的变化
Fig.4 The performance of the algorithms versus the angular spread
实验4 扩散角的影响。无线通信的实际应用中,角度扩散可达到10°。本实验令两个信源的扩散角度一致。设定GSNR为0 dB且特征指数α=1.2的脉冲噪声,图4给出了几种算法随扩散角度变化时的算法性能对比。图4表明当扩散角度越大,即多径效应越强时,算法的估计性能均有所下降。CDNC-ESPRIT算法对扩散角度不敏感,表现稳健,但在脉冲噪声下算法误差较大。EXC-NC-ESPRIT算法由于采用点源模型在对分布源信号进行估计时性能不如NC-ESPRIT-GCC算法,对比其他算法,本文算法表现出较好的性能。
5 结论
本文为解决脉冲噪声环境下传统相干分布式非圆信源DOA估计算法性能退化的问题,提出了一种基于广义复相关熵的DOA估计新方法。利用信号的非圆性扩展阵列输出数据,令扩展阵列输出的GCC矩阵取代传统的二阶统计量,结合ESPRIT算法实现脉冲噪声下的DOA估计。仿真结果表明,本文提出的NC-ESPRIT-GCC算法能够有效抑制脉冲噪声且受噪声特征指数的影响较小,可以在较低信噪比的情况下可以获得更好地估计性能。
附录
定理1的证明如下:
将
代入(10),有
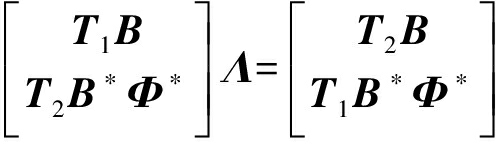
(13)
取第一行T1BΛ=T2B,该式说明B具有旋转不变性,这正是定理的假设,并已在文献[4]中给出证明。取第二行有
T2B*Φ*Λ=T1B*Φ*
(14)
Φ和Λ均为对角阵,可互换位置。因Φ*Φ=IP,对式(14)右乘Φ消去Φ*,得T2B*Λ=T1B*。再右乘Λ*,由Λ*Λ=IP得
T2B*=T1B*Λ*
(15)
对式(15)取共轭,有T1BΛ=T2B。综上,有J1BncΛ=J2Bnc。证毕。
[1] 韩英华, 汪晋宽, 宋昕, 等. 基于Schur-Hadamard积波束域传播因子的分布式信源参数联合估计[J]. 信号处理, 2008, 24(4): 534-537.
Han Yinghua, Wang Jinkuan, Song Xin, et al. Beamspace propagator method based on Schur-Hadamard product for joint parameter estimation of coherently distributed source[J]. Signal Processing, 2008, 24(4): 534-537.(in Chinese)
[2] 麻妍梅, 邓科, 殷勤业. 混合信源波达方向估计算法[J]. 信号处理, 2017, 33(11): 1468-1474.
Ma Yanmei, Deng Ke, Yin Qinye. Direction-of-arrival estimation for mixed sources[J]. Journal of Signal Processing, 2017, 33(11): 1468-1474.(in Chinese)
[3] Valaee S, Champagne B, Kabal P. Parametric localization of distributed sources[J]. IEEE Transactions on Signal Processing, 1995, 43(9): 2144-2153.
[4] Shahbazpanahi S, Valaee S, Bastani M H. Distributed source localization using ESPRIT algorithm[J]. IEEE Transactions on Signal Processing, 2001, 49(10): 2169-2178.
[5] Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995.
[6] Zhou Y, Fei Z, Yang S, et al. Joint angle estimation and signal reconstruction for coherently distributed sources in massive MIMO systems based on 2-D unitary ESPRIT[J]. IEEE Access, 2017, PP(99): 1-1.
[7] 代正亮, 巴斌, 张彦奎, 等. 回溯降维相干分布式非圆信号DOA快速估计[J]. 航空学报, 2017, 38(9): 269-278.
Dai Zhengliang, Ba Bin, Zhang Yankui, et al. Fast DOA estimation for coherently distributed noncircular sources by backtracking reduced dimension[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 269-278.(in Chinese)
[8] Yang X, Li G, Zheng Z, et al. 2D DOA estimation of coherently distributed noncircular sources[J]. Wireless Personal Communications, 2014, 78(2): 1095-1102.
[9] Wan L, Han G, Jiang J, et al. DOA estimation for coherently distributed sources considering circular and noncircular signals in massive MIMO systems[J]. IEEE Systems Journal, 2017, 11(1): 41- 49.
[10] Shao M, Nikias C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7): 986-1010.
[11] Liu T, Qiu T, Luan S. Cyclic correntropy: foundations and theories[J]. IEEE Access, 2018, 6: 34659-34669.
[12] Zhang J, Qiu T. The fractional lower order moments based ESPRIT algorithm for noncircular signals in impulsive noise environments[J]. Wireless Personal Communications, 2017, 96(7): 1673-1690.
[13] Steinwandt J, Roemer F, Haardt M, et al. R-dimensional ESPRIT-type algorithms for strictly second-order non-circular sources and their performance analysis[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4824- 4838.
[14] Santamaria I, Pokharel P P, Principe J C. Generalized correlation function: definition, properties, and application to blind equalization[J]. IEEE Transactions on Signal Processing, 2006, 54(6): 2187-2197.
[15] Guimaraes J P F, Fontes A I R, Rego J B A, et al. Complex correntropy: probabilistic interpretation and application to complex-valued data[J]. IEEE Signal Processing Letters, 2016, 24(1): 42- 45.
[16] 王鹏, 邱天爽, 金芳晓, 等. 脉冲噪声下基于稀疏表示的韧性DOA估计方法[J]. 电子学报, 2018, 46(7): 1537-1544.
Wang Peng, Qiu Tianshuang, Jin Fangxiao, et al. A robust DOA estimation method based on sparse representation for impulsive noise environments[J]. Acta Electronica Sinica, 2018, 46(7): 1537-1544.(in Chinese)
