1 引言
高斯过程(Gaussian process, GP)模型是一种有效的统计学习工具,可采用核方法和贝叶斯推理两类学习方式[1]。GP模型通过矩阵运算实现、结构清晰、模型的输出能提供概率信息[2],反映信号之间的时序特性。GP模型已被广泛应用在机器学习和模型识别中[3]。参数学习算法主要有极大似然估计(MLE)算法。
尽管GP模型具有诸多优势,但是在实际应用中依然存在着两个重要的问题:首先,高斯过程模型的协方差矩阵描述的是全体样本上的波动性,难以刻画分布在不同区域的多模态数据样本局部的波动性[4]。其次,学习参数时,需要对规模为N×N的协方差矩阵求逆,计算复杂度为O(N3),导致GP模型的计算效率较低[4]。为了解决GP模型中的这些问题,Tresp[5]于2000年提出了高斯过程混合模型。在此基础上,许多学者提出了不同形式的高斯过程混合模型。高斯过程混合模型主要包括样本输入X和样本输出Y,以及样本的类别标签Z。根据样本生成过程的不同,高斯过程混合模型可以分成两种形式:生成模型[6-7]和判别模型[8-9]。这两类模型的信息流动方向如下:判别模型“x→z→y”和生成模型“z→x→y”。相比于判别模型,生成模型有两大优势:第一,当缺失输入X时,可以通过输出Y反推出输入X;第二,样本输入X直观地反应样本输出的协方差。根据GP模型分量混合方式的不同,高斯过程混合模型也可以分成两类:基于输入空间上的混合,一般简称为MGP模型;基于输出空间上的混合,一般简称为mix-GP模型。本文所采用的高斯过程混合模型是基于输入空间混合的生成模型,因此在后文中称之为MGP模型。
学者常假定MGP模型中的均值函数恒为零,这样既减小了模型的计算量,又能够取得比较满意的结果。但是,在一些实际数据中,将均值函数设置为零过于粗糙,不能足够精确的展示数据的变化规律。Shi[10]首先提出了高斯过程函数回归(Gaussian process functional regression, GPFR)模型,通过B样条基函数的线性组合来表示均值函数,并在实验中取得了较好的结果。借助GPFR模型,Wu and Ma[11]提出了(mixture of GPFR, MGPFR)模型,即将MGP模型中的GP模型替换为GPFR模型。与高斯过程混合模型类似,高斯过程函数回归混合模型可根据高斯过程函数回归模型的混合方式分成输入方向的混合和输出方向的混合。前一种称之为MGPFR模型,后一种称之为mix-GPFR 模型。根据混合模型信息流动方向的不同可以分成生成模型和判别模型。在本文中涉及到的高斯过程函数回归混合模型是高斯过程函数回归模型在输入方向混合的生成模型,仍称之为MGPFR 模型。本文中的模型选择算法就是要选择出MGPFR模型中GPFR模型分量的个数。
在数据建模中,混合模型的模型选择是一个极其重要的问题。为解决这个问题,人们提出了如AIC,BIC,BYY等模型选择准则[12-14]。这些准则通过权衡对数似然函数和基于模型复杂度的惩罚项在高斯混合模型中得到了较好的模型选择结果。在mix-GP模型上,由于曲线族数据分布在统一的输入区间上,将曲线族数据分成不同的模式进行分类,这些准则也能取得了良好的结果。但在MGP模型上,由于样本点在输入空间的混合,而在各个GP 分量中,样本点间具有相关性,使得各个候选模型之间的对数似然函数的差异性较大,直接从样本进行模型选择是不可行的。由于对数似然函数的差异性较大,上述模型选择准则提供的惩罚项相对较小,上述准则倾向于选择较大的分量个数。针对这些问题,我们对零均值假设的MGP研究中提出了同步平衡准则(synchronously balancing criterion, SBC)[6],并在实验中取得了良好的结果[7]。这为本文的研究奠定了很好的理论基础。
实际上,在准则执行过程中,我们需要事先给定模型分量的候选集合。候选集合与模型选择正确率息息相关,当候选模型集合越大,模型选择正确率可能越高,计算效率越低,反之亦然。因此,有必要对自动模型选择算法进行探讨。目前,自动模型选择算法主要有:第一,基于贝叶斯学习算法,该算法非常依赖实现给定参数的先验分布;第二,采用Dirichlet过程[15]作为门限函数,但该算法的模型选择个数往往多于真实模型个数,降低了模型的泛化能力;第三,利用分合EM(Split and Merge, SMEM)算法[16]进行自动模型选择算法,该算法通过选择性执行分操作和合操作,实现动态模型选择。
MGPFR模型的参数学习算法主要有MCMC算法[17]、变分贝叶斯(VB)算法[18]和EM算法。当先验分布足够合理、样本个数趋于无穷时,MCMC算法能够得到足够精确的估计结果,但是该算法的计算效率较低[4]。VB假设参数和隐变量相互独立的条件太过粗糙,实验结果往往较差。EM算法是一种有效的学习混合模型的算法。由于MGPFR模型的Q函数过于复杂,往往需要在EM算法中加入某种近似策略,常用的近似策略主要有:变分EM算法、MCEM算法、硬分类(hart-cut) EM算法等。
Hard-cut EM算法[19]使用最大后验概率(MAP)原则将样本点分类到各个模型分量中。由于MGPFR模型中,大多数样本的后验概率近似呈现0-1分布的特征,在这些点上采用MAP原则分配样本,分类精度的降低可忽略。在少量的边缘点上采用MAP原则分类错误率较大,但是边缘点占比较低。所以,在MGPFR模型上采用hard-cut EM算法的总体精度仍在可接受范围内。
基于上述分析,本文首先将同步平衡准则推广到MGPFR模型,然后在hard-cut EM算法的框架下根据所推广的同步平衡准则建立MGPFR模型的模型选择和动态模型选择算法,并将其应用于曲线聚类分析上。
本文结构安排如下:第2节介绍GPFR模型和MGPFR模型;第3节推导MGPFR模型的模型选择准则,并建立动态模型选择算法;第4节给出动态模型选择算法的实验结果;第5节总结全文。
2 模型
2.1 GPFR模型
相比于GP模型,GPFR模型则有效地利用了均值函数。GPFR模型的均值函数使用一组B样条基函数φ={φ1(x),…,φh(x)}的线性组合来表示,即m(x)=φb,其中b是系数向量。y(x)是一个GPFR模型,则其在数学上定义如下:
y(x)=m(x)+τ(x)
(1)
其中τ(x)～GP(0,K(x,x′))。K(x,x′)是协方差函数,在本文中,我们则采用平方指数(Squared Exponential, SE)协方差函数:
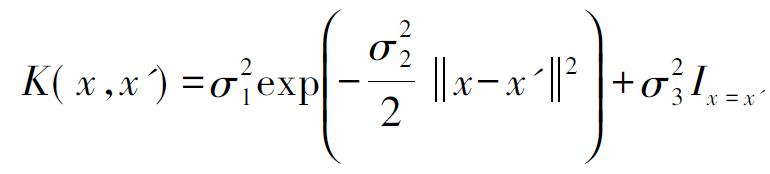
令参数为
那么,GPFR模型的参数就可以表示为(θ,b)。实际上对于这个模型,我们使用MLE即可有效地完成其参数学习。
2.2 MGPFR模型
假设曲线族数据集包含M条曲线(或时间序列)D={(xmn,ymn)|m=1,…,M;n=1,…,N},来自于包含有C个GPFR模型的MGPFR模型。每个GPFR模型表示为GPFRc,那么,MGPFR模型可以由以下三步骤描述:
1.引入隐变量
定义如下:
(2)
其中
2.在
的条件下,样本输入xmn服从均值为μc,协方差为
的均匀分布:
(3)
3.定义
为第m条曲线输入第c个GPFR模型的样本标号集合
为相应的输入输出。那么,
就可以定义第c个GPFR模型如下:
(4)
其中m=1,…,M,c=1,…,C。记MGPFR模型的参数集合{Θ,Ψ,b},其中
有了上面的定义,我们推导出MGPFR的对数似然函数
log p(Θ,Ψ,b|X,Y,Z)=
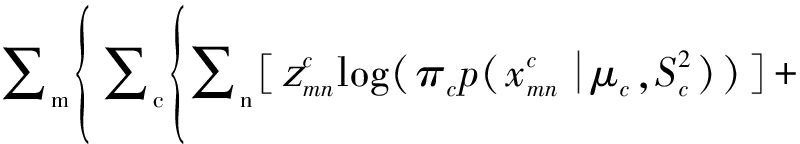
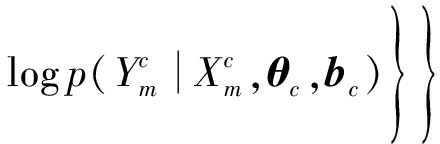
(5)
从上面三个步骤可以看出,MGPFR模型的信息流动方向为“zmn→xmn→ymn”,具备上述引言中提到的生成模型的优点。
3 算法设计
本文中采用的基本的参数学习框架为hard-cut EM算法,具体算法执行过程可参照文献[11,17]。
3.1 MGPFR模型的模型选择准则
在这一小节中,我们通过MGP模型的模型选择准则SBC推导出MGPFR模型的模型选择准则。有了上述的MGPFR模型的对数似然函数,我们将其变换成如下形式:
log p(Θ,Ψ,b|X,Y,Z)=∑m{logLMGPFRm}
(6)
其中logLMGPFRm表示如下:
logLMGPFRm=
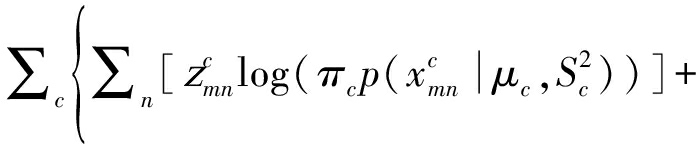
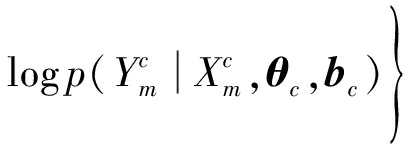
(7)
logLMGPFRm的形式和MGP模型的对数似然函数结构相似,而且M条数据是相互独立的。因此,我们将MGP模型的模型选择准则应用到M条曲线族数据的形式如下:
SBCMGPFR(C)=∑m{logLMGPFRm-δNmlogC}
(8)
不同于MGP模型,MGPFR模型中有M条数据。模型学习将更加稳定,对数似然函数的变化率也将更小,惩罚项系数δ的合理区间也将更小,这在后面的实验中得到了验证。
3.2 MGPFR模型的模型选择算法
结合MGPFR模型的模型选择准则和hard-cut EM算法,我们设计了MGPFR模型的模型选择算法,并选择出惩罚系数δ的合理区间。给定模型分量个数候选集合(Candidate Set, CS)。MGPFR模型选择算法可以通过以下步骤完成:
1.选择CS里的每一个元素c,执行hard-cut EM算法,并记录参数学习结果Θc,Ψc,bc和对数似然函数logLMGPFRc。
2.将步骤1中得到的logLMGPFRc应用到SBC中,计算每一个分量个数c∈CS的SBC目标函数:
SBCMGPFR(c)=∑m{logLMGPFRm-δNmlogc}
(9)
3.选择使得SBC目标函数最大的c*作为模型选择结果:
c*=arg maxc∈CS{SBCMGPFR(c)}
(10)
通过几下几个步骤则可获得SBC惩罚项系数的合理区间:首先,在MGPFR模型的模拟数据上,使用参数学习算法(hard-cut EM算法)独立重复试验多次,并记录每次参数学习结果的对数似然值(log-likelihood);其次,在实数轴上寻找出使得SBC准则选择正确模型个数的次数最多的惩罚项系数值;最后,将这些惩罚项系数所形成的区间设置为delta的合理区间。动态模型选择算法中的delta可在合理区间中取值。
3.3 MGPFR模型的动态模型选择算法
通过模型选择算法得到惩罚项系数的合理区间。基于分合EM算法,建立了MGPFR模型的动态模型选择算法——动态模型选择(Dynamic Model Selection, DMS)算法。算法涉及分准则、合准则和分操作、合操作。分准则的目的则是分裂“聚合度”最低的高斯过程函数回归分量,而合准则的目的是合并“相似度”最高的两个高斯过程函数回归分量。为此,我们选择了以下形式的分准则和合准则:利用两分量的后验概率分布向量的距离来刻画其“相似度”,而利用分量中的均样本对数似然函数值刻画分量的“聚合度”。
利用GPFR模型分量间的后验分布向量距离定义合准则
(11)
其中
是第m条曲线上样本点在第j个GPFR模型分量上的后验概率分布向量。Omerge(i, j)越大,说明两GPFR模型分量相似度越高,越可能被合并成一个GPFR模型分量。利用GPFR模型分量对数据的平均似然函数定义分准则
(12)
其中
是第m条曲线上第k个GPFR模型分量的对数似然函数,Nk为第k个GPFR模型分量的样本个数。平均对数似然函数值越小,该GPFR模型分量越趋向于被分成两个GPFR模型分量。通过上述两个准则选择出来执行分合操作的候选GPFR分量组。
假设当前混合模型中包含Ctemp个GPFR模型分量。分操作就是将分准则选出来的第k个GPFR模型一分为二,执行Ctemp+1的hard-cut EM算法,并判断是否接受分操作。合操作就是将合准则选出来的第i个和第j个GPFR模型合二为一,执行Ctemp-1的hard-cut EM算法,并判断是否接受合操作。
综上,MGPFR模型的动态模型选择算法可以描述如下:
1.初始化,设置初始分量个数Ctemp,随即设置参数{Θtemp,Ψtemp,btemp};
2.以{Θtemp,Ψtemp,btemp}为初始化,执行分量个数为Ctemp的hard-cut EM算法,计算
3.应用分合准则,选择出执行分合操作的GPFR模型分量组;
4.执行合操作,如果接受,返回步骤3;否则执行步骤5;
5.执行分操作,如果接受,返回步骤3;否则算法停止,并记录学习结果。
4 实验结果与分析
首先,在模拟数据上,通过模型选择算法寻找惩罚项系数δ的合理区间,并将之应用在动态模型选择算法中;其次,将动态模型选择算法应用在实际数据中。
4.1 模拟数据实验
生成了27个模拟数据[C,M,N]∈[3,4,5]×[50,70,100]×[200,250,300],其中C,M,N分别表示模型分量数、曲线条数和样本点数。各个GPFR模型的均值函数是连续的,并且相邻两个GPFR模型的均值函数是连续的。如图1所示C=4的MGPFR模型的均值函数图,其中横坐标表示自变量,纵坐标表示均值函数。在不同的区间上均值函数的结构趋势有差异。在此均值函数的作用下,生成的MGPFR模型的模拟数据也具有近似的走势形态,如图2所示,其中x轴表示输入X,y轴表示输出Y。
在27个模拟数据上,分别重复独立执行MGPFR模型的模型选择算法28次,统计算法模型选择正确率与惩罚项系数之间的关系。图3展示的是C=5,M=100,N=200。从图3中,其中横坐标表示惩罚项系数delta,纵坐标表示模型选择正确率。我们看到δ=0时,选择正确率仍然为100%,这说明MGPFR模型的对数似然函数具有足够的差异性;多条曲线数据更能体现出混合模型的信息,学习更稳定,在MGPFR模型上合理的惩罚项系数不像MGP模型的惩罚项系数那样大。上述结论在其他的模拟数据上也有相似的体现,综合27个模拟数据的模拟选择正确率,我们选择惩罚项系数的合理区间为δ∈(0.2,0.6)。
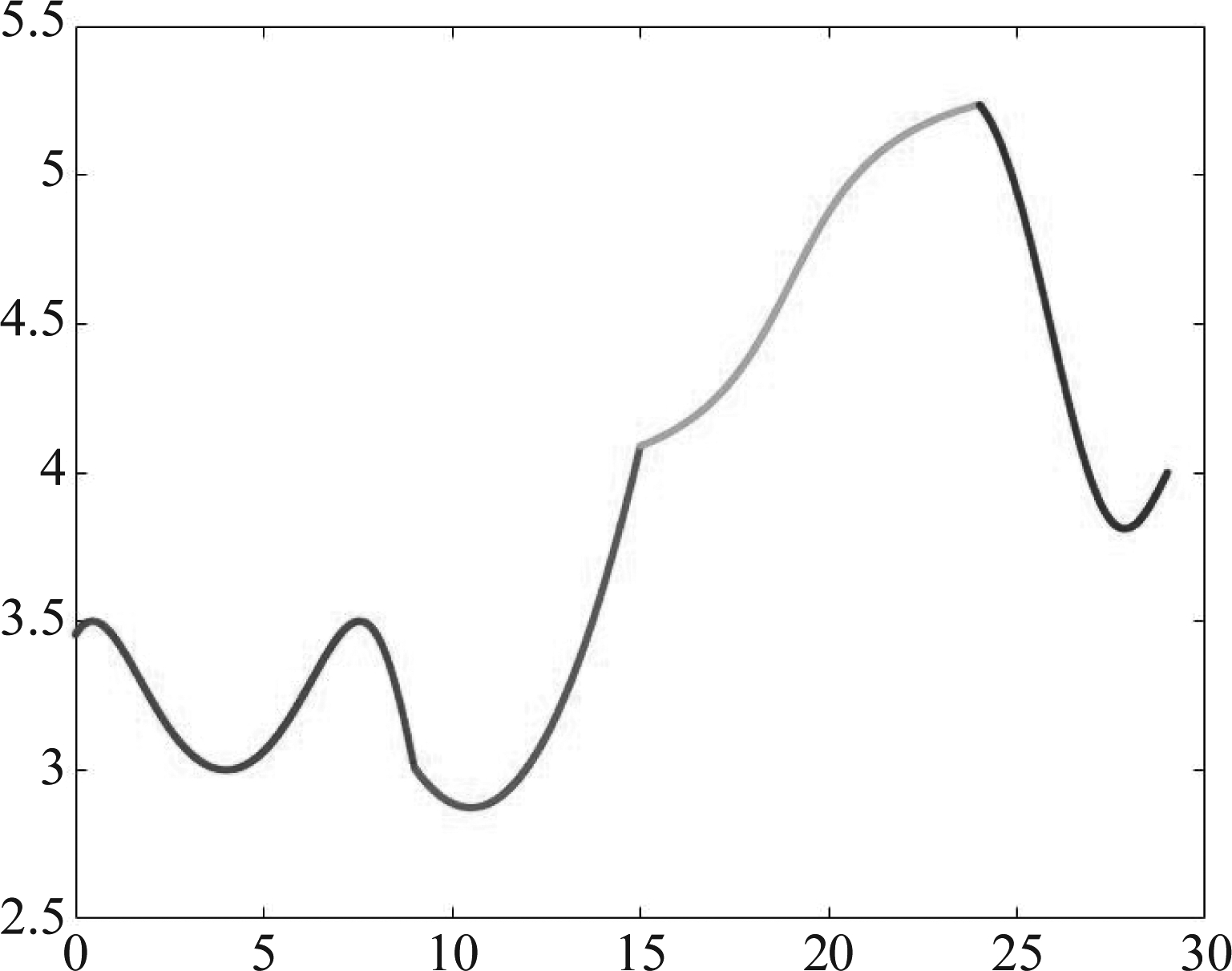
图1 C=4的MGPFR模型的均值函数
Fig.1 The mean function of MGPFR model with C=4
图2 C=4的MGPFR模型的模拟数据,其中M=100,N=200
Fig.2 Simulation data of the MGPFR model with C=4, M=100, and N=200
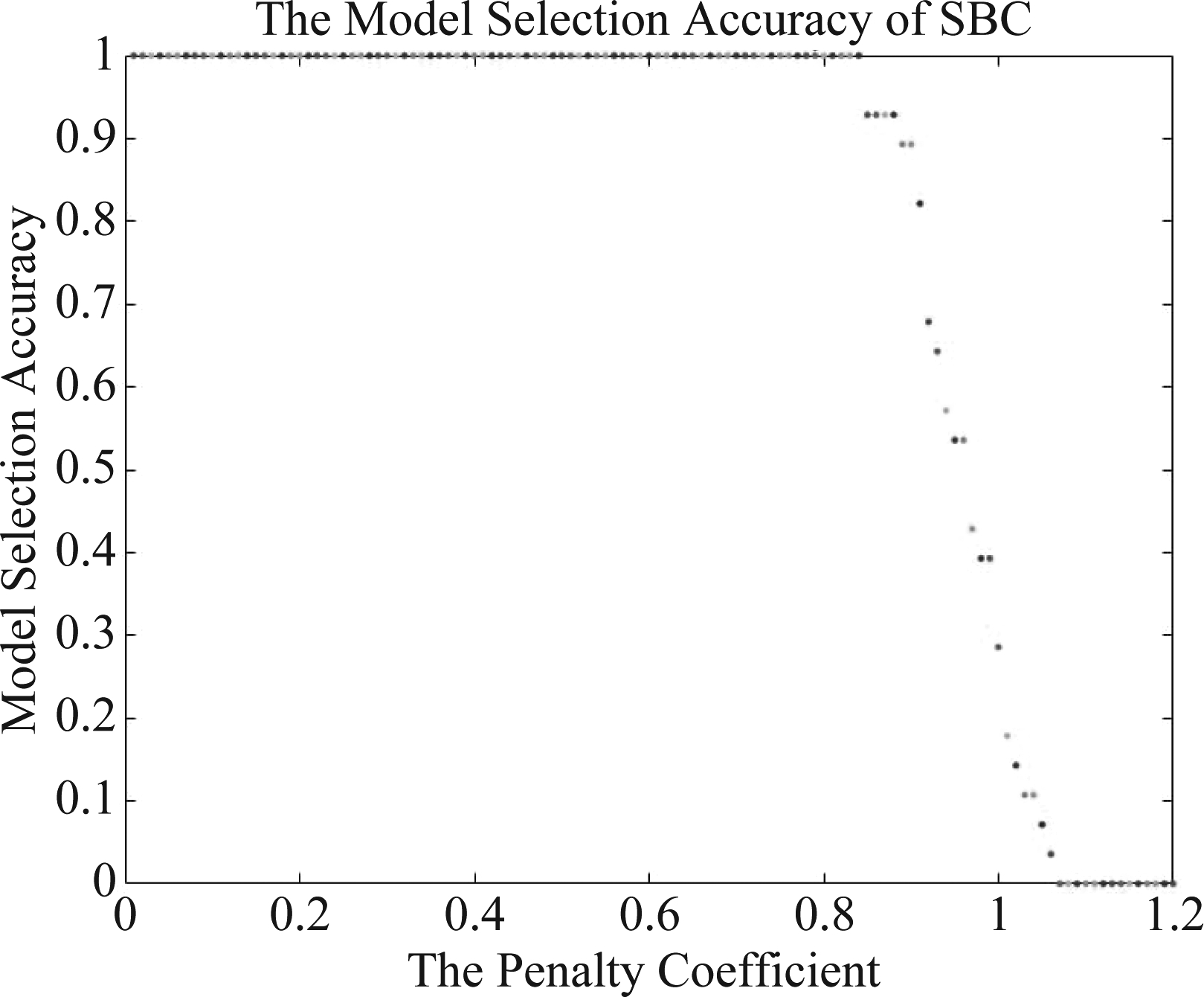
图3 惩罚项系数与模型选择正确率的关系
Fig.3 The relationship between the penalty coefficient and the correct rate of model selection
在模型选择正确的情况下,测试样本分类正确率如表1所示。在C相同的条件下,M相同的情况下,增加曲线条数,测试样本的样本分类正确率呈上升趋势;N相同的情况下,增加曲线上的样本数,测试样本的分类正确率也呈上升趋势。这是因为无论曲线条数的增加或者曲线中样本点的增加,都增强了MGPFR模型对数据的描述能力,这与我们的基本认知相符。
表1 测试样本的分类正确率
Tab.1 Classification accuracy on test data set
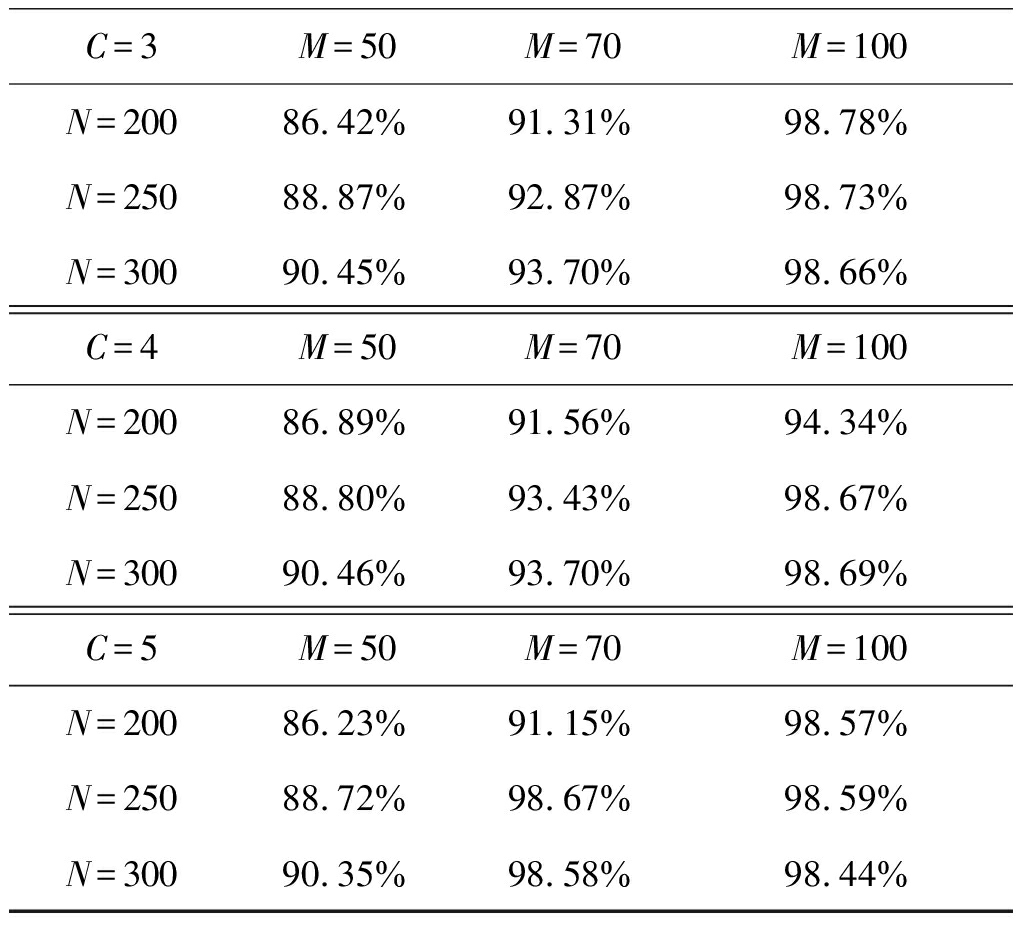
C=3M=50M=70M=100N=20086.42%91.31%98.78%N=25088.87%92.87%98.73%N=30090.45%93.70%98.66%C=4M=50M=70M=100N=20086.89%91.56%94.34%N=25088.80%93.43%98.67%N=30090.46%93.70%98.69%C=5M=50M=70M=100N=20086.23%91.15%98.57%N=25088.72%98.67%98.59%N=30090.35%98.58%98.44%
在上个实验中,我们得到了惩罚项系数的合理区间为δ∈(0.2,0.6)。在合理区间上随机选取11个惩罚项系数为δ,对每一个为δ,在27个模拟数据上分别执行动态模型选择算法28次。模型选择正确率由表2展示。测试样本分类正确率如表3所示。
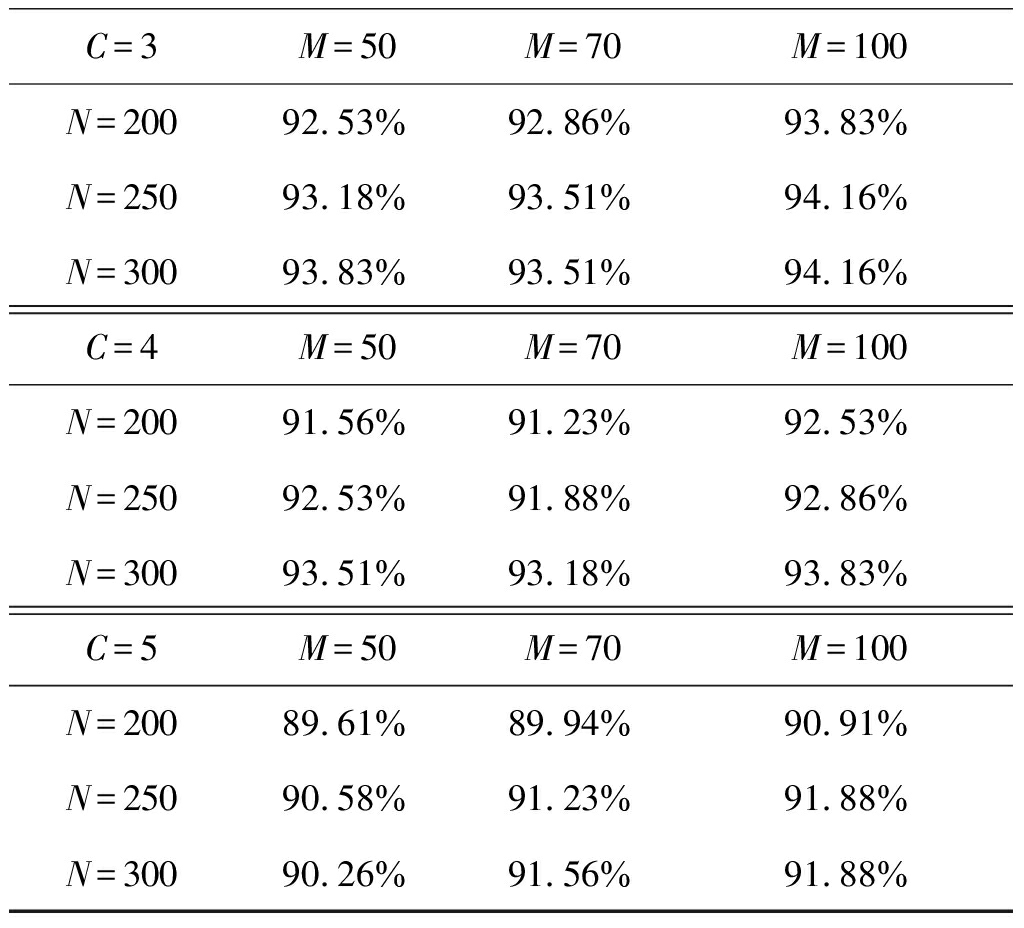
从表2中,我们可以看出,动态模型选择算法得到了很高的模型选择正确率。在C相同的条件下,固定N,模型选择正确率随着M的增加而增大;固定M模型选择正确率随着N的增大而增大,这和前面测试样本分类正确率得到的结论一致。之所以没有出现图3中展示的100%的模型选择正确率,是因为动态模型选择算法找到SBC的“凸结构”的顶点就停止运行,并返回模型选择结果。返回的“凸结构”可能是局部极值,而该算法没有跳出这种局部极值的能力。模型选择算法是在固定模型分量个数上的遍历,这使得该算法较大可能跳过局部“凸结构”,从而得到正确的模型选择。但前一种算法浪费大量计算资源,计算效率不及动态模型选择算法。动态模型选择算法也获得了很高的正确率,因此,综合计算效率和正确率,动态模型选择算法有优势。
表2 DMS算法在各个模拟数据上的模型选择正确率
Tab.2 Model selection accuracy of the DMS algorithm on various simulation data set
C=3M=50M=70M=100N=20092.53%92.86%93.83%N=25093.18%93.51%94.16%N=30093.83%93.51%94.16%C=4M=50M=70M=100N=20091.56%91.23%92.53%N=25092.53%91.88%92.86%N=30093.51%93.18%93.83%C=5M=50M=70M=100N=20089.61%89.94%90.91%N=25090.58%91.23%91.88%N=30090.26%91.56%91.88%
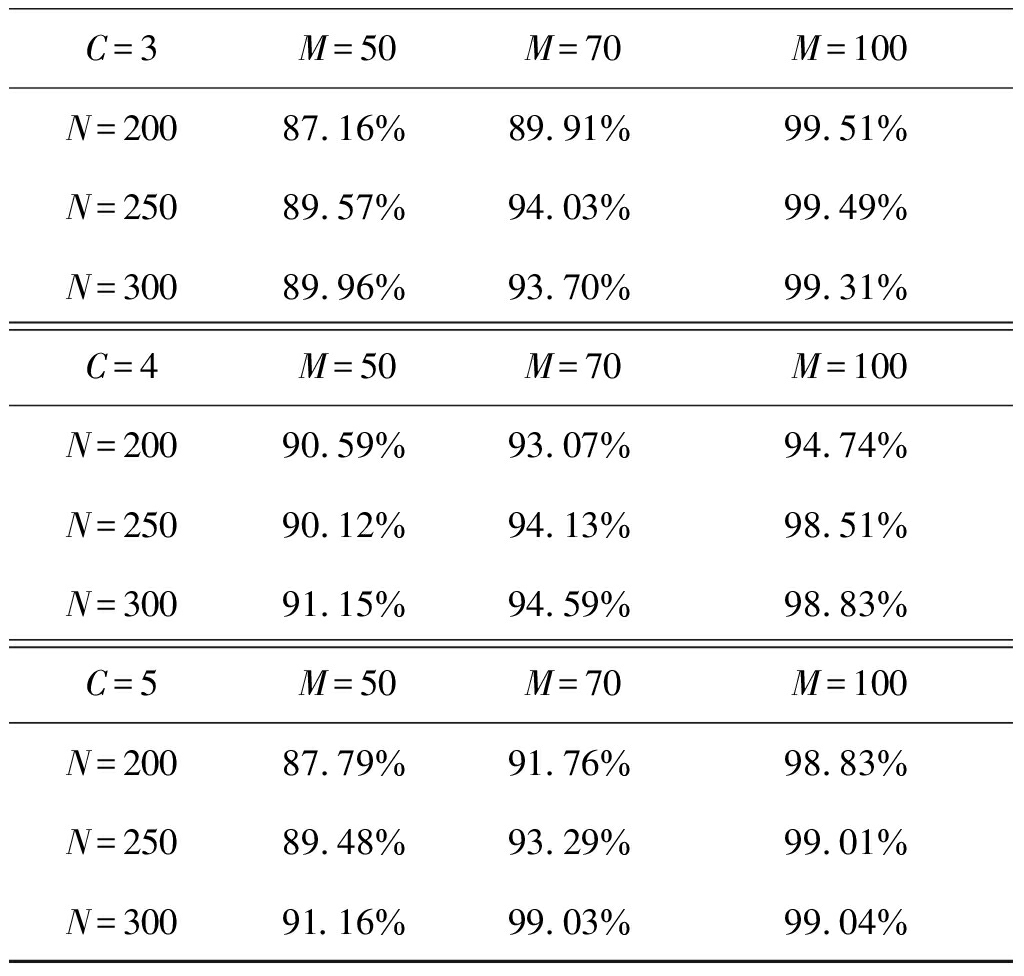
表3 DMS算法的测试样本分类正确率
Tab.3 Classification accuracy of the DMS algorithm on test data set
C=3M=50M=70M=100N=20087.16%89.91%99.51%N=25089.57%94.03%99.49%N=30089.96%93.70%99.31%C=4M=50M=70M=100N=20090.59%93.07%94.74%N=25090.12%94.13%98.51%N=30091.15%94.59%98.83%C=5M=50M=70M=100N=20087.79%91.76%98.83%N=25089.48%93.29%99.01%N=30091.16%99.03%99.04%
比较表1和表3,在相同的(C,M,N)的条件下,动态模型选择算法的样本分类正确率总体上高于模型选择算法的样本分类正确率。这是因为在学习的过程中,充分利用包含相邻分量个数MGPFR模型的结构相似性,加入分合操作,有效地躲避EM算法中的局部解,从而获得了更有的分类结果。
图4展示了C=3时,两种算法的对数似然函数的对比,其中分图中横坐标表示的是实验序号,纵坐标表示的是对数似然值,红色线条表示动态模型选择算法的对数似然函数值,蓝色线条代表模型选择算法的对数似然函数值。模拟数据包含70 条曲线,从上到下每一条曲线的样本点分别为300、250、200。从图4看到动态模型选择算法的对数似然函数值总体在模型选择算法的对数似然函数值上方,这说明动态模型选择算法学习更有效。
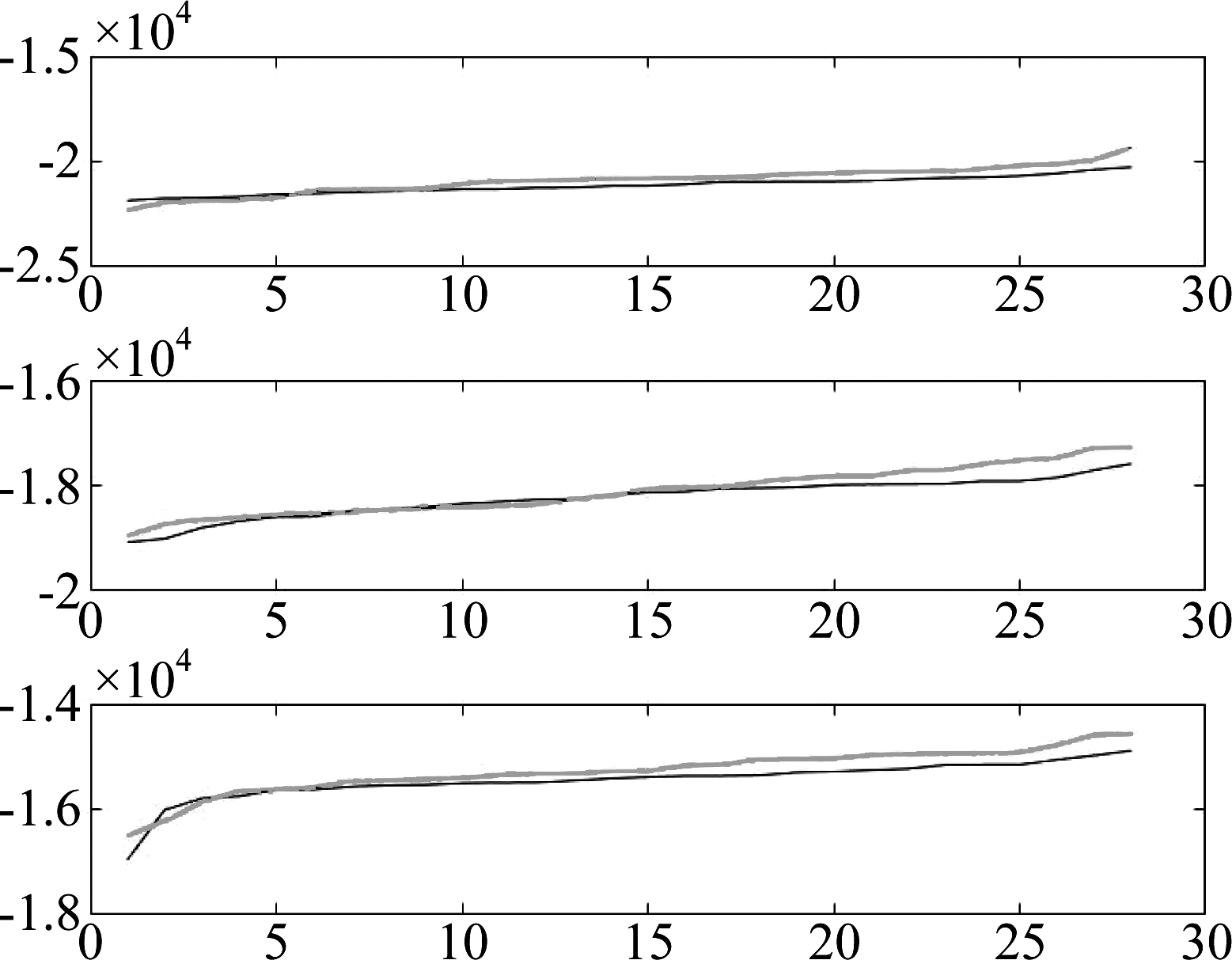
图4 两种算法的对数似然函数值对比
Fig.4 The Comparison of Log-likelihoods of the proposed two algorithms
4.2 实际数据实验
在这一节中,我们将动态模型选择算法应用在曲线族数据的分线分类上。我们在两组数据上实验:第一组是小孩身高数据[20],第二组是天气数据[21]。第一组数据记录了54个女孩和36个男孩从1岁到18岁的身高曲线。每条曲线31个点,其中21个点用作训练,10个点用作测试,如图5所示。第二组数据记录了加拿大两个大区(记作第一大区、第二大区)27个气象站的温度曲线,这两个大区的数据的重叠度较大,有些曲线的类别信息没有不太清晰。每条曲线73个点,其中36点用作训练37个点用作测试。
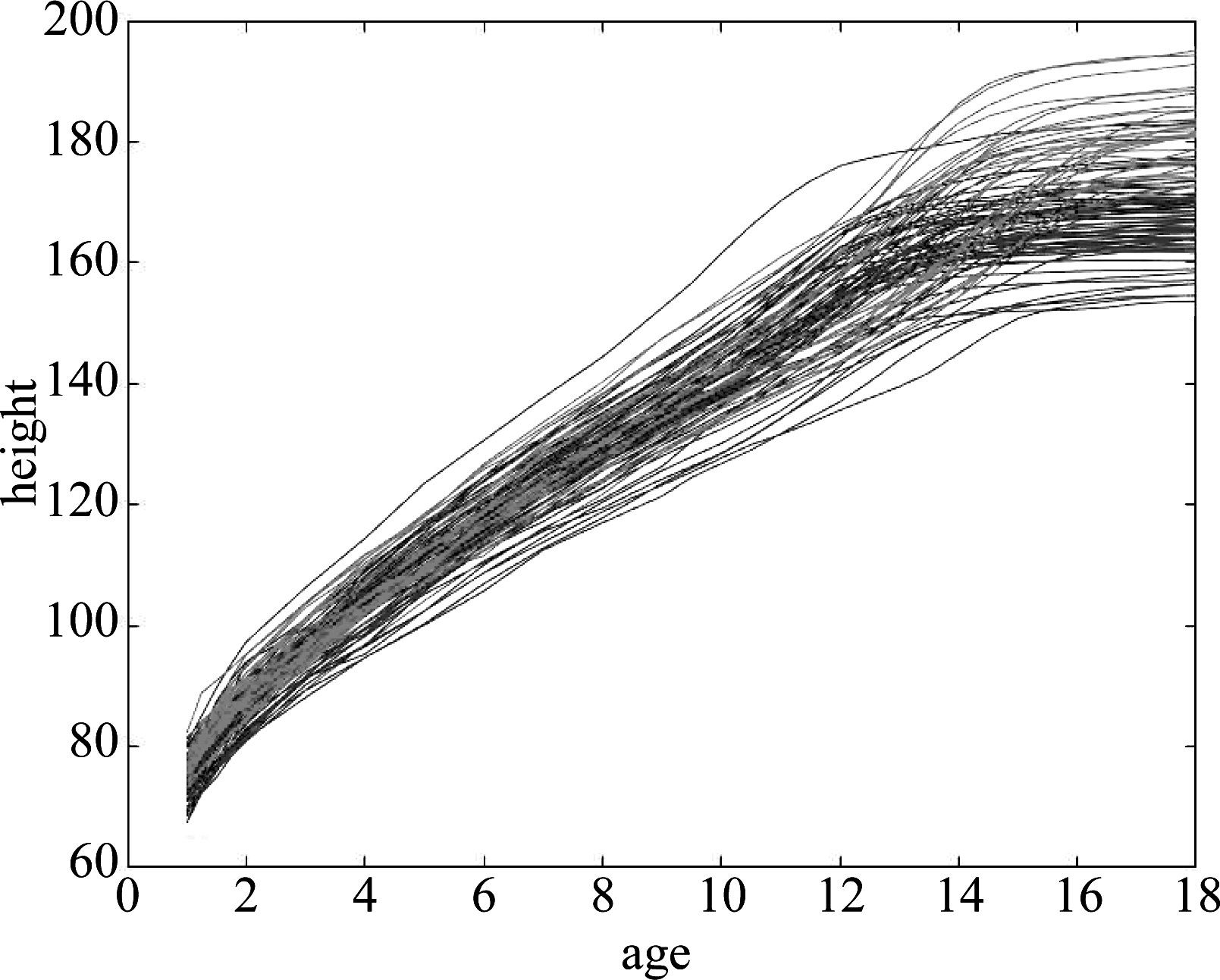
图5 伯克利小孩成长身高曲线
Fig.5 Berkeley Growth Study data
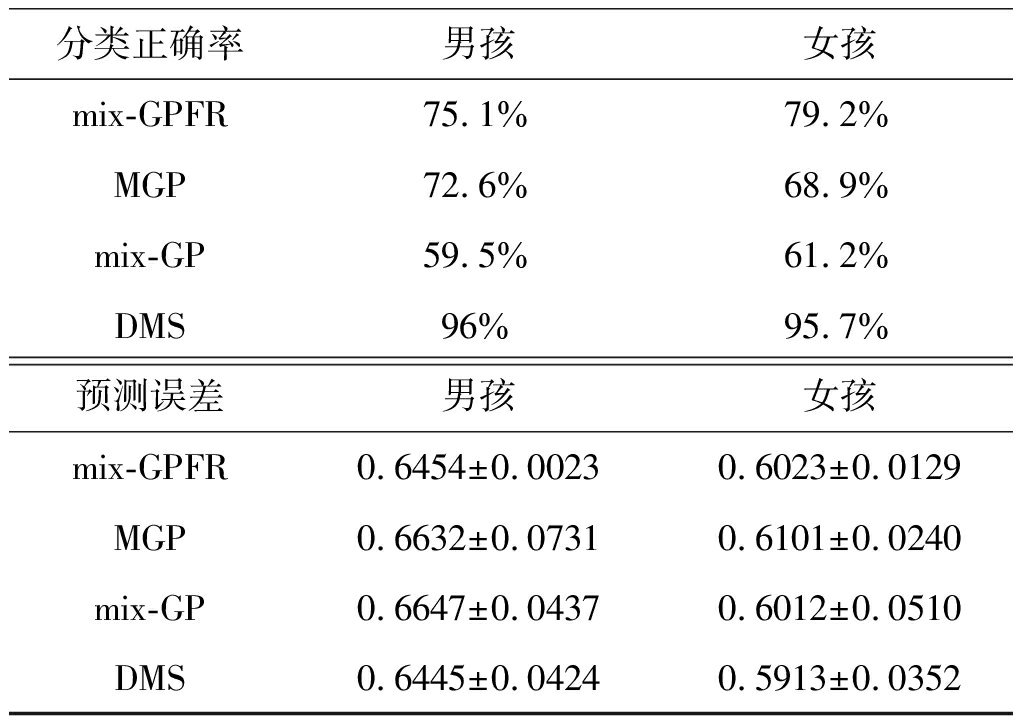
在第一组数据上执行动态模型选择算法和对比算法mix-GPFR、MGP、mix-GP,重复1000次实验。动态模型选择算法在男孩、女孩两类数据上都是1000 次选择了模型个数为2,显示了动态模型选择算法的稳定性。在年龄较小的阶段,身高增长得快,在年龄较大的时候,身高增长的较慢。在男孩的数据中,两个模型的分割点稳定在14 岁,在女孩的数据上,两个模型的分割点稳定在13 岁。这样的两个分割点在生理上能够得到解释:女性发育的早,男性发育的晚。表4展示了各算法的曲线分类正确率以及测试样本的预测误差。从表4展示结果可以看出,使用动态模型选择算法能够选择出对数据表达更加准确的MGPFR模型,从而使得MGPFR模型能够在曲线分类正确率以及测试样本上的预测误差都取得了比其他算法更加可靠精确的实验结果。
表4 各算法的曲线分类正确率以及测试样本的预测误差
Tab.4 The Comparison of curve classification correction rate and prediction error of each algorithm
分类正确率男孩女孩mix-GPFR75.1%79.2%MGP72.6%68.9%mix-GP59.5%61.2%DMS96%95.7%预测误差男孩女孩mix-GPFR0.6454±0.00230.6023±0.0129MGP0.6632±0.07310.6101±0.0240mix-GP0.6647±0.04370.6012±0.0510DMS0.6445±0.04240.5913±0.0352
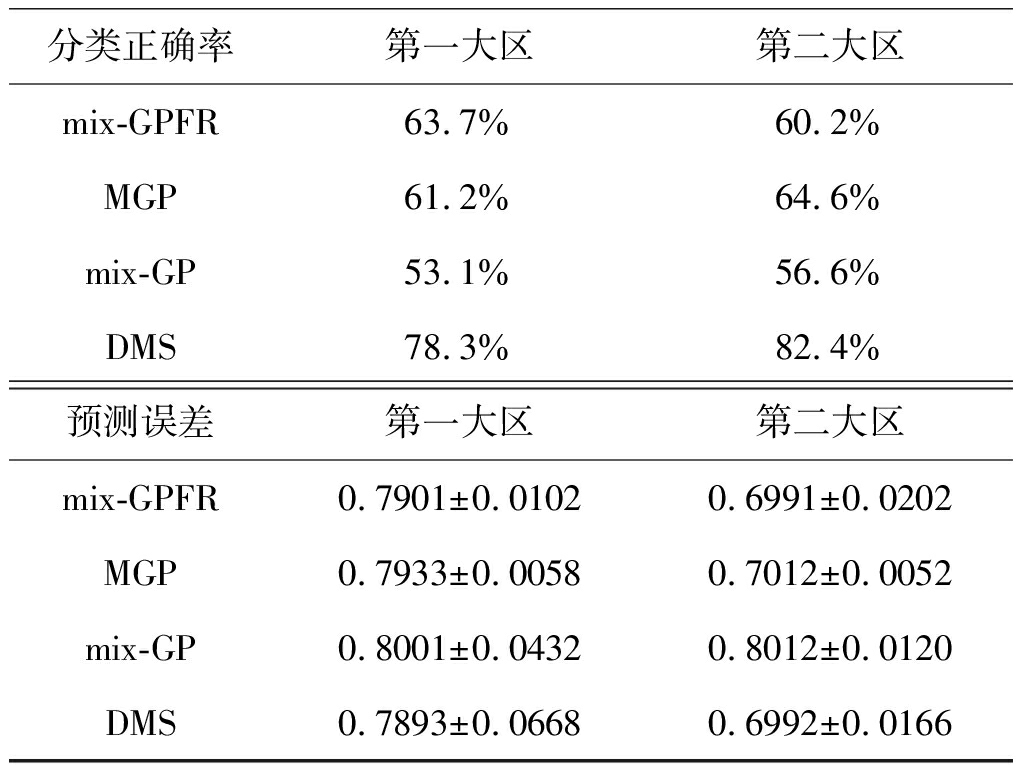
在第二组数据上执行动态模型选择算法和对比算法mix-GPFR、MGP、mix-GP,重复100次实验。表5展示了各算法的测试曲线的分类正确率与测试样本的预测误差。与第一组数据一样,无论在曲线分类正确率上,还是在测试样本的预测误差上,我们的算法都取得了最好的实验结果,并且优势较大。
表5 新算法和传统算法的曲线分类正确率以及测试样本的预测误差
Tab.5 Curve classification correction rates and prediction errors of the proposed algorithm and conventional algorithms
分类正确率第一大区第二大区mix-GPFR63.7%60.2%MGP61.2%64.6%mix-GP53.1%56.6%DMS78.3%82.4%预测误差第一大区第二大区mix-GPFR0.7901±0.01020.6991±0.0202MGP0.7933±0.00580.7012±0.0052mix-GP0.8001±0.04320.8012±0.0120DMS0.7893±0.06680.6992±0.0166
5 结论
MGP模型是一种有效的统计学习工具。在一定情况下,我们可假设其高斯过程的均值函数为零,并且MGP模型能够得到较满意的实验结果。但在许多情况,这样的假设是粗糙,我们则需要借助于B样条基函数将MGP模型推广到MGPFR模型。为了解决MGPFR模型的模型选择问题,本文从MGP模型的模型选择准则SBC出发,推导出了MGPFR模型的模型选择准则。进一步,我们结合hard-cut EM算法和模型选择准则建立了MGPFR模型的模型选择算法和动态模型选择算法。这两个算法在模拟数据上取得了较高的模型选择正确率和样本分类正确率。同时,我们将动态模型选择算法应用在曲线分类问题上,相对比其他算法,我们的算法取得了最好的曲线分类正确率和测试样本的预测误差。
[1] Murphy K P. Machine Learning: A Probabilistic Perspective[M]. MIT Press, 2012: 22-71.
[2] MacKay D J C. Introduction to Gaussian processes[J]. NATO ASI Series F Computer and Systems Sciences, 1998, 168: 133-166.
[3] Snelson E, Ghahramani Z, Rasmussen C E. Warped gaussian processes[C]∥Advances in Neural Information Processing Systems, 2004: 337-344.
[4] Yuan C, Neubauer C. Variational mixture of Gaussian process experts[C]∥Advances in Neural Information Processing Systems, 2009: 1897-1904.
[5] Tresp V. Mixtures of Gaussian processes[C]∥Advances in Neural Information Processing Systems, 2001: 654- 660.
[6] Zhao L, Chen Z, Ma J. An effective model selection criterion for mixtures of gaussian processes[C]∥International Symposium on Neural Networks. Springer, Cham, 2015: 345-354.
[7] Zhao L, Ma J. A dynamic model selection algorithm for mixtures of Gaussian processes[C]∥Signal Processing(ICSP), 2016 IEEE 13th International Conference on. IEEE, 2016: 1095-1099.
[8] Ross J, Dy J. Nonparametric mixture of Gaussian processes with constraints[C]∥International Conference on Machine Learning, 2013: 1346-1354.
[9] Stachniss C, Plagemann C, Lilienthal A J, et al. Gas distribution modeling using sparse Gaussian process mixture models[C]∥Robotics: Science and Systems Conference 2008, Zürich, Switzerland, June 25-28. MIT press, 2008: 310-317.
[10] Shi J Q, Murray-Smith R. Hierarchical Gaussian process mixtures for regression[J]. Statistics and Computing, 2005, 15(1): 31- 41.
[11] Wu D, Ma J. A Two-Layer Mixture Model of Gaussian Process Functional Regressions and Its MCMC EM Algorithm[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4894- 4904.
[12] Akaike H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.
[13] Schwarz G. Estimating the dimension of a model[J]. The Annals of Statistics, 1978, 6(2): 461- 464.
[14] Xu L. Bayesian Ying-Yang system, best harmony learning, and five action circling[J]. Frontiers of Electrical and Electronic Engineering in China, 2010, 5(3): 281-328.
[15] Rasmussen C E, Ghahramani Z. Infinite mixtures of Gaussian process experts[C]∥Advances in Neural Information Processing Systems, 2002: 881- 888.
[16] Ma J, He Q. A dynamic merge-or-split learning algorithm on gaussian mixture for automated model selection[C]∥International Conference on Intelligent Data Engineering and Automated Learning. Springer, Berlin, Heidelberg, 2005: 203-210.
[17] Ohishi Y, Mochihashi D, Kameoka H, et al. Mixture of Gaussian process experts for predicting sung melodic contour with expressive dynamic fluctuations[C]∥Acoustics, Speech and Signal Processing(ICASSP), 2014 IEEE International Conference on. IEEE, 2014: 3714-3718.
[18] Michalis K. Titsias. Variational heteroscedastic Gaussian process regression[C]∥International Conference on International Conference on Machine Learning, 2011: 841- 848.
[19] Chen Z, Ma J, Zhou Y. A precise hard-cut EM algorithm for mixtures of Gaussian processes[C]∥International Conference on Intelligent Computing. Springer, Cham, 2014: 68-75.
[20] Jones H E, Bayley N. The Berkeley growth study[J]. Child Development, 1941: 167-173.
[21] López-Pintado S, Romo J. On the concept of depth for functional data[J]. Journal of the American Statistical Association, 2009, 104(486): 718-734.
