1 引言
鬼成像(Ghost Imaging, GI)[1-3],又称关联成像(Correlated Imaging),是通过对信号光路和参考光路进行符合实现成像,是一种非定域成像。相比于传统成像,鬼成像对环境干扰的抵抗能力更强,因此鬼成像受到了广泛的应用[4-5]。
鬼成像最初是在1995年,由Pittman等人[6-7]基于量子纠缠光源实现的。2002年,Bennink等人[8-9]使用经典热光源也实现了鬼成像。相对于纠缠光源制备的复杂性,热光源实现鬼成像方案对实验设备要求更低,实现更为简单。因此,热光鬼成像成为近年来的研究热点,各种热光鬼成像方案相继被提出。2008年,Shapiro等人[10-11]提出了一种计算鬼成像方案(computational ghost imaging,CGI),参考光路的光场强度无需测量获取,可通过离线计算方式获取。2009年,Bromberg等人[12-13]在实验上实现了CGI。2009年,Katz等人[14-17]最先把压缩感知(Compressive sensing, CS)算法应用到鬼成像中,提出了一种压缩鬼成像方案(Compressive Ghost Imaging),利用CS算法突破了Nyquist采样频率极限,把数据的压缩和采样同时进行,使得鬼成像图像恢复所需的测量次数大大降低。
但是鬼成像仍然存在测量次数过多、成像质量较低等问题,因此,本文提出使用正交散斑代替随机散斑,通过使用离散余弦散斑照射物体和重建算法获得物体图像。该方案可以有效提高成像质量,减少测量次数。该方案本质上是根据物体的先验信息选取照射的物体散斑,是一种对散斑的优化方法,具有操作简便、效果显著的优势,可促进未来关联成像的实用化发展。
2 正交散斑的鬼成像方案
正交散斑的鬼成像方案示意图如图1所示,其中{Ii(x,y)}和{Bi}分别表示正交散斑的光场强度和桶探测值。首先激光通过数字微镜装置(Digital Micromirror Devices, DMD)后产生低频的DCT正交散斑,再照射到物体后,被桶探测器接收,最后把光场强度{Ii(x,y)}作为测量矩阵,桶探测值{Bi}作为测量值,通过CS重构算法恢复物体图像。
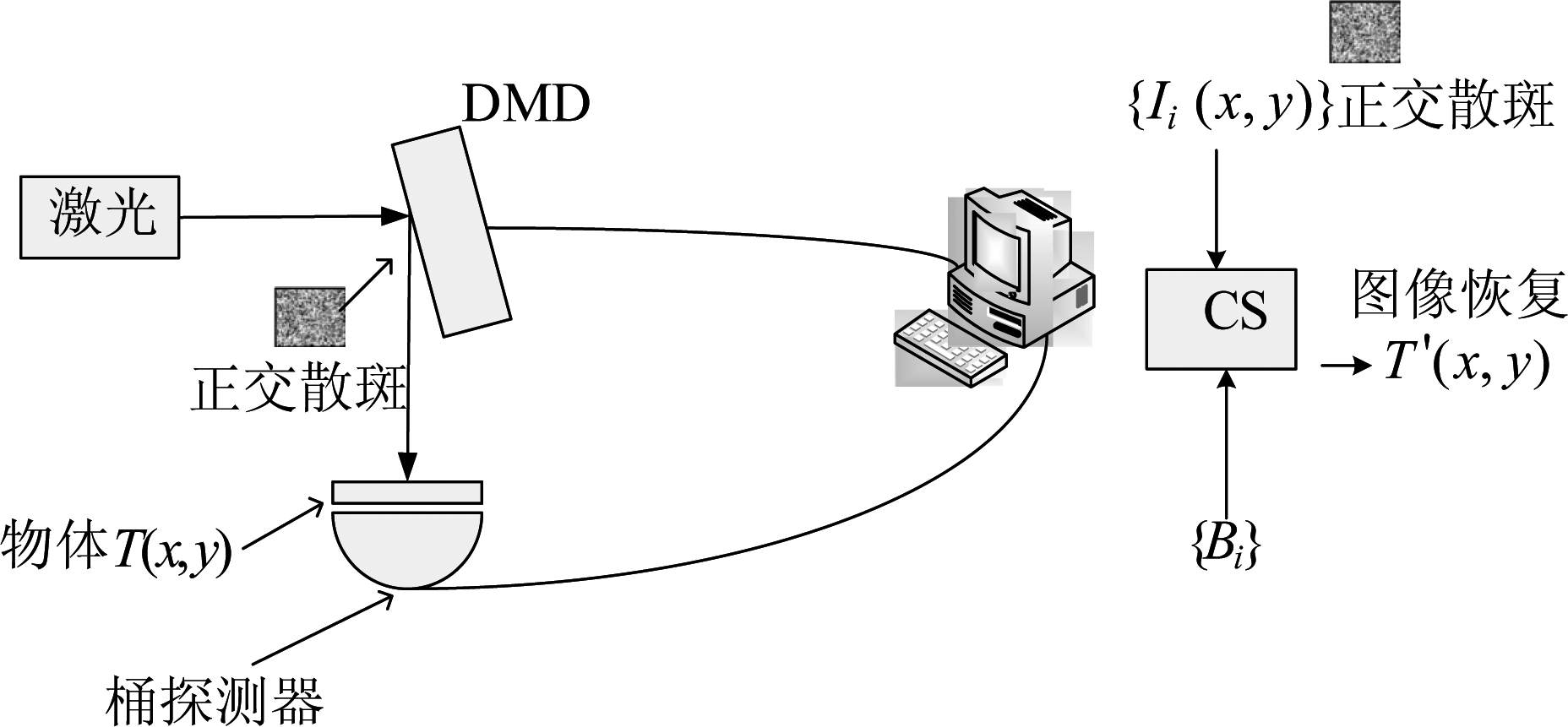
图1 正交散斑鬼成像方案示意图
Fig.1 Schematic diagram of orthogonal speckle ghost imaging scheme
方案的具体实现过程如下:(1)对物体稀疏表示。把物体T(x,y)拉长为一列X(X∈RN),由矩阵论的正交分解理论可知,X可用N个正交基来表示。
(1)
其中Ψ∈RN×N表示为Ψ={φ1,φ2,…,φN},φi∈RN是一个正交基,![]() 表示物体在正交基上的投影值。
表示物体在正交基上的投影值。
(2)选择对应的测量矩阵。在鬼成像中,成像过程可表示:
B=IX
(2)
其中,X∈RN表示待成像物体,I∈RM×N是测量矩阵,对应着相应散斑点的光场强度,M表示总共的测量次数,B∈RM是所有测量后获得的桶探测器值。
当总测量次数M=N时,因为Ψ是由一系列正交基组成的正交矩阵,可以令测量矩阵I等于物体正交分解矩阵Ψ的转置矩阵,即
I=Ψ-1=ΨT
(3)
式(2)可写为
B=IX=Ψ-1Ψβ=ΨTΨβ=β
(4)
第i次测量的桶探测器的值Bi可表示为:
(5)
由于φi∈RN是正交基,所以![]() 因此式(5)可化简为
因此式(5)可化简为
(6)
考虑到大部分物体经过DCT变换后,能量主要集中在低频部分,如图2所示,图像的左上表示低频部分,这意味着式(6)中β的大部分元素变为零,只有低频部分的β才不为0。

图2 经过DCT变换后的图片
Fig.2 Pictures transformed by DCT
正交基选择离散余弦基,其表示
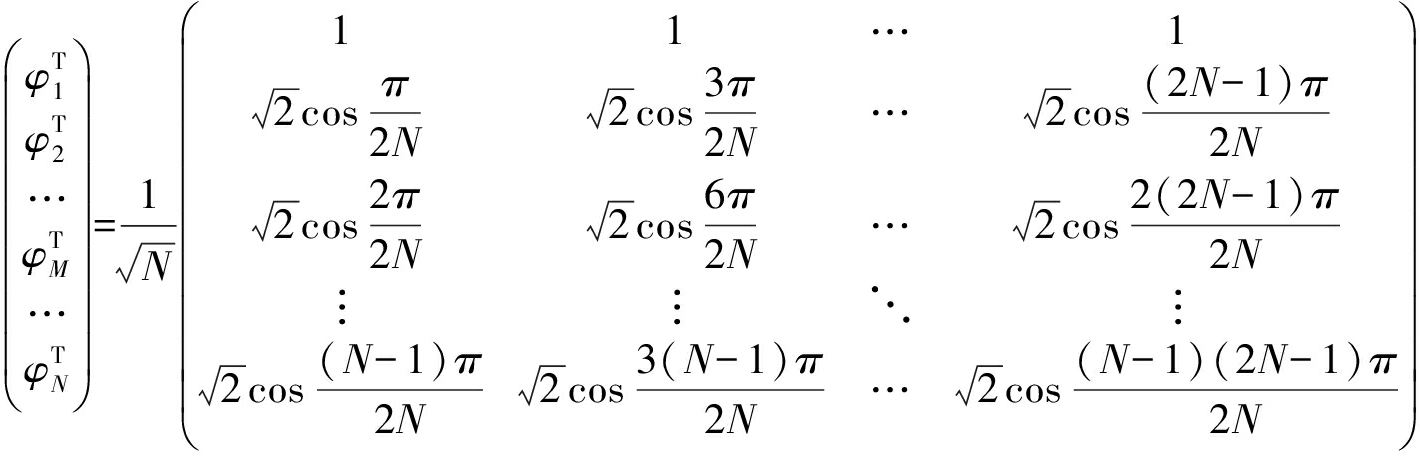
(7)
这时公式(4)可写为:
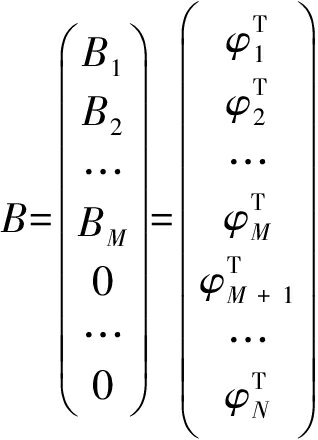
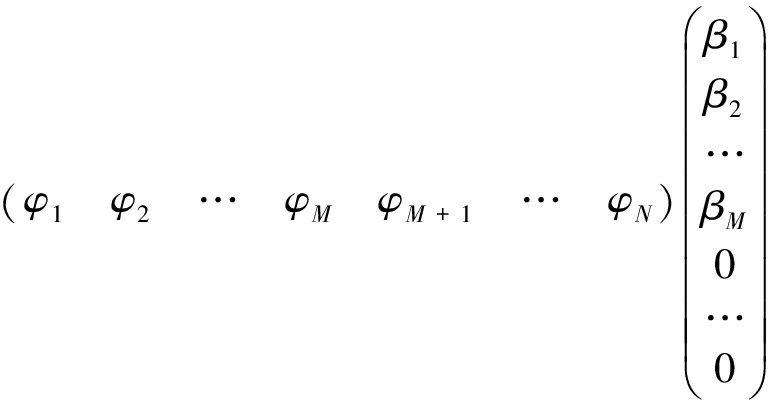
(8)
进一步化简为:
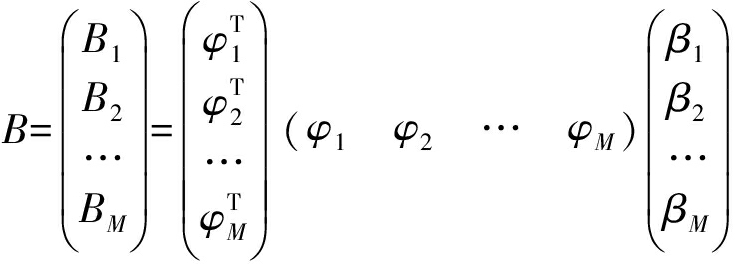
(9)
最后,利用正交散斑的特性I-1=I,可以求解出物体X:
X=I-1B=IB
(10)
因此在使用离散余弦基对原图像进行正交稀疏分解后,只需采用离散余弦基的低频分量作为正交散斑照射物体,即可对物体进行成像,而M≪N,因此鬼成像所需的测量次数大大减少。
3 实验结果与分析
为了定量的衡量恢复图像质量,引入峰值信噪比(Peak Signal-to-Noise Ratio,PSNR),其定义为:
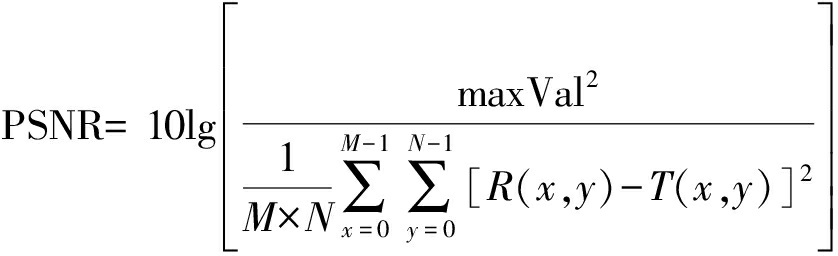
(11)
其中T(x,y)和R(x,y)是原始图像和恢复图像在像素点(x,y)上的光场强度,M×N表示图像的大小,max Val是图像最大的灰度值。由公式(10)可知,恢复图像的R(x,y)和原始图像的T(x,y)之间的差值越小,PSNR就越大,图像的恢复效果越好。
正交散斑的鬼成像方案实验装置图如图3所示。LED发射的光经过透镜后,通过由电脑控制的DMD(TI DLPC350)调制,产生低频部分的余弦正交散斑,再经过焦距f=300 mm的透镜,值得注意的是透镜只用来汇聚透过物体的所有光,没有成像功能。随后,正交余弦散斑照射到大小为32×32像素的物体,实验中采用的透射型物体NUPT是印刷在透明塑料片上。通过物体后,再通过透镜的汇聚后被桶探测器(Thorlabs S120C、PM100USB)接收测量。最后,通过CS算法恢复物体图像。
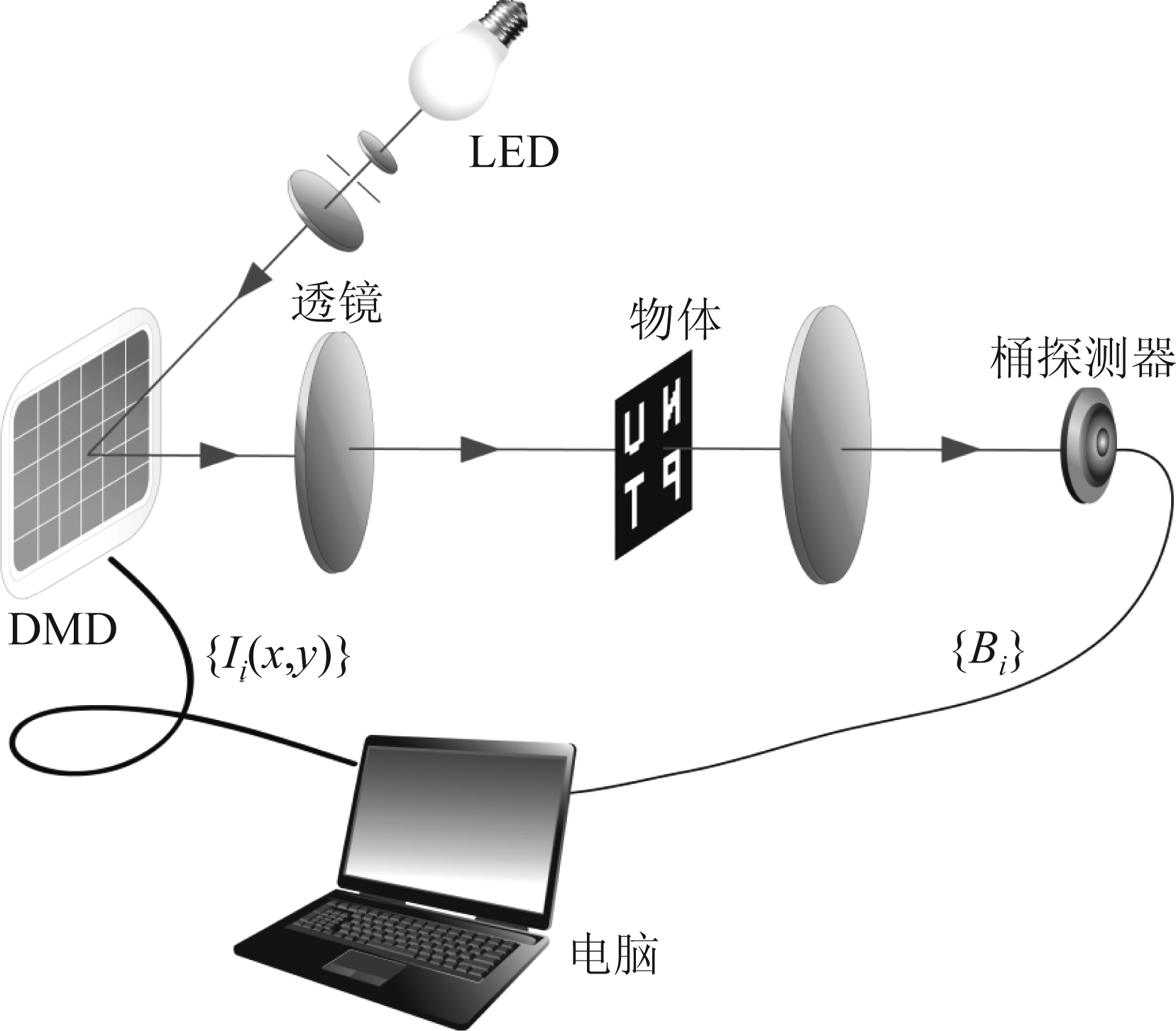
图3 实验装置图
Fig.3 Setup of the experiment
图4和图5是不同采样次数下使用随机高斯散斑和余弦低频正交散斑的图像恢复及其PSNR曲线图,其中scs代表使用余弦低频正交散斑,cs代表使用高斯随机散斑。由图4可知,正交散斑测量次数在500次时就可以会恢复出较高质量的图片,同样的测量次数下,正交散斑的恢复质量明显优于随机高斯散斑。由图5可以更清楚的看出,在同样的PSNR下,即图片质量相同的情况下,正交散斑所需的测量次数比高斯随机散斑大大减少。

图4 不同采样次数下使用随机高斯散斑和余弦低频正交散斑方案的“NUPT”结果图
Fig.4 NUPT Result Diagram Using Random Gauss Speckle and Cosine Low Frequency Orthogonal Speckle Scheme under Different Sampling Numbers
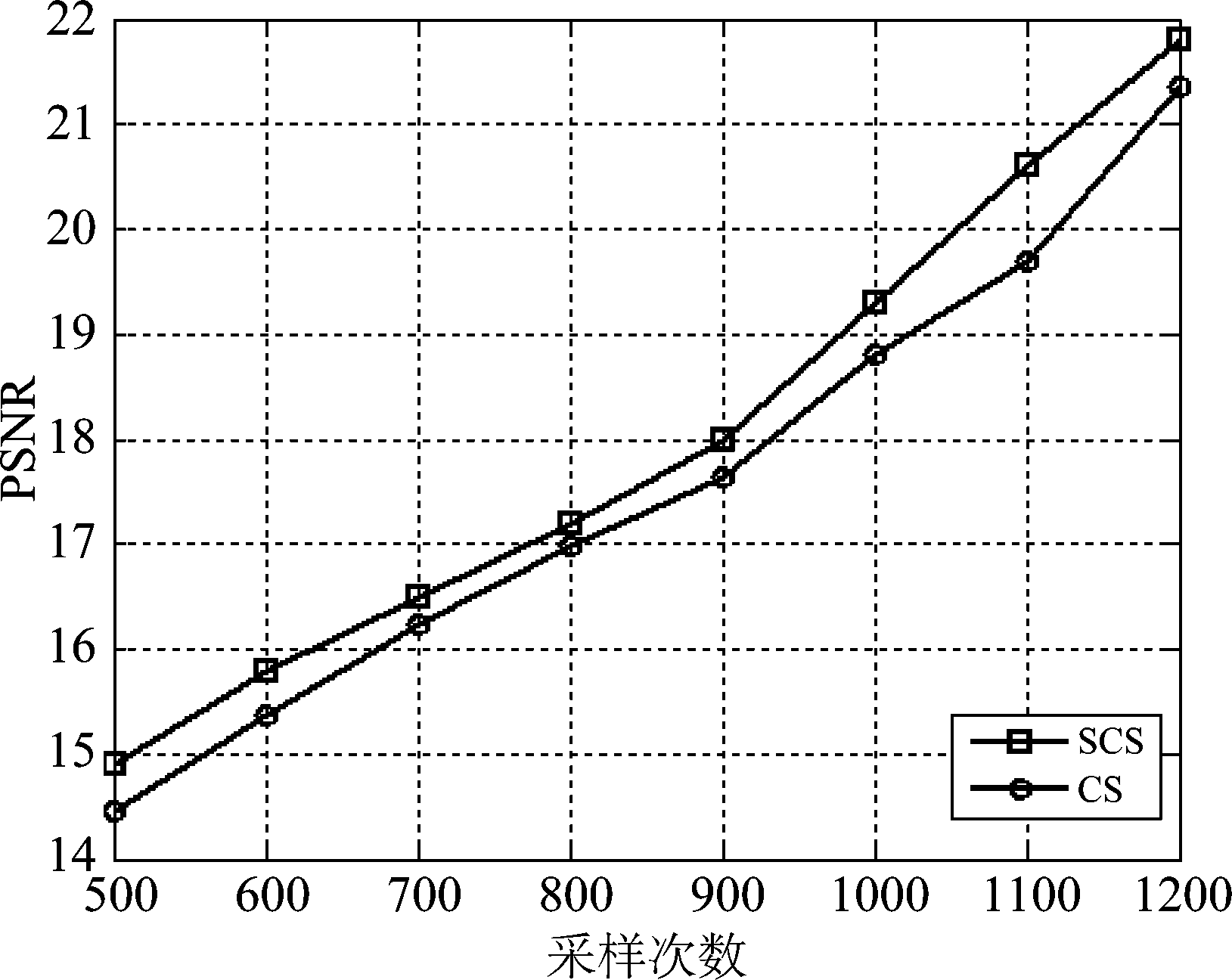
图5 “NUPT”图在两种散斑下的PSNR曲线图
Fig.5 PSNR Curve of “NUPT” Graph under Two Speckles
4 结论
本文研究了正交散斑鬼成像。首先对图像进行正交稀疏分解,测量矩阵选择正交分解基的转置矩阵,由于DCT分解使得图像能量主要集中在低频区,因此散斑选择离散余弦基的低频部分即可恢复出物体图像。实验结果表明,相比于使用随机高斯散斑,使用低频余弦分量的正交散斑鬼成像,恢复图像所需的测量次数大大减少,同样的测量次数,正交散斑鬼成像的图像恢复质量也更高。
[1] Pittman T B, Shih Y H, Strekalov D V, et al. Optical imaging by means of two-photon quantum entanglement[J]. Physical Review A, 1995, 52(5): R3429.
[2] Gatti A, Brambilla E, Bache M, et al. Correlated imaging, quantum and classical[J]. Physical Review A, 2004, 70(1): 013802.
[3] Cai Y, Zhu S Y. Ghost imaging with incoherent and partially coherent light radiation[J]. Physical Review E, 2005, 71(5): 056607.
[4] 崔丽君, 赵成强, 徐文东, 等. 强度关联激光成像雷达测量矩阵研究[J]. 中国激光, 2013 (9): 258-264.
Cui Lijun, Zhao Chengqiang, Xu Wendong, et al. Study on the measurement matrix of intensity correlation lidar[J]. Chinese Journal of Lasers, 2013 (9): 258-264.(in Chinese)
[5] Yang Z, Zhao L, Zhao X, et al. Lensless ghost imaging through the strongly scattering medium[J]. Chinese Physics B, 2015, 25(2): 024202.
[6] 韩申生, 龚文林, 陈明亮, 等. 基于稀疏和冗余表象的鬼成像雷达研究进展[J]. 红外与激光工程, 2015, 44(9): 2547-2555.
Han Shensheng, Gong Wenlin, Chen Mingliang, et al. Research progress of ghost imaging radar based on sparse and redundant images[J]. Infrared and Laser Engineering, 2015, 44(9): 2547-2555.(in Chinese)
[7] 仲亚军, 刘娇, 梁文强, 等. 针对多散斑图的差分压缩鬼成像方案研究[J]. 物理学报, 2015, 64(1): 88-94.
Zhong Yajun, Liu Jiao, Liang Wenqiang, et al. Research on Differential Compressed Ghost Imaging Scheme for Multi-Speckle Patterns[J]. Acta Physica Sinica, 2015, 64(1): 88-94.(in Chinese)
[8] 陈超, 赵生妹. 高阶差值筛选鬼成像方案研究[J]. 光学学报, 2014, 34(6): 611002.
Chen Chao, Zhao Shengmei. Study on ghost imaging scheme of high-order difference screening[J]. Acta Optica Sinica, 2014, 34(6): 611002.(in Chinese)
[9] Zhao Sheng-Mei, Zhuang Peng. Correspondence normalized ghost imaging on compressive sensing[J]. Chinese Physics B, 2014, 23(5): 054203.
[10] 白旭, 李永强, 赵生妹. 基于压缩感知的差分关联成像方案研究[J]. 物理学报, 2013, 62(4): 044209.
Bai Xu, Li Yongqiang, Zhao Shengmei. Differential correlation imaging based on compressed sensing[J]. Acta Physica Sinica, 2013, 62(4): 044209.(in Chinese)
[11] 曹非, 赵生妹. 基于计算鬼成像的双密钥光学加密方案[J]. 光学学报, 2017, 37(1): 0111001.
Cao Fei, Zhao Shengmei. Double Optical Secret Key Encryption Scheme Based On Computational Ghost Imaging[J]. Acta Optica Sinica, 2017, 37(1): 0111001.(in Chinese)
[12] 李恩荣, 陈明亮, 龚文林, 等. “鬼成像”系统的互信息[J]. 光学学报, 2013, 33(12): 93-98.
Li Enrong, Chen Mingliang, Gong Wenlin, et al. HMutual information of ghost imaging system[J]. Acta Optica Sinica, 2013, 33(12): 93-98.(in Chinese)
[13] 陈洁, 薄遵望, 韩申生. 高斯振幅调制下基于稀疏性的鬼成像[J]. 光学学报, 2013, 33(9): 135-139.
Chen Jie, Bo Zunwang, Han Shensheng. Ghost imaging based on sparsity under Gauss amplitude modulation[J]. Acta Optica Sinica, 2013, 33(9): 135-139.(in Chinese)
[14] Bennink R S, Bentley S J, Boyd R W. “Two-photon” coincidence imaging with a classical source[J]. Physical Review Letters, 2002, 89(11): 113601.
[15] Klyshko D N. Two-photon light: Influence of filtration and a new possible EPR experiment[J]. Physics Letters A, 1988, 128(3- 4): 133-137.
[16] Li C, Wang T, Pu J, et al. Ghost imaging with partially coherent light radiation through turbulent atmosphere[J]. Applied Physics B, 2010, 99(3): 599- 604.
[17] Abouraddy A F, Saleh B E A, Sergienko A V, et al. Role of entanglement in two-photon imaging[J]. Physical Review Letters, 2001, 87(12): 123602.
[18] 李永强, 白旭, 赵生妹, 等. 参考臂差分压缩关联成像方案研究[J]. 信号处理, 2014, 30(7): 836- 841.
Li Yongqiang, Bai Xu, Zhao Shengmei, et al. Study on Reference Differential Compressive Correlated Imaging Scheme[J]. Journal of Signal Processing, 2014, 30(7): 836- 841.(in Chinese)


