1 引言
波达方向(direction of arrival,DOA)估计是雷达、声呐、无线通信等领域的一个重要研究内容,有着非常广泛的应用[1]。基于常规波束形成的DOA估计方法,分辨性能较差,不能突破瑞利限。以多重信号分类(multiple signal classification, MUSIC)和ESPRIT(estimation of signal parameters by rotational invariance techniques)为代表的子空间方法,不受常规分辨率的限制,极大地推动了DOA估计方法的发展和应用。这类基于子空间的方法一般利用了信号的二阶统计特性,即接收数据的协方差矩阵。协方差矩阵的估计至少需要2M(M为阵元数)个独立同分布的快拍数据才能保证损失小于3 dB。然而,在高速、高机动等短时突发信号环境下,难以获得足够的独立同分布快拍数据。同时,由于受多径效应和敌方相干源干扰等的影响,估计的协方差矩阵会产生秩亏损,导致一般的子空间方法不能有效分辨目标信号。为此,直接采用单快拍进行DOA估计成为一种解决方法。
国内外学者提出了许多单快拍DOA估计方法,主要包括伪协方差矩阵构造方法[2- 6]、空间平滑类方法[7-9]、稀疏表示[10-13]等。文献[4]证明了直接采用单快拍数据构造的Toeplitz型伪协方差矩阵满足秩等于信源个数,可直接应用子空间类方法估计DOA,但其需要入射信号的初始相位为零。文献[2]和文献[3]分别采用对称阵和对单快拍数据做互相关处理的方式消除了对信号类型的限定,但是前者损失了一半的阵列孔径。文献[5]构造的伪协方差矩阵同样存在阵列孔径损失的缺点。空间平滑类算法也可用于估计协方差矩阵,但是在较少阵元数量时,协方差矩阵的秩不能有效恢复,且同样存在阵列孔径的损失。近年来,基于稀疏表示的DOA估计方法得到了很多关注,然而稀疏表示类方法面临着原子之间相关性与字典大小的矛盾,即DOA估计精度和计算量受空间角度划分的影响。
文献[14]提出了一种迭代超分辨(reiterative super-resolution,RISR)的空间谱估计方法,相对于传统的Capon或MUSIC等谱估计方法而言,可以处理单快拍数据,具有很高的分辨能力和估计精度。然而其DOA估计是通过空间谱峰搜索实现的,因此估计精度和运算量受空间角度划分的影响。迭代超分辨技术是基于迭代最小均方误差(reiterative minimum mean-square error,RMMSE)框架推导的,文献[15]基于加权最小二乘准则得到的迭代自适应方法与文献[14]的方法在本质上是相同的。本文基于最小方差无畸变响应原则重新推导了RISR算法,然后采用RISR估计阵列接收信号的协方差矩阵,并用无需空间谱峰搜索的求根MUSIC算法实现了对DOA的估计。仿真分析了空间角度划分、迭代次数、信噪比等参数对DOA分辨成功率和估计精度的影响。相比已有的方法,信源角度相距越近,本文方法的分辨能力越有优势。
2 离散信号模型
考虑包含M个全向阵元的等距线阵,阵元间距为半波长宽度。整个阵列在时刻t接收到的K(K<M)个方向的远场窄带信号,经AD采样后可表示为,
(1)
其中si(t)和a(θi)=[1 ejπsin θi … ejπ(M-1)sin θi]T分别为θi方向的信号和导向矢量,n(t)为零均值的复高斯随机噪声。基于空间搜索的方法在式(1)基础上,将整个观测空间划分为N(N>M)份。假设每个方向上都有潜在的信号,则式(1)可进一步表示为
x(t)=As(t)+n(t)
(2)
其中A=[a(θ1) a(θ2) … a(θN)]为N个方向的阵列流型矩阵,s(t)=[s1(t) s2(t) … sN(t)]T为信号向量。假设噪声与信号不相关,则阵列接收数据的协方差矩阵可写为,
R=E{x(t)xH(t)}=ARs(t)AH+Rn
(3)
其中E{·}表示统计期望,(·)H为共轭转置运算,Rs(t)=E{s(t)sH(t)}和Rn分别为信号和噪声协方差矩阵。基于子空间的方法需要估计接收数据的协方差矩阵R,一般通过下式估计,
(4)
然而在实际中,当独立同分布的快拍数不足或存在相干源时,
的估计会有较大误差或者产生秩亏损,从而导致DOA的估计和分辨性能变差。
3 基于迭代超分辨的单快拍DOA估计方法
针对上述问题,本文提出基于迭代超分辨的单快拍DOA估计方法,通过迭代估计接收数据的协方差矩阵,然后通过求根MUSIC和ESPRIT实现对DOA的估计。
3.1 基于迭代超分辨技术的协方差矩阵重构
本文基于最小方差无畸变响应原则重新推导了RISR。首先构造如下代价函数,
J(t)=E{‖s(t)-WH(t)x(t)‖2}
s.t. diag{WH(t)A}=1N×1
(5)
其中W(t)M×N为各个方向的滤波器权重。最小化式(5)可得,
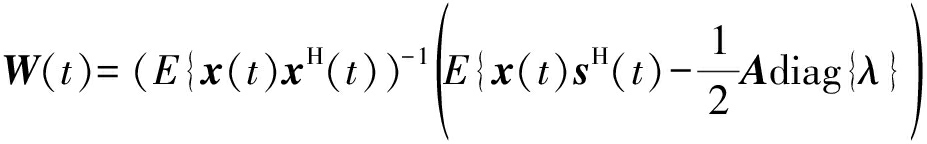
(6)
式中diag{·}表示对角化运算,λ为拉格朗日因子矢量。假设信号之间不相关,则(6)可简化为
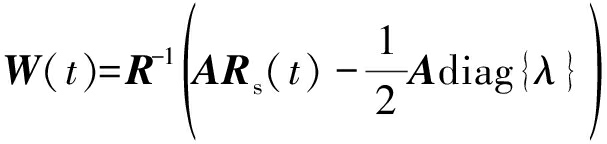
(7)
根据diag{WH(t)A}=1N×1可求得λ,带入上式后可得,
W(t)=R-1Adiag{1N×N./(AHR-1A)}
(8)
其中./表示元素点除运算。式(8)即为基于最小方差无畸变响应原则的RISR滤波器,虽然与文献[14]中的表达式有所不同,但其本质是相同的。由于接收数据的协方差矩阵R未知,因此需要通过式(3)迭代估计。信号协方差矩阵Rs(t)的初始值可通过常规波束形成得到,即
噪声协方差矩阵Rn可看作为对角加载项。通过上述推导可知,RISR每次迭代都需要估计阵列的协方差矩阵,因此可对多次迭代后的协方差矩阵应用求根MUSIC等无需谱峰搜索的DOA估计方法。
3.2 DOA估计
基于空间谱峰搜索的DOA估计方法的运算量与空间角度划分程度密切相关,更精细的角度划分可带来更高的估计精度和分辨能力,伴随而来的问题是更大的计算量。为避免谱峰搜索带来的高运算量,本文采用求根MUSIC算法实现DOA估计。
求根MUSIC的理论基础是Pisarenko分解[7],MUSIC算法是搜索下式的峰值来估计DOA,
(9)
其中Un为噪声子空间。定义p(z)=[1 z … zM-1]H,则
位于单位圆上的零点即对应信源的DOA。令pT(z-1)=pH(z),对式(9)变换可得,
(10)
求取式(10)中最接近单位圆的K个根即可得到信号的DOA,
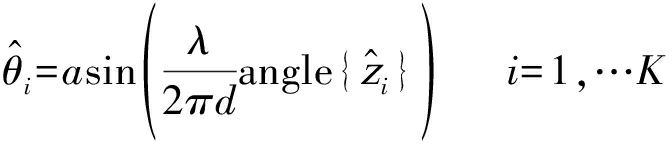
(11)
4 仿真分析
由上述推导可知,最终的DOA分辨性能和估计精度与RISR的网格划分程度、迭代次数和信噪比等参数相关。本节通过仿真分析各个参数对DOA分辨和估计性能的影响,以及将本文方法与文献[8]的空间平滑(forward-backward spatial smoothing, FBSS)方法、文献[5]的协方差重构(covariance matrix reconstruction, CMRC)和基于FOCUSS的稀疏表示DOA估计方法做了对比。阵列基本参数为M=13个阵元,阵元间距为半波长宽度,对应零点波束宽度为BW0=2asin(2/M)≈17.70°,或半功率点波束宽度BW0.5≈101.53/M=7.81°。假设两个信源的角度分别为θ1和θ2,若被估计的角度误差最大不超过(θ1-θ2)/2,则称这两个信源被成功分辨。对于FOCUSS算法而言,还需要信源个数估计正确才算一次成功的分辨。对于成功分辨的目标,通过下式计算其均方根误差,
(12)
其中
表示第p次分辨成功时的第k个DOA的估计值,P为分辨成功的次数。每种情况下的蒙特卡洛仿真实验次数为500。为了防止正确率太低时,RMSE统计失效,只计算P>100时的RMSE。
4.1 迭代次数对分辨性能和估计精度的影响
首先考虑两个目标分为位于0°和2.21°方向,即相隔1/8的零点波束宽度。固定网格划分间隔为0.1°,设置RISR迭代次数r以步长2从0至10变化,其中的0次迭代表示采用匹配滤波(matched filter, MF)估计协方差,信噪比以步长2从-5 dB至30 dB变化。仿真结果如图1所示,实线表示分辨正确率,点划线表示均方根误差。从图1可以看出,直接匹配滤波构造协方差矩阵的性能最差,而通过增加迭代次数可以提高分辨能力和估计精度,但是迭代6次之后,分辨正确率和RMSE逐渐收敛。
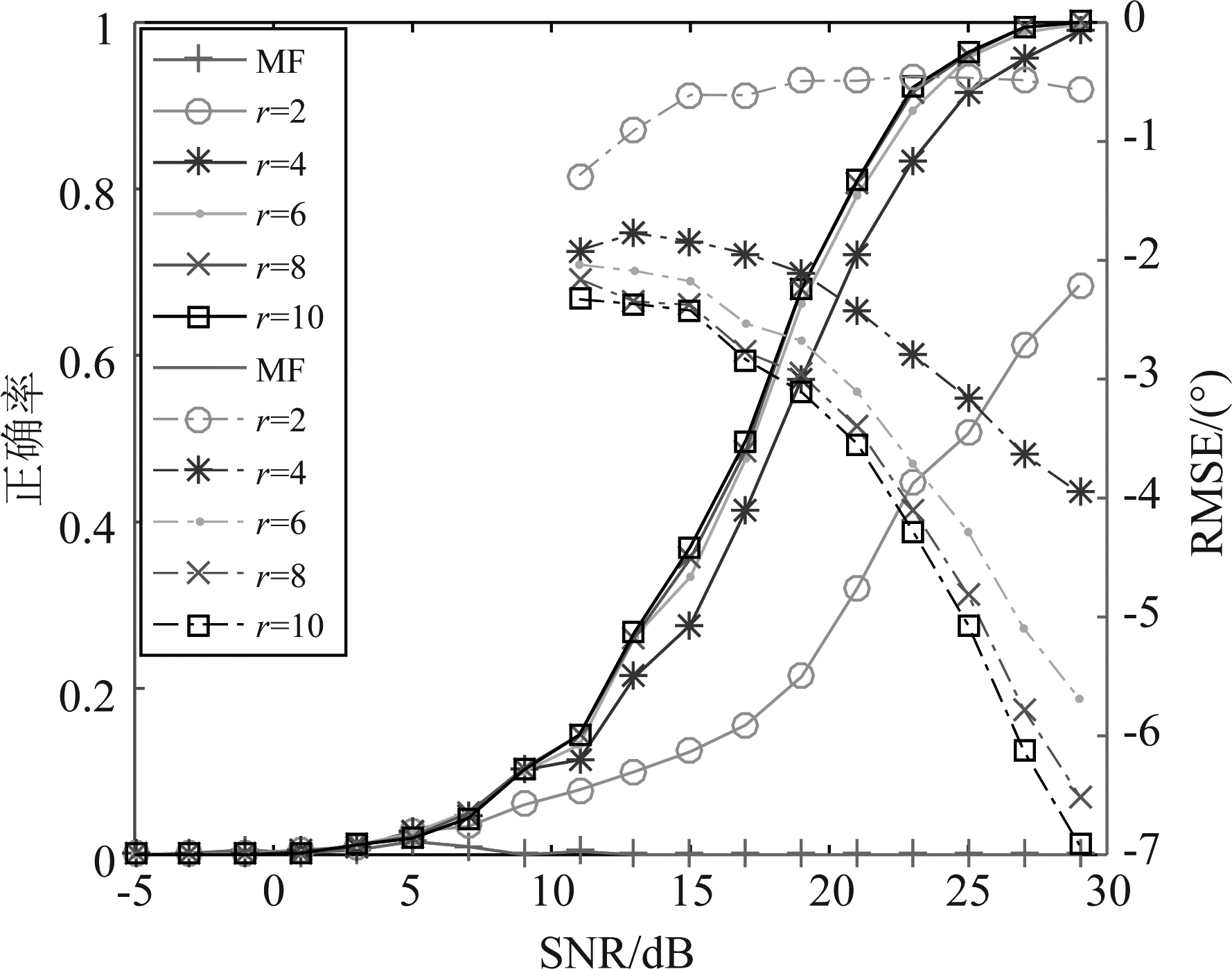
图1 迭代次数对分辨性能和估计精度的影响
Fig.1 Effect of iterations number on resolution performance and estimation accuracy
4.2 网格划分对分辨性能和估计精度的影响
固定迭代次数为5次,角度划分间隔为从2°至0.05°递减5次,其余设置同上,仿真结果如图2所示。可以看出,当角度划分Δθ=2°时,划分的刻度与信源角度最接近,此时模型失配程度最低,因此分辨正确率和估计精度都是最好的。当Δθ与信源角度差差别较大时,Δθ越小,分辨性能和估计精度越高,这同样是因为越小的网格划分对应着越低的模型失配。
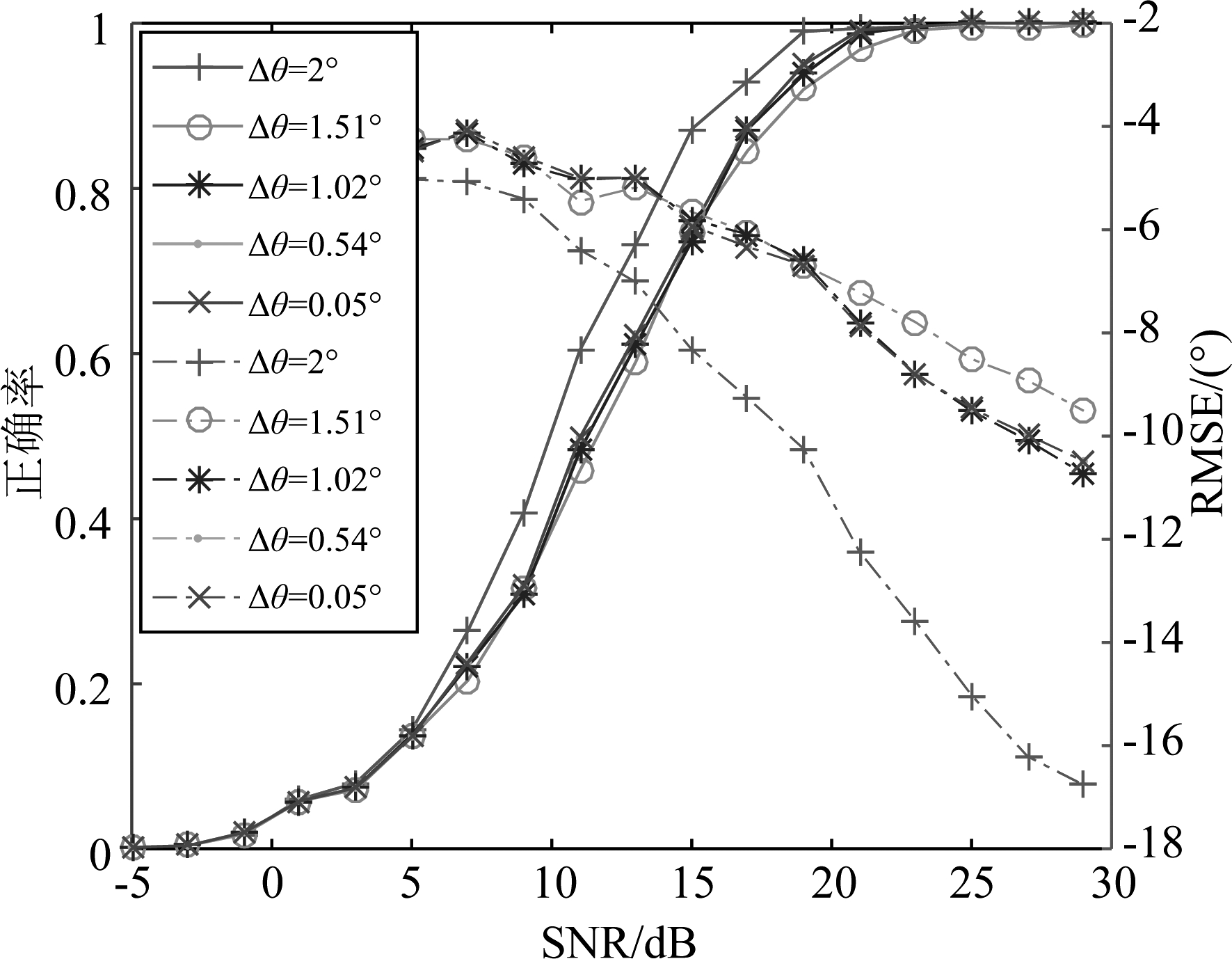
图2 网格划分对分辨性能和估计精度的影响
Fig.2 Effect of spatial partition on resolution performance and estimation accuracy
4.3 方法对比分析
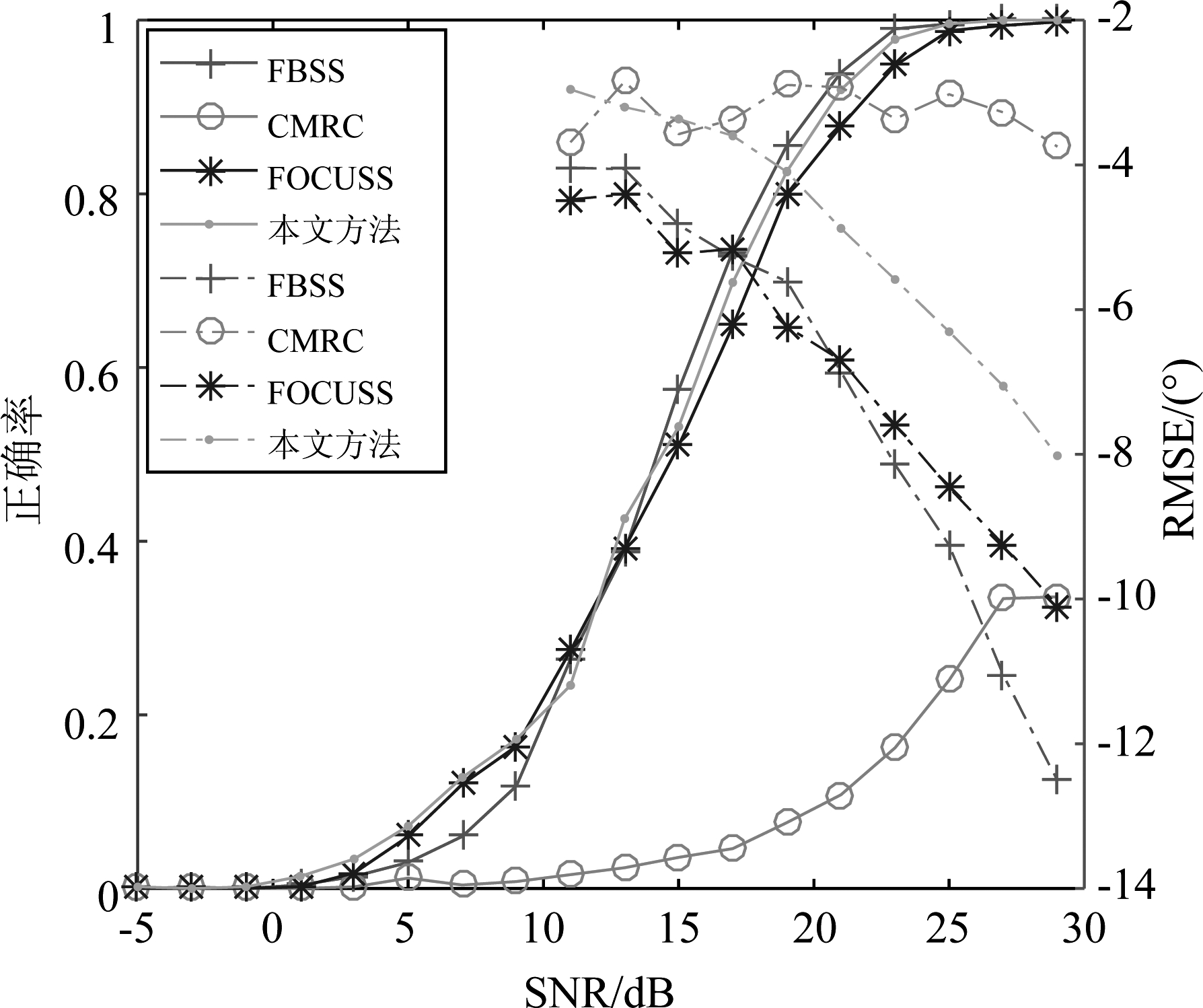
图3 两目标相距1/8零点波束宽度时的性能
Fig.3 Performance of two targets at a distance of 1/8 BW0.5
本小节对比分析本文方法与相关文献方法的性能。本文方法参数取Δθ=0.1°、r=5。空间平滑方法采用7个阵元前后向平滑计算协方差矩阵,然后采用求根MUSIC估计DOA。协方差重构方法采用三个阵元加权,加权系数α=1,构造的伪协方差矩阵维度为7。稀疏表示的DOA估计采用FOCUSS算法,空间角度划分精度为0.05°。考虑两个目标间隔分别为1/8和1/16的零点波束宽度,仿真结果见图3、4。从图3可以看出,基于空间平滑的FBSS方法分辨和估计性能最好,这是因为通过多次前后向平滑估计的协方差更准确,而采用单快拍直接构造伪协方差矩阵的CMRC方法性能较差。本文方法与FOCUSS方法在分辨正确率上接近,RMSE上稍差于FOCUSS方法。但是当两目标角度间隔进一步缩小时,此时CMRC和FOCUSS方法将完全失效,而本文方法在分辨性能和估计精度上都优于其余方法。
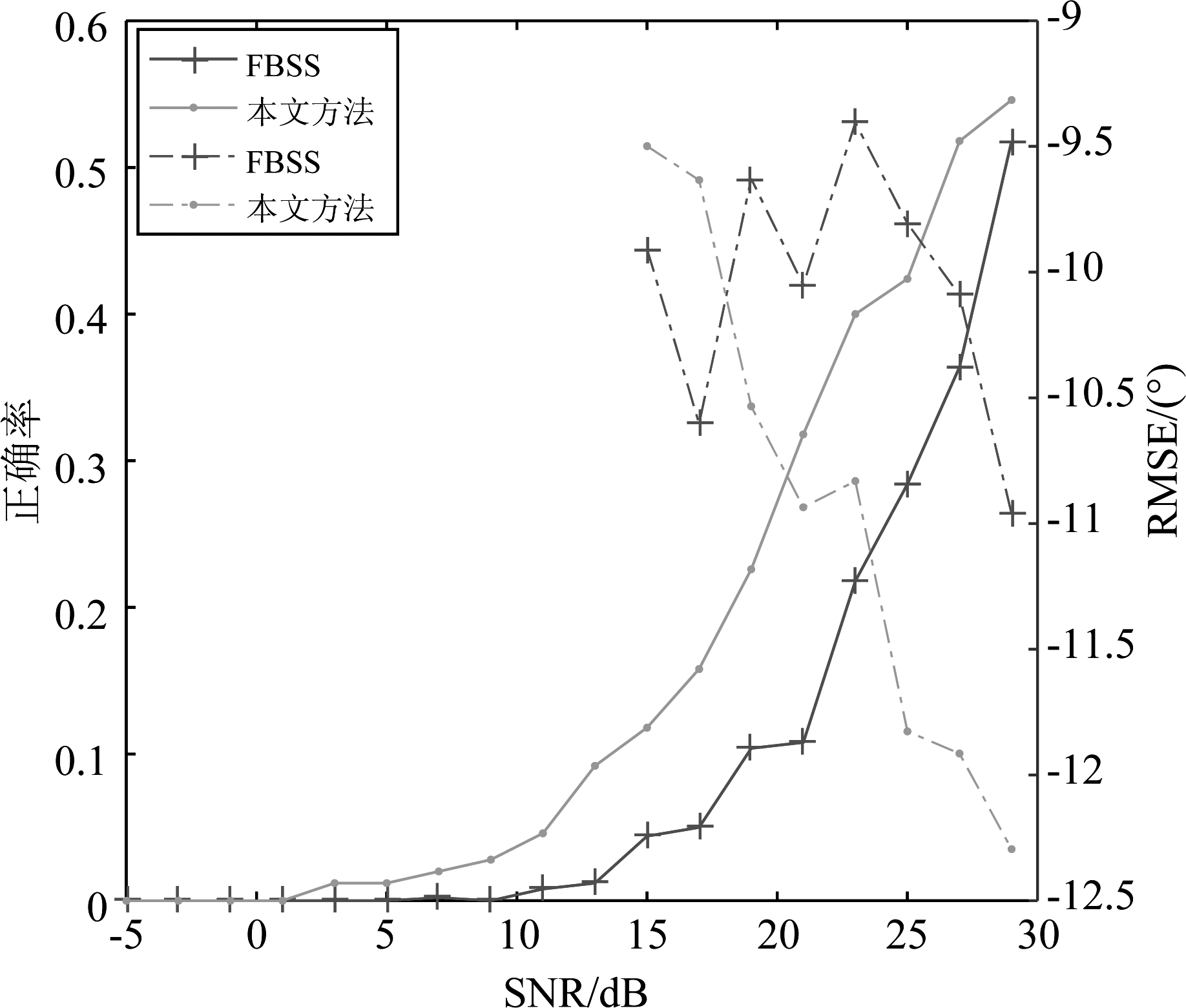
图4 两目标相距1/16零点波束宽度时的性能
Fig.4 Performance of two targets at a distance of 1/16 BW0.5
5 结论
综上,本文基于最小方差无畸变响应原则重新推导了RISR算法,采用RISR估计阵列接收信号的协方差矩阵,并用求根MUSIC算法实现对DOA的估计。该方法只需要单快拍数据,不需要空间谱峰搜索且没有阵列孔径损失。仿真分析了网格划分程度、迭代次数和信噪比等参数对DOA分辨性能和估计精度的影响,结果表明增加迭代次数可以提高对DOA的分辨能力和估计精度,网格划分的越精细(网格与目标DOA失配越小),DOA的分辨性能和估计精度越高。与已有的方法相比,信源角度相距越近,本文方法的分辨能力越有优势。
[1] 叶中付, 罗大为, 韦进强, 等. 相干信号波达方向估计技术综述[J]. 数据采集与处理, 2017, 32(2): 258- 265.
Ye Z F, Luo D W, Wei J Q. Review for Coherent DOA Estimation technique[J]. Journal of Data Acquisition & Processing, 2017, 32(2): 258- 265.(in Chinese)
[2] 王凌, 李国林, 李静, 等. 一种新的单次快拍二维ESPRIT算法[J]. 北京理工大学学报, 2013, 33(1): 99-104.
Wang L, Li G L, Li J, et al. A Novel Single Snapshot Two-Dimensional ESPRIT Algorithm[J]. Journal of Beijing Institute of Technology(Natural Science Edition), 2013, 33(1): 99-104.(in Chinese)
[3] 毛维平, 李国林, 谢鑫. 单快拍数据预处理的相干信号波达方向估计[J]. 上海交通大学学报, 2014, 48(10): 1362-1367.
Mao W P, Li G L, Xie X. DOA Estimation of Coherent Signals with Preprocessed Single Snapshot[J]. Journal of Shanghai Jiaotong University, 2014, 48(10): 1362-1367.(in Chinese)
[4] 谢鑫, 李国林, 刘华文. 采用单次快拍数据实现相干信号DOA估计[J]. 电子与信息学报, 2010, 32(3): 604- 608.
Xie X, Li G L, Liu H W. DOA Estimation of Coherent Signals Using one Snapshot[J]. Journal of Electronics & Information Technology, 2010, 32(3): 604- 608.(in Chinese)
[5] 蒋柏峰, 吕晓德, 向茂生. 一种基于阵列接收信号重排的单快拍DOA估计方法[J]. 电子与信息学报, 2014, 36(6): 1334-1339.
Jiang B F, Lv X D, Xiang M S. Single Snapshot DOA Estimation Method Based on Rearrangement of Array Receiving Signal[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1334-1339.(in Chinese)
[6] 王俊, 向洪, 魏少明, 等. 单快拍数据的分布式二维阵列测角方法研究[J]. 电子与信息学报, 2018, 40(6): 1375-1382.
Wang J, Xiang H, Wei S M, et al. 2-D DOA Estimation of Distributed Array with Single Snapshot[J]. Journal of Electronics & Information Technology, 2018, 40(6): 1375-1382.(in Chinese)
[7] Barabell A. Improving the Resolution Performance of Eigenstructure-based Direction-finding Algorithms[C]∥ICASSP’83. IEEE International Conference on Acoustics, Speech, and Signal Processing, 1983: 336-339.
[8] 刘晓娣, 周新力, 肖金光. 基于空间平滑的单快拍波达方向估计算法[J]. 探测与控制学报, 2015, 37(6): 66-70.
Liu X D, Zhou X L, Xiao J G. Single Snapshot DOA Estimation Algorithm Based on Spatial Smoothing[J]. Journal of Detection & Control, 2015, 37(6): 66-70.(in Chinese)
[9] Evans J E, Johnson J R, Sun D F. Application of Advanced Signal Processing Techniques to Angle of Arrival Estimation in ATC Navigation and Surveillance Systems[R]. MIT Lincoln Laboratory Technical Report, 1982.
[10] 赵春雷, 王亚梁, 毛兴鹏, 等. 基于压缩感知的高频地波雷达二维DOA估计[J]. 系统工程与电子技术, 2017, 39(4): 733-741.
Zhao C L, Wang Y L, Mao X P, et al. Compressive Sensing Based Two-dimensional DOA Estimation for High Frequency Surface Wave Radar[J]. Systems Engineering and Electronics, 2017, 39(4): 733-741.(in Chinese)
[11] Zamani H, Zayyani H, Marvasti F. An Iterative Dictionary Learning-Based Algorithm for DOA Estimation[J]. IEEE Communications Letters, 2016, 20(9): 1784-1787.
[12] Xu L, Wu R, Zhang X, et al. Joint Two-Dimensional DOA and Frequency Estimation for L-Shaped Array via Compressed Sensing PARAFAC Method[J]. IEEE Access, 2018, 6: 37204-37213.
[13] Uehashi S, Ogawa Y, Nishimura T, et al. Prediction of Time-Varying Multi-User MIMO Channels Based on DOA Estimation Using Compressed Sensing[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 565-577.
[14] Blunt S D, Chan T, Gerlach K. Robust DOA Estimation: The Reiterative Superresolution (RISR) Algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 332-346.
[15] Yardibi T, Li J, Stoica P, et al. Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 425- 443.
