1 引言
预测资源分配可以把无线网络资源提前分配给请求文件下载、视频点播等非实时业务的用户,从而充分利用服务完电话、视频会议等优先级较高的实时业务后网络的剩余资源,提升系统吞吐量或能效[2]。
在预测资源分配问题中,预测网络剩余资源是其中的关键问题之一。未来网络剩余资源(如可用带宽)可根据未来一段时间内的实时业务流量、利用排队论推导得到,因此网络剩余资源的预测问题可以转变为网络流量的预测问题[2]。
网络流量预测并不是一个新问题。为了进行动态准入控制,文献中往往采用自回归滑动平均模型[4]或可预测非平稳时间序列的自回归积分滑动平均模型(Autoregressive Integrated Moving Average model,ARIMA)[5]等线性模型进行短期流量预测。针对存在高突发的网络流量,文献[6]提出了基于自适应模板匹配的预测方法。在这类文献中,对历史流量数据的采样分辨率一般为毫秒级、需要对未来1至几秒后某个时间点的流量进行一步预测[4]。这些线性模型的方法训练和预测复杂度不高,但在进行长期流量预测时性能很差。随着深度学习等机器学习技术的快速发展,利用网络中实测的历史数据进行长期流量预测开始受到关注[6-10]。文献[7]使用高斯过程对流量的时变特性进行建模,从而预测蜂窝网络流量。文献[8]设计了利用自编码器和一种循环神经网络(Recurrent Neural Network,RNN)——长短期记忆(Long Short-Term Memory,LSTM)网络预测空时两维变化的蜂窝网络流量。文献[9]设计了深度置信网络对无线网络流量进行预测。文献[9]利用α-稳定模型建模了无线网络中各类业务的统计特性,基于该特性提出了基于字典学习的迭代方法来预测未来流量。这些方法基于粗采样分辨率(如小时或至少15分钟量级)的历史数据预测对未来一小时或15分钟后的流量进行单步预测,即对未来一个时间点的流量值进行预测,适于基站节能等应用。由于人类活动的潮汐效应,每天流量变化的规律性较强,故粗时间粒度的流量相对来说比较容易预测。然而,预测资源分配一般需要预测未来长度为几分钟的时间窗内每若干秒的残余带宽,即需要多步预测、所需预测信息的时间粒度通常为秒级[1-3]、所需预测的相对误差要小于20%[2]。对于在这样长度的未来时间窗内预测如此精细时间粒度的流量,目前尚未看到相关研究。
流量预测是一个时间序列预测问题,解决这个问题常用的RNN计算复杂度高、不能处理太远的长期依赖[11]。通过在RNN中引入注意力机制[12],可以对各个时间步的输出与所有时间步输入间的相关性进行建模,从而有效缓解这一问题。与传统基于RNN的序列-序列模型类似[11],全注意力机制(在部分文献中也被称为Transformer)具有编码器-解码器结构,其中编码器的输入为观测窗内的一段历史数据,解码器的输出为预测窗内的预测结果;与LSTM或门控循环神经网络(Gated Recurrent Unit,GRU)等RNN不同,全注意力机制不存在相邻时间步隐藏层之间的权重连接,因此能够充分利用图形处理器(Graphics Processing Unit,GPU)的并行计算能力。然而,文献[11]的全注意力机制是面向机器翻译问题提出的,如何把这种机制用于流量预测问题并不直接,对于流量预测问题是否相对于其他预测方法还有优势也未可知。
本文尝试基于全注意力机制设计神经网络对未来精细时间粒度的流量进行多步预测,利用一个每秒记录的实测流量数据集对这个网络进行训练和测试,在计算与样本复杂度和预测精度与延时等方面与现有的方法进行比较。为了分析注意力机制是否能提升流量预测的性能,我们与文献[14]中基于RNN的预测方法进行比较;为了分析采用神经网络预测流量是否有优势,与ARIMA模型这种传统的线性模型和支撑向量回归(Support Vector Regression,SVR)这种传统的非线性模型进行比较。为了给分析和评估预测资源分配方法提供预测误差模型,还对几种预测方法的误差统计特性进行了分析。最后,通过数值方法简要说明了全注意力机制的可解释性。
本文剩余部分安排如下。第2节介绍问题描述、神经网络结构设计与训练和测试过程。第3节为实验与数值结果。第4节总结全文。
符号定义:‖·‖1为1-范数,‖·‖2为2-范数,上标的正体字母T代表转置。
2 网络流量预测方法
本节提出利用全注意力机制对网络流量进行多步预测的方法。首先描述多步流量预测问题,然后介绍用于预测流量的神经网络结构,最后介绍训练和测试过程。
2.1 问题描述
把时间分为多个时隙,每一时隙长度为Δ。多步流量预测是根据一个时间序列预测另一个时间序列的问题,即利用一段长度为M个时隙的观测窗内的历史数据,对未来一段长为N个时隙的预测窗内各个时隙的流量进行预测,如图1所示。把观测窗内记录历史数据的时间间隔称为观测分辨率、预测窗内相邻两个时隙的时间间隔称为预测分辨率。为了简化符号,令观测分辨率和预测分辨率均为一个时隙的长度;当采用神经网络进行预测时两个分辨率不必相同。令预测窗开始时刻为第t个时隙结束的时刻,分别把观测窗和预测窗内每个时隙的流量数据记作向量
和
图1 问题描述
Fig.1 Problem Description
2.2 神经网络结构设计
下面首先从预测一般时间序列的角度介绍全注意力机制,然后利用这种机制设计用于进行预测流量的神经网络结构。
2.2.1 全注意力机制
对于时间序列预测问题,注意力机制建模了序列1中某一时隙(例如第TO个时隙)的值(称作目标值xTO)对序列2中每一个时隙(如第TS个时隙至第TE个时隙)的值(称作依赖序列xTS→TE=[xTS,…,xTE]T)的依赖程度[11](即相关性),依赖程度可由一组加权值
表示。为了与前文描述的流量预测问题相区分,在本子节出现的符号中与时间有关的下标都用大写的斜体字母T表示。此外,这里的序列1和序列2可以相同、也可以不同。在流量预测问题中,序列1和序列2可以是观测序列
或预测序列
在机器翻译领域中的研究发现,利用注意力机制可有效缓解传统序列预测模型(如循环神经网络)中依赖程度随预测时间增加而减小的现象[11]。文献[11]引入了如下的注意力函数来建模注意力机制:
yTO=f(xTO,xTS→TE,WV,WK,WQ)
(1)
其中,WV为dx×dν维的值(Value)参数矩阵,WK为dx×dk维的键(Key)参数矩阵,WQ为dx×dq维的查询(Query)参数矩阵,其中dx为依赖序列xTS→TE内每个元素的维度。在所考虑的流量预测问题中,每个元素为各个时隙内传输的字节数,因此dx=1。在其他问题中,dx可以大于1。例如,在机器翻译问题中,每个元素为句子中的单词经过词嵌入后的向量表示,dx为该向量的维度。
在式(1)中,矩阵WQ,WK,WV为需要通过反向传播等算法来进行监督学习的参数,其作用与全连接神经网络中的权重矩阵类似,可以把原始空间中的输入xTO和xTS→TE映射到另外的空间,使得在新的空间中进行分类、回归等任务更加容易。具体而言,把目标值与查询参数矩阵相乘,可以得到查询矩阵QTO,把依赖序列与键参数矩阵和值参数矩阵分别相乘,可得到键矩阵KTS→TE和值矩阵VTS→TE,即:
QTO=xTOWQ
(2)
KTS→TE=xTS→TEWK
(3)
VTS→TE=xTS→TEWV
(4)
其中矩阵QTO为xTO由WQ映射后在新空间中的表示,矩阵KTS→TE和VTS→TE为xTS→TE分别由WK和WV映射后在新空间中的表示。根据QTO和KTS→TE,可进一步得到反映依赖程度的加权值(即相关系数)向量:
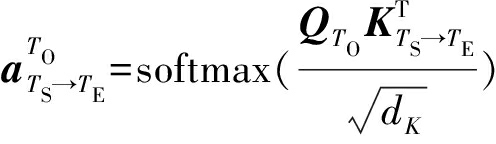
(5)
其中,运算softmax(x)=exp(-x)/‖exp(-x)‖1可把加权值归一化到(0,1)区间、且所有加权值之和为1。矩阵运算
可以衡量QTO和KTS→TE之间的相关性,即目标值xTO和依赖序列xTS,…,xTEVTS→TE在经过空间映射后的相关性。相关性越强,加权值越大。
利用
对矩阵中的各行进行加权,可得到注意力函数的输出:
(6)
进一步由式(4)可知,yTO可看作依赖序列xTS→TE经过空间映射后的加权和。
把式(2)～(5)代入式(6)中,可把注意力函数表示为:
yTO=f(xTO,xTS→TE,WV,WK,WQ)
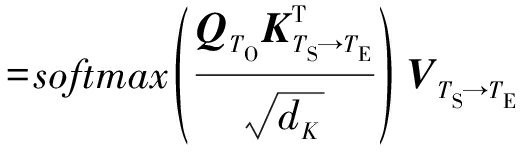
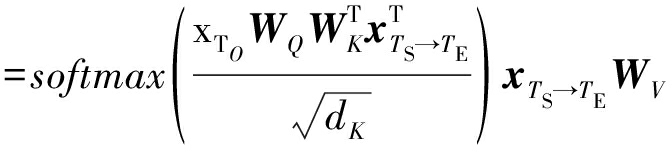
(7)
为了增强目标值与依赖序列之间注意力的表示能力,文献[11]进一步提出了多头注意力机制(Multi-head attention),即把H个WV、WK和WQ矩阵分别代入到式(7)中,从而产生多个注意力函数的输出。给WV、WK、WQ和yTO加入上标h,则多个注意力函数为:
……
(8)
把多个函数的输出级联在一起,即可得到多头注意力机制的输出
2.2.2 神经网络结构
用于多步流量预测的神经网络结构如图2所示,其中由完全注意力机制实现由编码器-解码器构成的序列-序列(Sequence-to-sequence,S2S)预测结构[12],而非使用LSTM等RNN实现。由图可见,在预测窗内的每一时隙(如第tq个时隙,图中解码器部分由实线表示,其余时隙由虚线表示),编码器的输入为观测窗内的流量数据
解码器的输入为观测窗内最后一个时隙的历史数据和预测窗内在第tq个时隙以前已经预测得到的流量数据
解码器在第tq个时隙的输出为该时隙的流量预测值
然后,在第tq+1个时隙,解码器把
反馈给解码器的输入,用于进行第tq+1个时隙的流量预测。
由以上叙述可看出,在利用上述网络进行预测时,解码器在预测窗内各个时隙的输出是顺序得到的,且在每一时隙内解码器的输入维度不同。为了保证网络结构不变,对于还未进行预测的时隙(即对于tq<τ<t+N时隙)给解码器输入设置缺省值
或
。这样,在预测窗的各个时隙内,解码器的输入维度均为预测窗的长度N。
图2所示的神经网络结构包含三种类型的中间层:自注意力层、编码器-解码器注意力层和全连接层。自注意力层和编码器-解码器注意力层都使用第2.2.1节所叙述的多头注意力机制实现,但对于不同种类的注意力层,目标值xTO和依赖序列xTS→TE有所不同:
·编码器内自注意力层的作用与由RNN构成的传统S2S模型(下文称作传统模型)中编码器内相邻时间步的权重连接类似,都用于表示编码器内每一时隙的输入受到编码器内所有时隙输入的影响,因此
图2 用于多步流量预测的神经网络结构
Fig.2 Neural network structure for multi-step traffic load prediction
·解码器内自注意力层的作用与传统模型中解码器内相邻时间步的权重连接类似,用于表示解码器内当前时隙tq的输入(即第tq-1个时隙的解码器输出)受到解码器内所有时隙的输入的影响,因此
·编码器-解码器注意力层的作用与传统模型中编码器和解码器之间的权重连接类似,用于衡量解码器内第tq个时隙的输出ytq对编码器输出zt-M+1,…,zt的依赖程度,因此xTO=ytq,xTS→TE=[zt-M+1,…,zt]T。
在传统RNN中,只存在相邻时隙之间的连接,因此表示目标值与依赖序列相关性的能力会随着二者时间间隔的增加而减弱。而由式(7)可知,自注意力层中包含了目标值和依赖序列中每个值之间的权重连接,因此表示能力比传统模型更强。
全连接层由权重矩阵、偏置向量和激活函数来表示。编码器内的权重矩阵和偏置向量分别记为We和be,解码器内的权重矩阵和偏置向量分别记为Wd和bd,激活函数为ReLU函数(σ(x)=max(x,0))。全连接层的输入为注意力层的输出(例如yt),全连接层的输出可表示为σ(Weyt+be)或σ(Wdyt+bd)。
综上所述,对于预测窗内各个时隙(以第tq个时隙为例),神经网络的输入与输出之间的关系可用如下的函数来表示:
(9)
其中,W表示神经网络中的所有参数,包括注意力函数中的系数矩阵
和全连接层的权重矩阵We、Wd及偏置向量be、bd。
在利用上述网络进行流量预测时,由于解码器各个时隙的输出是顺序得到的、且各个时隙的预测值有误差,因此这一误差会随着预测窗内时隙的增加而累积,即预测越远处的未来流量累计误差越大。
2.2.3 训练过程
为了使训练好的神经网络能够对流量的变化有足够强的泛化能力,训练集应当在每天的不同时间生成,即预测窗的开始时刻(第t个时隙结束时)应当在每天测量的历史数据中随机选择。编码器的输入为观测窗(即第t-M+1个时隙到第t个时隙)内的流量数据
解码器的期望输出(即用于监督学习的标签)为预测窗(即第t+1个时隙到第t+N个时隙)内的流量数据在训练过程中,把解码器的输入设为期望输出
而不是每一时隙内神经网络输出的预测值,是因为在训练过程中期望输出已知、可由训练样本得到,使用期望输出代替神经网络的实际输出可避免误差累积。为了与下文中的测试过程保持一致,对于当前时隙(例如第tq个时隙)以后的各个时隙τ>tq,均令xτ=0或xτ=-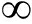。每个训练样本都由观测窗内的历史数据和预测窗内的期望输出
构成。
训练目标为使由神经网络实际与期望输出之间的经验均方误差(mean square error,MSE)最小,即:
(10)
其中,Ntrain为训练集的大小,
和
分别为由第n个训练样本得到的神经网络实际输出和第n个训练样本中的期望输出。在训练过程中,反向传播算法由迭代批梯度下降优化算法[13]实现,学习率由Adam算法[16]自适应更新。
2.2.4 测试过程
在预测窗开始时,首先给神经网络的编码器输入观测窗内的历史数据并给解码器的第一个时隙输入观测窗内最后一个时隙的历史数据xt,其余时隙输入缺省值(0或-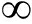)。其次,训练好的神经网络可输出第t+1个时隙的流量预测值
然后,使用
替换解码器内第二个时隙的缺省值,神经网络可输出
以此类推,直至顺序地输出预测窗内所有时隙内的流量预测值
3 实验与数值结果
本节利用实测的高分辨率流量数据集,来评估用所设计的神经网络在预测网络流量时的复杂度和预测性能,并通过数值结果理解全注意力机制的预测机理。
3.1 流量数据集与样本生成
所使用的原始数据集为在某校园网网关实测得到的流量数据,包含48天内有线和无线网络的流量,每天测量的时间为早晨8:00至10:00,记录的分辨率为1秒。图3为其中7天内实测的流量数据。
为了得到不同分辨率(即一个时隙的长度)Δ的流量数据集,每隔Δ秒对原始数据集每秒测量的流量数据求和。例如,若Δ=30秒,则每隔30秒对每秒测量的数据求和。如果没有特别说明,下面都使用30秒分辨率的数据集。
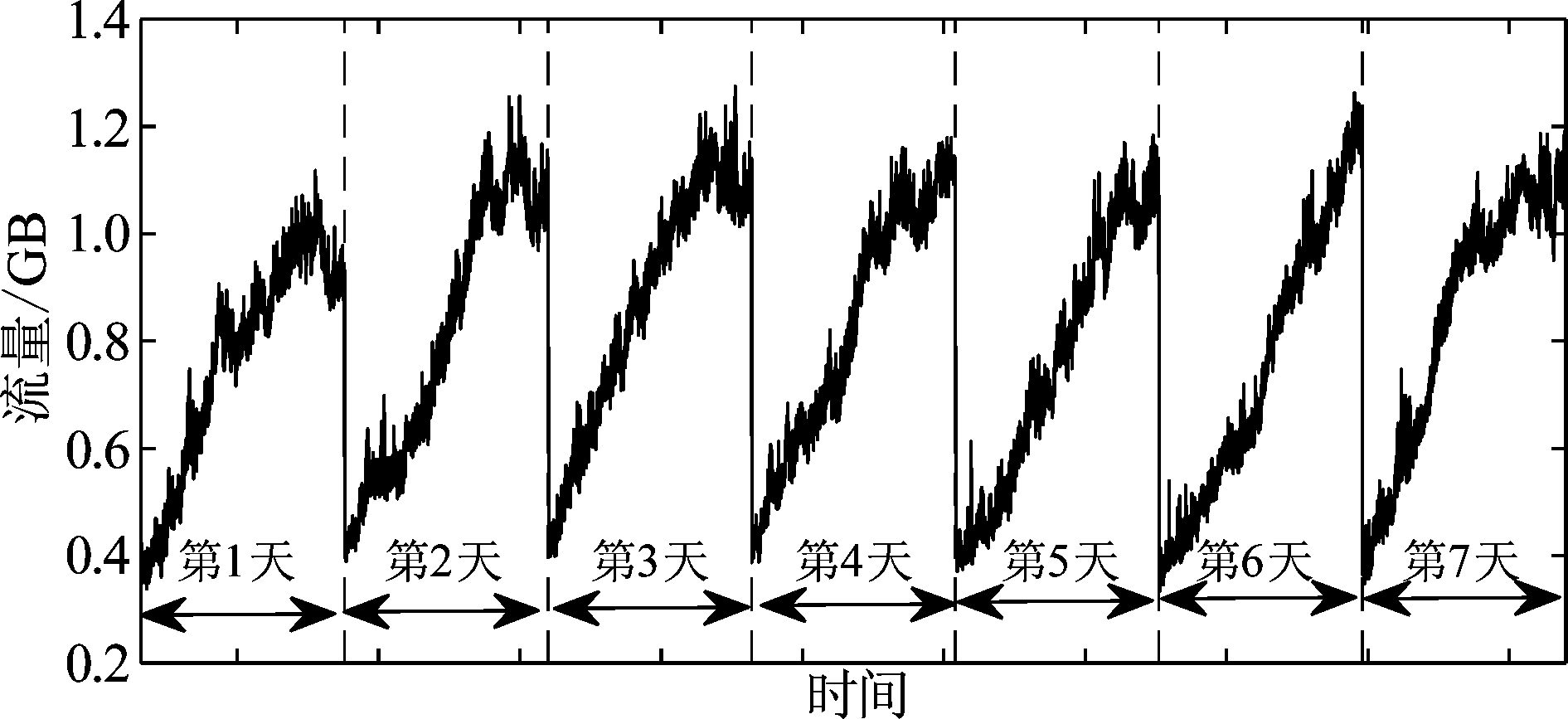
图3 秒级分辨率的实测流量数据
Fig.3 Real data of traffic load measured with one-second resolution
生成每个样本的方法如下。从每一天8:00的数据开始,把第一个时隙作为观测窗的开始、直至第M个时隙的数据作为样本中的输入,把第M+1个时隙作为预测窗的开始、直至第M+N个时隙的数据作为样本中的期望输出;然后在上一个观测窗的开始时刻加上X个时隙作为下一个样本中预测窗的开始,重复以上过程,直至使用完该天的数据;对于训练集,X=1;对于测试集,为了在连续的时间内得到流量预测,X=N。在后续仿真实验中,利用数据集中前32天数据生成的样本作为训练集,后16天数据生成的样本作为测试集从而评估流量预测的性能。
3.2 比较基准与性能指标
为了评估所设计的基于全注意力机制网络(图标为“注意力网络”)的性能,在实验中与S2S预测模型[13](图标为“S2S网络”)进行比较,从而分析引入注意力机制在哪方面有优势;还与文献[14]中提出的利用单输出方式进行多步序列预测的模型(图标为“GRU网络”)进行比较,从而分析引入编码器-解码器结构是否带来性能增益;为了分析神经网络相对于传统预测模型的优势,还与ARIMA[5]和SVR进行比较。其中,文献[14]中提出的预测模型如图4所示,对于第τ个时隙的期望输出xτ,RNN网络的输入为与时隙τ间隔为预测窗长度N的一段长为M-N的观测数据[xτ-M,…,xτ-N-1]T。利用该网络结构,给定观测窗数据通过将其分为N个长为M-N的序列[xt-M+1,…,xt-N]T,…,[xt-M+N+1,…,xt]T并分别输入到RNN网络中,网络可分别输出预测窗内各个时隙的预测值
为了降低训练复杂度,下面把文献[14]中采用的LSTM变为GRU,其超参数已经进行调节达到最优性能。实验结果表明,使用GRU预测的性能与LSTM网络相同,但训练时间仅为LSTM的2/3。为了进行公平比较,S2S模型的编码器和解码器也都采用GRU。
预测性能包括预测精度和预测延时,因为预测误差不能反映预测延时。预测精度可以由预测误差的均值和标准差来反映,也可以平均相对百分比误差(mean relative percentage error,MRPE)来表示:
(11)
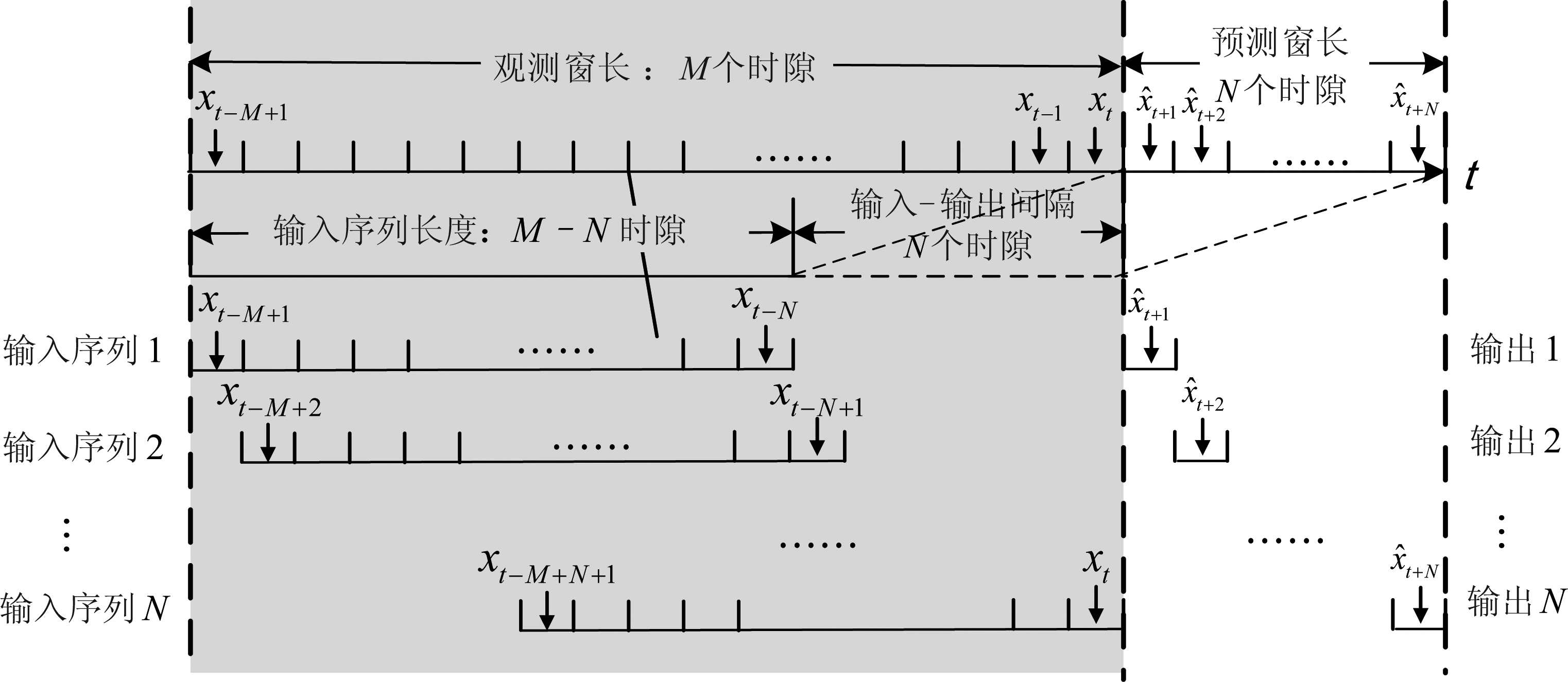
图4 利用单输出RNN网络进行多步预测[14]
Fig.4 Multi-time step prediction with single-output RNN
其中
为第n个测试样本在第t+i个时隙(即预测窗内第i个时隙)的神经网络输出,
为第n个测试样本在第t+i个时隙内的期望输出,Ntest为测试集大小。
实验中还将评估训练和测试阶段的计算复杂度。所有的实验均使用一台4核英特尔CPU、英伟达1080Ti GPU和32GB内存的计算机、在Python 3.6.0与Pytorch 1.0.0平台下实现。
3.3 超参数设置
通过实验发现,把每一时隙τ的单维流量数据xτ利用更细粒度的数据扩展至多维、即
可以达到更好的预测性能,其中
为第τ个时隙和第τ+1个时隙之间第i秒的流量数据,可以通过对以每秒分辨率记录的原始数据下采样得到。
图5是对多头注意力函数个数H和流量数据维数的实验结果。从图5(a)中可以看出,采用多头注意力比单头注意力的预测性能好,H=8时性能达到最优。从图5(b)中可以看出,考虑每时隙的多维流量数据比一维流量数据的预测性能好,综合考虑预测性能和训练复杂度,把流量数据维数选为4。
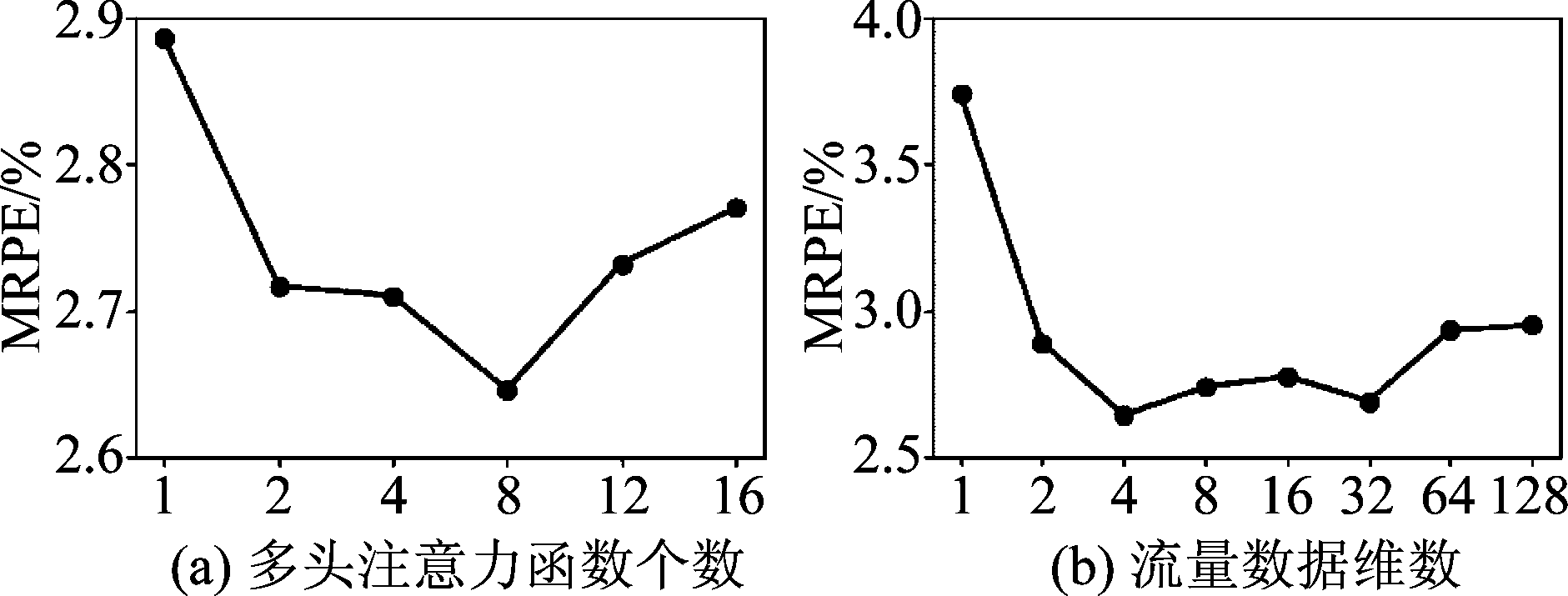
图5 超参数控制变量实验结果
Fig.5 Hyperparameters controlling variables
通过调参,可以得到表1所示的超参数,此时神经网络能够达到最好的性能。
如果没有特别说明,下面实验中的观测窗长度M=60Δ(当分辨率Δ为30秒时,观测窗长1800秒),预测窗长度N=1Δ～20Δ(当Δ为30秒时,预测窗长为30秒～600秒)。
表1 神经网络的超参数设置
Tab.1 Hyperparameters of neural network
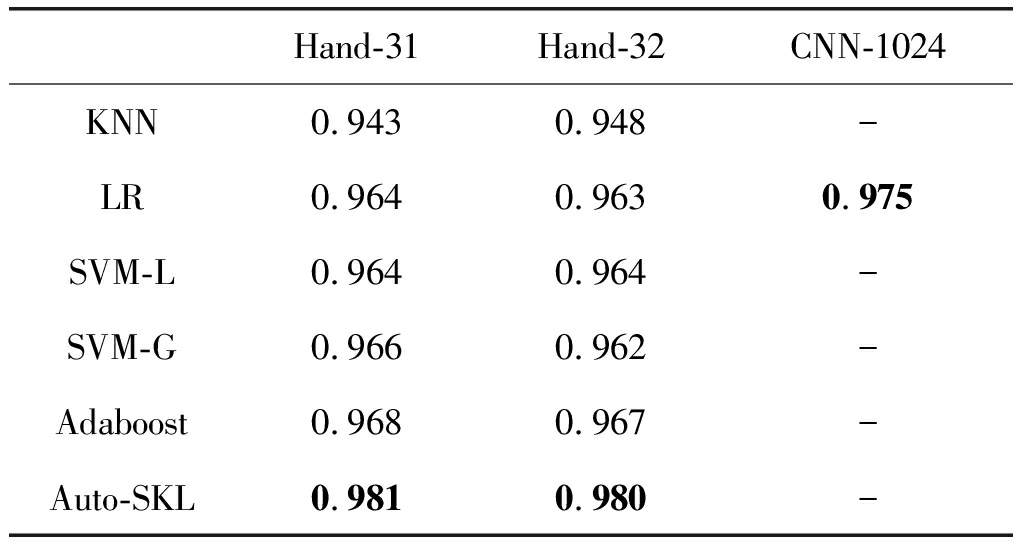
Hand-31Hand-32CNN-1024KNN0.9430.948-LR0.9640.9630.975SVM-L0.9640.964-SVM-G0.9660.962-Adaboost0.9680.967-Auto-SKL0.9810.980-
3.4 实验结果与分析
3.4.1 样本和时间复杂度
下面先比较“注意力网络”、“S2S网络”、“GRU网络”、ARIMA方法和SVR方法的训练和测试时间,其中观测窗包含60个时隙(即30分钟),预测窗包含10个时隙(即5分钟)。对于“注意力网络”、“S2S网络”、ARIMA方法和SVR方法,在测试集上接近最优性能所需的训练样本数为3000;对于“GRU网络”,在测试集上接近最优性能所需的训练样本数为5000。可见“注意力网络”、“S2S网络”、 ARIMA方法与SVR方法的样本复杂度相当,都低于“GRU网络”。
三种模型的测试集样本数均为192。实验结果如表2所示。
可以看出,“注意力网络”的训练和测试时间都短于“GRU网络”和“S2S网络”。这是因为“GRU网络”相邻时间步的隐含层输出存在权重连接,这一串行结构使其利用GPU的并行计算受到限制;而“注意力网络”不包含这种权重连接,因此能够利用GPU的并行计算能力提高训练和预测速度。此外,ARIMA和SVR方法的训练时间远小于各神经网络,SVR方法的测试时间小于其他方法。
表2 不同预测方法的训练和测试时间
Tab.2 Comparison of different methods in training time and testing time
神经网络注意力S2SGRUARIMASVR训练时间51秒2分39秒3分5秒2秒3秒测试时间50.8毫秒166.5毫秒80.8毫秒55.1毫秒30.0毫秒
3.4.2 预测性能
下面首先比较“注意力网络”、“S2S网络”和“GRU网络”这三种神经网络的预测性能。
图6为预测窗长为20个时隙时三种神经网络对预测窗内各个时隙流量预测的MRPE随着预测窗时隙标号i增长的变化。可以看出,当使用“GRU网络”进行预测时,MRPE在预测窗的各个时隙内变化不大,而使用“注意力网络”和“S2S网络”进行预测时,MRPE在预测窗内总体呈现上升趋势。这是因为:(1)“注意力网络”和“S2S网络”为多步输出模型,输入序列与所预测时隙间的相关性随两者时间间隔的增大而减小;(2)“注意力网络”和“S2S网络”在各个时隙的预测值会反馈到解码器的输入端来进行下一个时隙的预测,这一递归结构使得预测误差随时间增长不断累积,因此预测误差逐渐增大。与之相反,“GRU网络”使用单步输出模型进行多步预测,输入序列与预测点之间的时间间隔固定为预测窗长,不存在误差累积的问题,因此MRPE在整个预测窗内变化范围不大。为了验证上述解释,我们在同样的观测与预测窗长和观测分辨率下进行了两步预测,分别预测第10和第20个时隙的流量,此时对于第20个时隙的流量,“注意力网络”和“S2S网络”的MRPE为4.828%和5.044%,远小于图6中的“注意力网络”、“S2S网络”和“GRU网络”的相应值(6.736%、6.310%、5.150%)。更多的实验结果表明,使用SVR方法进行预测时,MRPE在预测窗内也呈现上升趋势;使用ARIMA方法进行预测时,MRPE在整个预测窗内变化范围不大,但远大于其他的预测方法。为了简洁,该结果并没有呈现在图6中。
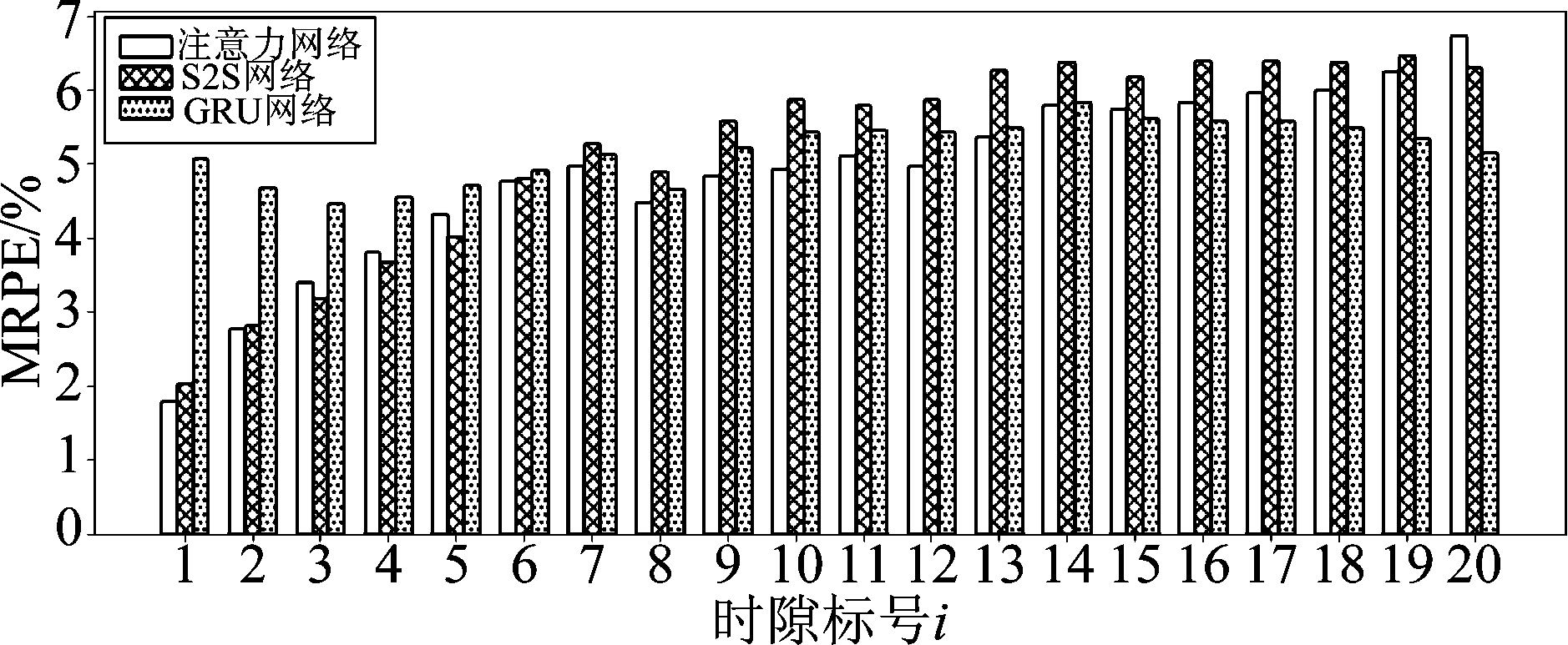
图6 MRPE随预测时间的变化,分辨率Δ=30秒,观测窗长为M =100Δ
Fig.6 MRPE versus time slot i in prediction window,Δ=30 s, M =100Δ
图7为预测窗长为N=5个时隙(即150秒)时“注意力网络”和“GRU网络”的预测结果(“S2S网络”的结果与“注意力网络”类似,故未给出)。尽管两种网络的整体预测效果相差不大,但是如果把其中一部分放大,可以看到“GRU网络”的预测结果存在一定程度上的滞后现象,即预测值的变化滞后于真实值的变化。这一滞后现象可由以下的方法验证。在图7下面子图的结果中,“GRU网络”预测值与真实值之间的MRPE为3.39%;而若把“GRU网络”的预测值向左侧平移5个时隙,则平移后的值与真实值之间的MRPE为1.51%。在图7上面子图的结果中,“注意力网络”网络的MRPE为2.89%,平移后的MRPE为2.48%。可以看出,“GRU网络”的MRPE在平移后下降较多。出现滞后现象的原因是“GRU网络”的输入与输出值之间始终相隔N=5个时隙,只能通过5个时隙之前的流量变化情况进行预测,因此无法较好地预测流量突变;而“注意力网络”和“S2S网络”的输入与输出值之间没有间隔。
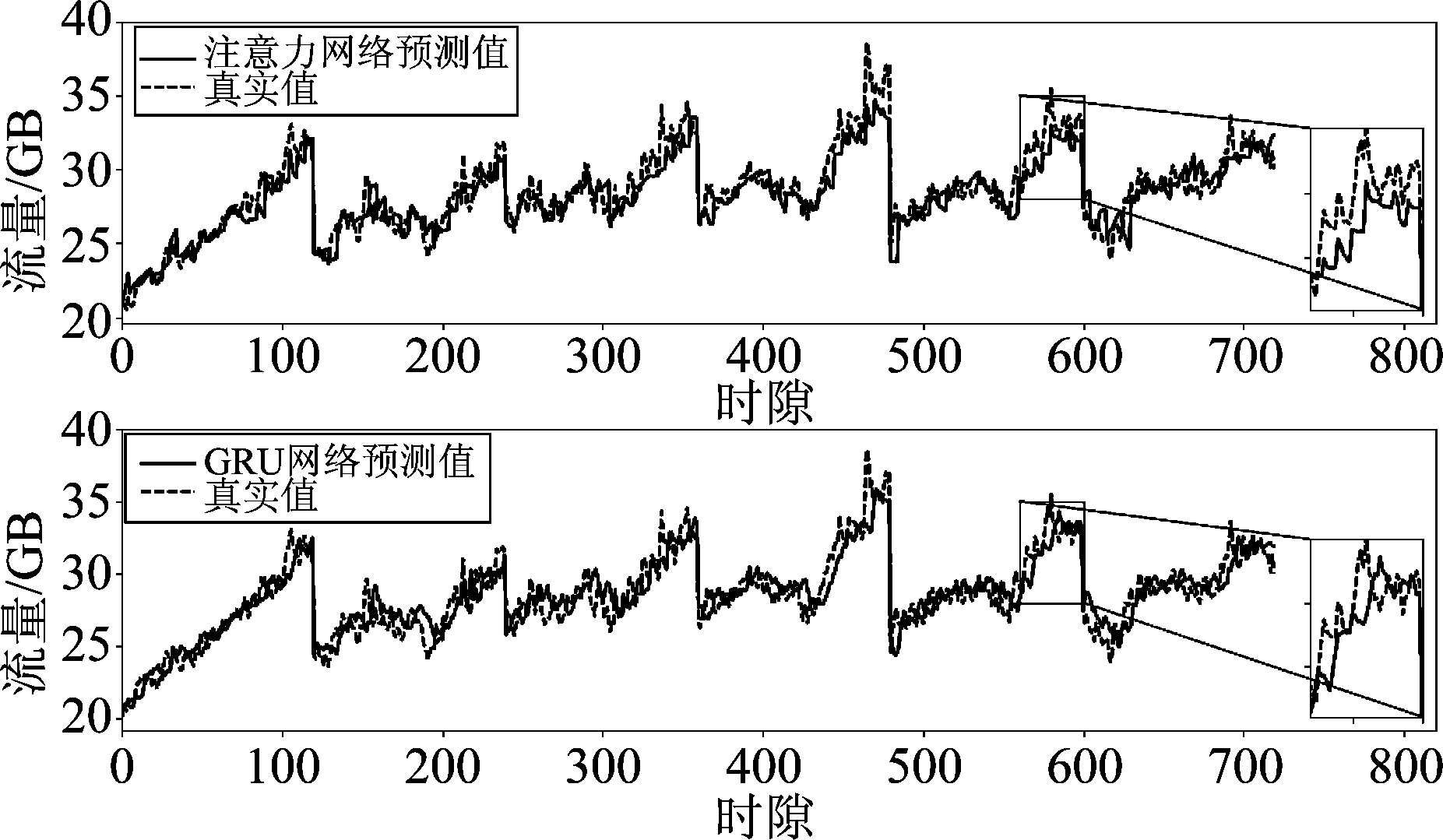
图7 不同网络的流量预测结果,分辨率Δ=30秒,预测窗长为N=5Δ (150秒)
Fig.7 Comparison of different neural networks in traffic load prediction, Δ=30 s, N=5Δ (150 s)
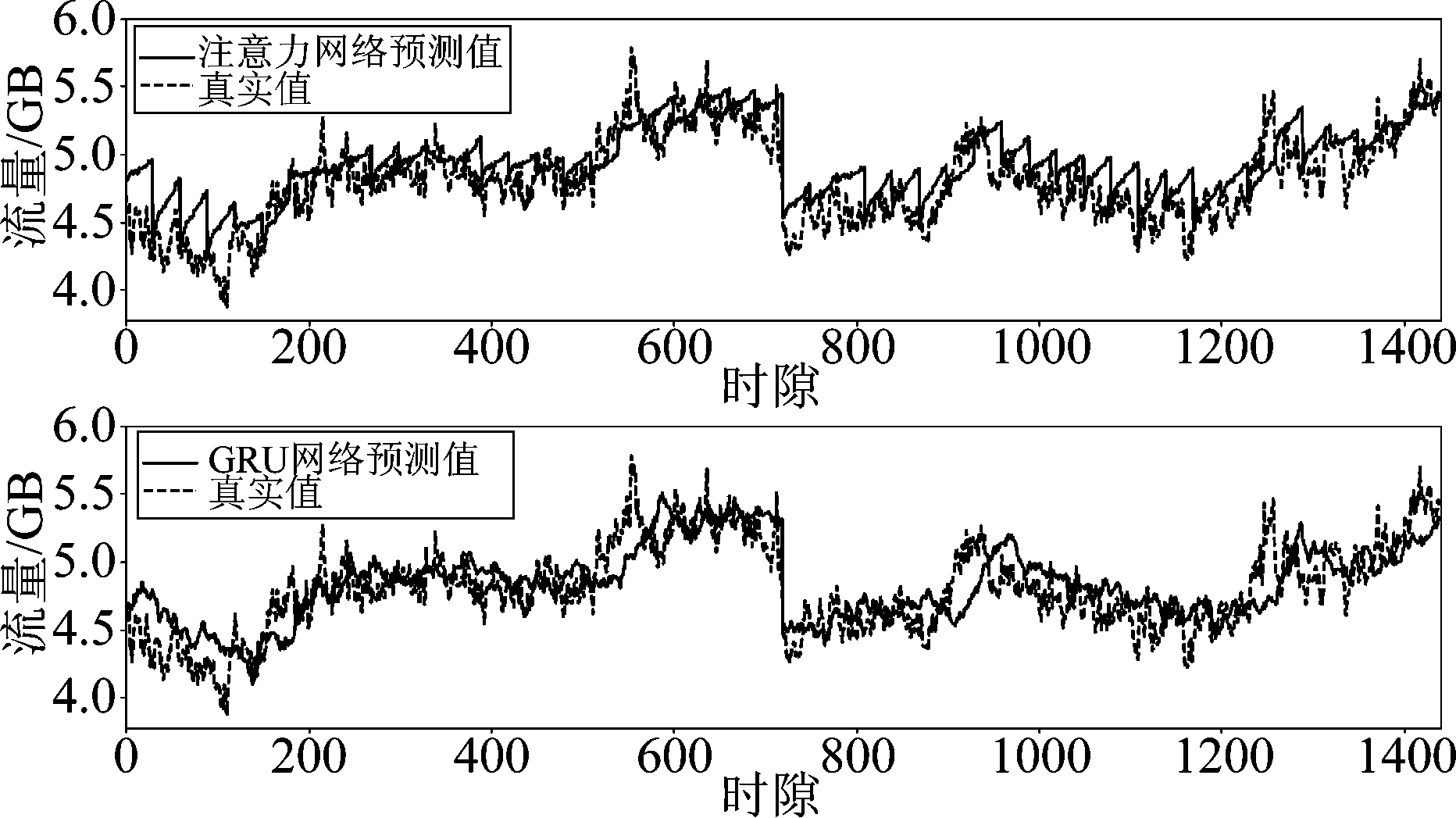
图8 高分辨率时的流量预测结果,Δ=5秒,预测窗长为N=30Δ(150秒)
Fig.8 Traffic load prediction with high resolution, Δ=5 s, N=30Δ(150s)
为了观察两种模型在更高分辨率时的预测性能,图8给出了在分辨率为5秒时的预测结果。观测窗长为M=360个时隙(1800秒),预测窗长为N=30个时隙(150秒),即两个窗长与图7相同。可以看出,预测性能相对于分辨率为30秒时的结果差。这是因为流量的短期变化存在更强的随机性,时间相关性更弱。
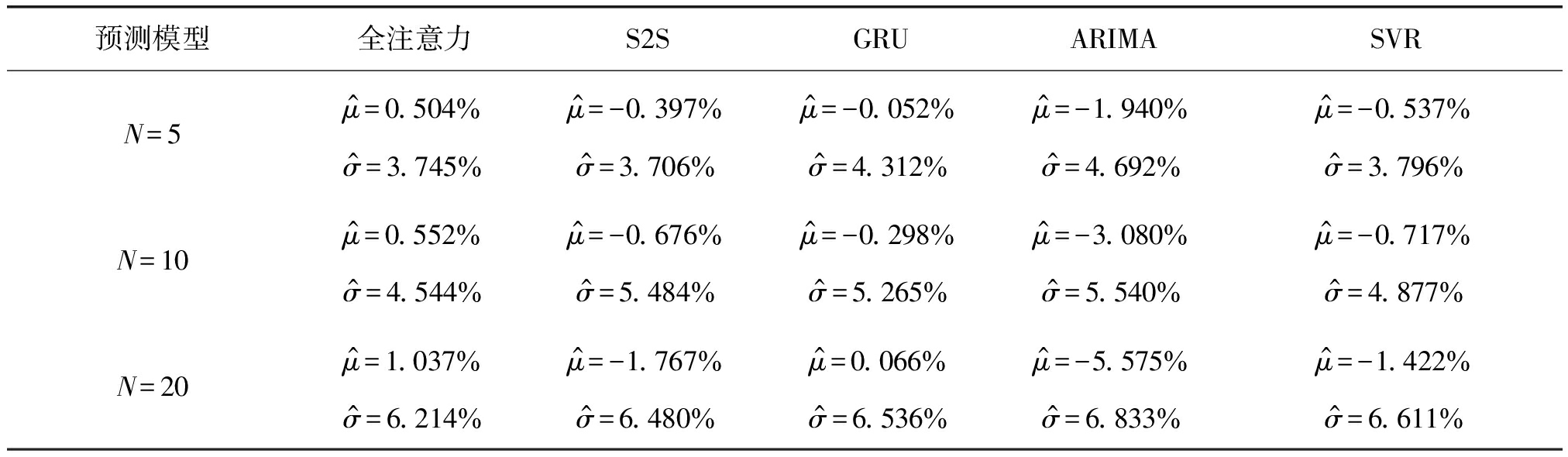
为了研究不同预测模型的误差统计特性,我们对预测结果的绝对和相对误差分布进行了拟合,其中相对误差为绝对误差除以真值。拟合结果表明,除ARIMA模型外,其他模型的绝对误差和相对误差的都大致服从高斯分布,而ARIMA模型的误差分布在一定范围内与高斯分布基本吻合、但比高斯分布的拖尾更长。表3列出了分辨率为30秒时五种预测模型的相对误差统计特性,其中
为对预测窗内所有时隙流量预测相对误差的均值,
表示相应的标准差。
从表中可以看出,随着预测窗长增长,所有预测模型的预测误差均值和标准差都会增大,而当预测窗长为10和20个时隙时,“注意力网络”的标准差最小。ARIMA模型的预测误差均值与标准差都大于其他模型,其中预测误差均值相对于其他模型差异较为明显。“注意力网络”的预测误差均值与标准差都略小于SVR方法。另外,ARIMA模型与“GRU网络”类似,存在预测延时现象,且延时现象更明显。
3.4.3 编码器-解码器注意力层的依赖程度分析
为了进一步理解注意力机制,以编码器-解码器间的注意力层为例,观察经过训练后神经网络学习到的依赖程度(即加权值
由于实测流量数据集具有非平稳的特点,因此序列值之间的相关性非常复杂。为了便于分析依赖程度与序列相关性之间的联系,考虑一个简单的时间序列——一阶自回归模型来生成训练和测试样本,其自相关系数与时隙间隔τ之间的关系如图9(a)所示,在时隙间隔τ≤4时,序列值之间的相关性较大。
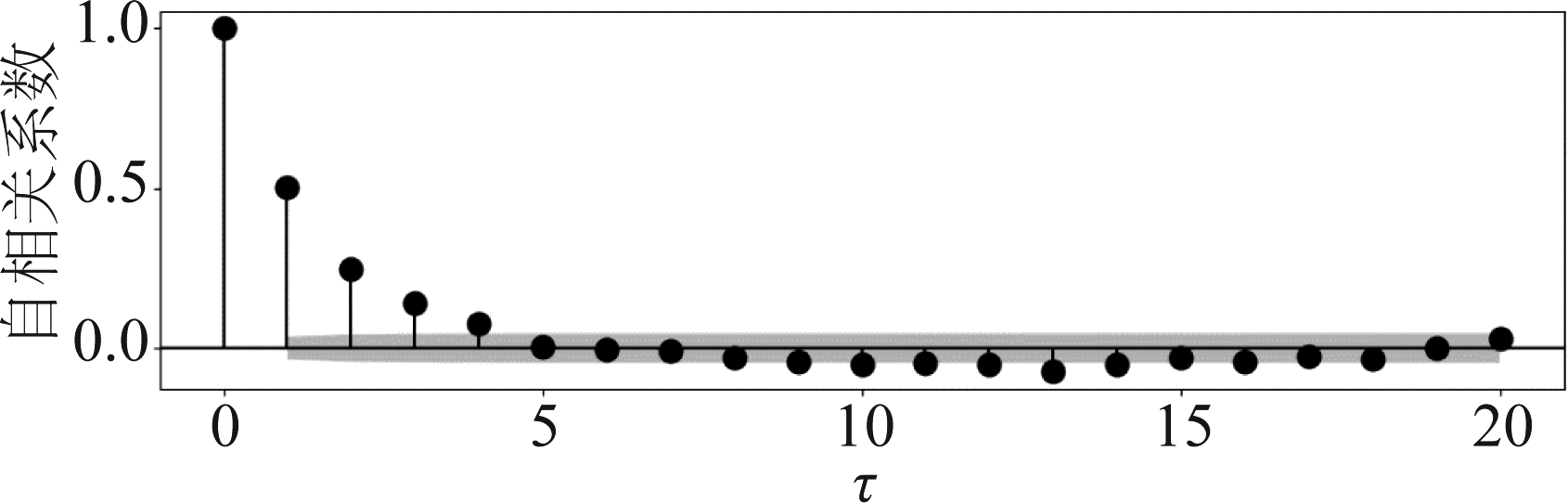
图9(a) 一阶自回归序列的自相关系数
Fig.9(a) Autocorrelation coeficient of first order autoregressive model
图9(b) 编码器-解码器注意力层内加权值的可视化图,M=20
Fig.9(b) Visualization of the weighting values in the encoder-decoder attention layer
图9(b)是训练完成后编码器-解码器注意力层内加权矩阵A=
...,
T的可视化图,图中的第i(i=0,1,2,3,4)行是观测(即第t-M+1到第t个时隙)序列对第t+i个时隙预测值的加权值
从图中可见,随着观测窗内时隙序号增加(即越靠近预测窗开始的时隙),加权值逐渐上升(即颜色变浅),最后5个时隙(即与预测窗开始的时隙间隔最小的5个时隙)的加权值较大,与该序列的自相关函数特点基本相符。随着预测窗内时隙序号的增加(即越远离预测窗开始的时隙),加权值逐渐下降,即相关性逐渐减弱。以上结果表明,注意力模型能够学习到相关性比较明显的序列之间的特征。
表3 不同预测模型相对误差统计特性的拟合结果
Tab.3 Statistics of relative errors of different prediction models
预测模型全注意力S2SGRUARIMASVRN=5μ^=0.504%σ^=3.745%μ^=-0.397%σ^=3.706%μ^=-0.052%σ^=4.312%μ^=-1.940%σ^=4.692%μ^=-0.537%σ^=3.796%N=10μ^=0.552%σ^=4.544%μ^=-0.676%σ^=5.484%μ^=-0.298%σ^=5.265%μ^=-3.080%σ^=5.540%μ^=-0.717%σ^=4.877%N=20μ^=1.037%σ^=6.214%μ^=-1.767%σ^=6.480%μ^=0.066%σ^=6.536%μ^=-5.575%σ^=6.833%μ^=-1.422%σ^=6.611%
4 结论
本文研究了如何把全注意力机制引入高分辨率多步流量预测的问题,在一个实测流量数据集上对所设计的预测方法进行了评估,并与其他两种基于循环神经网络的预测模型和传统线性、非线性预测模型进行了比较。研究结果表明,与其他基于神经网络的模型相比,基于全注意力机制网络具有可解释性、且时间复杂度最低、预测误差标准差较小;与基于编码-解码结构的模型相比,基于全注意力机制网络的样本复杂度相当;与SVR模型相比,基于全注意力机制网络的预测精度略高;ARIMA模型的预测误差远大于神经网络模型、且存在预测延时。
[1] Bui N, Widmer J. Data-driven Evaluation of Anticipatory Networking in LTE Network[J]. IEEE Trans. Mobile Comput., 2018, 17(10): 2252-2265.
[2] Yao C, Yang C, Xiong Z. Energy-Saving Predictive Resource Planning and Allocation[J]. IEEE Trans. Commun., 2016, 64(12): 5078-5095.
[3] Guo J, Yang C, Chih-Lin I. Exploiting Future Radio Resources with End-to-end Prediction by Deep Learning[J]. IEEE Access, 2018, 6(1): 75729-75747.
[4] Sadek N, Khotanzad A, Chen T. ATM Dynamic Bandwidth Allocation Using FARIMA Prediction Model[C]∥IEEE ICCCN 2013, 2013: 359-363.
[5] Zhang G P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model[J]. Neurocomputing, 2003, 50(none): 159-175.
[6] 高茜, 李广侠, 田湘, 等. 基于突发分离的自相似网络流量预测[J]. 信号处理, 2012, 28(2): 158-165.
Gao Q, Li G X, Tian X, et al. Self-similar Network Traffic Prediction Based on Burst Decomposition[J]. Signal Processing, 2012, 28(2): 158-165.(in Chinese)
[7] Xu Y, Xu W, Yin F, et al. High-Accuracy Wireless Traffic Prediction: A GP-Based Machine Learning Approach[C]∥IEEE GLOBECOM 2017, 2017: 1- 6.
[8] Wang J, Tang J, Xu Z, et al. Spatiotemporal Modeling and Prediction in Cellular Networks: A Big Data Enabled Deep Learning Approach[C]∥IEEE INFOCOM 2017, 2017: 1-9.
[9] Nie L, Jiang D, Yu S, et al. Network Traffic Prediction Based on Deep Belief Network in Wireless Mesh Backbone Networks[C]∥IEEE WCNC 2017, 2017: 1-5.
[10] Li R, Zhao Z, Zheng J, et al. The Learning and Prediction of Application-Level Traffic Data in Cellular Networks[J]. IEEE Trans. Wireless Commun., 2017, 16(6): 3899-3912.
[11] Vaswani A, Shazeer N, Parmar N, et al. Attention Is All You Need[C]∥NIPS 2017, 2017: 5998- 6008.
[12] Neubig G. Neural Machine Translation and Sequence-to-sequence Models: A Tutorial[J]. arXiv preprint arXiv: 1703.01619, 2017.
[13] Sutskever I, Vinyals O, Le Q V, et al. Sequence to Sequence Learning with Neural Networks[C]∥NIPS 2014, 2014: 3104-3112.
[14] Zhang W, Liu T, Yang C. Trajectory Prediction with Recurrent Neural Networks For Predictive Resource Allocation[C]∥IEEE ICSP 2018, 2018: 1- 6.
[15] Goodfellow I, Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT Press, 2016.
[16] Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[J]. arXiv preprint arXiv: 1412.6980, 2014.
