1 引言
随着船舶自动识别系统(Automatic Identification System, AIS)在全球范围内的普及和应用,海事主管机关及相关行业部门能够通过AIS数据准确的获取船舶位置、轨迹,并对船舶行为进行监视[1]。正常情况下,B类动态AIS数据信息上报的时间间隔通常为30 s[2],但是在实际过程中由于AIS设备的信息发送不及时、人为等不可靠因素,导致无法准确的判断船舶位置[3]。为解决船舶数据的完整性、连续性及精度等问题,基于AIS数据完整性地估计船舶航行轨迹成为目前亟待解决的难点之一[4]。
目前国内外针对运动轨迹预测的研究已经取得了系列的研究成果。Jaskolsk[5]等人通过离线时间序列轨迹数据预测船舶线性轨迹运动,在部分轨迹缺少传输链路的情况下提高轨迹质量。然而大多数情况下船舶的运动较为复杂,满足线性条件的情况较小。Sapankevych和Jiang[6]等人使用支持向量机的方法对轨迹数据进行时间序列上的预测,国内王艳锋[8]等人同样使用支持向量机算法对桥区水域失控船舶航迹进行预测。Simsir[9]等人通过神经网络解决了船舶在狭窄水域的轨迹预测问题,但是上述应用均存在训练样本效率低等问题。Qiao[10]等人将隐性马尔科夫模型HMM应用于移动对象的轨迹预测,但是在大数据环境下算法的运行时间较长,性能较低。Fossen[11]等人通过将船舶全局运动参数加入系统状态方程中,构建XKF滤波器完成对船舶运动模式的实时预测,但是模型在针对近180度的机动角度航迹问题时,存在误差较大等问题。周同驰[15]等人通过KTH和UCF-sports行为数据库提取的相对运动点轨迹能够描述对象的运动变化跟踪相对运动超像素内的兴趣点来产生轨迹,并采用轨迹的方向梯度、运动边缘、方向统计及其组合作为分类器的输入来识别行为。
本文针对AIS数据频率较低、运动模式变化较多、轨迹机动较大等情况,通过多项式拟合的方式构建轨迹模型补偿定位数据信息缺失、更新较慢的问题,进而对轨迹进行滤波预测。在研究船舶轨迹预测方面使用多项式卡尔曼滤波算法(Polynomial Kalman Filter, PKF)主要有以下两个方面的优势[12]:
(1)船舶的运动状态往往变化频繁,难以用简单的模型进行推算,多项式卡尔曼滤波算法能够通过对系统状态进行最优估计获取实时的运行状态估计和预测,对于我们掌握关注船舶的运动行为具有很重要的意义。
(2)多项式卡尔曼滤波算法对于变换运动状态的移动对象具有较高的自适应性,在研究轨迹预测上实时性较强。
2 船舶信息预处理
在实际的船舶信息数据获取过程中,由于AIS设备发生信号漂移或人为遮掩、篡改等原因,往往会存在AIS数据显示在陆地或航速出现超速异常等行为[13],为了保证数据的使用质量,需要对船舶AIS信息进行预处理。
某段时间内船舶的航行平均速度可由式(1)进行估算。
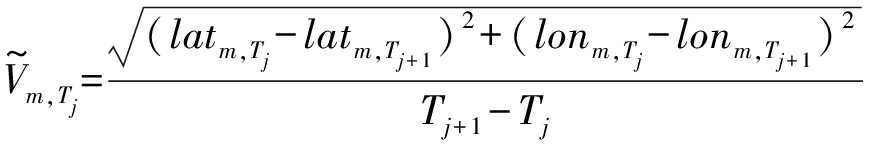
(1)
式中latm,Tj和lonm,Tj是船m在Tj时刻的经纬度坐标,此时船舶速度应满足:
Vm,Tj-bm(Tj+1-Tj)≤Vm,Tj≤Vm,Tj+am(Tj+1-Tj)
(2)
其中am和bm分别为船舶前进时的正向和反向加速度。当前的数据被鉴定为异常速度时,我们采取近两点的平均速度对数据进行更新。

(3)
对于数据的位置信息,同理我们可以通过式(4)进行检验。
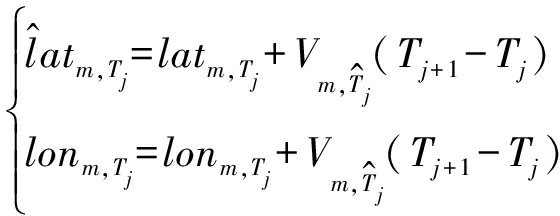
(4)
其中,![]() 和
和![]() 分别为船在Tj+1时刻的经纬度坐标。如果当前时刻经纬度坐标不满足式(4),则需要对位置信息进行如下变换。
分别为船在Tj+1时刻的经纬度坐标。如果当前时刻经纬度坐标不满足式(4),则需要对位置信息进行如下变换。
≤0.5am(Tj+1-Tj)2
(5)
AIS广播播报的船舶速度往往为当前时刻的速度情况,对应当前时刻的对地航向应将船舶速度转化为X、Y轴上的方向速度向量,如图1分解所示。其中航速在Tj时刻X轴和Y轴上的分量分别为Vx,Tj和Vy,Tj。
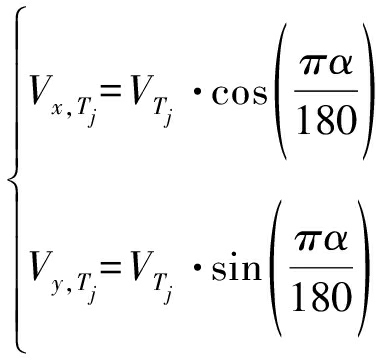
(6)
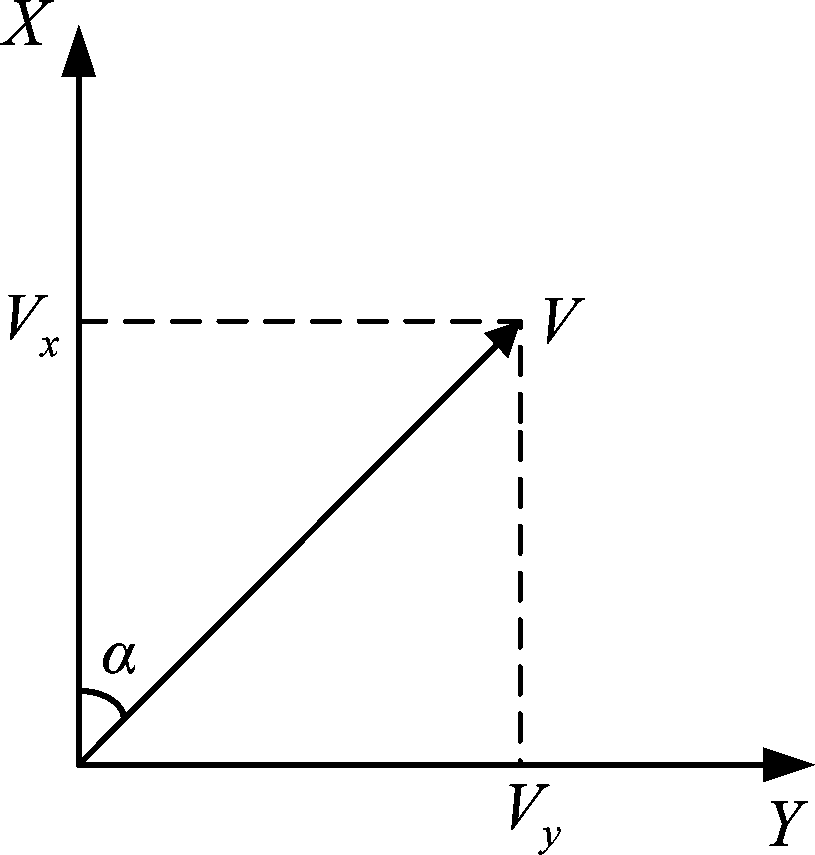
图1 船舶速度分解
Fig.1 Decomposition of ship speed
3 多项式卡尔曼滤波算法及建模
3.1 算法设计
工程应用中对船舶动态轨迹预测结果的实时性和准确性有非常高的要求。考虑到实测AIS数据很难满足匀速、线性的要求,利用多项式卡尔曼滤波能够解决目标运行的实际情况。设离散船舶航迹数据在Tj时刻的状态为
XTj=[latTj,lonTj,VTj,αTj]
(7)
αTj为当前时刻的对地航向。考虑到AIS数据分布上并非等时间间隔,当船舶位置坐标更新频率较低时,在预测下一时刻船舶位置往往会因为预测位置相隔时间太长而失去最佳修正位置,影响预测位置精度;当船舶位置坐标更新频率过快时,过于冗余的位置预测步长会导致滤波时间过慢,失去船舶位置实时预测的时效性。因此更新频率过快时,通过设置时间间隔阈值在获得的航迹点中随机选择一点替代整个航段;更新频率过低时,利用船舶速度及加速度对航线进行航迹点插值。此时式(7)可改进为
XTj=[latTj,lonTj,VTj,αTj,ωTj]
(8)
ωTj为当前时刻的加速度,ωTj与αTj之间的关系为
αTj=αTj-1+ΔtωTj-1
(9)
代入能够获得拟合航迹点的经纬坐标值。
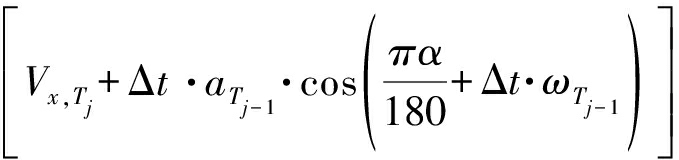
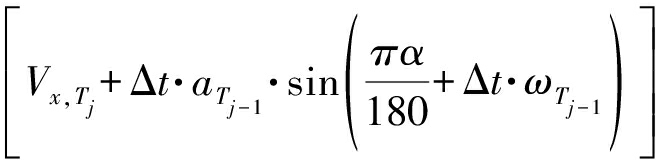
(10)
其中aTj-1为上一时刻船舶的加速度。
对于复杂的船舶运动模式,客观存在的航迹往往会表现出类似分段多项式的特征,因此多项式预测滤波器可以估计类似多项式形式的航迹未来值[14],通过迭代获取各数据点的自适应状态转移矩阵,通过扩展卡尔曼滤波算法得到航迹预测点。本文利用多项式模型拟合前Tj-1时刻航迹,多项式阶数的选择通过计算前Tj-1步的实际运行位置与多项式阶数从1开始预测位置的最小距离进行确定。当其小于阈值时,确定多项式阶数。此时目标的运行轨迹多项式为
(11)
其中X(t)为包括经纬度坐标随时间变化的多项式拟合曲线。此时模型的状态方程与测量方程分别为
xTj=FTj-1xTj-1+wTj-1
ZTj=HTjxTj+νTj
(12)
式中,xTj和xTj-1为两个时刻的状态向量,ZTj为Tj时刻的测量向量。wTj-1和νTj分别是过程噪声和测量噪声,且二者为相互独立、均值为零的高斯白噪声。FTj-1为Tj-1时刻的转移矩阵,由式(11)的多项式拟合轨迹由一阶泰勒展开得到的雅克比矩阵确定。HTj为该时刻的测量矩阵。
迭代过程中,状态向量的一步预测为:
(13)
系统状态向量的一步误差协方差矩阵为:
(14)
其中QTj-1为wTj-1的协方差矩阵。
卡尔曼增益为:
(15)
其中RTj为νTj的协方差矩阵。进而获得Tj时刻的状态估计。
(16)
更新误差协方差矩阵,迭代L次完成对轨迹的L步预测。
PTj=(I-GTjHTj)PTj|Tj-1
(17)
3.2 算法流程
基于多项式卡尔曼滤波的船舶轨迹预测算法详细步骤如表1所示。
表1 算法步骤
Tab.1 Steps of algorithm

算法1 基于多项式卡尔曼滤波的船舶轨迹预测算法Input:Trajectory data X={XT1,XT2,...,XTn}.Output: Root mean square error(RMSE).Algorithm:1.D=trajectoryPretreatment(X)2.F=Polyfit(D)3.initialParameters()4.for i=1 to L5.P=PKFPredict(D)6.E(i)=getRMSE(P)7.end8.RMSE= 1n∑Li=1E(i)()9.Output RMSE
(1)获取待处理的船舶轨迹数据集,通过速度、位置检验及插值、简化航迹后完成数据预处理(第一行)。
(2)确定轨迹参数模型,利用多项式拟合航迹获取状态方程及观测方程所需的F、H等参数(第二行)。
(3)确定初始时刻的状态估计值、误差协方差矩阵等,完成一步滤波(第三行)。
(4)对于待处理的L个轨迹点依次迭代获取状态估计值及下一步的预测误差协方差,并将预测值与真实值相比较,得到每个航迹点的均方根误差,结束迭代(第四到七行)。
(5)输出总体预测均方根误差(第八、九行)。
4 仿真分析
4.1 数据描述
以舟山海域附近为监测区域获取的ZHOUSHANHB船舶实测AIS数据为例,在集成开发环境为Matlab2014a下验证基于多项式卡尔曼滤波的船舶轨迹预测算法。实验参数设置如表2所示。
船舶整体航迹如图2所示,仿真时间共9.656秒。实验共分两个阶段:(1)利用多项式拟合船舶航行轨迹;(2)通过多项式获取航迹状态转移矩阵,经PKF算法得到航迹总体均方根误差。
表2 参数设置
Tab.2 Parameter settings
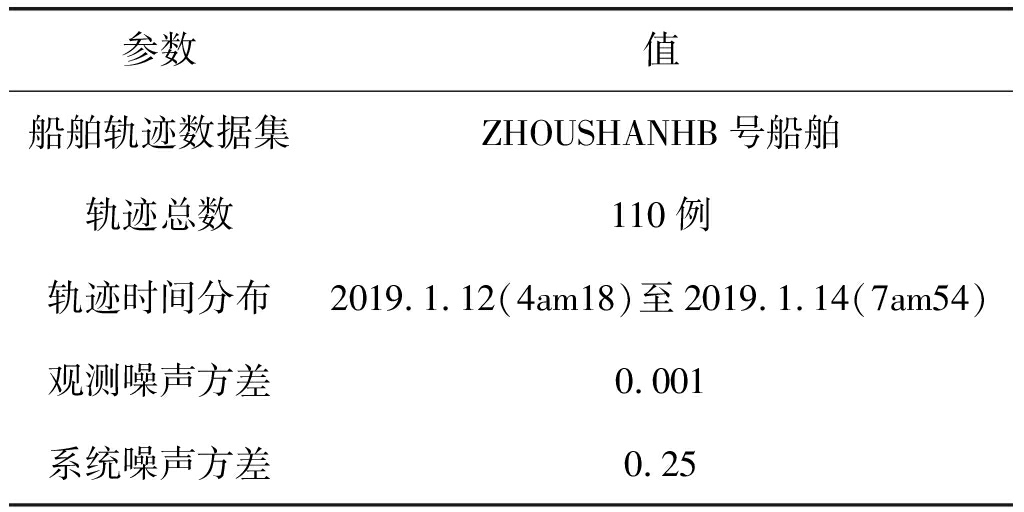
参数值船舶轨迹数据集ZHOUSHANHB号船舶轨迹总数110例轨迹时间分布2019.1.12(4am18)至2019.1.14(7am54)观测噪声方差0.001系统噪声方差0.25
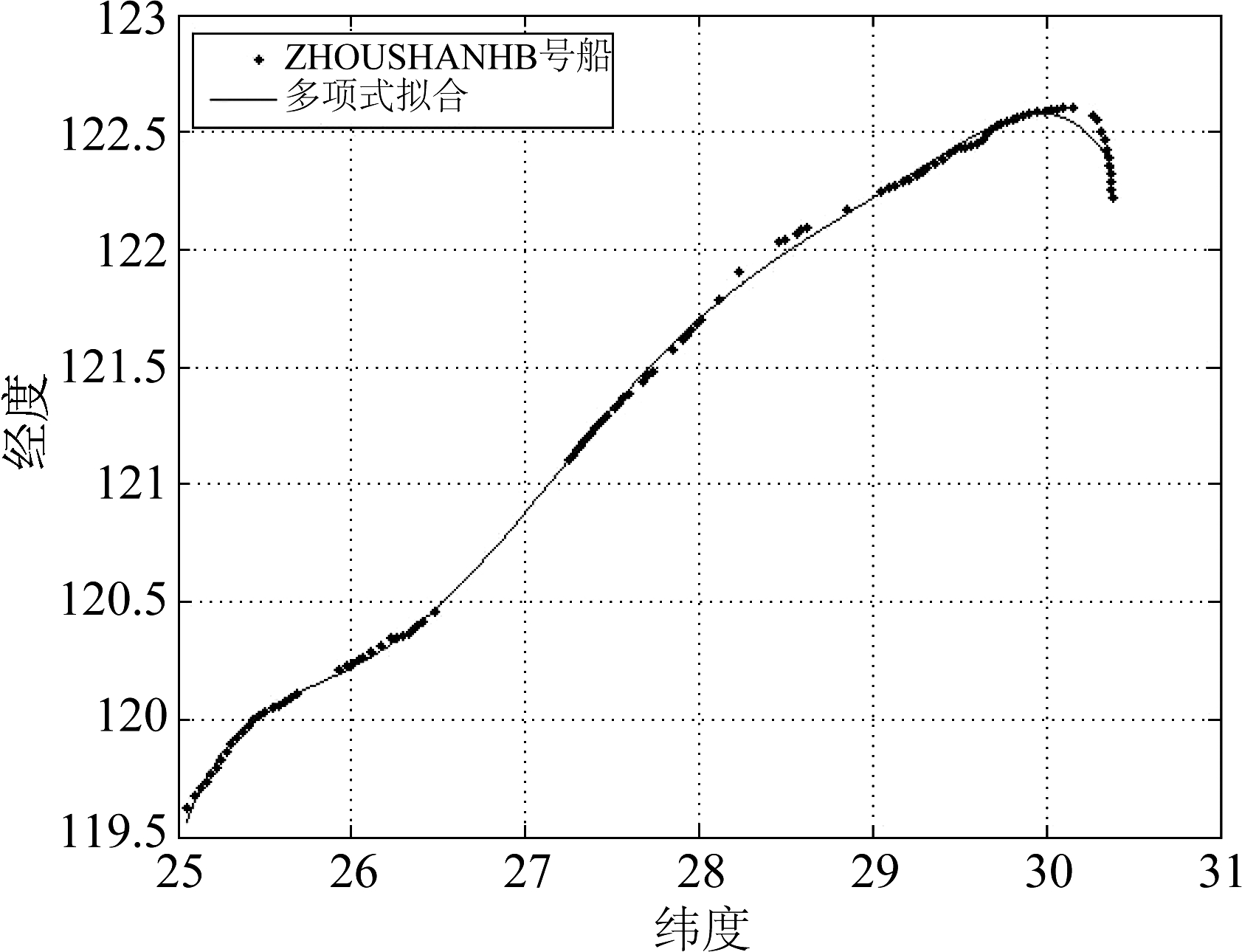
图2 ZHOUSHANHB号航迹及多项式航迹拟合效果
Fig.2 Trajectory and polynomial track fitting effect of vessel ZHOUSHANHB
4.2 实验结果分析
根据2.1小节中的轨迹预测方法,以实测AIS数据为原始数据,加上仿真软件产生的噪声误差模拟该船舶的历史存量AIS轨迹,确定本实验中轨迹的多项式拟合阶数为6阶。拟合效果如图2所示。仿真过程中图标的距离的基本单位均为度(°)。在仿真过程中,相邻两点的时间间隔并不均匀,但均满足数据预处理中设置的时间间隔阈值。最终获取的真实值、观测值与滤波航迹如图3所示。
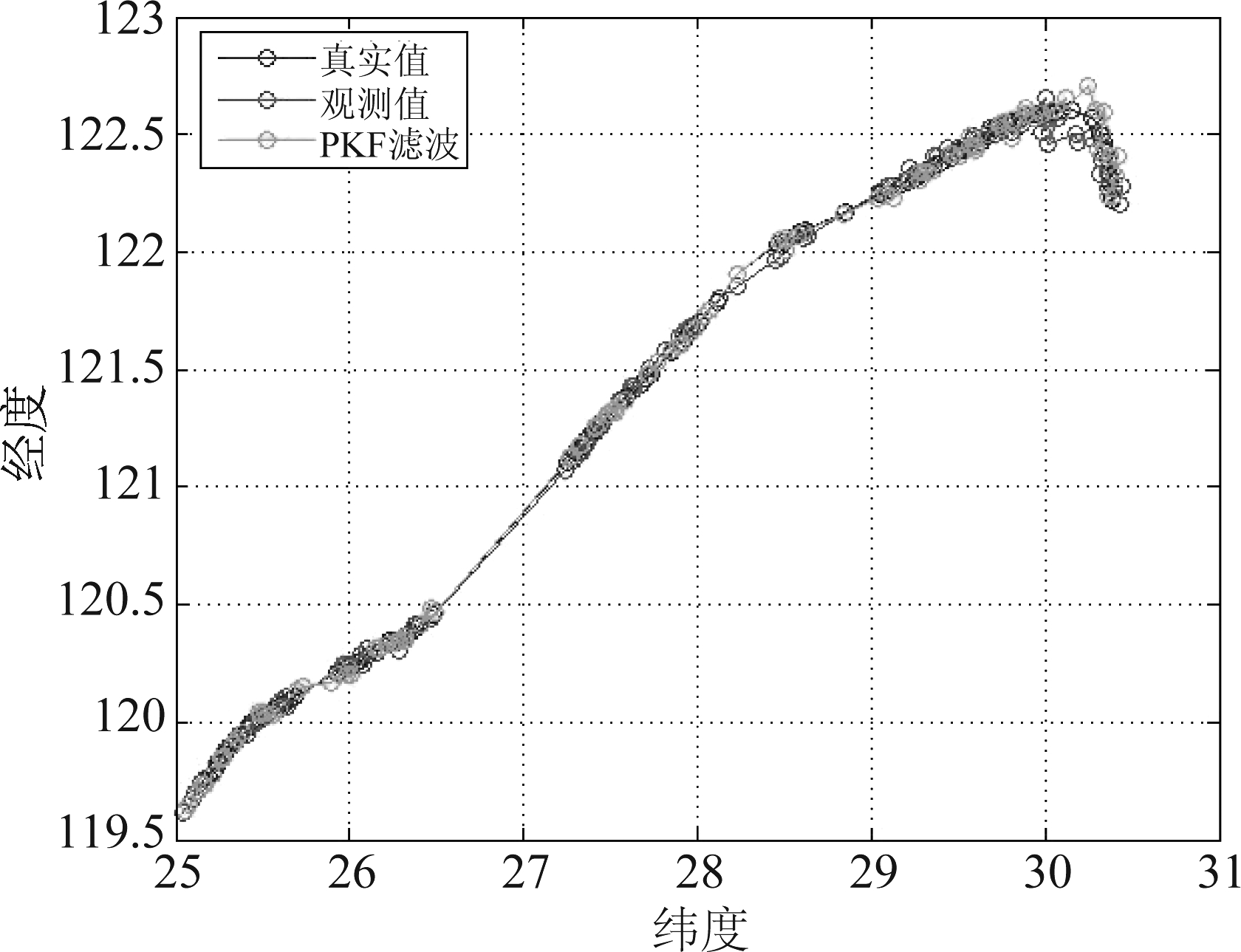
图3 目标轨迹的真实航迹、观测航迹与滤波航迹
Fig.3 Real, observation track and filter track of the target trajectory
从图3中可以看到,船舶实际轨迹与观测轨迹、PKF滤波轨迹几乎重合,预测效果良好,基本不受船舶大角度机动的影响。在阈值范围内,点迹时间间隔的差异对航迹的整体影响不大。图4为航迹各位置滤波偏差与系统状态返程偏差。可以看出PKF算法对实测AIS数据航迹有较好的滤波效果。时间上来说,程序整体运行时间为16.741秒,基本满足实际应用中对于航迹实时性的要求。
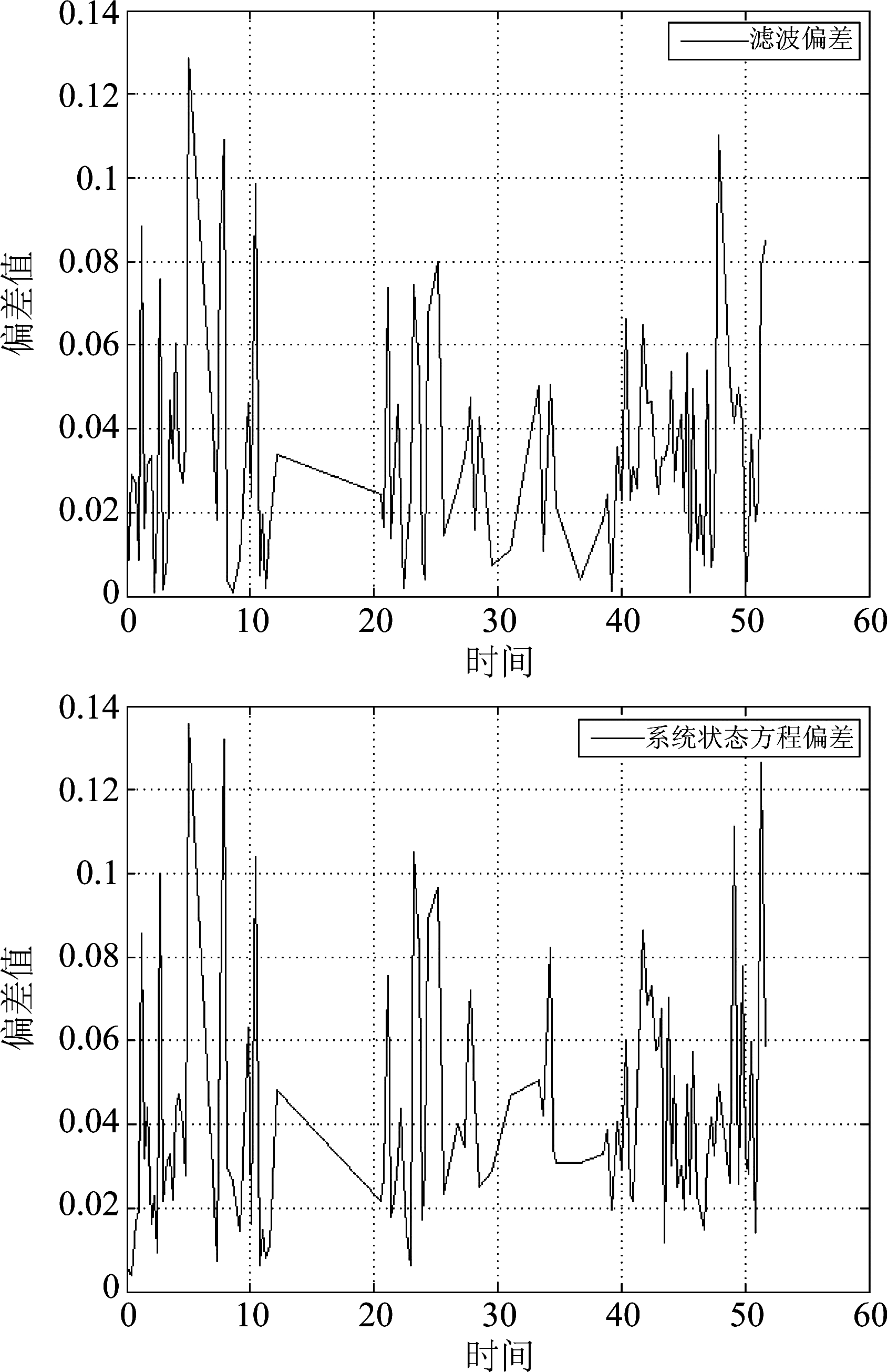
图4 航迹滤波偏差与系统状态方程偏差
Fig.4 Track filter deviation and system state equation deviation
5 结论
本文针对船舶在实际运动中存在的非线性、非匀速问题,提出来使用多项式卡尔曼滤波算法对船舶数据轨迹进行了预测处理。文中首先通过数据预处理获取质量较高、较为理想的轨迹数据,剔除掉航迹时间间隔过大对于预测效果的影响;根据部分航迹点构建轨迹多项式分布模型,确定多项式阶数,控制航迹存在的机动情况。进一步,利用PKF滤波算法,提高船舶的预测轨迹精度。算法具有较好的实时性、精确性。结果表明,基于多项式卡尔曼滤波的船舶轨迹预测算法具有较好的预测效果,能够应用于大多数海面对象轨迹分析场景,达到智能辅助预测船舶的位置的功能,可进一步为相关海事部门提供一种新的辅助手段。
[1] 靳智, 梁山, 曹芳平. 基于AIS的长江控制河段船舶视觉伺服跟踪研究[J]. 计算机应用, 2011, 31(12): 3414-3417.
Jin Zhi, Liang Shan, Cao Fangping. Visual Servo Tracking Method Based on Automatic Identification System For Vessels in Controlled Areas of Yangtze River[J]. Journal of Computer Applications, 2011, 31(12): 3414-3417.(in Chinese)
[2] IALA. Technical Clarifications on Recommendation ITU-RM. 1371-3[S]. IALA: IALA, 2003: 8-9.
[3] 赵帅兵, 唐诚, 梁山, 等. 基于改进卡尔曼滤波的控制河段船舶航迹预测[J]. 计算机应用, 2012, 32(11): 3247-3250.
Zhao Shuaibing, Tang Cheng, Liang Shan, et al. Track Prediction of Vessel in Controlled Waterway Based on Improved Kalman Filter[J]. Journal of Computer Applications, 2012, 32(11): 3247-3250.(in Chinese)
[4] 王伊冰, 阮林林, 陈琼冰, 等. 基于AIS数据的船舶航行轨迹估计研究[C]∥第九届中国卫星导航学术年会, 2018.
Wang Yibing, Ruan Linlin, Chen Qiongbing, et al. Estimation of Ship Navigation Trajectory Based on AIS Data[C]∥China Satellite Navigation Conference, CSNC, 2018.(in Chinese)
[5] Jaskolski K. Automatic Identification System Dynamic Data Estimation Based on Discrete Kalman Filter Algorithm[J]. Scientific Journal of Polish Naval Academy, 2017, 211(4): 71- 87.
[6] Sapankevych N, Sankar R. Time Series Prediction using Support Vector Machines: A survey[J]. IEEE Compute Intell. Mag., 2009, 4(2): 24-38.
[7] Jiang S, Jin H, Wei F. LS-SVM Application for Ship Course Model Predictive Control[J]. IEEE International Conference on Mechatronics and Automation(ICMA’13), 2013: 1615-1619.
[8] 王艳锋, 李红祥. 桥区水域失控船舶的航迹预测[J]. 武汉船舶职业技术学院学报, 2011, 10(4): 34-38.
Wang Yanfeng, Li Hongxiang. Track Prediction of Out of Control Ships in Bridge Area Waters[J]. Journal of Wuhan Institute of Shipbuilding Technology, 2011, 10(4): 34-38.(in Chinese)
[9] Simsir U, Ertugrul S. Prediction of Manually Controlled Vessels Position and Course Navigating in Narrow Waterways Using Artificial Neural Networks[J]. Applied Soft Computing, 2009, 9(4): 1217-1224.
[10] Qiao S, Han N, Zhu W. A Self-adaptive Parameter Selection Trajectory Prediction Approach via Hidden Markov Models[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 16(1): 284-296.
[11] Fossen S, Fossen T I. Exogenous Kalman Filter(XKF) for Visualization and Motion Prediction of Ships Using Live Automatic Identification System(AIS) Data[J]. Modeling, Identification and Control, 2018, 39(4): 233-244.
[12] 乔少杰, 韩楠, 朱新文, 等. 基于卡尔曼滤波的动态轨迹预测算法[J]. 电子学报, 2018, 46(2): 418- 423.
Qiao Shaojie, Han Nan, Zhu Xinwen, et al. A Dynamic Trajectory Prediction Algorithm Based on Kalman Filter[J]. Acta Electronica Sinica, 2018, 46(2): 418- 423.(in Chinese)
[13] 魏照坤, 周康, 魏明, 等. 基于AIS数据的船舶运动模式识别与应用[J]. 上海海事大学学报, 2016, 37(2): 18-23.
Wei Zhaokun. Zhou Kang, Wei Ming, et al. Ship Motion Pattern, Recognition and Application Based on AIS Data[J]. Journal of Shanghai Maritime University, 2016, 37(2): 18-23.(in Chinese)
[14] 董劲男, 邢千里, 班孝林. 多项式预测滤波技术在智能控制中的应用[J]. 长春师范学院学报, 2013, 32(2): 32-36.
Dong Jinnan, Xing Qianli, Ban Xiaolin. Application of Polynomial Predictive Filtering Technology in Intelligent Control[J]. Journal of Changchun Normal University, 2013, 32(2): 32-36.(in Chinese)
[15] 周同驰, 徐勤军, 周琳, 等. 基于有效轨迹和多重方向模式的行为识别[J]. 信号处理, 2016, 32(5): 519-527.
Zhou Tongchi, Xu Qinjun, Zhou Lin, et al. Action Recognition Based on Valid Trajectories and Multiple Directional Patterns[J]. Journal of Signal Processing, 2016, 32(5): 519-527.(in Chinese)

