1 引言
合成孔径雷达(Synthetic aperture radar,SAR)是一种可以全天时,全天候进行观测工作的仪器,可获得观测区域二维高分辨信息,其利用脉冲压缩获得距离高分辨,运动向合成孔径获得方位维高分辨。层析合成孔径雷达(SAR tomography,TomoSAR)是将合成孔径的思想扩展到高程方向,用以实现对目标三维信息的获取。
Reigbor等人[1]首次在实验室环境的理想条件下,利用机载系统开展了层析SAR的实验研究,验证了层析技术的可实施性。之后,Z. She等人[2-5]在星载SAR上测试了层析技术的可行性。2003年,Fornaro等人利用层析技术完成对ERS星载SAR数据的处理,进一步证实层析SAR技术的可行性。在层析SAR技术发展的同时,与之相应的数据处理算法亦被提出。傅里叶变换算法[6]最先被提出,但其需要在空间上均匀分布的采样基线,同时还要求相当大的孔径长度用以实现高程高分辨;但是在实际应用,基线数目少,分布不均匀,采样不规则等问题严重限制了层析成像的质量。为了解决上述问题,专家学者相继提出了MUSIC、Capon、SL1MMER等空间谱估计[1, 7- 8]方法,但由于这些算法严重依赖于对空间散射体数目的准确判断,影响了算法的稳定性。压缩感知(Compressive Sensing,CS)技术[9-10]的出现,在稀疏信号重建领域带来了新的风潮。在2010年,Joachim提出将CS理论应用于雷达领域[7],2011年,X.X.Zhu等人成功将CS理论应用于层析SAR[11],并分析比较了CS算法性能,文献[11]指出CS理论可最大限度的减少从信号中获取的测量数量,同时保留原始信号的全部信息,不需要模型选择提供关于分辨单元的散射体数量的先验信息,并且克服了由高程孔径限制引起的分辨率限制,实现超分辨[12]。
但是上述研究都是针对机载或星载等[13-15]观测距离远远大于目标结构尺寸的情况,同时使用雷达波段较低(X,C波段),对于近场条件下的层析处理研究并不充分。相对于远场低波段,在近场高波段信号数据处理中,每次测量的观测视角变化大,距离方位二维像畸变明显且高频影响严重,这些因素增加了层析处理的难度,传统的处理方式难以直接使用。
为解决上述问题,本文提出了一种适应于近场层析处理的方法与流程,解决了由于通道间的不一致性造成的图像散焦与栅瓣问题、SAR图像畸变旋转以及散射特性的改变造成的配准困难、以及成像投影关系的对应与压缩感知估计与层析维信息的关联问题。本文通过强点补偿通道间幅相误差改善二维成像质量,基于结构信息提取剔除强闪烁点影响提高配准质量,分析空间结构、建立映射模型估计层析维信息,最终实现对目标三维信息的估计重建。本研究改善了成像、配准与层析估计方法,并利用Ku波段雷达在近场(观测距离200 m)开展试验,完成了建筑物目标的三维信息估计与结构重建。
本文结构安排如下:第2节介绍了压缩感知理论与层析SAR成像原理,第3节分析了近场层析的难点与解决方法,第4节展示了试验结果,最后一节对全文做出总结。
2 基于压缩感知的SAR层析成像
2.1 压缩感知简介
压缩感知(Compressive sensing)是由Donoho与Candes等人在2004提出的一种采样理论。该理论利用信号的稀疏性或可压缩性,可以实现信号的采集、解码,是对传统Nyquist采样定理的极大变革。假设有一组长度为N的离散时间信号x,该信号在正交基上的映射为 s=Ψx,由信号理论可知,
x=ΨHs
(1)
式中,ΨH为N×N矩阵,s为N×1列向量。显然,x与s是同一信号的等价表示,x为时域表示,s为Ψ域表示。当信号x在Ψ基上有 K≪N 个非零值时,称s为x的稀疏系数,x是K稀疏信号。
用一组M×N维观测矩阵Φ,对目标信号x进行采集,获得长度为M的观测值y
y=Φx=ΦΨHs=Θs
(2)
将s信号的估计恢复问题转化为l0范数最小化问题,利用压缩感知理论完成对式(2)欠定方程组的求解。
(3)
有文献[10]指出,l1最小范数在一定条件下和l0范数最小化问题具有等价性,则
(4)
为了保证算法的收敛性,使得重构具有唯一解,观测矩阵与基矩阵的乘积需要满足等距约束准则(RIP)性质,即Θ=ΦΨH需要满足:
(5)
式中,δ  (0,1)为约束等距常数,X是一个具有K个非零值且位置与s相同的稀疏向量。RIP准则的一般等价情况是测量矩阵与基矩阵满足不相关性。
(0,1)为约束等距常数,X是一个具有K个非零值且位置与s相同的稀疏向量。RIP准则的一般等价情况是测量矩阵与基矩阵满足不相关性。
2.2 基于压缩感知的SAR层析成像
SAR层析技术是将合成孔径的方法应用于高程向的一种成像技术,即通过在不同轨道位置、不同时刻对同一目标区域进行多次数据采集,获取散射目标的空间相位变化信息,实现在垂直视线方向的合成孔径。层析SAR的观测几何构型如图1所示。
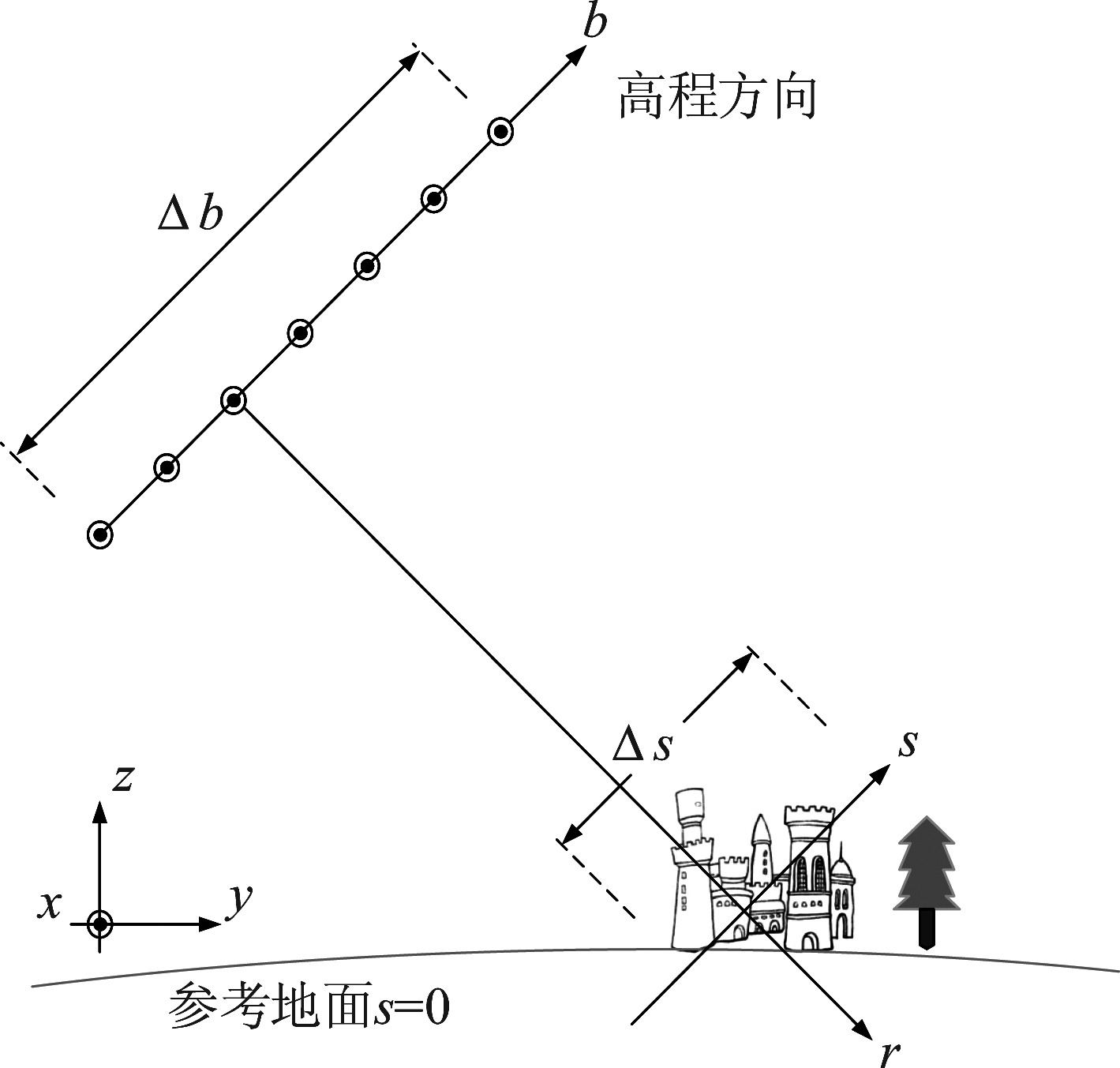
图1 SAR层析空间几何示意图
Fig.1 TomoSAR geometry
在单次SAR测量成像中,同一像素单元中斜距-方位一致的所有目标散射信息互相叠加。对区域目标进行不同高度的测量成像,得到M幅单视复数影像。经过图像配准后,M幅图像的相同位置的像素可以构成一个长度为M的散射特性序列:
rm={r1,r2,…,rM}
(6)
每一个像素的值都可以视为是目标在高程向上散射功率分布的积分[16-17],可以表示为:
(7)
式中,Δs为反射信号沿高程的分布范围,α(s)为目标在高程向的散射功率谱,ξm为采样空间频率,ξm=-2bm/(λr),bm为高程基线位置信息,λ为入射波长,r为中心斜距。对式(8)离散化,用矩阵形式表示,
r=Rα
(8)
式中,r是高程向的M个测量值rm,R是M × N的观测矩阵,Rmn=exp(-j 2πξmsn),α是长度为N的目标高程散射特性离散分布矢量,αn=α(sn)。sn(n=1,…,N)表示离散的高程位置。
根据压缩感知稀疏重构理论,利用观测矩阵R完成对目标信号α的重构,需要满足在2.1节中介绍的两个条件:信号的稀疏性与观测矩阵符合RIP准则。对于高波段层析SAR而言,高程向回波信号在空间域中仅包含少量的散射体作为非零元素,即在单位正交基底(Ψ=I)下是稀疏的,观测矩阵(Φ=R)是由随机分布的航迹位置决定的离散傅里叶矩阵,即观测矩阵是随机离散傅里叶变换矩阵,相关研究[16-17]分析中指出,其满足RIP准则。因此,K稀疏信号α可以通过l1范数最小化求解进行准确的重构:
(9)
3 地基MIMO SAR近场层析成像
3.1 难点分析
相较于传统星载与机载低频段层析SAR系统,使用高频段(Ku)地基MIMO SAR系统进行层析测量时有着显著的差异。在将测量距离缩小到与目标结构大小相近的测量范围时,测量位置的细微变化都会对成像结果带来显著影响[18]。以MIMO平台进行层析数据的获取,由于其本身的特性以及平台自身的固有的误差与技术缺陷,通道间的不一致性是客观存在的,其在成像中带来的影响表现为图像散焦,成像质量差。当测量距离较近时,孔径角度变化随位置移动变化明显,在成像结果中显现为图像有着明显的旋转变化与畸变,同时由于雷达高频段影响,目标散射特性变化剧烈,这都为配准带来了困难。最后,测量距离的缩短,限制了成像平面的选择,目标信息与成像结果的投影关系更为复杂,为三维信息的估计带来困难。
3.2 二维成像
在单视图像数据获取方面,本文选择了地基MIMO SAR平台完成对目标区域的观测测量,通过在纵深向的移动实现在层析向合成孔径。
采用后向投影算法进行二维成像。选择“距离-方位角”平面作为粗成像平面,以获得在测量区域中放置角反的距离方位角信息,用以对通道间幅相误差估计和补偿。孔径中心距离Rmid、孔径方位角θmid,则粗成像可以表示为:
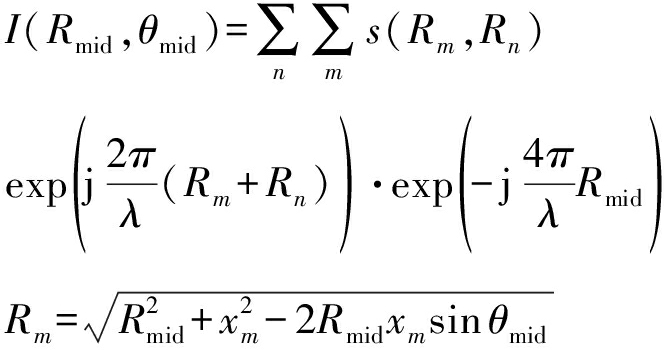
(10)
式中,xm为第m个发射通道的坐标,Rn有类似的定义。其中最后一项是保相处理,以便于后续三维成像。最终的成像平面设置为观测目标前方,以保证观测目标信息完整。
MIMO雷达收发分置且通道众多,由于工艺等问题的客观存在,通道间存在功率、链路的不一致性,会引入幅度和相位误差。通道间的幅相误差会严重影响图像的聚焦质量,导致严重的散焦和栅瓣。为了准确估计并补偿通道幅相误差,提高成像质量,本文选择分两步完成对目标的聚焦成像处理。首先进行粗成像,提取孤立散射强点位置信息,之后再进行精成像。
幅度误差的估计是利用孤立强散射点的幅度值,将各收发通道回波数据幅度进行归一化处理,如式(11)所示。
(11)
式中,m表示发射通道编号,n表示接收通道标号,AQ(m,n)为发射通道m发射,被n接收得到的回波数据中,目标Q的主瓣峰值幅度。
相位误差估计利用孤立散射点的相位信息。粗成像后,提取孤立散射强点的孔径中心距离Rmid、孔径中心方位角θmid,从而构造出孤立散射强点Q的理想徙动和相位信息,与一维距离像中提取出的散射点Q的相位历程做差,得到相位补偿项,即
φCompen(m,n)=-φerror(m,n)=φideal(m,n)-φreal(m,n)
(12)
式中,
(13)
3.3 图像配准
在做层析处理前,需要将目标所在像素单元匹配至同一位置,即多幅二维高分辨图像的同一位置像素对应于相同的目标。但是在近场环境下,图像畸变明显、散射特性变化剧烈,常规的基于孤立强点的配准效果[19]很差,为此,本文提出并采取了一种基于结构信息的近场图像配准策略,分两步完成对多轨图像的配准。
首先,基于图像边缘检测与提取,实现SAR图像对的像素级配准,克服近场散射点随SAR成像视角变化而发生闪烁的配准问题。根据图像目标边缘信息,对主、副图像进行目标与场景(杂波)的分割;对目标区域进行二值化处理,去除近场目标散射特性随SAR观测角度发生改变从而对配准造成的影响。副图像fS(x,y)可由主图像fM(μ,ν)平移变化得到,如式(14)所示。
fS(x,y)=fM(μ-x0,ν-y0)
(14)
式中,x,y对应于副图像像素坐标,μ,ν对应于主图像像素坐标,x0,y0表示图像偏移量。对fS(x,y)和fM(μ,ν)进行二维傅里叶变换,可得关系如式(15)所示。
FS(α,β)=FM(α,β)·e-j2π(αx0+βy0)
(15)
式中,FS,FM表示对应副、主图像的二维傅里叶变换,α,β表示原目标点对应频域坐标。利用相位相关法可求得图像整体偏移量函数fcor(x,y),完成对主副图像的粗配准,如式(16)所示。
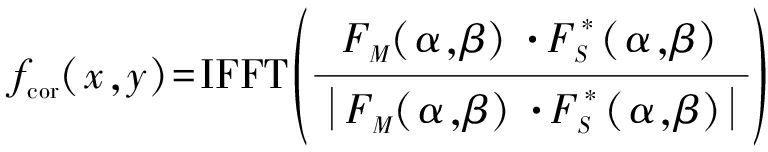
=δ(x-x0,y-y0)
(16)
式中*表示共轭。在粗配准的基础上,对提取的目标区域划分搜索窗与样本,采用相关函数测度的方法求取亚像素偏移量,计算过程如式(15)所示。
Cor(por,poa)=
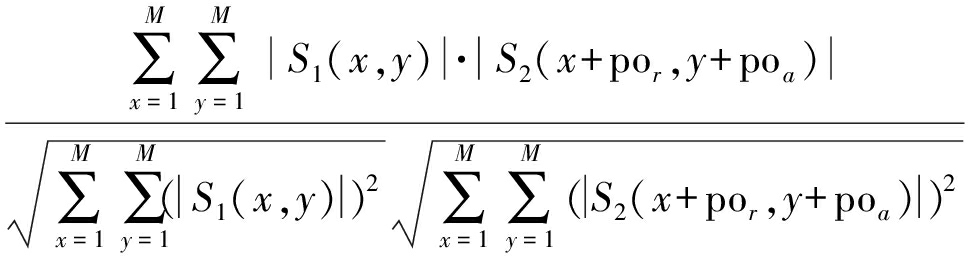
(17)
式中,S1和S2是主从图像,por和poa分别是距离向和方位向像素偏移。
然而,在近场图像中,会不可避免的出现一些低相干区域,比如闪烁强点,这会影响式(17)的计算结果,影响周围区域的配准结果。为解决闪烁强点的影响,保证像素偏移量提取精度与整体像素偏移量拟合精度,提出采用小样本窗对目标区域进行偏移量提取,同时基于偏移量直方图与偏移量梯度矩阵对闪烁控制点进行剔除。像素偏移的分布可用f(PO)表示,PO表示像素偏移量,可得式(18):
(18)
式中n表示f(PO)分布数,POk是使f(PO)达到最大值的偏移量。设偏移量PO设置最大和最小门限为T1与T2,则判断门限为:
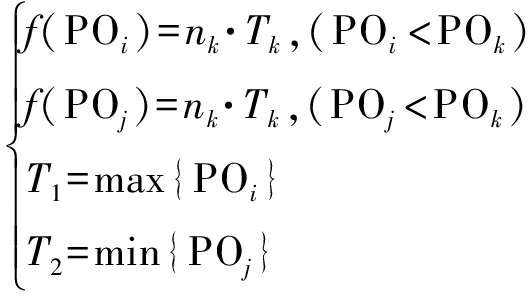
(19)
式中,nk表示f(PO)的最大值,Tk为衰减系数,Tk∈(0,1),通常选择0.01~0.05。超出门限的取样点计算值被认作是奇异点,或者是强闪烁点,这些强闪烁点可以通过邻域的采样点偏移量均值校正,保证像素偏移量提取精度,完成整体像素偏移量的高精度拟合,最终实现SAR图像对的精配准。
3.4 层析处理
经过3.4节处理之后单视二维图像按测量顺序排列,纵深向提取层析维数据。获取的测量值是稀疏非均匀的,通过解斜(deramp)处理,将高度维聚焦成像等效为高度维的空间谱估计问题。复数据测量向量r,观测矩阵为离散傅里叶矩阵R,映射矩阵为单位正交矩阵I,恢复矩阵Θ=IR,采用压缩感知算法,通过对空间谱谱峰位置的估计,提取目标的高度维信息。
高度维时域信号进行解斜处理,通过相位补偿,将空间中散乱分布的采样位置校正到一系列虚拟的采样位置上,实现高度维的聚焦效果,处理示意如图2所示。解斜处理信号形式如下为:
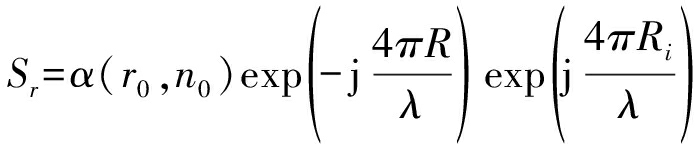
(20)
式中α表示回波强度,与观测斜距r与观测位置n有关,R表示采样点到目标的中心斜距,Ri表示位置校正时需要移动的距离,式中第三项即为解斜处理滤波器。

图2 空间采样解斜处理
Fig.2 Spatial sampling and deramp process
若高度维为传统的均匀过采样,则补偿二阶及高阶相位后,通过傅里叶变换即可实现高度维的成像,但在非均匀稀疏条件的约束下,无法直接使用傅里叶变换获取信号空间谱,所以利用压缩感知的框架完成对稀疏信号空间谱估计的求解。稀疏表示下的雷达测量结构如图3所示。
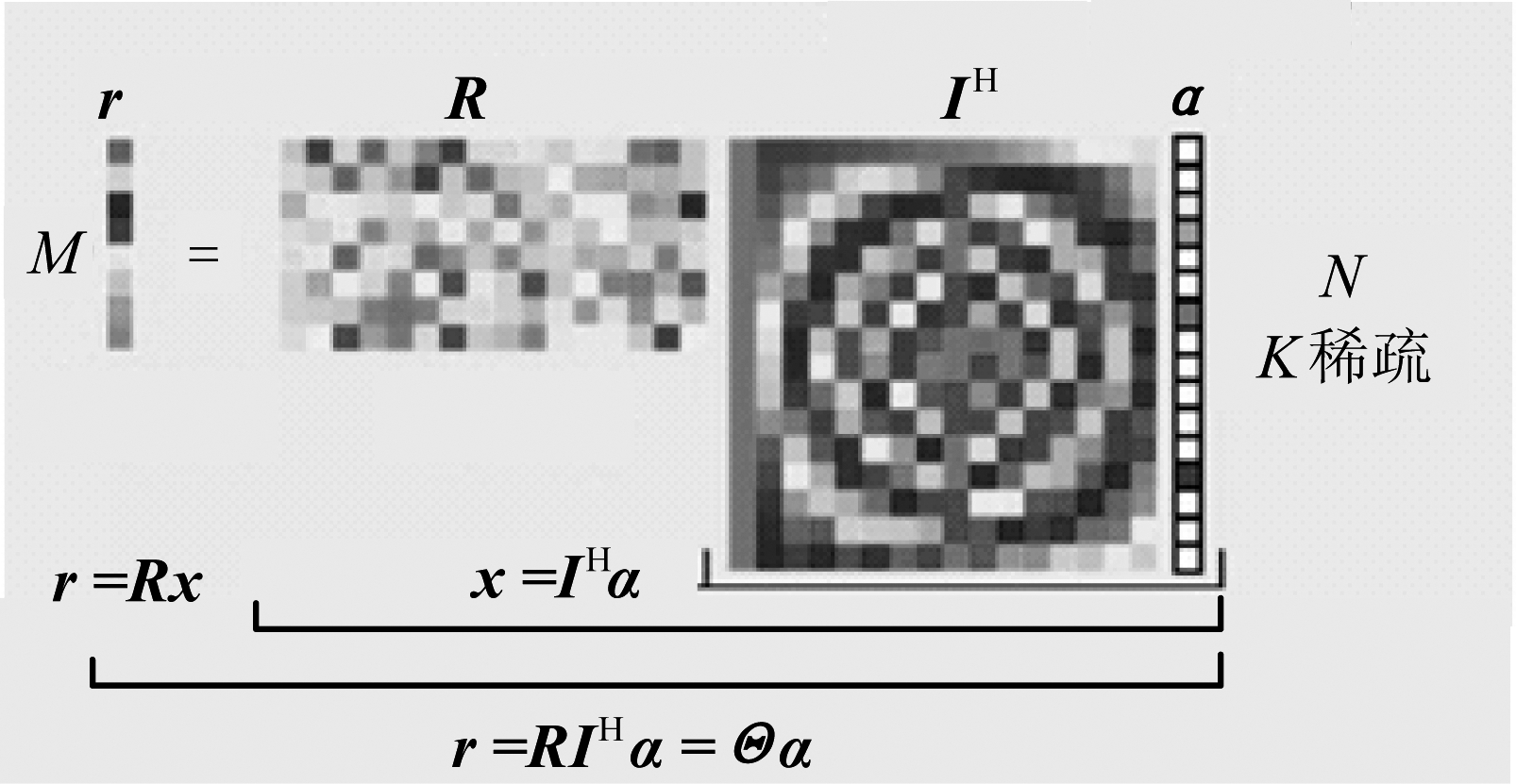
图3 压缩感知雷达矩阵表示框图
Fig.3 CS Radar matrix representation block diagram
利用正交匹配追踪算法[20]完成对式(9)的求解,即可完成对高度维空间谱谱峰位置的估计。高度维视角与空间谱估计结果有如下关系:
(21)
式中,R0表示解斜后的中心斜距,d表示均匀采样条件下的雷达位置间隔,d=λR0/(2H),H为层析向观测高度,θ表示高度维视角,k表示为空间谱估计结果。忽略高次项,斜距变化为正弦形式,对k做傅里叶变换,得到目标空域频谱Fk,目标层析信息的估计可表示为f(θ)=max(Fk)。
成像平面中的目标位置为T(xT,yT,zT),其真实空间位置为P(xp,yp,zp),两者应满足如下关系:(1)斜距相同;(2)α夹角相同,即x坐标一致。几何示意如图4所示。
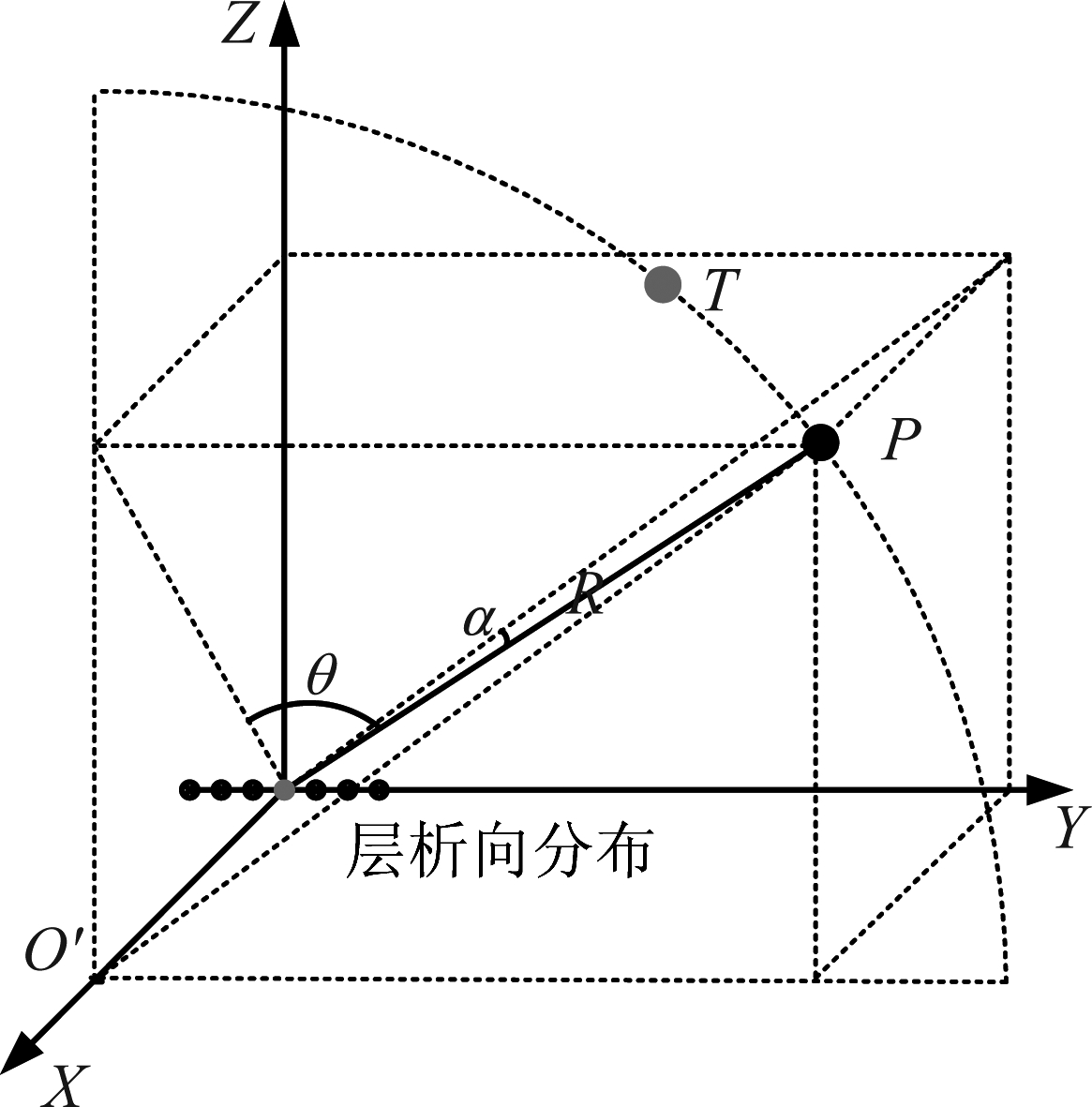
图4 目标与成像映射几何关系
Fig.4 Target and Mapping geometry
在图4中,雷达层析向为Y轴,坐标原点为层析向孔径中心,α为P与YoZ平面夹角,θ为P与XoZ平面夹角,定义其为空间前斜角。投影点T是P以在X轴上的投影O′为圆心,O′P为半径圆与成像平面的交点。通过联立斜距、高度维视角、投影映射几何分布,解算目标高度维信息,获得目标位置:
xp=xT
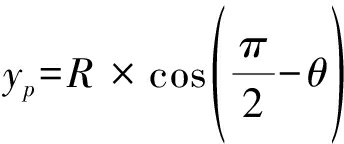
(22)
4 实验验证
4.1 实验场景
本实验观测场景如图5红色框选区域所示,观测目标是北京理工大学中心教学楼西侧面,通过层析SAR成像处理技术对大楼凹陷纵深分布进行估计成像。测量场景目标结构如图6所示,楼体凹陷部分约为40 m,大楼整体高度70 m。
在整个实验测量中,雷达沿Y轴移动并进行11次测量,层析向孔径中心距离楼面为120 m,基线分布总长为7.4 m。实验布置俯视场景如图7所示,数据来源于高德地图。
11轨测量位置为在7.4 m的基线里随机分布,手动完成对雷达平台的移动。雷达为调频连续波雷达,长度1.3 m,雷达样式如图8所示,具体平台参数如表1所示。

图5 北京理工大学中心教学楼西侧
Fig.5 The west of BIT Center Building
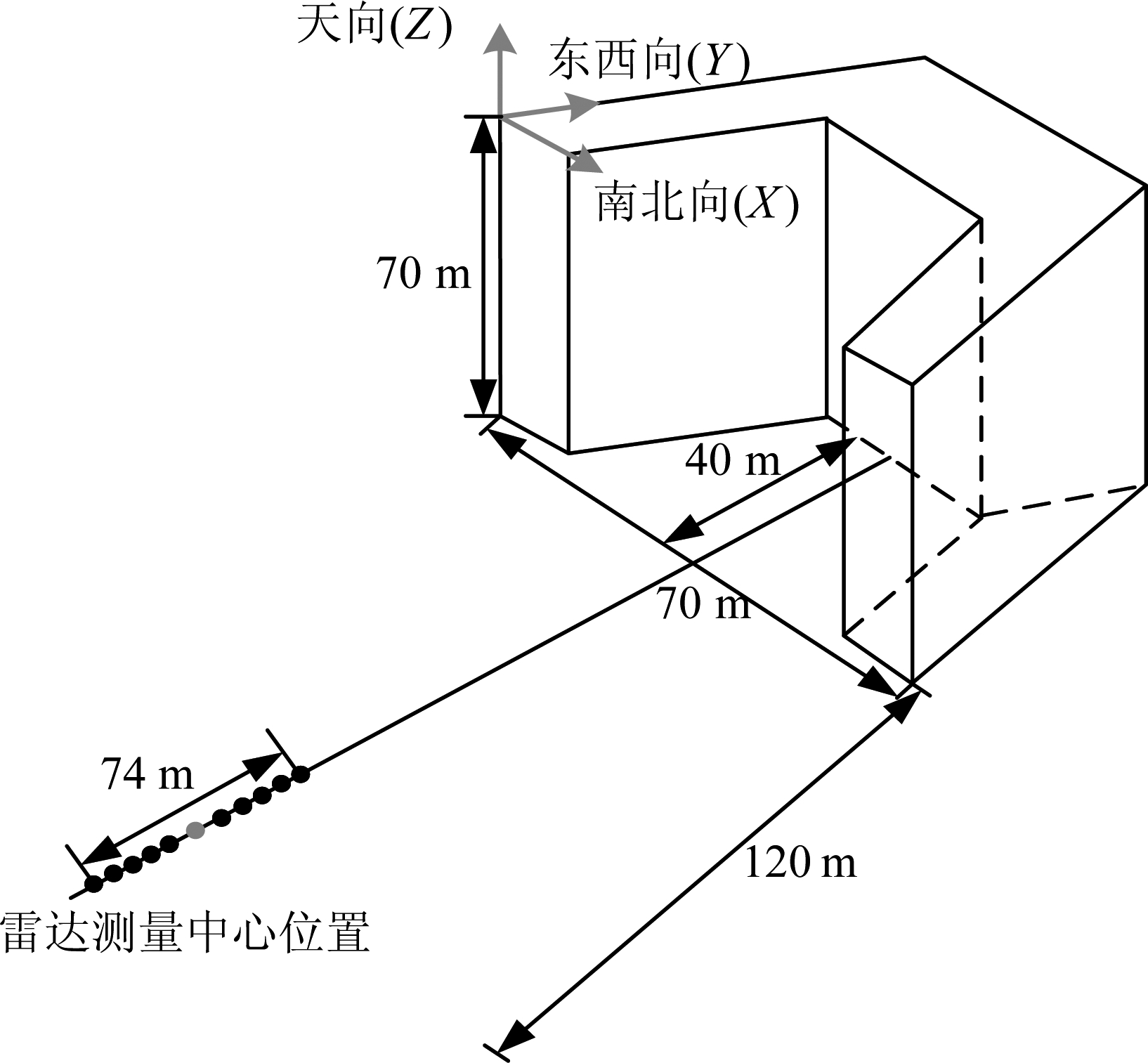
图6 测量场景三维结构图
Fig.6 Measurement Scene 3-D structure
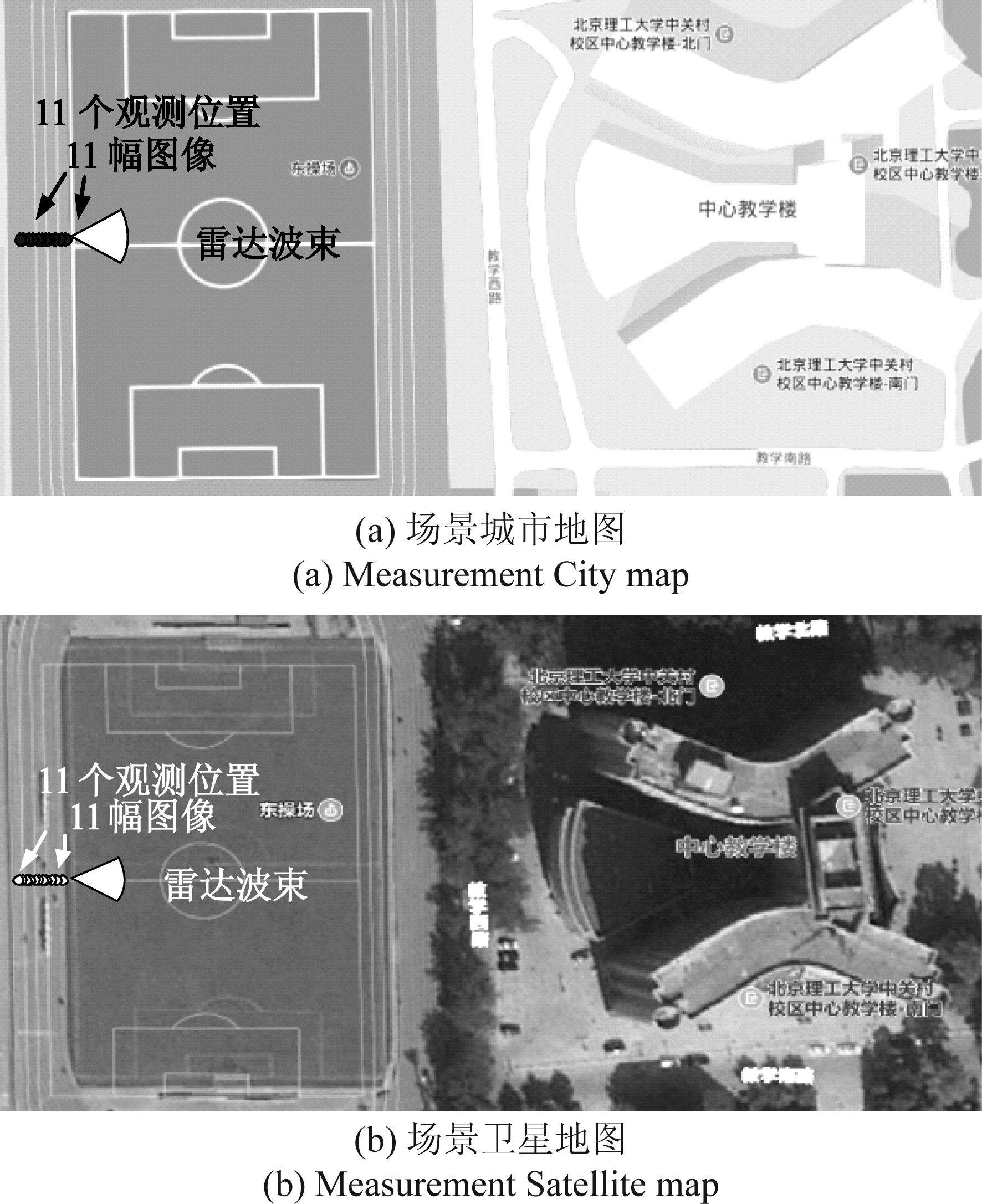
图7 测量场景二维平面图
Fig.7 Measurement Scene 2-D plan

图8 MIMO雷达
Fig.8 The picture of MIMO Radar
表1 MIMO雷达系统主要参数
Tab.1 Parameters of MIMO Radar

参数数值载频f0Ku带宽/GHz1重复周期/Hz2000占空比1发射阵元/接收阵元16/16等效合成孔径长度/m1.2
根据雷达系统参数以及投影平面的选择,实际成像结果中的相关分辨率为:在南北向(X)上,投影分辨率为0.73 m,在东西向(Y)上,雷达波束中心相对于地面存在15°的偏角,实际层析基线长度为1.915 m,投影分辨率约为1 m;在天向(Z)上,投影分辨率为0.25 m。
4.2 二维成像结果
二维成像结果如图9所示。图9(a)为没有经过补偿处理的单幅SAR数据图像,其栅瓣明显,散焦严重。图9(b)为经过3.2节方法进行通道间幅相误差补偿后的二维成像结果。图9(c)与(d)分别为对应红色选框点目标的二维刨面图,未加窗时的性能评估如表2所示。结果显示,经过通道间幅相误差补偿之后的峰值旁瓣比与积分旁瓣比有明显提高,成像质量有明显改善,方位向改善尤为明显。
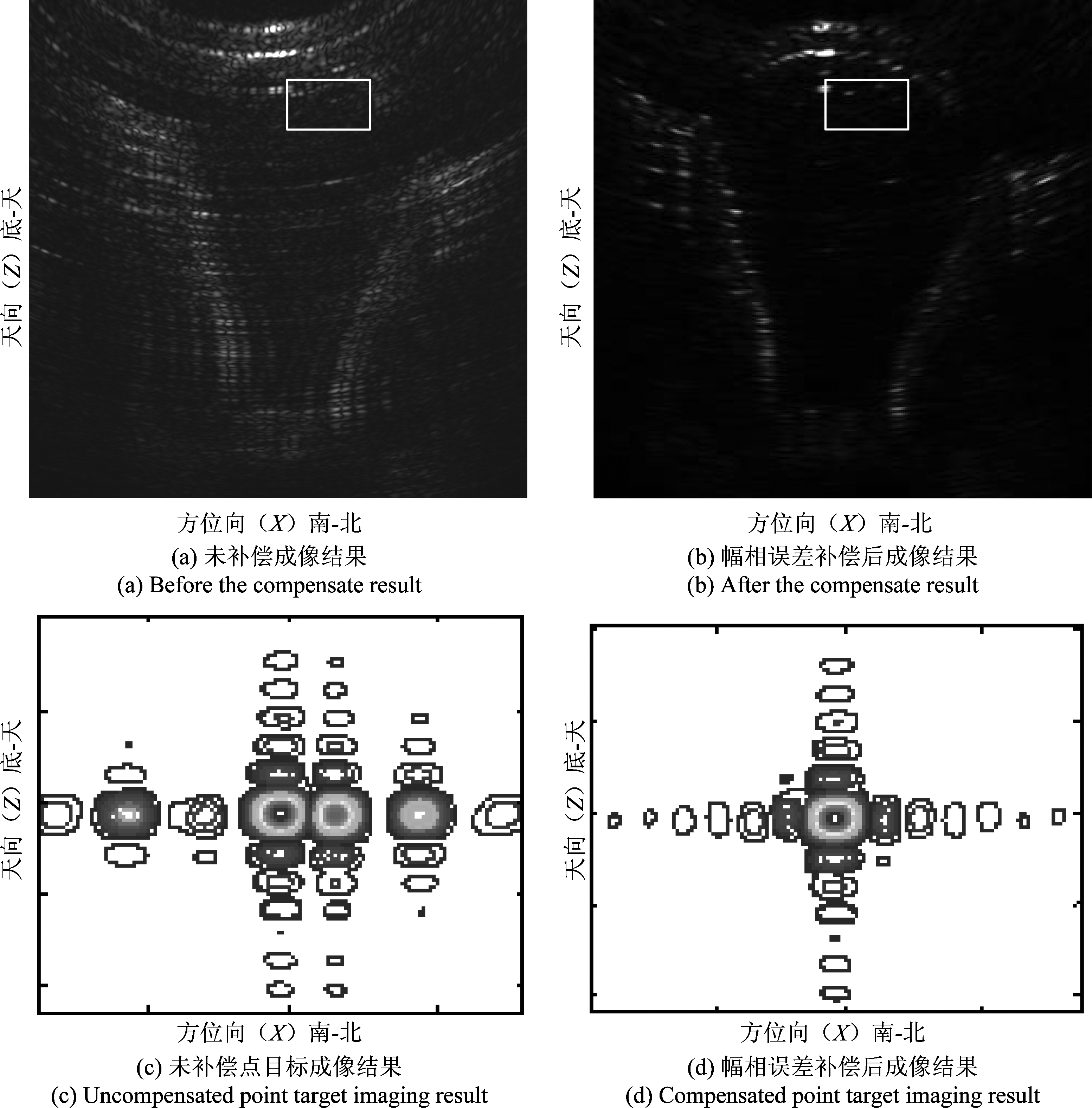
图9 二维SAR图像
Fig.9 2-D SAR figure
表2 二维成像点目标评估结果(未加窗)
Tab.2 2D imaging point target evaluation results(without window)
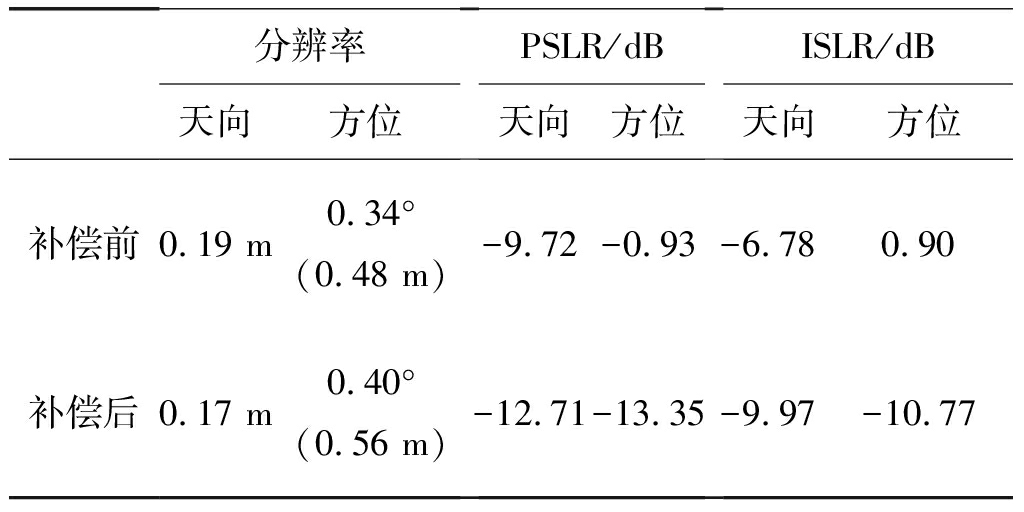
分辨率天向方位PSLR/dB天向方位ISLR/dB天向方位补偿前0.19 m0.34°(0.48 m)-9.72-0.93-6.780.90补偿后0.17 m0.40°(0.56 m)-12.71-13.35-9.97-10.77
4.3 配准结果
图10展示了在多幅SAR图像之间,散射特性的变化明显,这会对传统基于多强点的配准方式造成极大的干扰。
图11展示了在3.3节所介绍基于结构信息的图像配准方法下对主副图像二值化图形结构的提取结果。通过结构的对齐解决强闪烁点造成的影响。
最后图像的相干结果对比如图12所示。
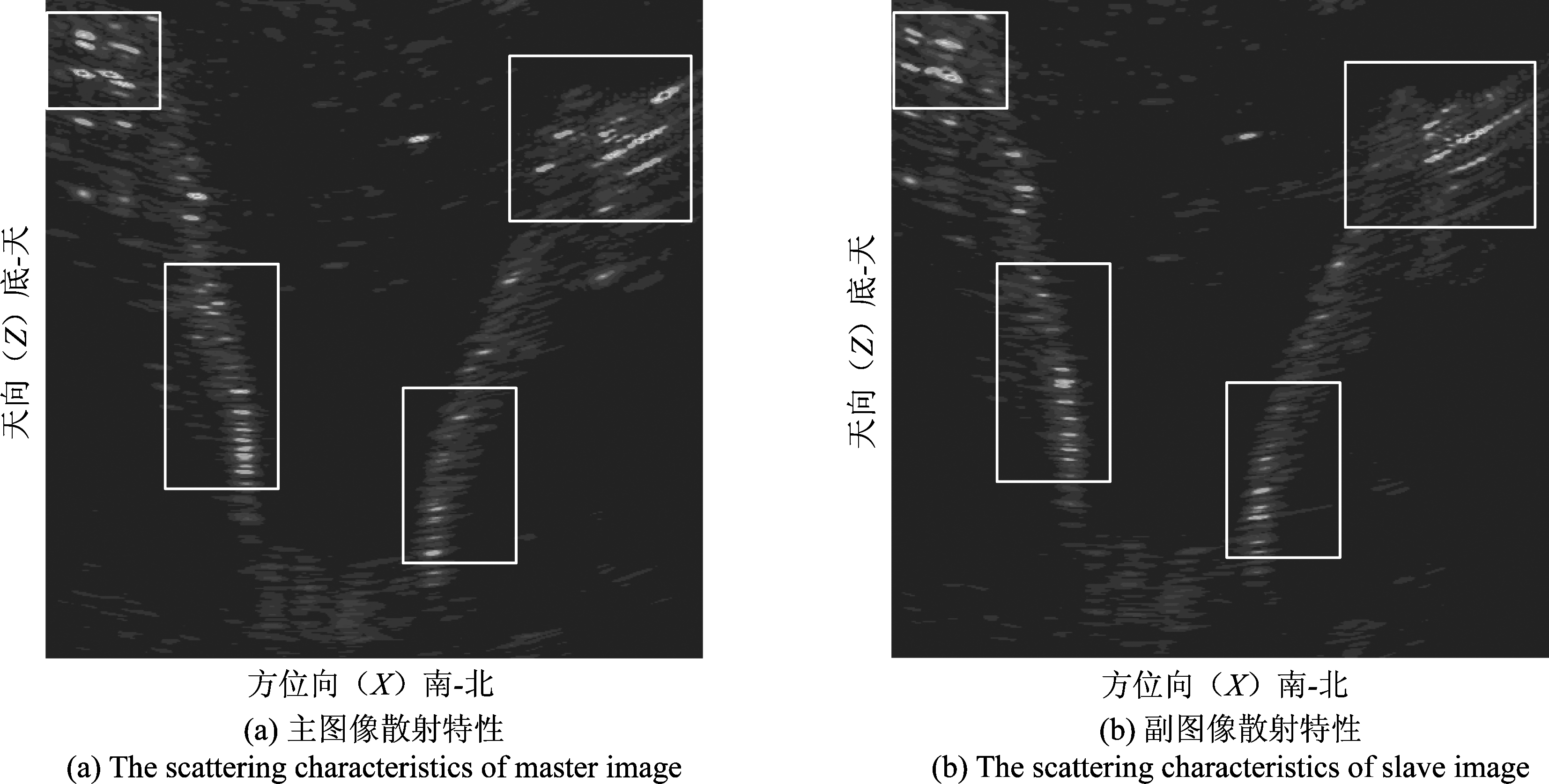
图10 不同视角下散射特性变化
Fig.10 The scattering characteristics change with different look angles

图11 主副图像二值化结构
Fig.11 The binary image of slave and master images
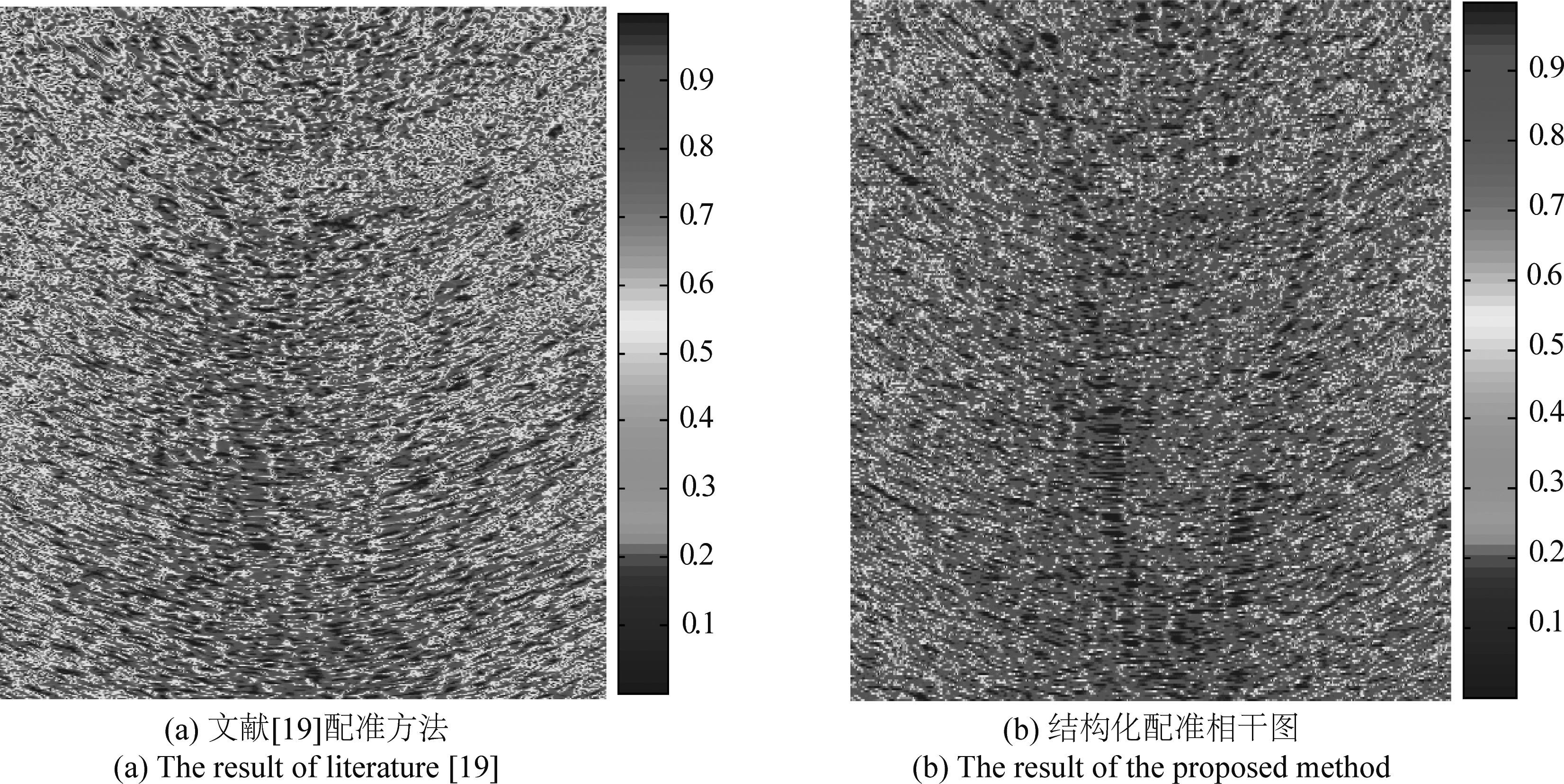
图12 配准相干图条纹图
Fig.12 The correlation coefficient maps after image registration
图12(a)为基于孤立散射强点方法配准[19]的主副SAR图像的相干条纹,通过图像中存在的强点散射信息完成对全幅图像的配准,但是由图10可以看出,在近场条件下,散射特性的剧烈变化使得图像中难以找到恒定的强点,最终的干涉结果也并不清晰。图12(b)为经过3.3节介绍方法处理的主副图像,结果显示出有明显的图纹痕迹,配准结果相较于传统方法有明显改善。
4.4 层析结果
以3.4节介绍的空间坐标系为基础,设在(-24,120,55)处有目标点A,在层析向总长度为7.25 m的测量基线上,随机选取11个测量位置,完成对目标的11次观测测量。相关雷达系统参数如表1所示,仿真结果如图13所示。
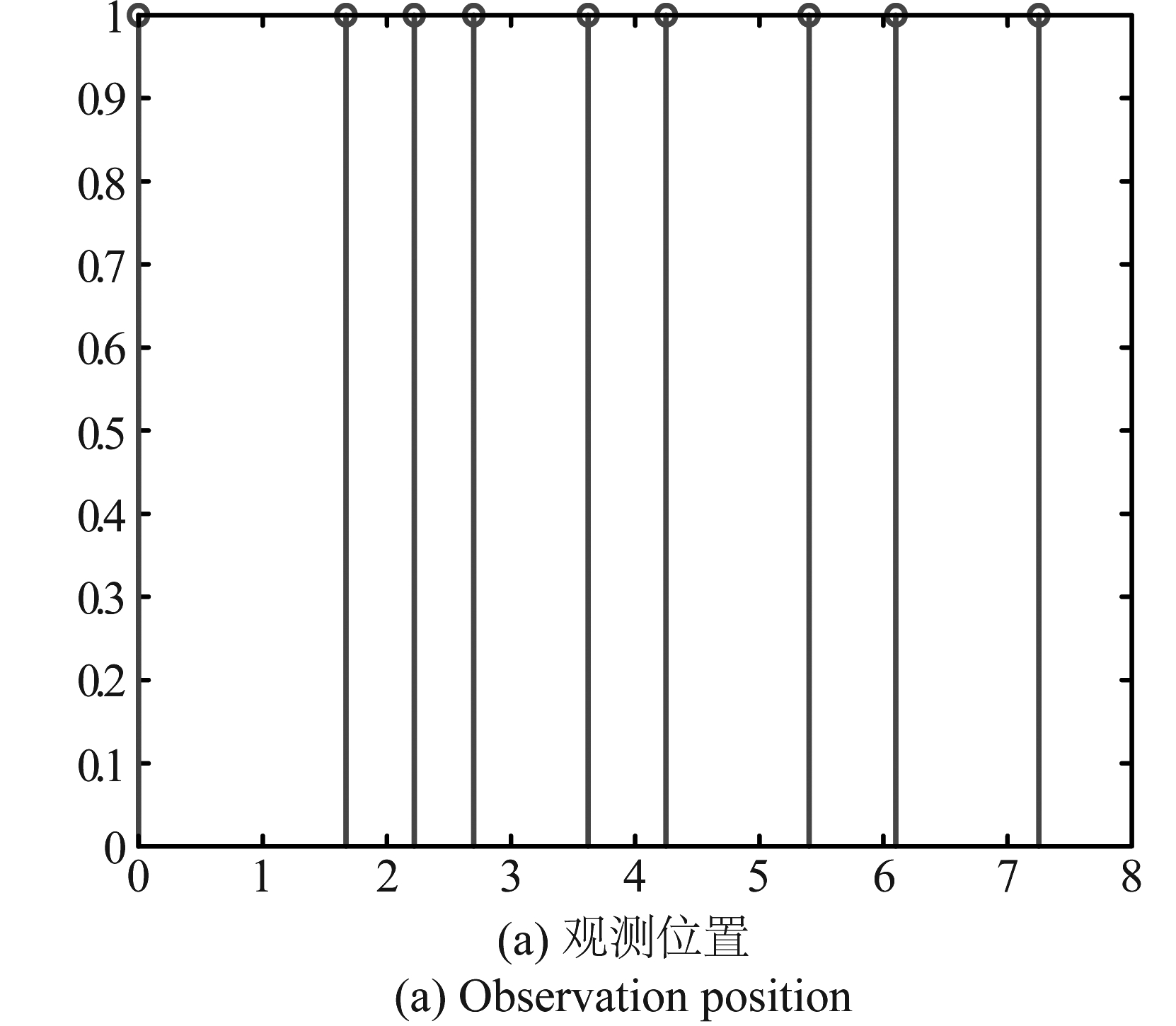
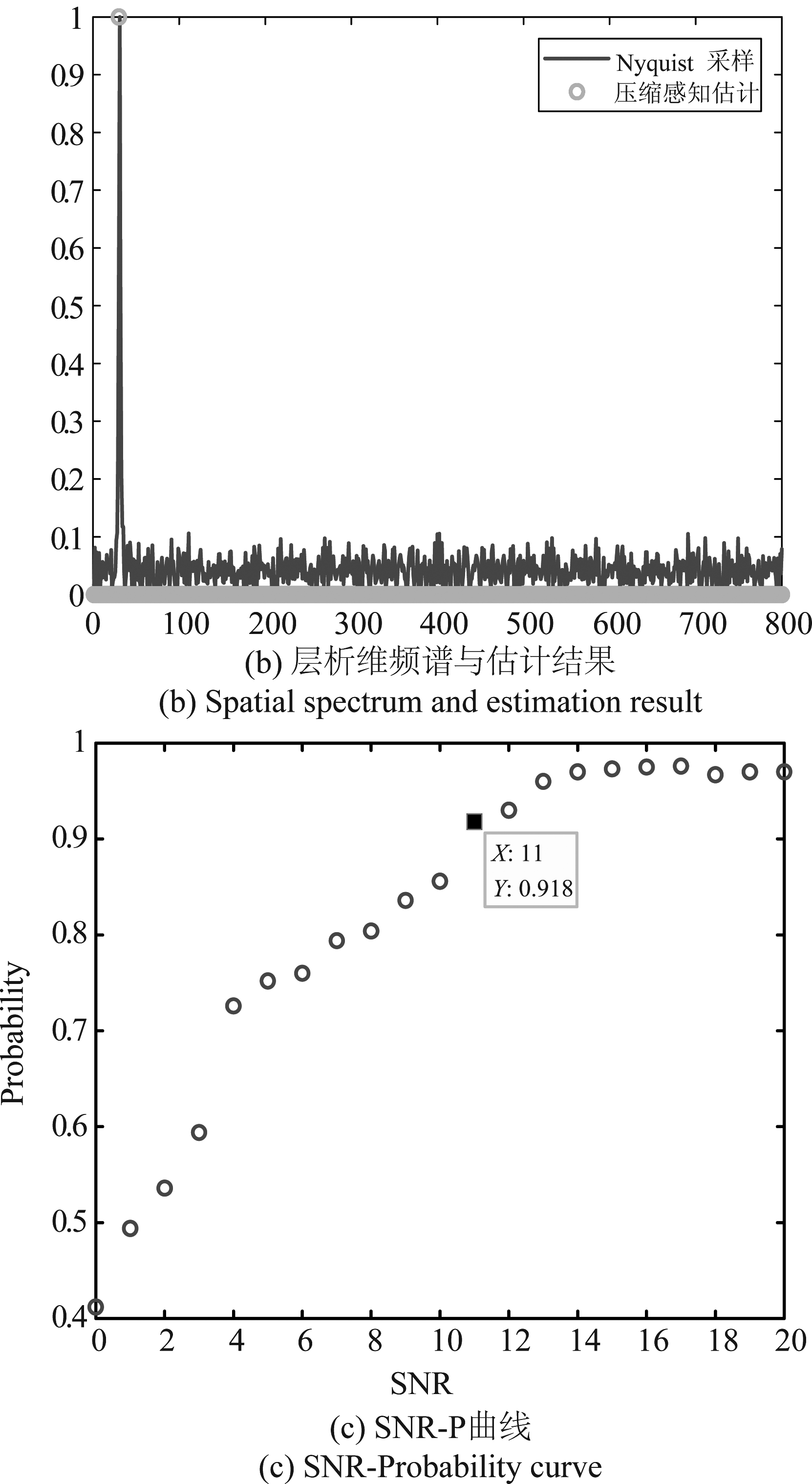
图13 仿真结果
Fig.13 Simulation results
图13(a)为起始为0,终点为7.25,总长为7.25 m的基线,在基线中随机分布共计11轨的测量位置,满足场景对应的稀疏非均匀采样条件。图13(b)展示在噪声环境下,层析维聚焦结果以及压缩感知估计结果,蓝色连续线表示在符合Nyquist采样定理下的,经过解斜处理后的聚焦结果,红色圆圈表示在压缩感知框架下估计恢复结果,仿真结果表明可以恢复得到高度维信号的谱峰位置信息。图13(c)展示了恢复概率随信噪比增加的变化情况,每组概率经过500次蒙特卡洛仿真统计,结果表明,在观测值取11次的情况下,SNR大于11 dB时即可获得90%以上的恢复正确概率,最终恢复概率保持在97%。层析估计处理方法主体为文献[20]中的OMP算法,运算量为O(MN),在估计过程,对全图逐像素点进行遍历,最终运算量为O(PMN),P表示单幅图像像素点总数,M表示测量数量,N表示原始信号长度(满采样条件下)。通过对实际层析运算处理记时,单次运行:11轨测量值,原始信号长度600点,900×101点像素,平均运行时间14 min,结果表明算法运算量具备可用性。
使用MIMO雷达获观测数据后,运用3.4节介绍方法进行处理,得到最后的结果如图14所示。图14(a)为北京理工大学中心教学楼卫星俯视图,图14(b)是对其观测测量的二维SAR图像,图14(c)是层析维即对观测大楼纵深进行估计,图14(d)展示了根据估计结果绘出的三维点云图。
通过卫星地图观测,以及全站仪对大楼中靶点A,B,C的观测测量,可获得目标大楼部分信息,如表3与图14(a)所示。最终获得目标大楼参考真值信息为:(70 m,40 m,58.5 m),分别对应大楼的长,纵深,以及高度值。实测数据测量结果如表4所示,可获得对应信息(72 m,41 m,59 m),通过对参考真值与测量数据的比较,两者结果相近,证明本文算法的有效性。
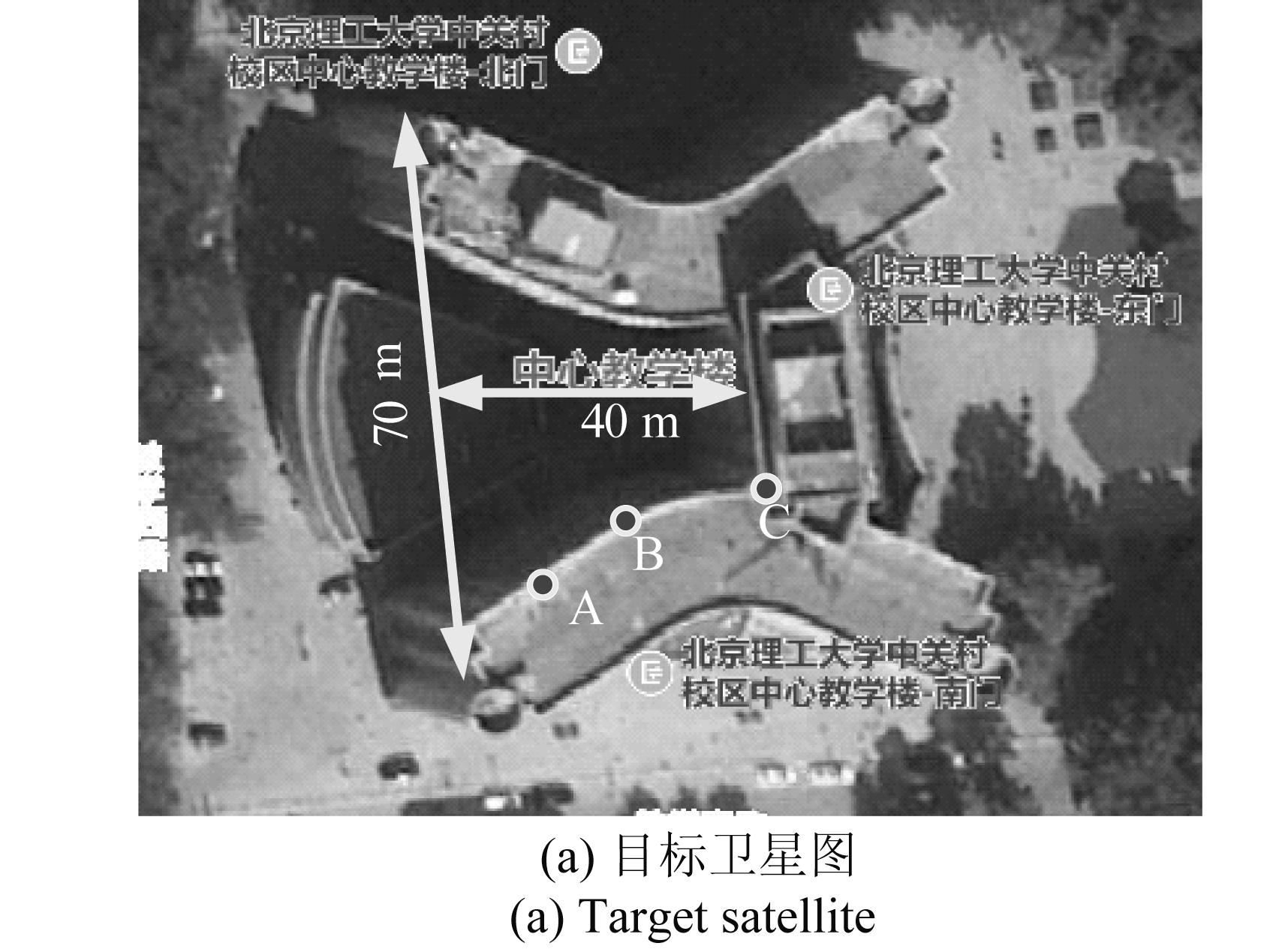

图14 实验测量结果图
Fig.14 Experiment measurement result
表3 大楼测量信息
Tab.3 Measurement information

目标坐标A(-11.2225,138.628,58.5454)B(-2.0623,-149.531,58.4068)C(7.9817,-169.107,58.56)
表4 大楼估计结果
Tab.4 Estimate result

目标坐标AB段高度59 m楼体纵深41 m楼体宽度72 m
5 结论
本文针对层析处理方法在近场应用中存在的不足开展了研究,分析了基于近场MIMO SAR层析处理的二维成像、多图配准以及层析估计问题。提出通过强点提取对通道间幅相误差进行补偿,改善二维成像质量;通过目标几何结构信息的提取,降低闪烁点的影响提高配准精度;通过建立映射估计关系,实现层析维的精确估计。最终利用MIMO SAR平台完成对北京理工大学中心教学楼层析SAR数据的获取成像,实现了目标三维信息的估计与目标三维点云的重建,后续拟在无人车载、机载平台层析等方面开展进一步研究。
[1] Reigber A, Moreira A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142-2152.
[2] Gini F, Lombardini F. Multilook APES for multibaseline SAR interferometry[J]. IEEE Transactions on Signal Processing, 2002, 50(7): 1800-1803.
[3] She Z, Gray D A, Bogner R E, et al. Three-dimensional space-borne synthetic aperture radar(SAR) imaging with multiple pass processing[J]. International Journal of Remote Sensing, 2002, 23(20): 4357- 4382.
[4] Fornaro G, Serafino F, Soldovieri F. Three-dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507-517.
[5] Fornaro G, Lombardini F, Serafino F, et al. Three-dimensional multipass SAR focusing: Experiments with long-term spaceborne data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 702-714.
[6] Knaell K K, Cardillo G P. Radar tomography for the generation of three-dimensional images[J]. IEE Proceedings-Radar, Sonar and Navigation, 1995, 142(2): 54- 60.
[7] Ender J H G. On compressive sensing applied to radar[J]. Signal Processing, 2010, 90(5): 1402-1414.
[8] Zhu X X, Bamler R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296- 4308.
[9] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[10] Candès E J. Compressive sampling[C]∥Proceedings of the International Congress of Mathematicians, 2006, 3: 1433-1452.
[11] Zhu X X, Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247-258.
[12] 刘记红, 徐少坤, 高勋章, 等. 压缩感知雷达成像技术综述[J]. 信号处理, 2011, 27(2): 251-260.
Liu Jihong, Xu Shaokun, Gao Xunzhang, et al. A Review of Radar Imaging Technique based on Compressed Sensing[J]. Signal Processing, 2011, 27(2): 251-260.(in Chinese)
[13] Shahzad M, Zhu X X. Automatic detection and reconstruction of 2-D/3-D building shapes from spaceborne TomoSAR point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1292-1310.
[14] Wang Y, Zhu X X. Automatic feature-based geometric fusion of multi-view TomoSAR point clouds in urban area[J]. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens., 2015, 8(3): 953-965.
[15] Budillon A, Johnsy A C, Schirinzi G. Sparsity based TomoSAR combining CS and GLRT[C]∥EUSAR 2018; 12th European Conference on Synthetic Aperture Radar. VDE, 2018: 1- 4.
[16] Budillon A, Evangelista A, Schirinzi G. Three-dimensional SAR focusing from multipass signals using compressive sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 488- 499.
[17] Zhu X X, Bamler R. Tomographic SAR inversion by L1-norm regularization—The compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839-3846.
[18] 王晶阳, 田卫明, 卢晓军, 等. 地基双基地MIMO成像雷达空间分辨特性分析[J]. 信号处理, 2018, 34(11): 1286-1296.
Wang Jingyang, Tian Weiming, Lu Xiaojun, et al. Analysis on Spatial Resolutions of Ground-based Bistatic MIMO Imaging Radar[J]. Journal of Signal Processing, 2018, 34(11): 1286-1296.(in Chinese)
[19] Serafino F. SAR Image Coregistration Based on Isolated Point Scatterers[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 354-358.
[20] Tropp J A, Gilbert A C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655- 4666.







