1 引言
当前,电磁辐射源定位在众多领域都有着广泛的应用需求,例如搜索和救援失事飞机和船只,定位非法干扰的地点——主要对无线电管理委员会管理违法电台,以及在反恐监控、部队安全保障等诸多方面。针对辐射源的目标定位技术主要包括到达角度(Angel of Arrival,AOA)[1]、达到时间差(Time Difference of Arrival,TDOA)[2]和接收信号强度指示(Receive Signal Strength Indication,RSSI)[3]等。其中,AOA测向设备对单站系统的复杂性有一定要求[4],而基于RSSI的定位技术在距离较远时误差较大[5]。TDOA技术除对系统时统精度有较高要求外,在定位精度和设备复杂度方面相较与前两者都有着较为明显的优势,而随着GPS和北斗授时系统的不断小型化,分布式TDOA系统的时统也不再是问题[6]。因此,一直以来围绕TDOA定位技术开展的研究很多[7-9]。其中关于非视距(Non-Line of Sight, NLOS)问题[7],最近的工作已经在TDOA系统中应用了凸优化来减少NLOS误差,但是该方法还存在凸包问题、参考节点选择问题以及处理大量由于非视距引起的测距误差等问题;而关于站点的布站方式[8],文献指出其布站的几何形式可以显著影响任何特定定位算法的潜在性能;关于TDOA定位精度的问题[9],可以在适当的TDOA测量噪声下,通过建立距离相关噪声模型,来提高基于TDOA的源定位的估计精度。
需要指出的是,非视距问题和站点几何位置影响是目前限制TDOA手段定位精度提升的最主要因素[7- 8]。特别是在城市环境下的应用,不仅要考虑天线高度以尽量避免遮挡,还要考虑布站的几何关系以获得最佳的控守区域,往往以上两者难以兼顾。当前,随着软件无线电平台的性能不断提高,体积不断减小,小型化多旋翼无人飞行器的逐渐普及,使升空载重量在5公斤以上的小型飞行平台完全可以胜任搭载定位系统的工作,因此,上述这一问题,可以利用无人机搭载定位系统在空中移动展开定位搜索的手段来解决。
将定位设备携带到空中,利用空中站点直接接收地面目标的辐射源信号,从而将目标的信息计算出来,这种方法优点是定位范围广,同时在空中也有效避免了多数条件下的非视距的影响。其中文献[10]和[11]讨论了移动条件下的定位问题,主要分析了为了获得精确持续的目标状态信息,无人机通过对目标状态的融合估计对移动目标进行在线建模,获得目标准确的当前状态,并对目标辐射源后续一段时域内的状态预测。但并没有就飞行器自身的续航能力限制问题展开讨论。为了保证飞行定位系统的正常工作,需要在考虑定位精度的同时保证飞行路径的优化,以解决续航的问题。
在近几年发表的文献中,对于无人机路径规划的算法比较多,如Voronoi法、概率地图法、遗传算法[12-14]等。其中符小卫等人[12]提出了一种在已知的雷达分布条件下的无人机路径规划算法:根据已知的雷达分布情况构建无人机可能飞行的路径集,用Voronoi图表示出来,利用Dijkstra算法搜索存在威胁的分布图,求解出大致的最短路径,在求出的最短路径的基础上,应用序列二次规划和三次样条曲线的方法求解最佳路径。方海洋等人[13]提出了基于MMTSP算法的多UAV协同侦察路径优化,是将地区的边界离散化并转化为有返回的多出发点的问题来得到最优路径。然而没有考虑目标的定位精度。McLain等人[14]提出了一种多无人机协同组队的想法:在满足机群编队要求的情况下,让单个的无人机分别计算自己的最佳航行轨迹,在这个算法中存在的不足是:人为情况下划分编队的因素会影响到航行路径规划的结果。上述研究都是仅针对飞行路径的优化问题,在优化中没有考虑飞行任务的变化。而将TDOA手段与无人机相结合,需要无人机在飞行过程中不断的定位,不断的更新飞行目的地,从而需要反复的更新路径规划。在这样的前提下,如何在保证高定位精度下,尽量控制飞行距离,是本文主要解决的问题,针对这一特殊问题,目前还鲜见公开的研究文献。本文提出了一种利用平均定位误差下界最小化的飞行路径规划模型,理论分析和仿真结论证明了方法的有效性。
2 问题描述
如前所述,将定位设备搭载在无人机上,多架无人机在空中针对辐射源目标进行定位,其中在本文中主要采用TDOA的方法进行定位研究。如图1所示。
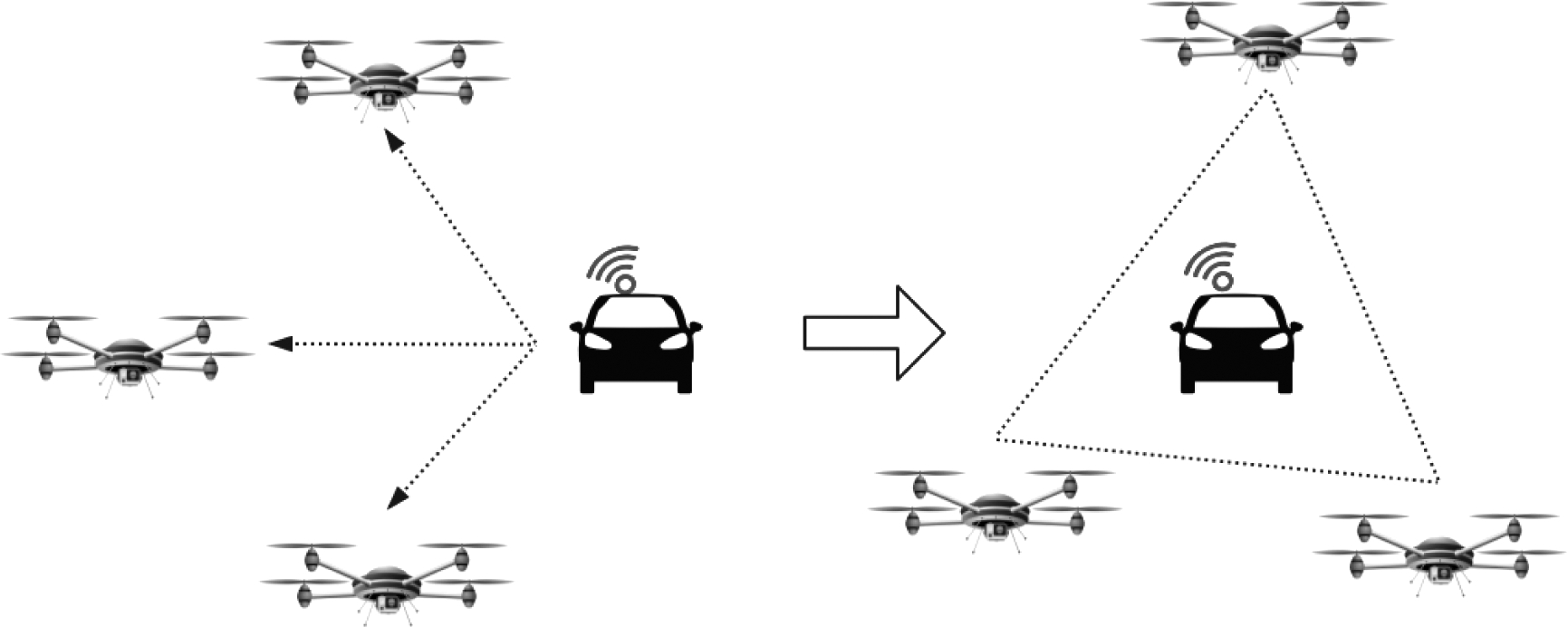
图1 无人机定位过程
Fig.1 The positioning process of unmanned aerial vehicles
设第k时刻第i架无人机的位置为:
...,m(无人机的位置由机上卫星定位系统获得,低空飞行不考虑自身定位误差),初始条件下,m架无人机在空中组成任意形状拓扑,完成目标定位后,依据目标定位位置,需要调整拓扑形状或者需要向目标飞行一段距离后进行二次定位,以此反复,来获得预定的定位精度,这期间受每次定位精度的影响,无人机的位置调整可能出现反复,特别是在目标较远,初始条件下构成短基线位置关系时,需要优化选择无人机逼近目标的飞行路径,尽量规避定位偏差带来的错误飞行路径,以尽量降低飞行时间,提高飞行定位系统的时效性。
3 多无人机协同侦察调度模型
多无人机协同侦察是由多架无人机从同一地点出发,飞到初始位置,通过每次更新迭代对目标源的定位位置来规划每次移动的路径,由于还要考虑到自身巡航时间的限制,用无人机在总的飞行路径中最短来达到节省能耗的目的。
3.1 模型假设
假设一共有m架无人机,第k时刻第i架无人机的位置为:s*
目标辐射源的位置为:θ*=[x,y]T。其中,用(⊗)*表示真实值,用(⊗)表示含有噪声的值。则第i架无人机到目标辐射源的距离为:
...,m
(1)
在第k时刻,目标辐射源到达第1架无人机和第i架无人机的时间差为:
...,m,其中c为光速,则令h*k(θ*
...,
表示为真实的距离差的集合。则观测到的距离差为:
hk(θ)=h*k(θ*)+Δr
(2)
θ表示测量出的辐射源的位置坐标。式(2)中的误差Δr服从标准正态分布规律N(0,R),其中
为测量噪声协方差矩阵。测量噪声协方差矩阵中的协方差是与目标源的距离有关[15],是关于真实距离d的函数。在相同的信道环境下,假设接收机的噪声功率是恒定的,则当目标源与无人机距离越近时,信号的接收功率越大,则接收到的信号的信噪比越高。其中,方差与信噪比的关系为[16]:
(3)
在式(3)中,γ为转发信号进入接收信道的信噪比,B为所处理信号的有效带宽,T为所处理信号的相关积累时间。同时,功率与距离的关系为:Pr=P0-10αlgd,其中,接收功率为Pr,发射功率为P0,α在自由空间中的取值为2。因此,当距离越远时,信号的接收功率就越小,在保持接收机的噪声功率恒定时,接收到的信号的信噪比就会越低。
综上,式(2)服从正态分布:hk(θ)-h*k(θ)～N(0,R),那么其概率密度函数为:
(4)
其对数似然函数为:
ρ(h|x,y)=ln(f(h))=
(5)
利用已给定条件,由此可推导出Fisher信息矩阵[17-18]:
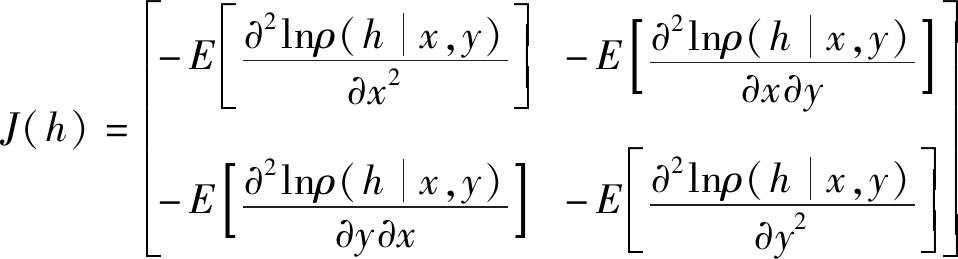
(6)
其中:
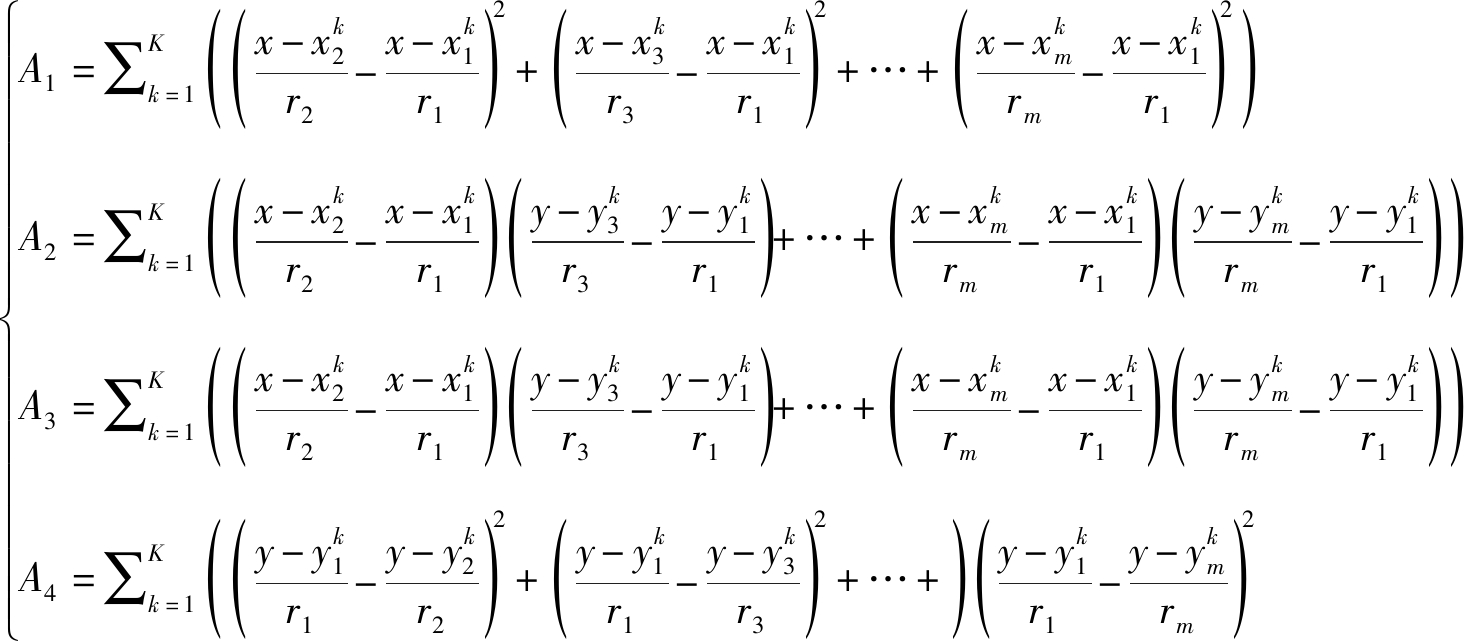
(7)
另外,关于辐射源目标位置的概率密度函数为:
f(s|s1,...,sm)=
(8)
为目标的真实位置坐标。因此当利用m架无人机进行实验时,随机变量的协方差矩阵为:
(9)
其中ρ为互相关系数,一般认为x与y是相互独立的,故ρ取0。在本文中,利用费舍尔信息矩阵的逆矩阵J-1(h)来定义式(9)的协方差矩阵。由于J-1(h)是无偏估计子所能达到的最小方差的下限[19]。因此,式(8)就可以认为是目标估计值关于真实值的“方差最小”的分布。
对式(8)的概率密度函数作如下仿真:以3架无人机为例,当3架无人机的中心位置距离目标源较近时,将距离设为800 m;当无人机的中心位置距离目标源较远时,将距离设为2000 m。如图2所示。
由上面的概率密度分布图可以看出,式(8)中的概率密度函数分布由无人机的位置和目标的位置决定。在无人机逐渐靠近目标源的过程中,概率密度分布有明显的变化。式(8)可以解释为目标位置的最优估计值关于真实值的概率分布,考虑在第k时刻定位的均方误差的期望为:
(10)
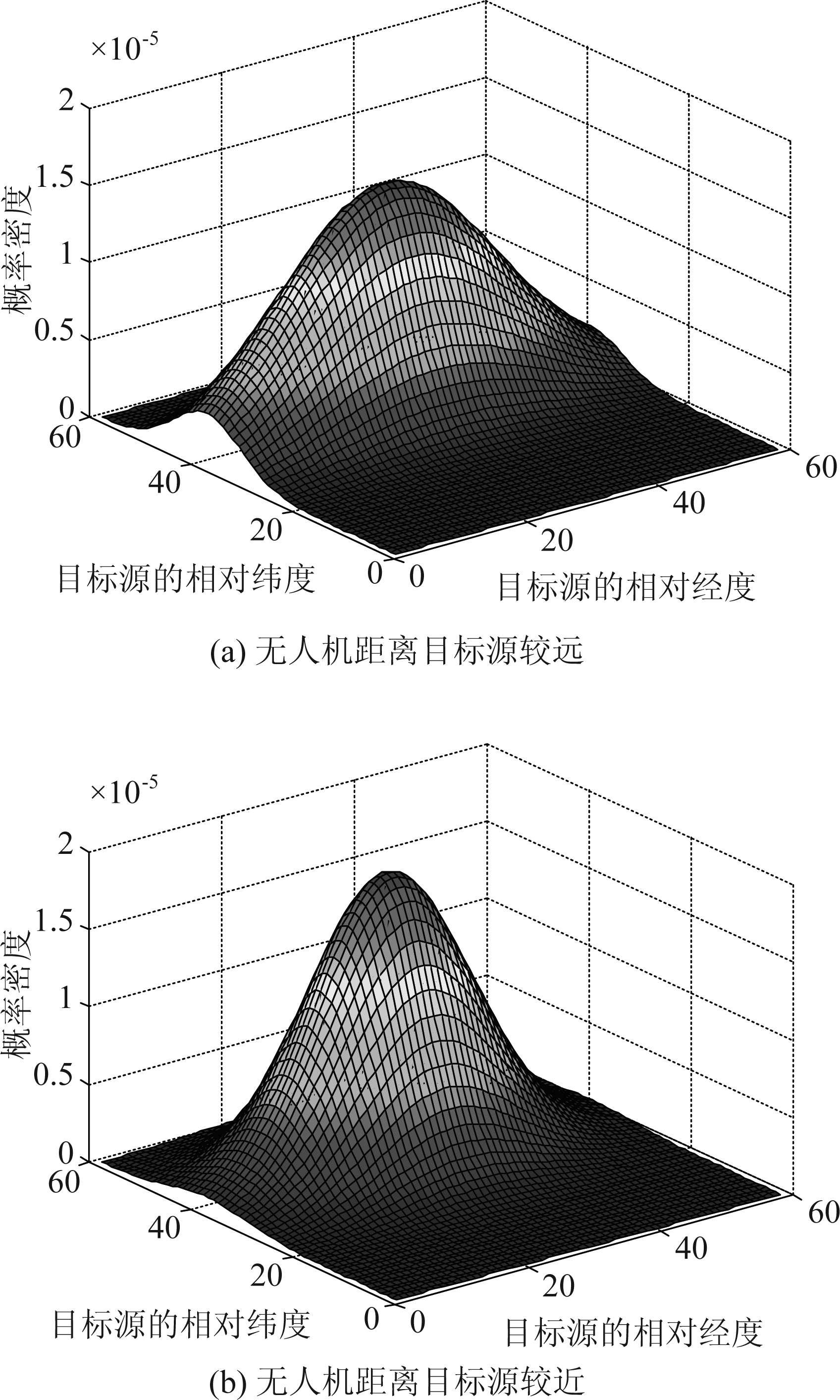
图2 不同距离条件下,概率密度函数的变化
Fig.2 The change of probability density function at different distances
是第k时刻定位的均方误差的期望的下界,其中k=1,2,…,K,该下界是关于无人机位置的函数,因此对飞行目标位置的求解转化为如下目标函数的优化问题:
...,sm)
(11)
即:
(12)
考虑到无人机飞行过程中出于接收功率限制、隐蔽探测等原因不能无限接近目标,应有约束条件:
...,m
(13)
综上,优化目标为:
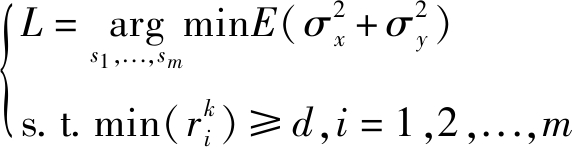
(14)
式(14)是在一次测量条件下获得的无人机最优位置估计,这为无人机下一时刻的飞行目的地提供了依据,设任意时刻获得一次关于目标的位置估计L,由L更新式(14),得到新的目标函数,求解该目标函数获得无人机当前应处于的最佳位置点,以此类推,直到当
小于预设阈值时结束定位过程。如前文所述,考虑到无人机的续航能力,所以要求在达到定位精度的同时要求飞行距离尽量的短。因此,在任意时刻,虽然获得了无人机关于目标定位的最佳位置,但需要考虑整体飞行距离最短的约束,此时,每一步的飞行距离转化为一个决策问题,即如何选择每一步的飞行路线,使得在达到定位精度要求的同时,总的飞行路径最短。
假设无人机飞行速度恒定且沿直线飞行,设存在关于时间的n个随机变量t1,t2,...,tn,上述问题就转化为:当无人机在完成当前定位之后,如何选择飞行时间Δti=ti-ti-1,i=1,2,...,n来进行下一次定位,使得在
达到预定精度的同时,
最短,其中i=1,2,...,n。
3.2 模型求解
在定位到初始目标位置后,多架无人机沿直线向初始定位目标移动,在理想条件下,接收站包围目标并呈等角布站是时差定位最优布站形式[20],因此在本文中考虑以等边三角形的形状包围初始的定位位置,进行二次定位。如果包围初始的定位位置后,为了得到最短的路径,计算出将正三角形绕定位点进行旋转,能使路径最短的包围角度。根据约束可以得出无人机的位置坐标,然后控制无人机以最短移动距离包围辐射源。而无人机的初始位置与目标源的距离的远近对定位性能也会产生一定的影响。如果本来无人机的位置与辐射源的位置距离比较远,则需要多次移动无人机,来得到最精确的辐射源坐标。
给出解决这个问题的两个算法:
1)谨慎型搜索模式。三架无人机从同一点出发,进行第一次定位后,计算最短路径,飞行最短路径的一段距离,接着进行第二次定位,并得到比第一次定位结果更精确的辐射源位置,再计算最短路径,飞行最短路径的一段距离,接着进行第三次定位,并重复之前的步骤,直到
小于等于设定的阈值时停止,得到精确的辐射源位置。
表1 谨慎搜索算法
Tab.1 Careful search algorithm
Step1 无人机进行第一次定位,无人机的几何中心位置为center1,并得到辐射源的第一次估计坐标location1;Step2 a.无人机初始位置与目标源的距离大于d0。飞行t1时刻,而t1满足:t1=(‖center1-location1‖/νUAV)∗kk=1-e-[a1-δ/E(σ2x+σ2y)]{,式中δ为衰减因子,其范围为5～10,可以得到新的位置center2。b.无人机初始位置与目标源的距离小于等于d0。在得到第一次估计坐标location1后,直接飞行至location1处;Step3 重复Step1,状态更新,得到新的辐射源的估计坐标loca-tion2,并重复Step2;Step4 当σ2x+σ2y小于等于预设阈值时,定位迭代结束,输出辐射源坐标locationn。
在上述算法中,当衰减因子δ=1时,k的值等于1,此时可以看成无人机在完成当前定位任务后,直接飞往当前定出的坐标点,从而来进行下一次的定位。因此下面给出方法二的算法:
2)贪婪型搜索模式。三架无人机从同一点出发,进行第一次定位,按最短的路径直接飞到定位的坐标点的周围并用正三角形的形式包围,接着继续进行后续的辐射源位置的迭代更新,直到σx+σy的值小于等于预设阈值时停止。
表2 贪婪搜索算法
Tab.2 Greedy search algorithm
Step1 无人机进行第一次定位,无人机的几何中心位置为center1,并得到辐射源的第一次估计坐标location1;Step2 无人机以最短路径直接飞行至初始坐标location1,重复Step1,状态更新,此时几何中心位置为center2,得到新的目标辐射源估计坐标location2;Step3 当σ2x+σ2y小于等于预设阈值时,定位迭代结束,输出辐射源坐标locationn。
4 计算机仿真分析
在本文中用MATLAB对所提出的算法进行仿真验证。这里采用三架无人机来进行实验,三架无人机从同一点开始出发,辐射源的位置分别设在距离无人机初始点位置较近与较远的点。
4.1 飞行算法对最短路径的影响
设三架无人机都从同一点起飞。利用无人机总的飞行的最短路径来比较和验证两种方法的应用范围,作如下仿真。
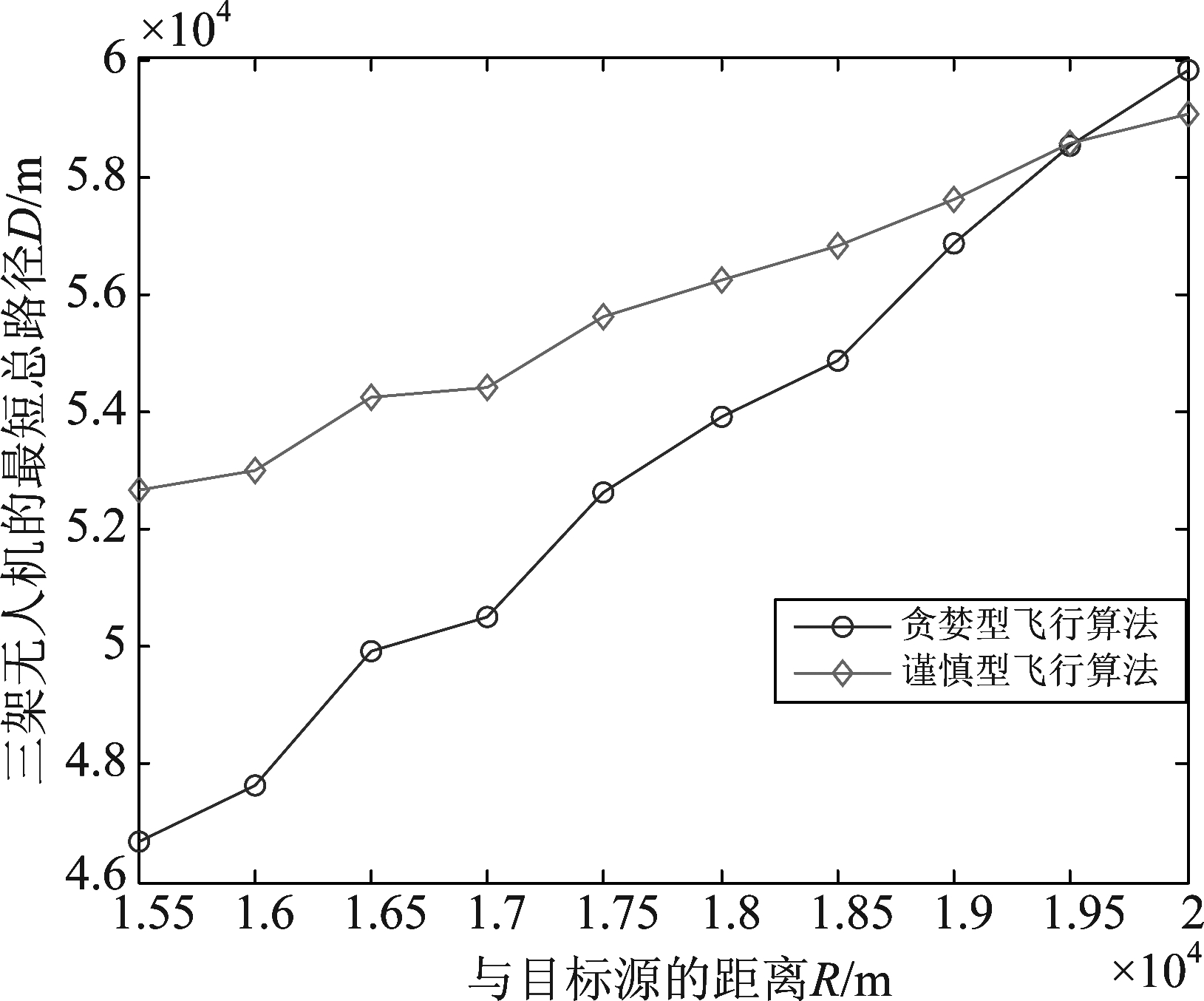
图3 不同飞行算法下的最短路径变化
Fig.3 The shortest path with different flight algorithms
由上面的图可以看出,在距离越来越远时,两种方法的总路径都在逐渐增大。然而,在距离增大的过程中,两条线逐渐相交,这说明随着距离的增大,谨慎型飞行算法逐渐比贪婪型算法的飞行路径更短,更有利于节省能耗。随着距离的增大,两种算法的定位精度在初始定位时的误差都比较大,然而在靠近目标源的过程中,谨慎型飞行算法对定位精度的修正比贪婪型算法的修正快速且准确,因此谨慎型飞行算法的总路径增加较慢。
4.2 定位精度对最短路径的影响
在这个仿真中,采用谨慎型飞行算法,对时延的误差分别增加10 ns、30 ns和60 ns,可以对不同时差测量精度时的理论定位精度进行分析,仿真结果如图4所示。
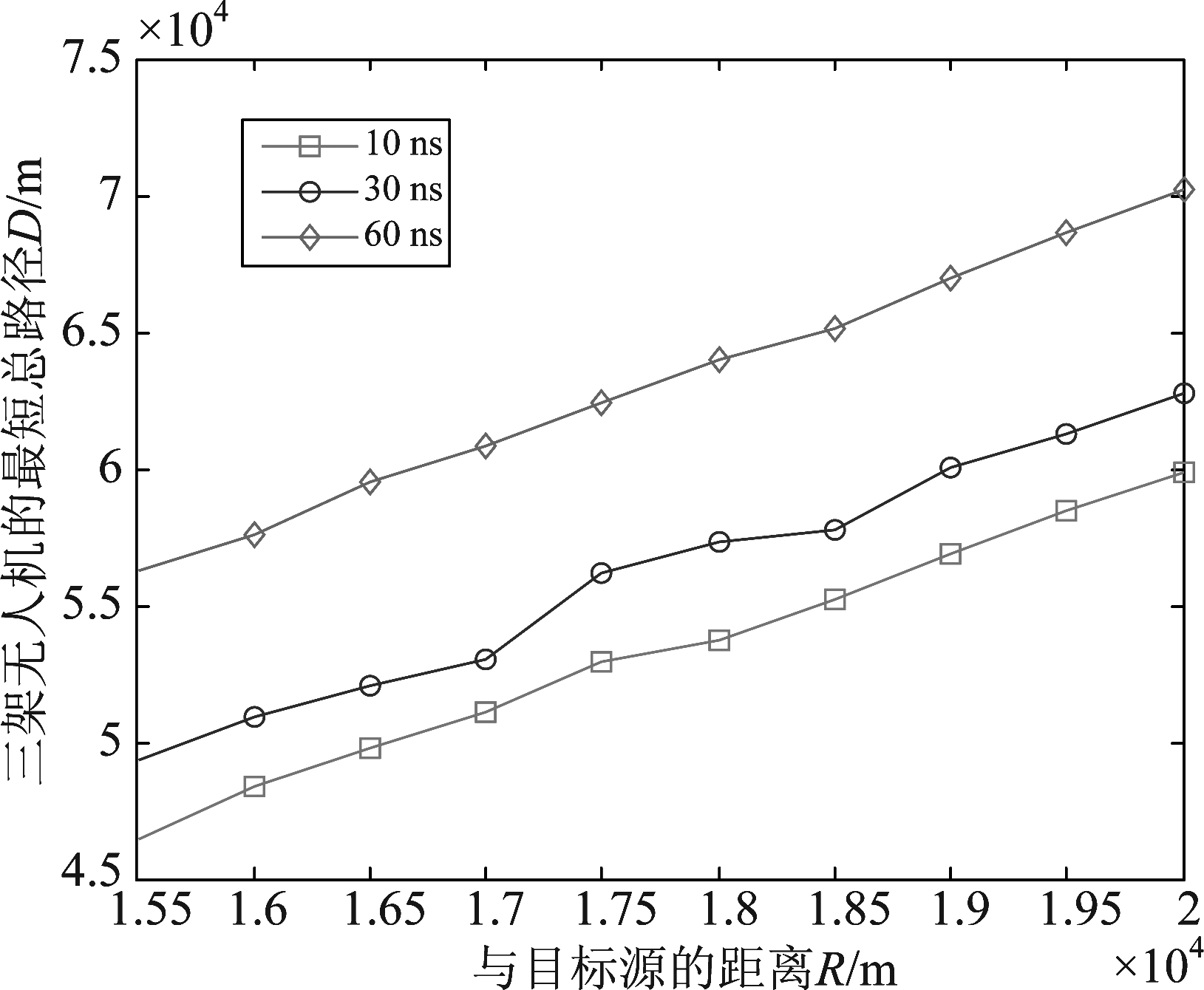
图4 不同时差测量精度下的最短路径变化
Fig.4 The shortest path with different time difference measurement accuracy
由上图可以看出,在该仿真条件下,随着测量精度的变差,可以导致理论的定位精度也随之变差,因此得到最直接的结果就是造成路径的增大。
4.3 飞行算法对定位精度的影响
在这个仿真中,假设无人机的初始位置是固定的,且距离目标源25公里,则在两种不同算法下,当无人机的飞行限制路径即飞行的总路径相同时,定位精度的比较结果如图5所示。
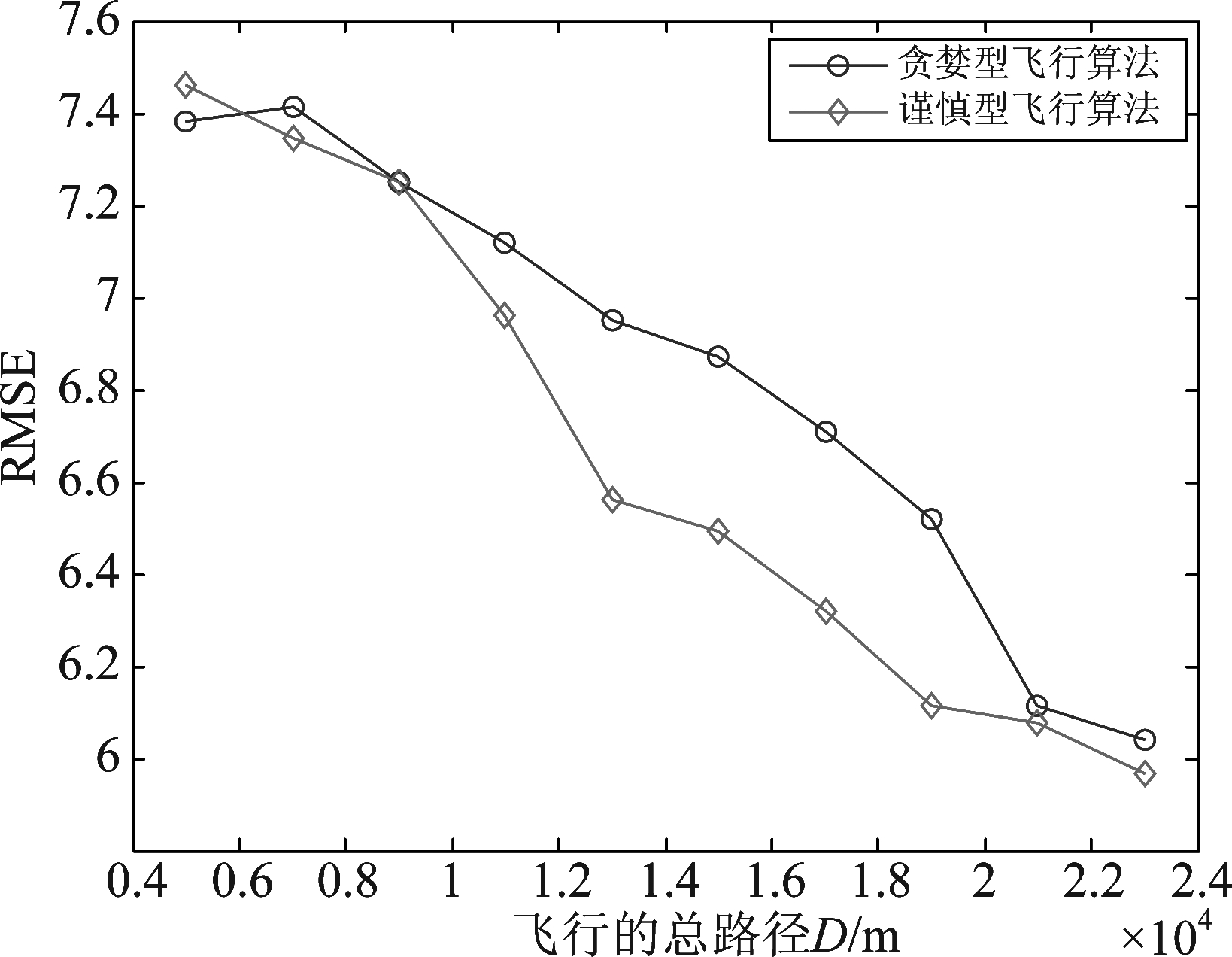
图5 相同飞行总路径下的定位精度比较
Fig.5 Comparison of positioning accuracy under the same flight path
由仿真图可以看出,当限定飞行的总路径远小于无人机初始位置与目标源之间的距离的时候,两种方法执行后的无人机仍然距离目标源较远,因此两种方法的定位精度都较低。然而随着飞行总路径的逐渐增大,两种方法下的定位精度都逐渐增高,且由于谨慎型飞行算法较大程度的避免错误飞行路线,因此它的定位精度比贪婪型飞行算法的定位精度高,假设无人机没有飞行总路径的限制,两者的定位精度最终将趋向一致。
4.4 与站点固定条件下的定位精度的对比
假设在30公里×30公里的正方形区域内,在区域内随机布置目标源,同时在目标源附近布设三个固定的站点进行定位,其中站点与目标源的距离逐渐增大。三架无人机的初始位置与地面站点位置相同,对比两种飞行算法与固定站点的定位精度。
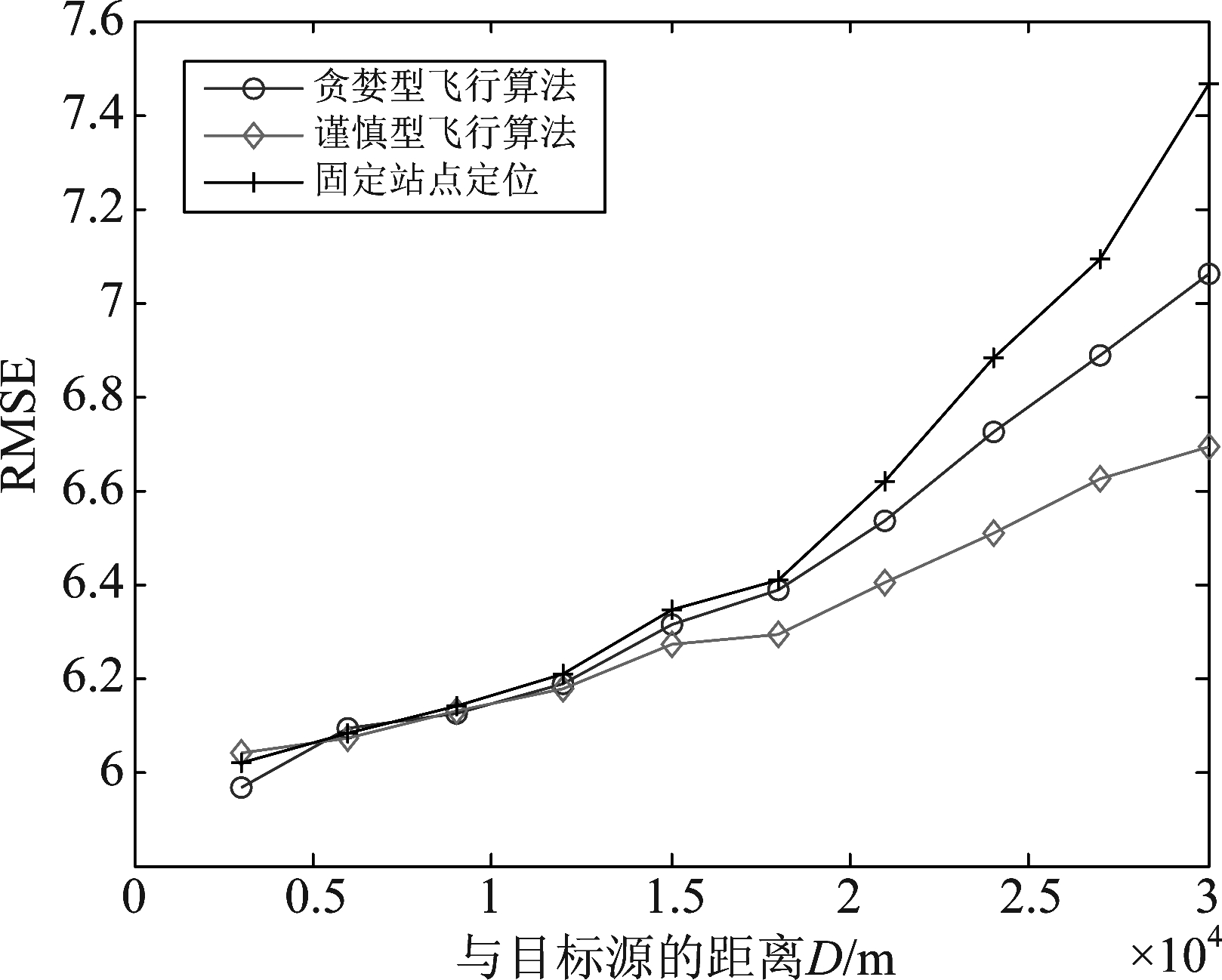
图6 与固定站点条件下的定位精度对比
Fig.6 Compared with the positioning accuracy of fixed station
由上图可以看出,在与目标源的距离较近的时候,三种方式的定位精度比较接近;随着距离的逐渐增大,三种方法的定位精度逐渐变差,其中固定站点的定位精度变化最快,而谨慎型飞行算法的定位精度变化最慢。
5 结论
将定位的设备携带到空中,在空间各个站点之间接收地面目标辐射源的辐射信号。通过利用对基于克拉美罗下界的概率密度分布的分析,可以在提高了定位精度同时降低计算的复杂度,另外突出了隐蔽,便于携带的优点。但是目前仅仅是针对固定的目标源的情况来定位,下一步,将对移动的目标源进行研究。
[1] Wu K, Ni W, Su T, et al. Robust Unambiguous Estimation of Angle-of-Arrival in Hybrid Array with Localized Analog Subarrays[J]. IEEE Transactions on Wireless Communications, 2018, PP(99): 1-1.
[2] Liu Y, Zhang Y, Qiu T, et al. Improved time difference of arrival estimation algorithms for cyclostationary signals in α-stable impulsive noise[J]. Digital Signal Processing, 2018, 76.
[3] Lao L H, Wong K Y. Detecting Hand Gestures with Wi-Fi Technology: Applications for Received-Signal-Strength Indicators in Interactive Interface Design[J]. IEEE Consumer Electronics Magazine, 2018, 7(2): 73- 82.
[4] Huang B, Yao Z, Cui X, et al. Angle-of-Arrival Assisted GNSS Collaborative Positioning[J]. Sensors, 2016, 16(6): 918.
[5] Abeywickrama S, Samarasinghe T, Ho C K, et al. Wireless Energy Beamforming Using Received Signal Strength Indicator Feedback[J]. IEEE Transactions on Signal Processing, 2017, 66(1): 224-235.
[6] Li W. A new TDOA estimation method in Three-satellite interference localization[J]. International Journal of Electronics, 2015, 102(5): 839- 854.
[7] Su Z, Shao G, Liu H. Semidefinite Programming for NLOS Error Mitigation in TDOA Localization[J]. IEEE Communications Letters, 2017, PP(99): 1-1.
[8] Bishop A N, Fidan B, Anderson B D O, et al. Optimality analysis of sensor-target localization geometries ☆[J]. Automatica, 2010, 46(3): 479- 492.
[9] Huang B, Xie L, Yang Z. TDOA-Based Source Localization With Distance-Dependent Noises[J]. Wireless Communications IEEE Transactions on, 2015, 14(1): 468- 480.
[10] 姜肖英. 多无人机对移动目标的侦察问题研究[D]. 南京:南京航空航天大学, 2012.
Jiang Xiaoying. Research on Moving Targets Surveillance of Multiple Unmanned Aerial Vehicles[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.(in Chinese)
[11] 王林. 多无人机协同目标跟踪问题建模与优化技术研究[D]. 长沙: 国防科学技术大学, 2011.
Wang Lin. Modeling and Optimization for Multi-UAVs Cooperative Target[D]. Changsha: Graduate School of National University of Defense Technology, 2011.(in Chinese)
[12] 符小卫, 高晓光. 一种无人机路径规划算法研究[J]. 系统仿真学报, 2004, 16(1): 20-21.
Fu Xiaowei, Gao Xiaoguang. Study on a Kind of Path Planning Algorithm for UAV[J]. Journal of System Simulation, 2004, 16(1): 20-21.(in Chinese)
[13] 方海洋, 杨廷鸿, 宗福兴, 等. 基于MMTSP算法的多无人机协同侦察路径优化[J]. 后勤工程学院学报, 2017, 33(3): 85-90.
Fang Haiyang, Yang Yanhong, Zong Fuxing, et al. Path Optimization of Multi-UAV Cooperative Reconnaissance Based on MMTSP Algorithm[J]. Journal of Logistical Engineering University, 2017, 33(3): 85-90.(in Chinese)
[14] Li S M, Boskovic J D, Seereeram S, et al. Autonomous hierarchical control of multiple unmanned combat air vehicles(UCAVs)[C]∥American Control Conference, 2002. Proceedings of the 2002. IEEE, 2002, 1: 274-279.
[15] 段凯宇, 张力军, 高玲, 等. 两种NLOS误差消除及TOA定位算法[J]. 信号处理, 2008, 24(4): 565-568.
Duan Kaiyu, Zhang Lijun, Gao Ling, et al. Two NLOS Error Elimination and TOA Location Algorithms[J]. Signal Processing, 2008, 24(4): 565-568.(in Chinese)
[16] Haworth D P, Smith N G, Bardelli R, et al. Interference localization for EUTELSAT satellites-the first european transmitter location system[J]. International Journal of Satellite Communications & Networking, 2015, 15(4): 155-183.
[17] Yang B, Scheuing J. Cramer-Rao bound and optimum sensor array for source localization from time differences of arrival[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing, 2005. Proceedings. IEEE, 2005: iv/961-iv/964 Vol. 4.
[18] 李红伟, 何青益, 李淳, 等. 运动多站无源时差定位的CRLB推导与分析[J]. 弹箭与制导学报, 2013, 33(6): 167-170.
Li Hongwei, He Qingyi, Li Chun, et al. Derivation and Analysis of CRLB for Moving Multi-station Passive Location Based on TDOA[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(6): 167-170.(in Chinese)
[19] Fowler Mark L, Chen Mo. Fisher-Information-Based Data Compression for Estimation Using Two Sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 1131-1137.
[20] 周成, 黄高明, 高俊. 时差定位最优布站方法研究[J]. 西安电子科技大学学报, 2016, 43(4): 123-127.
Zhou Cheng, Huang Gaoming, Gao jun. Optimum Sensor Array of Passive Localization from Time Differences of Arrival[J]. Journal of Xi Dian University, 2016, 43(4): 123-127.(in Chinese)
