1 引言
矩阵分解是实现高维的、大规模数据处理与分析的一种重要的方法,常用的传统矩阵分解的方法有奇异值分解(Singular Value Decomposition,SVD)、主成分分析(Principal Component Analysis,PCA)、矢量量化法(Vector Quantization,VQ)等[1- 4],使用上述方法进行矩阵分解时结果中可能会出现负值,但在实际应用中,负的数值为下一步的数据分析带来了很多困难。非负矩阵分解(Non-negative Matrix Factorization,NMF)算法由Lee和Seung于1999年在自然杂志上提出[5],NMF是一种基于特征空间低秩估计的降维技术,它在使特征维数降低的同时保证特征都非负,从而蕴含一定的物理意义。由于非负矩阵分解算法可以得到相对低维、纯加性、拥有一定稀疏特性的分解结果,具有收敛快、存储空间小的特点,作为一种有效的大规模高维数据处理方法,它被广泛应用于多个研究领域中,如文本分析与聚类、图像特征识别、语音分类与建模、盲信号分离、基因及细胞分析等。
Lee和Seung首先提出了一个以广义KL散度为优化目标函数的基本NMF模型算法,并将其应用于人脸图像表示[5];针对NMF算法的收敛性问题,Lee和Seung又提出了基于欧式距离测量的乘性迭代方法和基于广义的KL散度的乘性迭代算法[6]。Zhou J等人用小波变换来提取人脸图像的面部特征后,采用NMF来对高维面部特征图像数据进行降维以解决面部表情识别问题[7]。Ding Tu等人用层次化非负矩阵分解来研究文本流中的发现和跟踪问题,与已有的基线方法相比,在相同竞争效率的情况下取得了更好的性能[8]。Yong-Choon Cho等人用NMF算法来提取非负的光谱-声音信号特征,提出了一种基于NMF框架的编码变量推断方法,该方法在进行一般声音分类时,在噪声存在的情况下能够保证识别声学特性的鲁棒[9]。Wei J等人通过对老鼠大脑的分析将高维空间中的神经活动数据通过NMF映射到低维空间,用低维空间的连接性值来表达高维数据空间中神经元之间的连接,为脑网络分析提供了更好的描述[10]。
目前,越来越多的高维数据具有与时间相关的属性,而在使用NMF相关算法降维的过程中,如何有效获取所需低维非负表达的同时能够保留其时间属性是一个关键问题。目前的多数关于NMF算法的研究中并没有考虑到高维数据时间约束性问题[11-13]。
针对这一现状,本文提出了一种带时间约束的非负矩阵分解算法(Time Constraint Non-negative Matrix Factorization,TNMF),该方法通过构建包含时间属性的NMF模型,将高维数据的时间序列信息、维度以及分解前后误差等约束条件融合,共同构建时间约束模型,用于确定基矩阵的最优维数r,从而实现具有时间序列的高维数据的有效降维。将该方法应用于高维脑网络状态观测矩阵的降维实验结果显示,相对于K-means和t-SNE等降维算法,时间约束非负矩阵分解不但可以有效降低脑网络状态的特征数量,并且其在高维空间内的时间顺序被准确映射到低维空间内,同时在聚类指标上也得到了明显的提高。该方法不但为脑网络状态演化模型的研究提供了一种有效的解决方案,同时也为其他带有时间属性的高维数据分解提供了研究基础。
2 基于时间约束的NMF算法及原理
2.1 带时间属性的NMF模型构建
设{X(1),X(2),…,X(T)}表示高维时间序列数据的T个特征向量的集合,其中
表示第t(1≤t≤T)个时间点的特征向量。每个时间点的特征向量X(t)可以分解为X(t)≈W(t)(H(t))T,系数向量Hj(t)是第j个数据在基向量W(t)上的低维表示,每个时间点的Hj(t)是不同的,单个时间信息的分解变换可以表示为图1所示的包含时间序列信息的拓扑图。
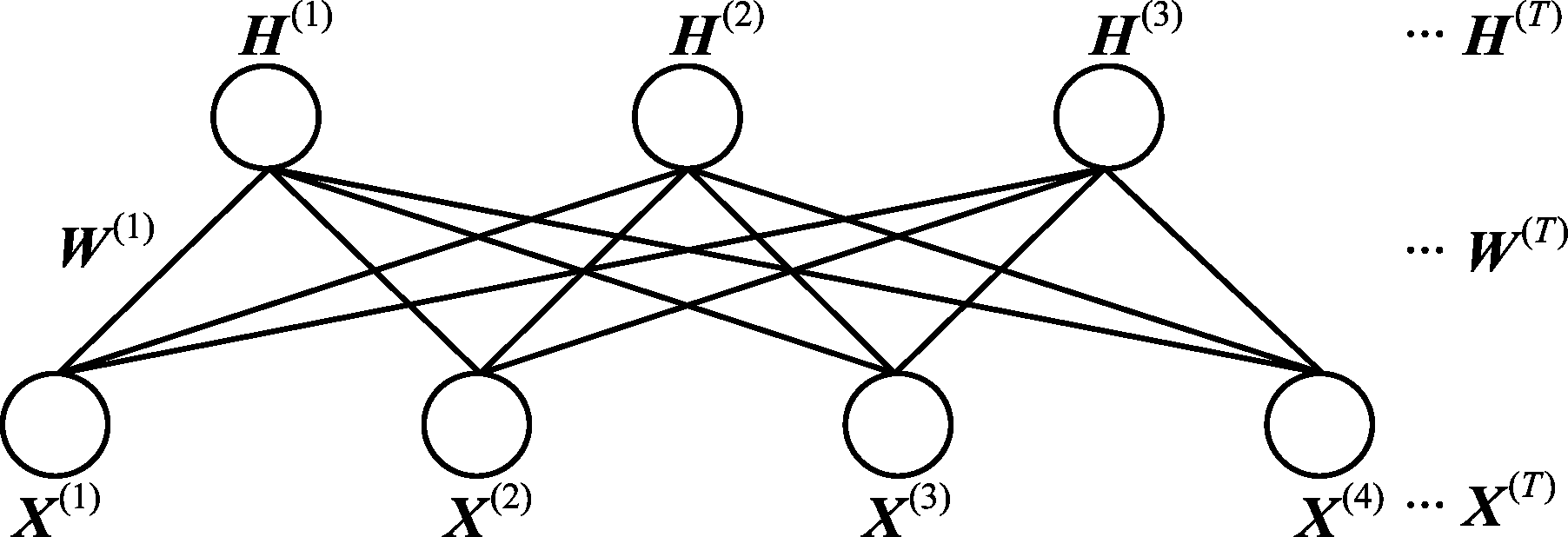
图1 包含时间序列信息的拓扑图
Fig.1 Topology diagram containing time series information
为了将单个时间点的矩阵分解信息融合到连续的时间序列中,需要确定每一个时间点X(t)的基矩阵W(t)。这里通过求解满足非负矩阵分解时的X(t)与W(t)(H(t))T的Frobenius范数[14]来实现,如公式(1)所示。
(1)
当该范数值满足在非负矩阵分解迭代条件下的最小值时,得到的就是最佳基矩阵。
为了研究方便,引入矩阵X,它是一个由m个时间点组成,每个时间点上有n个特征的矩阵,X可以用来表达一组时间序列的高维观测数据,其中行向量是一个时间点上的所有观测数据,而列向量则是一组随时间变化的某个观测数据。使用NMF算法,高维原始矩阵X可以分解为两个维数较低的非负矩阵乘积的一般形式,如公式(2)所示。
X=WH+E
(2)
上式中,X∈Rm×n为待分解矩阵,W∈Rm×r和H∈Rr×n为分解后的两个非负矩阵,E为逼近误差。
从几何意义上来讲,NMF算法能将高维的样本数据投影到由基向量张成的子空间上,每个样本在这个子空间上都有一种线性的表达方法,其投影系数是编码矩阵H中对应的列向量。
高维多时间序列矩阵X的分解过程如图2所示。
图2 多时间序列的分解过程
Fig.2 Decomposition process of multiple time series
其中W为基矩阵,H为系数矩阵。通过NMF分解,X中每一个列向量均为W中r个列向量的线性组合,H的向量则为相应的权值系数,r值的大小满足(n+m)r≪nm。这样W包含的列向量就可认为是对原始矩阵X进行线性估计而优化了的基,其结果是用r个基表示n个原始数据,从而达到降维的效果。
2.2 时间约束非负矩阵算法TNMF
在非负矩阵分解过程中,r值的选取决定了分解得到的基矩阵W和系数矩阵H,同时也影响了分解得到的低维特征的质量[15]。在本文的研究中,r值的大小除了受到非负、维数大小、分解误差大小的因素影响以外,还应满足高维数据的时间顺序约束,因此在上文的模型建立后,TNMF算法实现的关键就在于r值的确定。
本文以r值为变量,以具有时间序列的数据特征维度、时间序列信息以及NMF过程中的分解误差为参数,建立模型f(x),通过计算f(x)的最小值来为r值选取的提供合理的依据。建立的模型如公式(3)所示。
(3)
式(3)中T表示具有时间序列的高维数据矩阵的时间序列,∂表示每一个时间点数据具有的特征维度大小,r为原始数据矩阵X分解后基矩阵的列向量,即基矩阵的维度。当模型f(x)取最小值时,此时的r值即可确定为NMF对具有时间序列的高维数据矩阵分解时的最优r值,即计算
为了融合多时间点的时间序列信息,需要优化欧几里得距离,使其最小化,也就是找到目标函数
的收敛算法。本文使用Lee和Seung提出的乘法更新规则来优化NMF[6],如公式(4)和(5)所示。
(4)
(5)
其中V表示原始矩阵数据,即上文中的X。
计算的过程中,最初的矩阵W和H是随机选取的,只要其维度满足要求(n+m)r≪nm即可,在定义适当的迭代运算次数和误差值之后,按照式(4)和式(5)进行迭代计算,可求得最优的W和H,使得‖X-WH‖最小,即越接近零越好,此时高维矩阵就可分解为低维矩阵W和H。
2.3 TNMF算法的实现过程
TNMF算法的具体实现步骤如下:首先对具有时间序列的高维原始数据矩阵初始化;然后循环带入不同的r值,计算不同r值时时间序列模型f(x)的值;再取f(x)最小值时的r值作为降维的维度;最后以该r值为降维后基矩阵的维度,并对具有时间属性的高维原始数据矩阵降维分解。
输入参数:X,tol,iter,其中X为被分解的矩阵,tol为误差,iter为迭代次数输出参数:r(1)初始化矩阵X,r值由2循环至min(n,m),得到不同r值的矩阵W和H(2)固定矩阵W,迭代更新矩阵H:Haμ←Haμ(WTV)aμ(WTWH)aμ(3)固定矩阵H,迭代更新矩阵W:Wia←Wia(VHT)ia(WHHT)ia(4)计算f(x)=‖X-WH‖+r- ‖W‖+T∂‖X-WH‖()()2取最小值时的r输入参数:X,r,tol,iter,其中X为被分解的矩阵,r为分解后矩阵W的秩,tol为误差,iter为迭代次数输出参数:W、H(5)初始化矩阵X,得到矩阵W和H(6)固定矩阵W,迭代更新矩阵H:Haμ←Haμ(WTV)aμ(WTWH)aμ(7)固定矩阵H,迭代更新矩阵W:Wia←Wia(VHT)ia(WHHT)ia结束
3 实验验证及结果分析
3.1 实验数据背景
功能磁共振成像(functional Magnetic Resonance Imaging, fMRI)是一种重要的脑成像技术[16-17]。基于fMRI的脑网络重构技术为研究大脑的结构和功能特征提供了有效的方法,目前大多数相关研究假定在fMRI数据采集期间内大脑的活动处于静止的状态,事实上大脑处于时刻的变化当中,是一个活动和变化的整体[18-21]。人类大脑各个脑区之间的关系可以通过血氧水平依赖(Blood Oxygen Level Dependent,BOLD)信号的瞬间相关性表达,因此BOLD-fMRI对脑动态属性的研究有重要意义[22]。文献[23]通过研究系统的生物物理的BOLD-fMRI信号,为动物和人类的BOLD-fMRI的建模和解释提供了深入的见解。文献[24]通过研究静息态下的BOLD-fMRI与动态功能连接(Functional Connectivity Dynamics,FCD)的区域联系,研究结果表现出相似的空间模式,在大脑区域有显著的关联表明大脑协调和共同进化的潜在机制。
由于目前基于BOLD-fMRI信号所构建的脑网络动态数据包含了多个脑区在多个时间点的时空属性,因此其表现为高维数据结构,不能直接用于观测脑网络的特征、也不便于描述不同脑区之间的动态变化情况。目前大部分学者主要对脑网络的状态观测矩阵进行直接的降维处理,Vijay K等人采用K-means对高维的脑网络状态观测矩阵进行聚类分析[25],Panta S R等人用t-SNE算法将来自脑磁共振成像(Magnetic Resonance Imaging,MRI)扫描的大数据在保留数据集局部结构的同时,将输入数据集中每次扫描的次数降至二维[26]。杨保杰等人用深度自动编码器降维算法将高维的人脑网络空间表达映射到低维的本质特征空间中[27]。以上方法聚类的依据是数据在高维空间内的空间分布上的相似程度,但是对于脑状态等这类时间序列数据来说,除了空间关系外,状态在时间上所表现出的前后顺序关系是进一步观测其动态特性的重要基础[18-24]。因此降维过程中应该对映射到低维空间内的脑网络状态是否能够保留与时间的相关性,因此并不能作为进一步观测脑网络动态特性的依据。
本文采用2.2中所述的带时间序列的非负矩阵分解方法对高维脑网络状态观测矩阵进行降维,以保证降维结果中脑网络状态的时间属性得到保留的同时将其映射到低维空间,为后期脑网络动态演化方法的研究提供基础。
3.2 实验数据来源及预处理
本文将FCP公开脑网络数据库[28]中采集的20组脑网络数据样本组成样本集分别进行本文的实验。先对公开数据库下载的rs-fMRI数据样本用Python/FSLResting State Pipeline[29]进行数据预处理,提取BOLD信号,然后根据AAL(Anatomical Automatic Labeling)模板[30]将全脑共划分成90个脑区,并利用滑动窗口技术对BOLD-fMRI信号进行进一步的分析处理[31]。通过分析静息态脑功能磁共振的BOLD信号中的非线性特征,在基于滑动窗口的动态数据分析技术的基础上,对构建全脑动态特征矩阵过程中的不同非线性相关分析方法展开了对比研究,给出了构建脑网络中的阈值确定方法[32]。本文所用的实验数据共采集t=270个时间点,剔除了前9个不稳定时间点,滑动窗口尺寸w=20,窗口移动步长l=1,从而得到t-9-w+l=242个采样点上的脑网络状态观测窗口。在上述脑网络状态观测窗口中计算两两脑区的皮尔逊相关系数,得到90×90的脑区相关性矩阵,这里忽略脑区的自相关系数,把矩阵主对角线以上的元素每行从第1维到第4005维依次连接,得到大小为1×4005的向量。由此可以得到242个时间上的所有向量,从第1行到第242行首尾相连,构建出一个大小为242×4005具有时间属性的具有时间序列的高维脑网络状态观测向量性的高维脑网络状态观测矩阵。
3.3 基于TNMF算法的高维脑网络状态观测矩阵降维
以3.2中得到的242个具有时间属性的高维脑网络状态观测向量为对象,采用2.2中所述的方法,按照2.3节中所述的步骤,先用模型f(x)求取TNMF降维中的最优r值,通过求取f(x)的最小值来确定TNMF时基矩阵W的维度r,然后按照2.2方法寻找降维得到的基矩阵W。图4分别给出了6组不同样本数据的r值随f(x)变化的曲线。
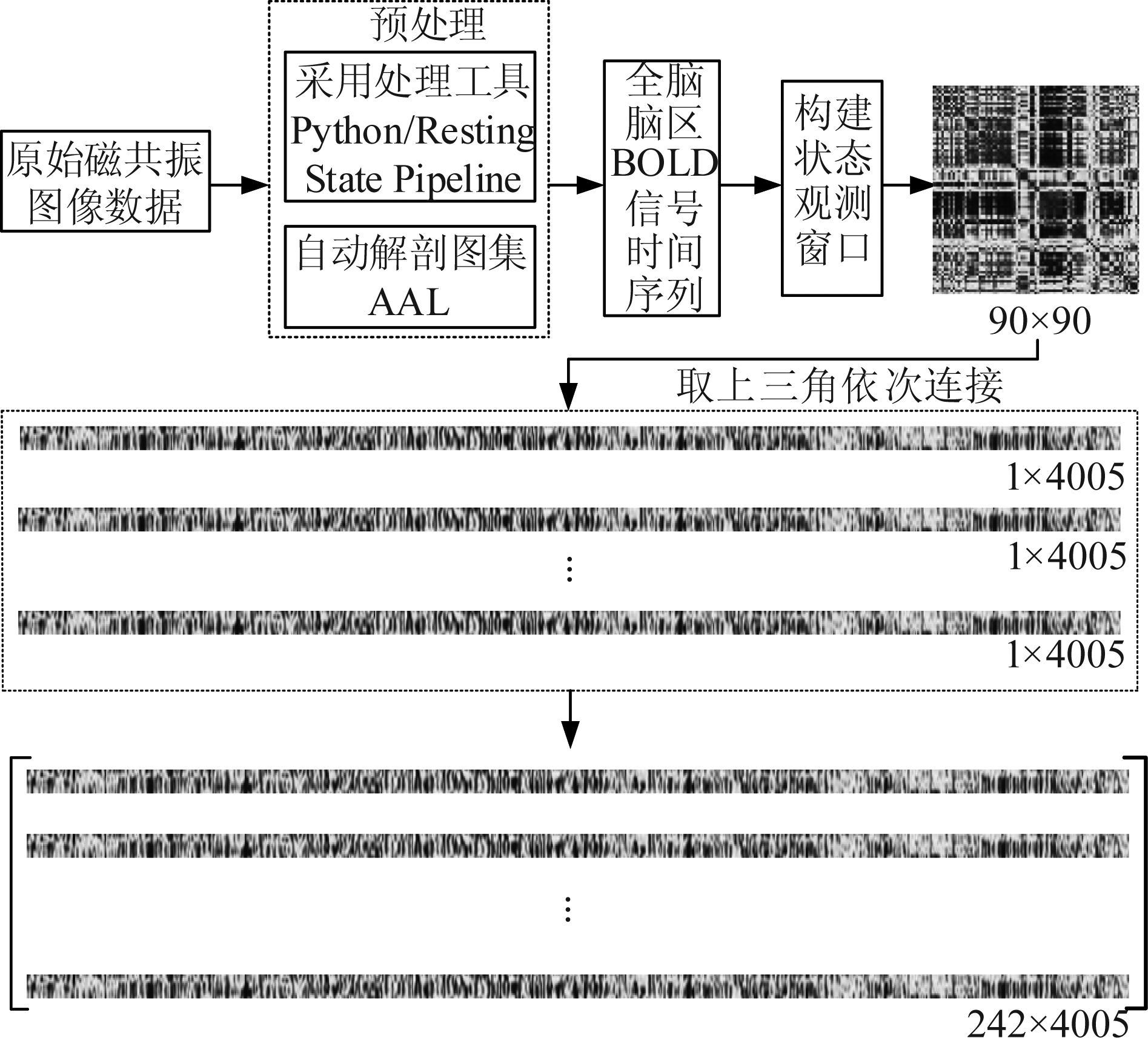
图3 具有时间序列的高维脑网络状态观测矩阵构建流程图
Fig.3 Flow chart of a higher-dimensional brain network state observation matrix with time series
由实验结果可知20组样本的r值分布情况,基矩阵W的维度r的取值范围均位于25-30之间,经计算,众数为28,算术平均值为27.5,因r值必须为整数,所以本文实验中对所有样本均选取r为28。20组样本集中f(x)取最小值时r的变化情况如图5所示。
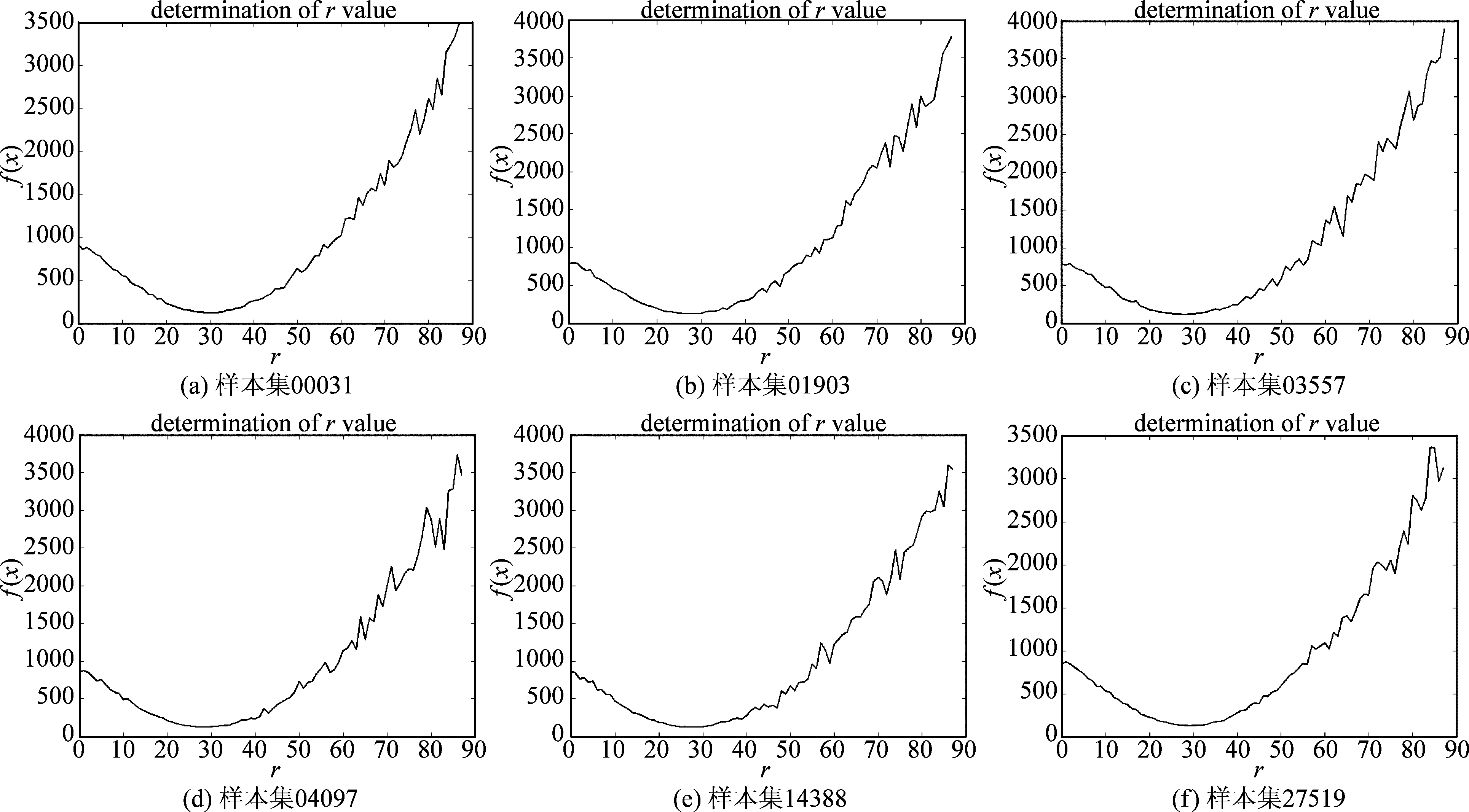
图4 数据样本集用TNMF时f(x)随r变化情况图
Fig.4 The change of f(x) with r when TNMF was used in data sample set
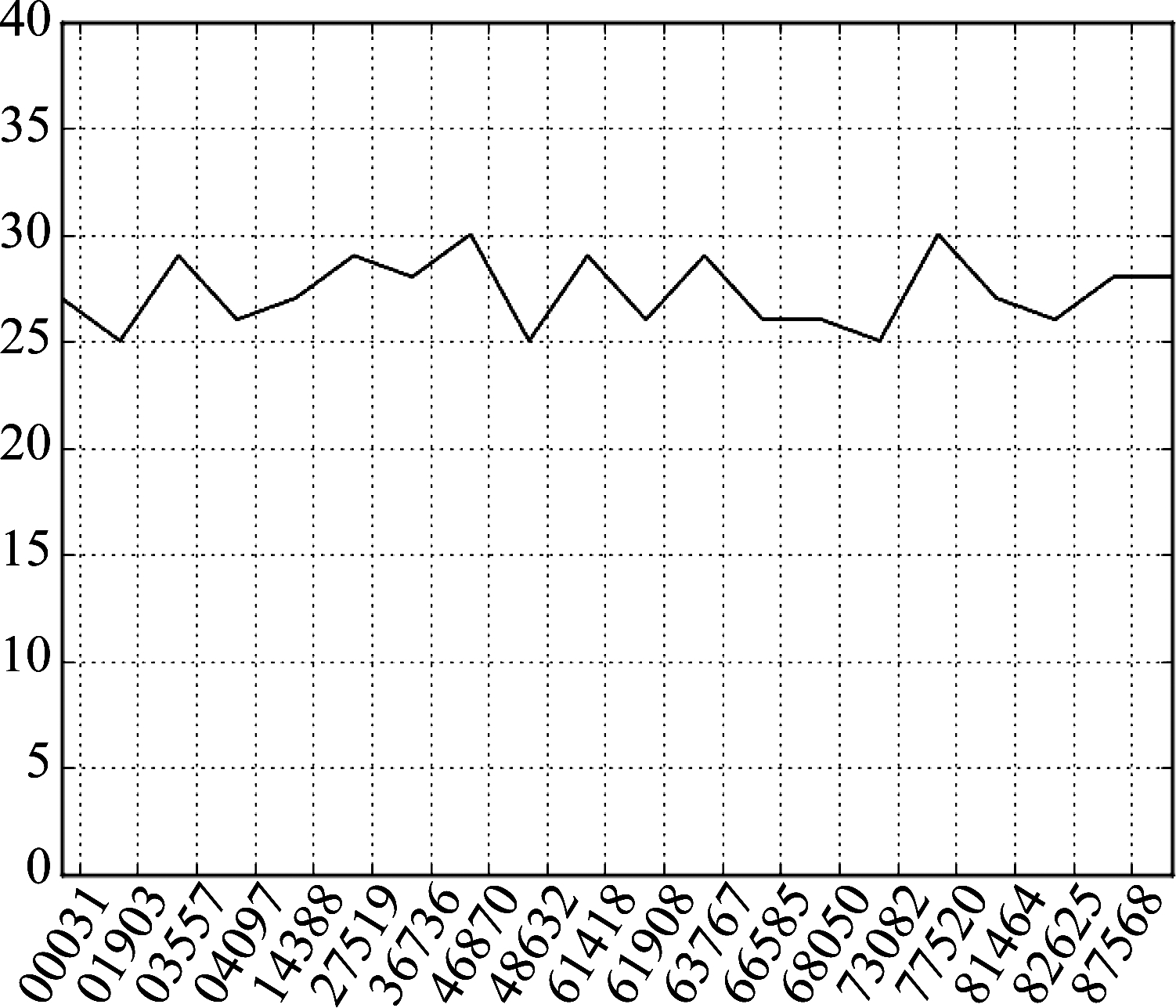
图5 20组样本集中f(x)取最小值时r的变化情况图
Fig.5 Change of r in 20 sets of sample sets when f(x) is the minimum value
为了证明本文建立的模型所选取的最优r值的准确性,任意选择三组样本,分别选取r值为10、50以及本文模型计算得到的28对脑网络状态观测矩阵进行降维及可视化对比,得到的结果如图6所示。
从图6可以看出,在使用NMF降维的过程中,不同的r值选取对降维结果有很大的影响,其中当r值取10和50时,高维脑网络状态在低维空间内的映射分布混乱,簇类不集中,簇间区别不明显,并且状态分布不能保证时间序列的连续性,降维结果不好。而当r取28时,降维结果显现出明显的聚类效果,脑网络状态自动地聚成几个不同的类,类间的界限清晰,并且状态随时间而有序分布,保留了这些状态在高维空间内的时间属性。由此可见TNMF能够较好地解决时间约束问题的降维。
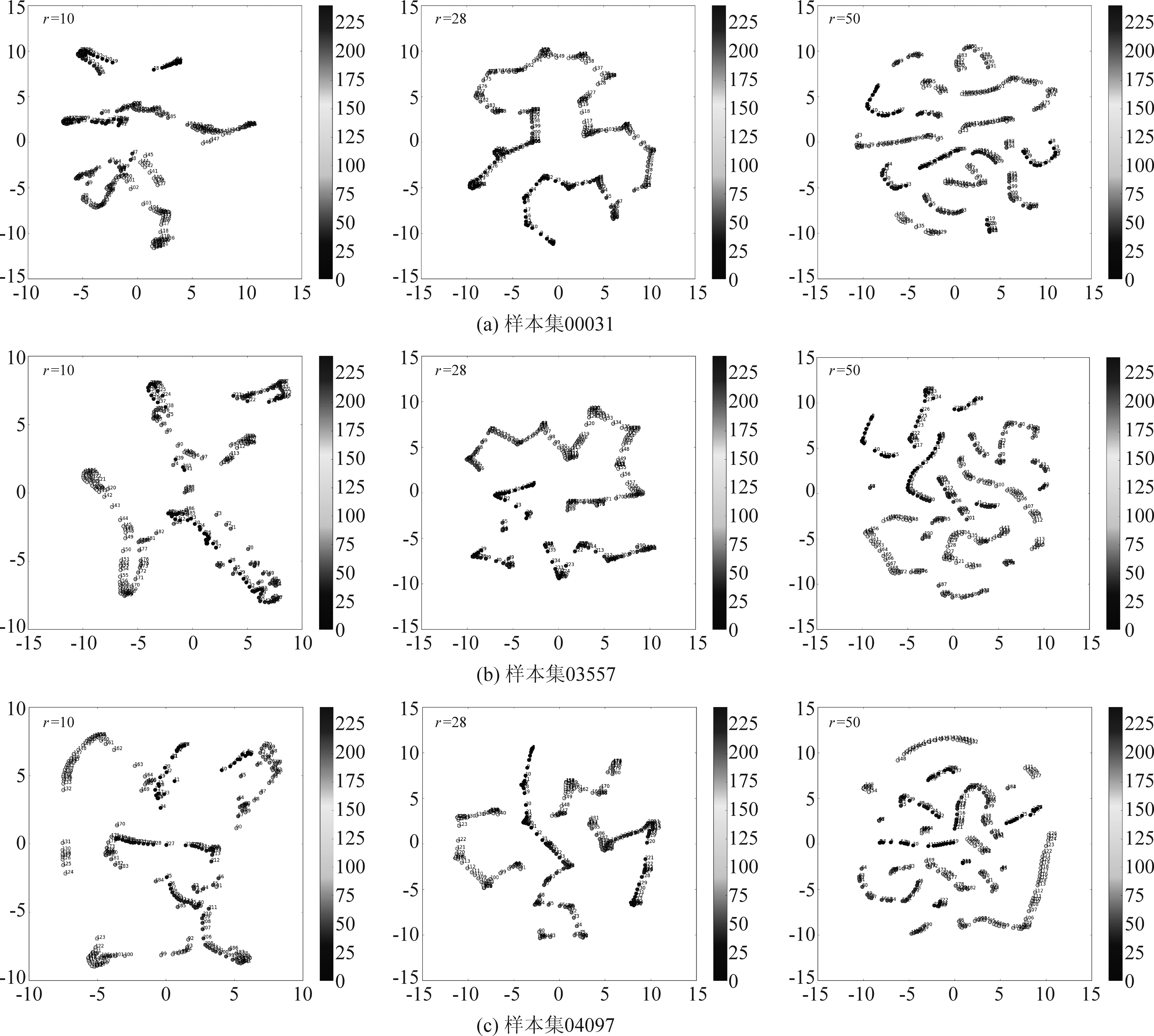
图6 三组不同样本集取不同的r值时降维可视化结果
Fig.6 Visualization results of dimensionality reduction when three different sets of samples take different values
为了进一步证明本文算法所选取的r值在降维结果上的优越性,分别对上述脑网络数据采用本文方法与传统t-SNE方法以及K-mean算法降维,并将其映射到二维空间内进行可视化。其中本文方法先按照最优的r值进行分解,然后再对基矩阵阵嵌入到二维空间内可视化。不同的降维方法的可视化实验结果如下图所示,其中方法1是先对242×4005的脑网络状态观测高维矩阵按本文所提的TNMF算法降到二维的聚类结果;方法2是直接用t-SNE将脑网络状态观测矩阵降到二维的聚类结果;方法3是直接用K-means将脑网络状态观测降到二维的聚类结果。
如图7所示,使用K-means方法进行聚类后,脑网络状态的分布是散乱的,没有明显的状态聚类效果,并且相近时间点的状态相互关系没有规律,不能反映出原始数据在高维空间内的时间序列信息;用t-SNE方法进行降维时,聚类结果中虽然有一部分能够反映出状态在时间上的前后关系,但是时间上距离较大的状态却出现了交叉现象,因而无法分辨状态在这些交叉点的归属,也不能明确脑网络状态的分布情况。使用本文TNMF方法进行降维后,所有状态均能保留其在高维空间内的时间属性先后关系,并且某些相近时间的状态在聚类结果中显示出更加紧密的相似关系,从而反映出不同脑网络状态在不同时间上的相似程度,可以作为进一步观测脑网络状态变化的依据。
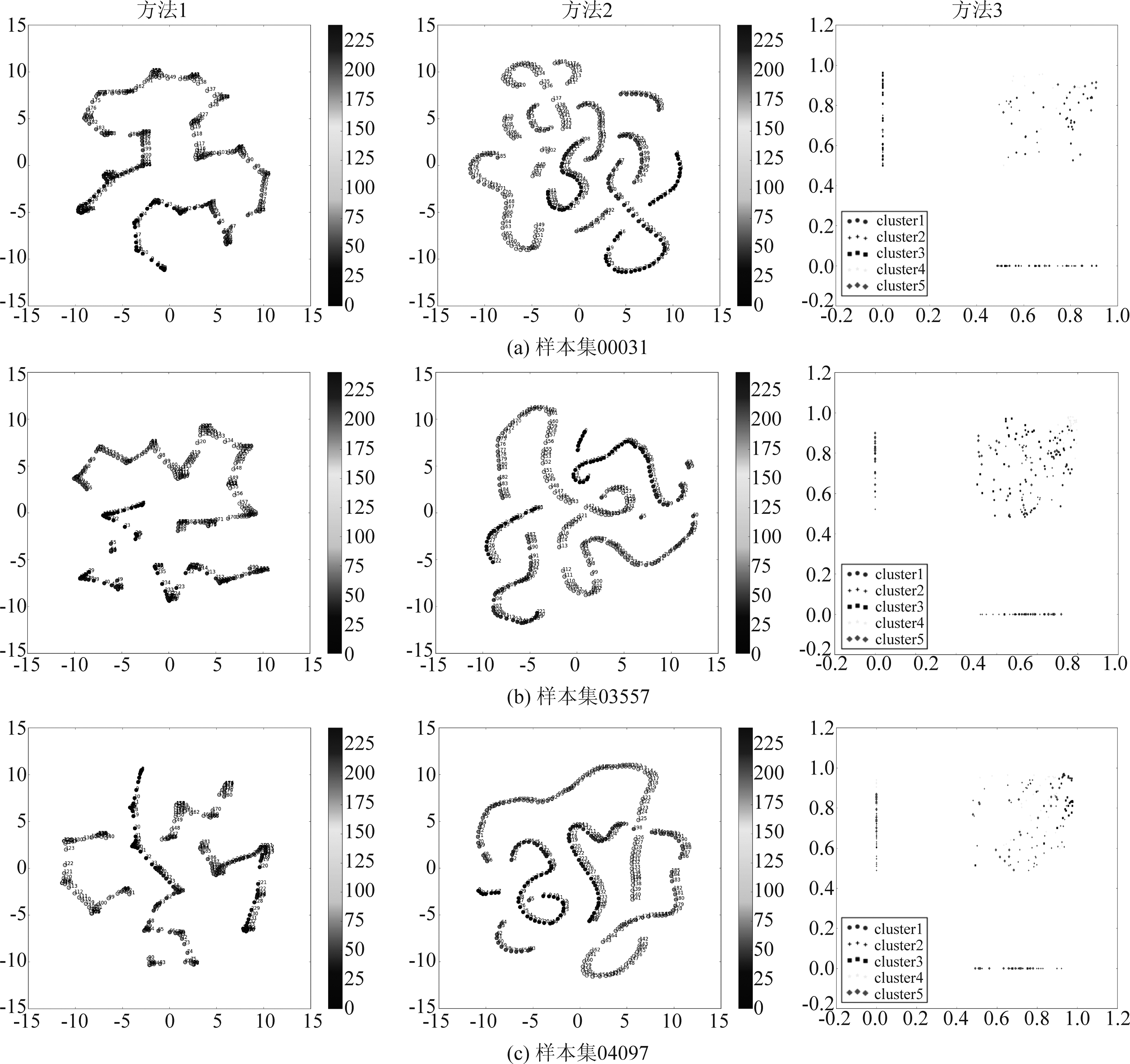
图7 三组不同的数据集用三种降维方法可视化结果对比
Fig.7 Comparison of visualization results of three groups of different data sets by three dimensional reduction methods
为了进一步证明本文算法的有效性,本文引入聚类性能度量指标对实验结果进行对比分析。由于K-means并没有实现对不同时间点状态的有效聚类,这里仅将本文算法与t-SNE算法的聚类指标进行对比。本文采用两个指标分别进行聚类结果的评价。DBI指数(Davies-Bouldin Index,简称DBI)[33-34]用于衡量同类脑网络状态观测矩阵样本的紧密程度及不同类脑网络状态观测矩阵样本的分散程度,DBI 越小,表示脑网络的聚类效果越好。Dunn指数(Dunn Index,简称DI)[35]用于衡量不同脑网络状态的分散情况,DI值越大,表示不同类簇间越分散,聚类效果越好。DBI和DI指标的计算公式如公式(6)和(7)所示。
(6)
公式(6)中k表示可视化聚类的类簇数,avg(C)表示簇C内样本间的平均距离,dcen(Ci,Cj)表示簇Ci与簇Cj中心点间的距离。
(7)
公式(7)中dmin(Ci,Cj)表示簇Ci与簇Cj最近样本间距离,diam(C)表示簇C内样本间的最远距离。
分别采用本文方法与t-SNE方法对3.2中20组公开数据进行降维,并分别计算其聚类结果的DBI和DI指标,可以得到如图8和图9所示的指标对比图。由图可知,使用本文方法聚类,DBI指标值有明显的降低,这说明同类脑网络状态的紧密程度有所增加,而不同脑网络状态之间更加分散,使得脑网络的聚类效果越好,更加有利于观察其随时间的变化。而DI指标值则有明显的增大,说明不同脑网络状态更加分散,聚类效果更加明显,更有助于划分脑网络的状态。
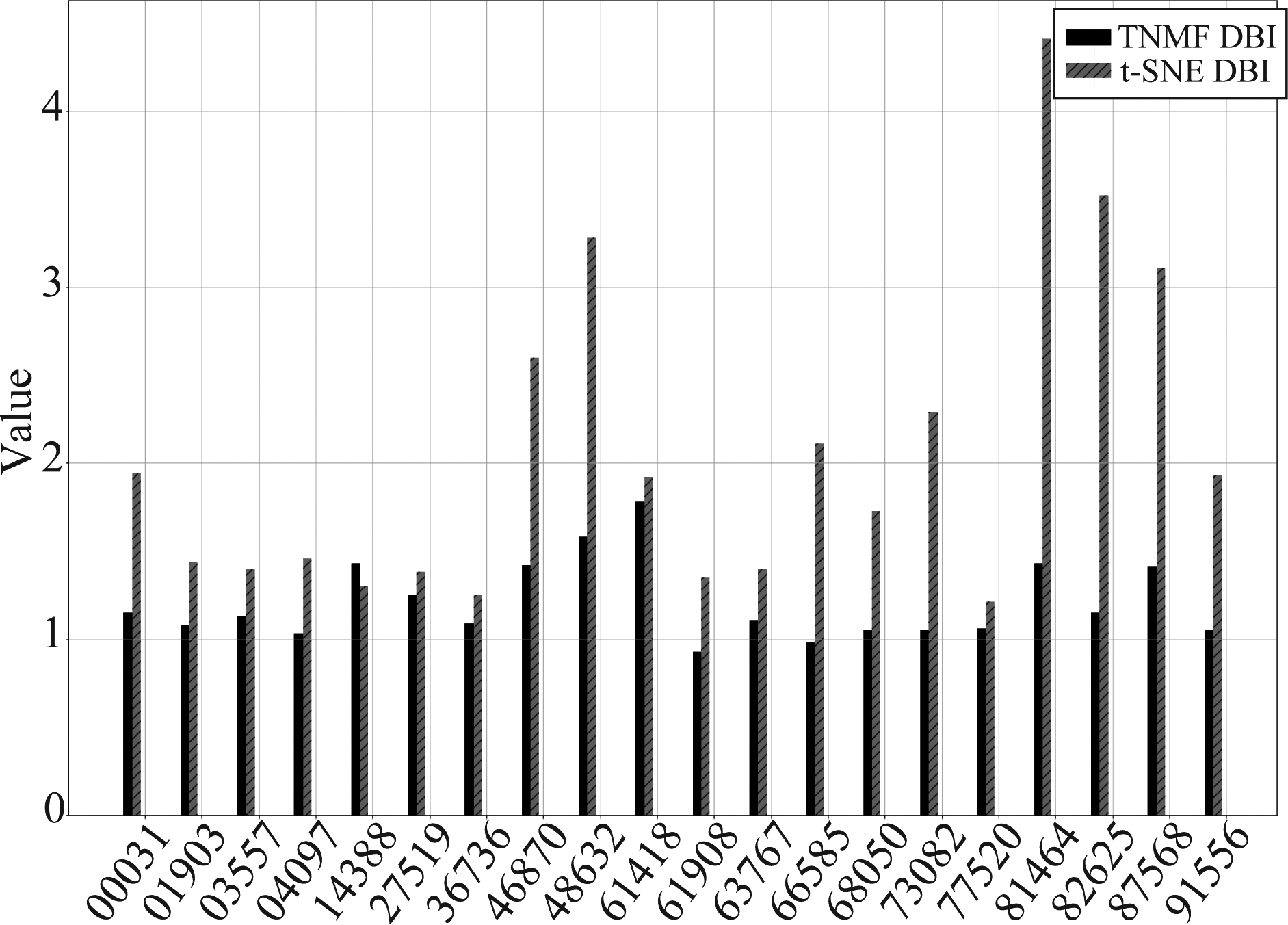
图8 DBI指标对比 Fig.8 Comparison of DBI indicators
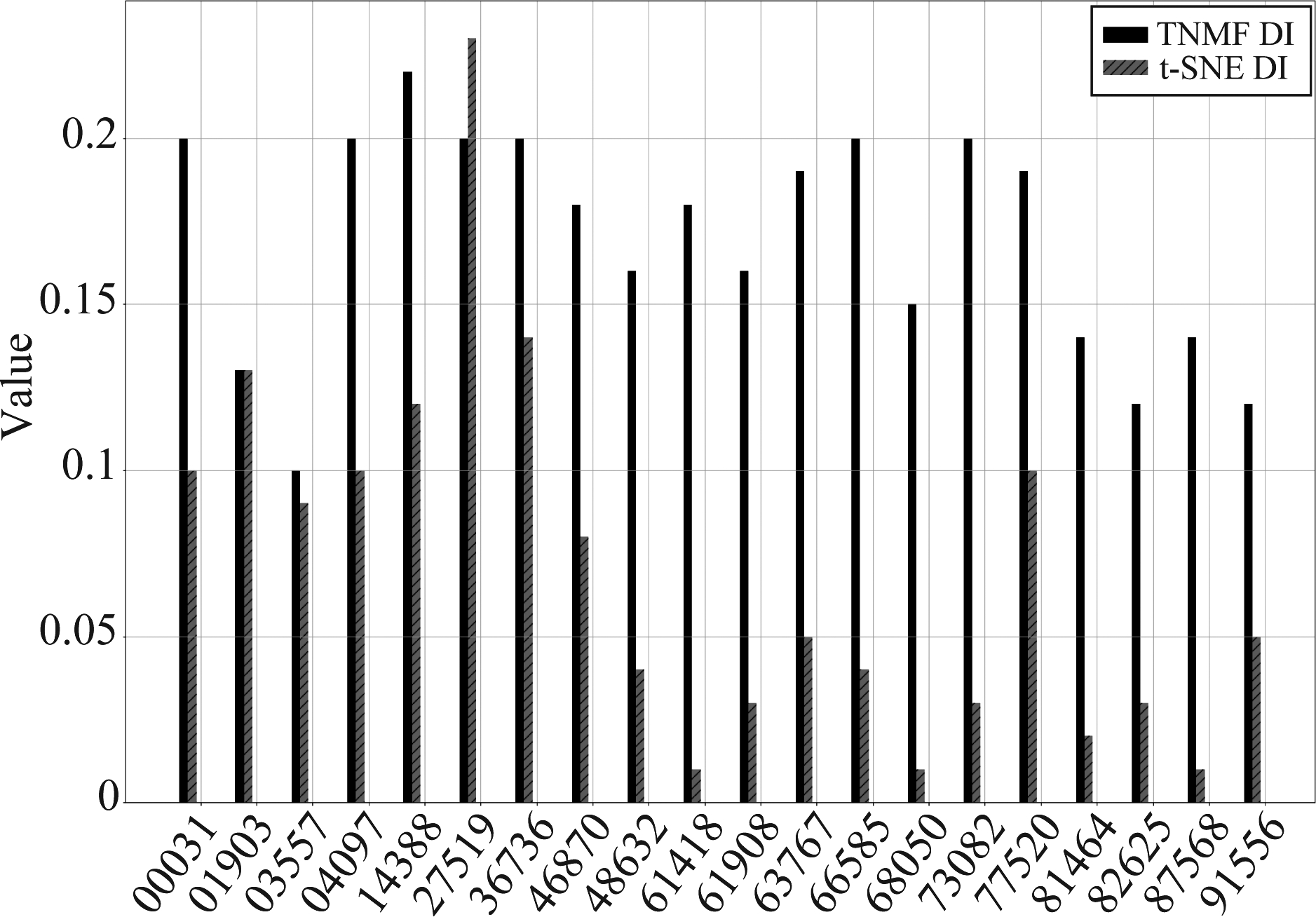
图9 DI指标对比
Fig.9 Comparison of DI indicators
其中 20组实验样本中,DBI指标中有一组样本14388的值有增加了9.8%,其他19组样本均有明显的降低,通过实验结果计算,20组样本数据的DBI指标平均下降了40.7%。20组实验样本中样本01903的DI值没有变化,样本27519的DI值下降了16.1%,其他18组样本的DI值均有明显的提高。通过计算可知20组样本数据的DI指标值平均上升了207.1%。实验结果证明,对于公开数据库中提供的数据。本文方法对绝大部分样本的降维效果是优于传统t-SNE方法,有明显改善和提高。两种指标的箱线图对比结果如图10所示。
已有研究表明,以fMRI的BOLD信号重构所得到的人脑功能网络个体差异性是较大的[17,19,22,24,36],这也是脑网络状态进行降维后得到的评价指标有所不同的原因。在实验过程中,为了更客观的评价算法的效果,我们对全部20组被试数据的r值和阈值等参数都采用了相同的设置,因而不能保证每一个被试个体在实验过程中的最优化,也出现了少数个体的评价指标不够理想的情况,如果想要得到更好的降维效果,可以通过对每一个个体分别设定不同的实验参数来实现,即自适应的参数选择方法,这也是我们在下一步研究中值得深入思考的方向。
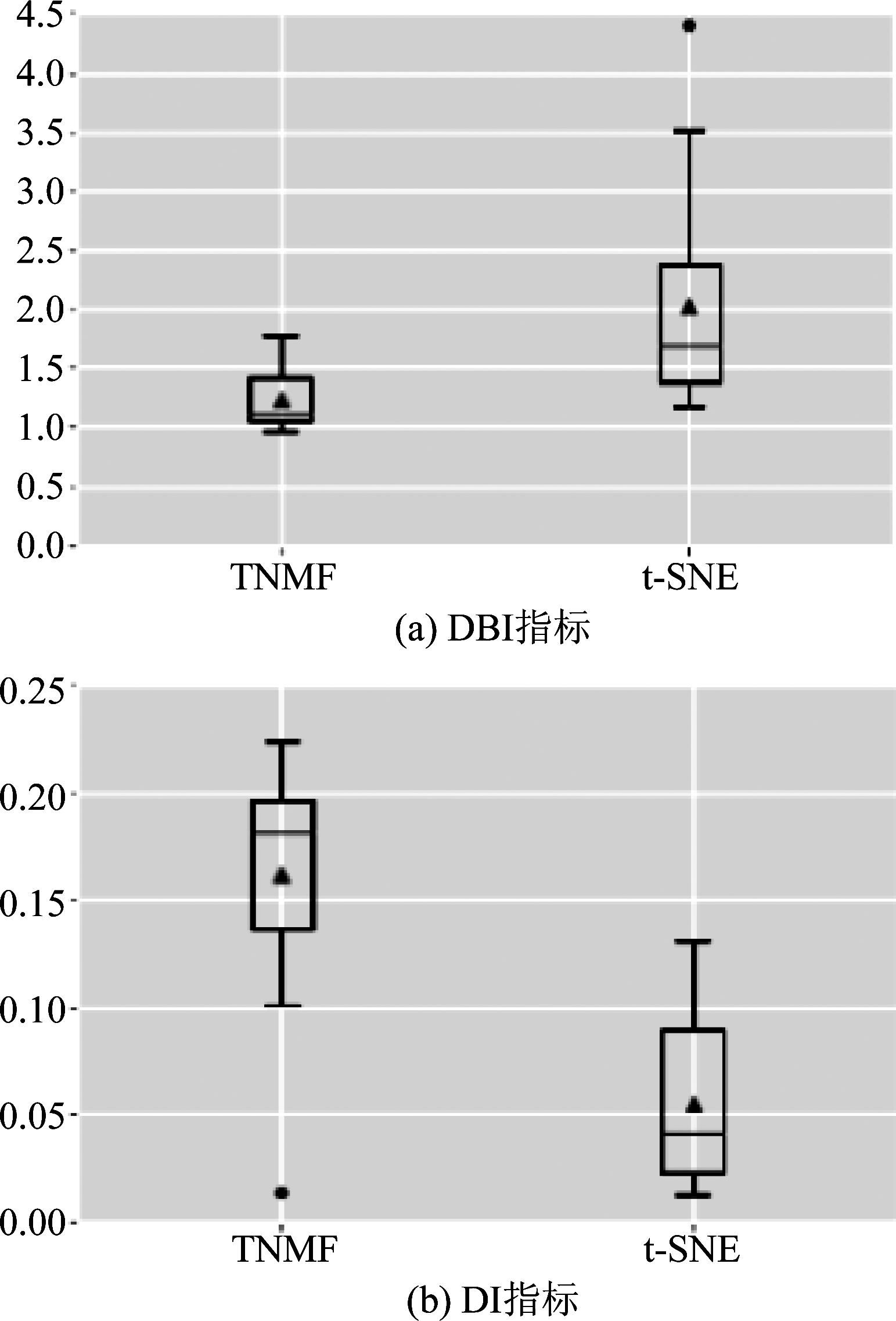
图10 DBI、DI指标对比评价箱线图
Fig.10 Comparison evaluation box diagram of DBI and DI indicators
4 结论
本文给出了一种带时间约束的非负矩阵分解算法TNMF降维算法,该算法针对高维时间序列数据在降维过程中必须保持其时间属性的要求,以寻找基矩阵的最优维度值为目标,综合考虑非负矩阵分解过程中的非负性、分解误差等约束条件,构建时间属性约束模型,从而确定基矩阵的维数r,实现具有时间约束的高维数据序列的有效降维。由于该方法以每一个时间点为基本单元展开非负矩阵的分解,在降维和特征提取过程中能够兼顾考虑数据在高维空间内具备的时间特征,因此对高维时间序列数据的降维更加适用。
目前在基于fMRI的动态脑功能网络的研究过程中,脑网络状态向量维数很高且与时间具有强相关性,因此将本文算法应用于动态脑功能网络的降维和特征提取,通过与现有的t-SNE算法、K-means算法和传统的NMF算法的实验对比可知,无论是在降维的可视化结果、状态的时间区间聚类效果,还是降维指标DBI、DI的改善结果上来看,本文算法都具有更好的效果,相比之下本文算法不仅能保留时间序列在高维空间内的时序关系,也能辨识出更明显的脑网络状态类别,并且不同状态组之间的差别更明显,而同组状态之间的相似性更大。
综上所述,本文所给出的TNMF算法将高维脑网络状态的时间观测序列数据降到一个相对低维的空间,既达到了降低维度便于观测的目的,又能使高维空间内数据的结构和时间属性得到较为完整的保留,同时该算法对于其他高维时间序列数据的降维具有一定的参考价值。
下一步的重点是在本文算法基础上完善时间属性约束模型,并且对不同样本的r值确定方法展开分析和研究,以推进TNMF在更广泛范围内的应用。
[1] Jia H, Ding S, Du M. Approximate normalized cuts without Eigen-decomposition[J]. Information Sciences, 2016, 374: 135-150.
[2] Zhang A, Xia D. Tensor SVD: Statistical and Computational Limits[J]. IEEE Transactions on Information Theory, 2018, PP(99): 1-1.
[3] Hong D, Balzano L, Fessler J A. Asymptotic performance of PCA for high-dimensional heteroscedastic data[J]. Journal of Multivariate Analysis, 2018.
[4] Lu Z M, Feng Y P. Image retrieval based on histograms of EOPs and VQ indices[J]. Electronics Letters, 2016, 52(20): 1683-1684.
[5] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-788.
[6] Lee D D, Seung H S. Algorithms for non-negative matrix factorization. In NIPS[J]. Advances in Neural Information Processing Systems, 2000, 13(6): 556-562.
[7] Zhou J, Zhang S, Mei H, et al. A method of facial expression recognition based on Gabor and NMF[J]. Pattern Recognition & Image Analysis, 2016, 26(1): 119-124.
[8] Tu D, Chen L, Lv MQ, et al. Hierarchical online NMF for detecting and tracking topic hierarchies in a text stream[J]. Pattern Recognition, 2018, 76: 203-214.
[9] Cho Y C, Choi S. Nonnegative features of spectro-temporal sounds for classification[J]. Pattern Recognition Letters, 2005, 26(9): 1327-1336.
[10] Wei J, Bai W, Liu T, et al. Functional connectivity changes during a working memory task in rat via NMF analysis[J]. Frontiers in Behavioral Neuroscience, 2015, 9(2): 2.
[11] Padilla P, Górriz J M, Ramírez J, et al. Analysis of SPECT brain images for the diagnosis of Alzheimer’s disease based on NMF for feature extraction[J]. Neuroscience Letters, 2010, 479(3): 192-196.
[12] Carel L, Alquier P. Simultaneous Dimension Reduction and Clustering via the NMF-EM Algorithm[J]. Statistics, 2018.
[13] 刘中健, 赵知劲, 尚俊娜. 快速NMF盲源分离算法[J]. 信号处理, 2014, 30(6): 699-705.
Liu Zhongjian, Zhao Zhijin, Shang Junna. Fast NMF Blind Source Separation Algorithm[J]. Journal of Signal Processing, 2014, 30(6): 699-705.(in Chinese)
[14] 刘正, 张国印, 陈志远. 基于特征加权和非负矩阵分解的多视角聚类算法[J]. 电子学报, 2016, 44(3): 535-540.
Liu Zheng, Zhang Guoyin, Chen Zhiyuan. A Multiview Clustering Algorithm Based on Feature Weighting and Non-negative Matrix Factorization[J]. Acta Electronica Sinica, 2016, 44(3): 535-540.(in Chinese)
[15] 侯小丽. 高维数据聚类中的神经网络降维方法研究[D]. 兰州: 兰州大学, 2015.
Hou Xiaoli. Neural network based dimensionality reduction and its application in high-dimensional data clustering[D]. Lanzhou: Lanzhou University, 2015.(in Chinese)
[16] Logothetis N K, Pauls J, Augath M, et al. Neurophysiological investigation of the basis of the fMRI signal[J]. Nature, 2001, 412(6843): 150.
[17] Greicius M D, Krasnow B, Reiss A L, et al. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis[J]. Proc Natl Acad Sci U S A, 2003, 100(1): 253-258.
[18] Fox M D, Snyder A Z, Vincent J L, et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks[J]. Proceedings of the National Academy of Sciences, 2005, 102(27): 9673-9678.
[19] Taubert M, Draganski B, Anwander A, et al. Dynamic properties of human brain structure: learning-related changes in cortical areas and associated fiberconnections[J]. Journal of Neuroscience the Official Journal of the Society for Neuroscience, 2010, 30(35): 11670-11677.
[20] Wang X, Wang Q. A novel image encryption algorithm based on dynamic S-boxes constructed by chaos[J]. Nonlinear Dynamics, 2014, 75(3): 567-576.
[21] Wang X, Liu L. Cryptanalysis of a parallel sub-image encryption methodwith high-dimensional chaos[J]. Nonlinear Dynamics, 2013, 73(73): 795- 800.
[22] Di X, Gohel S, Thielcke A, et al. Do all roads lead to Rome? A comparison of brain networks derived from inter-subject volumetric and metabolic covariance and moment-to-moment hemodynamic correlations in old individuals[J]. Brain Structure & Function, 2017, 222(8): 1-13.
[23] Kim SG. Biophysics of BOLD fMRI investigated with animal models[J]. J Magn Reson, 2018, 292: 82- 89.
[24] Fu Z, Tu Y, Di X, et al. Associations between Functional Connectivity Dynamics and BOLD Dynamics Are Heterogeneous Across Brain Networks[J]. Frontiers in Human Neuroscience, 2017, 11: 593.
[25] Vijay K, Selvakumar K. Brain FMRI clustering using interaction K-means algorithm with PCA[C]∥International Conference on Communications and Signal Processing. IEEE, 2015: 0909- 0913.
[26] Panta S R, Runtang W, Jill F, et al. A Tool for Interactive Data Visualization: Application to Over 10, 000 Brain Imaging and Phantom MRI Data Sets[J]. Frontiers in Neuroinformatics, 2016, 10.
[27] 杨保杰, 王彬, 薛洁, 等. 基于深度自动编码器的脑网络状态观测矩阵降维方法[J]. 传感器与微系统, 2017, 36(1): 9-12.
Yang Baojie, Wang Bin, Xue Jie, et al. Dynamic observation matrix of dimension reduction method for brain network based on deep autoencoder[J]. Transducer and Microsystem Technologies, 2017, 36(1): 9-12.(in Chinese)
[28] http:∥fcon_1000.projects.nitrc.org/fcpClassic/FcpTable.html.
[29] Brain Imaging & Analysis Center. Python/FSL Resting State Pipeline[DB/OL]. https:∥wiki.biac.duke.edu/biac:analysis:resting_pipeline.
[30] Tzouriomazoyer N, Landeau B, Papathanassiou D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain[J]. Neuroimage, 2002, 15(1): 273.
[31] 马洒洒, 王彬, 薛洁, 等. 基于同步多维数据流的脑网络动态特征辨识方法研究[J]. 计算机应用研究, 2017, 34(11): 3272-3276.
Ma Sasa, Wang Bin, Xue Jie, et al. Research of dynamic characteristic identification method for human brain network based on multidimensional synchronization data flow[J]. Application Research of Computers, 2017, 34(11): 3272-3276.(in Chinese)
[32] 龙雨涵, 王彬, 薛洁, 等. 非线性脑区相关性分析及动态脑网络构建方法[J]. 信号处理, 2018, 34(8): 963-973.
Long Yuhan, Wang Bin, Xue Jie, et al. Nonlinear Correlation Analysis Between Brain Regions and Dynamic Brain Network Construction Method[J]. Journal of Signal Processing, 2018, 34(8): 963-973.(in Chinese)
[33] 张开旭, 周昌乐. 基于自动编码器的中文词汇特征无监督学习[J]．中文信息学报, 2013, 27(5): 1-7.
Zhang Kaixu, Zhou Changle. UnsuperVised Feature Learning for Chinese Lexicon Based on Auto-Encoder[J]. Journal of Chinese Information Processing, 2013, 27(5): 1-7.(in Chinese)
[34] Hashimoto W, Nakamura T, Miyamoto S. Comparison and Evaluation of Different Cluster Validity Measures Including Their Kernelization[J]. Scis, 2009, 13: 204-209.
[35] Dunn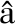
J C. Well-Separated Clusters and Optimal Fuzzy Partitions[J]. Journal of Cybernetics, 1974, 4(1): 95-104.
[36] Yang Z, Zuo X N, Mcmahon K L, et al. Genetic and Environmental Contributions to Functional Connectivity Architecture of the Human Brain[J]. Cerebral Cortex, 2016, 26(5): bhw027.
