1 引言
闪存(flash memory)是一种非易失性存储器,具有电可编程性和电可擦性,良好的可靠性、高存储密度和低成本使其成为一种主流存储器技术。利用置换来表示闪存单元电荷大小次序的等级调制方案(rank modulation)[1],开辟了闪存数据存储系统差错控制编码技术的新方向。RS码和BCH码等传统差错控制编码方法无法满足对大容量闪存设备的纠错需求[2],基于闪存系统的LDPC码编译码复杂度高[3],因此,置换码(permutation codes)作为一种多进制纠错码,其在闪存设备中的优势引起了广泛关注。
闪存设备的等级调制方案中,存储的数据由单元间电荷值的相对等级进行表示,可防止以电荷绝对等级存储形式易引发的错误,等级调制方案可有效避免闪存单元写操作中过度编程的风险,并降低由于电荷泄漏、读/写干扰、数据保持噪声等非对称错误产生的影响[4]。针对等级调制方案中存在的多种特殊错误类型,如“删除错误”[5]、“相邻对换错误”[6]、“移位错误”[7]、“强度有限错误”[8]等,可选取合适的距离度量来构造可纠正相应错误的纠错码。目前,用于研究置换码构造和性能分析的距离度量主要包括汉明(Hamming)距离[9]、Kendall τ距离[10]、Ulam距离[11]和切比雪夫(Chebyshev)距离[12]等。
作为置换码的一种推广,多重置换码(multi-permutation codes)可采用相近电荷值对闪存单元进行等级调制,降低设备电荷取值范围,并有效防止因单元间电荷差较小而导致的等级划分错误。近年来,学者们逐渐发现了多重置换码的应用价值。文献[10]提出了基于Kendall τ距离度量的系统置换码和系统多重置换码的构造方法。文献[13]中将置换码与多重置换码进行对比分析,多重置换码能够采用较小的电荷量级有效提高数据存储的可靠性和信息存储率,并提出了基于Ulam距离度量的多重置换码构造方法。文献[14]利用级联和递归技术提出了基于切比雪夫距离度量的可纠正强度有限错误的多重置换码构造方法。文献[15]中分别提出了纠单个和不超过t个删除错误的多重置换码构造方法。赵鹏等人提出了纠突发删除错误[16]和预定个数的相邻删除错误[17]的多重置换码构造和译码方法,并基于切比雪夫距离度量提出了两种多重置换码的一般构造方法[18]。
本文研究闪存单元等级调制下多重置换码发生移位错误(translocation error)的纠错问题。通常,电荷泄露可导致电荷减少,读取干扰可导致电荷增加。两种情况下,闪存单元电荷的相对等级次序将发生变化,表现为移位错误。本文在可纠正移位错误的置换码构造方法[7]的基础上,结合已有切比雪夫距离度量下多重置换码的构造方法[18],采用交织技术和不同的多重置换映射方法,提出一种基于切比雪夫距离度量的正则多重置换码的构造及其译码方法,用以纠正闪存设备等级调制下的单个“移位错误”。
文献[7]提出的基于Ulam距离度量的纠移位错误置换码的构造方法中,只考虑了右移位错误的译码问题。本文构造则提出了基于切比雪夫距离度量的多重置换码的构造方法,并考虑了所有可能发生的移位错误类型的译码问题。文献[18]给出的多重置换码一般构造方法(构造2)中,采用映射得到最小切比雪夫距离互不相同的多重置换子集,经过交织运算获得正则多重置换码,但未考虑闪存中具体错误类型的纠错问题及相应的译码方法。本文所提构造采用了与文献[18]不同的多重置换映射方法,得到最小切比雪夫距离相同的多重置换子集,并针对移位错误提出了正则多重置换码的交织构造方法及其译码方法。此外,文献[18]采用的映射限定了多重置换子集的个数,而本文构造中采用的映射仅限定多重置换子集的奇偶性,提高了映射的多重置换子集的个数,从而获得更高的码率。
2 置换和多重置换的基本概念
对于两个整数a和b,若a≤b,可定义一个连续整数集为[a,b]={a,a+1,…,b}。对于单一正整数n,可简化表示为[n]={1,2,…,n}。集合[n]上的一个置换记为σ=(σ(1),σ(2),…,σ(n)),所有置换构成的置换群记为Sn,且|Sn|=n!。一般地,任意有限集X上所有置换构成的置换群记为SX。
令e=(e(1),e(2),…,e(n))∈Sn,如果e(i)=i对所有i∈[n]恒成立,则e称为恒等置换。令i, j∈[n],恒等置换的移位定义如下。
定义1[7] 将恒等置换e∈Sn中元素i移动到j所处的位置,同时将i和j之间(包括j)的所有元素移动1个位置,当i<j时,元素i向右移位;当i>j时,元素i向左移位,统称恒等置换的一个“移位”。记为:
定义2[19] 对任意两个置换σ,π∈Sn,可将其复合置换定义为乘积运算σπ∈Sn,其各个元素确定为(σπ)(i)=σ(π(i)),i∈[n]。
对于任意i, j∈[n],当i<j时,移位e(i, j)和e(j,i)互逆,记为e(j,i)=e-1(i, j);当i=j时,必有e(i, j)=e。进一步,将σ中位置i上的元素移位到位置j,所得置换必为σ(i, j)=σe(i, j)。
定义3[19] 令置换σ∈Sn,若i<j且σ(i)>σ(j),称(σ(i),σ(j))为σ的一个逆序对,逆序对的总个数称为σ的逆序数。置换σ的逆序数为偶数时,称置换σ为偶置换,否则,称其为奇置换。
定义4[19] 令置换σ∈Sn和子集Q⊆[n],以σ中原有次序保留其属于Q的元素,并去掉其余元素,所得置换称为σ在Q上的投影,记为σ(Q)。
例1 设σ=(5,2,6,1,3,4)∈S6,Q={1,4,6},由定义4可得σ在Q上的投影为σ(Q)=(6,1,4)。
定义5[14] 令α=(α(1),α(2),…,α(n))和β=(β(1),β(2),…,β(n))是Sn中任意两个不同的置换,定义切比雪夫距离为
d
(α,β)=max{|α(i)-β(i)|:i∈[n]}
定义6[16] 给定l个向量πi=(πi,1,πi,2,…,πi,ni),i∈[l],其长度满足n1≥n2≥…≥nl≥n1-1,即彼此相差不超过1,令
对该组向量的元素进行交织(Interleaving),得到一个长度为n的向量π=(π(1),π(2),…,π(n)),记为π=π1∘π2∘…∘πl,其元素π(j)=πi,「j/l⎤, j∈[n],i≡j (modl),「x⎤表示不小于实数x的最小整数。
定义7 假设C⊆Sn是一个长度为n、基数为|C|=M的置换码,若d为该码中任意不同码字间的最小切比雪夫距离,则称C为一个(n,M,d)置换码。
给定l个置换码Ci,i∈[l],码长递减但相差不超过1,则根据定义6可构造一个交织码为
C=C1∘C2∘…∘Cl
={π1∘π2∘…∘πl:πi∈Ci,i∈[l]}
上述关于整数集、置换和置换码的定义,可直接推广到多重集、多重置换和多重置换码。
对于正整数m和正整数向量
可定义多重集(multiset)为
其中
称为重数向量,ri表示元素i∈[m]重复出现的次数,
表示该多重集元素总数。多重集
上的置换称为多重置换,所有多重置换的集合记为
特别地,当r1=r2=…=rm=r≥2时,称为正则(regular)多重集,简记为M(n,r),此时n=rm。类似地,正则多重集上的多重置换称为正则多重置换,且|SM(n,r)|=n!/(r!)m。下文中若不作特殊说明,多重集均指正则多重集,多重置换均指正则多重置换。
3 闪存等级调制的移位错误
在闪存等级调制体制中,闪存单元按其电荷值从高到低的相对等级次序进行分组存储数据,一组闪存单元的相对等级可表示为一个置换[1]。图1和图2的左图给出一个长度为9的闪存单元组的等级调制,其置换表示为σ=(5,2,7,9,1,6,3,4,8),表示第5单元的电荷值最高,而第8单元的电荷值最低。
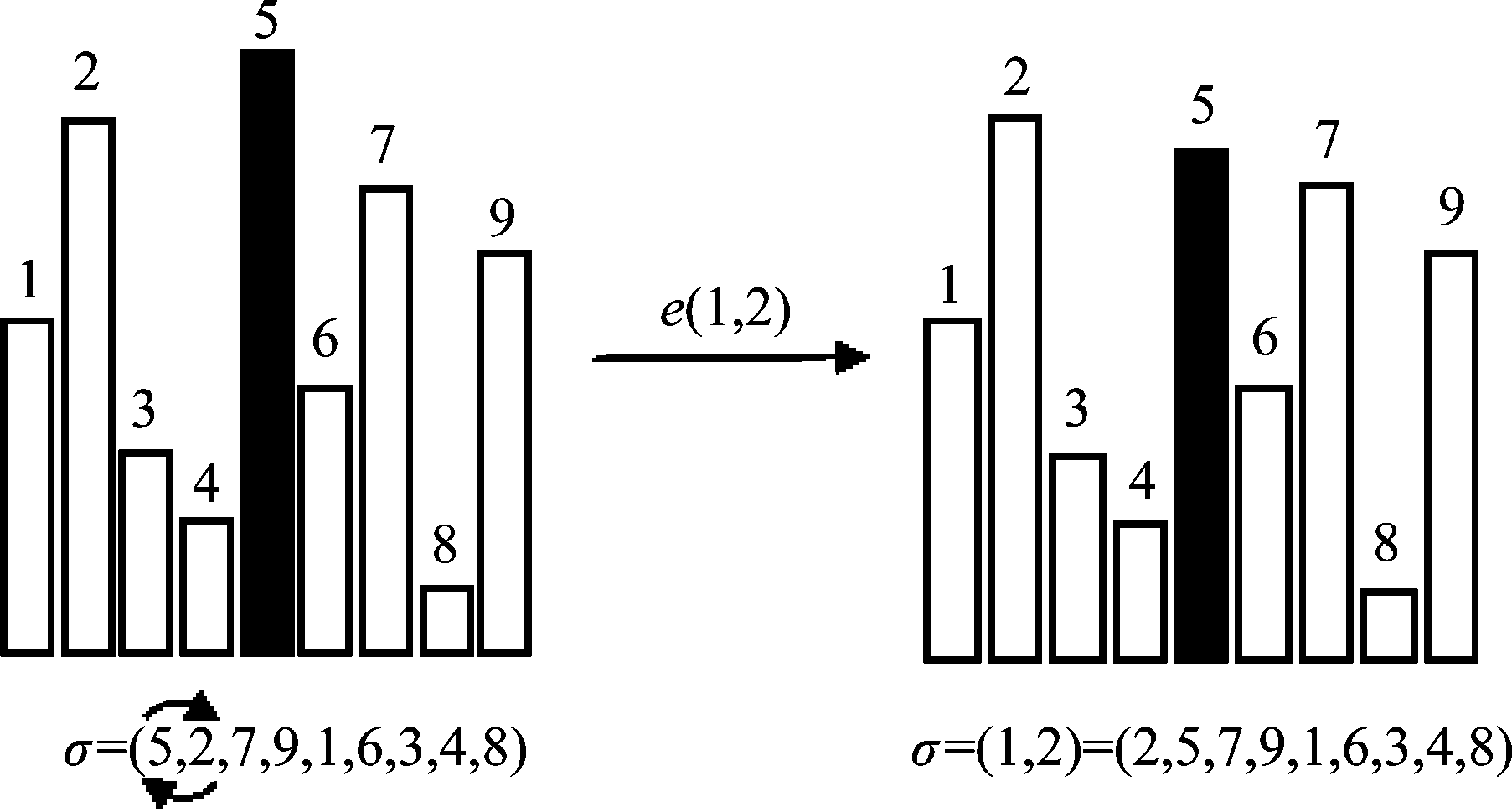
图1 相邻对换错误
Fig.1 Adjacent transposition error
闪存单元会面临电荷泄漏和读/写干扰等问题,电荷泄漏会导致闪存单元的电荷量减少,而读取干扰会导致闪存单元的电荷量增加。当某一闪存单元发生小幅度的电荷泄漏或增加时,其电荷相对等级在置换表示中会发生相邻移位,称为“相邻移位错误”。如图1右图中,单元5的电荷量在泄漏后低于单元2的电荷量,使元素5移位到元素2之后,从而使置换表示由σ变为σ(1,2)。
当某一闪存单元的电荷泄漏或增加速度远高于其他单元时,发生较大幅度的电荷泄漏或增加,可使其电荷相对等级在置换表示中移动多个位置,称为“移位错误”[16]。如图2右图中,单元5的电荷量在泄漏后远低于所有其他单元的电荷量,使置换改变σ(1,9)。
图2 移位错误
Fig.2 Translocation error
一般地,等级调制置换表示中所发生的移位错误可记为e(i, j),表示位置i的元素移位到位置j。令α,β∈Sn,α表示存储置换,β表示读取置换,假设仅发生单个移位错误e(i, j),即β=αe(i, j),则可能发生的错误图样包括如下三类:
1)相邻错误(|j-i|=1):
β=(β1,…,βi-1,βi,βi+1,βi+2,…,βn)
=(α1,…,αi-1,αi+1,αi,αi+2,…,αn)
2)右移位错误(i<j):
β=(β1,…,βi-1,βi,βi+1,…,βj-1,βj,βj+1,…,βn)
=(α1,…,αi-1,αi+1,αi+2,…,αj,αi,αj+1,…,αn)
3)左移位错误(i>j):
β=(β1,…,βj-1,βj,βj+1,…,βi-1,βi,βi+1,…,βn)
=(α1,…,αj-1,αi,αj,…,αi-2,αi-1,αi+1,…,αn)
闪存单元组的电荷等级也可表示多重置换,由电荷泄漏/增加引起置换移位错误的描述,同样适合于多重置换。
4 多重置换码构造与译码
本节针对闪存多重置换等级调制中发生的单个移位错误,提出一种基于切比雪夫距离度量的多重置换码的构造,并给出了译码方法。
4.1 构造方法
首先建立一种多重置换之间映射关系。
定义8 给定正整数n,h,r,满足r|h,令mh=h/r和mn=n/r,定义多重集
和
并定义子集Q={q(1)r,q(2)r,…,q(mh)r}⊆M(n,r),其中{q(1),q(2),…,q(mh)}⊆[mn],且q(1)<q(2)<…<q(mh)。则可建立映射φQ:SM(h,r)→SQ,将任意π=(π(1),π(2),…,π(h))∈SM(h,r)映射为φQ(π)=(φ(1),φ(2),…,φ(h))∈SQ,其中φ(i)=q(π(i)),i∈[h]。很显然,φQ(π)与π一一对应,且各自元素的大小顺序一致,即具有相同的奇偶性。
例2 令n=8,h=6,r=2,Q={12,42,62}⊆M(8,2),π=(3,2,2,1,3,1)∈SM(6,2),由定义8得φQ(π)=(6,4,4,1,6,1)∈SQ。
应用定义6的交织方法和定义8的多重置换映射,提出可纠正单个移位错误的多重置换码构造。
构造:给定正整数m,r≥2,d<m,且d|m,令n=rm,h=n/d,将多重集M(n,r)划分为d个互不相交的子集
Ql={j∈M(n,r):j≡l (mod d)},l∈[d]
且|Ql|=h。令
为SM(h,r)中所有偶多重置换构成的子集,构造一个n长的多重置换码为
本构造中亦可将偶多重置换子集替换为奇多重置换子集
定理1 构造所得的多重置换码C是SM(n,r)中一个码长为n=rm、最小切比雪夫距离为d、能够纠正单个移位错误的(n,M,d)多重置换码,其中
(1)
证明 下面基于偶置换子集的码构造为例进行证明。令α=(α(1),α(2),…,α(n))和β=(β(1),β(2),…,β(n))为码C中任意两个不同的码字,则至少存在一个k∈[n],使得α(k)≠β(k)。同时由构造可知,α(k)和β(k)属于同一子集Ql,且α(k)≡β(k)≡l (mod d)。因此,|α(k)-β(k)|必为d的正整数倍数,即|α(k)-β(k)|≥d。从而证得码C的最小切比雪夫距离为d。
由于定义8的多置换映射具有一一对应特性,且
中任意多重置换都将被映射到d个不同子集Ql的置换集SQl中,从而构造得到唯一的交织码字。因此,码C包含的码字数目
已
由参数关系n=rm和h=n/d即可推得式(1)。
码C可纠正单个移位错误在译码部分证明。
4.2 译码方法
假设某个n长闪存单元组等级调制的码字为α=(α(1),α(2),…,α(n))∈C,实际读取时发生单个移位错误,不妨记为e(i, j),i, j∈[n],使得码字α中位置i的元素值移位到位置j。令读取码字记为β=(β(1),β(2),…,β(n))∉C,有β=α(i, j)。为了纠正该移位错误,只需确定i和j的值,即可唯一地恢复原码字为α=β(j,i)。
由构造可知,对任意k∈[n],码字α同时满足两个条件:α(k)≡k (mod d)和α(k)-α(k-1)≡1 (mod d),其中引入了零哑元α(0)=β(0)=0。读取码字β由于包含了移位错误e(i, j),从位置i到位置j之间的元素不再同时满足这两个条件。当发生右移位错误时,β中位置i的元素值同时满足条件β(i)-β(i-1)≡2 (mod d)和β(i+1)-β(i)≡1 (mod d);当发生左移位错误时,同时满足条件β(i)-β(i-1)≡1 (mod d)和β(i+1)-β(i)≡2 (mod d)。
下面,通过以下步骤确定i和j的值。
1)首先确定一对位置值kmin和kmax为:
kmin=min{k∈[n]:β(k)≢k(mod d)}
kmax=max{k∈[n]:β(k)≢k (mod d)}
[kmin,kmax]为发生移位的位置区间。
2)其次判断kmin是否同时满足如下条件:
β(kmin)-β(kmin-1)≡2 (mod d)
β(kmin+1)-β(kmin)≡1 (mod d)
此时,e(i, j)为右移位错误;
如果kmin不能同时满足条件,则kmax必然同时满足如下条件:
β(kmax)-β(kmax-1)≡1 (mod d)
β(kmax+1)-β(kmax)≡2 (mod d)
此时,e(i, j)为左移位错误。
3)确定i的精确值和j的可能值:
当e(i, j)为右移位错误时,此时i<j,可直接确定i=kmin。若β(kmax)≢β(kmax+1)(mod d),可直接确定j=kmax;否则, j有两种可能取值:j1=kmax或j2=kmax+1,此时,位置i的元素值移位到位置j1与移位到j2可能得到相同的移位区间, j的精确值还需验证。
类似地,当e(i, j)为左移位错误时,此时i>j,直接确定i=kmax。若β(kmin)≢β(kmin-1)(mod d),可直接确定j=kmin;否则, j有两种可能取值:j1=kmin-1或j2=kmin。
4)最后确定j的精确值,恢复码字:
当j只有一种取值时,原码字可唯一地恢复为α=β(j,i),译码结束。
当j存在两种可能的取值j1或j2时,根据定义有j2-j1=1,原码字相应可恢复为α′=β(j1,i)或α″=β(j2,i)。
当β(j1)=β(j2)时,任意确定j=j1或j=j2,此时唯一有α=α′=α″,译码结束。
当β(j1)≠β(j2)时,必有α′≠α″,此时需对α′和α″分别验证来确定其中的正确码字,从而唯一确定j的取值。由定义4得α′的投影集为
若其中所有的投影置换奇偶性一致,则α′为正确码字,否则α″为正确码字。
下面通过具体的例子来验证该构造方法及其译码方法的有效性。
例3 令正整数m=9,r=2,d=3,则n=18,h=6,令C表示构造采用获得的n长多重置换码。多重集M(n,r)根据模d同余关系划分为3个子集:Q1={12,42,72},Q2={22,52,82},Q3={32,62,92}。任取3个偶多重置换
经定义8的映射和定义6的交织,生成一个码字φQ1(α1)∘φQ2(α2)∘φQ3(α3)∈C。
假定α1=(3,1,3,2,1,2),α2=(1,3,3,1,2,2),α3=(3,2,1,3,1,2),可得φQ1(α1)=(7,1,7,4,1,4),φQ2(α2)=(2,8,8,2,5,5),φQ3(α3)=(9,6,3,9,3,6)。则交织生成的码字为α=φQ1(α1)∘φQ2(α2)∘φQ3(α3)=(7,2,9,1,8,6,7,8,3,4,2,9,1,5,3,4,5,6)∈C。
假定实际读取的置换码字发生单个移位错误e(i, j),下面列举三种移位错误的译码实例。
1)假定发生移位错误e(5,10),实际读取码字为β=(7,2,9,1,6,7,8,3,4,8,2,9,1,5,3,4,5,6)∉C。
首先确定kmin和kmax的值为:
kmin=min{k∈[18]:β(k)≢k (mod 3)}=5
kmax=max{k∈[18]:β(k)≢k (mod 3)}=10
由于β(5)-β(4)≡2 (mod 3),β(6)-β(5)≡ 1 (mod 3),因此,可判断发生右移位错误e(i, j),并直接确定i=kmin=5。
其次,因为β(10)≡β(11)(mod 3),所以j有两种可能取值:j1=kmax=10或j2=kmax+1=11。由于β(10)≠β(11),原码字相应可恢复为α′=β(10,5)=(7,2,9,1,8,6,7,8,3,4,2,9,1,5,3,4,5,6),或者为α″=β(11,5)=(7,2,9,1,2,6,7,8,3,4,8,9,1,5,3,4,5,6)。
最后,需要对α′和α″分别验证来确定其中的正确码字。由定义4得α′的投影集
由于
均为偶多重置换,则α′为正确码字,恢复的原码字为α=α′=(7,2,9,1,8,6,7,8,3,4,2, 9,1,5,3,4,5,6)。可确定i=5, j=10,译码结束。
2)假定发生移位错误e(5,11),实际读取码字为β=(7,2,9,1,6,7,8,3,4,2,8,9,1,5,3,4,5,6)∉C。
首先确定kmin和kmax的值为:
kmin=min{k∈[18]:β(k)≢k (mod 3)}=5
kmax=max{k∈[18]:β(k)≢k (mod 3)}=10
其次,同理得与1)相同的分析结果,发生右移位错误e(i, j),i=5, j的两种可能取值为j1=10或j2=11。由于β(10)≠β(11),原码字相应可恢复为α′=β(10,5)=(7,2,9,1,2,6,7,8,3,4,8,9,1,5,3,4,5,6),或者为α″=β(11,5)=(7,2,9,1,8,6,7,8,3,4,2,9,1,5, 3,4,5,6)。
最后,验证α′和α″,α′的投影集由于α′Q2为奇多重置换,则α″为正确码字,恢复的原码字为α=α″=(7,2,9,1,8,6,7,8, 3,4,2,9,1,5,3,4,5,6)。由此可确定i=5, j=11,译码结束。
3)假定发生移位错误e(9,2),实际读取码字为β=(7,3,2,9,1,8,6,7,8,4,2,9,1,5,3,4,5,6)∉C。
首先确定kmin和kmax的值为:
kmin=min{k∈[18]:β(k)≢k (mod 3)}=2
kmax=max{k∈[18]:β(k)≢k (mod 3)}=9
由于β(3)-β(2)≢2 (mod 3),β(4)-β(3)≢1 (mod 3),不满足右移位错误条件,可判断为左移位错误e(i, j),满足β(9)-β(8)≡1 (mod 3),β(10)-β(9)≡2 (mod 3),并直接确定i=kmax=9。
其次,由于β(1)≢β(2)(mod 3),可直接确定j=kmin=2。因此,可直接恢复原码字为α=β(2,9)=(7,2,9,1,8,6,7,8,3,4,2,9,1,5,3,4,5,6)。可确定i=9, j=2,译码结束。
由以上三种移位错误实例可看出,当j有两种可能取值时,即存在β(j1)≡β(j2)(mod d),如1)和2),此时必须对α′和α″的投影集的奇偶性进行验证才可确定j的取值,从而恢复正确的码字;当j的值可唯一确定时,如3),可直接确定i和j的值,从而恢复正确的码字。
定理2 构造所得的(n,M,d)多重置换码C的码率可表示为
其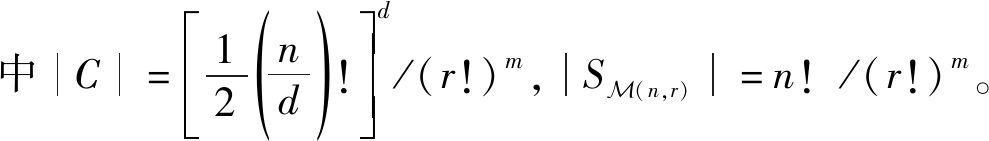
所以,当n→时,码C的渐进码率为
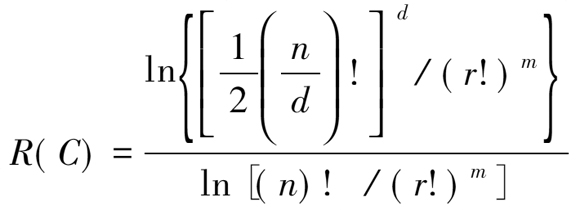
5 结论
基于切比雪夫距离度量,利用交织技术和多重置换映射,提出了正则多重置换码的一种构造方法,可纠正闪存等级调制置换表示的单个“移位错误”,并给出了相应的译码方法,渐进分析证明该编码方法可获得渐进码率1,最后给出实例验证。
[1] Jiang A, Mateescu R, Schwartz M, et al. Rank modulation for flash memories[J]. IEEE Transactions on Information Theory, 2009, 55(6): 2659-2673.
[2] 吴刚, 张邦宁, 郭道省. 非理想同步下BCH码盲识别的改进算法[J]. 信号处理, 2016, 32(6): 746-754.
Wu Gang, Zhang Bangning, Guo Daoxing. Improved algorithm for blind recognition of BCH codes under imperfect synchronization[J]. Journal of Signal Processing, 2016, 32(6): 746-754.(in Chinese)
[3] 肖旻. 基于闪存系统的多进制LDPC码译码研究[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(5): 626- 629.
Xiao Min. Decoding for non-binary LDPC codes in flash memory systems[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2014, 26(5): 626- 629.(in Chinese)
[4] Jiang A, Schwartz M, Bruck J. Correcting charge-constrained errors in the rank-modulation scheme[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2112-2120.
[5] Chee Y M, Ling S, Nguyen T T, et al. Permutation codes correcting a single burst deletion II: Stable deletions[C]∥IEEE International Symposium on Information Theory. Aachen: IEEE Press, 2017: 2688-2692.
[6] Gabrys R, Yaakobi E, Milenkovic O. Codes in the Damerau distance for deletion and adjacent transposition correction[J]. IEEE Transactions on Information Theory, 2018, 64(4): 2550-2570.
[7] Farnoud F, Skachek V, Milenkovic O. Error-correction in flash memories via codes in the Ulam metric[J]. IEEE Transactions on Information Theory, 2013, 59(5): 3003-3020.
[8] Yehezkeally Y, Schwartz M. Limited-magnitude error-correcting gray codes for rank modulation[J]. IEEE Transactions on Information Theory, 2017, 63(9): 5774-5792.
[9] Zhou H, Schwartz M, Jiang A, et al. Systematic error-correcting codes for rank modulation[J]. IEEE Transactions on Information Theory, 2015, 61(1): 17-32.
[10] Buzaglo S, Yaakobi E, Etzion T, et al. Systematic error-correcting codes for permutations and multi-permutations[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3113-3124.
[11] Kong J, Hagiwara M. Nonexistence of perfect permutation codes in the Ulam metric[C]∥International Symposium on Information Theory and Its Applications. Monterey: IEEE Press, 2016: 691- 695.
[12] 韩辉, 慕建君, 焦晓鹏. 切比雪夫距离下系统置换码的编译码算法[J]. 西安电子科技大学学报: 自然科学版, 2018, 45(6): 26-30.
Han Hui, Mu Jianjun, Jiao Xiaopeng. Coding and decoding algorithms for systematic permutation codes at the Chebyshev distance[J]. Journal of Xidian University: Natural Science Edition, 2018, 45(6): 26-30.(in Chinese)
[13] Farnoud F, Milenkovic O. Multipermutation codes in the Ulam metric for nonvolatile memories[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(5): 919-932.
[14] Shieh M Z, Tsai S C. Decoding frequency permutation arrays under Chebyshev distance[J]. IEEE Transactions on Information Theory, 2010, 56(11): 5730-5737.
[15] Sala F, Gabrys R, Dolecek L. Deletions in multipermutations[C]∥IEEE International Symposium on Information Theory. Honolulu: IEEE Press, 2014: 1-5.
[16] Zhao Peng, Mu Jianjun, He Yucheng, et al. Multipermutation Codes correcting a burst of deletions[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2018, 101(2): 535-538.
[17] Zhao Peng, Mu Jianjun, Jiao Xiaopeng. Multipermutation codes correcting a predetermined number of adjacent deletions[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2017, 100(10): 2176-2179.
[18] 赵鹏, 慕建君, 焦晓鹏. 切比雪夫距离度量下多重置换码的新构造方法[J]. 西安电子科技大学学报: 自然科学版, 2018, 45(4): 51-56.
Zhao Peng, Mu Jianjun, Jiao Xiaopeng. New construction methods for multipermutation codes under the Chebyshev distance metric[J]. Journal of Xidian University: Natural Science Edition, 2018, 45(4): 51-56.(in Chinese)
[19] Rotman J J. A first course in abstract algebra with applications[M]. Third Edition. Upper Saddle River: Prentice Hall, 2005.
