1 引言
随着人类社会的快速发展,陆地资源如石油、煤炭等已经面临枯竭,海洋资源成为各国争相抢占、探索和开发的领域,由于人类身体极限的约束,深海探索只能依靠潜水器等机器设备,我国自主研发的“蛟龙号载入潜水器”于2009年至今为我们传来了大量珍贵的海洋图片,填补了我国在海洋资源探索的空白,在此大环境下,水下探险,深海考古,海底资源勘探保护等领域也有了长足的发展。但由于海底坏境的特殊性,由潜水器采集到的视频和图片大多都有严重的质量退化和颜色失真情况,所以通过技术手段对海底图像进行恢复和增强对海洋环境的探索和监护都有非常重大的意义[1-2]。水下图像成像可以视为目标景物到摄像机之间直接传输、光的吸收、光的散射三个部分的线性叠加,其中散射分为前向散射和后向散射,前向散射指的是光在水下传播过程中随机改变它的传播路径,后向散射指的是反射光在到达目标景物之前就被水或者水中的悬浮物所反射,从而被摄像机所接受到。而水中的悬浮物不仅会增大后向散射的影响,也会给采集到的图像带来较大的噪声,导致图像质量退化。
由于可见光的吸收、光的反射和散射等不良因素的影响,使得水下图像退化。例如,不同波长的光在水下有不同的衰减率,红色光最先消失,随着水深的增加,其他颜色的光也随之开始不同程度的衰减,由于蓝色光拥有最短的波长,具有最强的穿透能力,因此在水下的传播距离最远,这就是为什么大多数水下图像以蓝绿色为主的原因。
在本文中,我们提出一种新的无色恒常性原理与白平衡方法,并将它命名为无色恒常白平衡(CLCWB)方法。我们将输入图像转到YCbCr颜色空间,对蓝色色度通道、红色色度通道进行非线性无色检测。最后利用无色检测结果进行白平衡,能够矫正各类极端偏色图像的颜色。
2 现有的白平衡技术
2.1 灰度世界假设[3-4]
灰度世界法假设自然界景物对于光线的平均反射的均值在总体上是个定值,这个定值近似地为“灰色”。在给定图片的白平衡算法中,灰色世界假设图片中的反射面足够丰富,以至于可以作为自然界景物的一个缩影,此时一个场景的反射率平均值为消色差。然而,当图像中有颜色一致的大物体时,这种方法就失败了。
2.2 镜面反射法[5-6]
根据图像形成理论,对于纯白色的反射面而言,无论光源是什么颜色,最终反射后的颜色总能完全表现出光源的颜色。如果景物中有纯白的部分,那么就可以直接从这些像素中提取出光源信息。这种方法假设图片中一定有纯白色面存在,那么在经典光源下,图片中所有像素点三个信道的最大值都应该等于255,或者是一个给定的纯白色的值。在任何其他的光源下,图片纯白色点的像素值就会小于经典光源下的纯白色,并且这些点将代表整幅图片中最亮的点。那么只要将各信道的值按比例规一化到最大值(纯白色)就可以获得在经典光源下的图片了。
2.3 动态阈值自动白平衡[7]
这个算法通过对图片的ycbcr色空间的分析来确定参考白点,为自适应白平衡算法。该算法选择参考白点的阈值是动态变化的,所以对于不同的图片,其阈值也不同。通过对图片的cb、cr坐标空间的分析,接近白色的区域是包含着参考白点的。依此对图片分区,找出参考白点,然后在通过von kvies model来调整图片,实现白平衡。这个算法包括了两个步骤:寻找参考白点,白点调整。
2.4 UCM[8] (Unsupervised Colour Correction Method)
2003年,R. Fisher提出对比度校正算法,校正公式如下:
(1)
其中,Po为对比度校正之后的像素值,Pi是当前像素值,a是灰度下限,即为0,b为灰度上限255,c是当前图像中存在的最小像素值,d是当前图像中出现的最大像素值。
该方法首先通过均衡化颜色值来减少颜色转换。其次,通过公式(1)的变形将最低颜色分量直方图拉伸到最大(即右侧),如图1(a)。最大颜色分量直方图拉伸到最小(即左侧),如图1(c)。适中分量直方图向两侧拉伸,如图1(b)。最后,利用HSI色彩模型的饱和度和亮度分量进行对比度校正。
2.5 Nicolas Limare方法
2011年,Nicolas Limare提出了基于直方图拉伸的白平衡方法,通过计算累计直方图,截断前后s%,在全局上进行拉伸,如图2。但仅仅部分场景效果良好,原因为:(1)参数s需人为设定,未达到自适应性;(2)全局直方图拉伸,在水下红色分量极低情况下效果较差。
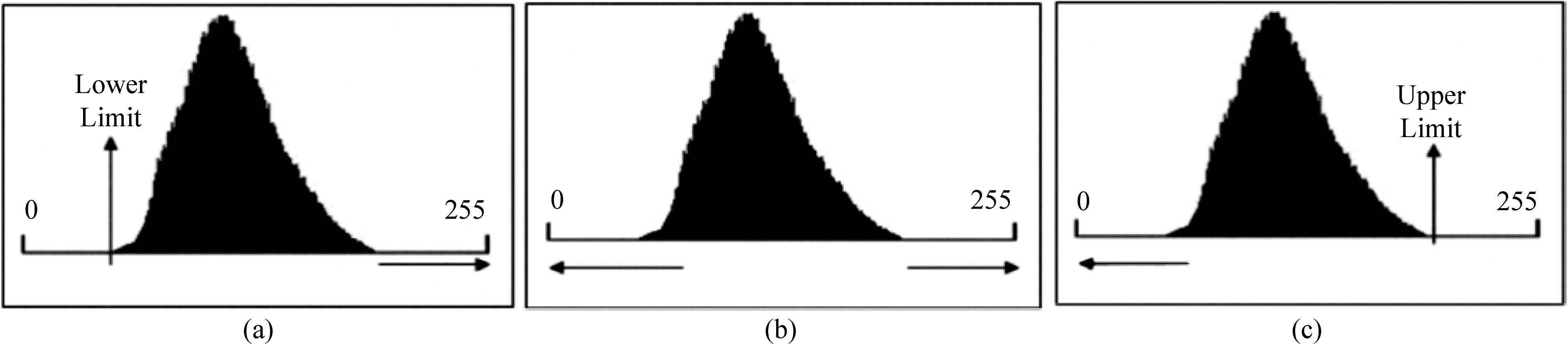
图1 (a)上侧对比度校正,(b)两侧对比度校正,(c)下侧对比度校正
Fig.1 (a) Upper Contrast Correction, (b) Contrast Correction to Both Sides, (c) Lower Contrast Correction
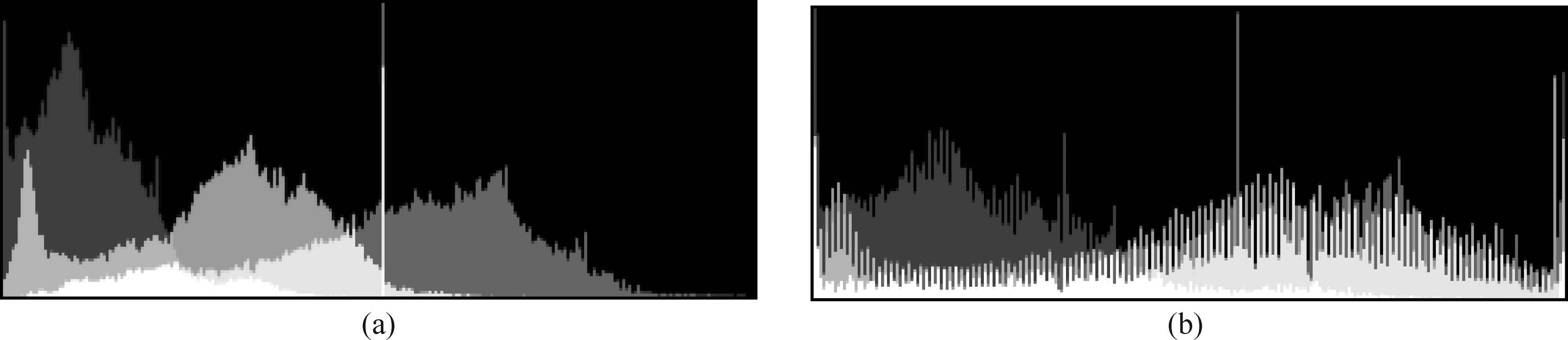
图2 Nicolas Limare算法直方图分布. (a)原图三通道直方图,(b)结果三通道直方图
Fig.2 Nicolas Limare method effect histogram. (a) original histogram, (b) result histogram
在此基础上,2014年,Fu[9]等人采取一种基于统计方法的颜色校正方法,他通过计算每个通道的均值和方差来重新规定三通道各自的最大值和最小值,通过最值来限定直方图的拉伸范围,公式如下:
(2)
(3)
(4)
其中,![]() 和
和![]() 分别为c通道的均值和均方误差(MSE);μ是一个参数来控制图像的动态;
分别为c通道的均值和均方误差(MSE);μ是一个参数来控制图像的动态;![]() 是c通道的最大值和最小值,最后得到彩色校正后的图像。
是c通道的最大值和最小值,最后得到彩色校正后的图像。
3 本文算法
在上一节的介绍中,我们发现这些传统的白平衡算法,均是通过线性的方式,计算一个值(灰度世界假设计算中间灰度,完美反射法计算最亮的点),由这些值来计算色偏校正的增益。总的来说,就是利用线性方式,对三通道进行统一处理,这样做会出现颜色过饱和失真的现象。图3是灰度世界假设,完美反射法,灰度拉伸等白平衡方法及本文算法的处理效果及直方图分布情况。
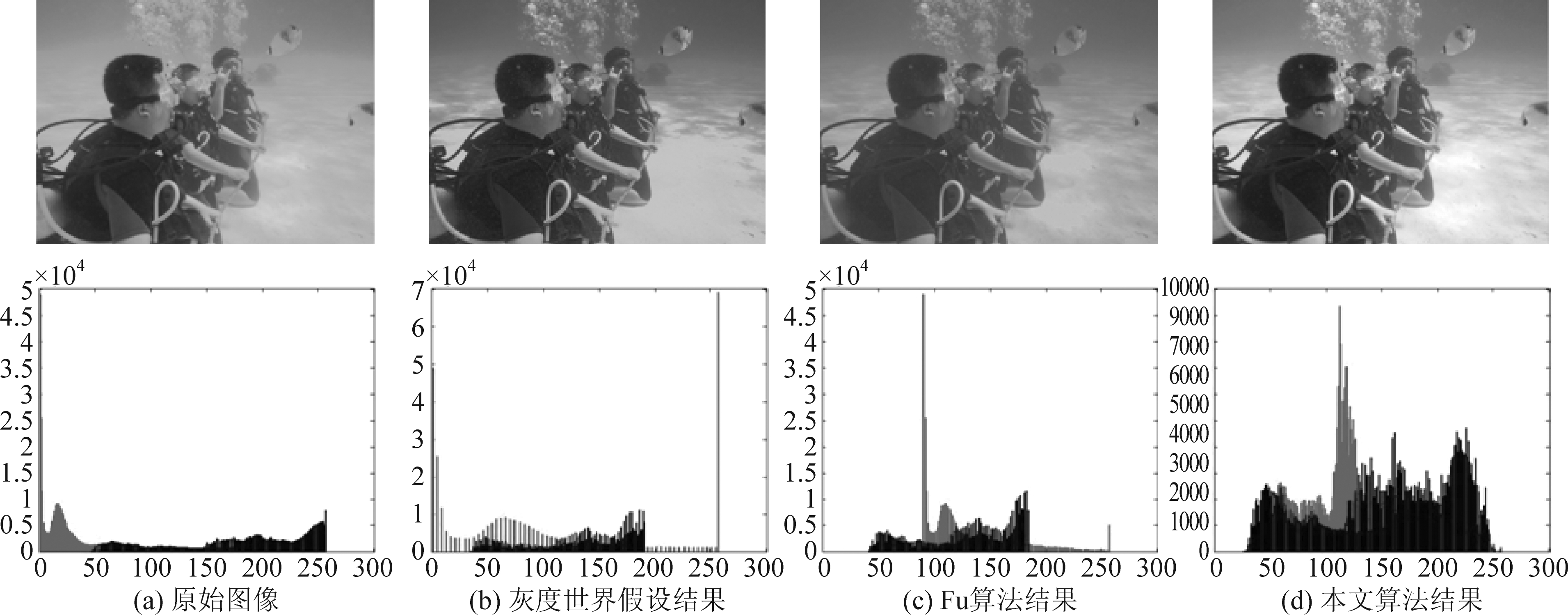
图3 经典算法效果及直方图分布
Fig.3 Classical algorithm effect and histogram distribution
从以上几种算法的效果及直方图分布可以看出,由于光的波长原因,水底图像的红色分量一般都分布在较低灰度级,而对偏色图片进行线性统一处理,会导致过度拉伸,在一些正常区域或者不该发生变化的区域都或多或少地有变红的现象发生,比如水底的白色砂砾,潜水员的白色气泡,黑色潜水服等。这些都彰显了传统线性模式下统一处理的弊端。因此,本文提出无色恒常性原理及白平衡方法。
3.1 无色恒常性原理
这里指出的无色恒常性,相对于传统颜色恒常性,有着独特的定义。它指的是色度调整前后颜色感知效果不应该发生较大变化的无色或色度较弱的区域,如图4所示,像水面波纹、气泡的白色,砂砾的白色,海豹身体的黑色,不管算法如何进行调整,这些区域都不应该发生变化,因此通过非线性方式检测图像中的无色区域计算色度权重,实现对图像中无色区域的保护,对偏色区域的偏色消除。
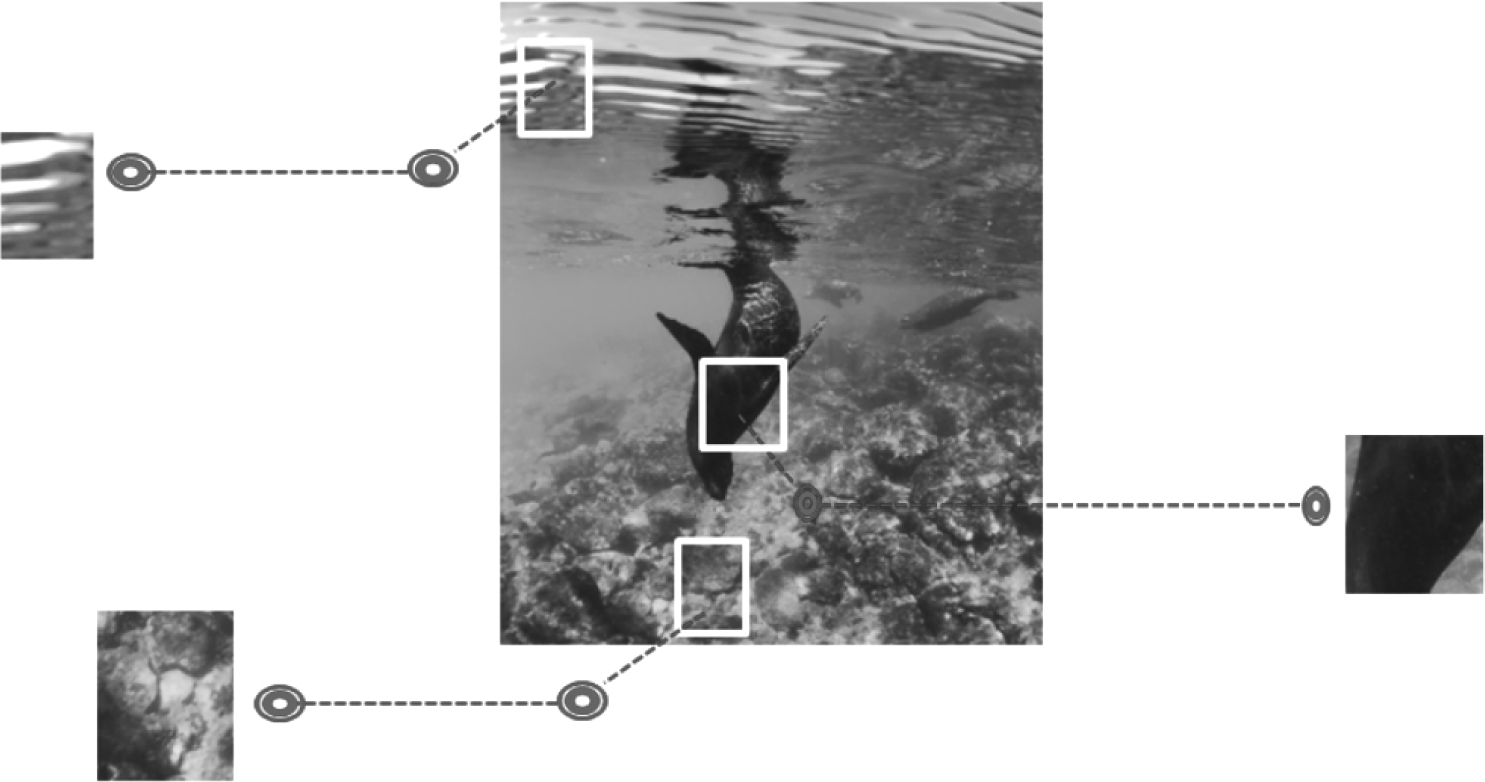
图4 无色区域示例
Fig.4 Colorless region
由于输入图像通道为RGB,首先将其转换到YCbCr空间,如公式(5):
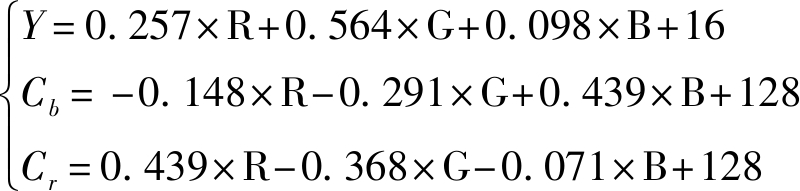
(5)
Cb,Cr反映的是RGB输入信号蓝色部分、红色部分分别与RGB信号亮度值之间的差异。因此,根据YCbCr通道与RGB通道之间的转换关系可知,R、B、G三通道中最亮的点(255,255,255)、最暗的点(0,0,0)以及R、G、B值都相等的点在Cb、Cr通道中的值都为128。因此,我们定义这些点为“无色点”,即RGB彩色模型中黑白点的连线,如图5所示。不论怎样偏移,这些点都不应该变化。同样地,在做色彩校正的时候,这些点也是不做任何调整的,即所谓的“无色恒常性”。
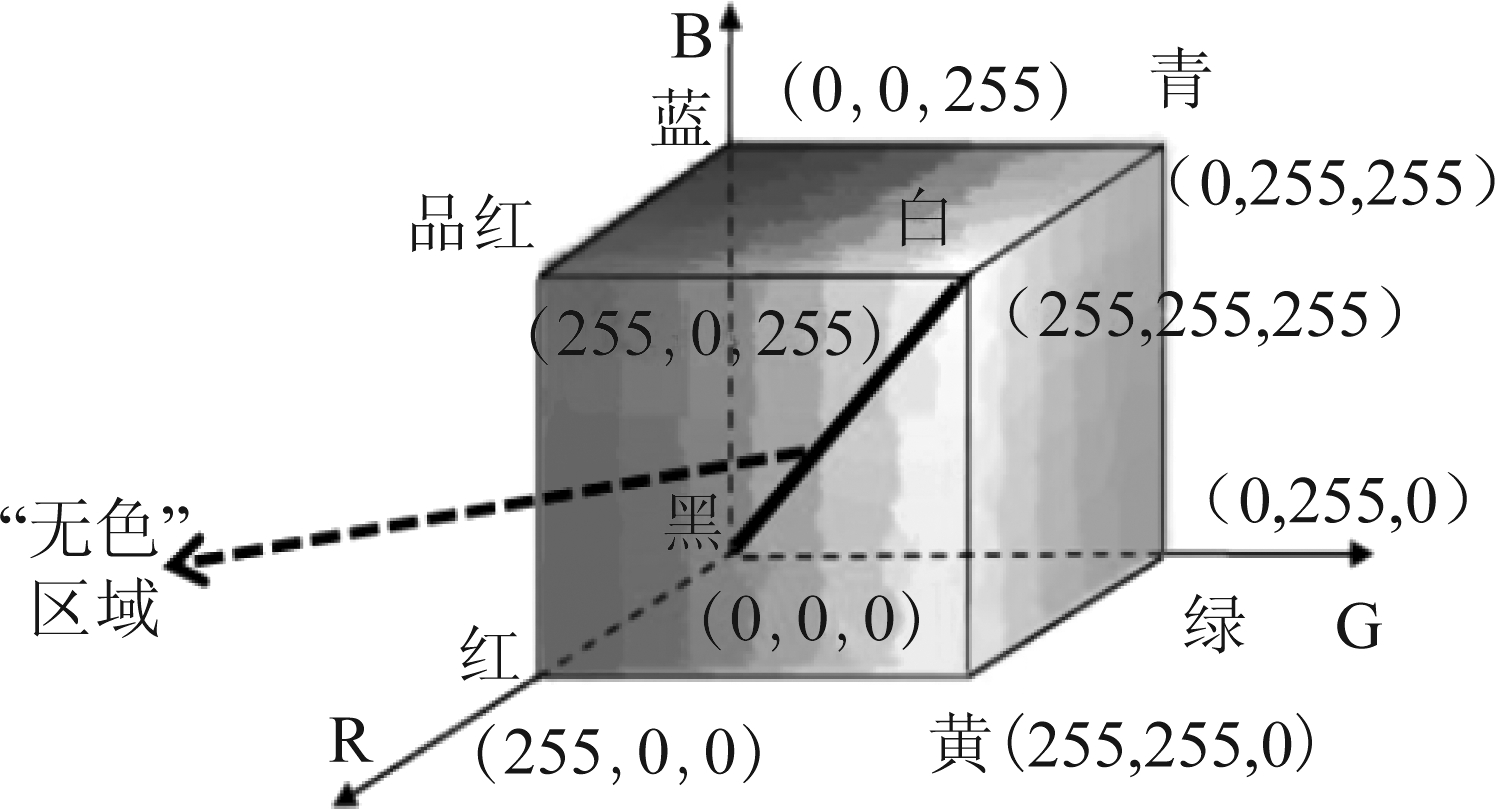
图5 无色区域的定义
Fig.5 Definition of Colorless region
3.2 具体算法
算法流程如图7所示,本文算法对输入图像进行亮色分离,亮度调整有直方图的相关算法[10-16],本文中简单地采用CLAHE(Contrast limited adaptive histogram equalization)算法进行亮度增强。CLAHE与传统的HE的不同之处在于,它将对比度限制在一个截断门限上,以截断直方图中的峰值。剪切后的像素被重新分配到每个灰度级别。截断门限越高,对比度增强越大,如图6(b)所示。截断门限计算如下:
(6)
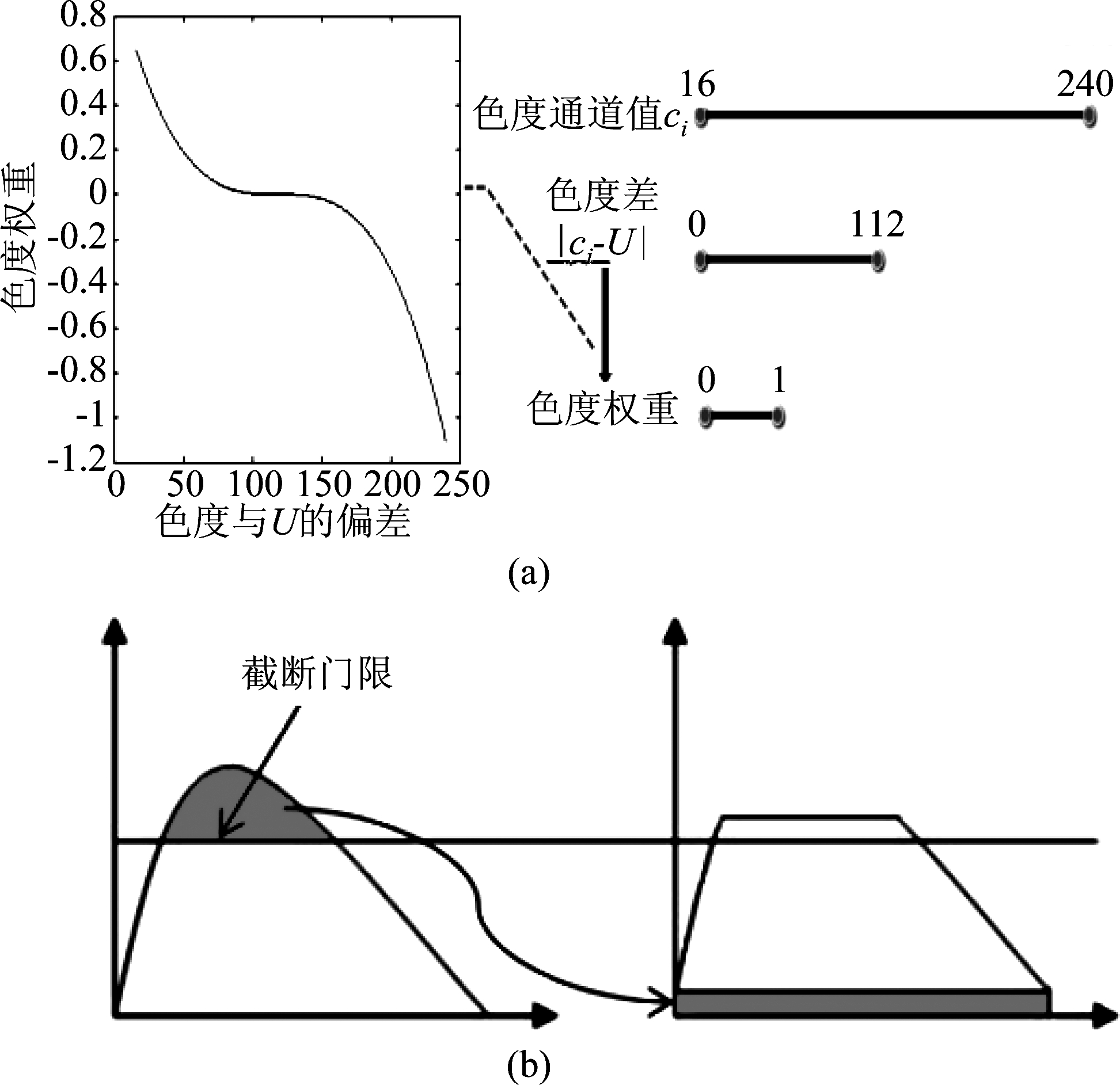
图6 (a)色度权重的计算,(b) 直方图重分配 Fig.6 (a) calculation of chroma weight,
(b) Histogram redistribution

图7 本文算法的整体框架
Fig.7 The framework of our algorithm
其中,M为图像的像素个数,N为图像灰度的动态范围,Smax为最大斜率,α为截断因子,当接近于0时,截断门限为M/N,当接近于100时,对比度大大增强。因此,截断门限是调节对比度增强的关键因素。然后通过剪切直方图的累积分布函数(CDF)得到映射函数:
(7)
T(l)=cdf(l)×lmax
(8)
其中,T(l)为映射函数,l为像素灰度级,lmax为图像最大像素值。
色度计算过程如下:Cb,Cr通道为蓝色色度通道和红色色度通道。对于Cb,Cr通道采用非线性的形式计算通道中每个像素的色度权重,色度权重按照以下公式获取:
(9)
其中,Ci为色度空间,数值大约在(16,240)之间。i=b,r。U为中心灰度值,对于8比特图像,U为128。在此基础上,其他像素值相对于无色区域来说,都有一定差异,差值越小,越接近于“无色”,则调整地越少。计算出来的无色权重的具体意义为:定义黑、白、灰为无色区域,在权重图中归一化为1,每个像素点相对于无色区域存在偏移量,即为|Ci-U|,在(0,112)之间。通过公式(9)得到的权重归一化在(0,1)范围内。如图8(a)所示。
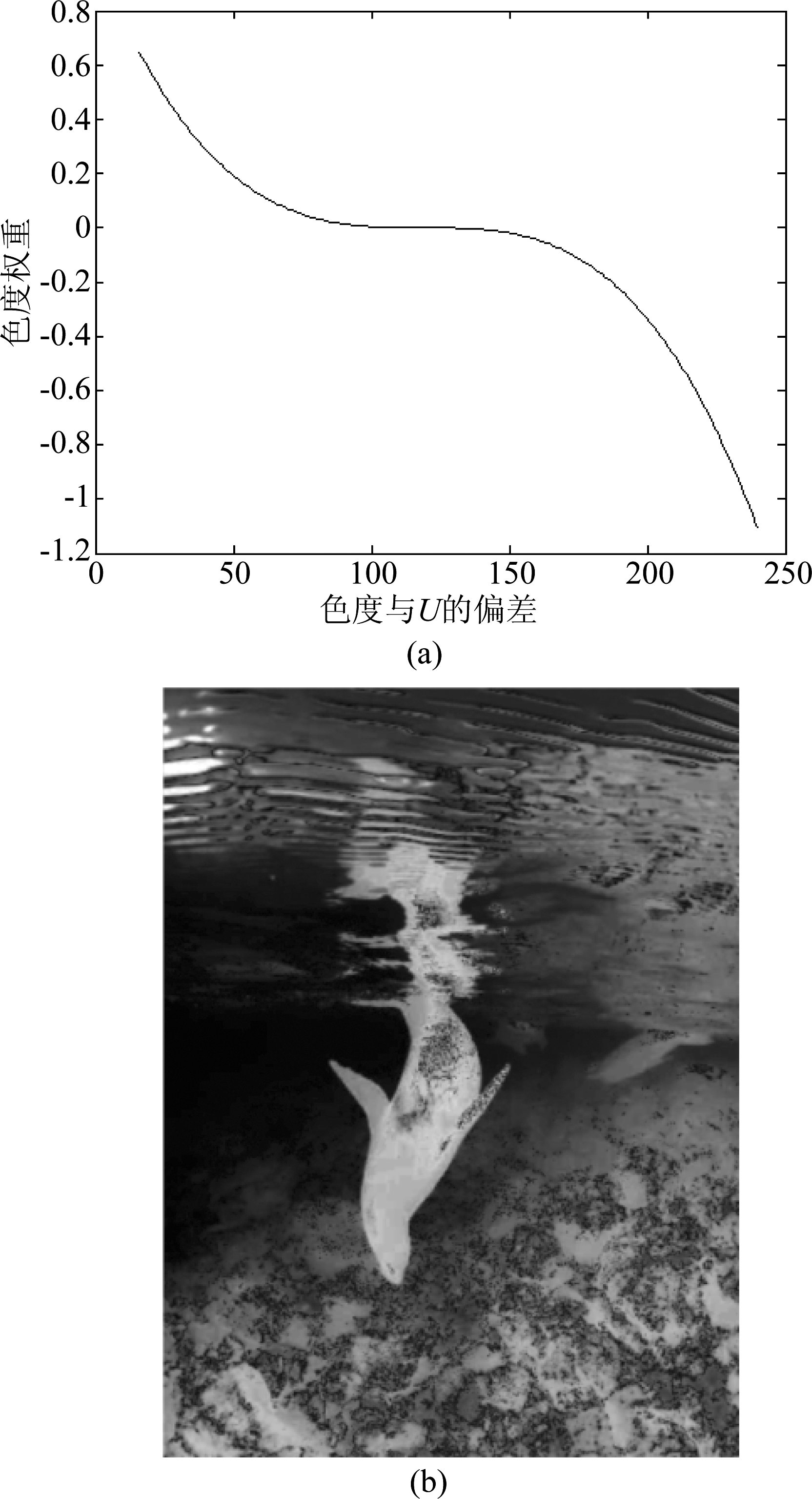
图8 (a)色度权重曲线,(b)色度权重图 Fig.8 (a) Chroma weight curve, (b) Chroma weight map
将两个色度权重通道中坐标相同的权重值进行比较,保留每个坐标位置对应权重值的最小值,存入总色度权重通道矩阵W。如公式(10)所示,结果如图8(b)。而对于一些图片没有黑白区域,则不需要进行保护,例如绿色的水、沙尘等,在处理过程中不进行处理,因此,通过色度通道的均值比例来简单判断图片的类型,如公式(11)。其中Mcb,Mcr分别为cb,cr通道的均值。
W=min(WCb,WCr)
(10)
(11)
本文最终的图像偏色校正方法以灰度世界假设为基础进行改进,在YCbCr空间中的灰度世界假设校正公式如(12)
I′Ci=ICi-MCi+128
(12)
其中,ICi和I′Ci分别是色度调整前后的图像,MCi为各个通道的均值,其思想为将图像的整体色度均值平移至128左右,从而校正色偏。图像全局的色度平移是导致校正后颜色失真的原因,本文采用改进的加权灰度世界算法,通过无色恒常性计算图像的总偏色权重,使不同的像素点得到不同程度的颜色校正。公式如下:
C′i=GainCi×(Ci-(1-W′)×MCi+W′×128)+128
(13)
当某一像素的总偏色权重接近1时,根据无色恒常性原理所述,该像素值接近黑色或白色,是需要进行保护的像素,带入加权灰度世界假设校正公式中,相当于色度减去128再加上128,该像素的颜色不发生变化,能够防止其产生颜色失真,而当某一像素的总偏色权重远离1时,说明该像素存在一定程度的偏色,需要进行正常校正。其中,Gainci为原色彩通道的调整系数,定义如下:
(14)
至此,无色恒常白平衡(CLCWB)算法步骤如下:

无色恒常白平衡(CLCWB)算法输入:彩色图像输出:彩色图像的恢复结果1.Begin2.输入数字图像并转为YCbCr通道,对应公式(5)3.获取亮度通道,直方图操作,得到亮度通道的增强图像Y′4.计算Cb、Cr通道的色度权重wcb,wcr,对应公式(9)5.取两通道色度权重最小,为总色度权重通道矩阵w,对应公式(10)6.根据色度通道均值更新w,对应公式(11)7.用总色度权重通道矩阵w计算新的蓝色和红色色度通道,记为C′b,C′r,对应公式(13)8.将得到的Y′,C′b,C′r结合成输出彩色图像End
4 实验及结果分析
4.1 主观评价
为了验证本文算法的性能,采用了多种公开的图像数据库进行测试。本节选取六组图像进行增强效果对比与分析,实验结果如图9至图10所示。

图9 鱼
Fig.9 Fish

图10 雕像
Fig.10 Statue

图11 非水下场景测试图
Fig.11 Non-underwater scene test diagram
从图9和图10的水下场景的对比结果可以看出,本文算法色彩校正适当,不会像灰度世界假设的结果那样,大片面积由于红色分量过度拉伸,导致的红色过饱和。Nicolas方法在图10中,偏黑区域变得更黑,也出现了颜色的过饱和失真。由此可见,本文算法很好地保护了这些需要保护的区域,体现了“无色恒常性”。Fu算法在这几张图上都明显效果不足,在图9,图10中很明显地看出,完美反射法由于以最亮的像素作为参考白点,因此亮度会过度增强,白色部分会过曝,丢失细节。Retinex算法在水下会导致颜色失真,出现不和谐的色斑。本文算法与上述方法最大的不同在于它采用的是非线性的方式来考量每个像素,计算出每个像素是否偏色,且该校正多少。摒除了线性方式可能会过饱和、失真的弊端,而从图11的非水下场景偏色的对比结果也可以看出,非水下场景中,不论是室内、室外、人物还是色彩丰富的物体,本文算法也可以很好地进行颜色恢复和校正。
4.2 客观评价
水下彩色图像质量评价(UCIQE)[17]是目前针对水下彩色图像质量评价的非参考模型,但在实际计算过程中,经常与主观判断相悖,因此本文中并没有采用此评价指标。为了能更准确地体现实验结果,本文采用了色彩分量相关性和NIQE(Natural Image Quality Evaluator)两种客观评价指标来衡量各种算法的增强结果。
(1)色彩分量相关性(rcolor):表示RGB色彩空间的各个颜色分量之间的相关性,反映图像三分量灰度变化的一致性,值越大越好,公式如下:
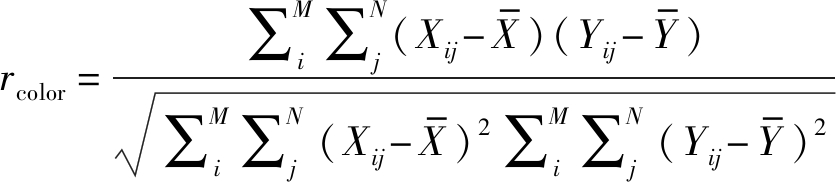
(15)
其中,![]() 表示RGB图像中任意两个颜色通道X、Y的均值,Xij、Yij为图像中像素值。
表示RGB图像中任意两个颜色通道X、Y的均值,Xij、Yij为图像中像素值。
(2)NIQE是Mittal[18]等人在2013年提出的一种无参考图像质量评价算法,它根据待评价图像特征模型参数与预先建立的模型参数之间的距离来评价图像质量。NIQE算法评价值与人眼感知结果具有较好的一致性,其NIQE数值越小代表图像质量越好。
图12为部分测试图片,表1至表2给出了各评价指标的测试结果。

图12 部分测试图
Fig.12 Part of the test image
表1 色彩分量相关性指标
Tab.1 Color component correlation index
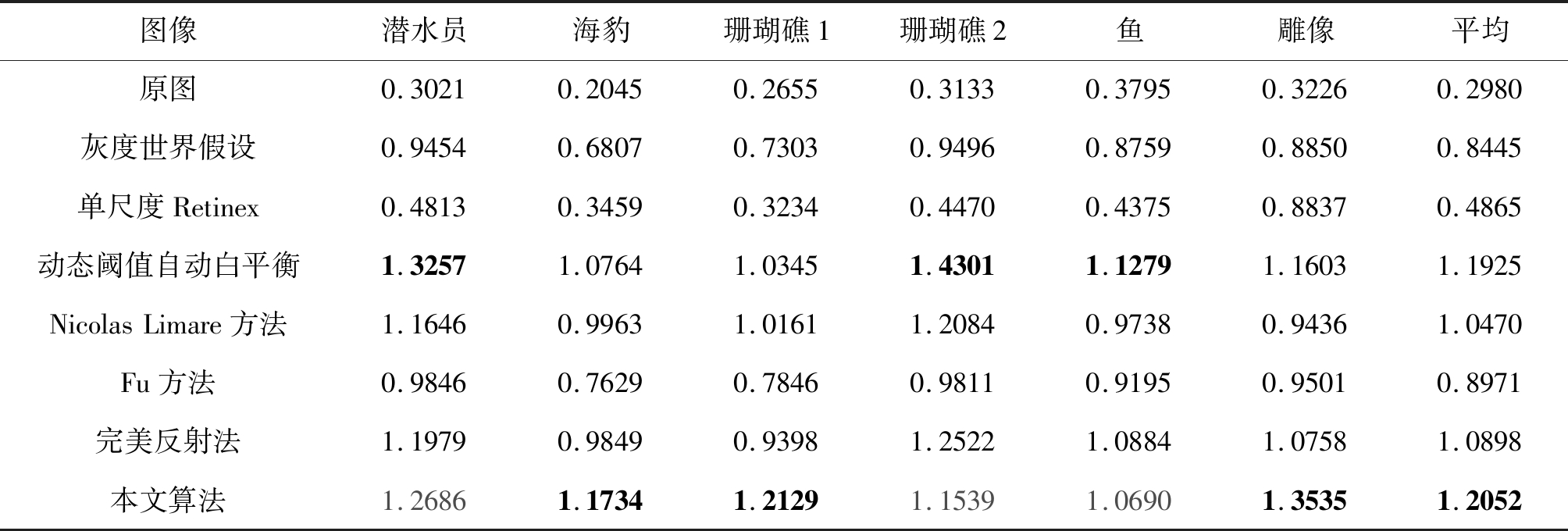
图像潜水员海豹珊瑚礁1珊瑚礁2鱼雕像平均原图0.30210.20450.26550.31330.37950.32260.2980灰度世界假设0.94540.68070.73030.94960.87590.88500.8445单尺度Retinex0.48130.34590.32340.44700.43750.88370.4865动态阈值自动白平衡1.32571.07641.03451.43011.12791.16031.1925NicolasLimare方法1.16460.99631.01611.20840.97380.94361.0470Fu方法0.98460.76290.78460.98110.91950.95010.8971完美反射法1.19790.98490.93981.25221.08841.07581.0898本文算法1.26861.17341.21291.15391.06901.35351.2052
表2 NIQE评价指标
Tab.2 Evaluation index of NIQE
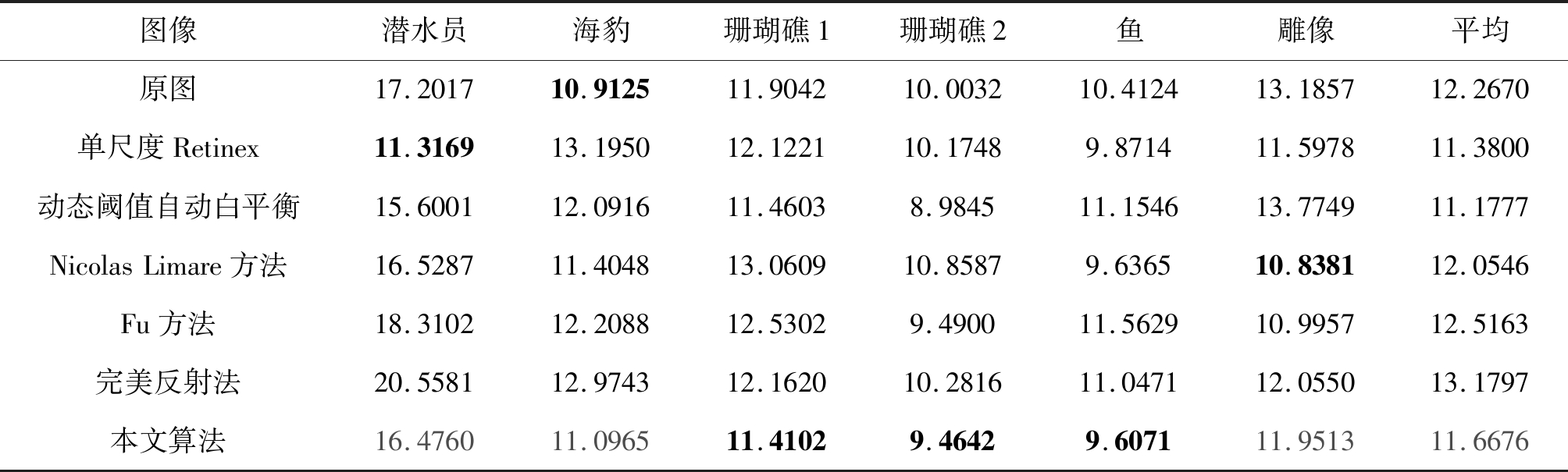
图像潜水员海豹珊瑚礁1珊瑚礁2鱼雕像平均原图17.201710.912511.904210.003210.412413.185712.2670单尺度Retinex11.316913.195012.122110.17489.871411.597811.3800动态阈值自动白平衡15.600112.091611.46038.984511.154613.774911.1777NicolasLimare方法16.528711.404813.060910.85879.636510.838112.0546Fu方法18.310212.208812.53029.490011.562910.995712.5163完美反射法20.558112.974312.162010.281611.047112.055013.1797本文算法16.476011.096511.41029.46429.607111.951311.6676
以上各表中,红色加粗标注的数据表示最优指标、从表1中数据可知,本文的算法色彩相关性指标均比较大,意味着图像三分量灰度变化一致性较好,反之,像灰度世界假设和单尺度Retinex算法,此项数据偏小,这就意味着在色彩校正过程中,三个通道变化程度差异很大,容易导致过饱和失真现象。表2为自然图像质量评价指标,可以看出本文算法与上述诸多算法相比拥有较小的NIQE值,视觉效果也更好,这也与主观评测的结果相符。
5 结论
本文在研究了大量白平衡算法之后,针对传统白平衡方法会对不应该发生较大变化的无色或色度较弱区域产生不良偏色的缺点,提出了一种新的无色恒常性原理,并依此设计了一种白平衡方法。本文算法通过非线性的方式计算色度分量,计算每个像素对应的色度权重,根据新的线性加权算法重新计算每个像素的色度,实现对图像中无色区域的保护以及偏色区域的色彩校正。
对比实验验证了本文思想的科学性和算法的实用性,针对水下偏色和自然环境中的偏色情况,CLCWB算法克服了传统白平衡方法的缺点,获得了较好的视觉感知效果。且算法复杂度低,具有鲁棒性。
[1] Wang N, Qi L, Dong J, et al. Two-stage underwater image restoration based on a physical model[C]∥Eighth International Conference on Graphic & Image Processing. International Society for Optics and Photonics, 2017.
[2] Li M D, Liu J Y,Yang W H, et al. Structure-revealing low-light image enhancement via robust retinex model[J].IEEE Transactions on Image Processing, 2018, 27(6): 2828-2841.
[3] 朱贵冬, 沈理, 王今觉. 基于Von-Kries色适应的分区颜色校正方法[J]. 计算机工程与科学, 2007, 29(2): 50-52.
Zhu G D, Shen L, Wang J J. Partition color correction method based on von-Kries color adaptation[J]. Computer Engineering and Science, 2007, 29(2): 50-52.(in Chinese)
[4] 谷元保, 付宇卓. 一种基于灰度世界模型自动白平衡方法[J]. 计算机仿真, 2005, 22(9): 185-188.
Gu Y B, Fu Y Z. An automatic white balance method based on the world model of gray scale[J]. Computer Simulation, 2005, 22(9): 185-188.(in Chinese)
[5] Huo J Y, Chang Y L, Wang J, et al. Robust automatic white balance algorithm using gray color point in images[J]. IEEE Transactions on Consumer Electronics Society, 2006, 52(2): 541-546.
[6] 周荣政,何捷,洪志良.自适应的数码相机自动白平衡算法[J]. 计算机辅助设计与图形学学报,2005,17(3): 529-533.
Zhou R Z, He J, Hong Z L. Adaptive white balance algorithm for digital camera[J]. Journal of Computer-Aided Design, 2005, 17(3): 529-533.(in Chinese)
[7] Weng C C, Chen H, Fuh C S. A novel automatic white balance method for digital still cameras[C]∥Circuits and Systems, 2005. ISCAS 2005. IEEE International Symposium on. IEEE, 2005.
[8] Iqbal K, Odetayo M O, James A E, et al. Enhancing the low quality images using unsupervised color correction method[C]∥IEEE International Conference on Systems Man & Cybernetics. IEEE, 2010.
[9] Zhuang P, Huang Y, et al. A retinex-based enhancing approach for single underwater image[C]∥IEEE International Conference on Image Processing. IEEE, 2015.
[10] Abhisek P, Paritosh B, Santi P M, et al. Plateau limit-based tri-histogram equalisation for image enhancement[J]. IET Image Processing, 2018, 12(9): 1617-1625.
[11] Cao G, Tian H W, Yu L F, et al. Acceleration of histogram-based contrast enhancement via selective downsampling[J]. IET Image Processing, 2018, 12(3):447- 452.
[12] Chang Y, Jung C, Ke P,et al. Automatic contrast limited adaptive histogram equalization with dual gamma correction[J]. IEEE Access, 2018, 6(99):1-1.
[13] Wang Y, Chen Q, Zhang B.Image enhancement based on equal area dualistic sub-image histogram equalization method[J]. IEEE Transactions on Consumer Electronics, 1999, 45(1): 68-75.
[14] Yao Z, Zhou Q, Lai Z, et al. Image enhancement based on bi-histogram equalization with non-parametric modified technology[C]∥2016 IEEE 22nd International Conference on Parallel and Distributed Systems(ICPADS). IEEE, 2016.
[15] Shanmugavadivu P, Balasubramanian K. Thresholded and optimized histogram equalization for contrast enhancement of images[J]. Computers & Electrical Engineering, 2014, 40(3): 757-768.
[16] Gautam C, Tiwari N. Efficient color image contrast enhancement using range limited bi-histogram equalization with adaptive gamma correction[C]∥International Conference on Industrial Instrumentation & Control. IEEE, 2015.
[17] Yang M, Sowmya A. An underwater color image quality evaluation metric[J]. IEEE Transactions on Image Processing, 2015, 24(12): 6062- 6071.
[18] Mittal A, Soundararajan R, Bovik A C. Making a “completely blind” image quality analyzer[J]. IEEE Signal Processing Letters, 2013, 20(3): 209-212.



