1 引言
随着高铁在中国乃至世界的快速发展,对轨道质量的要求越来越高,为了高铁运行的安全性、以及高速运行对轨道的苛刻要求,对轨道表面的缺陷检测显得尤其重要。由于高速车轮与轨道间的摩擦、压力作用,轨道表面会出现多种多样的损伤,这些损伤形态、大小不一,且可能随机出现在任意位置。由于缺陷缺乏周期性的形状特性,以及轨道线路非常长,因此对于轨道表面的缺陷检测是铁路运营维护中的一大重点难题。传统的人工检测效率低,依赖大量的人力,且主观性强。对于全国12.1万公里的铁路线,要想靠人工检测几乎不可能。
近年来,铁轨无损检测方面得到了大量的关注,例如[1]中应用差分涡流检测系统得到裂纹检测信号的幅值和相位变化信号,通过大量试验对不同长度、深度的缺陷样本进行了检测分析。[2]中基于概率图模型构建扣件子图邻域纹理图和初始引导图与被定位图之间的置信图,并通过计算置信图的最大极值点实现对扣件子图中心点的快速定位。在无损检测中,基于CCD相机拍摄的图像的缺陷检测因其成本低、抗干扰性强等特点,在铁轨表面缺陷检测中得到了很好的发展[3-10]。
铁轨表面离散缺陷检测系统一般来说包含三个部分[7],即:图像获取子系统(image acquisition subsystem, IAS),图像处理子系统(image processing subsystem, IPS),以及自动控制模块(automatic control block)。通过CCD相机,在固定LED光源下对铁轨表面进行拍摄得到高质量的铁轨表面图像,然后通过缺陷检测软件实现缺陷的自动检测和定位。而控制模块将自动的控制LED光源,调整亮度,保证获取到高质量、清晰的铁轨表面图像。在获得铁轨表面图像之后,[7]提出了一种从粗到细的多层次铁轨缺陷检测方法,粗检测算法通过利用mean shift算法来检测背景梯度变化密度,从而建立背景模型;进一步,其精细检测算法为每个像素定义一个显著性函数,通过阈值判断该像素是属于缺陷还是噪声,并同时定位出缺陷位置,精细检测算法可以极大的抑制噪声的影响,提高缺陷检测准确率。在[8]中,提出了一种PEME(proportion emphasized maximum entropy)阈值法来提取缺陷区域。其首先提出局部MLC(Michelson-like contrast)方法来提高铁轨图像背景和缺陷区域的对比度,使得缺陷区域更黑而背景区域更加明亮。然后计算背景和前景灰度级概率分布,并极大化背景和前景熵来确定前景和背景的分割阈值,实现缺陷与背景的分割。在[9]中, 提出了一种改进的Perona-Malik(P-M)扩散系数方法来提高图像质量,然后利用自适应阈值二值化方法进行缺陷检测。在[10]中,Li等提出了首先将铁轨图像进行局部规范化(local normalization,LN),去除光照带来的影响,并将局部规范化之后的图像向横轴和纵轴方向投影,称为基于投影剖面缺陷定位(defect localization based on projection profile,DLBP)。对投影结果的连续非零值区域进行定位,从而得到水平和竖直方向上的缺陷区域坐标,实现对缺陷区域的定位。在[11]中,提出了局部对比度测量法和改进的最大熵法来对铁轨图像进行对比度增强和自动阈值分割。[12]中描述了一个铁轨表面缺陷检测系统的软硬件构成,但是从缺陷检测的算法来看,主要是基于传统边缘提取、形态学的算法。上述的这些算法中,主要还是基于图像预处理、形态学、边缘提取等图像处理的方法来实现缺陷检测,而这些方法中,一个较大的问题是其中涉及许多参数的手工调整,而且受到图像背景、光照等问题的影响很大,在普适性和鲁棒性上还有待进一步的提高。
近年来,低秩矩阵分解(低秩矩阵重构)得到了学术界广泛的关注[13-20],其被广泛应用到人脸识别、图像恢复、去噪及数据重构等。低秩矩阵重构的目的在于从被大而稀疏的有误差的数据中恢复出原始具有低秩结构的矩阵。一般而言,一个被噪声干扰的矩阵,可以通过低秩矩阵理论分解为一个低秩矩阵和一个稀疏误差矩阵之和,分解得到的低秩矩阵可以看成是对原始无噪声的矩阵的重构(或逼近),而稀疏误差矩阵则是噪声部分。在低秩矩阵重构中,最经典的模型即鲁棒主成分分析(robust principal component analysis, RPCA)模型[13],另外还有基于l1范数的主成分分析(principal component analysis based on l1-norm, PCAL1)[14-15]、广义低秩矩阵逼近(generalized low-rank approximations of matrices, GLRAM)模型[16]、鲁棒广义低秩矩阵逼近模型(robust generalized low-rank approximations of matrices, RGLRAM)[17]。考虑到稀疏大噪声的特点,[18]中提出了对低秩部分核范数和稀疏部分l1范数联合极小化的鲁棒广义低秩分解模型。[19]中进一步考虑TV范数在图像边缘保持方面的优越性,提出了联合核范数、TV范数以及1-范数联合极小化问题,得到了较好的图像重构效果。在[20]中,将低秩矩阵逼近理论运用到了TFT-LCD缺陷检测中,由于TFT-LCD图像具有横竖条纹纹理,其可以建模为一个低秩矩阵,而前景缺陷图像也同样可建模为一个稀疏矩阵,因此可以通过核范数与1范数联合极小化实现背景和前景的分离,最终提取缺陷区域。进一步,RPCA模型在[21]中被用于铝箔表面缺陷检测,实现缺陷区域与背景的有效分割。[22]中则针对于LCD显示屏缺陷检测,提出了先行压缩采样后列压缩采样的压缩感知方法,并给出了相关的压缩感知电路实现方案。在[23]中,针对纺织物的缺陷检测,提出了基于块矩阵特征值分解的低秩表示算法,建立了核范数和2,1范数联合极小化的低秩表示模型。通过将图像分割为图像块实现降维,并利用块矩阵的特征值分解替代整体图像上的奇异值分解,提高缺陷检测的准确度和效率。[24]中考虑到纺织品图像中的高斯噪声,将原始图像分解为低秩背景、噪声矩阵及稀疏缺陷矩阵,并用F范数来描述高斯噪声,使得分解得到的稀疏缺陷矩阵中噪声的干扰极大的减小。[25]中,首先利用具有多尺度和多方向的Gabor滤波器得到纺织品图像的Gabor特征,然后对这些特征图进行分块,并将这些块中的特征向量重新组成一个特征矩阵,最后利用RPCA模型实现稀疏矩阵(缺陷矩阵)的分割。
从上可以看出,低秩矩阵重构在缺陷检测中具有鲁棒性好,适应面广的特点,且分解过程中需要考虑的参数少,性能稳定。在本文中,考虑到铁轨背景一般来说比较光滑,而缺陷部分则可以看作为稀疏噪声或野点,因此,通过低秩矩阵分解理论,可以较好的对缺陷进行分离,去除背景干扰,实现缺陷的检测。
2 低秩矩阵分解模型
图1列出了在不同光照下,四幅典型的带缺陷的铁轨表面图像,可以看到,由于铁轨表面反光、光照不均匀等问题,不同时间段、不同位置的铁轨得到的铁轨表面均有所不同,但是图像背景均呈现出有规律性的纵向条纹,其本质上来说应该是一个低秩矩阵,这为我们利用低秩矩阵分解理论来实现缺陷和背景的分离奠定了十分良好的基础。

图1 不同光照下的铁轨缺陷图像
Fig.1 Rail track defective images under different illuminations
在铁轨表面图像中,缺陷区域分布、形状、大小具有很强的随机性。但是总的来说,缺陷区域与背景相比较,所占的面积较小,而且由于缺陷发生位置及形状大小的随机性,使得缺陷对于背景来说呈现一种稀疏性,因此,若能将原始图像分离成前景和背景两张图像,前景缺陷图像则可以看成是一个具有稀疏性的矩阵。因此,根据鲁棒主成分分析理论,对于铁轨的成分分解可以由以下模型来建立:
(1)
其中,原始铁轨缺陷图像为Dm×n。记对应的铁轨背景矩阵为Am×n,稀疏的前景缺陷图像矩阵为Em×n。 ||·||0表示l0-范数,即矩阵中非零元素的个数,λ>0为权重参数。模型(1)的目标是通过极小化背景矩阵A的秩与稀疏矩阵E的零范数,使得将原始带缺陷的铁轨图像能分解为一个背景低秩矩阵A和前景缺陷矩阵E之和,从而达到缺陷分离的效果。
然而,式(1)中零范数是非凸且不连续的函数,该式的极小化问题是一个NP-难问题。在[26]中,提出了对式(1)中的代价函数进行松弛,并且松弛的结果仍然可以保证A的低秩性和E的稀疏性,凸松弛后的优化问题称为主成份追踪(Principal Component Pursuit, PCP),即将式(1)转化为下述优化问题:
(2)
其中||A||*=∑i σi(A)表示A的核范数,σi(A)为A的第i个奇异值,||·||1表示l1-范数,即矩阵中所有元素的绝对值之和。λ>0为权重参数,[26]中建议![]() 其中C为一个常数,一般可以取1。式(2)对应的拉格朗日函数如下:
其中C为一个常数,一般可以取1。式(2)对应的拉格朗日函数如下:
L(A,E,Y,μ)=||A||*+λ||E||1+
(3)
上述问题可以通过非精确的拉格朗日乘子法(Inexact augmented Lagrange multiplier method, IALM)予以求解[27],求解算法如下:

算法1 非精确拉格朗日乘子法求解RPCA问题输入:观测矩阵D∈Rm×n,齄.1.Y0=D/J(D);E0=0;μ0>0;ρ>1;k=0;2.执行下列循环直到D-Ak+1-Ek+1FDF<δ;3.(U,Σ,V)=svd(D-Ek+μ-1kYk);4.Ak+1=USμ-1k[Σ]VT;5.Ek+1=S齄μ-1k[D-Ak+1+μ-1kYk];6.Yk+1=Yk+μk(D-Ak+1-Ek+1];μk+1=ρμk.7.k=k+1.输出:Ak,Ek.
其中,J(D)=max(||D||2,λ-1||D|| ),Sε[x]表示软阈值操作,即:
),Sε[x]表示软阈值操作,即:
Sε[x]≐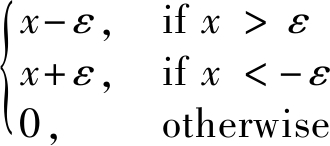
(4)
上述算法1的收敛性证明可以参考[27]。通过上述迭代算法,对于给定的带缺陷的铁轨表面图像,可以分解为两个矩阵之和,由于缺陷具有稀疏性,其绝大部分的成分将会被分解到矩阵E中。利用上述算法对图1中的4幅图像进行低秩矩阵分解。得到的结果如图2所示。

图2 低秩矩阵分解后得到的稀疏矩阵显示结果,
分别对应图1中的4幅图像
Fig.2 The sparse matrix image after low-rank matrix decomposition, these four figures correspond to the figures shown in the Fig.1, respectively
从图2可以看出,经过算法1对原始缺陷图像进行低秩矩阵分解之后,得到的稀疏矩阵基本只包含了缺陷部分,而背景区域则被去除掉了,背景变成了一片均匀的灰色,而缺陷区域则是黑色,这使得缺陷部分很好的凸显出来。而且对于不同的光照具有较好的鲁棒性(图1中的4幅图像中包含了三种光照条件,(a)和(b)的光照条件一样,而(c)、(d)的光照条件是另外两种)。这使得后续的缺陷检测定位变得更加容易和准确。
3 缺陷检测与定位
上述的低秩矩阵分解模型仅仅是将缺陷前景从原始图像中分解出来,但是要判断某一张图像是否有缺陷、缺陷的大小是否符合安全标准还需要进一步对缺陷区域进行定位,若定位到的缺陷区域面积过小,则可以忽略,否则应该予以标记出来并提示。从图2看到,在稀疏矩阵中,背景区域已经基本全部被去除,对于没有包含有缺陷像素的那些行,其行像素值在竖直方向上的累积量(即每一行像素值之和)应该近似的相等,而若某一行穿过了某一个缺陷区域,则这一行的像素值累积量应该有所变化。基于此思路,我们分别计算稀疏矩阵E每一行的像素值累积量,即![]() 对每一个E∈Rm×n将会得到一个向量,记为p∈Rm×1。图2中四幅图像得到的像素值累积量如图3所示。
对每一个E∈Rm×n将会得到一个向量,记为p∈Rm×1。图2中四幅图像得到的像素值累积量如图3所示。
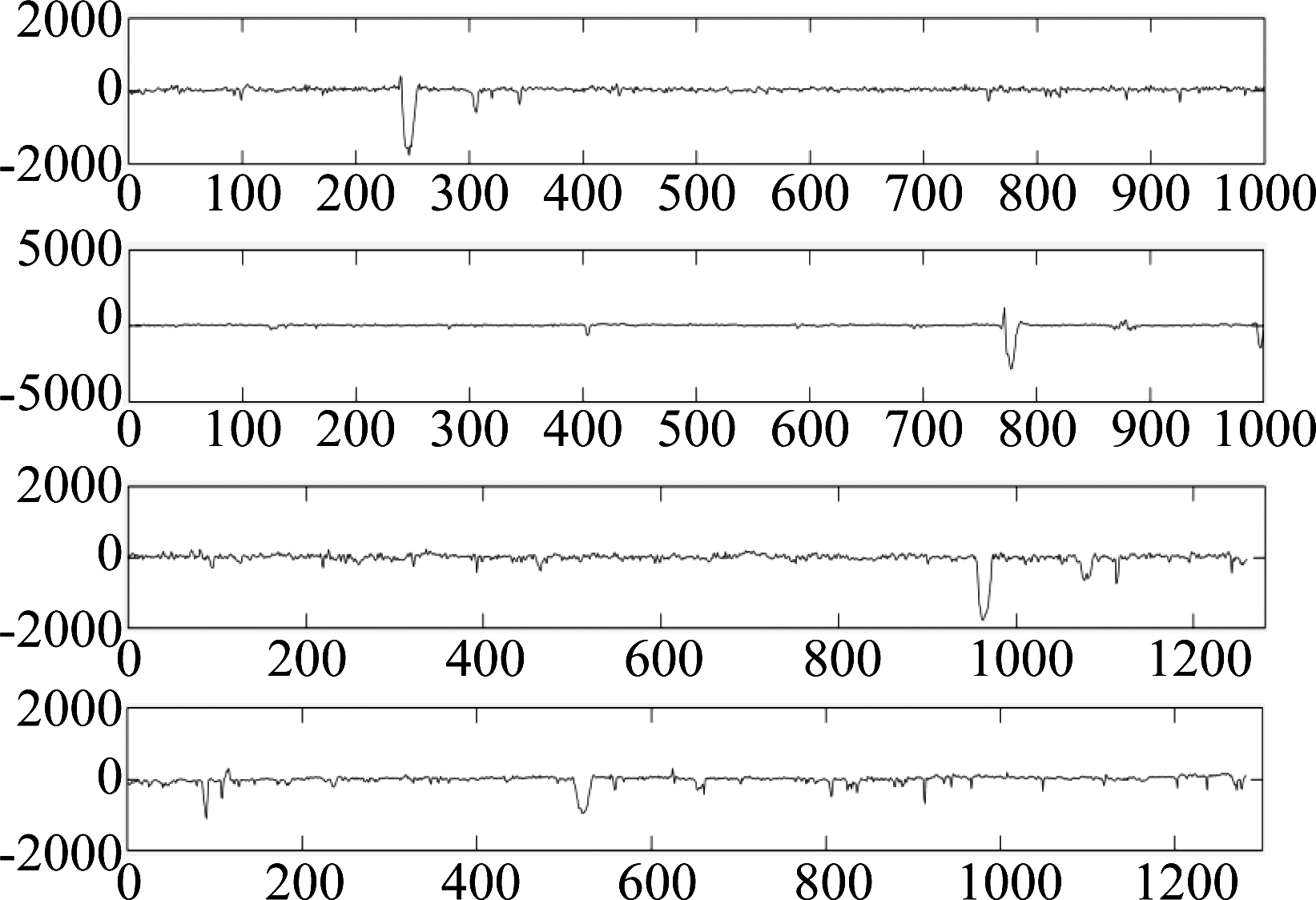
图3 稀疏矩阵E竖直方向上的像素值累积量图,从上至下分别对应于图2中的四幅图
Fig.3 The pixel accumulation values of the sparse matrix E along the vertical direction. The four subfigures here correspond to the 4 images shown in the Fig.2
图3中可以明显的看到,对于缺陷像素的那些行,其累积量明显小于未穿越缺陷的那些行,图中每一个向下的突变区域均对应一个缺陷区域,而且突变区域与正常区域有着十分明显的区别度。为了定位缺陷区域,我们只需在图3的基础上设置一个阈值,将图3进行二值化,即可确定每一个缺陷区域的行起始位置和结束位置。二值化过程如下:
(5)
其中τ=β·min(p), β 为一个常数,min(p)为向量p中元素的最小值。以图3中的第一幅图为例,设置β=0.3,得到结果如下,为了便于比较,我们将对应的稀疏矩阵E进行转置并绘图放在一起。
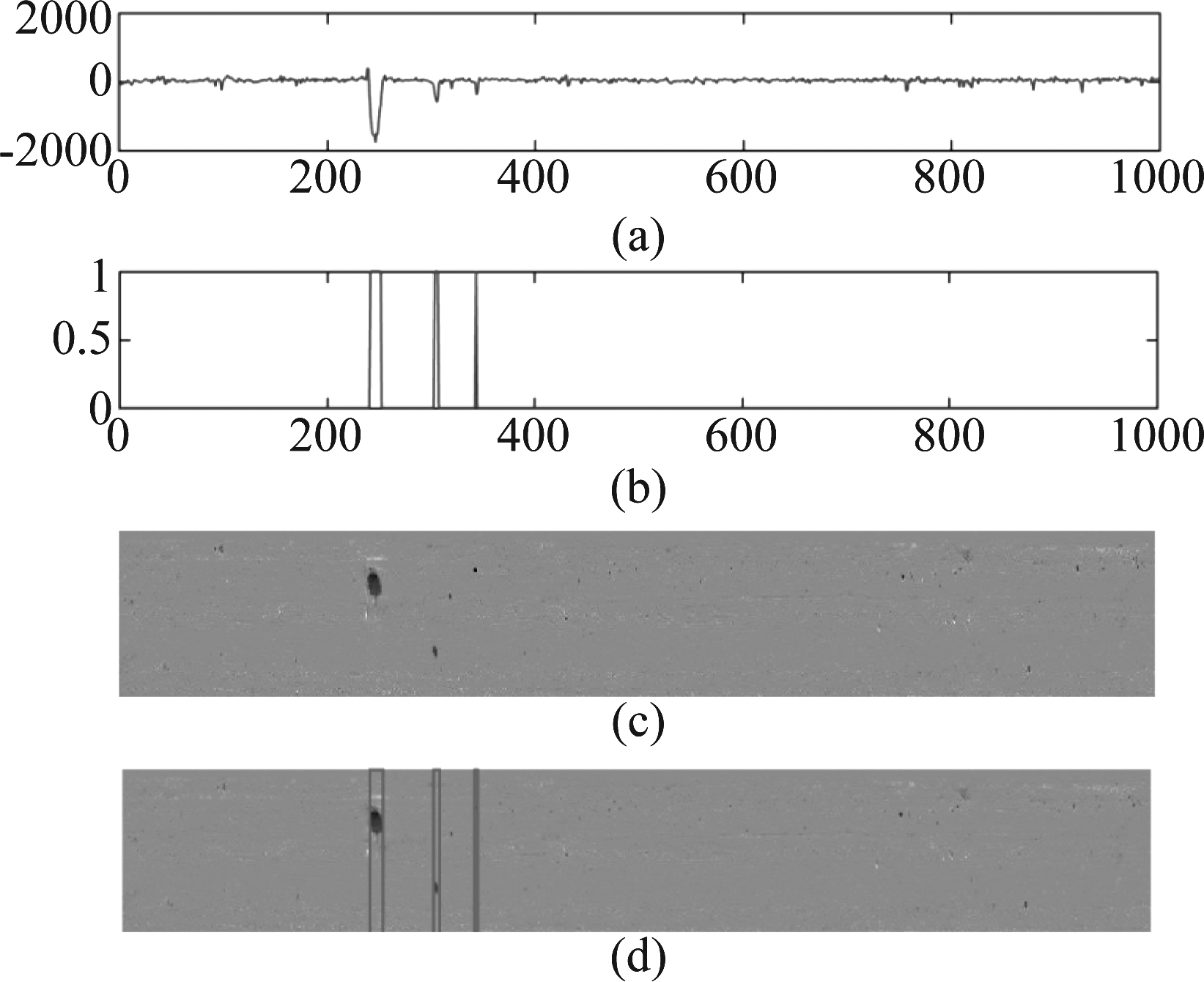
图4 稀疏矩阵竖直方向上像素值累积量二值化结果
Fig.4 The binarization results of the pixel accumulation values of the sparse matrix along the vertical direction
从上图看到,稀疏矩阵行向量像素值累积量二值化向量中,非零值区间对应着相应的缺陷区域,因此,我们只需对此二值化向量从第一个元素开始查找其每一个从0变为1的突变点,以及从1变为0的突变点,即可得到各个缺陷区域的行起始位置和行结束位置,从而确定出缺陷行坐标,根据行坐标对缺陷进行标记的结果如图4(d)所示。最后,由于铁轨图像很窄,因此确定了每一个缺陷的行坐标之后,根据行起始和结束位置截取出这一小段的图像块,一般来说,在这样的小图像块中,背景像素值变化很小,因此可以直接进行二值化操作,二值化阈值设置与式(5)相同,即可得到缺陷区域的二值图像,根据8联通区域查找二值图像中的最大联通区域即可认为是缺陷区域,最终确定缺陷在水平方向上的范围。综合上述的行坐标查找和列坐标查找结果,便可利用矩形框对缺陷区域进行标记。对图1中的4幅图像进行上述操作后,检测结果如下。

图5 图像缺陷检测定位结果,最左侧为直线
指示的小缺陷的放大图
Fig.5 Defect detection and localization results. The image at the left is an enlarged view of the small defect indicated by the straight line
从图5可以看到,上述算法已经取得了较好的缺陷检测和定位结果,尤其对于第1、2幅图,对缺陷的定位十分准确。但是,许多很细小的缺陷也被检测出来了,这些细小的缺陷可能只占据几个像素,对于铁路安全来说并不影响,在实际应用中不计入缺陷中,因此,为了降低误检率,需要去除这些细小的缺陷点。在此,根据图4中行坐标检测的结果,若某一个突变区域像素个数小于3(包含起始点和结束点),则该缺陷可认为太小予以忽略,经过这样处理后的缺陷检测定位结果如图6所示,可以看到,这样的检测结果更加清晰明确,很好的降低了误检率。

图6 去除细小缺陷之后的检测定位结果
Fig.6 Defect detection and localization results after removing tiny defects
4 算法时间复杂度分析
上述缺陷检测过程中,计算量包括三个方面:(1)IALM算法;(2)基于行像素值累积量的缺陷行坐标定位;(3)基于图像块二值化的缺陷列坐标定位。对于IALM算法,其算法复杂度为O(k*m*n*(m+n))→O(N4);对于基于行像素值累积量的缺陷行坐标定位算法,算法复杂度为O(m)。而对于基于图像块二值化的缺陷区域列坐标定位,算法复杂度为O(n)。因此整体检测过程算法复杂度为O(N4)。
5 实验结果与分析
首先,我们给出算法1的收敛曲线,对图1中4幅带缺陷的铁轨图像,利用IALM算法进行图像分解,4幅图像分别迭代了39、38、38、39次后达到预定误差阈值δ=10-7,迭代停止。不同的迭代次数及重构误差![]() 关系如下图所示,其中
关系如下图所示,其中![]() 和
和![]() 表示每次迭代过程中得到的原始图像的低秩图像和稀疏图像的逼近。
表示每次迭代过程中得到的原始图像的低秩图像和稀疏图像的逼近。
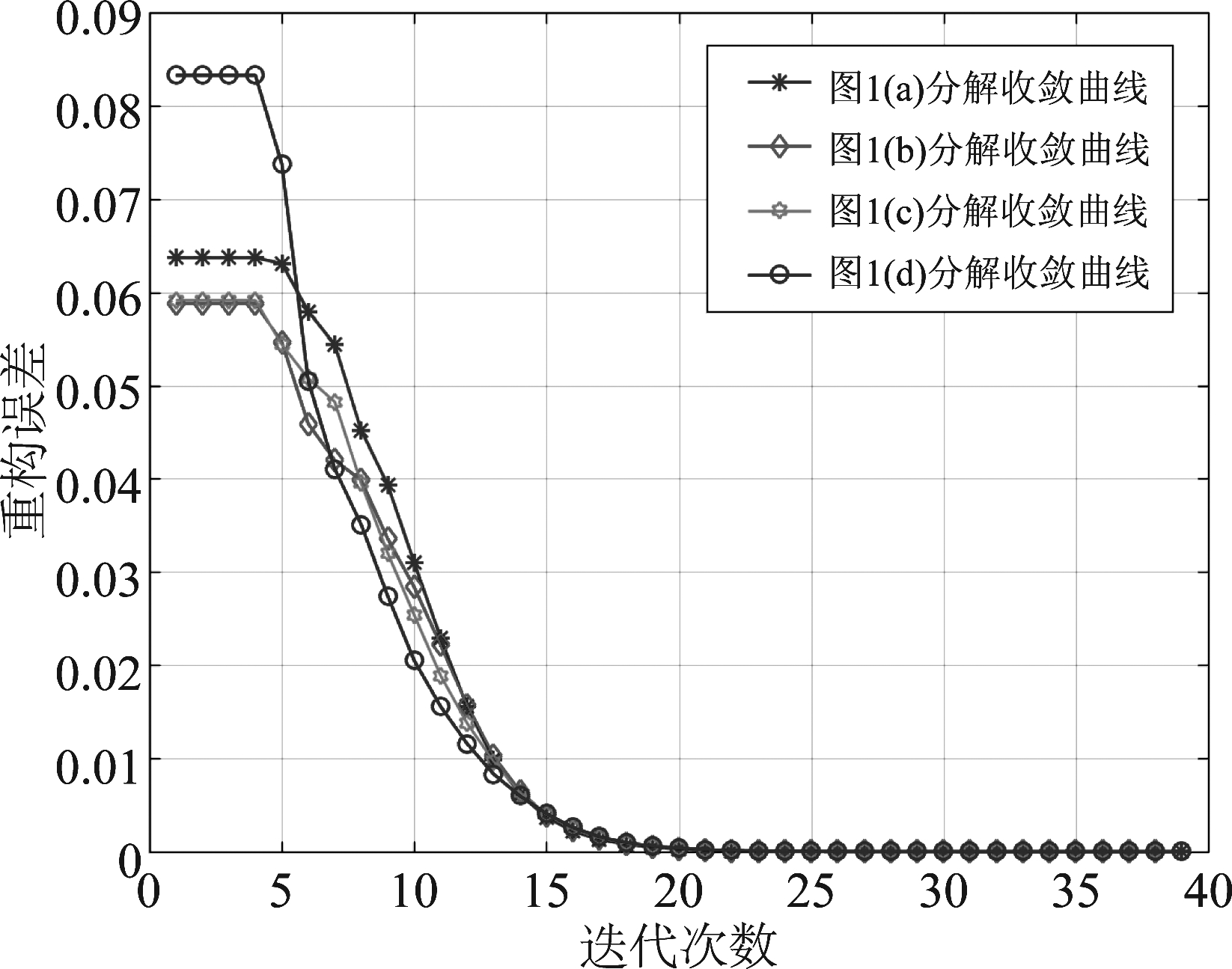
图7 图1中4幅图像用算法1进行分解得到的收敛曲线
Fig.7 Convergence curves of the images shown in Fig.1 by using Algorithm 1
为了验证本文提出算法的有效性,我们使用了两个数据库[7]进行实验验证,第一个是Type-Ⅰ RSDDs(rail surface discrete defects)数据库,其中包含了67张高铁铁轨图像;第二个是Type-Ⅱ RSDDs数据库,其中包含了128个普通/重载铁路铁轨图像。实验在Surface 3笔记本电脑上利用matlab 2016b进行编程实现。由于本文最终结果是用一个红色方框把缺陷定位标记出来,因此在进行实验结果比较时采用缺陷级的评价标准,共有三个指标,分别是准确率(Pre)、召回率及F-measure,分别定义如下:
Pre=TPd/P
Rec=TP′d/N
F=2*Pre*Rec/(Pre+Rec)
(6)
其中TPd表示正确检测到的缺陷个数,TP′d表示某一个检测到的区域映射到Ground truth上,被判定为正确检测的缺陷个数;P表示全部被正确检测到的缺陷个数;N表示ground truth中手动标记出来的缺陷总数。设第s个检测到的缺陷面积为area(s),而ground truth中某一个缺陷的面积为area(GT),则TPd定义为:
(7)
TP′d定义为:
(8)
其中,![]() 表示统计满足括号内的条件的检测到的缺陷个数。
表示统计满足括号内的条件的检测到的缺陷个数。
在本文提出的算法中,有两个参数对算法性能有着较大的影响,一个是式(5)中的常数β,另外一个是细小缺陷的评价标准。对于细小缺陷,经过咨询铁路安全专家,确定为缺陷面积不超过4个像素点的缺陷可以忽略不计。对于常数β,我们从两个数据库中各自随机挑选出20%的图像进行测试,得到β与F-measure的关系曲线如下。
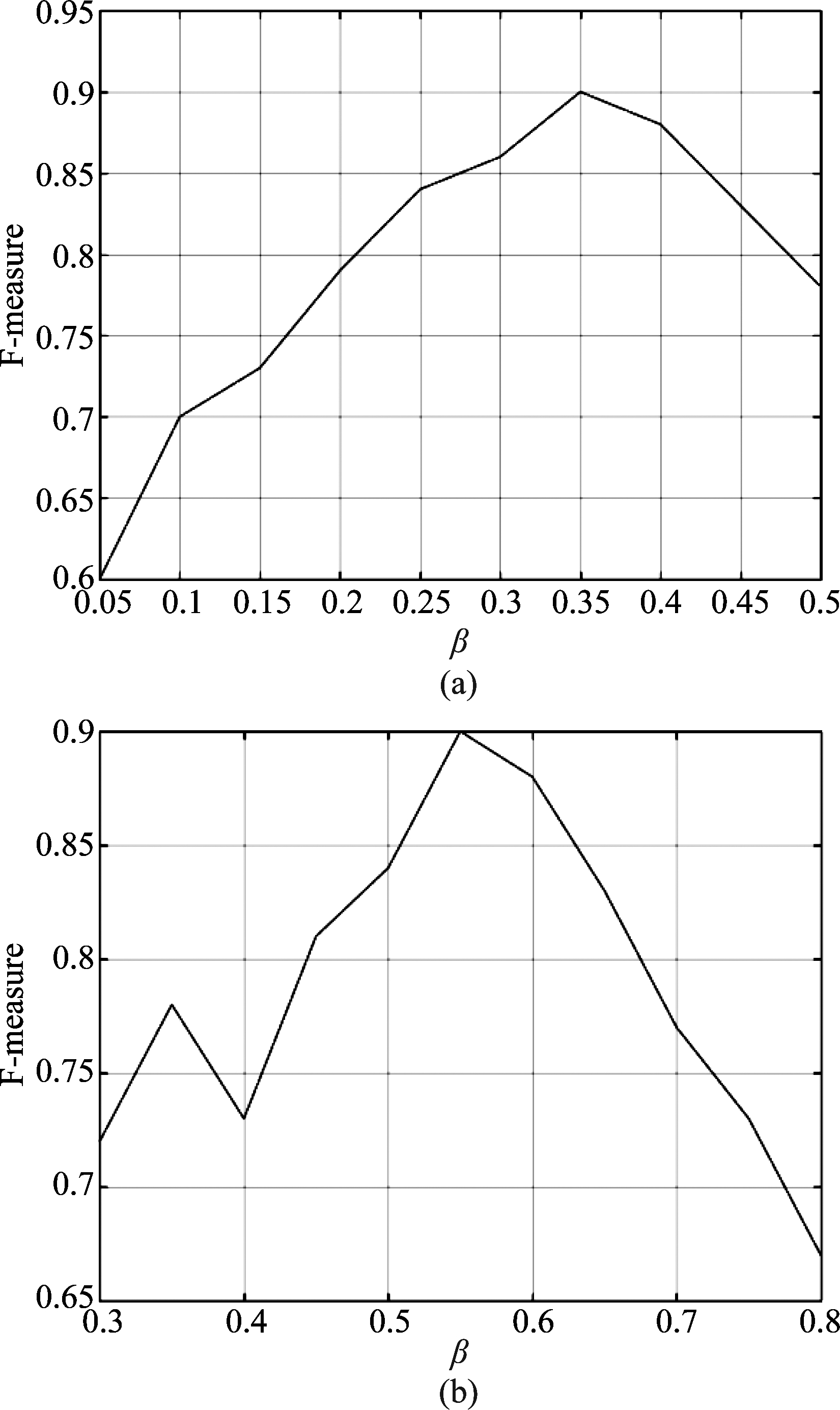
图8 β与F-measure关系曲线图. (a) Type-Ⅰ RSDDs, (b) Type-Ⅱ RSDDs
Fig.8 The relations of β and F-measure. (a) Type-Ⅰ RSDDs, (b) Type-Ⅱ RSDDs
从图8可以看到,对于Type-Ⅰ RSDDs,β=0.35比较合适,而对于Type-Ⅱ RSDDs,β=0.55得到最好的结果。根据这一参数选择,本文算法与已有文献算法的比较结果如下表1和表2所示。
从上述两个表可以看到,本文算法取得了较好的结果,在F-measure以及召回率上结果均为最好,但是准确率有所欠缺,这意味着误检率较高。为了进一步验证本文算法的有效性,我们另外使用了文献[7]以外的100张图像进行实验,由于我们没有[7-10]文献中的源程序,因此此处仅给出本文算法的结果。100张图像中,Type Ⅰ和Type Ⅱ型铁轨各有50张,对Type Ⅰ型铁轨图像,利用本文算法得到的Pre, Rec, F-measure值分别为85.23、92.55、89.41,对Type Ⅱ型的50张图像,实验结果的三个指标值分别为85.01、91.78、88.7。结果与表1、2中两个数据库的结果基本一致。另外,我们统计了程序运行时间,一幅图像从读入到定位出缺陷区域坐标,在matlab中程序运行平均时间为1.44 s。为了更加直观的展示实验结果,图9和10中展示了对Type-Ⅰ和Type-Ⅱ RSDDs数据库中一些图像的缺陷检测结果。可以看到,我们的算法在缺陷定位方面具有较好的效果。
表1 Type-Ⅰ RSDDs数据库上缺陷检测结果比较
Tab.1 The comparison of defect detection results on the Type-Ⅰ RSDDs dataset
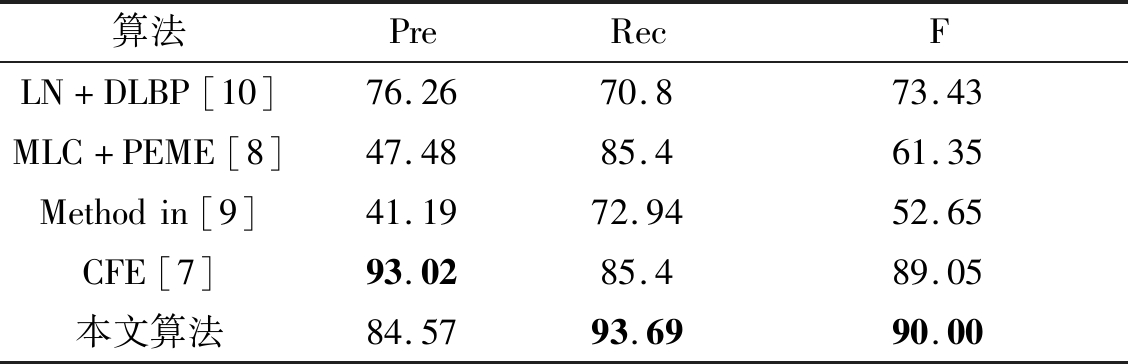
算法PreRecFLN+DLBP[10]76.2670.873.43MLC+PEME[8]47.4885.461.35Methodin[9]41.1972.9452.65CFE[7]93.0285.489.05本文算法84.5793.6990.00
表2 Type-Ⅱ RSDDs数据库上缺陷检测结果比较
Tab.2 The comparison of defect detection results on the Type-Ⅱ RSDDs dataset
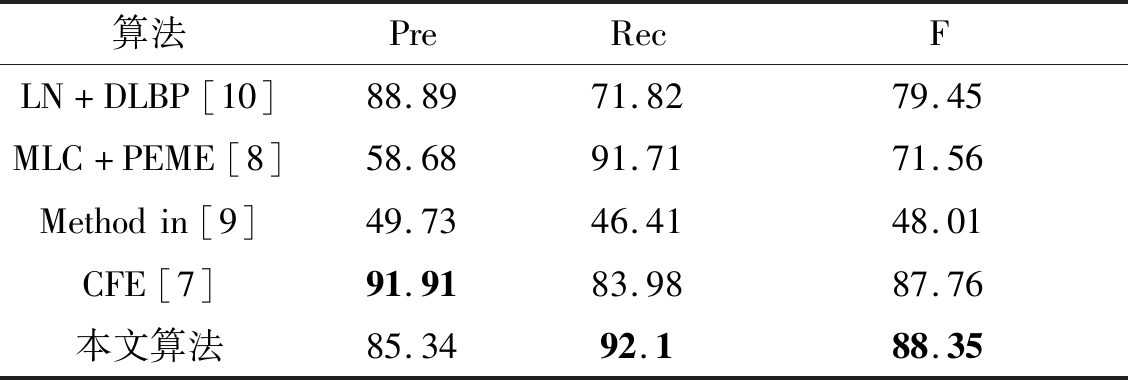
算法PreRecFLN+DLBP[10]88.8971.8279.45MLC+PEME[8]58.6891.7171.56Methodin[9]49.7346.4148.01CFE[7]91.9183.9887.76本文算法85.3492.188.35

图9 不同方法在Type-Ⅰ RSDDs数据库上缺陷
检测结果.(a) 原始图像中的缺陷部位,(b) 人工标注
基准,(c) LN+DLBP,(d) MLC+PEME,(e) [9]中
算法结果,(f) CFE,(g) 本文算法结果 Fig.9 Defect detection results of different method on the Type-Ⅰ RSDDs dataset. (a) Defective part in the original image, (b) Ground truth, (c) LN+DLBP, (d) MLC+PEME, (e) Method in [9], (f) CFE, (g) The result obtained by our method

图10 不同方法在Type-Ⅱ RSDDs数据库上
缺陷检测结果.(a) 原始图像中的缺陷部位,
(b) 人工标注基准,(c) LN+DLBP,(d) MLC+PEME,
(e) [9]中算法结果,(f) CFE,(g) 本文算法结果
Fig.10 Defect detection results of different method on the Type-Ⅱ RSDDs dataset. (a) Defective part in the original image, (b) Ground truth, (c) LN+DLBP, (d) MLC+PEME, (e) Method in [9], (f) CFE, (g) The result obtained by our method
6 结论
在本文中,基于铁轨表面图像具有纵向规律性条纹的特点,将铁轨表面缺陷检测问题转化为低秩矩阵分解问题,提出利用鲁棒主成分分析方法对原始缺陷图像进行低秩背景和缺陷前景图像的分离;其次,提出通过计算前景稀疏缺陷图像在竖直方向上的像素值累积量,然后通过阈值判断实现对缺陷的检测和定位,实验结果表明,与已有算法相比较,本文算法取得了较好的缺陷检测结果。
[1] 许鹏, 朱晨露, 徐中行, 等. 基于差分涡流检测的铁轨裂纹特征识别方法[J]. 无损检测, 2018, 40(12): 7-11.
Xu Peng, Zhu Chenlu, Xu Zhongxing, et al. Rail Crack Identification Method based on Differential Eddy Current Testing[J]. Nondestructive Detection, 2018, 40(12): 7-11.(in Chinese)
[2] 戴鹏, 王胜春, 杜馨瑜, 等. 基于半监督深度学习的无砟轨道扣件缺陷图像识别方法[J]. 中国铁道科学, 2018, 39(4): 45-51.
Dai Peng, Wang Shengchun, Du Xinyu, et al. Image recognition Method for the Fastener Defect of Ballastless Track based on Semi-Supervised Deep Learning[J]. China Railway Science, 2018, 39(4): 45-51.(in Chinese)
[3] 刘孟轲, 吴洋, 王逊. 基于卷积神经网络的轨道表面缺陷检测技术实现[J]. 现代计算机, 2017, 10(中): 65- 69.
Liu Mengke, Wu Yang, Wang Xun. Implementation of Track Surface Defect Inspection Based on Convolutional Neural Network[J]. Modern Computer, 2017, 10(Middle): 65- 69.(in Chinese)
[4] 茅正冲, 邬锋. 基于图像传感器的铁轨表面缺陷视觉检测算法[J]. 传感器与微系统, 2015, 34(9): 141-144.
Mao Zhengchong, Wu Feng. Visual Detection Algorithm for Rail Surface Defects based on Image Sensor[J]. Transducer and Microsystem Technologies, 2015, 34(9): 141-144.(in Chinese)
[5] 刘雄祥. 基于卷积神经网络的铁轨表面缺陷识别研究[D]. 西南科技大学硕士论文, 2018.
Liu Xiongxiang. Research on Rail Surface Defect Recognition based on Convolutional Neural Network[D]. Thesis for Master Degree of the Southwest University of Science and Technology, 2018.(in Chinese)
[6] 宋亚帆, 潘迪夫, 韩锟. 复杂环境下基于视觉显著性特征的铁轨识别方法[J]. 铁道科学与工程学报, 2018, 15(4): 57- 65.
Song Yafan, Pan Difu, Han Kun. Track Detection Approach in Complex Environment based on Saliency Features[J]. Journal of Railway Science and Engineering, 2018, 15(4): 57- 65.(in Chinese)
[7] Gan Jinrui, Li Qingyong, Wang Jianzhu, et al. A Hierarchical Extractor-Based Visual Rail Surface Inspection System[J]. IEEE Sensors Journal, 2017, 17(23): 7935-7944.
[8] Li Qingyong, Ren Shengwei. A visual detection system for rail surface defects[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C(Applications and Reviews), 2012, 42(6): 1531-1542.
[9] He Zhendong, Wang Yaonan, Yin Feng, et al. Surface Defect Detection for High-speed Rails Using an Inverse P-M Diffusion Model[J]. Sensor Review, 2016, 36(1): 86-97.
[10] Li Qingyong, Ren Shengwei. A Real-Time Visual Inspection System for Discrete Surface Defects of Rail Heads[J]. IEEE Transactions on Instrumentation & Measurement, 2012, 61(8): 2189-2199.
[11] 邬锋, 茅正冲. 铁轨表面缺陷图像增强与分割算法[J]. 计算机仿真, 2015, 32(10): 159-162.
Wu Feng, Mao Zhengchong. Enhancement and Segmentation Algorithm for Rail Surface Defects Image[J]. Computer Simulation, 2015, 32(10): 159-162.(in Chinese)
[12] 王海涛, 甄理, 杨春霞, 等. 基于计算机视觉的铁轨表面缺陷检测系统[J]. 无损检测, 2011, 33(11): 38- 41.
Wang Haitao, Zhen Li, Yang Chunxia, et al. Rail Surface Defects Dection System based on Computer Vision Technology[J].Nondestructive Detection, 2011, 33(11): 38- 41.(in Chinese)
[13] Cand`es E J, Li Xiaodong, Ma Yi, et al. Robust Principal Component Analysis?[J]. Journal of the ACM, 2011, 58(3): 1-37.
[14] Kwak N. Principal Component Analysis based on L1-norm Maximization[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(9): 1672-1680.
[15] Markopoulos P P, Karystinos G N, Pados D A. Optimal Algorithms for L1-subspace Signal Processing[J]. IEEE Transactions on Signal Processing, 2014, 62(19): 5046-5058.
[16] Ye Jieping. Generalized low rank approximations of matrices[J]. Machine Learning, 2005, 61(1-3): 167-191.
[17] Shi Jiarong, Yang Wei, Zheng Xiuyun. Robust Generalized Low Rank Approximations of Matrices[J]. PLoS One, 2015, 10(9): Art. no. e0138028.
[18] Wang Hengyou, Cen Yigang, He Zhihai, et al. Robust Generalized Low-Rank Decomposition of Multi-matrices for Image Recovery[J]. IEEE Transactions on Multimedia, 2017, 9(5): 969-983.
[19] Wang Hengyou, Cen Yigang, He Zhihai, et al. Reweighted Low-Rank Matrix Analysis With Structural Smoothness for Image Denoising[J]. IEEE Transactions on Image Processing, 2018, 27(4): 1777-1792.
[20] Cen Yigang, Zhao Ruizhen, Cen Lihui, et al. Defect Inspection for TFT-LCD Images based on the Low-rank Matrix Reconstruction[J]. Neurocomputing, 2015, 149: 1206-1215.
[21] 王辉, 孙洪. 鲁棒主成分分析的铝箔表面缺陷检测方法[J]. 信号处理, 2017, 33(4): 577-582.
Wang Hui, Sun Hong. Robust Principal Component Analysis for Aluminum Foil Surface Defects Detection[J]. Journal of Signal Processing, 2017, 33(4): 577-582.(in Chinese)
[22] 冯奇, 黄建军, 张源, 等. LCD 缺陷检测系统的图像压缩感知方法[J]. 信号处理, 2018, 34(1): 72- 80.
Feng Qi, Huang Jianjun, Zhang Yuan, et al, An Image Compressive Sensing Method for LCD Mura Detection System[J]. Journal of Signal Processing, 2018, 34(1): 72- 80.(in Chinese)
[23] Li Peng, Liang Junli, Shen Xubang, et al, Textile Fabric Defect Detection based on Low-rank Representation[J]. Multimedia Tools and Applications, 2017(3): 1-26.
[24] Cao Junjie, Wang Nannan, Zhang Jie, et al. Detection of Varied Defects in Diverse Fabric Images via Modified RPCA with Noise Term and Defect Prior[J]. International Journal of Clothing Science and Technology, 2016, 28(4): 516-529.
[25] Zhang Duo, Gao Guangshuai, Li Chunlei. Fabric Defect Detection Algorithm based on Gabor Filter and Low-rank Decomposition[C]∥Eighth International Conference on Digital Image Processing. International Society for Optics and Photonics, 2016.
[26] Wright J, Peng Yigang, Ma Yi, et al. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-rank Matrices by Convex Optimization[C]∥Advances in Neural Information Processing Systems, 2009, 3.
[27] Lin Zhouchen, Chen Minming, Ma Yi. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices[EB/OL]. Eprint Arxiv, 2010, 9.

