1 引言
CNN深度神经网络可分为两部分,一是卷积层,主要作用是特征提取与抽象化;二是全连接层,主要作用是在特征空间的分类。其中卷积的过程可以看成是卷积核的图像模式与被分类图像的图像模式的匹配滤波的过程。对于特定的图像分类来说,如果训练后的卷积核能表征待分类图像特有的局部几何特性,则这些几何特性就更容易被检测出来。
在CNN深度神经网络中,每个卷积层是由多个卷积核组成的子网络。卷积层之间是层层递进的关系,前一层子网络提取特征的质量会影响后一层子网络对特征抽象的质量。其中第一层卷积核子网络对对整个网络的全局优化尤其重要。另外CNN卷积神经网络是一个非线性映射优化训练过程与初始条件有较大的关系。因此在CNN神经网络训练中,卷积核初始化是非常重要的。针对深度神经网络的训练,一些研究人员提出了很多针对性的训练方法[1-10,14-16],其中有对网络权值初始化方法的研究[1-4,6-7,8,15],有些是对初始化后的权值如何约束其分布的研究[5-6,8,10,16]。
当前最为常用的初始化方法是Xavier[1],卷积核权值为均匀分布,值的范围由所在层的输入维度n和输出维度m决定,但因为Xavier推导过程中的假设条件之一是激活函数是线性的,不适用于ReLU等非线性激活函数。于是有学者针对ReLU激活函数适用的问题,在Xavier基础上的提出了改进发方法MSRA[2],卷积核初始后是一个均值为0方差为2/n的高斯分布。OrthoNorm[13]为一种正交矩阵初始化方法,比近似正交的高斯噪声更好,同时该方法也适用于非线性网络。LSUV[6]的方法将正交初始化扩展到迭代过程,首先使用单位方差的高斯噪声替代权值,然后将它们分解为具有QR或SVD分解的标准正交基,并使用其中一个分量替换权值。
Xavier方法中权值初始化的范围由输入和输出神经元的数量自动决定,能在一定程度上解决超梯度弥散的问题,使得信号在网络中可以传递得更深。Xavier和MSRA初始化方法可以保证每层神经元输入输出方差一致,服从相同的分布,可以避免后层激活函数的输出值趋向于0。在均匀分布或高斯分布等初始化条件下,当网络很深时,会产生与深度无关的学习速度的延迟,通过将权重矩阵初始化为正交的方法,可以解决这一问题。LSUV初始化方法中,它不仅利用了正交性,而且还利用了每层输出的单位方差。
上述初始化方法都有较好的适用性,对应的网络针对不同数据集都能够达到一个较好的结果。但是在网络训练的过程中,通过各种初始化方法的卷积核与训练样本是相互独立的,卷积核与训练图像样本中具有代表性的局部模式是一个低概率的匹配事件,只有在通过多次迭代训练后,卷积核才能较好的与样本中的局部模式匹配。而对于一个特定的数据集,可以通过提取典型样本图像中具有代表性的局部模式作为初始化卷积核,使得网络在开始训练时,卷积核即可利用匹配滤波较好提取图像中的局部模式,能够使网络训练以较大的概率在聚集收敛域附近,则能够使网络快速进入全局最优状态,从而更有利于网络的最终判别精度。
本文通过提取典型图像样本中局部模式生成与之相关的候选卷积核。再用卷积核对CNN网络第一层进行初始化,使得卷积网络中第一层卷积核与训练样本中具有代表性的局部模式特征在一定程度上存在匹配的关系,根据卷积理论可知该卷积子网络提权样本特征的能力自然更强。本文主要贡献:(1)首次提出从训练样本中提取卷积核的方法。卷积核与训练样本具有内在的关联,与样本中的典型局部模式是匹配的,在网络开始训练之前,卷积核能够在一定程度上提取较好的样本特征,目前并没有发现使用类似方法提取卷积核的相关文献;(2)提出了一种局部模式子图拓扑结构相似性度量的方法,以连通分量拓扑属性为依据对子图进行分类,对相同拓扑性质结构的子图进行势函数聚类获取样本图像中的典型局部模式子图集合;(3)该卷积核子网络在网络优化空间上具有导向性,能够加速网络收敛、使得训练时间更短,并且在一定程度上提高分类精度。
2 本文方法的基本思想
根据卷积公式(1)我们可知,卷积的过程实质上就是滤波,特征的提取则可看成是匹配滤波,因此在CNN网络训练中权值矩阵与训练样本关联越大,输出就越强,特征提取的效果就越好。匹配滤波可看成是双方面的事情,要求滤波器和样本中的结构特征在形状结构上有较好的匹配度,才能起到较好的反应。
(1)
对训练样本中同一类别集合来说,同类目标样本的特征具有较大相似性,因此从同类样本中随机抽取部分图片提取出来的典型局部特征可在一定程度上代表本类样本的主要特征。对训练样本集合的每个子集进行处理,随机挑选部分图像构造典型图像子集;对图像进行分块处理,构造出候选卷积核局部模式子图集合;对集合中子图进行拓扑特征描述,提取子图的拓扑特征并进行粗分类及筛选获得同拓扑结构卷积核局部模式子图集合;对同拓扑结构子图进行势函数聚类,获得代表该类拓扑结构的典型局部模式子图集合。最后挑选出与CNN网络卷积核个数匹配的卷积核。整个流程图如图1。
图1 卷积核提取流程图
Fig.1 Convolution kernel extraction flow chart
3 卷积核初始化方法
3.1 由已标注样本图像构造候选卷积核集合
设已标注训练样本集合为T={W1,…,WC},共C类样本子集。对每类样本子集有
每类样本子集包含n张图片。在样本子集中挑选图像动态范围和图像熵均高于均值的图片作为典型图像进行候选操作。动态范围相对较大的图像其对比度相对更好,熵表示图像中平均信息量的多少。对任意一张图片可分别求得其动态范围和熵。设图片的大小为N×N,动态范围如式(2)
k=1,…,n,x=0,…,N-1,y=0,…,N-1
(2)
其中
为图像
的最大像素值,
为图像
的最小像素值。则样本子集的平均动态范围如式(3)
(3)
图片的一维熵如式(4)
(4)
其中ho表示某个灰度在该图像中出现的概率,则样本子集的平均熵如式(5)
(5)
对样本子集进行筛选,挑选出动态范围和熵都大于对应的平均值,筛选如式(6)
(6)
筛选后获得样本集G(Yd)中图片像素的动态范围和熵都大于平均值,可认为其图片中目标的动态范围较大且信息量也较为丰富。从子集G(Yd)中随机挑选m张图片,其特征即可代表该类样本的主要特征,设对G(Yd)子集随机挑选的图片作为候选集合J(Yd),则有
(7)
对候选集合J(Yd)中图片
进行归一化处理,如式(8)
k=1,…,m;x=0,…,N-1;y=0,…,N-1
(8)
归一化后的样本图像
像素值范围为[0,1],归一化后的候选图片集合如式(9)
(9)
设卷积核大小为a*a,按照卷积核大小对图片进行切块处理,步长设为1时,大小为N×N的图片可切成子块数量V=(N-a+1)(N-a+1),则归一化后的子块集合如式(10)
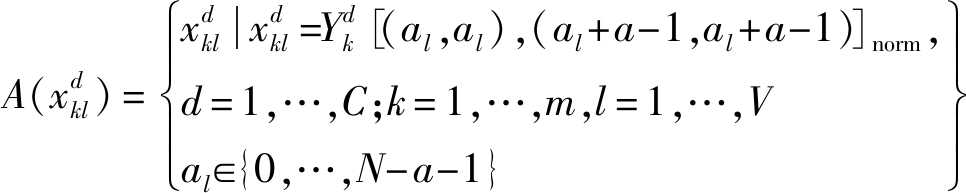
(10)
表示第d类样本子集的第k张归一化后的图片,[(al,al),(al+a-1,al+a-1)]为图片中子块的对角坐标,表示中子块四个角的坐标{(al,al),(al,al+a-1),(al+a-1,al),(al+a-1,al+a-1)}。
3.2 候选卷积核集合的拓扑粗分类方法
滤波器提取特征能力由其形状结构决定,而权值只是在某一定程度上影响滤波的性能,但并不能改变滤波器的功能,通过符号化处理能够在一定程度上清晰滤波器的形状结构,泛化滤波器的性能。因此先对子块模板进行去均值化处理,再进行符号化处理。设子块模板
的均值为
子块去均值化处理如式(11)
(11)
中的值是对应范围为(-1,1),对应的子块去均值化处理集合为
对子图模板
进行符号化处理得到
如式(12)
(12)
δt是阈值,符号化后子图对应的集合为
令符号化子图
对应的连通域数量为
卷积核提取特征跟其形状结构密切关联,从其拓扑结构属性来看,连通域个数越多,其提取的特征个数越多。从实际存在的卷积核特点来看,连通分量为0的卷积核可认为是平凡解,不具有提取特征的能力,连通分量大于5个的卷积核一般可认为是以提取纹理特征为主,这类以提取纹理特征的卷积核其形状结构相对更为平凡,没有明显的特点,我们更在意的是卷积核形状结构的不一样,所以主要考虑的是连通域数量大于0且小于5的卷积核,由式(13)可得
(13)
z为连通分量数,b为当前连通分量集合元素的个数。集合
与符号化后的子块集合
及去均值化子块集合
的子块均有一个对应关系。
3.3 基于势函数聚类的候选卷积核生成
根据同类连通域滤波器在不同区域的势函数[17]度量进行分类。在一个集合样本中,每个点的势值可表示其所在空间样本密度,势值越大则该样本所处空间密度越大;反之,势值越小则该样本所处空间密度则越小。同样,势值相同的点在空间中的位置是重合的,即它们对应的滤波器形状结构也一样;势值越相近,对应的点在空间中位置也越接近,则表示对应的滤波器形状结构也相近。因此势值最大点对应的滤波器形状结构可以在一定程度上代表其附近点对应的滤波器形状结构。这种势值的度量考虑到样本之间的距离信息,可以将训练样本空间的全局分布信息有效利用起来。
给定样本集合,通过统计样本空间中每个样本点的势值,即可建立起集合中每个样本的势值度量,把子块
转换成一个多维行向量
则有,对于同类集合中的一对向量
作用势计算如(14)
(14)
其中s,t=1,…,b,s≠t。在样本空间中,
采用欧式距离度量,当
时,
值最大;当
之间的距离无穷大时,的值趋于零;Λ是常数,为距离加权因子,用来控制势函数的衰减速度。对于向量
将同类集合fz中其他所有向量对
的作用势进行累加,可得:
(15)
其中b为fz+z-中样本的个数,由此可得出同类集合fz中向量对所有其他向量作用势累加的集合ρw
(16)
对于同类集合fz中样本点的分布密集程度可在ρw中体现出来,密集度越高,对应样本点作用势的累加和就越大,即可把高密度区域对应的样本向量分为一类。则集合ρw中最大势如式(17)
ρwmax=max{ρw}
(17)
通过选择作用势最大值ρwmax对应的样本向量点作为高斯核函数中心,标准差为σk,通过更新公式来选择每次更新后的最大势值,更新公式为(18)
s=1,2,…,b,s≠t
(18)
上式中,
代表fz更新后的样本势值。根据高斯函数的分布特点,当势累加集合ρw中样本
距离中心
较近时,其势值被抵消较大;当距离较远时,其势值被抵消的较小。标准差σq表示最大势函数对应该样本的代表范围,σq值越大,则表示该样本代表的范围越大,最终聚类的类别会更少;σq值越小则表示该样本代表的范围越小,最终聚类的类别会更多。通过更新公式不断迭代,从而获得所有次迭代时最大势值列表Γz
(19)
其中g为迭代次数,由最大势值列表Γz可知对应子块符号化后的集合Z(fΓz)和原始子块去均值化的集合B(fΓz)。当满足下式时,则停止更新
(20)
这里δρ为阈值,是一个相对值,值的大小为迭代前最大势值的千分之一。
3.4 训练CNN网络的卷积核初始化
集合Z(fΓz)中的子块是为了更好提取拓扑特征而进行了符号化的数值,为了使CNN中的卷积核与样本更匹配,所以我们选择的是与Z(fΓz)对应的去均值化集合B(fΓz)作为初始化卷积核。势函数聚类是一种自动聚类的方法,只能通过σk的大小来选择样本代表的范围,最终滤波器个数并不是确定的,但CNN的首层卷积核个数是确定的,实际上去均值化集合B(fΓz)的数量要远多于CNN首层的卷积核个数,为了使得提取从样本子块中提取的卷积核数量与网络首层卷积核数量一致。还需要对去均值化的子块集合B(fΓz)进行挑选,设集合B(fΓz)中的子块总的数量为Bm,gz为当前类别z的子块数量,则有
(21)
当前CNN网络首层需要的卷积核数量为B0,在进行势函数聚类的过程中通过对σk的大小进行调整,使得各类别最大势个数的总和如式(22)
(22)
所以对去均值化的子块集合B(fΓz)中的每个子类,我们只需要取前
数量的子块组成新的卷积核集合B(fτz)即可,其中,
⊂
为用于初始化CNN首层的卷积核集合。
4 实验及分析
本文实验是在PyTorch框架上完成,使用的GPU为GTX1080,实验使用的网络为DenseNet[11],使用的公开数据集为CIFAR-10,CIFAR-100,SVHN,分别对比的初始化方法为Xavier[1]、MSRA[2]、OrthoNorm[13]、LSUV[6]。
4.1 参数选择及训练
对样本子集进行挑选时,采取的方法是每类样本随机挑选m=10张图片,在对子块进行符号化处理时,阈值δt=0.01,在进行卷积核子图的拓扑特征判断连通分量时,选取的是8邻域的方法,在基于拓扑划分的粗分类及筛选时,选择的正负连通分量均不大于4,在进行势函数聚类时,阈值δρ为迭代前最大势值的千分之一。因为训练所用网络DenseNet的第一层卷积核为192个,核的大小为5×5,本文所用比较的初始化方法均在同样参数条件下进行,为保证实验的公平,本方法提取的卷积核数量也为192个,大小为5×5。
在实际训练中,按照原始初始化方式对所有层权值进行初始化,然后使用我们方法生成的卷积核改变网络第一层的权值。实验主要比较的就是替换网络第一层权值前后的结果,为保证实验的公平,除了对每种初始化方法的第一层进行了改变,其他都保证一样,训练的epoch为300。
4.2 实验结果及分析
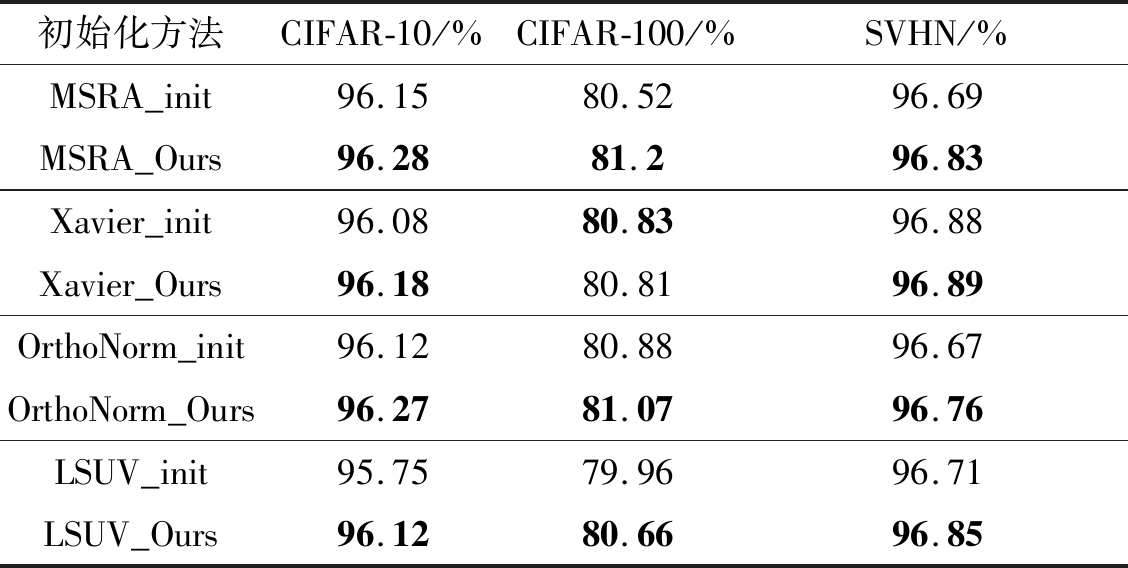
实验最终的结果如表1所示,分别给出了四组对比算法在CIFAR-10\100、SVHN数据集上的分类精度,可以看到,在对比原始初始化方法,我们的方法明显有效,适应对每种算法的改进。CIAFR-10中,我们的方法优于比较方法,最高分类精度为96.28,对应的方法是MSRA_Ours,而比较方法的分类精度为96.15。CIAFR-100数据集中,最高分类精度为81.2,对应算法为MSRA_Ours,比较方法的分类精度80.52。我们的方法有三组结果比对比方法更好,只有Xavier_Ours方法比Xavier_init方法略低。在SVHN数据集中,我们的方法均优于比较方法,最高分类精度为96.89,相应的方法是Xavier_Ours,比较方法的分类精度96.88,差别不大。总体来看,通过我们方法提取的卷积核虽然只改变了第一层权值,但最终分类精度却能明显提高,并且对所有比较方法都适用。
三个数据集CIFAR-10、CIFAR-100和SVHN训练初期结果如图2、图3和图4,图2(左)表示数据集在训练周期epoch0时四组对比方法loss相减后的趋势图,分别是我们方法训练的loss减去对应方法的loss,如式(23)
表1 四组不同初始化方法下,CIAFR-10\100、SVHN的Accuracy
Tab.1 The CIFAR-10\100, SVHN corresponds to the accuracy of four groups of different initialization methods
初始化方法CIFAR-10/%CIFAR-100/%SVHN/%MSRA_init96.1580.5296.69MSRA_Ours96.2881.296.83Xavier_init96.0880.8396.88Xavier_Ours96.1880.8196.89OrthoNorm_init96.1280.8896.67OrthoNorm_Ours96.2781.0796.76LSUV_init95.7579.9696.71LSUV_Ours96.1280.6696.85
loss_subtraction=lossmethod_ours-lossmethod_init
(23)
式中method分别为MSRA、Xavier、Orthonorm、LSUV四种方法,method_init为method原始方法直接进行初始化,method_ours为使用提取的卷积核在method_init基础上又再初始化了第一层, 结果小于0则表示我们方法训练的loss下降更快,图2(右)则是左图对应的测试精度相减后的趋势图,分别是我们方法测试的精度减去对应方法的精度,如式(24)
accuracy_subtraction=accuracymethod_ours-accuracymethod_init
(24)
式中method与式(15)一样,结果大于0则表示我们方法的精度更高。可以清楚看到,训练初期,loss相减趋势图中,均明显小于0,loss差值最小也有0.2,最大的差值平均都在0.4左右;对应的精度相减趋势图中,均明显大于0,平均优势至少都在7个百分点的精度,精度差值最大达到了17.5以上,表明即从训练开始,我们的方法收敛速度就更快,并且精度高还稳定,也就是说从训练开始即表现出了更好的优化方向。图3中,loss差值从开始几乎一样慢慢增大到0.15～0.25,差距呈加大趋势,表明我们方法在第一个训练周期收敛速度越来越快;四组分类精度差值在1～8之间,表明我们方法的分类精度在第一训练周期更高且稳定。图4中,loss差值均小于0,其中我们方法在MSRA和Xavier中收敛更快一点,在Orthonorm和LSUV中明显收敛更快;分组分类精度差值在1～9之间,表明我们方法的分类精度在第一训练周期更高且稳定。
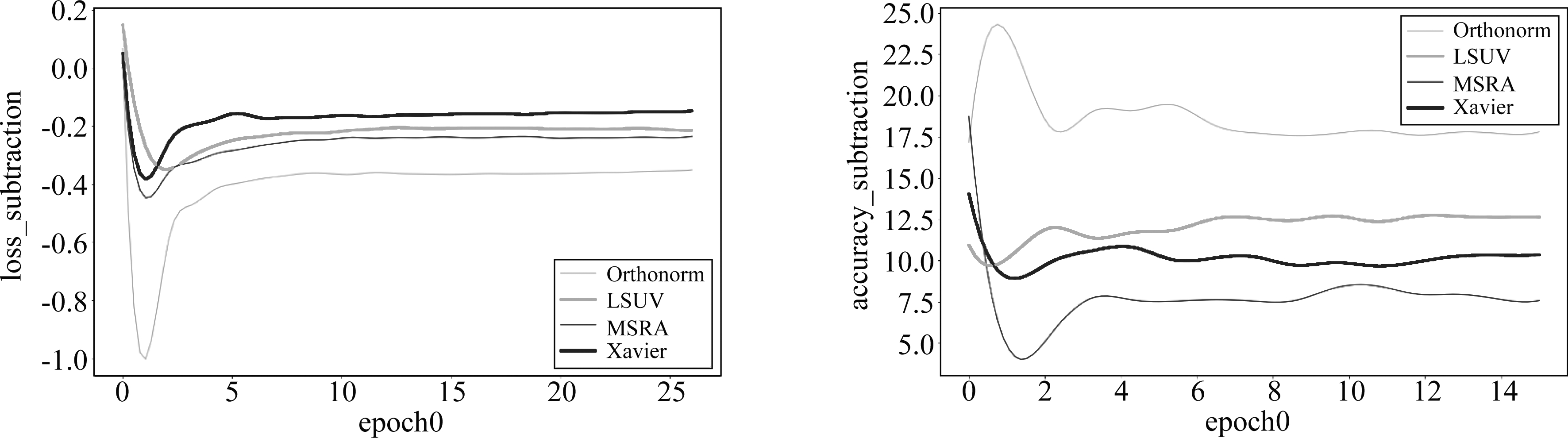
图2 四组对比算法的loss和精度相减曲线(CIFAR-10,epoch0)
Fig.2 Loss and accuracy subtraction curves of four groups of comparison algorithms(CIFAR-10,epoch0)
图3 四组对比算法的loss和精度相减曲线(CIFAR-100,epoch0)
Fig.3 Loss and accuracy subtraction curves of four groups of comparison algorithms(CIFAR-100,epoch0)
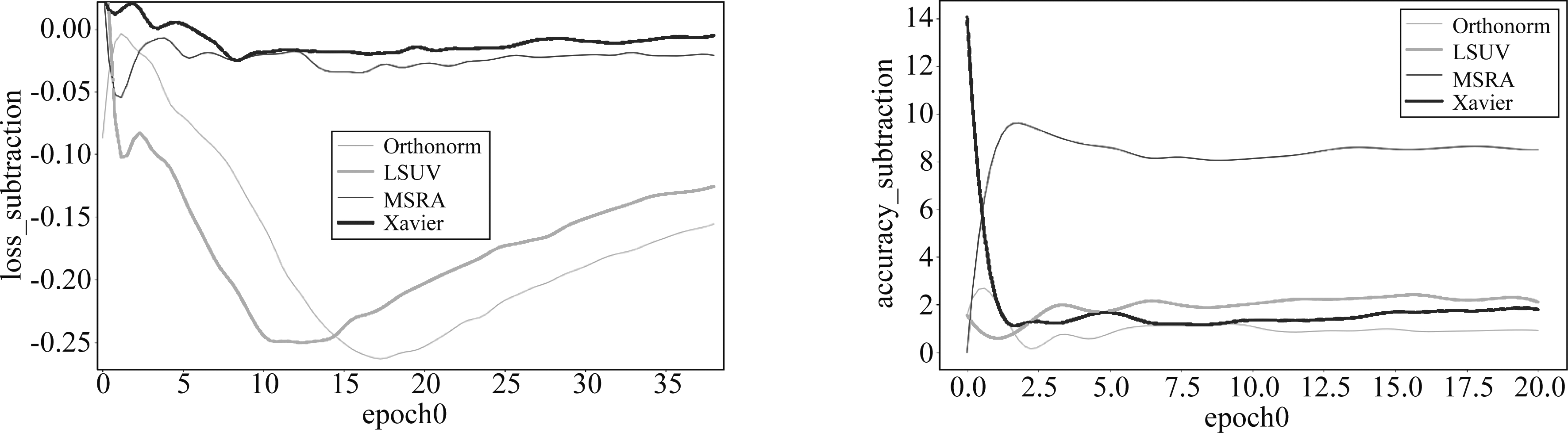
图4 四组对比算法的loss和精度相减曲线(SVHN,epoch0)
Fig.4 Loss and accuracy subtraction curves of four groups of comparison algorithms(SVHN,epoch0)
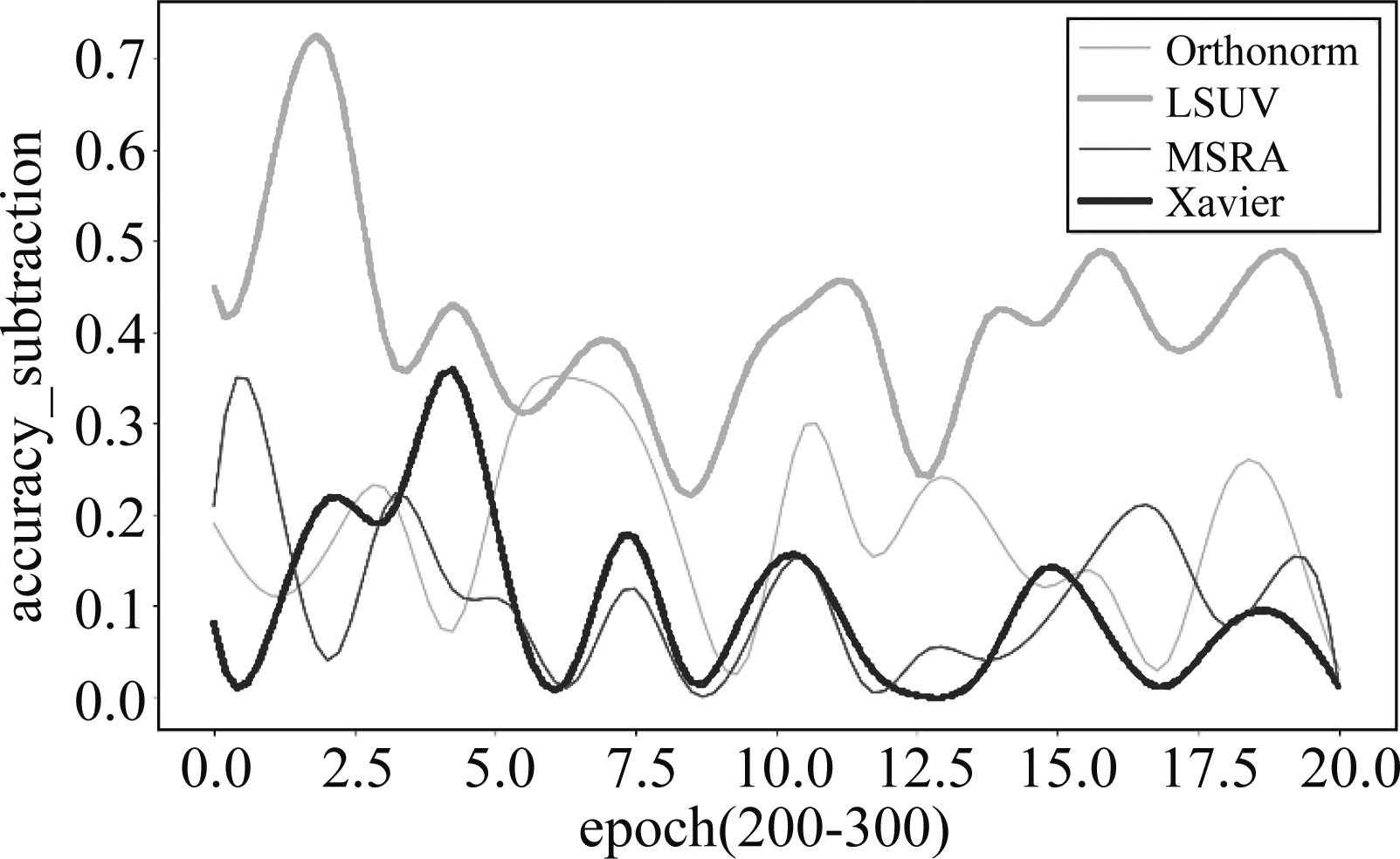
图5 四组对比算法的精度相减曲线
(CIFAR-10,epoch 200-300)
Fig.5 Accuracy subtraction curves of four groups of comparison algorithms(CIFAR-10,epoch 200-300)
三个数据集CIFAR-10、CIFAR-100和SVHN后期的精度相减结果如图5、图6和图7,公式如(16),图5表示数据集在训练周期epoch200-300时四组对比方法测试精度相减后的趋势图,结果大于0则表示我们方法的精度更高。可以清楚看到,训练后期,精度相减趋势图中,绝大部分大于0,整体趋势明显是大于0的,范围在0.05～0.5之间,即表明整个训练后期,我们的方法整体精度更好,也更稳定。图6的范围在0.1～0.9之间,表现出了明显的优势。图7的范围0～0.2,整体大于0。从这三幅图可看出,在不同的数据集上,均可明显看出我们的方法精度更高而且稳定。
一个好的网络初始权重一开始就与样本有着内在关联,能够对样本进行匹配,所以其优化方向在同一网络中也会更好。从结果可看出首层有较好的初始化能够对最终的训练结果起到一个明显的促进作用,即网络的这种优化组合处在一个较优的空间,离最优点更近,因此最终的精度也会更高。
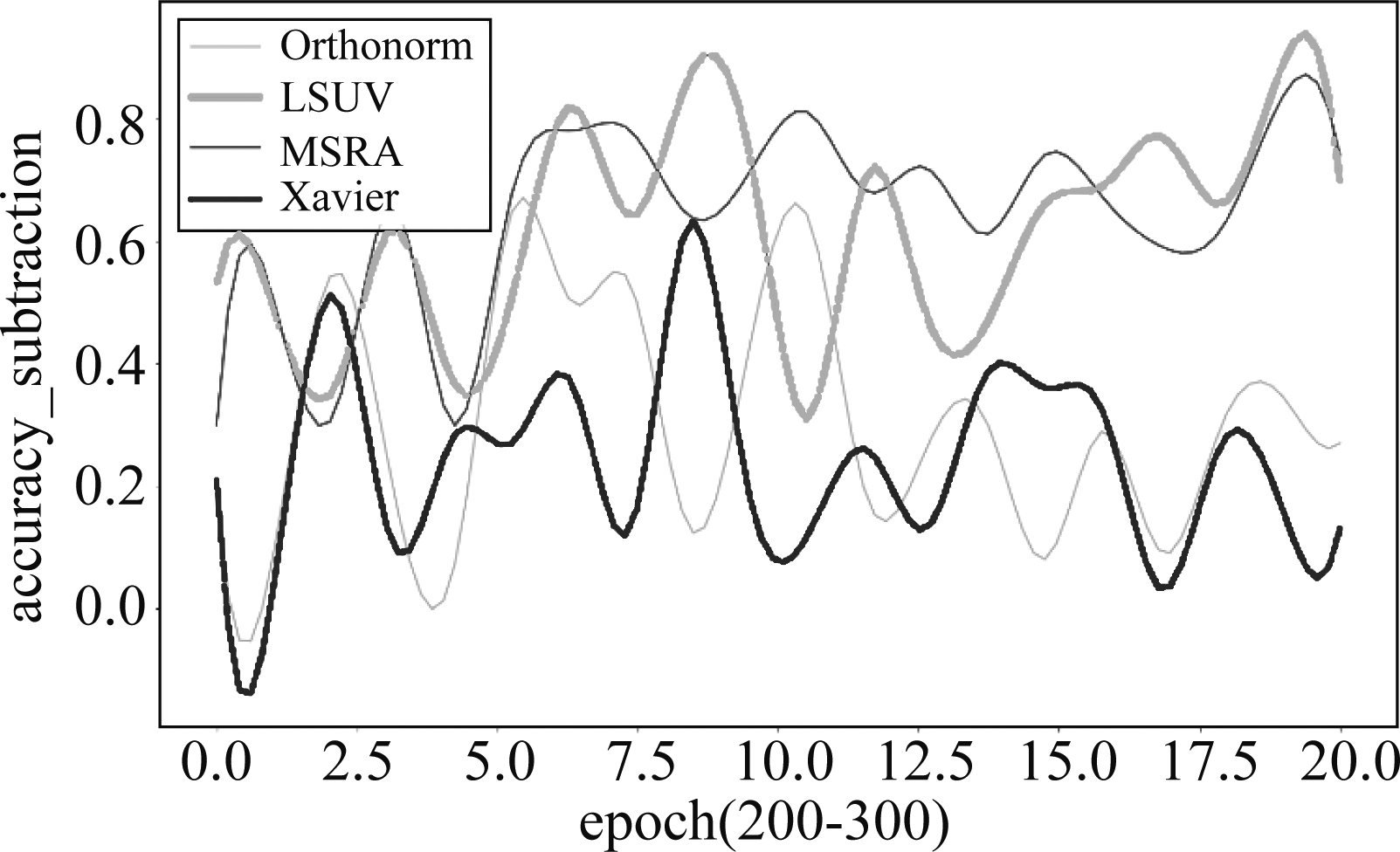
图6 四组对比算法的精度相减曲线(CIFAR-100,epoch 200-300)
Fig.6 Accuracy subtraction curves of four groups of comparison algorithms(CIFAR-100,epoch 200-300)
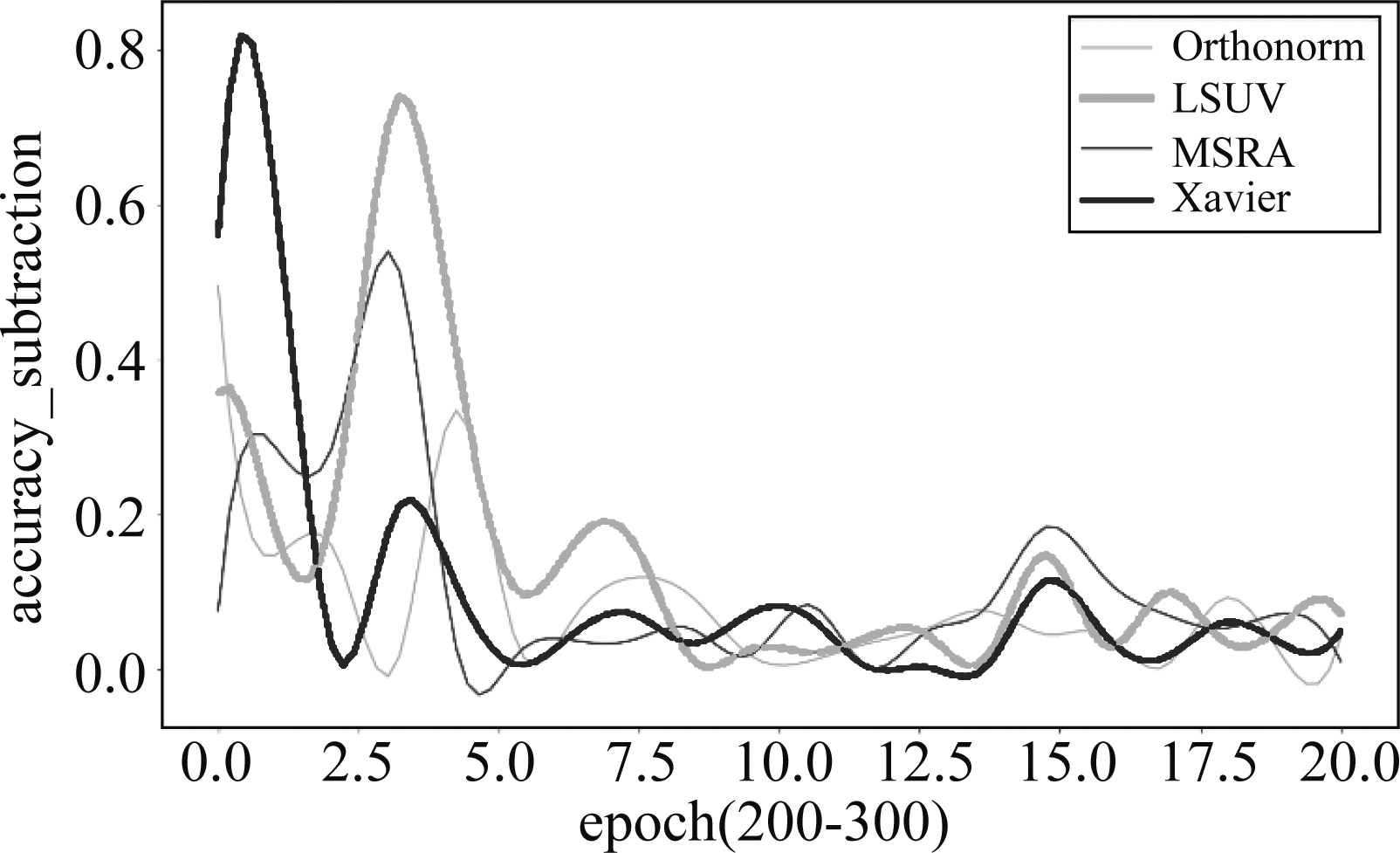
图7 四组对比算法的精度相减曲线(SVHN,epoch 200-300)
Fig.7 Accuracy subtraction curves of four groups of comparison algorithms(SVHN,epoch 200-300)
5 结论
本文采用典型样本图像中局部特征模式对应子图作为候选卷积核的方法,对CNN卷积核进行初始化。通过对图像块去均值化、符号化处理,并进行拓扑粗分类,采用势函数聚类的方法找到候选卷积核。候选卷积核源自于图像样本中的局部特征模式,样本与卷积核进行卷积的过程一定程度上可视为匹配滤波。通过在图像训练集中选取一部分典型的样本图像,并构造出与卷积核相同大小的子图作为图像局部模式矢量集合。首先对局部模式子图进行去均值化、符号化处理,并应用拓扑特性进行粗分类,采用势函数聚类的方法获取样本图像中的典型局部模式子图模式集,用它们作为CNN的初始卷积核进行训练。卷积核组成的局部特征模式的网络,在训练过程可明显提高图像样本典型特征的提取质量。实验结果表明,在同一实验条件下,对CIFAR10\100和SVHN数据集的训练中,我们方法在网络训练初期收敛速度明显更快,引导了网络的优化方向,并且分类精度也有一定程度的提高。
[1] Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[J]. Journal of Machine Learning Research, 2010: 249-256.
[2] He K, Zhang X, Ren S, et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification[J]. International Conference on Computer Vision, 2015: 1026-1034.
[3] Luan S, Chen C, Zhang B, et al. Gabor Convolutional Networks[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4357- 4366.
[4] 胡正平, 何薇, 王蒙, 等. Gabor调制的深度多层子空间人脸特征提取算法[J]. 信号处理, 2017, 33(3): 338-345.
Hu Zhengping, He Wei, Wang Meng, et al. Face Feature Extraction Algorithm Based on Deep Subspace with Gabor Filter Modulation[J]. Journal of Signal Processing, 2017, 33(3): 338-345.(in Chinese)
[5] Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[J]. International Conference on Machine Learning, 2015: 448- 456.
[6] Mishkin D, Matas J. All you need is a good init[J]. International Conference on Learning Representations, 2016: 1-13.
[7] Xie D, Xiong J, Pu S, et al. All You Need is Beyond a Good Init: Exploring Better Solution for Training Extremely Deep Convolutional Neural Networks with Orthonormality and Modulation[J]. Computer Vision and Pattern Recognition, 2017: 5075-5084.
[8] Ozay M, Okatani T. Optimization on Submanifolds of Convolution Kernels in CNNs[J]. arXiv: Computer Vision and Pattern Recognition, 2016: 1-9. http:∥arxiv.org/abs/1610.07008.
[9] Kumar S K. On weight initialization in deep neural networks[J]. arXiv: Learning, 2017: 1-9. http:∥arxiv.org/abs/1704.08863.
[10] Hendrycks D, Gimpel K. Adjusting for Dropout Variance in Batch Normalization and Weight Initialization[J]. arXiv: Learning, 2017: 1-10. http:∥arxiv.org/abs/1607.02488.
[11] Huang G, Liu Z, Der Maaten L V, et al. Densely Connected Convolutional Networks[J]. Computer Vision and Pattern Recognition, 2017: 2261-2269.
[12] He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[J]. Computer Vision and Pattern Recognition, 2016: 770-778.
[13] Saxe A M, Mcclelland J L, Ganguli S, et al. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks[J]. International Conference on Learning Representations, 2014: 1-22. http:∥arxiv.org/abs/1312.6120.
[14] Seyfioglu M S, Gurbuz S Z. Deep Neural Network Initialization Methods for Micro-Doppler Classification With Low Training Sample Support[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(12): 2462-2466.
[15] Krizhevsky A, Sutskever I, Hinton G E, et al. ImageNet Classification with Deep Convolutional Neural Networks[C]∥Neural Information Processing Systems, 2012: 1097-1105.
[16] Ba J L, Kiros J R., Hinton G E. Layer Normalization[J]. 2016: 1-14. arXiv: 1607. 06450v1.
[17] Wen H, Xie W, Pei J, et al. An incremental learning algorithm for the hybrid RBF-BP network classifier[J]. EURASIP Journal on Advances in Signal Processing, 2016: 1-15. https:∥doi.org/10.1186/s13634- 016- 0357- 8.
