1 引言
无论在军事领域还是民用领域,GNSS全球导航卫星系统,特别是全球定位系统(Global Positioning System, GPS)的应用非常广泛,而且发挥着举足轻重的作用。但是由于GPS卫星离地面很远,平均轨道高度达20200 km,卫星信号到达地面时已经非常微弱[1],非常容易受到干扰。由于GPS信号采用了扩频结构,具有一定的抗干扰能力,但是当有意或者无意的干扰信号功率很大时,会影响接收机的定位性能,甚至不能够定位[1-3]。因此对有效的抗干扰技术是GPS信号处理领域的研究热点。
由于强干扰的存在,仅凭GPS信号的扩频特性不能抑制干扰,对传统的接收机有很大的影响。当前的针对导航信号抗强干扰的方法主要有时域/频域滤波技术[4- 6]、空域滤波技术[7-11]、空时域联合滤波技术。时域/频域滤波技术利用适当的FIR或IIR滤波器在干扰频率处设置陷波实现干扰抑制,但是这种方法需要知道干扰信号的特性,当存在多个干扰时难以达到有效的干扰抑制效果。而空时域联合滤波技术往往计算复杂度高,难以满足实时性要求。利用多天线空域信号处理的方法来可以抑制窄带、宽带等不同类型的干扰,而且复杂度相比于空时联合处理的方法也低。文献[7]中提出了一种功率倒置(Power Inversion, PI)算法,此方法在约束输出功率最小的情况下得到一组阵列系数,用这组系数直接对多天线数据进行合并。文献[8]中进行了改进,针对强干扰和欺骗式干扰提出了一种级联式的抑制方法。但是这种盲波束形成方法虽然能抑制强干扰,但是也在一定程度上抑制了信号,而且没有对卫星方向进行估计,对空域信息利用的不够充分。文献[9]中提出了CLEAN算法,先利用子空间方法估计干扰空间,通过投影抑制干扰,再分别估计每颗卫星信号的来波方向,再在此基础上做波束形成,但是此方法依次对各个卫星信号的角度进行估计,相互之间影响较大,角度估计性能不高。文献[10-11]的RELAX方法有一定程度的改善,但是由于增加了迭代搜索的过程,运算复杂度更大。而且这几种方法都不能够对卫星信号来向进行实时跟踪。
基于上述的原因,本文提出了一种新的多天线抗干扰GPS接收机的设计方法,由于强干扰的存在,在捕获阶段先利用子空间方法获得干扰空间,然后将接收信号投影到与干扰正交的空间上实现干扰抑制,然后利用GPS信号的周期特性进行角度、小数倍频偏的联合估计,而且通过扩展阵元可以得到更好的估计结果。得到配对的小数倍频偏和角度后,分别对每颗卫星做波束形成,进而分别估计出整数倍频偏和时延。然后根据获得的初值,对卫星进行跟踪,本文提出的方法在增加了角度环,可以同时对卫星的角度、频偏、时延进行跟踪,相比于其他方法,在卫星角度发生变化时,不需要重新捕获,结构更加稳定。
2 信号模型
GPS接收机接收到多颗卫星信号的总和,同时还会受到干扰的影响,在接收阵列为均匀线阵时,接收到的信号可表示为:
(1)
其中:导向矢量
表示入射角度,M为阵元个数,d为阵元间距,λ表示入射信号波长。sl(t)表示卫星l的信号,L是可见卫星个数, jq(t)表示第q个干扰信号,Q是干扰源个数,n(t)表示高斯白噪声。由于GPS信号是扩频信号,可以表示为:
sl(t)=dl(t-τl)cl(t-τl)ej2πfl(t-τl)
(2)
式中,dl(t),cl(t)分别是卫星l的导航电文和C/A码,τl, fl是相应卫星的时延和多普勒频移。
3 抗干扰GPS接收机结构设计
由于卫星距离地面很远,而且信号的格式是公开的,所以很容易受到有意或者无意的干扰,本文利用多天线提供空域角度信息,然后在空域上实现干扰抑制。GPS接收机物理层信号处理主要包括两个过程:信号的捕获和卫星信号的跟踪,如图1所示。
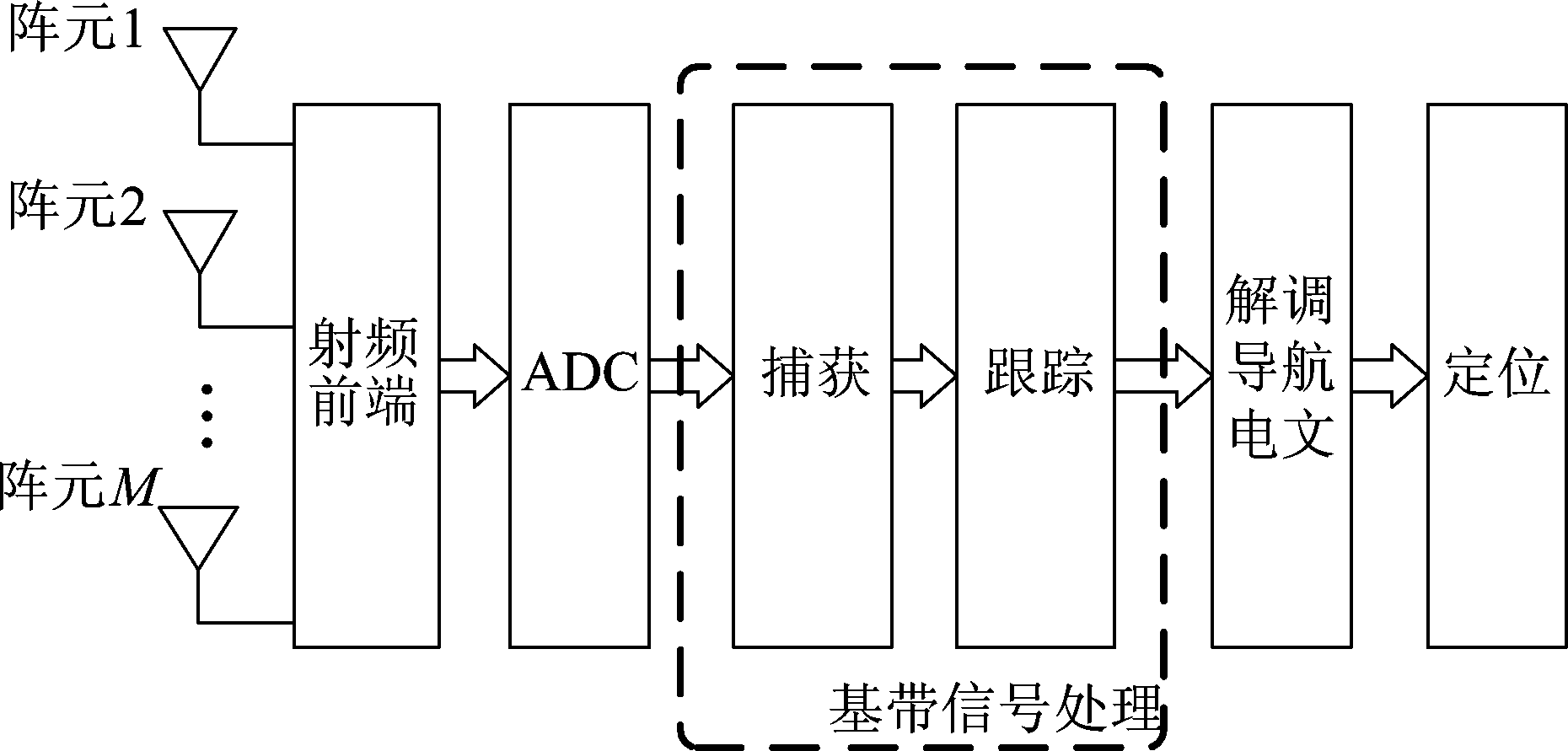
图1 GPS接收机结构
Fig.1 The structure of the GPS receiver
在处理基带信号时,不同于传统的单天线接收机只需要对多普勒频偏和码相进行估计,多天线抗干扰接收机往往需要同时获得卫星的角度信息,此信息可用于抗干扰,虽然类似于功率倒置方式的盲波束形成抗干扰方式不需要角度的先验信息,但是这类方法通常抗干扰性能较弱,并且还可能抑制信号功率,所以准确估计信号和干扰的角度有很大的益处。在这种情况下,本文分别对捕获和跟踪阶段参数估计方法进行了研究。
3.1 信号的捕获
信号捕获就是要确定当前的可见卫星,并且获得可见卫星的初始参数,主要包括码初相和载波频偏,还有信号的入射方向(DOA),本文的捕获过程参数估计的结构如图2所示,对干扰进行投影抑制后,先进行角度和小数倍频偏的联合估计,再分别对每颗卫星做波束形成,在每个通道分别估计单颗卫星的时延和整数倍频偏。
先利用GPS信号的周期性,对来波方向和小数倍频偏进行估计。由于卫星距离地面很远,解扩前信号淹没在噪声中,而干扰通常来源于地面,所以干扰信号的功率
远远大于信号功率
从式(1)的接收信号模型出发,可以计算出自相关矩阵为:
(3)
式中
为噪声功率,I表示单位矩阵。
因为干扰信号功率大,所以对自相关矩阵进行特征分解后,最大的Q个特征值对应的特征向量张成干扰空间,而由于信号功率太小,与噪声空间混杂在一起。这样,选取Q个最大特征值对应的特征向量张成Uj,从而获得投影矩阵
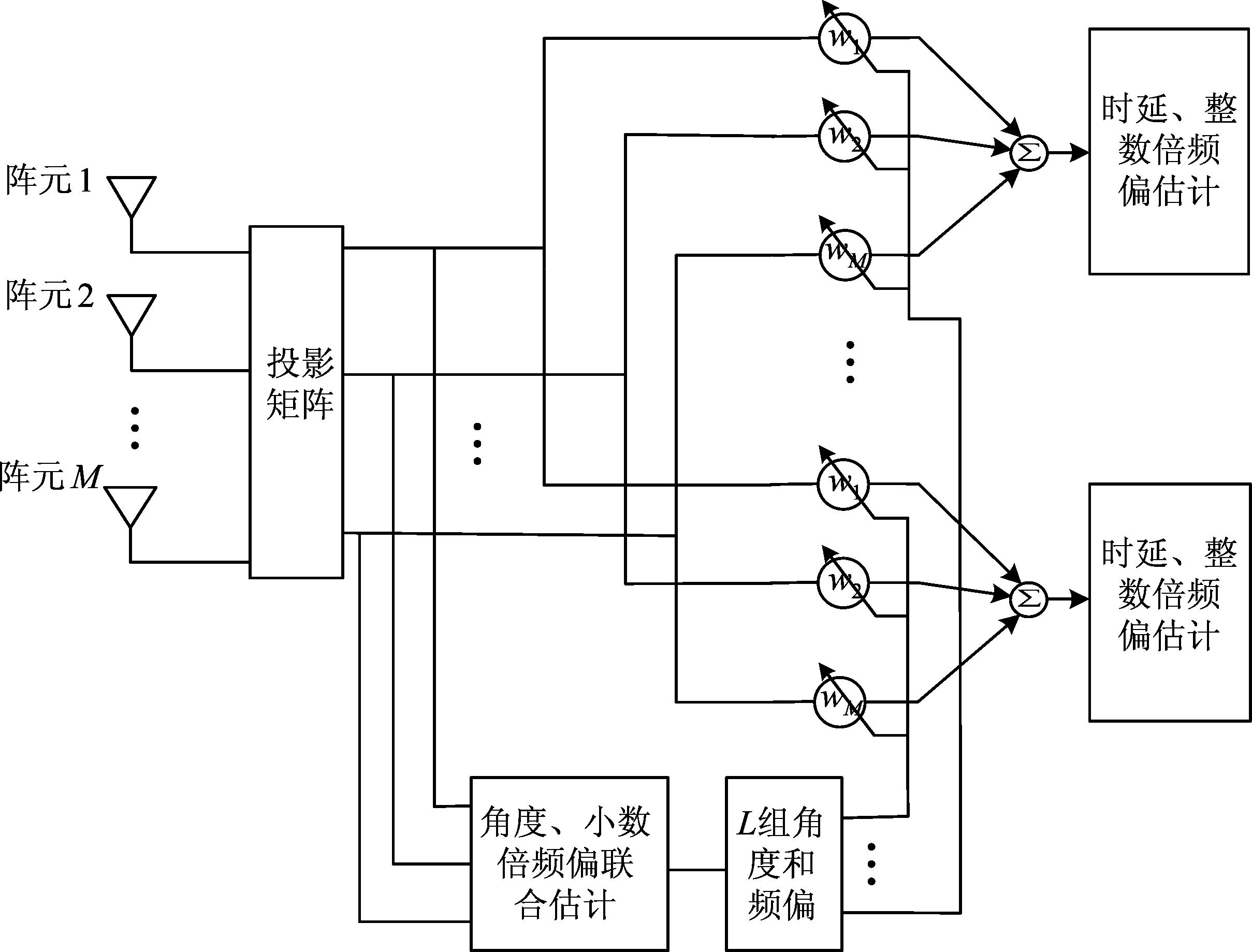
图2 捕获过程信号处理流程
Fig.2 Signal flow diagram of acquisition stage
(4)
由于投影矩阵和干扰空间正交,所以可以用投影矩阵对接收信号中的干扰进行抑制,此时接收信号可以表示为
(5)
其中:定义
为投影后的导向矢量,S=[s1(t),s2(t),…,sL(t)]T是信号矩阵。
由于GPS数据码的周期为20 ms,而CA码的周期为T=1 ms,从式(5)可以推导出,x(t)延迟p ms(p<20)后的表达式可以表示为
(6)
构造如下的信号结构:
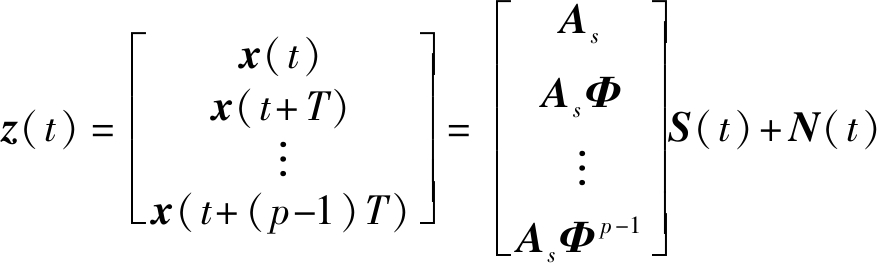
(7)
其中:Φ=diag{ej2πf1T,…,ej2πfLT}。
从式(7)的模型可以看出,包含在对角矩阵Φ中的多普勒频偏可以利用旋转不变子空间(ESPRIT)方法[12]估计频偏,由于T=1 ms,频率估计存在模糊,模糊间隔为1 kHz,所以此处得到的是小数倍频偏。在运用ESPRIT方法的时候,需要对z(t)的自相关矩阵进行特征分解,可以获得信号空间和噪声空间的特征向量,分别记为Us和UN,对应的特征值分别构成对角矩阵Σs和ΣN,那么自相关矩阵可以表示为:
这样,导向矢量中含有的角度信息可以通过搜索获得
(8)
式中
至此,角度和小数倍频偏已经获得,在估计时延时,先用最小方差无失真响应MVDR波束形成器对分别对每颗卫星形成波束,波束系数为
(9)
其中:R=E{xxH}表示相关函数。那么经过波束形成后的信号为
(10)
最后再分别对每一颗卫星的时延和整数倍频偏进行最大似然搜索:
slocal(t)=c(t-τ)ej2π(fint+fp)t
(11)
其中y表示y(t)多个时刻采样点构成的列向量。这样,捕获阶段就获得了可见卫星的角度、频偏和时延值,用于后续的跟踪过程。
3.2 多天线跟踪环路
多天线接收可以提供空域角度信息,考虑跟踪阶段,捕获阶段已获得角度、频偏、码相的初值。考虑到和单天线跟踪环路[1]相结合的思路,增加角度环路,利用超前滞后的波束分别对接收信号进行合并,计算获得两个支路的功率,对其进行比较,调整本地波束的参数(角度的正弦值)。经过一段时间的跟踪,环路趋于稳定。具体结构如下图3。
从图3可以看出,角度环对卫星的角度进行跟踪,并将获得的信号角度用于生成即时波束,将多天线的接收信号进行合并,同时提高了信噪比,然后再将此数据输入传统的单天线跟踪环路,此环路包括了码环和载波环,分别对码相和载波频率进行跟踪,同时单天线跟踪的结果用于对信号进行解扩,将解扩后的信号输入角度环,分别用超前滞后波束对输入信号进行合并,再利用两路的功率差异调整本地波束生成。下面主要对角度环的信号流变化进行推导,假设当前跟踪的卫星编号为i,并且由于各个卫星之间的扩频码不相关,而且扩频码和干扰、噪声也不相关,所以解扩后的信号可以表示为
(12)
此处的超前滞后波束的结构也采用导向矢量的结构,只是超前滞后分别调整了里面参量的值,此处记
并且超前滞后的间隔为δα,这样超前滞后波束分别可以表示为
所以超前滞后波束对输入信号进行合并后的结果为
图3 跟踪环路结构
Fig.3 The structure of tracking loop
(13)
可以看出,当即时波束对准输入信号方向时,超前滞后波束两路输出功率相等。所以鉴相器可以通过计算两路功率的差值来调整本地波束的方向,鉴相器输出如下
(14)
环路滤波器可以设计不同阶数的滤波器,此处采用一个简单的全通滤波器,这样调整后的波束参数为
(15)
式中,κ是一个和收敛速度相关的系数。
从式(15)可以看出,当超前滞后波束两路的相关值相等时,即时波束的参数αi也稳定下来,变成一个常数,而且此值正好等于实际信号的入射方向,而当输入信号方向慢变时,超前滞后两路的相关值也发生,从而作用于本地波束生成器,直到达到新的稳定。通过这样一个过程,角度环实现了对角度的跟踪,单天线跟踪环路对于码相和多普勒频偏也有相似的效果,所以整个跟踪环路通过角度环、码环、载波环相嵌套的方式,实现了对输入多天线信号的各个参数的跟踪,并且由于针对卫星信号方向做了波束形成,所以从空域上实现了抗干扰。
3.3 复杂度的分析
用L表示卫星数目,M表示天线阵元数目。考虑几种方法的差异:功率倒置PI算法主要在于矩阵求逆,复杂度为O(M3),复杂度是最低的,但是估计性能也最差(可以从后面的仿真结果中看出)。CLEAN算法复杂度主要在于空域角度搜索部分,搜索点数记为Se,那么复杂度为O(LSeM),RELAX算法由于存在迭代过程,记迭代次数为Iter,那么复杂度为O(L(L+1)Iter/2·SeM)。本文提出的算法角度估计包含一个特征分解和搜索过程,复杂度为O(M3)+O(LSeM)。虽然复杂度比CLEAN算法更高,但是角度估计精度的提升明显,并且获得了配对的小数倍频偏,有利于时延的估计。再考虑跟踪阶段,CLEAN、RELAX算法只跟踪载波和码相信息,而不跟踪角度信息,当角度发生变化时,要重新捕获,而本文的方法会同时跟踪角度信息,记跟踪阶段需要重新捕获的次数为Cre,一个扩频码周期内的采样点数为Nc,这样CLEAN、RELAX方法的总体复杂度分别为O(CreLSeM+3LNc)、O(CreL(L+1)Iter·SeM/2+3LNc),而本文的算法的复杂度为O(M3+LSeM+3LNc+3LM),实际中Se和Cre都远大于天线数M,所以从总体复杂度来看,本文算法的复杂度更低。
4 仿真结果分析
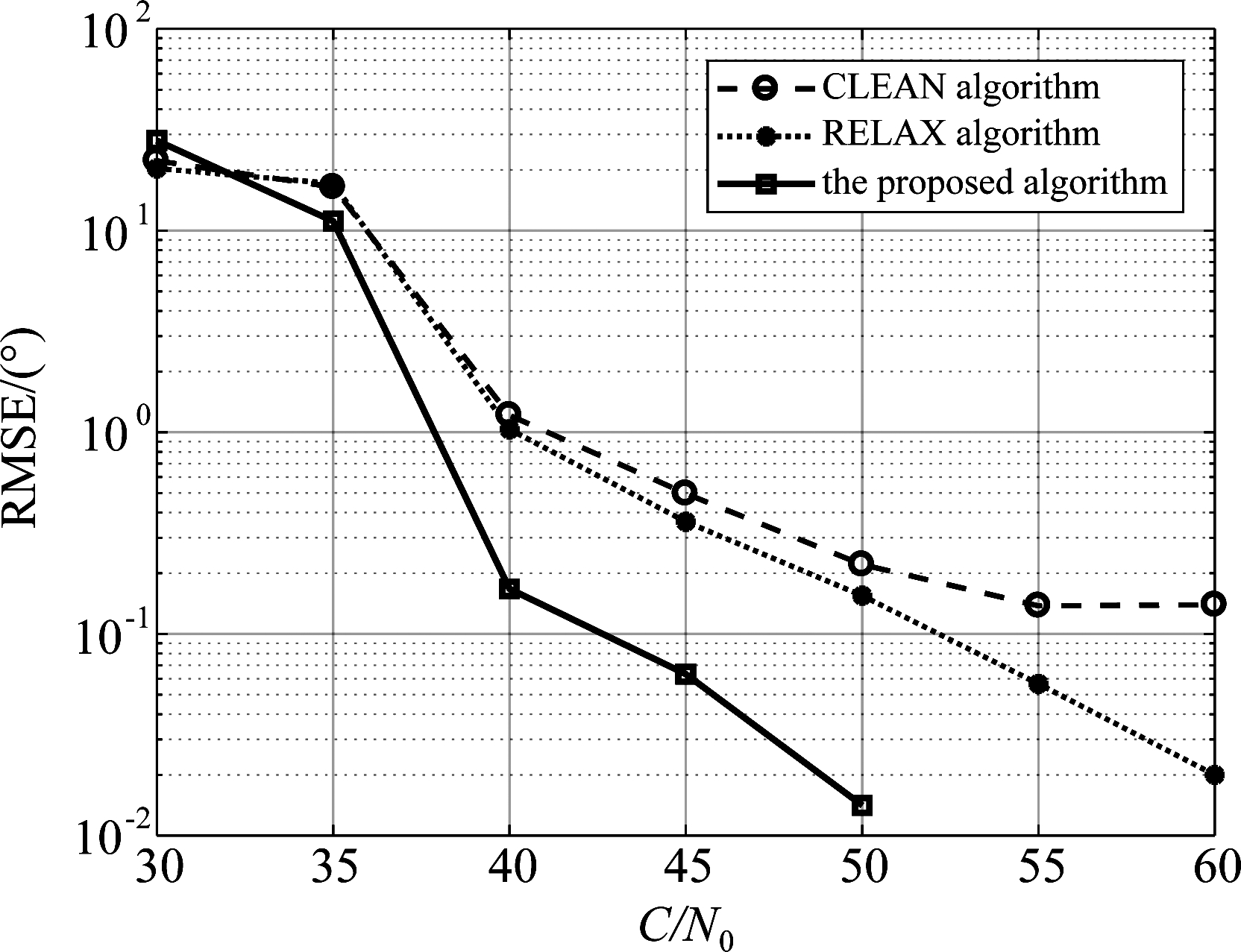
图4 捕获阶段角度估计误差
Fig.4 RMSEs of DOA estimated for GPS signal at acquisition stage
由于本文所提抗干扰的方法主要是针对导航接收机中的捕获和跟踪模块,并且卫星角度估计精度对应了干扰抑制的能力,时延和频偏的估计性能直接影响了接收机的定位精度,时延、频偏估计越精确,则定位精度越高,所以仿真中分别对捕获和跟踪阶段的参数估计性能进行了研究。仿真中采用的实验条件如下:接收天线采用十阵元均匀线阵,阵元间距为半波长(实际上本文所提方法扩展了阵元数目,采用更少的阵元也能捕获卫星信号,但阵元数目过少时CLEAN、RELAX算法无法正常工作,为保证对比的公平性,采用了十个阵元)。三颗卫星信号的prn编号为[3,1,7],入射方向为[-30°, 0°, 15°],存在一个强干扰,由于干扰通常都来自于地面,所以设置干扰入射方向为70°,并且干扰功率比噪声功率大20 dB。用PR表示信号功率,定义载噪比为C/N0=10log10(PR/N0),单位为dB·Hz,其中N0是噪声功率谱密度。从图4可以看到在捕获阶段角度估计误差曲线,CLEAN算法[9]估计性能最差。RELAX算法[10]通过用反复迭代性能得到了提升,但是复杂度过高。由于本文提出的角度、小数倍频偏联合估计方法由于扩展了阵元数目,所以角度估计结果得到了大幅度提高。并且由于获得了对应的小数倍频偏,所以在捕获阶段估计卫星时延时需要的搜索次数更少。图5展示了小数倍频偏对于捕获概率的影响,仿真了三颗卫星信号入射,单天线接收时已知小数倍频偏和未知小数倍频偏时漏捕概率随载噪比的变化,从图中可以看出获得小数倍频偏后对捕获概率有很大的提升,本文提出的方法获得了小数倍频偏,相比于CLEAN、RELAX算法,捕获概率也更高。
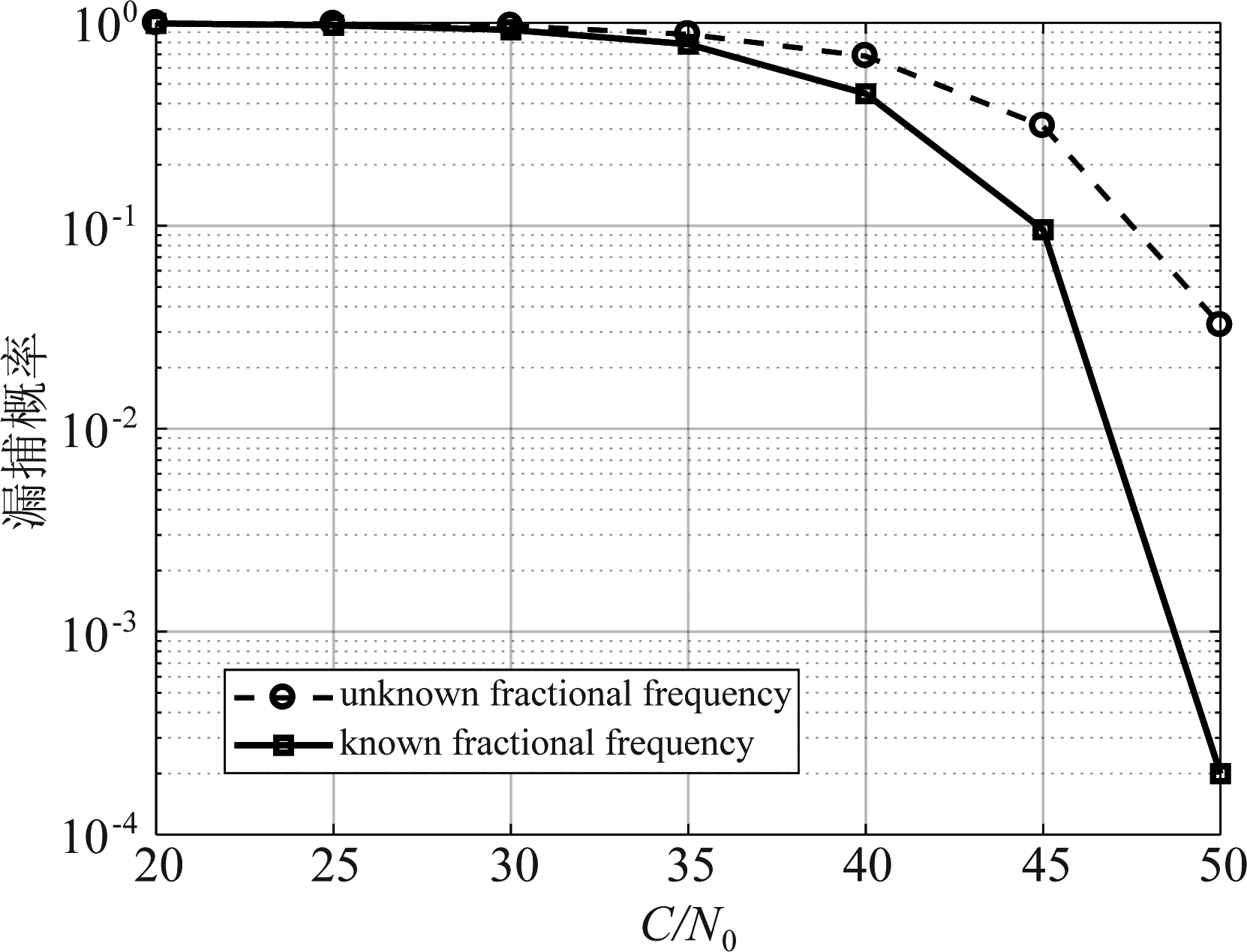
图5 漏捕概率随载噪比的变化曲线
Fig.5 Missing probability with/without the fractional frequency versus C/N0
在捕获到卫星信号后,转入跟踪环路。图6和图7分别是卫星prn=3跟踪阶段的时延误差和频率误差,信号和干扰的参数设置同上,仿真采用的码环的超前滞后鉴相间隔为1个CA码片,码环和载波环的噪声带宽分别为2 Hz和25 Hz,阻尼系数为0.7。通常接收机的工作范围为35到50 dB·Hz,可以看到由于功率倒置(PI)算法只形成了一个波束,高信噪比下卫星信号收到抑制并且卫星之间干扰变大,所以性能最差;其他三种算法都针对不同的卫星做了波束形成,获得了阵列增益,并且都充分利用了GPS信号的扩频增益,所以性能基本一致。但是从图8中可以看到,由于CLEAN、RELAX算法在估计到卫星信号的角度信息后,就分别利用波束形成合并了接收信号,结构上虽然比较简单,但是丧失了对卫星信号角度进行跟踪的能力。而本文提出的新的跟踪结构,可以对每一颗卫星信号的入射角度进行跟踪,并且可以看出估计误差也较小。从图8中也可以看到由于投影矩阵对角度跟踪环路的影响,所以随载噪比提高,角度跟踪误差稳定在0.1°左右,但是此精度已经足够跟踪卫星信号,而且较低载噪比下角度跟踪误差也远小于1°,也可以准确跟踪卫星。这样在卫星运动过程中也就不需要重新捕获,正如复杂度分析部分的计算,降低了复杂度。
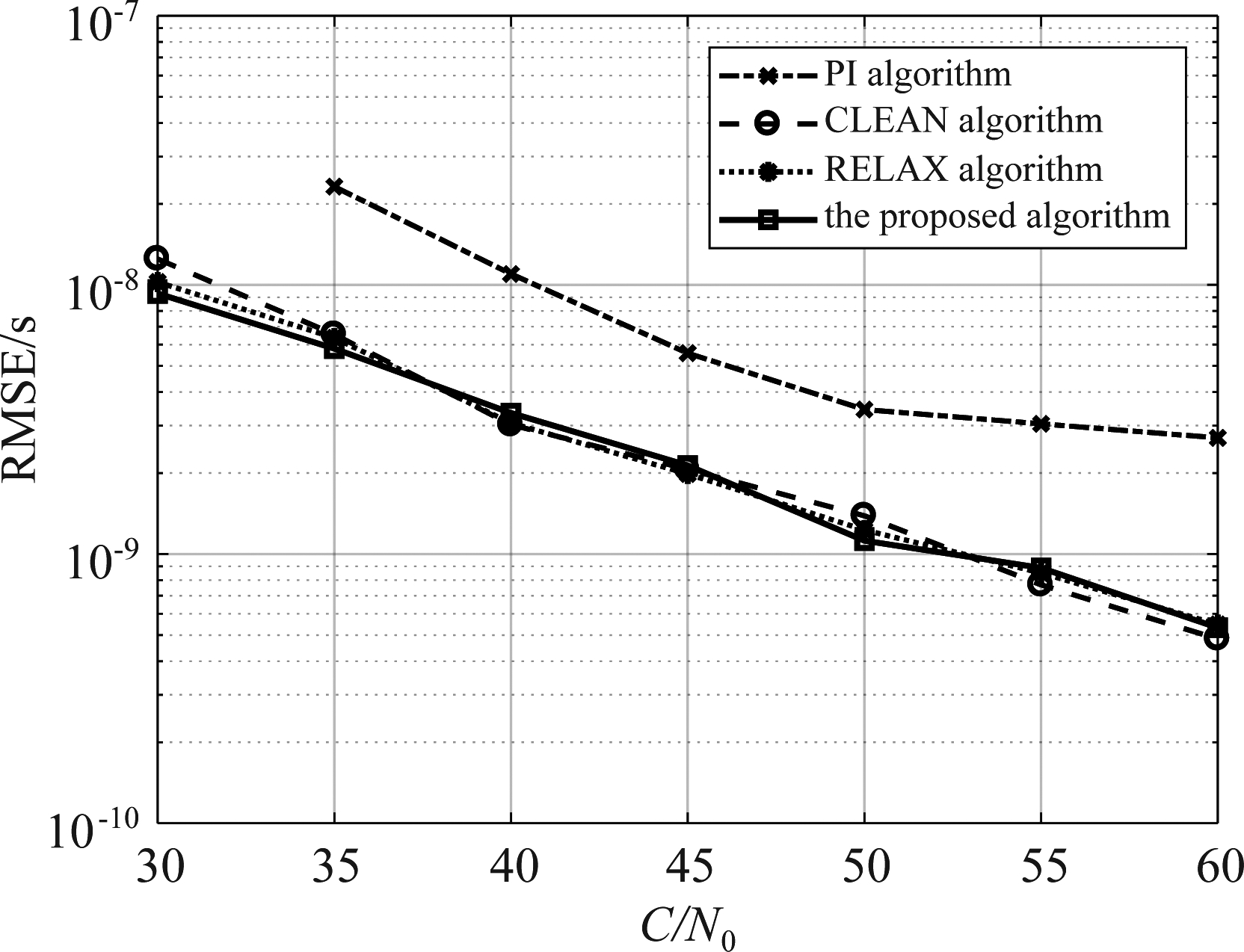
图6 跟踪阶段时延误差
Fig.6 RMSEs of delay estimated for GPS signal at tracking stage
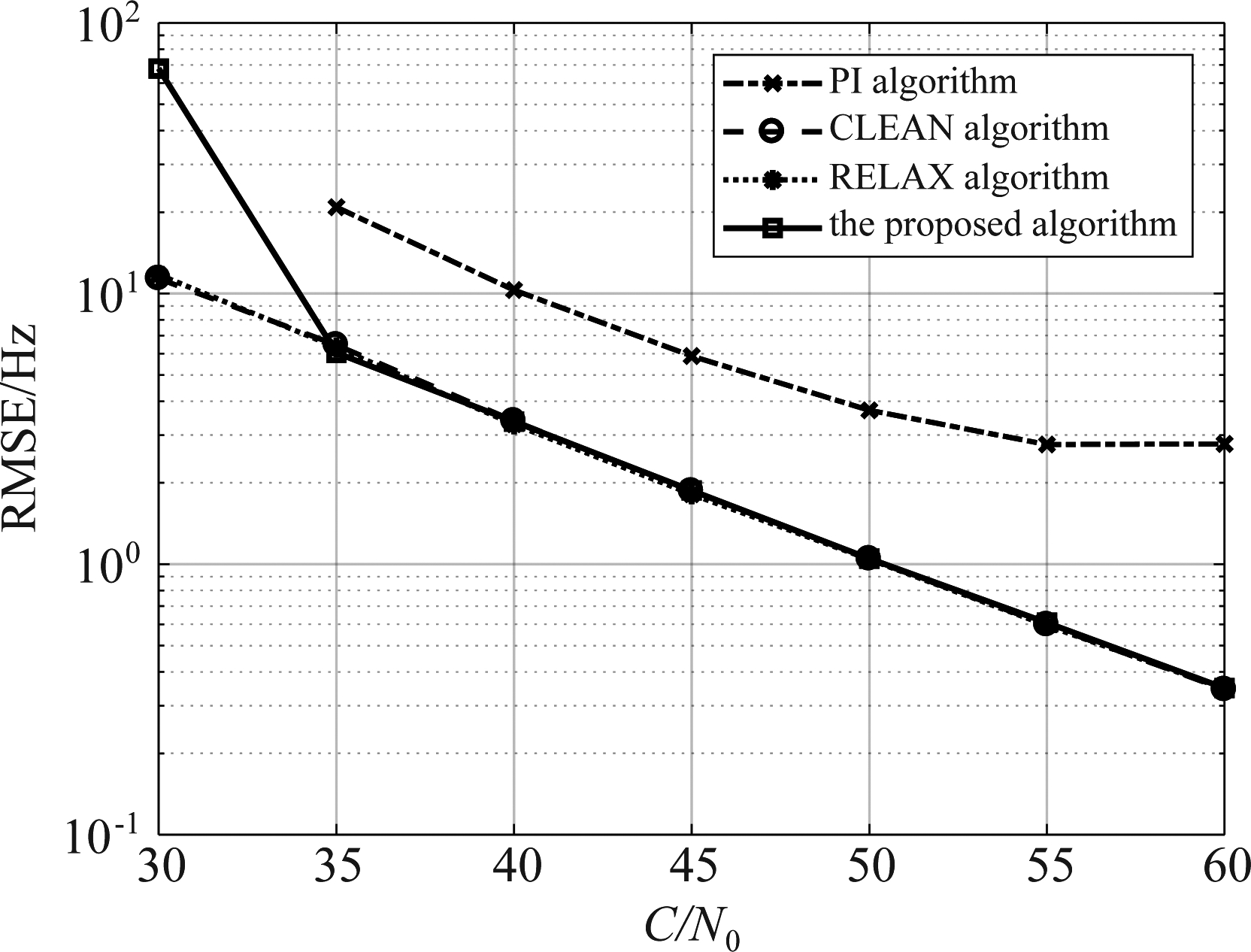
图7 跟踪阶段时延频率误差
Fig.7 RMSEs of frequency offset estimated for GPS signal at tracking stage
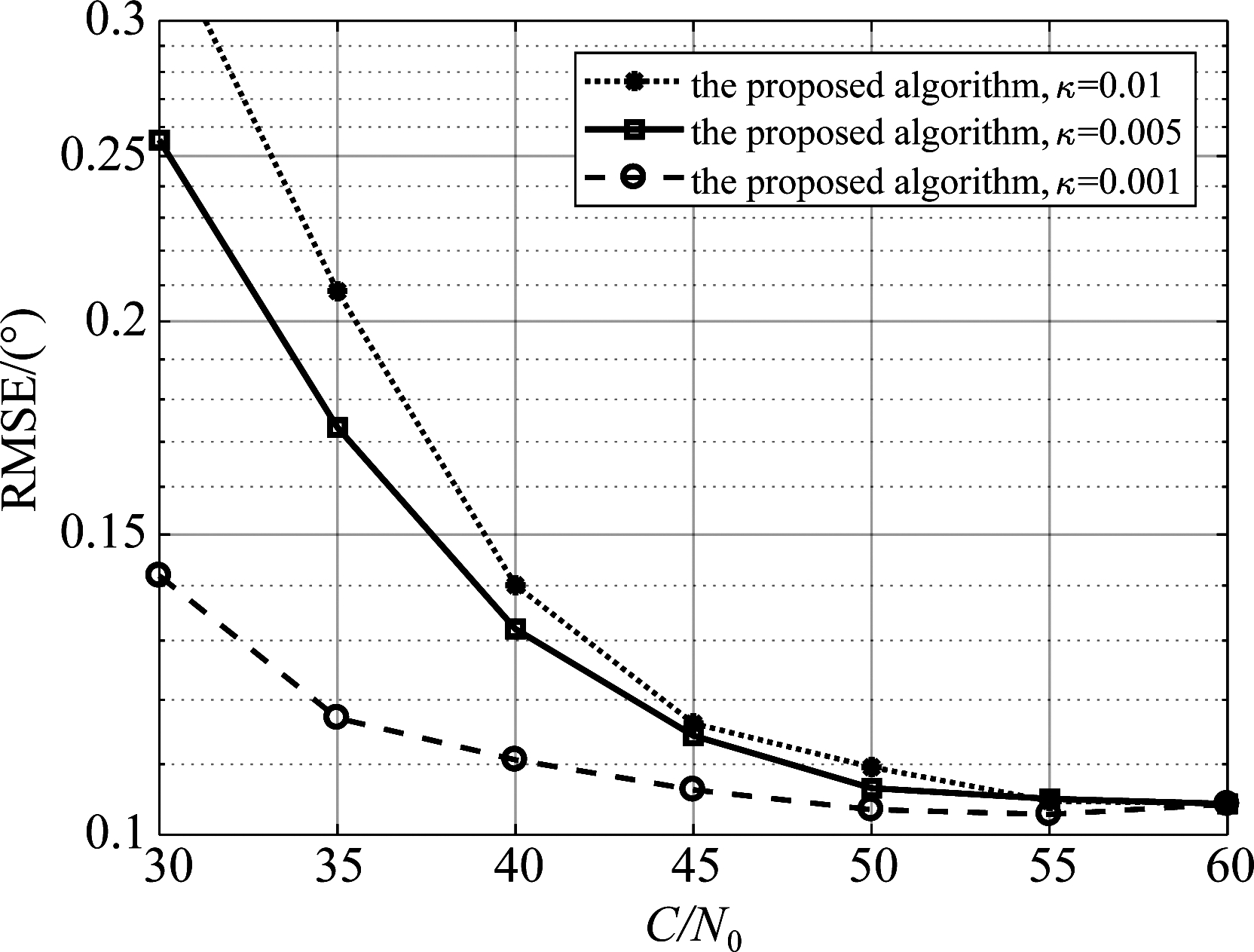
图8 跟踪阶段角度误差
Fig.8 RMSEs of DOA estimated for GPS signal at tracking stage
5 结论
本文在传统单天线GPS接收机的基础上,提出了一种多天线抗干扰GPS接收机中角度、时延、频偏的估计和跟踪方法,利用多天线扩展出新的自由度用于抗干扰,同时提高了时延、频偏的估计性能,对以后续的定位精度提高有很大益处。相比于CLEAN、RELAX类多天线抗干扰算法,角度参数估计性能得到了提升,同时由于多天线提供的空域信息,可以利用角度信息进行投影实现干扰的抑制。在捕获阶段,干扰信号通常来源于地面,功率远远高于信号功率,利用这一特性,利用子空间投影抑制干扰后,再捕获可见卫星,确定初始频偏和码相,提高了捕获概率;在跟踪阶段,利用了波束形成,每个跟踪通道只接收某一方向上的单颗卫星信号,从而也可以达到对干扰和噪声的抑制。而且由于存在角度环路,时刻跟踪卫星信号的入射角度,相比于CLEAN、RELAX算法,在卫星角度发生改变时不需要重新进行捕获,提高了系统的稳健性,并且降低了运算复杂度。
[1] Misra P, Enge P. Global Positioning System: Signals, Measurements, and Performance[M]. Lincoln, MA: Ganga-Jamuna Press, 2004.
[2] 贾琼琼, 吴仁彪, 王文益, 等. 基于空域信号分离的多径干扰抑制算法[J]. 交通运输工程学报, 2017, 17(2): 151-158.
Jia Qiongqiong, Wu Renbiao, Wang Wenyi, et al. Multipath interference suppression algorithm based on spatial signal separation[J]. Journal of Traffic and Transportation Engineering, 2017, 17(2): 151-158.(in Chinese)
[3] Rezaei M J, Abedi M, Mosavi M R. New GPS anti-jamming system based on multiple short-time Fourier transform[J]. IET Radar Sonar & Navigation, 2016, 10(4): 807- 815.
[4] Chien Y R. Design of GPS Anti-Jamming Systems Using Adaptive Notch Filters[J]. IEEE Systems Journal, 2017, 9(2): 451- 460.
[5] Rao K, S. Swamy M. New approach for suppression of FM jamming in GPS receivers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(4): 1464-1474.
[6] Soderstrand M A, Johnson T G, Strandberg R H, et al. Suppression of multiple narrow-band interference using real-time adaptive notch filters[J]. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 2002, 44(3): 217-225.
[7] Gecan A, Zoltowski M. Power Minimization Techniques for GPS Null Steering Antenna[C]∥in Proc. 8th Int. Tech. Meeting of the Satellite Division of Institute of Navigation, Palm Springs, CA, Sept. 12-15, 1995(ION, Fairfax, 1995): 861- 868.
[8] 包莉娜, 吴仁彪, 王文益, 等. 两级结构的卫星导航压制式和欺骗式干扰联合抑制算法[J]. 信号处理, 2015, 31(9): 1041-1046.
Bao Lina, Wu Renbiao, Wang Wenyi, et al. Two-step GPS Interference Suppression Algorithm for Spoofing and Jamming[J]. Journal of Signal Processing, 2015, 31(9): 1041-1046.(in Chinese)
[9] Lu Dan, Liu Haitao, Wu Renbiao. Global positioning system anti-jamming algorithm based on period repetitive CLEAN[J]. IET Radar, Sonar & Navigation, 2013, 7(2): 164-169.
[10] Li Jian, Zheng Dunming, Stoica P. Angle and waveform estimation via RELAX[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 1077-1087.
[11] Liu Zhengshe, Li Jian. Implementation of the RELAX algorithm[J]. IEEE Transactions on Aerospace & Electronic Systems, 2002, 34(2): 657- 664.
[12] Sharma K, Santosh S. A Review on ESPRIT-Estimation of Signal Parameters via Rotational Invariance Techniques[J]. International Journal of Engineering Research, 2013, 2(3).
