1 引言
随着互联网的高速发展,移动数据流量正以指数速度快速增长,据文献[1]预测,到2021年,全球数据流量将会达到2016年的8倍之多,其中,视频业务所产生的流量将占据总流量的70%以上。为了应对这种情况,减轻海量流量给蜂窝网络带来的巨大压力,可以在靠近终端用户的位置部署多个小型基站。然而,小基站是通过容量有限的回传链路连接到核心网,这使得在数据请求高峰期,很难保证用户的服务质量(Quality of Service,QoS)。为了解决这种问题,文献[2]提出一种网络边缘分布式缓存方案,分布式缓存的思想是在小基站上部署存储单元,可以根据一定的缓存策略将流行文件存储在这些单元中。如果小基站中已缓存有用户所请求的视频文件,则无需通过回传链路就能满足用户请求。为了更好地实施边缘缓存,文献[3]进一步提出移动网络运营商(Mobile Network Operator, MNO)可以通过与视频服务提供商(Video Service Provider, VSP)进行合作,使得视频内容得以缓存到边缘节点。因此,网络运营商需要制定一种激励机制来鼓励视频服务提供商分享并提前缓存它们的热门内容。
近来,受到文献[2]以及[3]的启发,大量文献从不同的层面对内容缓存工作进行了研究,例如分层视频传输的最优化缓存策略、D2D(设备到设备)网络、分层缓存、回传链路受限的多小区场景等。文献[4]指出,流行视频内容在短时间内的重复下载给蜂窝网链路带来了巨大的传输压力。为解决这种问题,文献[5]提出了一种智能定价机制来最大化运营商的收益并最小化向用户收取的费用。通过D2D网络,用户之间可以相互交易自身已缓存好的数据来减少自身的开销,运营商制定了区分高峰时段和非高峰时段的动态定价模型以最大化自身收益。文献[6]将基站和用户之间的缓存激励问题建模为Stackelberg博弈,通过预测用户行为,基站制定奖励策略,对帮助基站卸载流量压力的用户进行奖励,对于基站制定的奖励,用户可以决定是否帮助基站缓存视频并帮助其他用户分享视频。
然而上述工作大都聚焦于D2D网络中的缓存资源分配,从网络运营商和视频服务提供商的角度讨论较少,例如,视频服务提供商提前缓存多少视频到边缘节点中能最大化自身效用？因此,本文的主要工作是:(1)提出一种多个运营商和多个视频服务提供商之间的缓存激励策略,并将该缓存激励问题建模为多主多从Stackelberg博弈问题[7],其中,网络运营商充当领导者,视频服务提供商充当跟随者。网络运营商通过预测视频服务提供商的缓存请求来制定单位存储空间的价格策略,以最大化自身利益;另一方面,由于网络运营商提供的存储空间有限,视频服务提供商并不能将自身的视频文件全部缓存到边缘节点中,因此,视频服务提供商根据运营商的价格策略,彼此竞争来决定在各个运营商处的缓存空间购买量。(2)论文证明了在运营商价格给定的情况下,视频服务提供商之间的非合作博弈存在纳什均衡点。(3)论文利用分布式迭代算法对多主多从Stackelberg博弈问题进行了求解,保证网络运营商和视频服务提供商都达到了最优效用。
本文其余部分内容安排如下:第2部分阐述多主多从Stackelberg博弈基本理论知识;第3部分为系统模型与算法描述;第4部分为算法求解;第5部分为仿真结果与分析;最后一部分为结论与展望。
2 多主多从Stackelberg博弈
博弈论在通信领域中已得到广泛应用,其中,Stackelberg博弈是一种较为经典的博弈模型。博弈模型的要素通常包括博弈的参与者、参与者的策略和参与者的收益。为了最大化自身利益和总体利益,博弈参与者之间可能存在合作关系和非合作关系。通常情况下,当所有参与者均达到最大收益,并且任何个体都无法通过私自改变自身策略得到更大的收益时,称此状态为均衡状态。我们的目标就是利用Stackelberg博弈模型求出激励缓存资源分配问题的均衡解。
Stackelberg博弈是一种上下级之间的博弈问题,博弈中的参与者分属于两种不平等地位,即领导者和跟随者。在博弈模型中,领导者通过预测跟随者的反应首先做出决策,随后,跟随者对领导者的决策做出最优反应。所谓预测,即领导者在决定自己的决策的时候,充分了解跟随者会如何行动——这意味着领导者可以知道跟随者的反应函数。因此,领导者自然会预期到自己决策对跟随者的影响。正是在考虑到这种影响的情况下,领导性者的决策将是一个以跟随者的反应函数为约束的利润最大化变量。在Stackelberg模型中,领导者的决策不再需要自己的反应函数。
在多主多从Stackelberg博弈模型中,假设同时存在a个领导者和b个跟随者,分别用集合A={1,2,...,a}和集合B={1,2,...,b}表示。领导者的策略集表示为X=(x1,x2,...,xa),领导者n的收益表示为Uoa;跟随者的策略集表示为Y=(y1,y2,...,yb),收益表示为Uνb。
在给定领导者策略为X的情况下,跟随者之间进行非合作博弈,其纳什均衡点集合表示为
(1)
其中,
表示跟随者b的最佳策略,
表示除了跟随者b,其他所有跟随者的最佳策略集合。对于满足式(1)的任意策略
...,
称Y*为一个非合作博弈的纳什均衡点。
对于多主多从Stackelbrg博弈问题,可分为领导者决策和跟随者决策两个过程。博弈问题可由G={x,y,Uo(x,y),Uν(x,y)}表示,其中,a∈A,b∈B。对于满足式(2)的策略(x*,y*)∈X×Y,称策略(x*,y*)为一个多主多从Stackelberg博弈的子博弈完美纳什均衡点。
(2)
其中,a∈A,Y*∈S(X)。
3 系统模型与算法描述
3.1 系统模型
考虑如图1所示的场景,假设系统中存在n个存储空间大小不同的网络运营商和m个需求不同的视频服务提供商,网络运营商集合表示为N={1,2,...,n},视频服务提供商集合表示为M={1,2,...,m}。其中,每个网络运营商都有若干个边缘节点,以提供缓存服务,运营商ν提供的缓存空间上限为Cν。m个视频服务提供商彼此竞争n个网络运营商的存储空间,为了提升自身所服务用户观看视频时的QoS,视频服务提供商向网络运营商购买一定的存储空间将热门视频内容缓存到靠近用户的边缘节点中,如果用户请求的视频已经缓存在边缘节点中,则边缘节点可立即响应用户请求,否则,需要通过向核心网发送请求,将用户请求的视频发送至用户处。网络运营商制定单位存储空间的价格来最大化自身的收益。
图1 系统模型
Fig.1 Syetem Model
由于存在多个网络运营商供选择,且各网络运营商的存储空间上限不同,对于视频服务提供商来说,可以选择在多个运营商处购买不同的缓存空间,因此,视频服务提供商将根据不同运营商制定的价格策略来决定在各运营商处的缓存购买量,以最大化自身利益。
3.2 Stackelberg博弈模型
本文模型中存在两类参与者:领导者和跟随者。其中,n个网络运营商充当领导者,m个视频服务提供商充当跟随者。领导者是存储空间的拥有者并制定相应的价格策略,跟随者是缓存资源的需求者,根据领导者给出的价格策略决定自身的缓存需求量。一方面,所有的视频服务提供商想尽可能多地将自身视频内容缓存到边缘节点中,这可以提升自身服务用户的QoS;另一方面,购买缓存资源需要向网络运营商支付一定的费用,因此,在Stackelberg博弈模型中缓存激励机制受制于移动网络运营商为提升自身利益所制定的单位存储空间价格。
对于网络运营商ν来说,ν∈M,其策略为单位存储空间价格pν。对于视频服务提供商u来说,u∈N,其策略为在各运营商处的缓存需求策略suν,suν表示在网络运营商ν处购买的缓存空间,且满足0≤suν≤Cν。所有视频服务提供商在网络运营商ν处的总缓存请求量应满足
不失一般性,假设视频服务提供商u的视频文件集是按视频流行度从高到低降序排列的,用户请求视频h的概率zh服从Zipf分布[8]:
(3)
其中,c为常数,0<αu<1表示视频服务提供商u的流行视频内容的分布度,αu越大,表示流行视频内容分布越集中。
视频服务提供商和网络运营商之间的博弈分为两部分。在第一阶段,网络运营商首先公布单位存储空间的价格,并向所有视频服务提供商公告此策略。视频服务提供商收到不同运营商的价格策略后,彼此竞争,确定在各运营商处的缓存需求策略。此时,视频服务提供商之间的竞争是一个非合作博弈问题,纳什均衡为该问题的解。在第二阶段,网络运营商根据视频服务提供商的缓存需求策略,重新制定自身的价格策略,以获取更高的收益。
3.3 效用函数
对于网络运营商和视频服务提供商来说,效用函数表示的是博弈参与者在博弈过程中获得的满意程度,接下来,我们将分别分析网络运营商和视频服务提供商的效用函数。
3.3.1 网络运营商的效用函数
对于网络运营商来说,其收益是视频服务提供商购买缓存空间向其支付的费用。对于网络运营商ν,其效用函数定义如下
Uoν=pν·Sν
(4)
其中,Sν表示所有视频服务提供商在网络运营商ν处购买的缓存空间总量,即
如果网络运营商的定价过低,即使出售其全部存储空间,也不会获得较高的收益。相反,如果网络运营商的定价过高,则大多数视频服务提供商将不会购买其存储空间,这也会导致运营商收益较低。所以,网络运营商需要制定合适的价格,以保证获得较高的收益。为使网络运营商ν获得最优效用,其最佳定价
应满足
(5)
其中,
和s*表示除运营商ν之外,博弈的其他参与者均满足最优策略。
3.3.2 视频服务提供商的效用函数
给定各运营商的单位存储空间价格策略p,所有视频服务提供商彼此竞争决定自身的缓存需求策略。视频服务提供商的效用函数定义为收入减去支出。
对于视频服务提供商u,其支出Zu即为购买缓存空间所花费的费用,定义为
(6)
实际上,视频服务提供商(如YouTube)很关心自身所服务用户观看视频时的满意度。此处的用户满意度可以用观看视频的时延或网络吞吐量来衡量,是Su的增函数,其中Su表示视频服务提供商u在所有运营商处购买的缓存空间总量,表示为
同时用户满意度函数也是关于S-u的减函数,S-u表示除视频服务提供商u外,其他所有视频服务提供商的缓存购买总量。
所以,视频服务提供商的收入可以定义为自身所服务用户观看视频时的满意度。由于满意度函数是视频服务提供商购买的缓存总量的增函数,根据文献[9],这里用对数函数来表示视频服务提供商基于缓存购买量的收益函数,为了便于分析,每个视频服务提供商在各运营商处获得存储空间后,根据按流行度降序排列的文件集缓存自身受欢迎的视频文件,直到存储空间已满。收益函数定义为
(7)
其中,λu>0表示视频服务提供商u的收益因子,0<αu<1表示视频服务提供商的流行视频内容的分布度,αu越大,表示流行视频内容分布越集中。
因此,视频服务提供商u的效用函数可表示为
(8)
视频服务提供商根据收到的网络运营商价格策略,制定自身的最优缓存需求策略,由于网络运营商提供的存储空间有限,因此视频服务商之间的缓存需求策略会相互影响,视频服务提供商的最优缓存需求策略满足下式
(9)
3.4 视频服务提供商纳什均衡点存在性
在给定网络运营商单位存储空间价格策略后,视频服务提供商之间存在竞争关系,即非合作博弈,每个视频服务提供商彼此竞争在各运营商处的缓存空间,且其缓存策略会间接对其他视频服务提供商的缓存策略造成影响。
纳什均衡,又称非合作博弈均衡,在纳什均衡解下,非合作博弈的所有参与者均达到了最优效用,任何参与者都无法通过私自改变自身策略获得更高收益。然而,纳什均衡解不一定存在,有些非合作博弈可能没有纳什均衡解,而有的非合作博弈可能存在多个纳什均衡解。现对纳什均衡解的存在性进行分析。
定理1 假设网络运营商给出的单位存储空间价格策略为p=(p1,p2,...,pn),在此价格策略下,视频服务提供商之间存在非合作博弈,效用函数为Ucu(p,suν,s-uν),其中,u∈N,ν∈M,则此非合作博弈存在纳什均衡点
证明 对于任意视频服务提供商的缓存需求策略suν,显然属于欧氏空间的有界闭集,且视频服务提供商的效用函数Ucu在缓存需求策略空间上是连续的。下面对Ucu的函数特性进行分析,一阶偏导数为
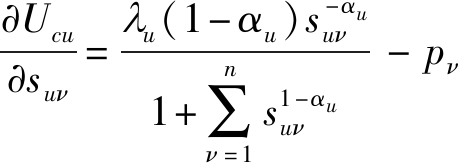
(10)
对其求二阶偏导,可得
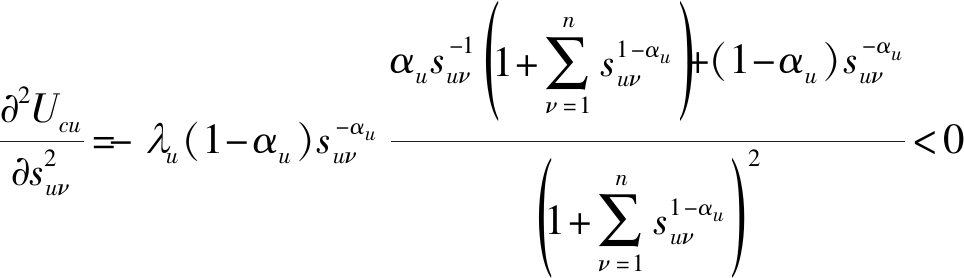
(11)
其中,0<αu<1,λu>0,suν≥0,视频服务提供商的二阶偏导数为负,保证了效用函数为严格凹函数,由此保证了纳什均衡点的存在性[10]。
由上可知,对于网络运营商的任意一组价格策略,总能得到视频服务提供商缓存需求策略的纳什均衡点,则说明,在运营商最优价格策略的情况下,一定能得到视频服务提供商的最优缓存策略,使得博弈的全体参与者,均达到最大收益,即存在多主多从Stackelberg子博弈完美纳什均衡。
4 算法求解
本节,我们对上述多主多从Stackelberg博弈模型进行求解。对于传统的一主多从Stackelberg博弈模型求解,一般用的是反向归纳法,这种方法要求博弈的参与者知道其他所有参与者的信息,显然,这一方法对于求解多主多从Stackelberg博弈模型很难实现。受文献[11]启发,每个博弈参与者仅需要局部信息就能做出决策,本文根据进化博弈的最优动态反应,利用如下算法进行求解:
假设跟随者的行动是完全理性的,领导者的行动是有限理性的,也就是说,在网络运营商给出价格策略时,视频服务提供商立即根据此价格策略彼此竞争达到均衡,网络运营商之间的价格均衡不是一步达到的,需要通过多次迭代不断进行调整,从而得到均衡解。
具体来说,假设在t时刻,网络运营商向所有的视频服务提供商公布单位存储空间的价格策略p(t)=(p1t,p2t,...,pnt),视频服务提供商根据收到的价格策略,并结合自身需求调整在各运营商处的缓存需求量,使自身利益达到最大。视频服务提供商的缓存需求变化率与自身效用函数的梯度成正比。视频服务提供商在博弈过程中需要经过数次迭代才能达到纳什均衡,称τ时刻到τ+1时刻的时间间隔为视频服务提供商的一次迭代周期,用Δτ表示。在迭代周期Δτ内,视频服务提供商的缓存需求迭代公式为
(12)
其中,表示k>0表示视频服务提供商的缓存策略迭代步长,
表示效用函数的梯度,由下式给出
(13)
由于视频服务提供商的效用函数满足凹函数特性,因此,经过多次迭代之后,视频服务提供商的缓存需求策略可收敛到纳什均衡点。
在所有视频服务提供商达到纳什均衡后,网络运营商在t+1时刻根据各视频服务提供商的缓存需求策略,通过价格迭代公式调整自身价格策略,价格迭代公式如下
(14)
其中,l>0表示网络运营商价格策略迭代步长,t时刻到t+1时刻的时间间隔称为网络运营商的一次迭代周期Δt。网络运营商效用函数对于价格的偏导数可以通过一个小的变化量θ(如θ=10-4)来计算
(15)
在视频服务提供商的缓存需求策略达到纳什均衡前,网络运营商应保持价格策略不变,直到所有视频服务提供商得到最优缓存需求策略,这一过程所用时间即是网络运营商的一次迭代周期Δt,因此,一个Δt包含多个Δτ。对于整个激励缓存分配系统而言,网络运营商作为领导者,根据各视频服务提供商的缓存需求策略动态调整自身价格策略,使自身收益达到最大,此价格策略称为最优价格策略,在此价格下,视频服务提供商达到均衡的缓存需求策略称为最优缓存策略。迭代的最终结果是,所有的视频服务提供商和网络运营商均达到了纳什均衡(p*,s*),即子博弈完美纳什均衡。在此均衡状态下,博弈的任何参与者均无法通过私自改变策略得到更高的收益。
迭代算法伪代码描述如下:
MNOset N={1,2,...,n};
VSPset M={1,2,...,m};
t=0;
Initialize pν, for ∀ν∈N; suν, for∀u∈M,ν∈N;
while (the termination conditions are not met)do
for (MNO ν, ν=1,...,n)do
MNO ν adjusts price strategy pν according to (14) and (15);
end for
while (|suν(τ+1)-suν(τ)|>ε)do
during each epoch Δτ, each VSP u adjusts its caching demand strategy suν by equation (12) and (13);
end while;
if (|pν(t+1)-pν(t)|≤ε) then
break
else
t=t+1;
end if
end while
整个迭代算法过程分为网络运营商价格策略调整阶段和视频服务提供商缓存需求策略调整阶段,给定各参数的初始值后,执行以下过程:
1)网络运营商价格策略调整:在t时刻,网络运营商根据式(14)和式(15)调整自身的价格,并将价格策略公布。
2)视频服务提供商缓存需求策略调整:视频服务提供商在新价格策略下,在每个迭代周期Δτ内,根据式(12)和式(13)调整在各运营商处的缓存需求,直到所有视频服务提供商均达到最大收益,调整后策略与调整前策略之差绝对值小于等于收敛精度ε,即达到纳什均衡。
3)如果在t+1时刻,所有网络运营商收益均达到最大,调整后策略与调整前策略之差绝对值小于等于收敛精度ε,则迭代结束。否则,返回过程1)继续调整价格策略。
5 仿真与分析
在本节中,我们对提出的缓存激励算法进行仿真分析并验证其性能。仿真环境为MATLAB R2018a, Inter(R)Core(TM)i5-3230 CPU、4G内存、Windows 8 Sp1(64位)。仿真环境中存在2个不同的网络运营商,每个网络运营商都有若干个边缘缓存节点。运营商1提供的存储空间为200 GB,运营商2提供的存储空间为300 GB。在运营商覆盖区域中,3个视频服务提供商彼此竞争这些存储空间,仿真中,每个视频服务提供商的初始缓存需求策略均设为0.1 GB,对应的参数α分别为0.3、0.6和0.9。网络运营商的初始价格策略均为0.1。收敛精度ε为10-3,缓存策略迭代步长k和价格策略迭代步长l均为0.1,视频服务提供商的收益因子λu为200。下面对仿真结果进行分析。
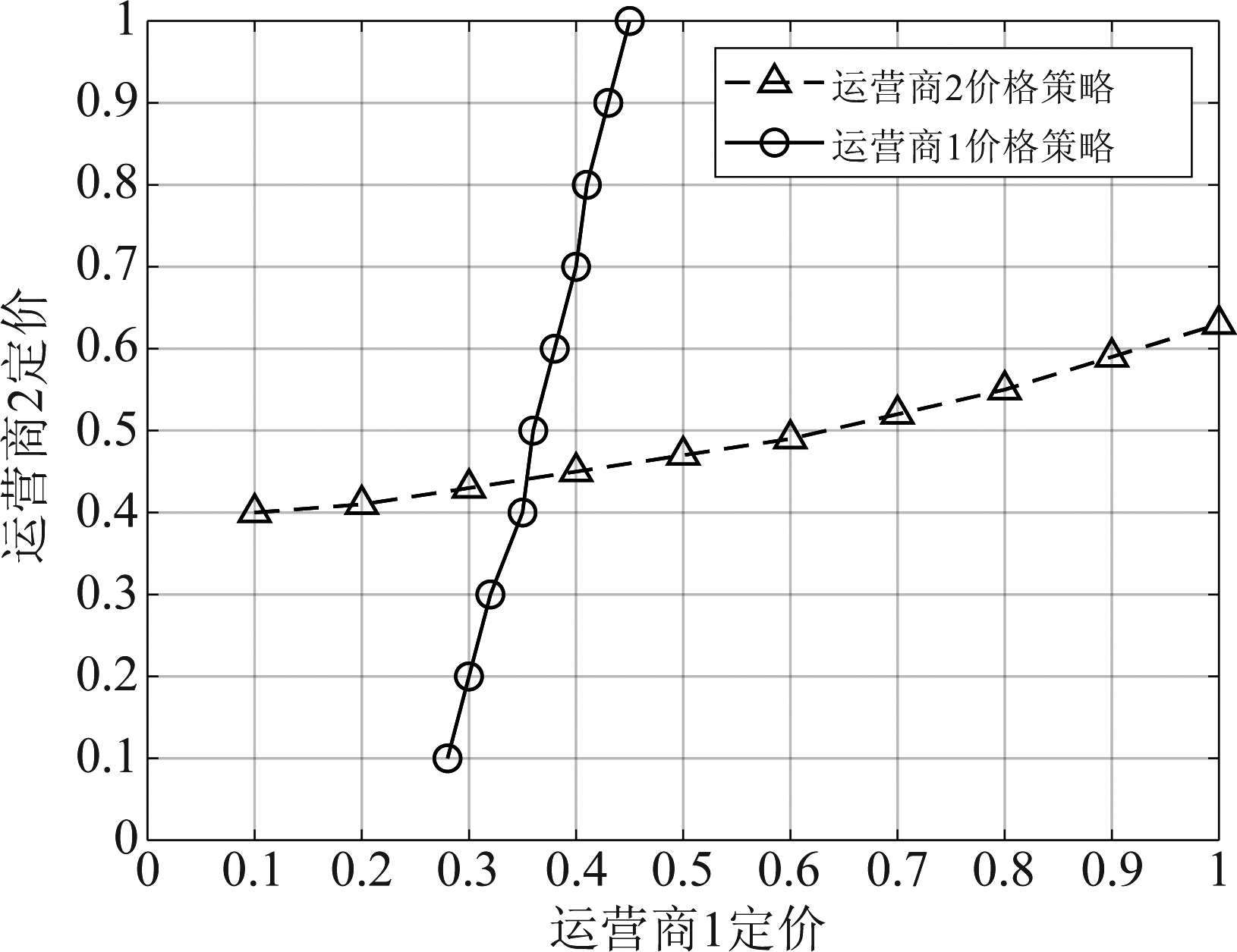
图2 运营商之间的最优价格曲线
Fig.2 Optimal Prices of MNO1 and MNO2
图2给出了两个网络运营商之间的价格动态变化关系曲线。图中两条曲线分别表示运营商1的最优价格曲线和运营商2的最优价格曲线。两条曲线上的点分别表示某运营商针对另一运营商价格的最优价格策略。两条曲线的交点表示两运营商的价格均衡点,在此价格策略下,两运营商收益均达到最大,任何一方改变自身的价格策略,均不能使自身效用增加。
图3显示的是给定运营商最佳定价的情况下,各视频服务提供商在网络运营商1处所购买的缓存空间总量,由于网络运营商1提供的存储空间有限,所以各视频服务提供商根据运营商1的定价策略,相互竞争存储空间。由图可知,对于不同的α值,α越大,说明流行视频文件的分布越集中,用户访问命中已缓存视频的概率越高,所以,缓存较少数量的视频内容即可获得较高的收益。
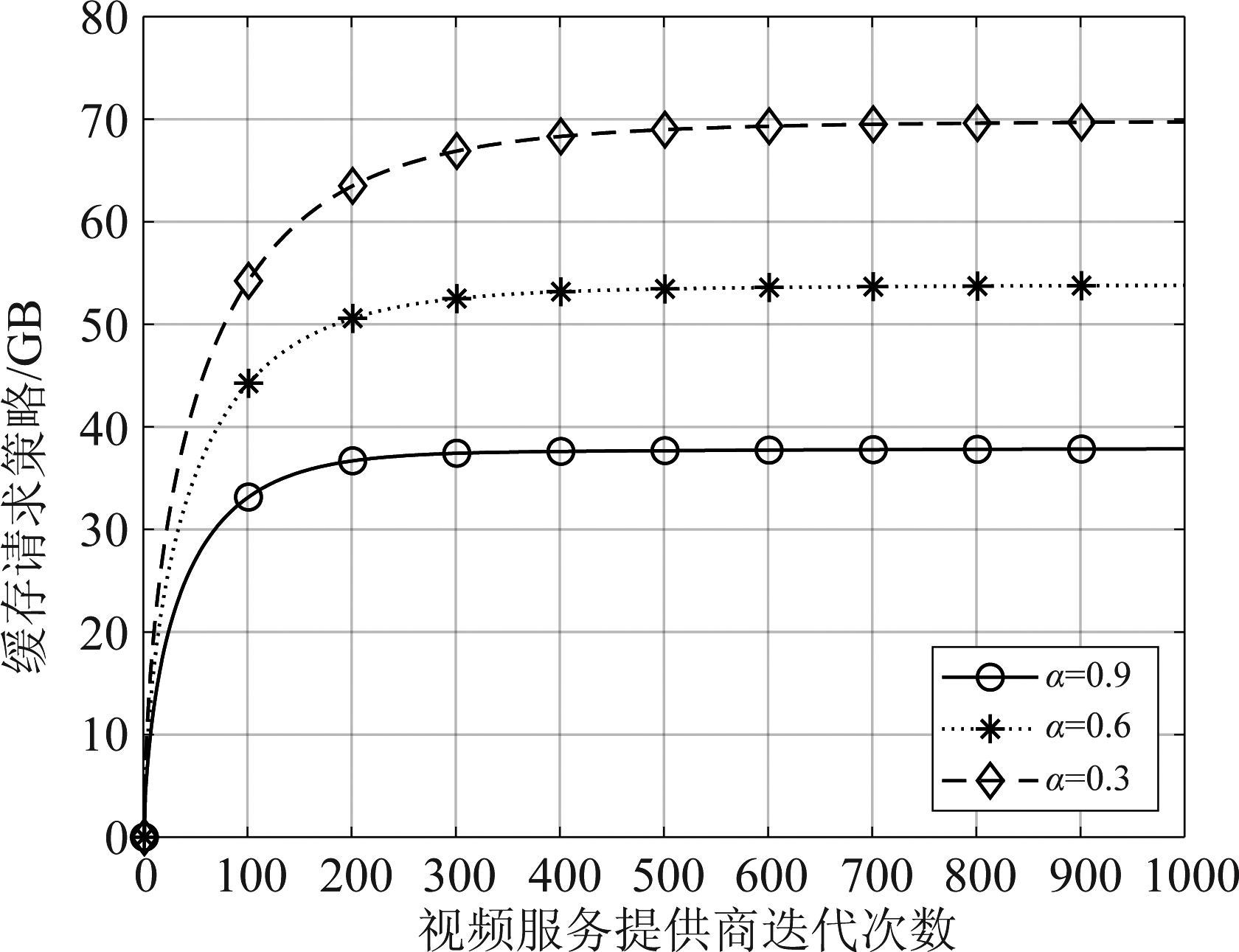
图3 视频服务提供商缓存购买量曲线
Fig.3 VSP’s caching quantity versus number of iteration
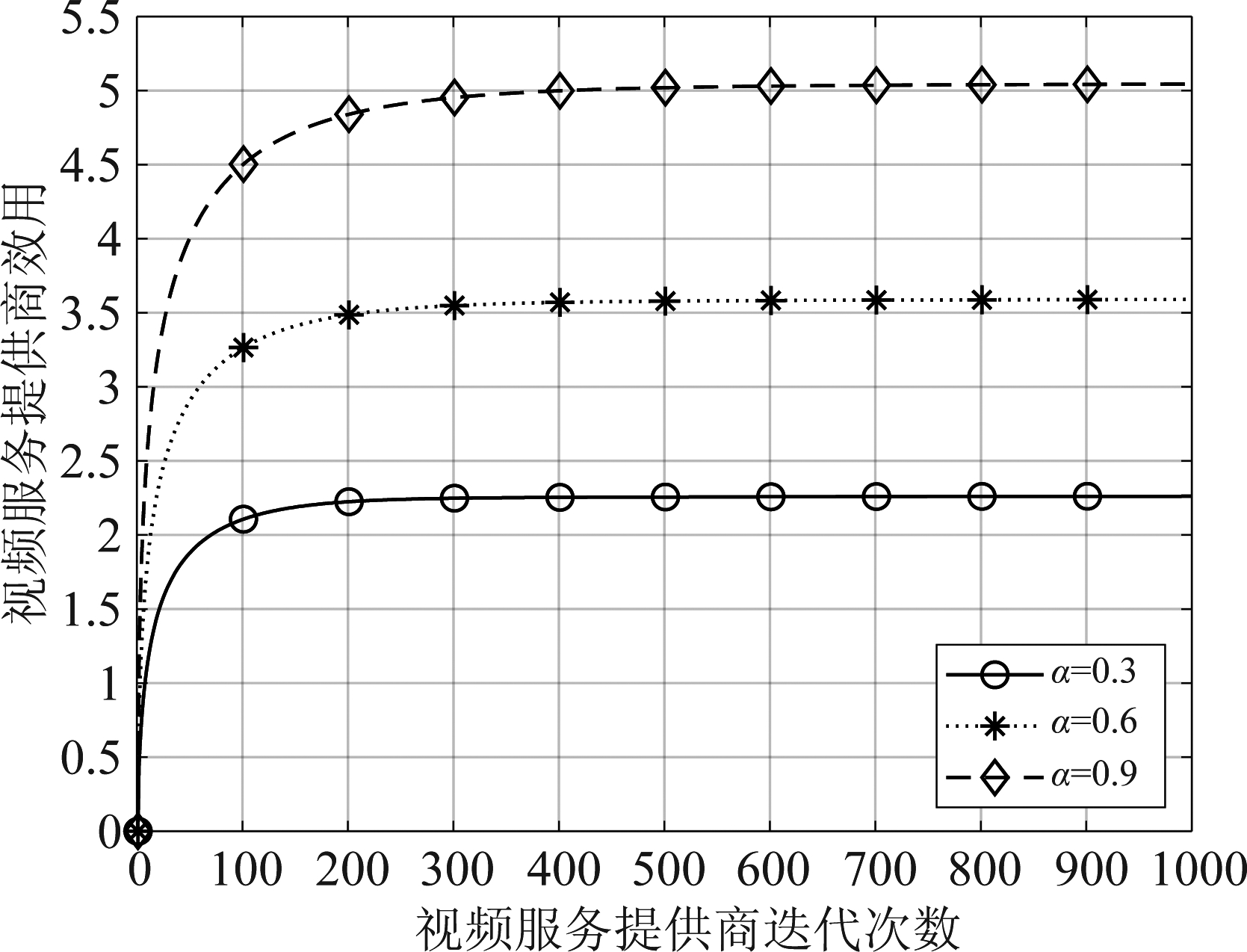
图4 视频服务提供商效用变化曲线
Fig.4 VSP’s utility versus number of iteration
图4显示的是在运营商最佳定价的情况下,视频服务提供商在迭代过程中,各自效用函数的变化曲线。由图可知,对于不同α值的视频服务提供商,随着迭代次数的增加,视频服务提供商的收益均收敛到最大值。由于α越大,表示用户访问的视频文件分布越集中,所以,虽然视频服务提供商1(α=0.3)的缓存空间购买总量较多,但其缓存命中率较低,其效用在三者中最低。注意,造成效用低的原因也可能是缓存空间的购买成本过大。
图5给出了随着缓存空间购买量的增加,本文算法与用户QoS优先算法的单位成本收益对比。单位成本收益定义为视频服务提供商的收益与购买缓存空间所花费的成本之比。用户QoS优先算法是指为了最大化所服务用户的QoS,视频服务提供商不考虑运营商的定价情况,尽可能多地购买缓存空间。由于不考虑网络运营商的定价,虽然视频服务提供商有较多的缓存空间,但其支出成本很高,所以其平均单位成本收益较低。本文算法综合考虑不同网络运营商的定价,视频服务提供商的单位成本收益较高,随着缓存空间购买量的增加,逐渐趋于平稳。
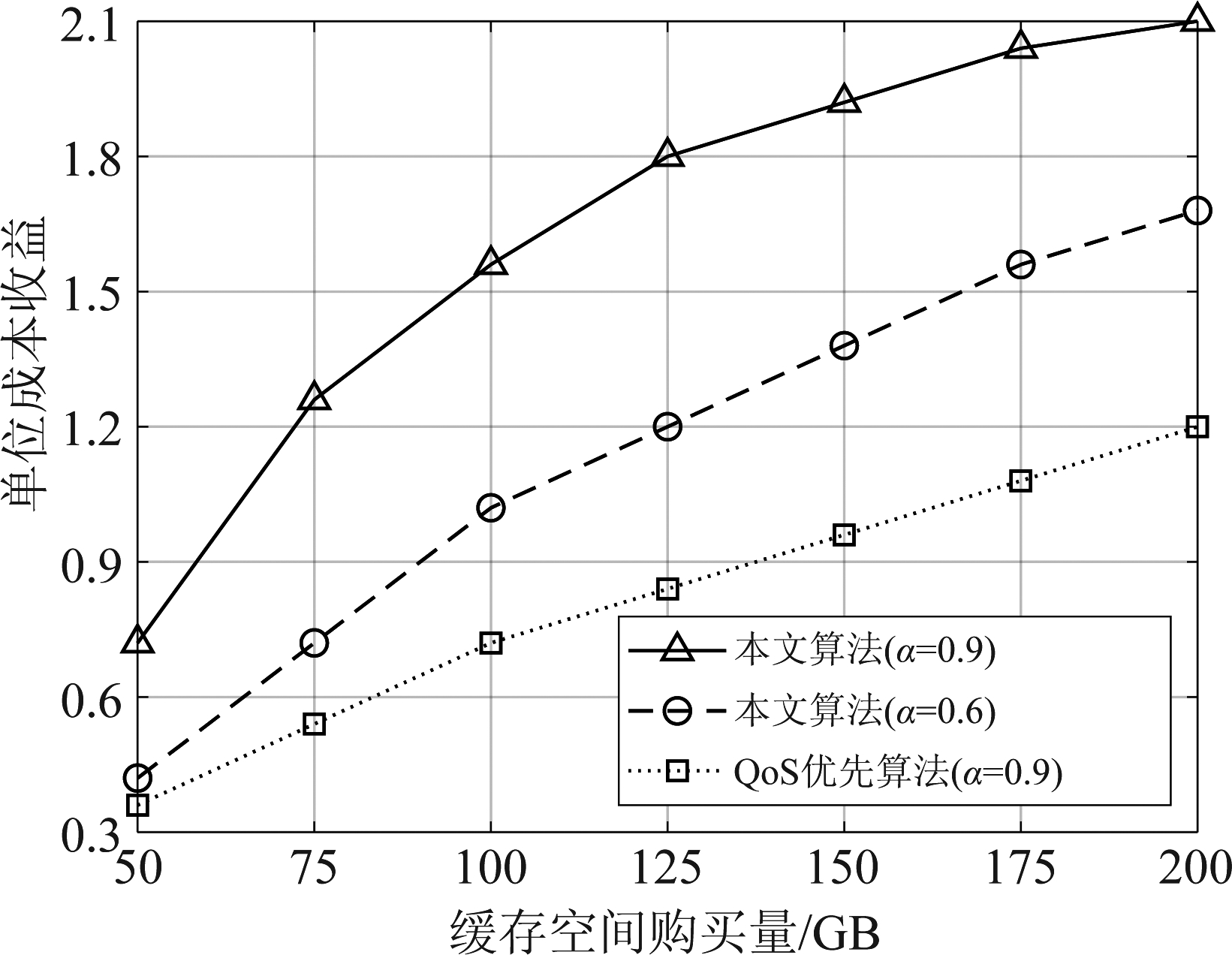
图5 不同算法的单位成本收益对比
Fig.5 Comparison of unit cost and income of different algorithms
6 结论
在本文中,我们利用多主多从Stackelberg博弈对多运营商多视频服务提供商之间的缓存激励问题进行建模,证明了视频提供商效用函数满足凹函数特性,保证了视频服务提供商之间非合作博弈纳什均衡点的存在。通过视频服务提供商的缓存迭代公式以及网络运营商的价格迭代公式,利用分布式迭代算法对博弈问题进行求解,在运营商最优定价的情况下,得到各视频服务提供商的最优缓存策略,网络运营商和视频服务提供商均获得了最大收益。本文尚未考虑相同视频内容的重复缓存、运营商的运营成本等因素,下一步工作将综合考虑不同网络运营商之间合作以及运营商成本等因素,进一步完善效用函数的构建。
[1] Cisco. Cisco visual networking index: global mobile data traffic forecast update, 2016-2021[OL]. White Paper, https:∥www.cisco.com/c/en/us/solutions/collateral/service-provider/visual-networking-index-vni/white-paper-c11-738429.html, 2017.
[2] Bastug E, Bennis M, Debbah, Mérouane. Living on the edge: The role of proactive caching in 5G wireless networks[J]. IEEE Communications Magazine, 2014, 52(8): 82- 89.
[3] Paschos G, Ejder Ba
Land I, et al. Wireless Caching: Technical Misconceptions and Business Barriers[J]. IEEE Communications Magazine, 2016, 54(8): 16-22.
[4] Ramanan B A, Drabeck L M, Haner M, et al. Cacheability analysis of HTTP traffic in an operational LTE network[C]∥in Proc. Wireless Telecommun. Symp.(WTS), Phoenix, AZ, USA, 2013: 1- 8.
[5] Hosny S, Alotaibi F, El Gamal H, et al. Towards a mobile content marketplace[C]∥2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications(SPAWC), Stockholm, 2015: 675- 679.
[6] Chen Z, Liu Y, Zhou B, et al. Caching incentive design in wireless D2D networks: A Stackelberg game approach[C]∥IEEE International Conference on Communications. IEEE, Kuala Lumpur, 2016: 1- 6.
[7] 田厚平, 郭亚军, 王学军. 一类基于进化博弈的多主多从Stackelberg对策算法[J]. 系统工程学报, 2005(3): 303-307.
Tian Houping, Guo Yajun, Wang Xuejun. A Multi-master and Multi-slave Stackelberg Game Algorithm Based on Evolutionary Game[J]. Journal of Systems Engineering, 2005(3): 303-307.(in Chinese)
[8] Yang C, Yao Y, Chen Z, et al. Analysis on Cache-enabled Wireless Heterogeneous Networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(1): 131-145.
[9] Shen F, Hamidouche K, Bastug E, et al. A Stackelberg Game for Incentive Proactive Caching Mechanisms in Wireless Networks[C]∥Global Communications Conference. IEEE, Washington, DC, 2016: 1- 6.
[10] ALPCAN T, BASAR T. A game-theoretic framework for congestion control in general topology networks[C]∥Proceedings of the 41st IEEE Conference on Decision and Control. Las Vegas, Nevada, USA, 2002: 1218-1224.
[11] 姜永, 陈山枝, 胡博. 异构无线网络中基于Stackelberg博弈的分布式定价和资源分配算法[J]. 通信学报, 2013, 34(1): 61- 68.
Jiang Yong, Chen Shanzhi, Hu Bo. Stackelberg games-based distributed algorithm of pricing and resource allocation in heterogeneous wireless networks[J]. Journal on Communications, 2013, 34(1): 61- 68.(in Chinese)
