1 引言
随着移动互联网和智能终端技术的快速发展,视频点播(VoD,Video on Demand)已成为移动通信系统中最热门的业务,带来移动数据流量的爆炸式增长[1]。为了满足移动用户的VoD业务需求,内容分发网络(CDN,Content Delivery Network)的概念最近被引入到移动通信系统中,称为无线边缘缓存[2]。
无线边缘缓存与有线CDN相比的主要区别之一是边缘缓存节点的存储容量通常较小[3]。这导致传统适用于CDN的被动式缓存策略在无线边缘缓存中的性能一般较差。为了提高缓存性能,已有文献对主动式边缘缓存策略进行了优化设计,例如文献[4]和[5]优化了异构网的概率缓存策略来最大化成功传输概率和区域频谱效率,文献[6]研究了小小区网络中缓存和推荐策略的联合优化,文献[7]和[8]研究了多播网络中的主动缓存策略,文献[9]和[10]研究了设备间直接通信网络中的缓存策略。
文件库大小对主动式边缘缓存的性能有着重要影响。文献[11]指出主动式缓存的命中率取决于存储空间与文件库大小的比值。这意味着为了达到相同的缓存性能,所需的存储资源随着文件库增大而增长。文献[12]指出当存储资源给定时,随着文件库大小的增长,典型缓存算法的性能都会下降。可见,文件库大小对于无线边缘缓存的性能和资源开销具有直接影响,分析文件库大小及其与系统参数之间的内在联系具有重要的研究意义。
值得指出的是,无线边缘缓存所涉及的文件库并不能包含视频网站发布的全部内容,这是因为移动网络通常只能观测到那些被移动用户请求过的视频[注]通过与视频网站在内容共享方面进行合作,移动网络运营商未来有可能获得视频网站发布的全部内容,但目前这种合作机制还并不完善。。因此,面向无线边缘缓存,需要分析的文件库是指用户请求的所有文件。文献[13]对用户请求的文件库大小进行了猜测。考虑到用户趋向于请求热门视频,因此作者推测用户请求的文件数会随着请求数呈亚线性增长。如此较慢的文件库增长速度符合无线边缘缓存的要求,但这一猜测缺少严格的理论分析和实测数据的验证。
本文面向无线边缘缓存,对用户请求的文件库大小进行理论分析和数据验证。基于Zipf文件流行度模型[14],分析了用户请求的文件库大小与请求数、视频网站文件总数、流行度参数等因素的内在关系。研究结果表明,相对于视频网站的文件数,当用户请求数较少时,请求的文件库大小随请求数线性增长,而当用户请求数较多时,请求的文件库大小随请求数呈负指数增长。我们通过仿真对所得到理论结果的准确性进行了验证,并通过实测数据验证了结论的有效性。
论文剩余内容安排如下:第2节介绍系统模型,第3节介绍理论分析结果,第4节进行仿真和数据验证,第5节对本文进行总结。
2 系统模型
考虑给定区域内(例如宏小区或微小区)用户对一个视频网站进行访问。设视频网站发布的视频总数为N,视频流行度服从Zipf分布,即第i个流行视频的请求概率为[13]:
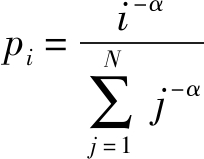
(1)
其中α为Zipf分布参数,它刻画了视频请求概率分布的倾斜程度,α越大则表示用户对热门视频的请求越集中。
为了分析用户请求的视频数,假设用户对视频的请求过程统计独立同分布,即每次请求都会以概率pi对第i个流行视频发起请求。当给定区域内的用户发起M次请求时,第i个流行视频被请求的概率可以表示为:
qi=1-(1-pi)M
(2)
其中(1-pi)M为M次请求都未请求第i个流行视频的概率。
针对用户对视频的随机请求,定义移动网络在给定区域内(如一个宏小区或微小区)所能观测到的平均视频数为用于在该区域设计边缘缓存的文件库大小,记为Nf。由式(2)可得,当用户发起M次请求后移动网络所能观测的视频数的均值为:
(3)
从式(3)中可以看出,视频文件库的大小Nf与视频网站的文件总数N、用户请求数M和视频流行度参数α有关。下面将分析它们之间的内在联系。
3 视频文件库大小分析
为了得到视频文件库大小Nf的显示表达式,首先对视频流行度pi的表达式进行以下近似:
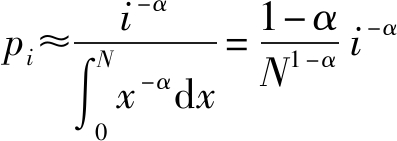
(4)
其中将离散求和近似为连续积分![]() 其准确性随着N的增加而提高。由于视频网站的文件总数N通常很大,因此该近似具有很好的准确性。
其准确性随着N的增加而提高。由于视频网站的文件总数N通常很大,因此该近似具有很好的准确性。
由此,式(3)可以近似为:
(5)
式(5)可以进一步近似为:
(6)
其中第一步近似与式(4)类似,把离散求和近似为连续积分,当N较大时该近似准确;第二步近似考虑一阶泰勒近似e-t≈1-t,该近似在t≪1时准确,在式(6)中![]() 其取值范围为
其取值范围为![]() 由于在实际情况下N较大,因此t≪1成立,即该近似准确;最后一步等式来自变量替换y=x-α。
由于在实际情况下N较大,因此t≪1成立,即该近似准确;最后一步等式来自变量替换y=x-α。
经过上述近似和变换,得到了Nf与参数N、M和α的连续显示表达式。在此基础上,下面将对Nf与这些参数之间的渐近关系进行分析。考虑到式(6)的积分项对于任意流行度参数α通常很难进行化简,并且在实际场景下流行度参数α通常小于1,为了得到具有显示表达式的理论关系,下面将分别考虑α→0和α=0.5两种特殊情况,然后再通过仿真来说明在这两种情况下得到的结论同样适用于α为任意值的场景。
3.1 情况一:α→0
当α→0时,由式(1)可知视频流行度![]() 即所有视频具有相同的流行度。此时,由式(3)可得视频文件库大小Nf为:
即所有视频具有相同的流行度。此时,由式(3)可得视频文件库大小Nf为:
(7)
进一步考虑在实际情况下视频网站的文件总数N通常很大,则上式可以表示为:
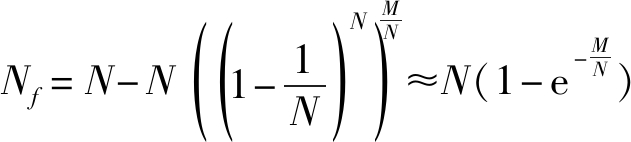
(8)
其中近似来自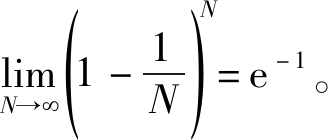 当请求数M≪N时,由一阶泰勒近似可得
当请求数M≪N时,由一阶泰勒近似可得![]() 因此由式(8)可得Nf≈M。
因此由式(8)可得Nf≈M。
可见,如果所有视频具有相同的流行度(即α→0),则Nf会以负指数速度趋于视频网站的文件总数N(即式(8)),若用户的请求数M较少,则平均请求视频数Nf等于请求数M,这是因为此时所有视频具有相同的请求概率。
3.2 情况二:α=0.5
选择α=0.5进行分析是由于此时式(6)中![]() 的指数项为整数,以便于得到解析的理论关系。
的指数项为整数,以便于得到解析的理论关系。
利用如下的积分公式:
(9)
以及分部积分法,可以把式(6)给出的Nf表达式进一步表示为:
(10)
其中![]() 为指数积分函数,E1(x)=-Ei(-x)为一阶指数积分函数。
为指数积分函数,E1(x)=-Ei(-x)为一阶指数积分函数。
根据[15],E1(x)可以准确近似为:
(11)
其中![]()
把式(11)代入式(10)得到的平均请求视频数Nf表达式仍然比较复杂,难以直接得到Nf与视频网站的文件总数N和用户请求数M间的简洁关系。为此,下面考虑M≪N和M≫N两种场景。
(1)M≪N
当M≪N时,式(10)中的![]() 可以近似为:
可以近似为:

(12)
其中第一步近似考虑了当![]() 时,式(11)中参数q≈0,h≈1;第二步近似考虑了
时,式(11)中参数q≈0,h≈1;第二步近似考虑了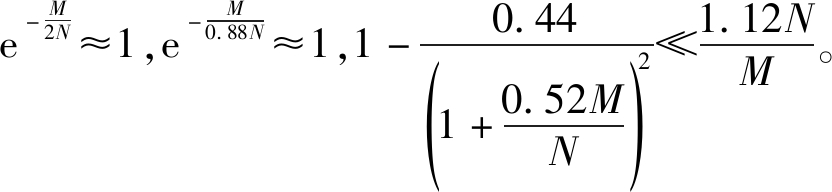
类似地,![]() 可以近似为:
可以近似为:
(13)
进一步考虑M≪N时的以下一阶泰勒近似结果:
(14)
经过简单计算可由式(10)得到Nf的近似表达式为:
(15)
式(15)表明,当请求数M较小时,平均请求视频数Nf随M近似线性增长。
(2)M≫N
当M≫N时,式(10)中的![]() 可以近似为:
可以近似为:
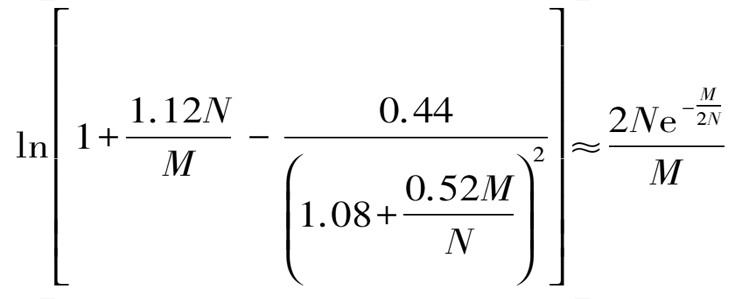
(16)
其中第一步近似考虑了当![]() 时,式(11)中参数q很大,因此h≈h
时,式(11)中参数q很大,因此h≈h ;第二步近似考虑了
;第二步近似考虑了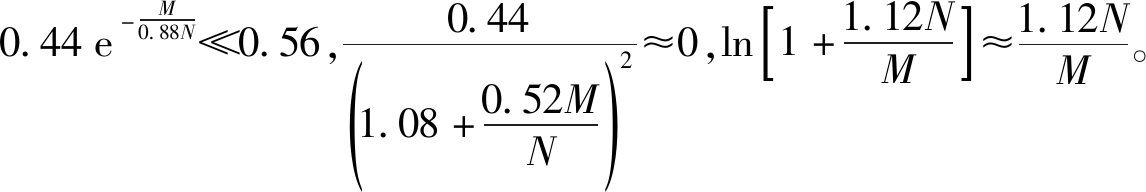
类似地,![]() 可以近似为:
可以近似为:
(17)
把式(16)和(17)代入式(10)并进行简单计算,可得到Nf的近似表达式为:
(18)
式(18)表明,当请求数M较大时,平均请求视频数Nf随M呈负指数增长,增速越来越慢。
3.3 分析结果讨论
表1对以上两种情况的分析结果进行了总结。
表1 文件库大小分析结果
Tab.1 Analytical results of file catalogue size
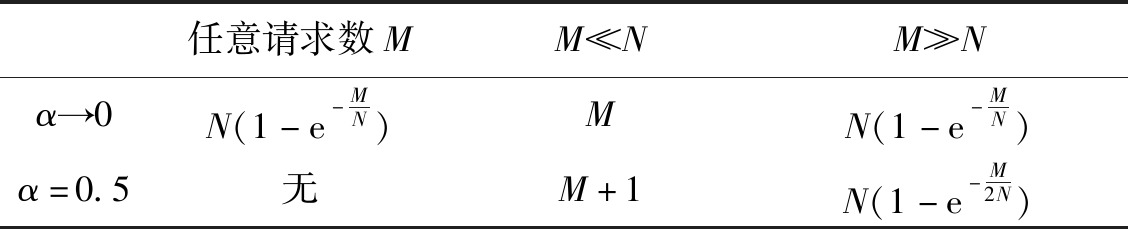
任意请求数MM≪NM≫Nα→0N(1-e-MN)MN(1-e-MN)α=0.5无M+1N(1-e-M2N)
从表1中可以看出,无论是α→0还是α=0.5,视频文件库大小Nf与请求数M、视频网站文件总数N之间呈现类似的关系,即当请求数M较小时,Nf随M线性增长,当请求数M较大时,Nf随M按负指数增长。需要说明的是,表1所列结果是在视频流行度服从Zipf分布的假设下得到的,当这一假设不成立时,Nf与M和N之间的关系可能会发生改变。
在实际场景中,典型视频网站的文件数N通常在百万至千万级别,而蜂窝小区级区域内用户的请求数通常有限,例如下一节给出的某校园网100天内对一个典型视频网站的请求次数约为十万量级,可见实际系统一般工作在M≪N场景。此时,文件库大小随请求数的增长并非如文献[12]所推测的亚线性关系,而是线性增长。
文件库大小增长速度较快对提升无线边缘缓存性能带来很大的挑战,这意味着在保证相同缓存命中率的条件下需要部署更多的存储资源。另一方面,由于视频请求数与区域覆盖面积有关,不同类型的小区(例如宏小区和微小区)的请求数(或请求到达率)通常不同,因此所对应的视频文件库大小也会不同。在面向异构网设计缓存策略时应该考虑这一差异,而现有工作一般假设所有小区的文件库相同。
4 仿真和实测数据验证
本节通过仿真来验证在第3节理论推导中所引入的近似的准确性,并基于在校园网中采集的爱奇艺(iQIYI)视频网站的请求记录来验证所得出理论结果的正确性。
4.1 近似准确性验证
首先,在推导平均视频请求数(6)时,我们引入连续积分来近似离散求和,并使用了一次泰勒近似。为了验证近似的合理性,在α=0.7和0.5、N=100、M取值范围为0~1000时对准确理论表达式(3)和近似表达式(6)进行了比较,结果如图1所示。可以看出,近似表达式和解析表达式的趋势一致、且相对误差较小。
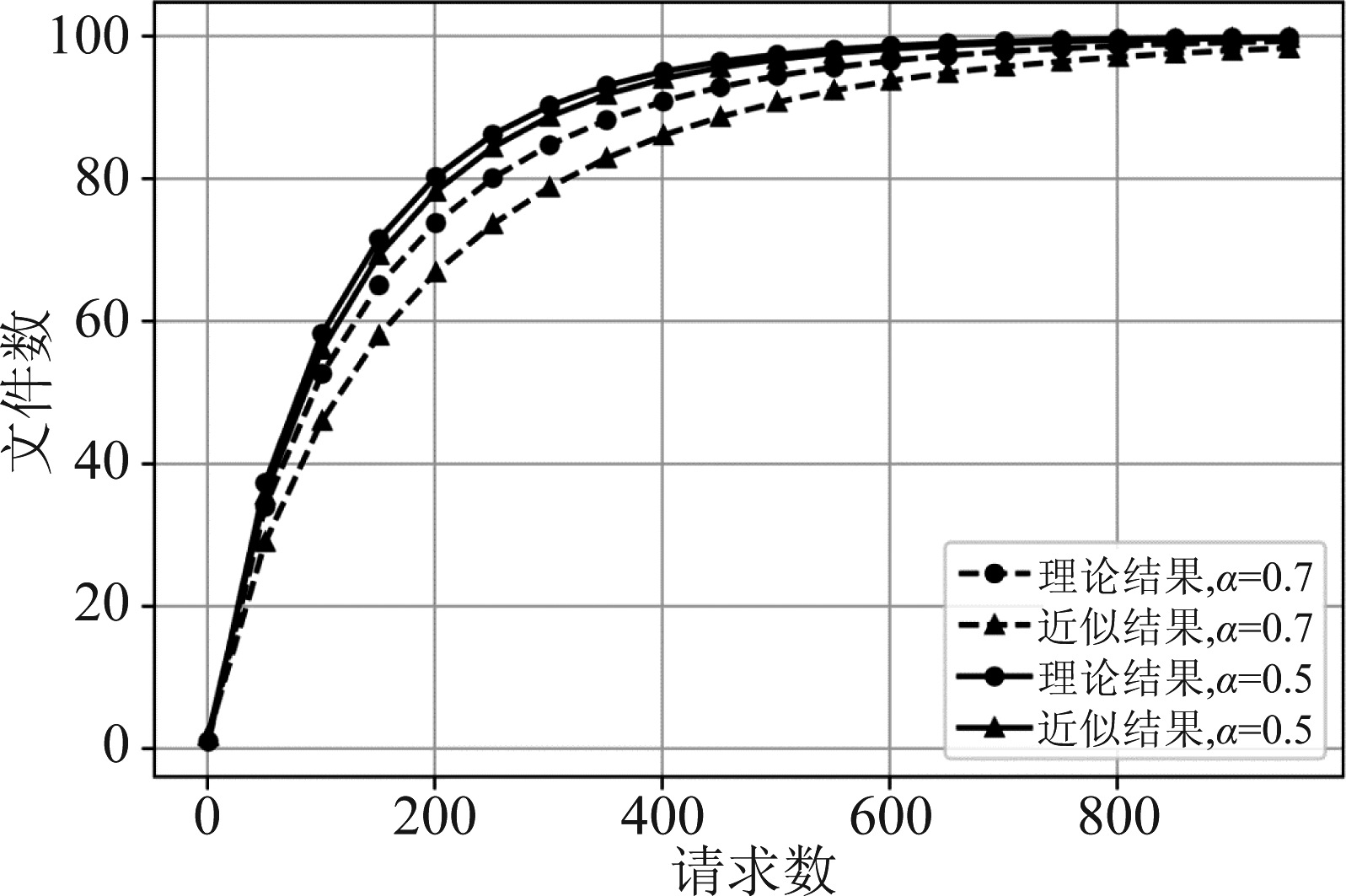
图1 近似表达式的准确性
Fig.1 Accuracy of the approximate expressions
其次,为了验证在α→0情况下式(8)中近似结果的准确性,在a=0.1、N=100、M取值范围为0~1000的情况下,比较近似结果和式(3)给出的理论结果,如图2(a)所示。可以看出,式(8)的近似很准确,同时当M≪N时,Nf≈M成立。为了验证当α=0.5时,M≪N和M≫N两种情况下近似表达式(16)和(19)的准确性,在α=0.5、N=100、M取值范围为0~1000时比较了理论和近似结果,结果如图2(b)所示。可以看出当M<0.2N或M>8N时,近似结果很准确。为了进一步说明在α=0.5、M≫N情况下近似表达式(19)的准确性,图2(c)给出了近似结果与理论结果之间的比值,可以看出随着M的增加,两者之间的差距越来越小。
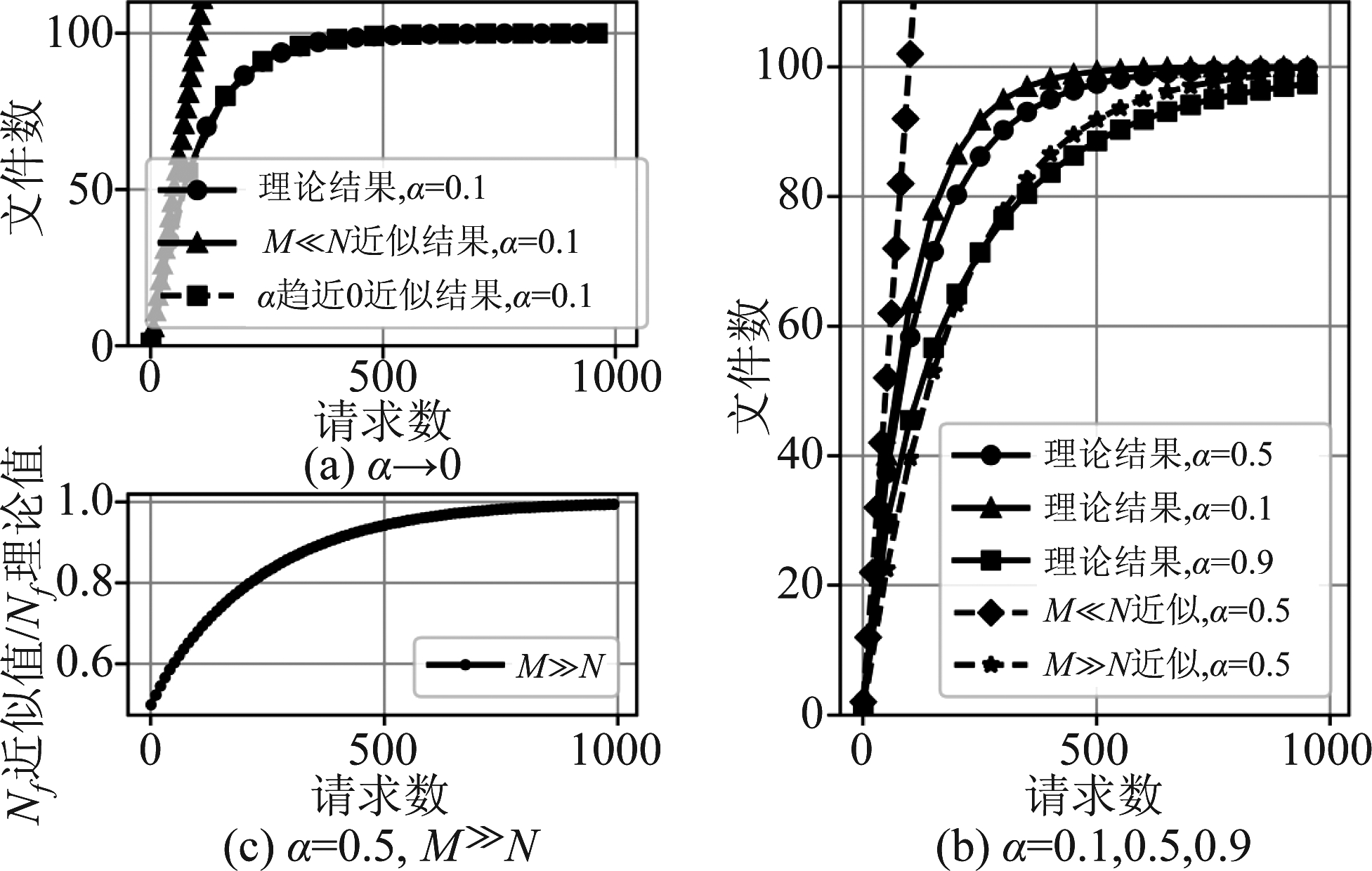
图2 理论结果准确性验证
Fig.2 Accuracy validation of the theoretical results
最后,为了验证所得到的文件库大小Nf随M先线性增长、后负指数增长的规律适用于任意α,在图2(b)中给出了α=0.1和α=0.9时的理论结果,从中可以观察到类似的增长规律。
4.2 实测数据验证
本节基于在某校园网中采集的爱奇艺视频网站匿名请求记录来验证理论分析结果的有效性。数据集包含校园网连续100天内9179位匿名用户对爱奇艺视频的请求记录,其中总请求数为131066,请求的总视频数为46754,视频流行度服从参数为0.7334的Zipf分布,拟合结果如图3所示。
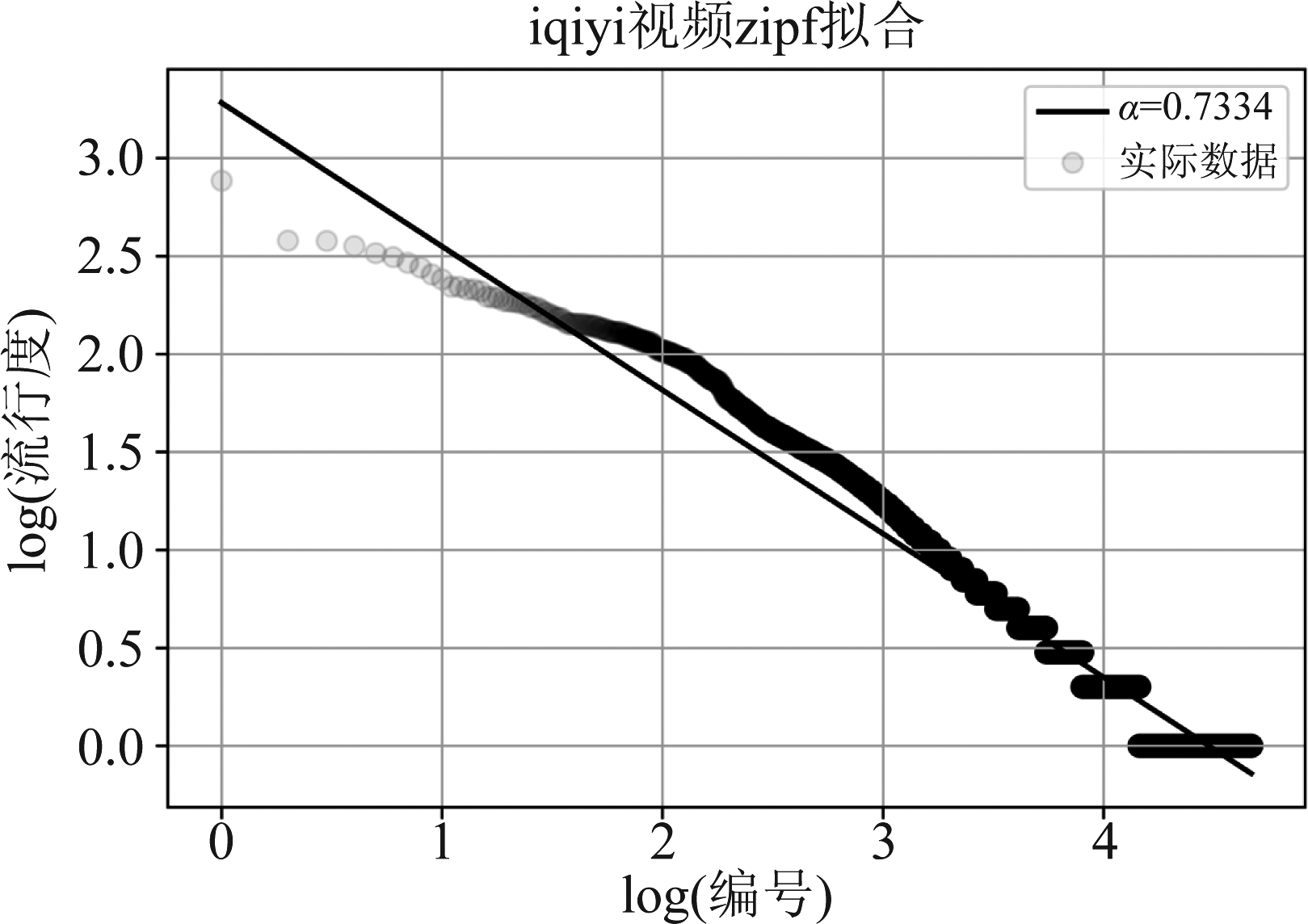
图3 爱奇艺数据集下视频流行度的Zipf拟合
Fig.3 Zipf fitting of video popularity distribution under the iQIYI DataSet
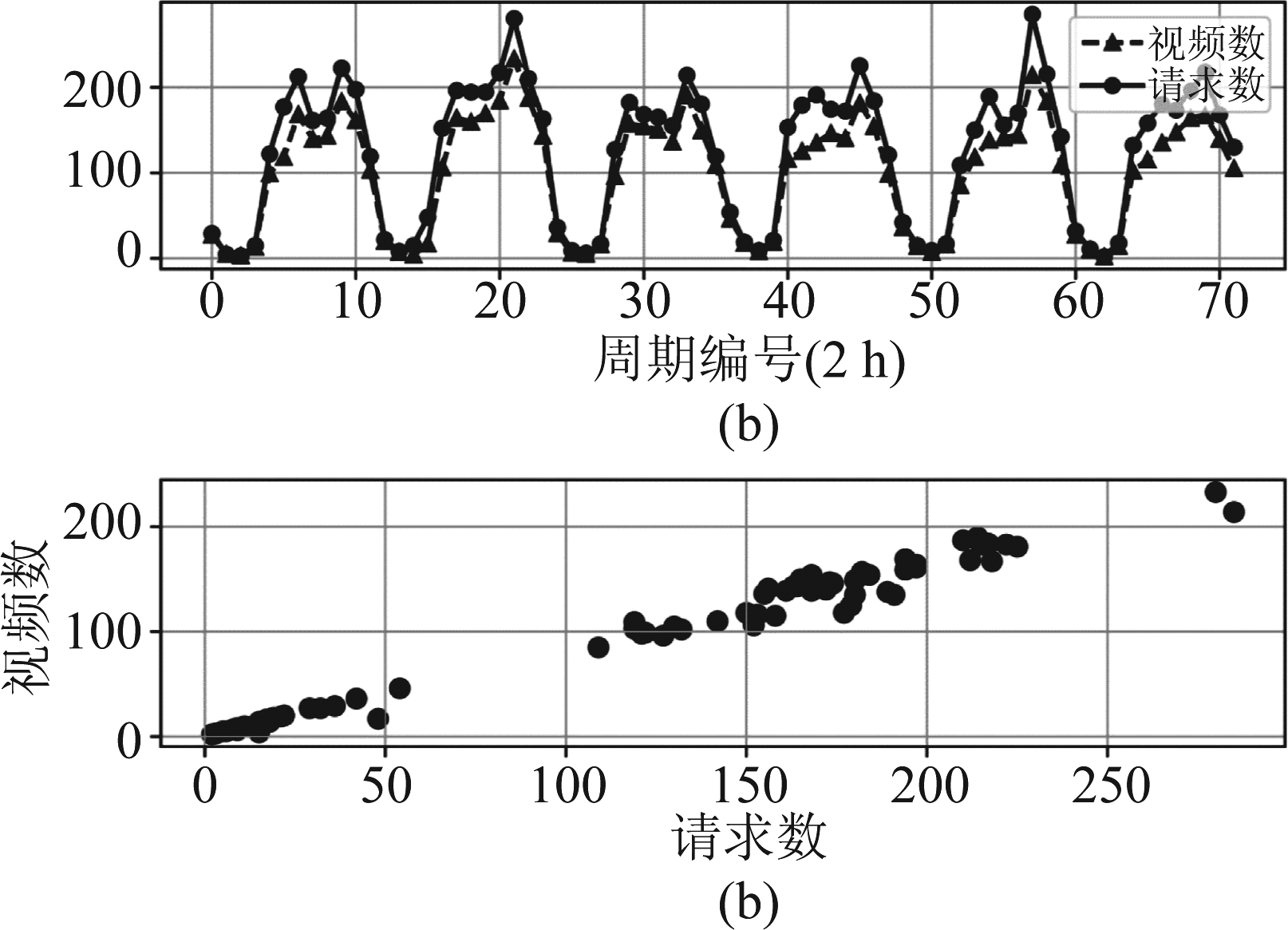
图4 爱奇艺数据集下请求的视频数Nf与请求数M的关系
Fig.4 The number of requested videos Nf v.s. the number of requests M under the iQIYI DataSet
首先,基于采集的数据集,以两小时为周期统计连续6天中每个周期内用户发起的请求数M和请求的视频数Nf,结果如图4(a)所示。可以看出,用户的请求数(或请求到达率)不是恒定的,而是呈现周期性变化,周期为一天,且请求的视频数Nf随着请求数M同步变化。在图4(b)中,我们把图4(a)中的结果以散点图的形式表示,其中横轴为请求数M,纵轴为视频数Nf。可以看出,Nf随M近似线性增长。这是因爱奇艺网站的视频总数N远大于请求数M,根据表1给出的理论分析结果,此时Nf~M关系位于线性增长区域。
图5(a)给出了100天内用户请求的视频数Nf随请求数M的增长关系。与图4(b)相比,虽然图5(a)的横轴取值范围更大(最大请求数为131066),但仍远远小于爱奇艺网站的视频总数N,因此Nf~M关系仍然接近线性。
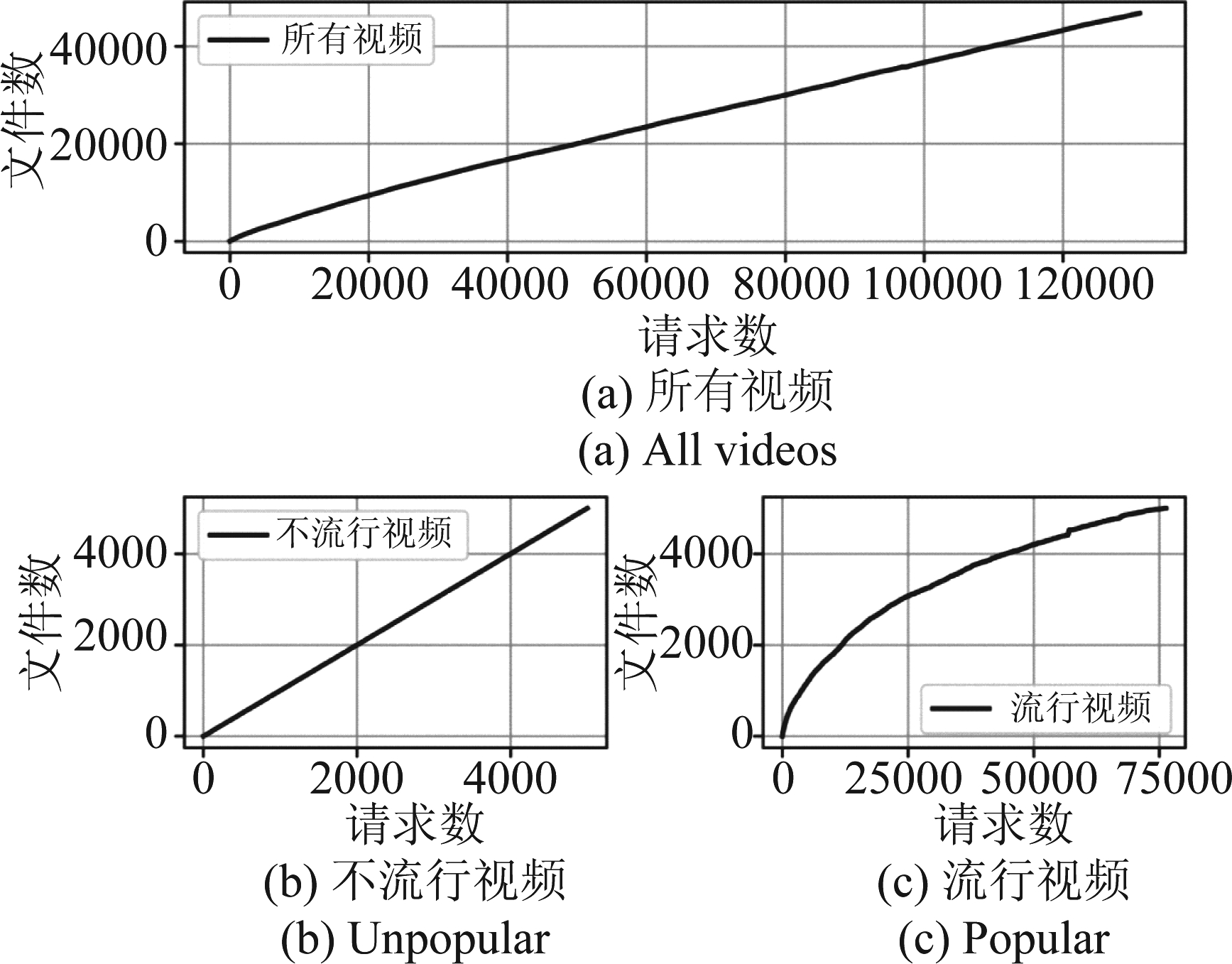
图5 流行视频和不流行视频的Nf~M关系
Fig.5 Nf~M relationships for popular and unpopular videos
为了观察Nf~M关系的亚线性增长区域,我们从采集的爱奇艺数据集中人为抽取出两个子集。具体来说,假设有两个小型视频网站,每个网站只有5000部视频,即N=5000。其中第一个网站的视频是从爱奇艺数据集中抽取的5000部不流行视频,第二个网站的视频是从爱奇艺数据集中抽取的5000部最流行视频。然后,我们从爱奇艺数据集中抽取出这两个模拟网站的请求记录,得到Nf~M关系曲线如图5(b)和5(c)所示。
在图5(b)中,不流行视频组成的模拟网站的视频流行度参数约为α=0,用户对它的请求数较少,因此Nf~M处于近似线性增长区。在图5(c)中,流行视频组成的模拟网站的请求数M远多于文件数N=5000,因此Nf~M关系由线性增长区过渡到了负指数增长区域。
5 结论
文件库大小对无线边缘缓存的性能具有重要的影响。本文对文件库大小与用户请求数、文件总数、流行度参数等因素的内在关系进行了渐近分析。研究结果表明,相对于文件总数,当请求数较少时,文件库大小随请求数线性增长,否则,文件库大小随请求数呈负指数增长。仿真结果和实测数据验证了所得理论结果的准确性。在实际系统中,无线边缘节点覆盖范围内的用户请求数通常远小于视频网站的文件总数,因此用户请求的文件库大小随请求数线性增长。文件库大小增长速度较快一方面对提升无线边缘缓存性能带来严峻挑战,另一方面也说明在面向异构网设计缓存策略时应考虑不同类型小区具有不同大小的文件库。
[1] Index C V N. Cisco Visual Networking Index: Forecast and Methodology, 2016-2021[J]. Complete Visual Networking Index (VNI) Forecast, 2017, 12(1): 749-759.
[2] Golrezaei N, Dimakis A G, Molisch A F, et al. Wireless video content delivery through distributed caching and peer-to-peer gossiping[C]∥Signals, Systems and Computers(ASILOMAR), 2011 Conference Record of the Forty Fifth Asilomar Conference on. IEEE, 2011: 1177-1180.
[3] Liu D, Chen B, Yang C, et al. Caching at the wireless edge: design aspects, challenges, and future directions[J]. IEEE Communications Magazine, 2016, 54(9): 22-28.
[4] Li K, Yang C, Chen Z, et al. Optimization and analysis of probabilistic caching in N-tier heterogeneous networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(2): 1283-1297.
[5] Liu D, Yang C. Caching policy toward maximal success probability and area spectral efficiency of cache-enabled HetNets[J]. IEEE Transactions on Communications, 2017, 65(6): 2699-2714.
[6] Chatzieleftheriou L E, Karaliopoulos M, Koutsopoulos I. Jointly optimizing content caching and recommendations in small cell networks[J]. IEEE Transactions on Mobile Computing, 2019, 18(1): 125-138.
[7] Cui Y, Wang Z, Yang Y, et al. Joint and competitive caching designs in large-scale multi-tier wireless multicasting networks[J]. IEEE Transactions on Communications, 2018, 66(7): 3108-3121.
[8] Hong J P, Chae S H, Lee K. Network throughput gain of multicast with user caching in heavy traffic downlink[J]. IEEE Access, 2018.
[9] Chen B, Yang C. Caching policy for cache-enabled D2D communications by learning user preference[J]. IEEE Transactions on Communications, 2018, 66(12): 6586- 6601.
[10] Ji M, Caire G, Molisch A F. Fundamental limits of caching in wireless D2D networks[J]. IEEE Transactions on Information Theory, 2016, 62(2): 849- 869.
[11] Leconte M, Paschos G, Gkatzikis L, et al. Placing dynamic content in caches with small population[C]∥INFOCOM 2016-The 35th Annual IEEE International Conference on Computer Communications, IEEE. IEEE, 2016: 1-9.
[12] Zhang N, Zheng K, Tao M. Using grouped linear prediction and accelerated reinforcement learning for online content caching[C]∥2018 IEEE International Conference on Communications Workshops(ICC Workshops). IEEE, 2018: 1- 6.
[13] Golrezaei N, Molisch A F, Dimakis A G, et al. Femtocaching and device-to-device collaboration: A new architecture for wireless video distribution[J]. IEEE Communications Magazine, 2013, 51(4): 142-149.
[14] Chen Y, Zhang B, Liu Y, et al. Measurement and modeling of video watching time in a large-scale internet video-on-demand system[J]. IEEE Transactions on Multimedia, 2013, 15(8): 2087-2098.
[15] Barry D A, Parlange J Y, Li L. Approximation for the exponential integral(Theis well function)[J]. Journal of Hydrology, 2000, 227(1- 4): 287-291.



