1 引言
三维合成孔径雷达(3D-SAR)能够获取观测场景中被测目标的三维分布及散射特性,在三维地形测绘、人体表面三维成像等领域得到了广泛应用[1-13]。目前较为常见的三维成像应用几何包括平面孔径几何[1- 6]、柱面孔径几何和球面孔径几何[7-13],相应成像算法的研究也在近些年被大量展开。相比而言,平面孔径几何结构简单且具有均匀的波数域采样,对于波数域成像算法更为适用;而柱面几何和球面几何能够获取目标更全面的散射信息。理论上,只要几何模型能够形成一个立体波数空间,就具备实现三维分辨的可能[9]。本文将阵列天线与弧形曲面孔径几何相结合,给出了一种新的弧形阵列3D-SAR系统模型。不同于现有的三维成像几何模型,本文设计系统能够实现高效的数据采集和更为宽广的观测视角,为大面积地形测绘、高效人体安检等应用提供了一种新的解决思路与可能[14-16]。
为了更好地迎合轻量化、便携化的雷达系统发展趋势和降低系统成本,本文所设计的弧形阵列3D-SAR系统采用调频连续波(FMCW)信号体制[17-18],并在高度向利用一维弧形阵列运动扫描实现二维弧形曲面孔径。基于所设计的系统模型,本文提出了一种弧形阵列3D-SAR波数域成像算法,首先利用快速傅里叶变换将信号变换到波数域,在波数域利用卷积法求解出被测目标在柱坐标系下的三维频谱,利用插值变换将其转化到笛卡尔坐标系下,最后通过三维逆傅里叶变换(IFFT)获取被测目标的三维精准聚焦[19-22]。
本文首先给出了弧形阵列3D-SAR系统的成像几何与信号模型;在此基础之上,提出了一种应用于FMCW信号的弧形阵列3D-SAR波数域成像算法,通过波数域卷积及空间变换,避免了距离近似等引起的相位误差,实现了目标的高效精准聚焦。最后,通过单点目标仿真,对成像算法性能进行了验证;通过多点目标仿真对所设计系统及成像算法的有效性进行了验证。
2 弧形阵列3D-SAR系统信号模型
弧形阵列3D-SAR系统的观测几何如图1所示。一维弧形阵列天线沿Z轴正方向运动,实现二维曲面孔径,起始位置的Z轴坐标为0,被观测目标位于圆弧曲面外侧。在实际应用过程中,弧形阵列通常有两种工作方式[23],一种是聚束模式,即弧形阵列的所有阵元天线均指向同一片观测区域,可获得更长的合成孔径有效长度,从而实现较高的方位分辨率;另一种模式是条带式,即弧形阵列的阵元天线指向阵元各自所在的方位角度方向,可获取更宽广的方位观测视角,本文设计的弧形阵列工作在该模式下。在高度向上,若观测区域的高度向观测范围大于弧形阵列在高度向上的运动总长度H,则在成像过程中需要进行高度向补零操作,以防止高度向上出现目标卷绕,将回波信号的高度向尺寸补零至观测场景的高度向尺寸即可[20]。
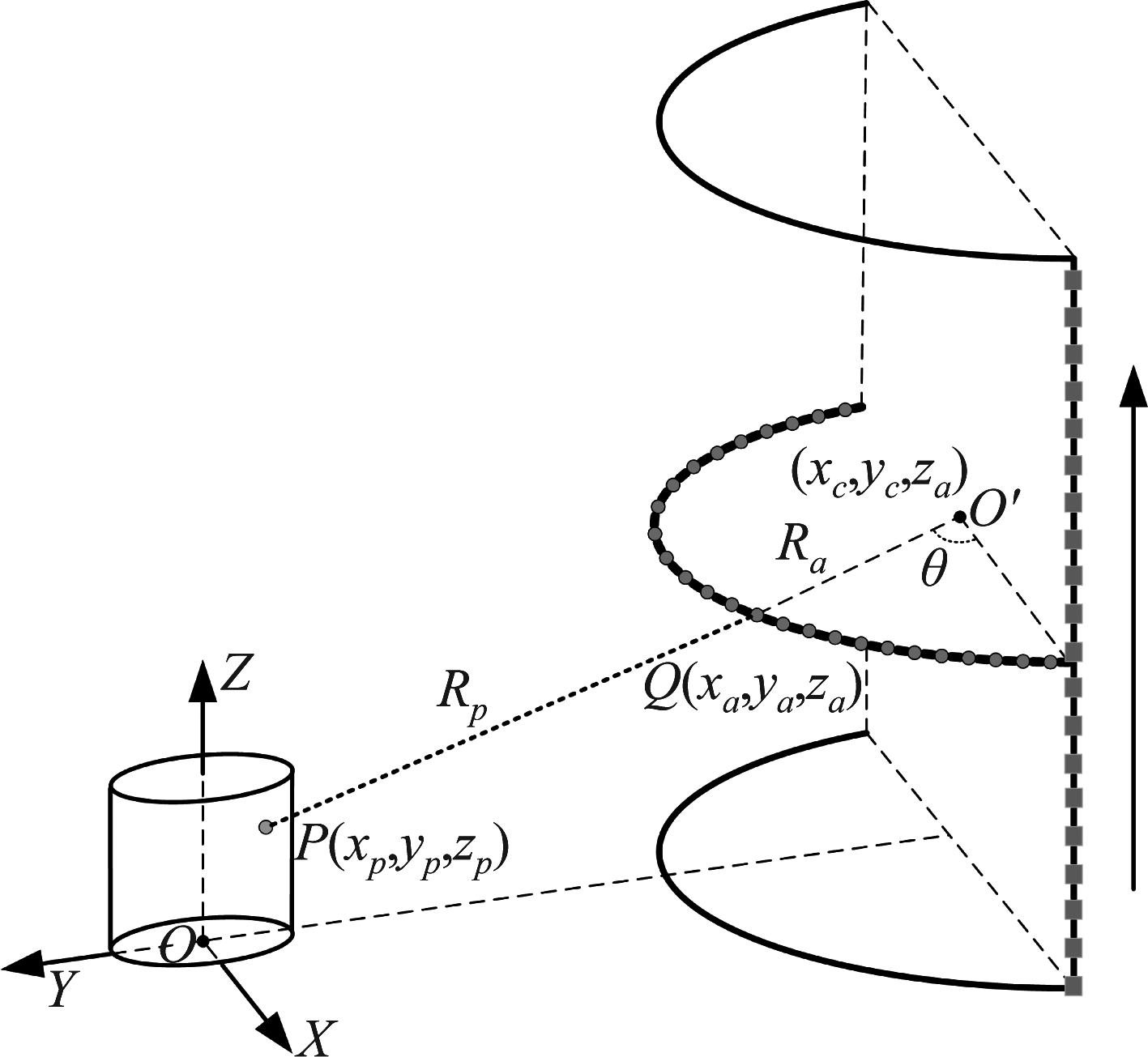
图1 弧形阵列3D-SAR系统观测几何
Fig.1 Observation geometry of arc array 3D-SAR system
弧形阵列的圆弧中心坐标为O′(xc, yc, za),圆弧半径为Ra,位于Q点的天线阵元与X正轴夹角为θ,收发阵元采用伪单站工作模式,利用相位中心等效法获取收发阵元的等效相位中心和采样间隔,收发天线阵元的等效相位中心点Q的坐标为
(xa,ya,za)=(xc+Racos θ,yc+Rasin θ,za)
(1)
发射信号采用线性调频连续波,其表达式如下:
ST=exp[j(2πf0t+πKt2)]
(2)
其中, f0是信号载频,K是调频斜率,t是信号快时间。
设信号在τ时刻发射,对应的等效相位中心Q到目标P的瞬时斜距为Rp(τ),信号接收时间为τ+τd,对应的瞬时斜距为Rp(τ+τd),因此,可得回波延迟时间τd方程式如下:
(3)
其中,
(4)
(5)
c是光速,ν是阵列运动速度。对公式(3)进行二次方程求解,可得
(6)
其中,za=ντ。则点目标的回波信号可表示为
SR=ST(t-τd)
(7)
取雷达到坐标原点的距离为参考距离Rref,则参考信号为
Sref=ST(t-τref)
(8)
其中,
(9)
将参考信号Sref与接收到的回波信号SR进行混频,可得解调后的信号为
exp[-j 2πf(τd-τref)]·exp[jπK(τd-τref)2]
(10)
其中,σ(xp,yp,zp)为目标散射系数, f=f0+K(t-τref),exp[jπK(τd-τ)2]为残余视频项(RVP)。
由于ν≪c,公式(6)可近似为
(11)
经过RVP补偿和参考相位函数H1=exp(-j 2πfτref)补偿后的解线调频信号如下:
SIF=σ(xp,yp,zp)·exp(-j 2πfτd)
≈σ(xp,yp,zp)·exp{jΦ}
(12)
其中,
(13)
3 弧形阵列3D-SAR成像处理算法
不同于平面孔径3D-SAR,基于弧形阵列的曲面孔径3D-SAR信号是柱坐标系下获取的,因此在波数域不能直接使用快速傅里叶变换(FFT)进行方位向和斜距向的信号处理。首先我们给出信号在直角坐标系下的瞬时波数表达式[21]:
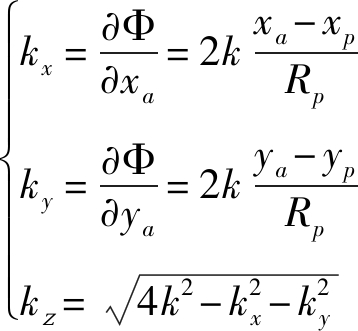
(14)
其中,k=2πf /c是空间波数。
对解线调频信号SIF在Z方向上做傅里叶变换,可得
S(f,θ,kz)=σ(xp,yp,zp)·
(15)
对于三维立体目标,可得
(16)
将公式(1)带入到公式(16)可得
(17)
其中,![]()
为了求解式(17),首先简化信号模型,分析自由空间的格林函数:
(18)
则h(x,y,kr)的二维傅里叶变换结果可以表示为:
H(kx,ky,kr)=exp(-jkxRa)
(19)
然后h(x,y,kr)进行空间移位,可得
=h(x-xc,y-yc,kr)
(20)
由傅里叶变换的性质,可得g0(x,y,kr)的二维傅里叶变换为
G0(kx,ky,kr)=H(kx,ky,kr)·exp(-jkxxc-jkyyc)
=exp(-jkxRa)·exp(-jkxxc-jkyyc)
(21)
而式(17)中的格林函数为
g(x,y,kr)=
(22)
可以看出,g(x,y,kr)是由g0(x,y,kr)在(x, y)空域做了角度为θ的旋转所得,故其二维频谱也相当于做了角度为θ的旋转[14],故可得g(x,y,kr)的二维频谱为
G(kx,ky,kr)=exp[-j(kxcos θ+kysin θ)Ra]·exp(-jΦc)
=exp[-jkrcos(θ-φ)Ra]·exp(-jΦc)
(23)
其中,![]() 为波数支持域,θs是由天线波束宽度决定的有效最大方位角, Φc=krcos φxc+krsin φyc是参考位置决定的相位因子。
为波数支持域,θs是由天线波束宽度决定的有效最大方位角, Φc=krcos φxc+krsin φyc是参考位置决定的相位因子。
因此,根据Parseval’s理论[14-16]可得
exp[-j(kxcos θ+kysin θ)Ra]·exp(-jΦc)dkxdky
(24)
将上式中的二维积分转换到极坐标系下,可得
(25)
令Gφ(kr,θ,kz)=exp[-jkrcos(θ)Ra],则可得式(25)中的卷积关系式如下:
σ(kr,θ,kz)⊗Gφ(kr,θ,kz)
(26)
对式(26)等式两边同时对θ进行傅里叶变换,并由时频对应关系可得[19-21]
Sc(kr,kθ,kz)=σ(kr,kθ,kz)·
FFTθ[Gφ(kr,θ,kz)]·exp(-jΦc)
(27)
因此可得柱坐标系下的三维频谱为
σ(kr,θ,kz)=IFFTθ[Sc(kr,kθ,kz)·H2]·H3
(28)
其中,![]() 方位补偿函数,H3=exp(jΦc)为参考距离相位补偿函数。
方位补偿函数,H3=exp(jΦc)为参考距离相位补偿函数。
然后将柱坐标系下的三维频谱插值到直角坐标系,坐标映射关系如下
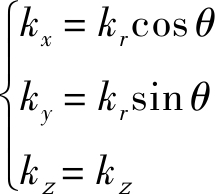
(29)
对插值后的频谱进行三维IFFT,可得目标散射系数为:
σ(x,y,z)=IFFT3D[σ(kx,ky,kz)]
(30)
弧形阵列3D-SAR波数域成像算法流程图如图2所示。
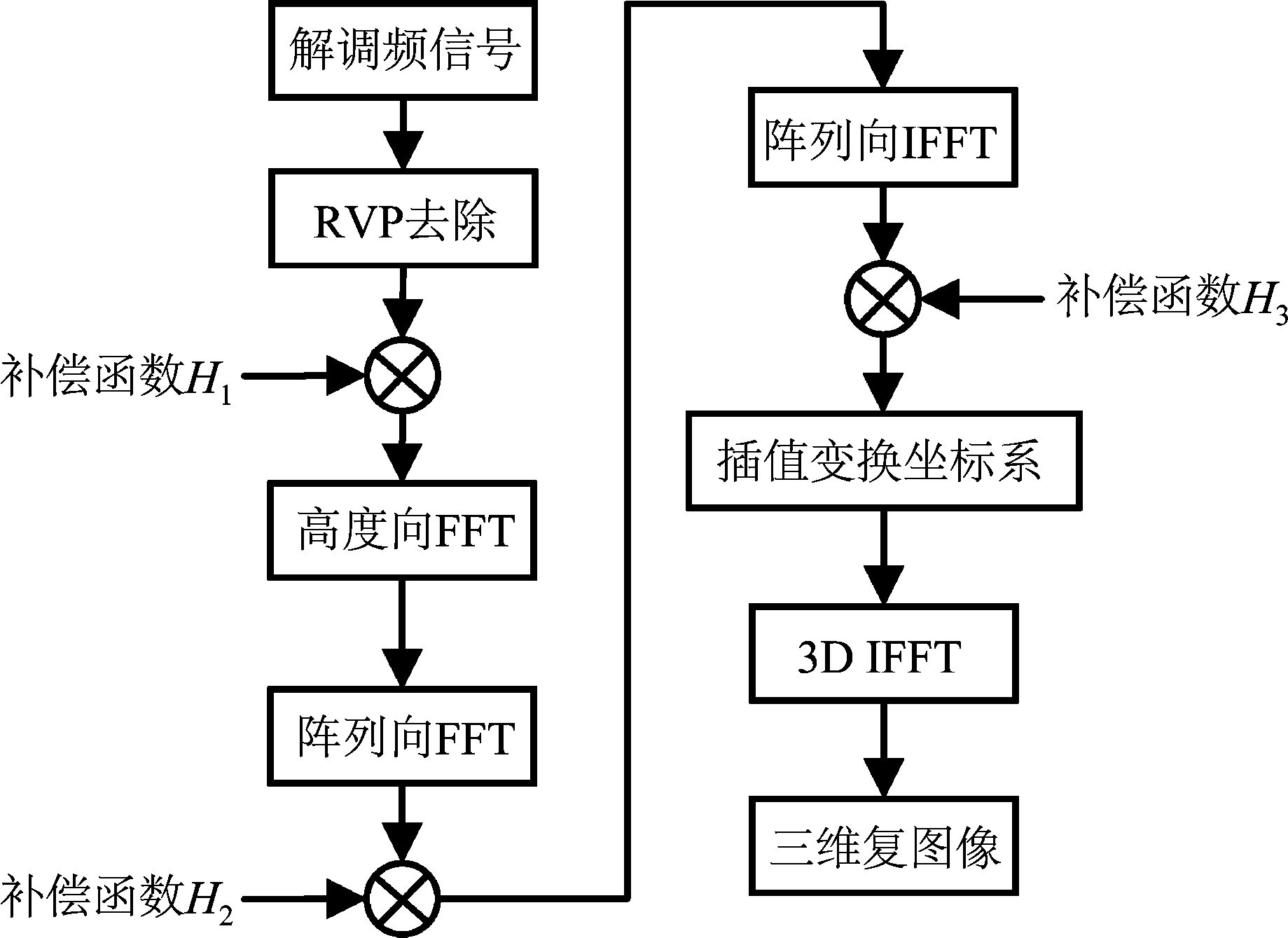
图2 弧形阵列3D-SAR波数域成像算法流程图
Fig.2 Flow chart of wavenumber domain imaging algorithm for arc array 3D-SAR
4 弧形阵列3D-SAR成像仿真实验
为了验证本文设计的弧形阵列3D-SAR系统和提出的波数域三维成像算法的有效性,进行了立体空间下的点目标成像仿真实验。首先,进行单点目标成像仿真,通过将本文提出的三维波数域成像算法的成像结果与三维后向投影(BP)算法的成像结果相对比分析,验证本文提出算法的成像性能。由于3D-SAR成像具有空变特性,故还需进行多点目标成像仿真,对所设计系统的有效性及成像算法做进一步的验证。系统仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters

参数参数值中心频率/GHz35信号带宽/GHz10调频斜率GHz/s106弧形阵列半径/m0.6弧形阵列采样间隔/(°)0.3弧形阵列等效阵元数目201高度向采样间隔/m0.006高度向采样点数101阵列中心x坐标/m0阵列中心y坐标/m-3
单点目标位置坐标为(x=0 m,y=1 m,z=0.3 m),其成像仿真结果如图3所示,从三维点目标成像结果分别在三个平面的投影结果可以看出,本文提出的弧形阵列3D-SAR成像算法使得点目标实现了良好的聚焦效果。为了定量地评估所提出算法的成像性能,我们将成像结果的图像质量指标与三维BP算法的成像结果进行了对比。三维BP算法是一种无近似误差的精准成像算法,可以适用于任何成像几何模型下,但其三维成像效率太低,故往往很难在实际中得到广泛应用,但其具有良好成像精度,故可与本文提出算法的成像结果进行对照,以验证本文算法的成像性能。两种算法的成像结果在各平面投影得到的质量参数如表2所示,从点目标的各方向上的成像指标可以看出,本文提出算法的成像结果与三维BP算法结果具有相当的图像质量,从而验证了本文提出算法的成像性能。而从两种算法成像所需要的时间来看,本文提出算法的成像效率要远远高于三维BP算法,更具有实际应用价值。
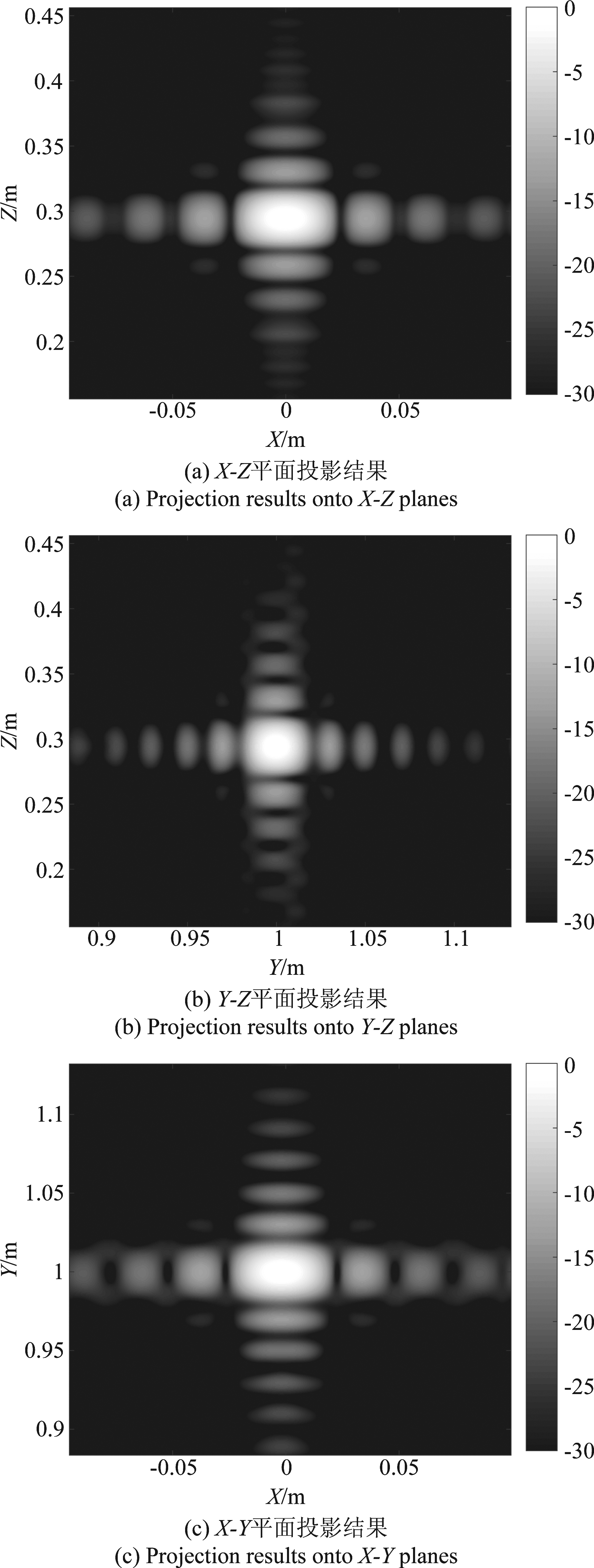
图3 单点目标成像仿真
Fig.3 Single-point target imaging simulation
表2 图像质量参数
Tab.2 Image quality parameters

算法参数X方向Y方向Z方向本文算法IRW/m0.02130.01330.0218PLSR/dB-13.275-13.341-13.275ISLR/dB-10.386-11.113-10.897成像时间38.26seconds3D-BP算法IRW/m0.02090.01330.0212PLSR/dB-13.286-13.322-13.261ISLR/dB-10.422-11.264-11.082成像时间2hoursand125seconds
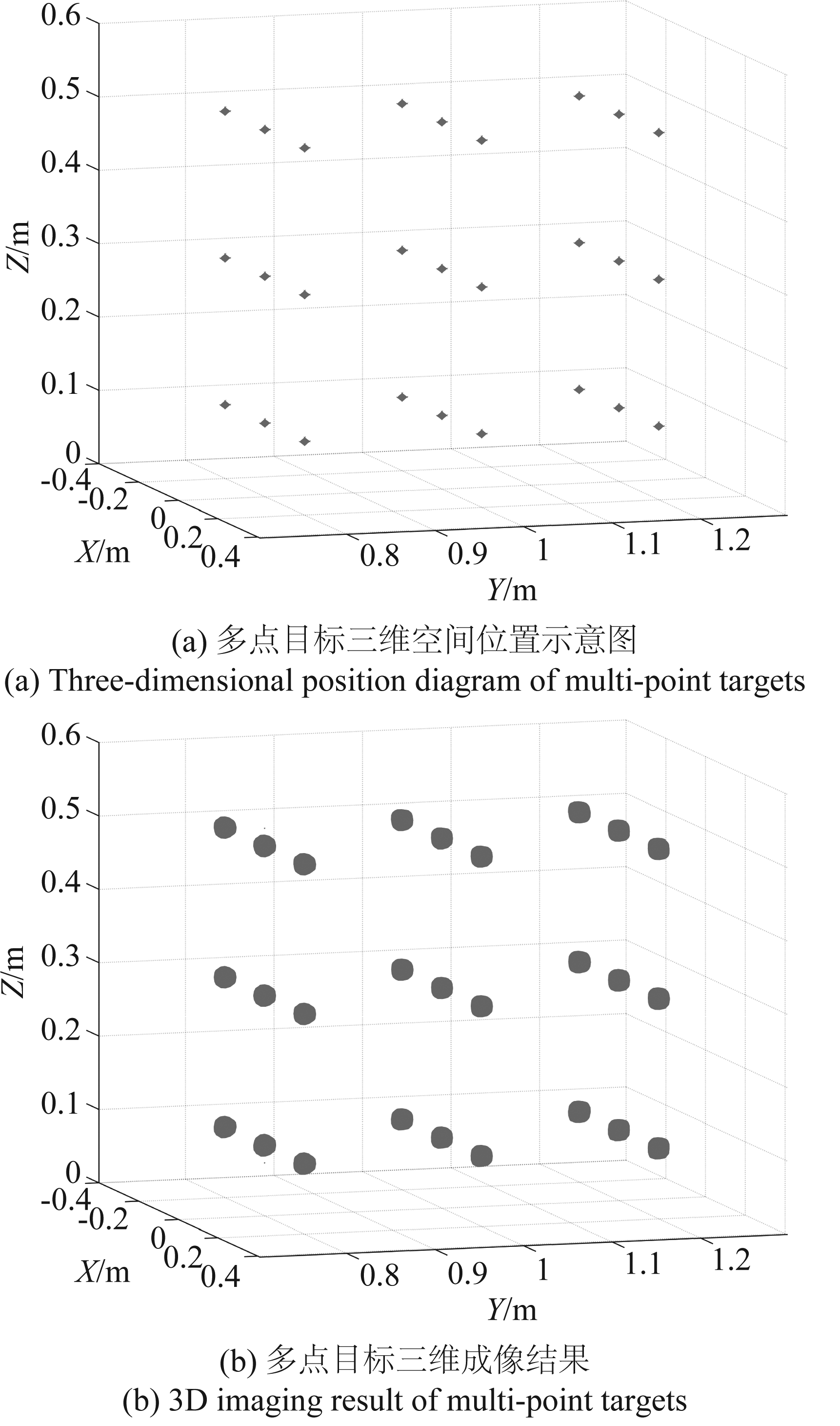
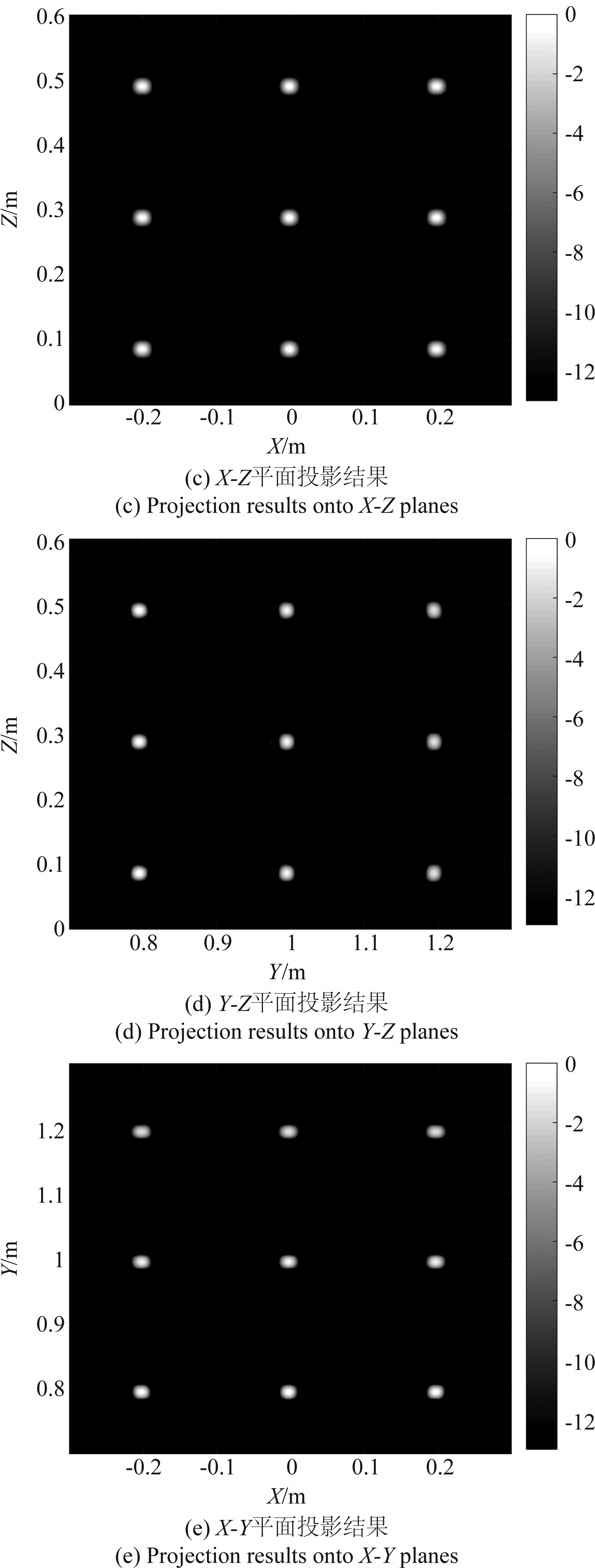
图4 多点目标成像仿真
Fig.4 Multi-point targets imaging simulation
为了进一步验证成像算法的有效性,进行了多目标仿真实验,点目标分布如图4(a)所示,27个点目标均匀分布在三维空间场景中。利用本文算法得到的成像结果如图4(b)~(e)所示,图4(b)为多目标的三维成像结果,可以看出,各点目标均得到了良好的聚焦,且与预先设定的点目标空间位置均一一对应。图4(c)~(e)为多点目标的成像结果在各平面的投影,从投影结果可以看出,本文提出算法使被测目标在三维空间的各方向上均达到了较为理想的成像结果。以上结果进一步验证了本文设计的弧形阵3D-SAR系统模型及成像算法的有效性。
5 结论
不同于现有的3D-SAR成像系统,本文设计了一种弧形曲面几何下的3D-SAR系统模型,在该模型下利用弧形阵列天线实现高效的数据采集和宽视角三维成像。为了降低系统成本和便携化,本文将FMCW信号体制引入到系统设计中,并提出了一种应用于FMCW信号的弧形阵列3D-SAR波数域成像算法,通过在波数域进行卷积与插值变换,实现了对被测目标的精准聚焦。最后,将本文算法的单点目标成像仿真结果与三维BP算法的成像结果进行了对比,验证了本文提出算法良好的成像性能;通过三维空间多点目标仿真验证了本文所设计系统模型及提出算法的有效性。
[1] Klare J, Brenner A, Ender J. A new airborne radar for 3D imaging-image formation using the ARTINO principle[C]∥Proceeding of European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006: 1- 4.
[2] Han K, Wang Y, Tan W, et al. Efficient pseudopolar format algorithm for down-looking linear-array SAR 3-D imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(3): 572-576.
[3] Peng X, Tan W, Hong W, et al. Airborne DLSLA 3-D SAR image reconstruction by combination of polar formatting and, L1 regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 213-226.
[4] 张凯, 杜小勇, 王壮. 基于压缩感知的空间目标三维雷达成像方法[J]. 信号处理, 2011, 27(9): 1406-1411.
Zhang Kai, Du Xiaoyong, Wang Zhuang. Three-dimensional imaging technique of space objects based on compressive sensing[J]. Signal Processing, 2011, 27(9): 1406-1411.(in Chinese)
[5] Sheen D M, Mcmakin D L, Hall T E. Three-dimensional millimeter-wave imaging for concealed weapon detection[J]. IEEE Transactions on Microwave Theory Techniques, 2001, 49(9): 1581-1592.
[6] Sheen D M, Mcmakin D L, Hall T E. Near-field three-dimensional radar imaging techniques and applications[J]. Applied Optics, 2010, 49(19): 83-93.
[7] Fortuny-Guasch J, Lopez-Sanchez J M. Extension of the 3-D range migration algorithm to cylindrical and spherical scanning geometries[J]. IEEE Transactions on Antennas & Propagation, 2002, 49(10): 1434-1444.
[8] Tan W, Hong W, Wang Y. A novel spherical-wave three-dimensional imaging algorithm for microwave cylindrical scanning geometries[J]. Progress In Electromagnetics Research, 2011, 111: 43-70.
[9] 谭维贤. 合成孔径雷达三维成像理论与方法研究[D]. 北京: 中国科学院电子学研究所, 2009.
Tan Weixian. Study on theory and algorithms for three-dimensional synthetic aperture radar imaging[D]. Beijing: Institute of Electronics, Chinese Academy of Scences, 2009.(in Chinese)
[10] Ren B, Li S, Sun H, et al. Modified cylindrical holographic algorithm for three-dimensional millimeter wave imaging[J]. Progress In Electromagnetics Research, 2012, 128: 519-537.
[11] 朱荣强, 周剑雄, 付强. 柱面阵三维成像的降维时域相关法[J]. 信号处理, 2016, 32(7): 779-786.
Zhu Rongqiang, Zhou Jianxiong, Fu Qiang. Demension-reduced time domain correlation algorithm for 3-D cylindrical array imaging[J]. Journal of Signal Processing, 2016, 32(7): 779-786.(in Chinese)
[12] Zhang Y, Deng B, Yang Q, et al. Near-field three-dimensional planar millimeter-wave holographic imaging by using frequency scaling algorithm[J]. Sensors, 2017, 17(10): 2438-2452.
[13] Amin N V, Mansouri E, Kavehvash Z, et al. Low-cost three-dimensional millimeter-wave holographic imaging system based on a frequency-scanning antenna[J]. Appl Opt, 2018, 57(1): A65-A75.
[14] 吴世有, 高航, 李超, 等. 太赫兹MIMO弧形阵列方位向成像算法研究[J]. 电子与信息学报, 2018, 40(4): 860- 866.
Wu Shiyou, Gao Hang, Li Chao, et al. Research on MIMO THz azimuth imaging algorithm base on arc antenna array[J]. Journal of Electronics and Information Technology, 2018, 40(4): 860- 866.(in Chinese)
[15] 黄平平, 谭维贤, 苏莹, 等. 直升机载弧形阵列MIMO微波成像技术研究[J]. 雷达学报, 2015, 4(1): 11-19.
Huang Pingping, Tan Weixian, Su Ying, et al. Research on helicopter-borne MIMO microwave imaging technology base on arc antenna array[J]. Journal of Radars, 2015, 4(1): 11-19.(in Chinese)
[16] Huang Z, Sun J, Tan W, et al. Investigation of wavenumber domain imaging algorithm for ground-based arc array SAR[J]. Sensors, 2017, 17(12): 2950.
[17] Meta A, Hoogeboom P, Ligthart L P. Signal processing for FMCW SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3519-3532.
[18] Wang R, Loffeld O, Nies H, et al. Focus FMCW SAR data using the wavenumber domain algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2109-2118.
[19] Soumekh M. Reconnaissance with slant plane circular SAR imaging[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 1996, 5(8): 1252-1265.
[20] Soumekh M. Synthetic aperture radar signal processing with MATLAB algorithms[M]. John Wiley & Sons, New York, 1999.
[21] Lin Y, Hong W, Tan W, et al. Extension of range migration algorithm to squint circular SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 651- 655.
[22] Zhu R, Zhou J, Jiang G, et al. Range migration algorithm for near-field MIMO-SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(12): 2280-2284.
[23] Lee H, Lee J H, Kim K E, et al. Development of a Truck-Mounted Arc-Scanning Synthetic Aperture Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2773-2779.
