1 引言
合成孔径雷达能够进行全天时、全天候的高分辨率成像[1]。由于SAR图像具有相位信息,因此可以通过对SAR图像做干涉提取成像区域的形变信息。这是一种非接触式且高精度的形变信息提取技术。鉴于SAR系统具备了上述优势,它成为了地面形变监测的重要手段之一[2-3]。地基合成孔径雷达(GBSAR)是一种近年来备受关注的SAR系统。它的重访周期短,监测精度高,可以对一个特定场景长时间连续监测[4],并实时反馈监测信息。因此GBSAR被广泛应用于建筑物的形变监测以及滑坡预警[5- 8]。
传统的GBSAR系统的天线沿着直线轨道扫描[9-10],因此系统的视场不能在一次观测中覆盖全部周围的场景。一种新的GBSAR观测模式ArcSAR能够解决上述问题。ArcSAR的合成孔径通过附在旋臂末端的天线旋转生成[11-12],在保证系统分辨率的前提下,能够在一次观测中覆盖周边360°大范围场景。目前,多个团队正在研究ArcSAR系统并已经将它应用于地面形变监测[13-15]。
尽管近年来ArcSAR的可行性及独特优势已经被验证,但它的成像算法研究仍存在难点:ArcSAR的天线运动轨迹为弧线,这种特殊的运动轨迹给成像算法增加了难度。目前处理弧线运动轨迹的算法是针对圆迹SAR的[16-17],但圆迹SAR与ArcSAR几何模型不同(圆迹SAR是围绕探测区域做弧线运动从而获取该区域的SAR图像。ArcSAR是通过旋转天线对平台周围区域进行成像),因此针对圆迹SAR的成像算法不适用于ArcSAR。使用时域成像算法虽然能够得到ArcSAR的高精度成像结果,但时域成像算法计算效率较低。因此我们需要一种适用于ArcSAR系统的频域成像算法。文献[18]提出了极坐标格式下的RD算法。该算法中回波相位的斜距表达式被泰勒展开并忽略了高于二次的相位项,这种近似方法适用于方位向波束宽度较小(即合成孔径较小)的情况[18],如果方位向波束宽度较大,该近似方法会导致图像质量明显下降。文献[9]中也提出了一种快速成像算法。该算法以旋转中心与目标的距离远大于旋转半径为前提,对天线相位中心到目标的斜距做泰勒展开,并保留一阶项。这种近似会降低成像质量,且方位向成像角度受到了限制,尽管文中提出使用分割策略对成像区域进行分块成像,但这样就不能在一次观测中完成系统周边360°场景的成像。本文提出一种新的ArcSAR快速成像算法,信号的聚焦在频域进行,利用二维频域匹配滤波对距离徙动和相位进行补偿。并且可以处理宽波束信号,这有效提高了合成孔径长度进而保证成像精度。此外,本文提出的快速算法能够在一次观测中完成系统周边360°场景的成像,并获得良好的成像结果。
本文其余部分安排如下。第2部分介绍ArcSAR几何模型和信号模型。第3部分对算法的原理进行论述。并分析算法误差,推导算法的适用条件。第4部分利用仿真实验对算法的适用条件进行验证,并对时域成像算法和本文提出的快速成像算法的成像效率和成像质量进行比较。最后,结论总结。
2 ArcSAR的几何模型和信号模型
ArcSAR系统具有一个旋转平台,由旋转平台中心延伸出的旋臂可以进行360°旋转,旋臂搭载了用于收发信号的天线。因此,该系统的视场能够覆盖大范围场景。此外,与直线扫描GBSAR的合成孔径不同(直线扫描GBSAR的合成孔径通过天线沿直线轨道扫描生成,合成孔径大小即天线沿直线轨道运动距离,与天线波束宽度无关),ArcSAR系统的合成孔径通过附在旋臂末端的天线旋转生成,合成孔径大小受天线波束宽度影响,波束宽度越大,波束照射目标的时间就越久,合成孔径就越大,系统的成像精度就越高。
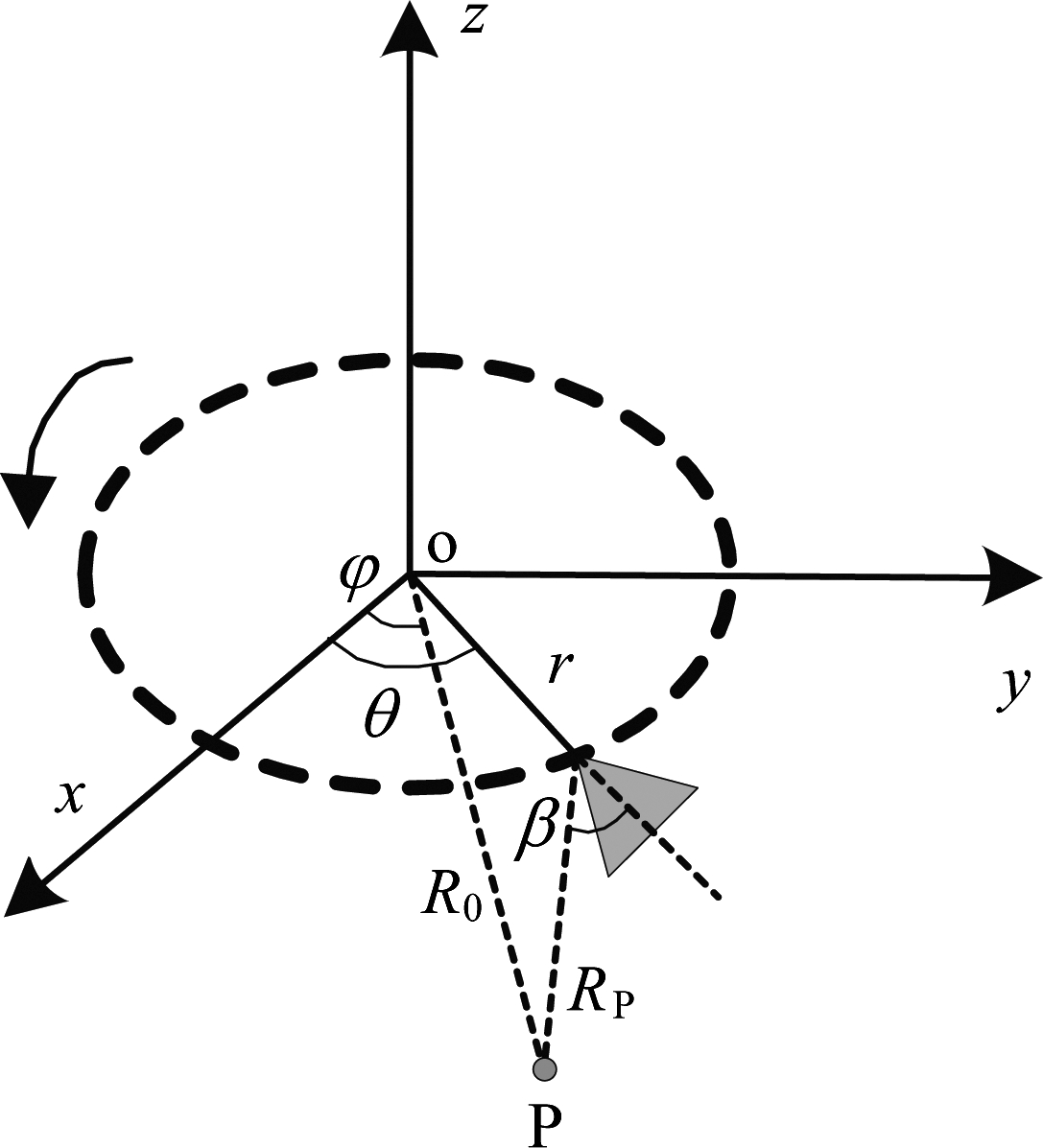
图1 ArcSAR几何模型
Fig.1 Geometric model of ArcSAR
图1给出了ArcSAR的几何模型。我们选取系统的旋转平面为成像平面(本文后续关于算法的讨论也都选取系统的旋转平面做为成像平面);P为点目标点(假设P在成像平面上);r为旋臂长度,即ArcSAR的旋转半径;θ为旋臂旋转角度,即方位向角度;φ为目标位置的方位角;β为瞬时斜视角;R0为目标与旋转中心的瞬时距离;Rp为目标与天线相位中心的瞬时距离,它是关于θ的函数,随着旋臂的旋转Rp的大小也会发生改变,根据图1给出的几何关系,我们可以得到Rp的表达式:
(1)
已知了天线与目标的距离关于θ的关系。我们可以得到ArcSAR的信号模型,以线性调频信号为例,假设回波信号的散射系数为δp,则目标P的回波信号S(θ,tr)可以表示为:
S(θ,tr)=δprect((tr-2Rp/C)/Tp)·rect((θ-φ)/θbw)·
exp(jπKr(tr-2Rp/C)2)·exp(-j4πRp/λ)
(2)
其中,tr为系统距离向时间,C为光速,Tp为回波信号脉宽,θbw为天线波束宽度,Kr为线性调频率,λ为回波信号波长。
3 ArcSAR快速成像算法理论
3.1 二维频域信号
快速算法的算法流程图如图2所示。
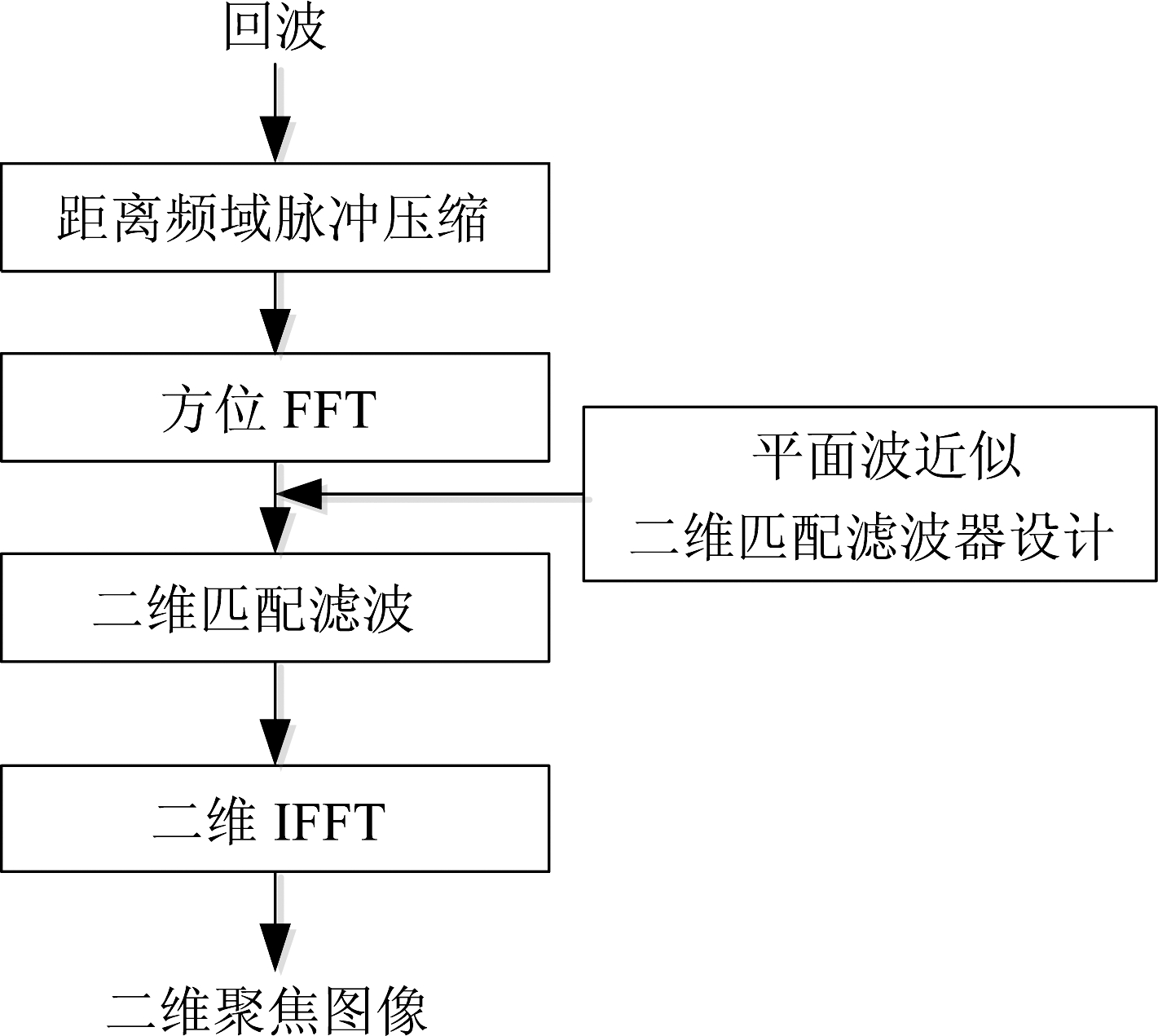
图2 算法流程图
Fig.2 Flowchart of the proposed algorithm
本小节我们会推导出回波信号S(θ,tr)经距离向频域脉冲压缩和方位向FFT后,所得的二维频域信号的形式。首先,我们对回波信号进行距离向脉冲压缩,脉冲压缩后的信号如下所示:
S(θ, f)=δp·rect((θ-φ)/θbw)·
rect(f/Br)·exp[-j4π(f+fc)Rp/C]
(3)
其中f为发射信号基带频率,Br为发射信号带宽,fc为发射信号中心频率。由于回波信号在方位向具有移不变特性,即距离旋转中心相同距离的目标(即R0相同),即使它们的方位角φ不同,但它们的距离徙动的形式是一样的。在频域,相同R0,不同方位角φ的目标的频谱只相差线性相位。因此为方便后续的推导,我们假设目标位置的方位角φ=0,并忽略常数项δp。因此S(θ,f)可以重写为:
S(θ, f)=rect(θ/θbw)·rect(f/Br)·
exp[-j4π(f+fc)Rp/C]
(4)
Rp的表达式可以重写为:
(5)
然后,我们对式(4)做方位向的傅里叶变换,并通过驻定相位定理获取信号S(θ,f)的二维频域表达式:
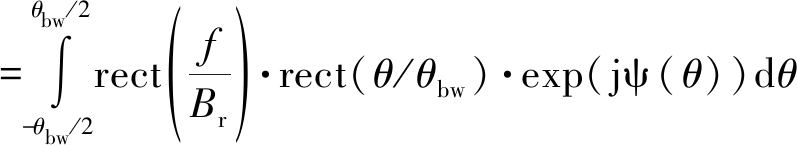
(6)
其中, fθ为旋臂旋转角度θ的频域表达形式,即方位频率。积分相位ψ (θ)可以表示为:
(7)
已知驻留点满足dψ (θ)/dθ=0,因此:
(8)
将式(5)代入式(8),我们可以可得fθ与θ的关系式:
(9)
将式(9)代入式(6),我们可以得出信号S2df(fθ,f)的二维频域形式:
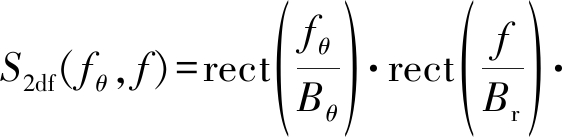
(10)
其中,Bθ为方位向带宽。
3.2 二维频域匹配滤波
接下来需要对二维频域信号S2d(fθ,f)做频域匹配滤波,从而实现信号的距离徙动和相位的校正。
二维频域匹配滤波器可以表示为:
exp(j 2πfθ·θ(fθ))
(11)
由式(11)可以看出,θ和Rp都是关于方位频率fθ的函数,因此我们能够推导出θ和Rp关于fθ的表达式。此处,我们假设目标处于远场,并使用平面波近似,因此Rp(fθ)-R0可以近似为:
Rp-R0≈-rcos β
(12)
式(12)近似结果的具体推导过程将在3.3小节呈现。根据图1所给出的系统几何关系,可知:
(13)
根据上式,sin β可以表示为:
sin β=R0sin θ/Rp
(14)
将上式代入式(8),可以推知方位频率fθ与斜视角正弦值sin β的关系:
(15)
通过式(15)可以发现, fθ与sin β成正比例关系。由式(15)我们可以获得β关于fθ的表达式:
(16)
将上式代入式(12),就能够获得Rp关于fθ的表达式:
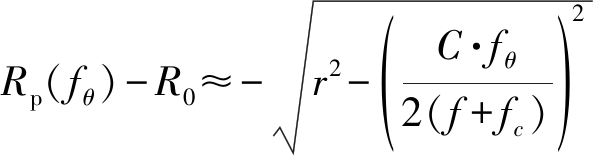
(17)
已知在远场条件下,根据平面波近似我们可以视方位向角度θ和瞬时斜视角β近似相等(该近似具体说明会在3.3小节呈现),即:
(18)
由此θ和Rp关于fθ的函数我们均已获得,将式(17)和式(18)代入式(11),可得二维频域匹配滤波器的表达式为:


(19)
让二维频域信号S2df(fθ,f)与频域匹配滤波器H1(fθ,f)相乘,滤波结果可以表示为:
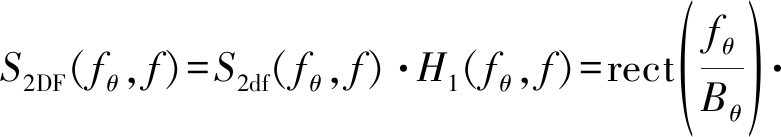
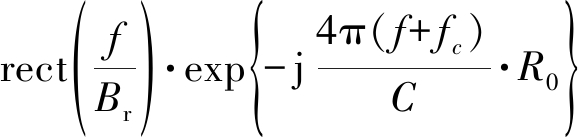
(20)
最后,对滤波结果S2DF(fθ,f)做二维傅里叶逆变换,即可获得点目标在极坐标格式下的时域SAR图像。
3.3 算法适用条件
本文提出的快速算法使用了平面波近似,这种近似是以假设目标处于远场为前提的。因此该算法使用前需要判定目标是否满足远场条件。本节我们首先对上一小节中式(12)和(18)通过平面波近似得出的近似结果加以说明。然后对本文提出算法的适用条件进行讨论。
我们给出图1几何模型的x-y二维俯视图,如图3所示。
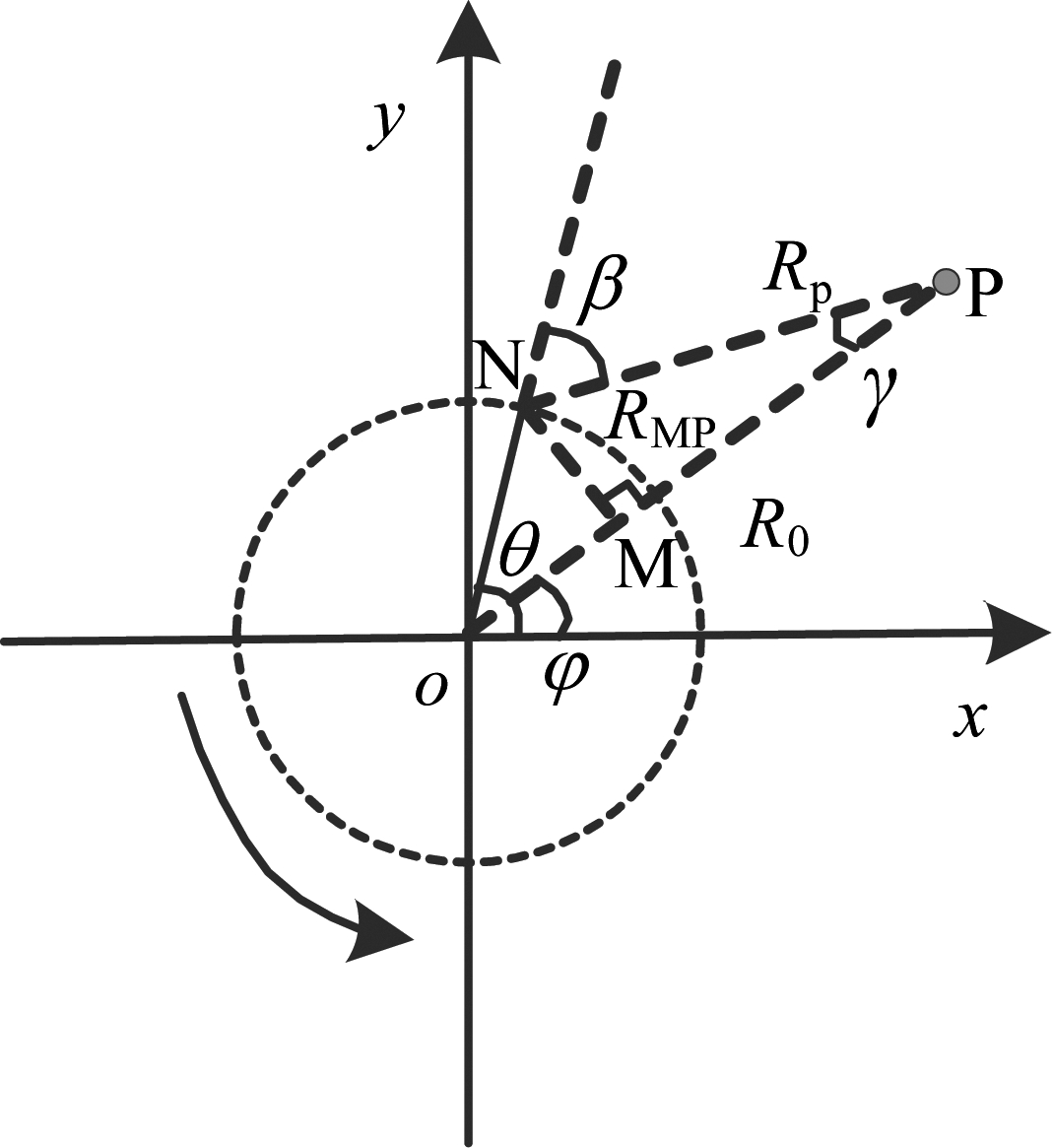
图3 平面波近似几何示意图
Fig.3 Geometric schematic of plane wave approximation
N为系统收发天线所在位置,在目标P处于远场的前提下,一束球面雷达波从N发射到目标P,并由目标P反射回N。通过平面波近似,我们将由P反射回N的球面雷达回波近似为一束平面波,该平面波的波面垂直于MN,NP与MP近似平行,且由N到P的距离Rp和由M到P的距离RMP近似相等,即:
Rp≈RMP=R0-rcos(θ-φ)
(21)
由于线段NP与线段MP平行,故θ-φ≈β,在3.2小节的讨论中我们假设目标位置的方位角φ=0,因此可知θ≈β(即式(18)所使用的近似结果),将θ≈β代入式(21),可以得到Rp≈R0-rcos β,即式(12)所使用的结论。
接下来我们对本文提出算法的适用条件进行讨论:上述近似结果Rp≈R0-rcos β,这种近似会带来斜距误差,若要近似成立,斜距误差所引起相位误差不能大于π/4[19],即斜距误差不能大于λ/16, 如下所示:
(22)
其中Δr0是Rp由于平面波近似所产生的斜距误差。由图2的几何关系,Δr0可以表示为:
Δr0=Rp-RMP=Rp-Rpcos γ
(23)
其中,
(24)
将式(1)代入式(24),可得
(25)
将式(25)和式(1)代入式(21),我们就得到了本文提出的快速成像算法的适用条件:
(26)
当实验参数满足上式时,由平面波近似造成的斜距误差小于λ/16,平面波近似成立,本文提出的快速算法能够对回波进行良好的聚焦成像。此外,根据图3几何关系,如果R0大小已知,波束宽度为θbw的波束对场景内某一点目标扫描,当旋臂旋转角度θ∈[0, θbw/2]时,波束才能够照射到这一目标。因此R0大小已知时,θ=θbw/2处的斜距误差最大。
4 算法验证
4.1 算法适用条件验证
本节我们利用仿真实验和仿真结果的质量分析,对上一节最后得出的算法的适用条件进行验证。必要的实验参数如表1所示。
表1 实验参数
Tab.1 Experiment parameters

参数名称参数值信号载频/GHz信号带宽/GHz信号速率/(m/s)扫描角度/(°)方位向波束宽度/(°)旋转半径/m1713e8360601
通过上一节得出的算法适用条件可知,本次实验中,当ArcSAR旋转中心与目标径向距离(即距离向距离R0)大于115.1512 m时,场景中的目标符合远场条件,利用本文提出的快速算法处理回波将获得良好的成像结果。我们在系统周围设置24个点目标(这些目标处于系统的旋转平面上),以系统旋转中心o为圆心,每隔45°设置三个点目标,共设八组,每组的
三个目标径向距离相隔100 m。系统与点阵最近径向距离115 m,最远径向距离315 m。目标分布如图4所示。点阵的成像结果如图5所示,坐标系横轴为距离向,纵轴为方位向(旋臂旋转过的角度θ)。

图4 目标分布
Fig.4 Targets distribution
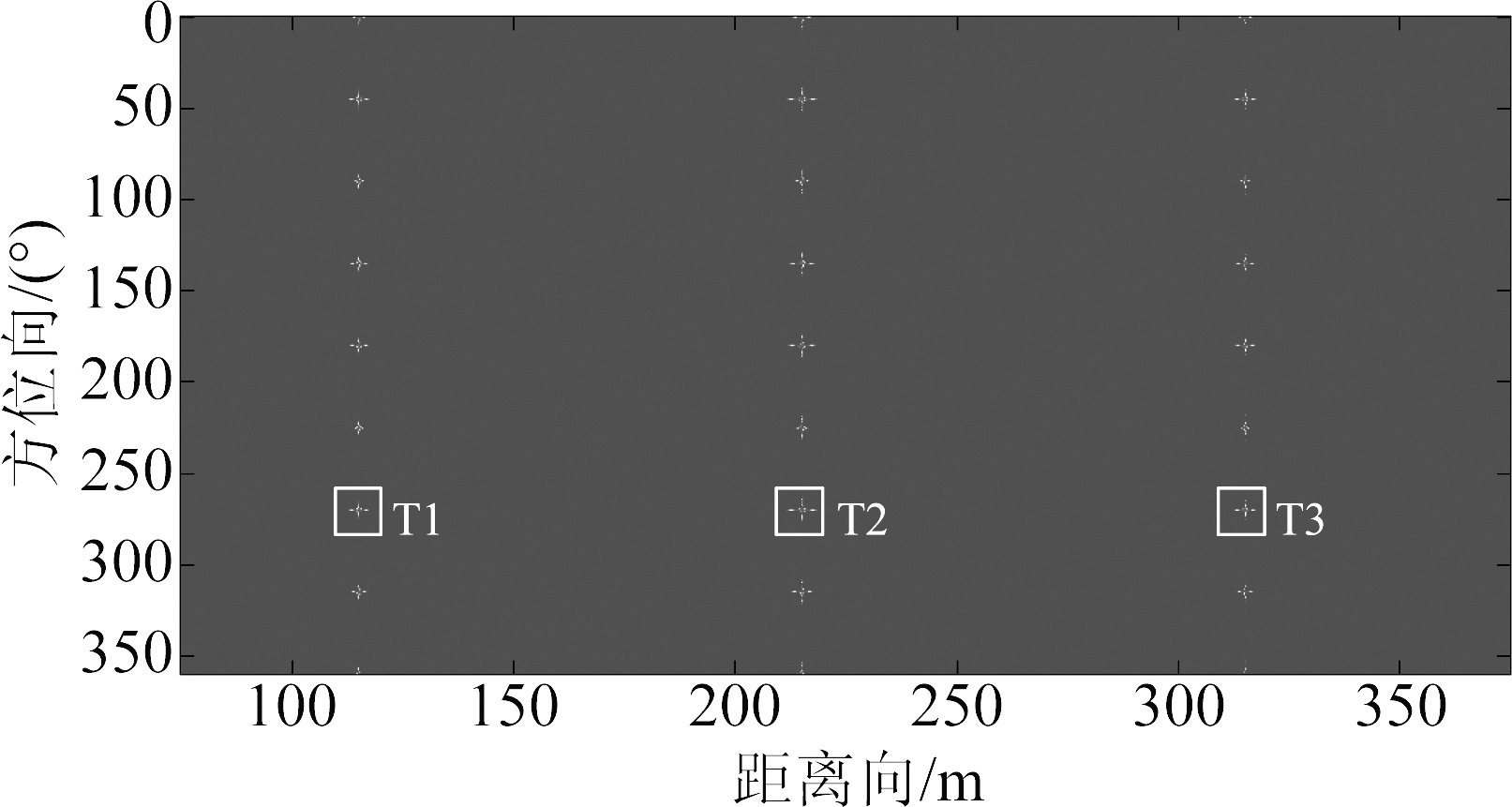
图5 ArcSAR系统360°扫描成像结果
Fig.5 ArcSAR 360° imaging result
我们选取目标T1、T2、T3的成像结果进行质量分析,它们的极坐标分别为(115 m, 270°),(215 m, 270°),(315 m, 270°),位置在图4中和图5中已被标出。对图5中T1、T2、T3成像结果切片并做20倍升采样,成像结果如图6、图7、图8所示。点目标质量参数如表2所示。
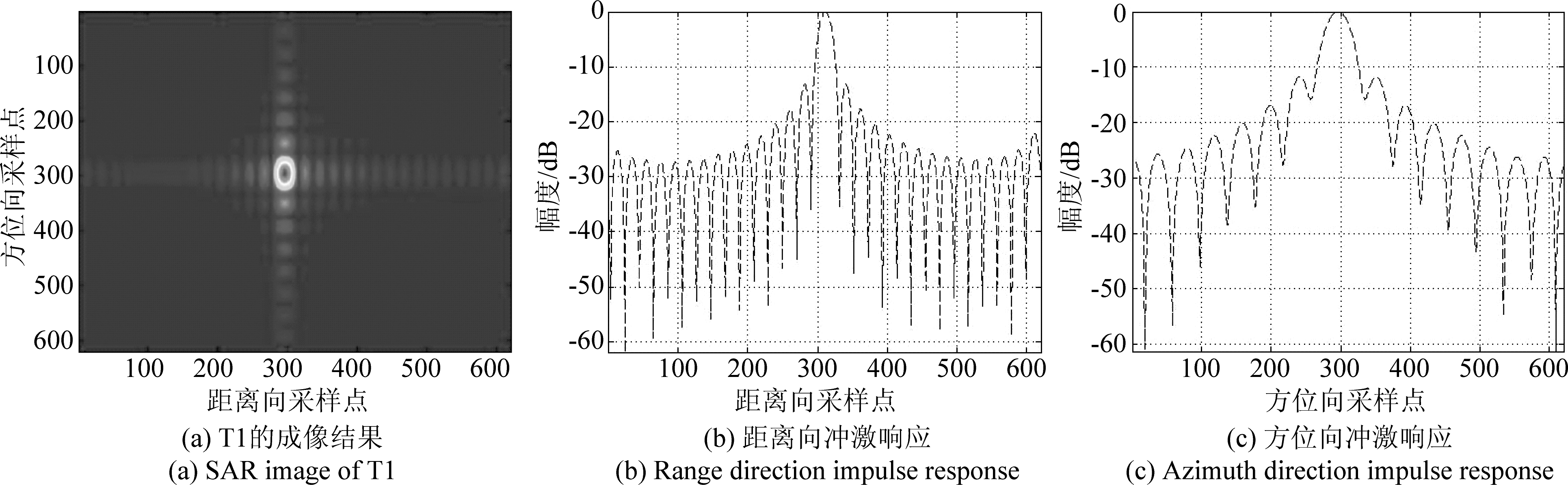
图6 T1的目标质量分析
Fig.6 Target Quality Analysis of T1
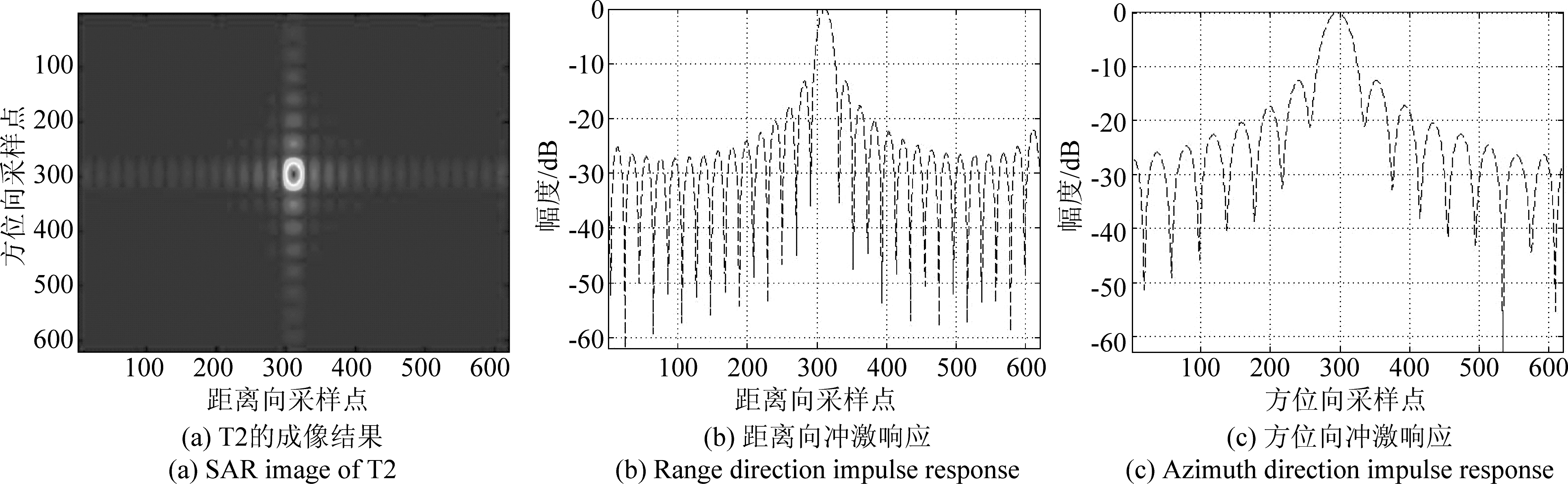
图7 T2的目标质量分析
Fig.7 Target Quality Analysis of T2
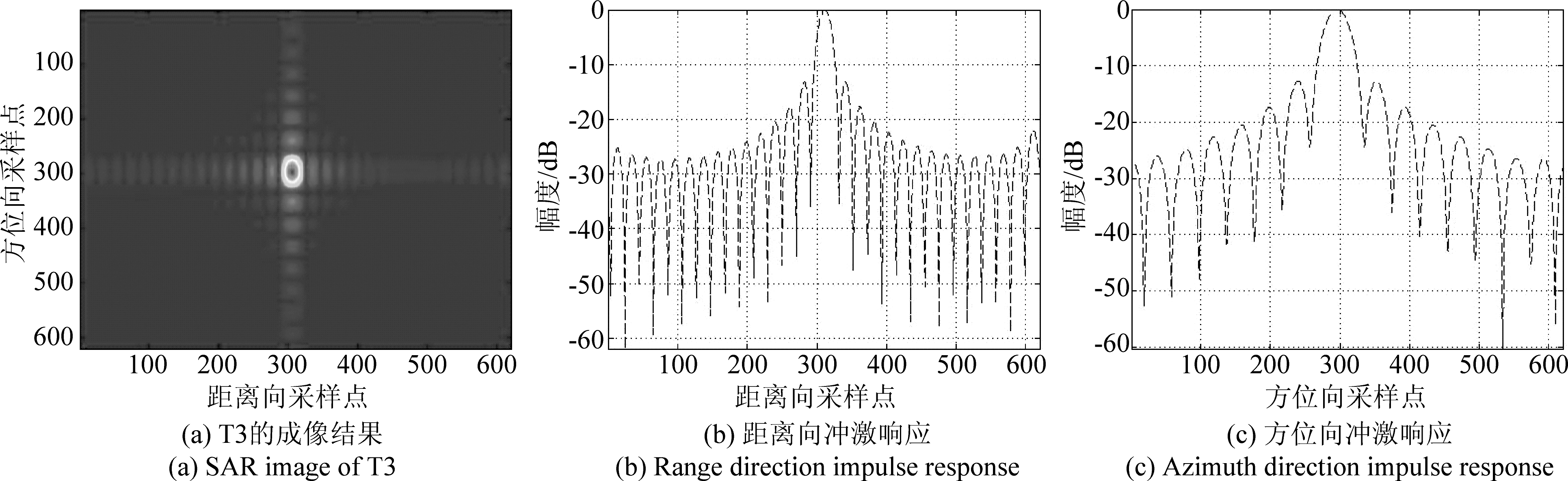
图8 T3的目标质量分析
Fig.8 Target Quality Analysis of T3
表2 仿真结果质量参数
Tab.2 Quality parameters of simulation results

目标名称极坐标/(m,°)距离向分辨率/m距离向PSLR/dB方位向分辨率/m方位向PSLR/dBT1(115,270)0.15-13.230.90-11.83T2T3(215,270)(315,270)0.150.15-13.21-13.221.682.46-12.56-12.78
从图6、图7、图8的成像结果能够看出,当目标符合远场条件时,成像效果良好。从表2可以看出,随着距离向距离的增加,目标的方位向峰值旁瓣比有所提升,成像质量逐渐变好。
4.2 快速成像算法与时域算法的对比验证
若成像场景为一个N×N的矩阵,时域算法需要进行逐像素的操作,因此计算量的量级为N×N×Ls,其中Ls为ArcSAR系统合成孔径内方位向的采样条数。本文提出的快速算法的主要操作是在方位向和距离向使用傅里叶变换,因此计算量的量级为N×N×log2N。可见,相同的场景大小,本文提出的快速算法的计算量远小于时域算法,具备更高的计算效率。为验证本文提出的快速算法与时域算法相比,具有更高的成像效率,且具备较好的成像质量。我们对相同场景中的一个点目标分别使用时域算法和本文提出的快速成像算法进行成像仿真实验,并对比两种成像算法仿真结果的成像质量和成像所需时间。
我们选取的时域成像算法为后向投影算法(BP算法),必要的实验参数见表1,选取图4中的点目标T1,分别使用BP算法和本文提出的快速算法对点目标进行成像仿真实验,并对成像结果切片做20倍升采样,成像结果如图9所示。
两种算法成像结果的质量参数和成像时间的对比如表3所示。本文提出的快速算法成像时间约为1.97 s,时域算法成像时间为77.22 s。时域算法成像时间约为本文提出的快速算法成像时间的39.20倍。通过表3的对比可以看出,本文提出的快速算法与时域算法相比,计算效率更高,且具备较好的成像质量。

图9 BP算法和快速成像算法的点目标成像仿真
Fig.9 SAR imaging simulation of BP algorithm and fast imaging algorithm
表3 BP算法和快速成像算法的仿真结果质量参数
Tab.3 Quality parameters of simulation results of BP algorithm and fast imaging algorithm

算法名称距离向分辨率/m距离向PSLR/dB方位向分辨率/m方位向PSLR/dB成像时间/s快速算法0.15-13.230.90-11.831.97BP算法0.15-13.220.88-13.1577.22
5 结论
本文提出了一种针对ArcSAR的快速成像算法。这是一种频域算法,信号的聚焦、距离徙动和相位的校正皆在频域进行。与传统时域算法相比,该算法的计算效率更高,能够满足ArcSAR系统实时监测的需求。由于算法在对距离徙动和相位校正的过程中使用了平面波近似,因此该算法适用于ArcSAR的远场成像,在远场条件下可以获得良好的成像结果。此外,该算法能够处理宽波束信号,且能够通过一次算法处理对系统周边360°的场景成像,这有效提升了ArcSAR系统的成像效率。本文目前的算法推导是基于目标与成像平面没有高度差的假设。未来会继续分析验证该算法对具有高度的目标的有效性。
[1] 秦玉亮, 王建涛, 王宏强, 等. 弹载合成孔径雷达技术研究综述[J]. 信号处理, 2009, 25(4): 630- 635.
Qin Yuliang, Wang Jiantao, Wang Hongqiang, et al. Overview on Missile-borne Synthetic Aperture Radar[J]. Signal Processing, 2009, 25(4): 630- 635.(in Chinese)
[2] 林圣, 王震, 丁泽刚, 等. 多频干涉SAR局部条纹频率估计方法[J]. 信号处理, 2017, 33(3): 314-318.
Lin Sheng, Wang Zhen, Ding Zegang, et al. Local Fringe Frequencies Estimation Method Based on Multi-Frequency InSAR[J]. Journal of Signal Processing, 2017, 33(3): 314-318.(in Chinese)
[3] 王力宝, 许稼, 皇甫堪, 等. 基于干涉图的星载MIMO-SAR动目标检测[J]. 信号处理, 2010, 26(1): 23-27.
Wang Libao, Xu Jia, Huangfu Kan, et al. Moving target detection for spaceborne MIMO-SAR based on interferogram[J]. Signal Processing, 2010, 26(1): 23-27.(in Chinese)
[4] 路满, 宋红军, 罗运华. 基于调频连续波信号的圆弧式合成孔径雷达成像[J]. 雷达学报, 2016, 5(4): 425- 433.
Lu Man, Song Hongjun, Luo Yunhua. Imaging Algorithm for Arc Synthetic Aperture Radar Using Frequency Modulated Continuous Wave[J]. Journal of Radars, 2016, 5(4): 425- 433.(in Chinese)
[5] Wang Yanping, Qi Yaolong, Tan Weixian, et al. Experimental Study on Deformation Monitoring Based on GB-SAR[C]∥IET Radar 2015, 2015, 1- 4.
[6] Yang Xiaolin, Wang Yanping, Qi Yaolong, et al. Experiment Study on Deformation Monitoring Using Ground-Based SAR[C]∥Asian-Pacific Conference on Synthetic Aperture Radar(APSAR 2013), 2013.
[7] Zhu Mao, Hu Cheng, Zeng Tao, et al. Experimental results and analysis for GBSAR deformation measurement[C]∥IET International Radar Conference 2015, 2015.
[8] Peng Xueming, Lu Xuguang, Tan Weixian, et al. Ku-Band step frequency Ground-Based SAR system and experiments[C]∥IET International Radar Conference 2013, 2013: 1-5
[9] Luo Yunhua, Song Hongjun, Wang Robert, et al. Signal processing of Arc FMCW SAR[C]∥Conference Proceedings of 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), 2013:412- 415.
[10] Andrea Carolina Flores Rodriguez, Gustavo Fraidenraich, Tarcísio A. P. Soares, et al. Optimal and Suboptimal Velocity Estimators for ArcSAR With Distributed Target[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 252-256.
[11] Garmatyuk D S, Narayanan R M. Ultra-wideband continuous-wave random noise arc-SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(12): 2543-2552.
[12] Hoonyol Lee, Seong-Jun Cho, Kwang-Eun Kim. A ground-based Arc-scanning synthetic aperture radar(ArcSAR) system and focusing algorithms[J]. 2010 IEEE International Geoscience and Remote Sensing Symposium, 2010: 3490-3493.
[13] Luo Yunhua, Song Hongjun, Wang Robert, et al. Arc FMCW SAR and Applications in Ground Monitoring[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5989-5998.
[14] Pieraccini M, Miccinesi L. ArcSAR for detecting target elevation[J]. Electronics Letters, 2016, 52(18): 1559-1561.
[15] Massimiliano Pieraccini, Lapo Miccinesi. ArcSAR: Theory, Simulations, and Experimental Verification[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(1): 293-301.
[16] 赵月, 林赟, 王彦平, 等. 基于圆迹SAR的目标方位散射特征提取研究[J]. 信号处理, 2017, 33(4): 613- 617.
Zhao Yue, Lin Yun, Wang Yanping, et al. Target Feature Extraction on Azimuth Angles Based on Circular-SAR[J]. Journal of Signal Processing, 2017, 33(4): 613- 617.(in Chinese)
[17] Wang Yanping, Lin Yun, Tan Weixian, et al. Polar Format Algorithm for Circular SAR[C]∥EUSAR, 2010: 1- 4.
[18] Hoonyol Lee, Jae-Hee Lee, Kwang-Eun Kim, et al. Development of a Truck-Mounted Arc-Scanning Synthetic Aperture Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2773-2779.
[19] 吴雄峰, 王彦平, 吴一戎, 等. 圆周合成孔径雷达投影共焦三维成像算法[J]. 系统工程与电子技术, 2008, 30(10): 1874-1878, 1933.
Wu Xiongfeng, Wang Yanping, Wu Yirong, et al. Projected confocal 3-D imaging algorithm for circular SAR[J]. Systems Engineering and Electronics, 2008, 30(10): 1874-1878, 1933.(in Chinese)



