1 引言
随着移动数据业务需求的爆炸式增长,无线通信对频谱资源的需求逐年攀升。根据思科公司2017年的年度互联网预测,2021年全球数据流量将超过3300万亿兆字节,其中移动设备所占用的比例将占总流量的73%[1]。如何大幅度提升通信系统容量来应对流量增长需求迫在眉睫。但传统3 GHz以下的频谱资源的利用已趋于饱和,频谱利用率也已逼近香农极限,仅在现有授权频段上提升系统容量已是杯水车薪。因此拓展新的频谱资源势在必行。采用毫米波频段通信可以突破可用频谱资源匮乏的瓶颈,满足未来移动数据业务的需求。同时毫米波无线通信技术拥有带宽极宽、易小型化的优势,此外60 GHz的毫米波还具有无需授权使用的优势[2]。因此,毫米波无线通信技术有望成为5G通信的关键技术之一,特别适合高速率、大容量通信。
虽然毫米波频段提供了丰富的带宽资源,但与传统频段相比,普通的平面电磁波在该频段上存在很高的路径损耗,严重影响了系统容量。近年来因波前为涡旋形状而具备轨道角动量(Orbital Angular Momentum, OAM)的电磁波(又称涡旋电磁波)在毫米波频段所展现的信息携带能力越来越受到关注[3-5]。轨道角动量的相位函数为ejlφ,其中l是拓扑电荷数,用于表示OAM模态。理论上模态数是无穷的,这意味着可以构成无穷维的希尔伯特空间(高维性);同时具有不同模态的OAM波束是相互正交的(正交性)[6-7]。因此,将OAM模态应用到无线通信中理论上可以实现更高的传输速率。在文献[8]中,作者在视距条件下的60 GHz的毫米波频段实现了32 Gbit/s的总传输速率和16 bit/s/Hz的频谱利用率。该实验结果表明在该频段进行OAM复用通信可以减少波束传播过程中的能量损耗,增加传输距离,且能减少收发器的尺寸。文献[9]中提出了一种基于OAM空间调制的毫米波通信系统,相较于OAM-MIMO系统能量效率大幅提升并对于毫米波的路径衰减有更好的鲁棒性。
OAM毫米波呈螺旋状分布,这就使得它不能像普通平面波那样在主方向处处都可接收到信号能量,如果不在特定方位进行接收,相当一部分能量无法被接收端捕捉[10]。受限于OAM波的能量辐射特性,文献[11]首次指出,当收发两端均匀环形阵列(Uniform Circular Array, UCA)同心共轴高度对齐时,OAM毫米波系统可以提供与多输入多输出系统(Multiple-Input Multiple-Output,MIMO)相同的性能,但当发送和接收阵列之间存在微小的倾斜角度时,将严重影响接受端模态检测的准确性,OAM毫米波系统性能将严重降低。文献[12]中作者运用MIMO的信道模型,研究了在角度偏移时OAM毫米波通信系统的信道模型和信道容量,从而验证了上述结论。但是该模型中是采用UCA的多天线系统产生OAM毫米波的,其分析过程是基于传统的MIMO传输模型,考虑了收发天线阵元之间的路径衰减,但并不涉及多路OAM毫米波信号传输模型的建立与分析,同时也不适用于其他产生OAM毫米波的天线系统。此外该文只针对收发两端收发天线共轴但存在角度偏移情形下的信道进行了建模,该模型并不适于收发天线平行非共轴的场景。因此,如何建立更加普适的OAM毫米波系统信道模型具有重要的研究意义。
当轨道角动量用于无线通信传输时,一旦信道环境受到干扰,OAM模态的能量会以一定的概率发生转移,从而发生模态间的串扰。文献[13]曾在无线环境中用光波进行实验,得到了其因湍流而发生跃迁的能量分布。基于这种模态跃迁特性,本文将接收端的信号建模成不同路径OAM毫米波信号的叠加,通过理论分析推导出收发端横向轴偏移下模态迁移的分布,将系统信道建模成多元离散无记忆信道模型。
本文其他部分安排如下:第2节建立了OAM毫米波通信系统传输模型;第3节基于OAM毫米波的模态迁移特性对信道进行了建模,并推导了收发端横向轴偏移情况下的系统容量表达式;第4节对仿真结果进行了分析;最后阐明结论并总结全文。
2 系统模型
本文所研究的OAM毫米波系统如图1所示,其包含多个收发天线对,用于生成和接收不同的OAM毫米波信号。每条链路发送端均传输一个单一的OAM模态,则该系统中存在多个互相正交的OAM模态,能够增大系统容量。
具体来说,当某条链路被分配使用模态li时,原本携带信息的平面波经相应参量的空间相位调制后成为具有|li|个拓扑电荷的涡旋毫米波,其中li的正负表示波束的自旋方向,我们假设li取正整数(顺时针方向),则发送端生成的含有OAM模态li的毫米波载波信号可以表示为
Φli(r,θ,t)=Uli(r,θ)ej(ωst+φs(t))
(1)
其中ωs和φs(t)分别是该OAM毫米波的频率和瞬时相位。Uli(r,θ)表示天线阵列生成的OAM模态li,其表达式为
Uli(r,θ)=Rli(r)ejliθ
(2)
其中r和θ分别表示极坐标下OAM波束的半径和方位角,ejliθ是OAM毫米波的空间相位,引起涡旋相位。Rli(r)表示OAM毫米波的振幅,其中拉盖尔-高斯模式的OAM毫米波振幅为
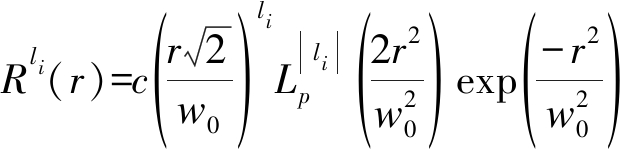
(3)
其中w0是零阶高斯束腰半径。L(·)是连带拉盖尔多项式。li表示发送的OAM模态,p表示径向模态
表示归一化常数,当考虑p=0时,
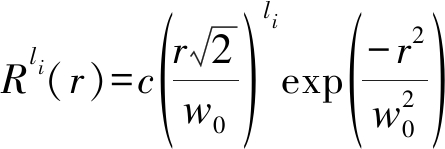
(4)
发送端携带有数据信息的OAM毫米波已调信号为
(5)
其中P是系统发送功率,si(t)是调制信号。因此,图1中进入传输信道前的发送信号E(r,θ,t)可以看作是m路OAM毫米波信号的线性叠加
(6)
在OAM毫米波通信系统中,接收端的信号可能会受到大气湍流、天线增益、路径衰减以及加性噪声等因素的影响,其数学表达形式为发送信号与传输函数的卷积
E′(r,θ,t)=E(r,θ,t)⊗h(r,θ,d,t)+n(t)
(7)
其中d表示收发两端的距离,即路径长度。⊗表示卷积,n(t)表示信道中的加性高斯白噪声。在接收端只需通过相应的逆相位控制和空间滤波的方式就可以将各模态波束分离,包含不同OAM模态的毫米波信号在接收端通过不同的接收天线接收。利用OAM波束的天然正交特性解调恢复出各路信号信息Si(t),该解调过程数学表达式如下
Si′(t)=〈Φli′(r,θ,t)|E′(r,θ,t)〉
⊗h(r,θ,d,t)〉
+ni(t)·Φli′(r,θ,t)
(8)
其中〈·|·〉表示内积,ni(t)表示第i个子信道的加性高斯白噪声。
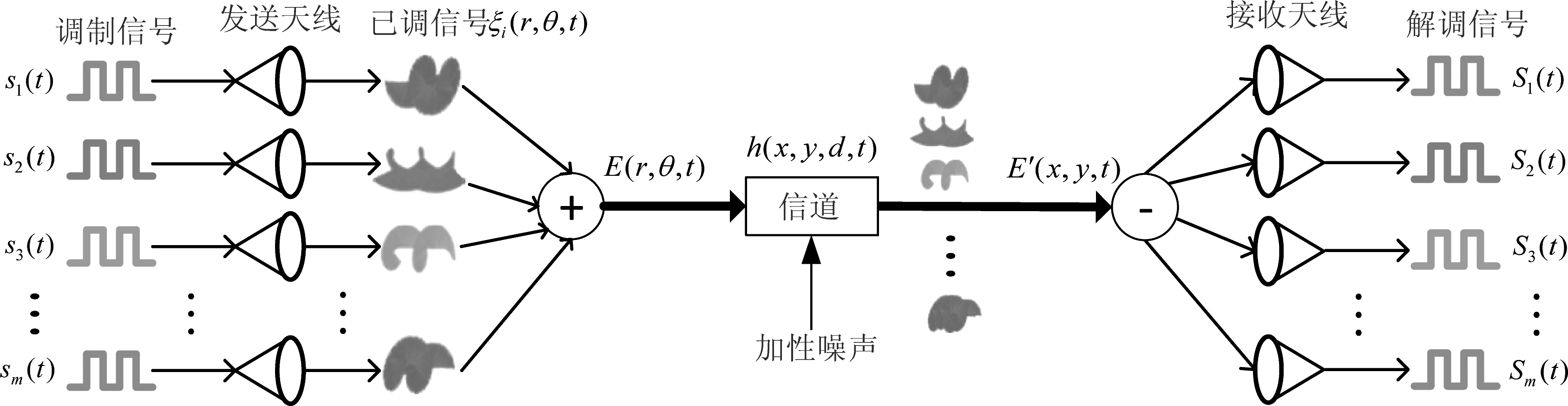
图1 OAM毫米波系统模型
Fig.1 Diagram of OAM millimeter wave system
3 信道建模与容量分析
OAM理论上具有无穷多个正交态,我们正是利用这一特性在收发两端之间建立多条子信道进行传输。而在实际的传输过程中,必须额外考虑大气湍流和收发偏移等因素带来的模态跃迁问题。模态迁移是指OAM模态在传输过程中,某个模态的能量可能部分由其他模态迁移得到,其本身的能量也可能部分泄露到其他模态。此时接收端接收到的信号虽仍彼此正交,但已产生了不同程度的失真。也就是说,原先单路子信道传输携带单一模态的OAM毫米波信号,由于模态能量迁移的影响,接收端检测到的毫米波信号不仅仅携带单一模态的轨道角动量,而是以一定的概率取不同的模态值,从而错误地将其恢复为多个模态叠加的毫米波信号。因此在数学表达上,接收到的失真的OAM毫米波信号可以看成是多个相互正交的OAM模态的叠加
(9)
其中αli′(t)是与大气湍流、收发偏移、天线增益以及路径衰减等因素有关的失真系数。本文将重点聚焦于收发偏移情形下的失真系数推导。
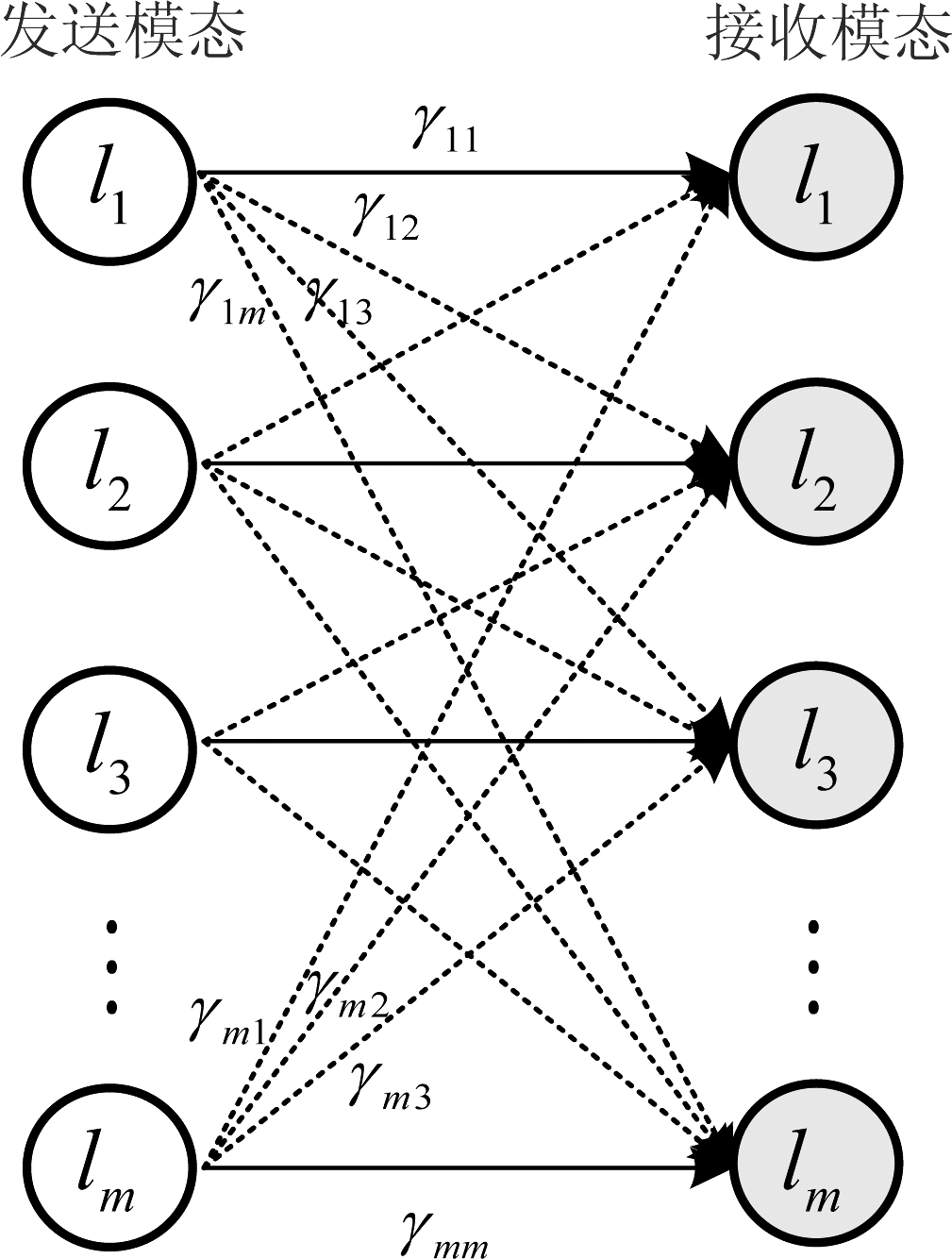
图2 OAM模态能量迁移
Fig.2 Energy transition of OAM modes
横向偏移情形下的OAM模态迁移如图2所示。无失真情况下,每个子信道传输的信号仅含有单个OAM模态li,即该路信号收发两端使用同一模态分别进行发送和检测,如图2中的实线箭头所示。一旦OAM毫米波系统收发两端发生横向轴偏移,模态间的能量发生迁移,如图2中的虚线箭头所示。其中γii′表示实际传输中收发两端模态之间的子信道特性系数,即发送端模态为li而接收端变为模态li′时的信道特性系数。此时每一路信号可能变得不再纯粹,将导致接收端检测的精度大大受限。从理论上来说,模态跃迁带来的潜在干扰信号的分布会制约OAM毫米波通信系统的容量上限。这就使得本系统信道模型有别于传统无线衰落模型,必须同时考虑收发端之间的路径衰减和偏移时跃迁模态的分布特性。
假设整个系统处于大气湍流环境下,发送端天线产生带有OAM 模态的毫米波信号,可用拉盖尔高斯波束的形式来表征单纯OAM模态毫米波的空间和相位特性,如式(3)所示。图3中给出了收发两端天线产生横向轴偏移在笛卡尔坐标系下的几何模型。坐标原点O表示发送端天线轴心,Z轴表示收发端轴对准时波束轴指向方向。实际接收端轴心位置发生横向偏移,位于O′Z′方向。因此,图中OO′表示收发两端的横向轴偏移。x0和y0分别为收发天线在X轴和Y轴方向上相对位移,引起OAM模态间串扰,实际传输中该位移是随时间t变化的变量,即x0(t)和y0(t)。该情形下的传输函数h(x,y,d,t)的表达式如下
(10)
其中,B是天线增益系数,λ表示波长,k=2π/λ表示波数,δ(·)是狄拉克函数。
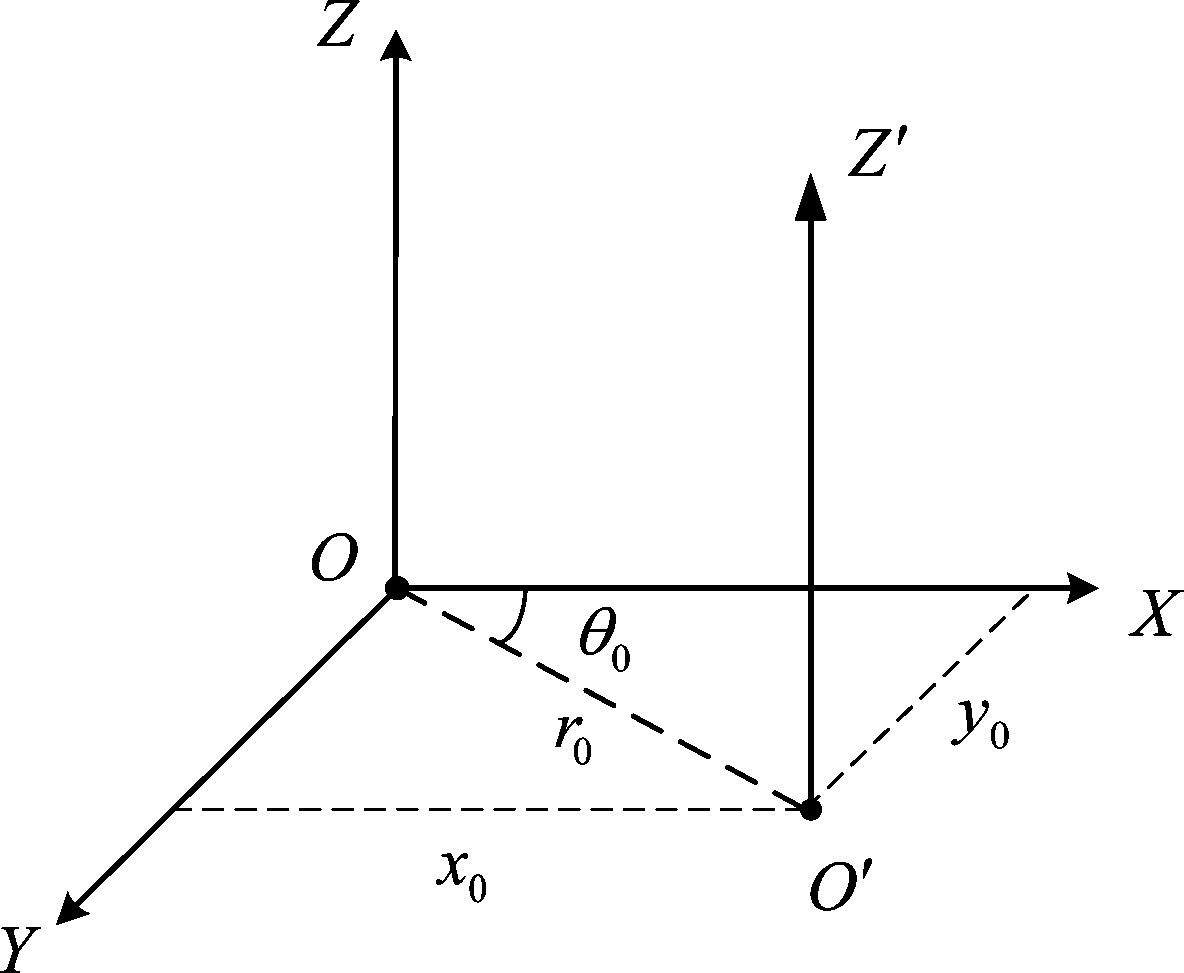
图3 收发两端天线横向轴偏移的几何模型
Fig.3 The geometrical model of the transmit antenna and
the receive antenna in the off-axis misalignment case
为了更加直观地表现收发偏移的情形,给定一组极坐标参数r0和θ0用于表示收发设备之间的偏移程度,其中r0表示横向轴偏移的距离,即OO′的长度,θ0表示收发端天线轴心间的偏移夹角,且满足x0=r0cos θ0,y0=r0sin θ0。因此,式(10)中的传输函数可以转换为极坐标下的形式并代入式(7),可得接收端的OAM毫米波信号为
E′(r,θ,t)=E(r,θ,t)⊗
δ(rcos θ-r0(t)cos θ0(t),rsin θ-r0(t)sin θ0(t))+n(t)
(11)
将上式与式(9)联立,我们可以得到接收端不同模态之间的功率相关系数(失真系数)为
αli′(t)=〈Uli′(r,θ)|E′(r,θ,t)〉
Uli′*(r,θ)E′(r,θ,t)rdrdθ
(12)
该系数反应了OAM模态迁移的分布特性。进一步将式(2)和(7)代入上式中的被积函数表达式,可以得到αli′(t)的表达式
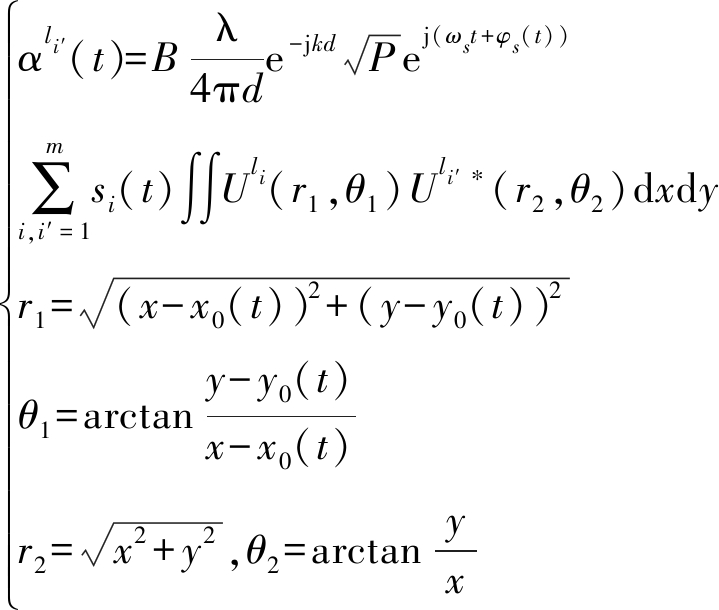
(13)
信道特性与调制信号si(t)和OAM毫米波的频率和瞬时相位无关,即
可以得到信道特性系数γii′(t)的一般表达式
(14)
同理,将式(2)代入上式中的被积函数,可得其具体数学表达式
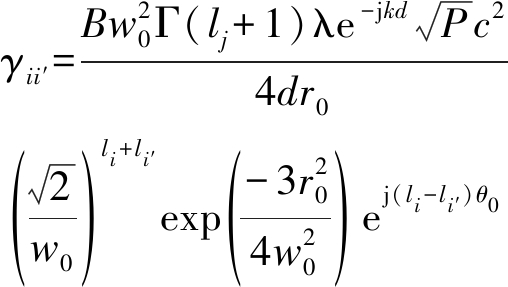
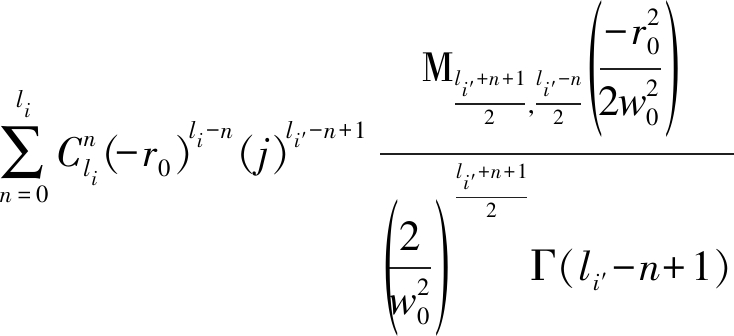
(15)
其中Jν(·)是ν阶贝塞尔函数,Γ(·)是伽玛函数,Μλ,μ(·)是Whittaker函数,
表示从0到li个不同元素中取出n个元素的一个组合。则接收端接收到OAM模态为li′的毫米波信号上携带的调制信号为
其中信道特性系数γii′构成了信道传输矩阵H,具体表示如下
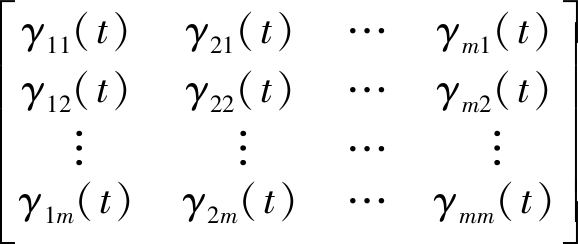
(16)
为了推导OAM毫米波通信系统的容量,首先需要对信道矩阵进行奇异值分解(Singular Value Decomposition, SVD),其具体表达式如下
H=ULVH
(17)
U和V均为m×m阶的酉矩阵,L为对角阵且
对角阵的元素顺序按
排列,其中
是信道矩阵H的奇异值,r=rank(H)。
在上一部分中,我们建立了一个收发两端均包含m个OAM模态的系统模型,因此最终得到的信道传输矩阵阶数为m×m。假设每条链路的发射功率相等,那么该OAM毫米波系统的信道总容量是各子信道的容量的总和,其表达式如下
(18)
其中
是接收端的噪声方差,Pi表示各子信道的发送功率。
4 仿真结果与分析
下面给出OAM系统信道容量在给定参数下的数值结果。在仿真中,假设发送端功率P=1 W,且该功率以平均分配的方式分配给各子信道,即各信道功率相等。其他默认的仿真参数设置如下:载波频率f=60 GHz,天线增益系数B=105,零阶高斯束腰半径w0=0.001 m,发射天线和接收天线之间的距离为30 m,带宽为20 MHz。
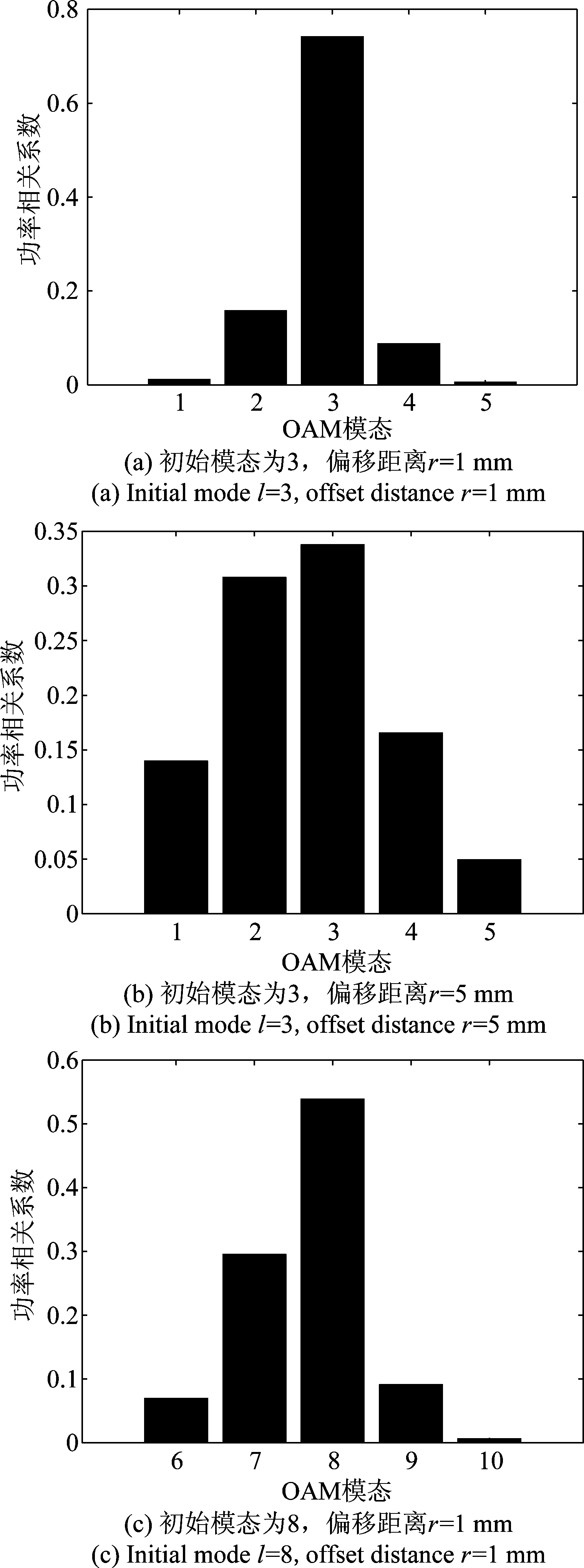
图4 不同初始发送模态和不同偏移距离下的OAM模态功率分布(归一化)
Fig.4 Power distribution between OAM modes with different initial modes and offset distances (normalized)
如上文所述,式(15)中的信道特性系数γii′(t)的物理意义是模态li(发送端)迁移到模态li′(接收端)的功率转移量。因此,结合式(16)中的矩阵分布,取某一列的所有元素并分别取模,即得到该列对应的初始模态转移到其他各模态的功率以自身所携带的剩余功率值,将计算结果归一化处理后可以得到图4中的OAM模态功率分布图。仿真结果显示,不同的初始发送模态受到不同距离的横向轴偏移干扰时,OAM模态之间会发生不同的能量迁移。其中图(a)和(b)表明,当选择相同的初始发送模态时,由于横向轴偏移的存在,l≠0的OAM波束在传输过程中会存在波束发射效果,该毫米波信号波束携带的模态的能量会产生泄露,且泄露到相邻模态的能量是高于非相邻模态的,也就是说相邻模态之间发生跃迁和串扰的概率是最高的。且偏移距离越大,模态间的能量泄露越剧烈,接收端模态检测的误差也会随之急剧增加。此外,对比图(a)和图(c)可以发现,初始发送模态较大时,其能量泄露到其他模态的程度较大,接收端检测到原模态的概率会减小,说明其抵抗横向轴偏移的能力较差。这是因为OAM波束的发散角度随着l数值的变大而增大,即发散越来越强烈。因此l较大的模态群组的不同模态之间其由于横向偏移而导致发生模态能量的迁移概率必然会更高,从而导致其模态的能量泄露更加严重。
图5中给出了理想信道下,传统MIMO毫米波系统和OAM毫米波系统容量随信噪比变化的曲线。我们可以看出,两种系统的容量均随着信噪比的增大而增大。同时在相同的信噪比下,4模态OAM毫米波通信系统的容量大于4×4 MIMO(发射天线和接收天线数目均为4)毫米波通信系统的容量, 2模态OAM毫米波通信系统的容量大于2×2 MIMO毫米波通信系统的容量。由该结果可以看出,OAM毫米波通信在系统传输速率方面的性能是优于传统的MIMO毫米波系统的。
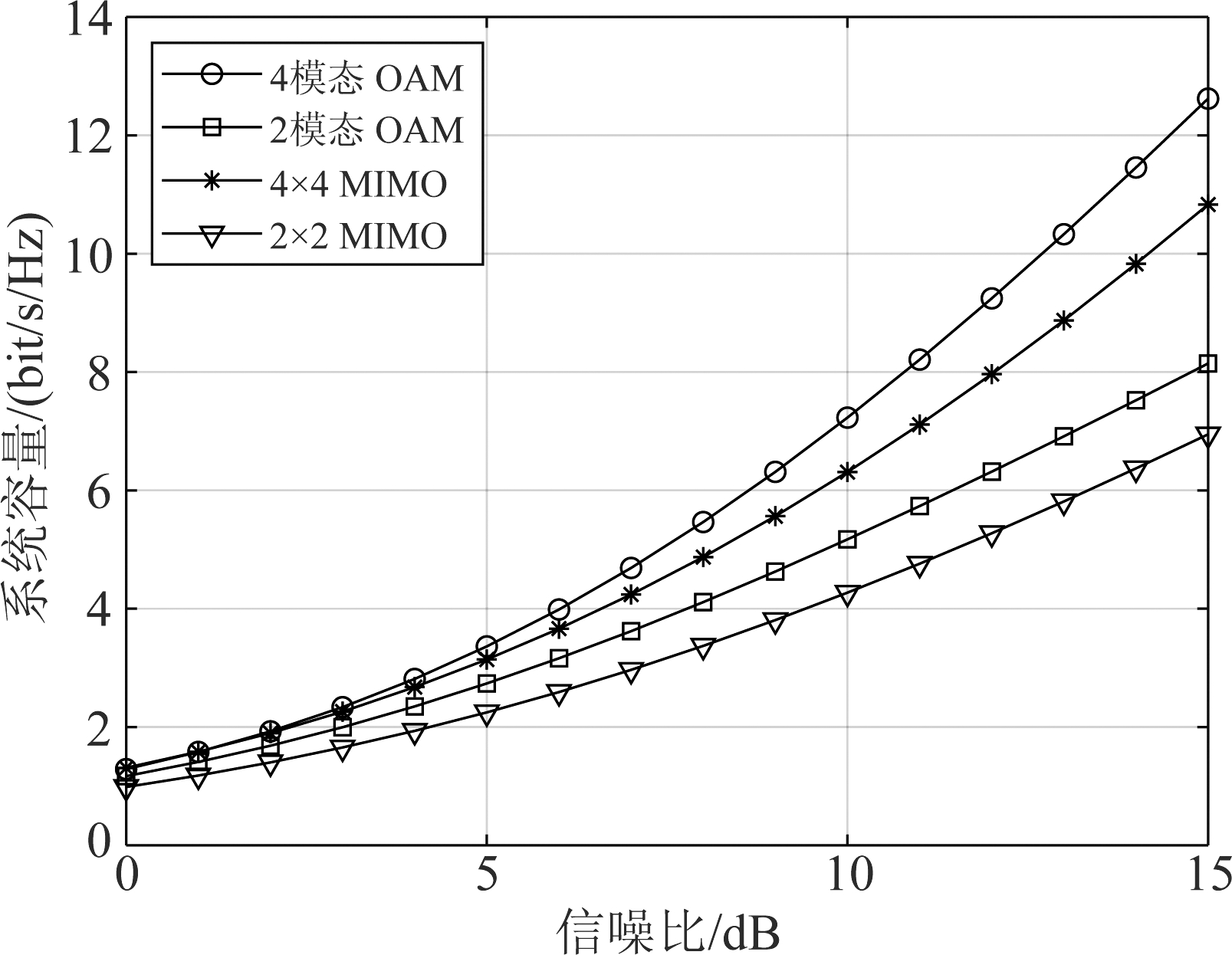
图5 MIMO毫米波系统和OAM毫米波系统容量随传输信噪比的变化情况
Fig.5 Capacity of conventional MIMO and OAM millimeter wave communication systems with respect to the transmission SNR
图6给出的是给定不同模态数目下系统容量与传输信噪比的关系曲线。其中选定的8模态群组为{l=1,2,…,8},4模态群组为{l=1,2,…,4}。可以看出,对于不同的模态数,系统容量都随着信噪比的增大而增大,且模态数目越多,系统容量更大。将偏移距离设定为1 mm,此时由于存在模态之间的跃迁和串扰,系统容量有明显下降,例如有偏移时8模态的系统容量在15 dB信噪比下约为8.2 bit/s/Hz,该值甚至小于同信噪比无偏移下4模态的系统容量(约12.6 bit/s/Hz)。因此收发两端天线产生横向轴偏移会使得OAM毫米波系统性能明显下降,OAM毫米波的收发对齐是一个不容忽视的问题。
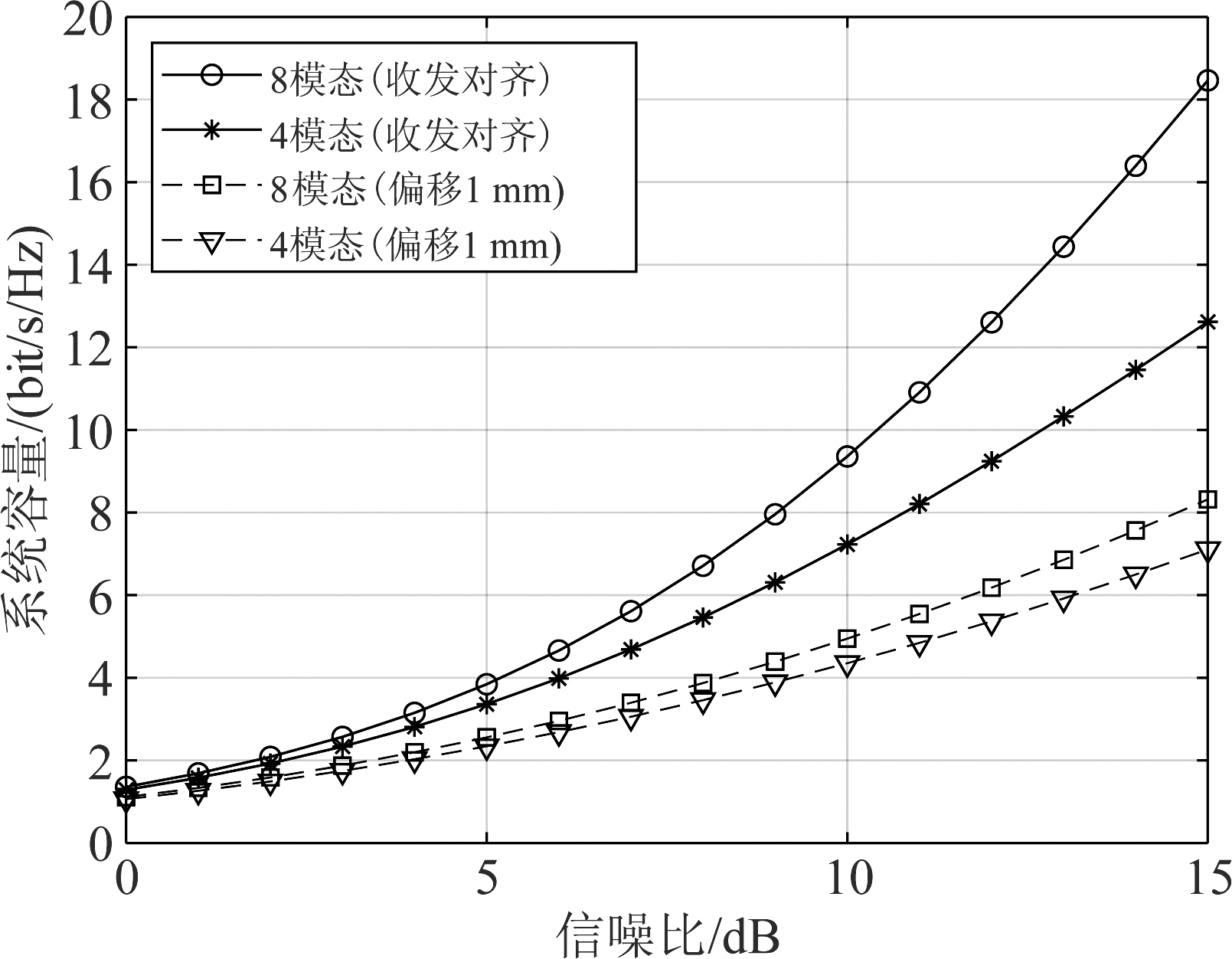
图6 轴对准和轴偏移时OAM毫米波系统容量随传输信噪比的变化情况
Fig.6 Capacity of OAM millimeter wave communication systems with respect to the transmission SNR both in the alignment and off-axis misalignment case
图7具体描绘了不同模态数目下系统容量与横向偏移距离的具体关系曲线,其中给定传输信噪比为30 dB,选定的8模态群组为{l=1,2,…,8},4模态群组为{l=1,2,3,4},2模态群组为{l=1,2}。可以发现随着收发端横向偏移距离的增大,模态迁移导致模态之间的能量泄露概率增大,因此系统容量呈现显著下降的趋势。以8模态为例,当横向偏移为1 mm时,系统容量大约为24 bit/s/Hz,然而当横向偏移增加到5 mm时,容量急剧下降到约10 bit/s/Hz。可见,轨道角动量对横向偏移十分敏感,横向偏移的存在使得OAM毫米波系统的性能受到了严重的限制。同时当偏移达到一定距离之后,系统容量不再减少。这就说明当收发两端的偏移超过某一限定值后,模态之间的干扰分布将趋于一个稳态,系统容量不再减少。值得一提的是,当偏移距离大于3 mm时,8模态和4模态的系统容量均小于2模态的系统容量。这说明模态数目越大的系统随着偏移距离增大,系统性能下降得越明显。且由于模态数目更多,其发生模态迁移的概率更大,更容易产生模态间的串扰。
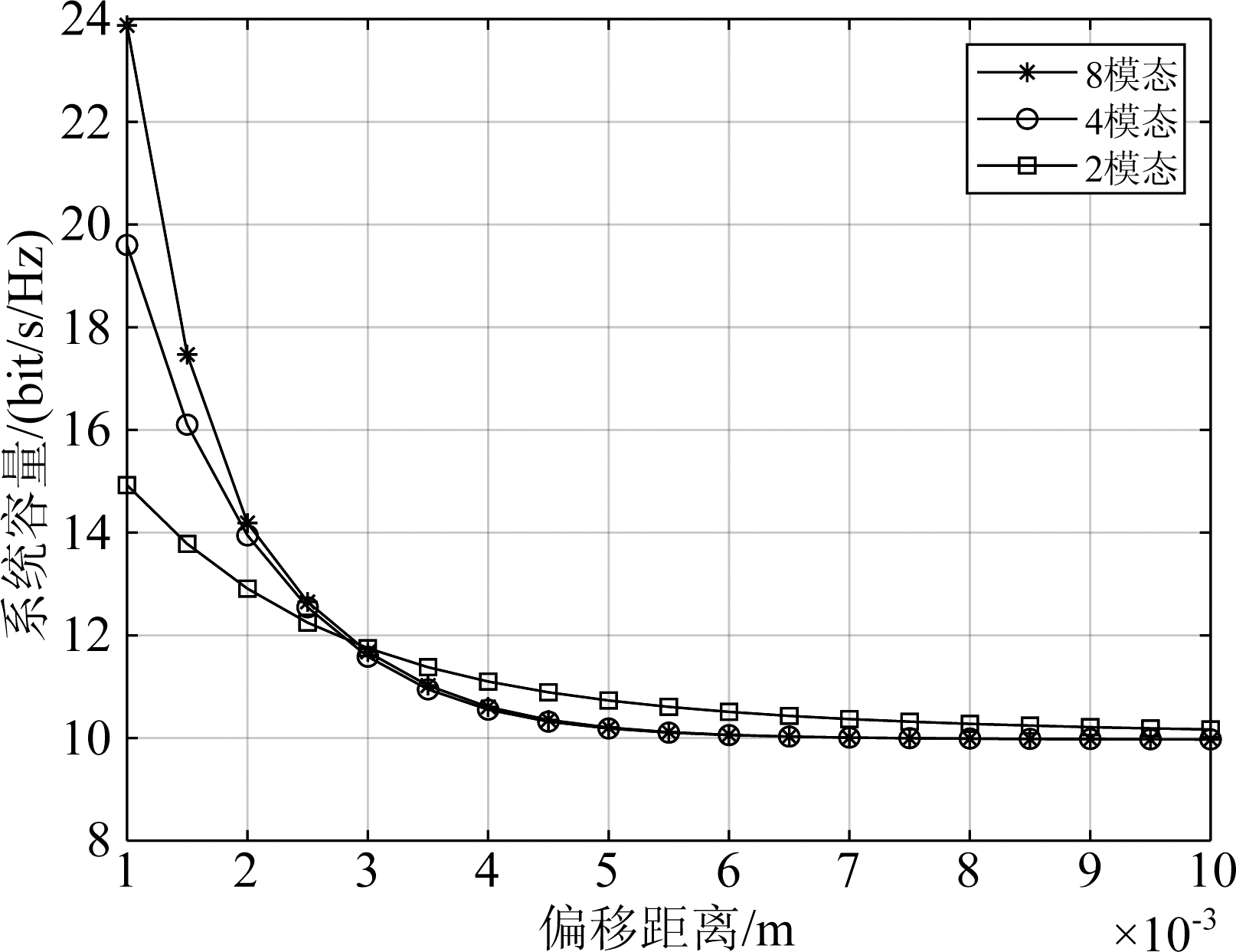
图7 OAM毫米波系统容量与偏移距离的关系(信噪比为30 dB)
Fig.7 The relationship between the capacity of OAM millimeter system and the offset distance (SNR=30 dB)
图8和图9给出了不同模态的组合选择方式与系统容量之间的关系曲线,从系统容量的角度验证了图4中给出的OAM模态功率分布与初始发送模态和偏移距离之间的关系。以4模态群组为例,给定偏移距离为1 mm。图8中具体考虑了三种不同的OAM模态组合方案,分别采用不同的模态间隔Δl。模态群组分别为{l=1,2,3,4},{l=1,3,5,7},{l=1,4,7,10},对应的模态间隔为Δl=1,2,3。从图中的仿真结果可以发现,在相同的偏移距离下,模态间隔越大,模态间发生能量泄露的概率减小,因此模态间串扰的可能性降低,系统容量也更大。图9则描绘了当模态间隔恒定,不同模态群组与系统容量之间的关系曲线。给定模态间隔Δl=1,选择的不同模态群组{l=1,2,3,4},{l=5,6,7,8},{l=9,10,11,12}。由仿真结果可以看出,在相同的偏移距离下,当l取值较大时,由于OAM波束的发散更加强烈,此时模态之间的能量迁移更严重,因此系统容量相对较小。
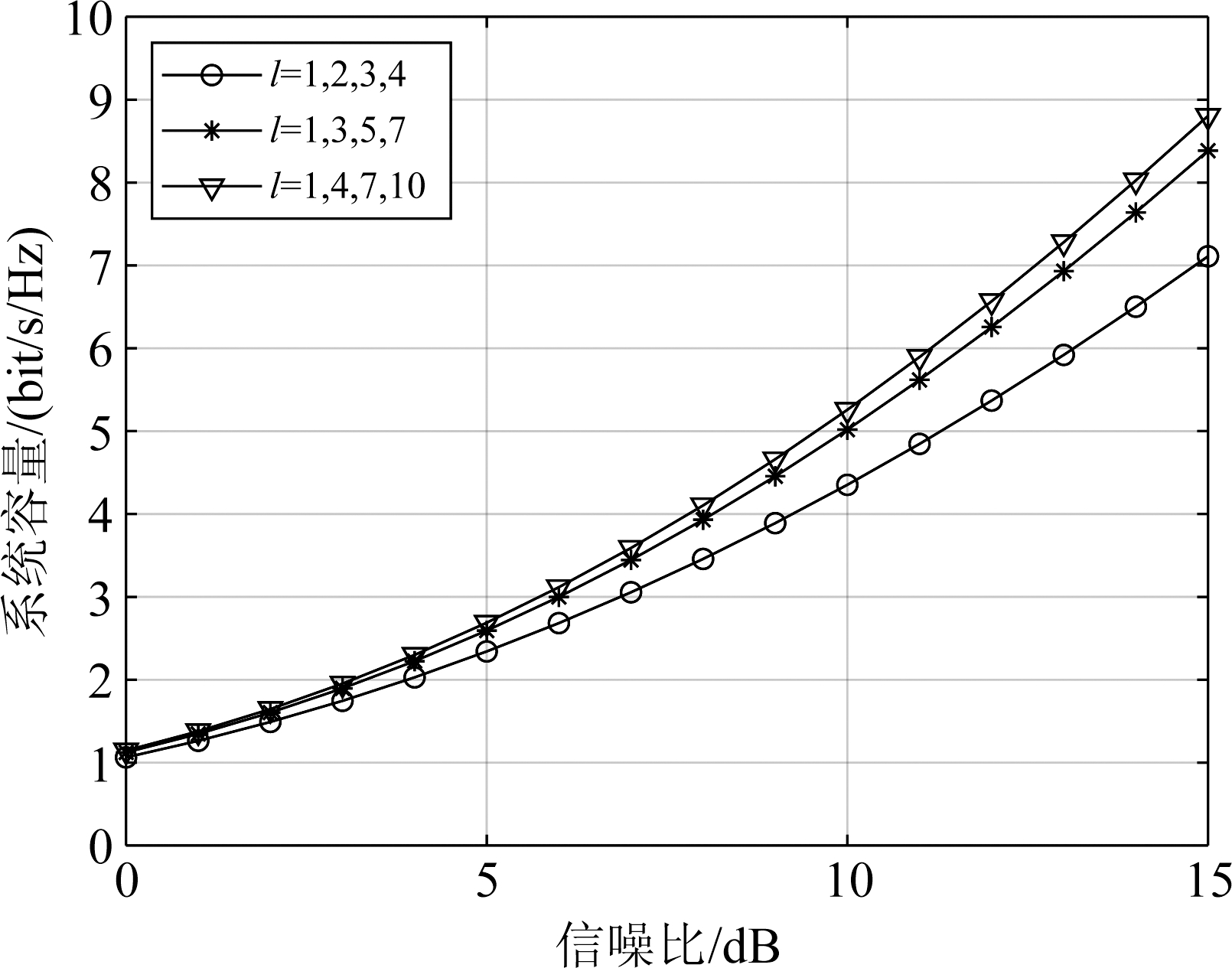
图8 模态间隔Δl=1,2,3的模态群组的OAM毫米波系统容量随传输信噪比的变化情况(模态群组容量为4)
Fig.8 Capacity of OAM millimeter wave communication systems with respect to the transmission SNR, 4 OAM modes and mode interval Δl=1,2,3
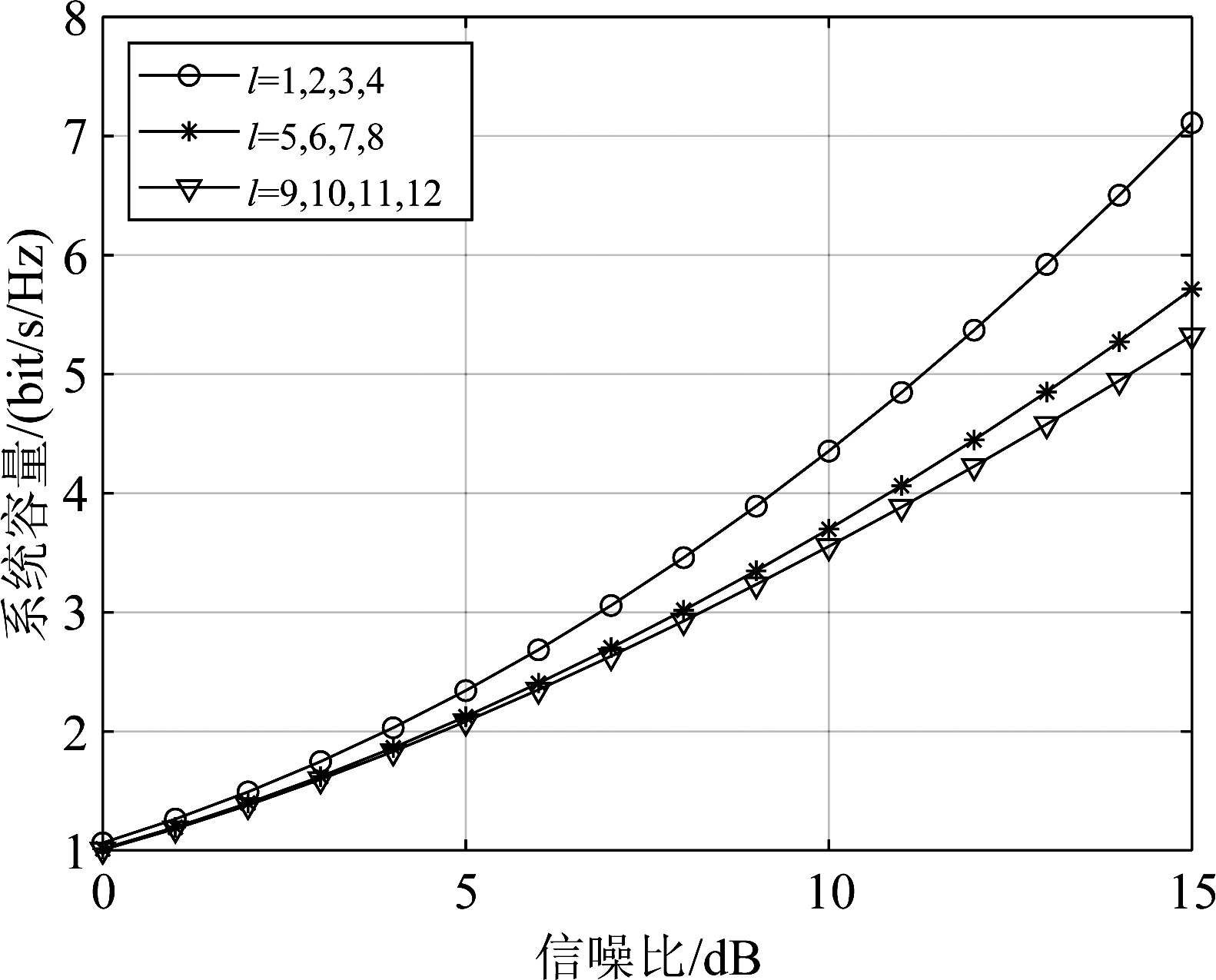
图9 模态间隔Δl=1的不同模态群组的OAM毫米波系统容量随传输信噪比的变化情况(模态群组容量为4)
Fig.9 Capacity of OAM millimeter wave communication systems with respect to the transmission SNR, 4 OAM modes and mode interval Δl=1
5 结论
本文建立了一种OAM毫米波通信系统并针对其传输信号时收发两端天线产生横向轴偏移的情形,结合OAM毫米波的模态迁移特性,对系统进行了信道建模,理论推导了有偏移下的模态功率分布,构建了系统信道传输矩阵。并基于该矩阵对系统进行了容量分析。实验仿真结果表明了系统容量会随着偏移距离的增大而呈现下降趋势,并最终趋于稳定。模态数目越大的系统容量下降趋势更加明显。而且在收发偏移时,当系统选用模态值较小的模态群组和模态间隔较大的模态群组时,系统容量更大,即此时受偏移影响较小。这为提升偏移场景下的系统容量提供了可行的思路。同时,未来的研究工作也可以着眼于轴偏移的校准方案设计,从而进一步优化系统性能。
[1] Cisco visual networking index: Global mobile data traffic forecast update 2016-2021 white paper[Online]. Available: http:∥www.cisco.com.
[2] Olver A D. Millimetrewave systems-Past, present and future[J]. IEE Proceedings F-Radar and Signal Processing, 1989, 136(1): 35-52.
[3] Allen L, Beijersbergen M W, Spreeuw R J C, et al. Orbital angular momentum of light and transformation of Laguerre Gaussian Laser modes[J]. Physical Review A, 1992, 45(11): 8185- 8189.
[4] Babiker M. IV The Orbital Angular Momentum of Light[J]. Progress in Optics, 1999, 39(1-3): 291-372.
[5] MilesPadgett, Allen L. Light with a twist in its tail[J]. Contemporary Physics, 2000, 41(5): 275-285.
[6] Yao A M, Padgett M J. Orbital angular momentum: origins, behavior and applications[J]. Advances in Optics & Photonics, 2011, 3(2): 161-204.
[7] Soskin M S, Gorshkov V N, Vasnetsov M V, et al. Topological charge and angular momentum of light beams carrying optical vortices[J]. Physical Review A, 1997, 56(5): 4064- 4075.
[8] Yan Y, Li L, Zhao Z, et al. 32-Gbit/s 60-GHz millimeter-wave wireless communication using orbital angular momentum and polarization multiplexing[C]∥2016 IEEE International Conference on Communications. IEEE, 2016: 1- 6.
[9] Ge X, Zi R, Xiong X, et al. Millimeter Wave Communications with OAM-SM Scheme for Future Mobile Networks[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 2163-2177.
[10] Nguyen D K, Pascal O, Sokoloff J, et al. Discussion about the link budget for electromagnetic wave with orbital angular momentum[C]∥European Conference on Antennas & Propagation. IEEE, 2014: 1117-1121.
[11] Cagliero A, Gaffoglio R. On the Spectral Efficiency Limits of an OAM-based Multiplexing Scheme[J]. IEEE Antennas & Wireless Propagation Letters, 2017, 16(99): 900-903.
[12] Zhang N Y, Feng W, Ge N. On the restriction of utilizing orbital angular momentum in radio communications[C]∥2013 8th International Conference on Communications and Networking in China(CHINACOM). IEEE Computer Society, 2013: 271-275.
[13] Zhao S M, Wang L, Zou L, et al. Both channel coding and wavefront correction on the turbulence mitigation of optical communications using orbital angular momentum multiplexing[J]. Optics Communications, 2016, 376: 92-98.
