1 引言
解决非线性滤波的最优方案是得到其条件后验概率的完整描述,然而精确闭式解需要无穷多的参数,因此需要近似[1]。泰勒级数思想通过对非线性函数进行线性化近似,对高阶项目采用逼近或忽略。其中最为广泛使用的是一阶扩展卡尔曼滤波器(EKF)[2],该方法易于实现。由于线性化带来不可避免的估计误差,对于强非线性动态系统,扩展卡尔曼滤波器的估计性能下降并可能产生发散。无迹卡尔曼(UKF)滤波器是一种基于无迹变换(unscented transform)的滤波算法[3]。该算法从统计学的角度近似后验分布,避免了非线性函数的线性化计算。估计精度高于扩展卡尔曼滤波算法,适用范围广[4]。近年来,粒子滤波器(PF)是有效解决非高斯、非线性估计问题的滤波算法,其基本思想是通过带权重的采样粒子以在线方式完整地表示估计状态的后验分布,然而粒子贫化及计算量大是主要挑战[5-6]。
文献[7-8]表明,迭代步骤的引入(比如,迭代扩展卡尔曼滤波IEKF、迭代无迹卡尔曼滤波IUKF)可以提高相应估计器(EKF,UKF)的鲁棒性和准确性。文献[9]指出,对于弱可观测的非线性动态系统,估计结果可能无法收敛到全局最优的情况,可利用与参数相关联的约束信息进行迭代优化以改进滤波效果。文献[10]指出,非线性量测函数的近似仅在可行区域中是准确的。从而,对于非线性状态估计,可以将一些特定约束信息视为潜在先验知识,以修正的后验概率分布的近似过程。近年来,诸多约束状态估计算法相继涌现,没有单一的最优方法将约束结合到非线性动态状态估计过程中[11]。较为常见的方法有截断法,数值优化法等。文献[12]提出截断无迹卡尔曼滤波器(TUKF),可以有效处理多模型似然函数情况,滤波性能优于单一的传统卡尔曼型滤波器。文献[13]提出约束迭代无迹卡尔曼滤波器(CIUKF)不仅可以用于估计目标的动态状态,而且可以用于检测和识别模型参数的变化。上述算法中的约束条件均为硬约束,需要严格满足。
在此基础上,本文将量测软约束新息引入无迹卡尔曼滤波的实施过程,提出了平滑约束无迹卡尔曼(SCUKF)算法。采用数值优化近似求解修正先验概率统计量,将采样西格玛点限制在可行域内,从而,提高计算效率并平滑更新过程中可能存在的野值问题。仿真实验表明了该算法的有效性。
2 无迹卡尔曼算法
2.1 无迹变换
无迹变换的基本思想为,用固定数量的参数去近似一个高斯分布比近似任意发的非线性函数或变换更容易实现。其实现步骤为:
步骤1 根据采样规则[4],利用修正先验概率的均值和方差产生满足约束条件的2nx+1个sigma点xi以及相应的权值wi。
i=1,…,nx
i=1,…,nx
(1)
其中,nx 是状态变量的维数,λ是尺寸因子,决定周围西格玛点的范围,可以为nx+λ≠0的任意值
是(nx+λ)Px均方根的第 i 列,该矩阵均方根的求解可由Cholesky分解得到。 wi是第i个粒子的权值,并且
步骤2 将sigma点代入状态方程,加权计算预测均值
和预测协方差Px
(2)
i=0,…,2nx
(3)
步骤3 时间更新,加权计算量测均值
预测协方差pzz以及状态与测量的互协方差px z
(4)
(5)
(6)
该算法对于高斯输入量的非线性函数可以精确到三阶,对于非高斯输入的近似,至少可以精确到二阶。而EKF则是将非线性函数做泰勒基数展开,仅仅保留一阶。
2.2 无迹卡尔曼滤波
将无迹变换应用于卡尔曼滤波,就可以得到无迹卡尔曼滤波算法。初始化,并通过数值期望计算原始先验概率的均值和方差。
步骤4 计算增益Kk+1,状态均值
和方差Pk+1
(7)
(8)
(9)
对非线性系统采用标准无迹卡尔曼算法进行滤波估计的处理过程,可采用状态量增广的方法对状态向量及其方差进行了扩维处理。在状态噪声与量测噪声不相关的情况下,也可以不进行扩维处理。无迹卡尔曼算法适用于任何非线性模型,无需估算雅可比矩阵,实现简单,估计精度比扩展卡尔曼要高。
但无迹卡尔曼滤波算法本身也存在一些缺陷,在数值计算中往往存在舍入误差等问题,而无迹卡尔曼对数值计算误差较为敏感,因此在无迹卡尔曼滤波的递推过程中,由于计算误差等因素的影响,有时会出现滤波状态协方差不对称或非正定,从而导致滤波器发散,影响滤波算法的收敛速度和稳定性。
3 平滑约束无迹卡尔曼滤波算法
3.1 问题描述
动态系统模型中状态随时间变化过程可描述为一个离散马尔科夫过程
xk=fk(xk-1)+νk
(10)
zk=hk(xk)+ek
(11)
式中,k表示离散时间,xk和zk分别是k时刻系统的状态和观测序列。fk,hk分别表示相应量测空间上的一些确定的非线性函数。νk和ek分别是相互独立的过程噪声和观测噪声,为了统计简单,将其假设为加性白高斯噪声。
在实践中,噪声总是有界的,因为没有噪声可以提供无限大的值。在可行区域内,可合理假设加性噪声的概率密度函数具有有界的连通支持,数学表述为
p(ek)=0, if ek∉R
(12)
其中,R表示满足约束条件的状态的n维联通区域可行区域。
考虑量测软约束条件,根据贝叶斯公式可得,修正先验概率P1(·)是原始先验概率P0(·)的截断,可表示为,
P1(xk|xk-1,zk)∝pg(zk|xk)P0(x1:k-1|z1:k-1)/εk,
s.t.{xk,zk}∈R
(13)
式中,εk是归一化常数,pg(·) 是指示函数。
3.2 近似可行域中心
非线性观测约束信息作为先验知识,只影响目标的位置矢量。不同于硬约束,软约束仅需要近似满足而不是完全满足边界条件。根据最大后验估计理论,定义可行域的中心点为
(14)
式中,上标c表示约束。
定义fik≅
分别表示
在
处的雅克比和海森矩阵。将其展开成泰勒二阶级数来得到
的近似初始优化值。
本文选择待估计参量的自然对数为障碍函数,采用牛顿内点法[14]近似求解全局最小值。可不加证明认为观测方程(11)是可局部线性化的,从而,问题转化为求解无约束增广目标函数(15),
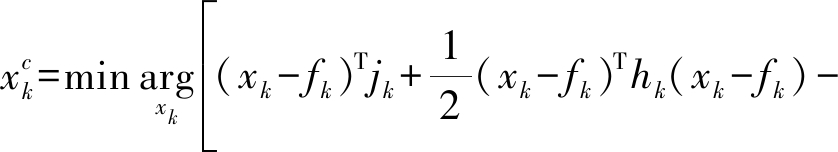
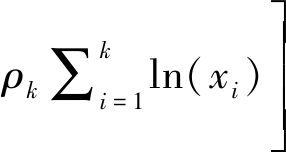
(15)
该方法的基本思想是保持每一个迭代点xk是可行域 R 的内点,对于不满足约束区域的点,当迭代点靠近边界时,增广目标函数值骤然增大,以示“惩罚”,并阻止迭代点穿越边界。该算法结构简单,适应性强。但是,初始点要求选择为一个严格的可行点。定义Ck={i|fik∈Rk},如果均值在可行域,计算均值,将其定为初值,即,
(16)
否则,取权值最大的数值作为初值,即,
(17)
通过拟牛顿迭代方法可得遍历全局最优解为:
(18)
其中α*是步长。di是搜索方向,若x0∈R,α*=1。
由可行域的中心,计算其一阶矩作为正态分布方差
最终,修正的先验概率密度近似为正态分布,即,
3.3 时间更新
数值优化估计器的本质是递归优化,关键步骤是更新,找到最优的观测预测
根据修正先验概率的均值和方差产生满足约束条件的2nx+1个西格玛点
以及相应的权值
将其代入状态方程,加权计算预测均值
和预测协方差
具体公式可参考2.2节列出的卡尔曼更新过程。通过数值优化近似全局最优解,减小了传统UKF舍入误差等问题。另外,为了解决数值计算误差敏感问题,在式(5)计算新息的过程中,考虑到量测噪声在输出端并不一定呈线性,对系统状态进行扩维处理。从而,提高了滤波算法的收敛速度和稳定性。
4 仿真结果及分析
4.1 一维单变量增长模型
为了比较提出算法的估计性能,对于高度非线性、非静态的动态离散时间系统进行仿真比较,公式可表示为
(19)
其中νk是过程噪声,假设是零均值高斯分布;观测噪声ek零均值、方差为0.01的高斯分布。模型系数为常数α=1,β=1,γ=0.5。对于每次蒙特卡洛仿真,取状态初值x0为[0,1]间的均匀分布。相关粒子滤波算法的粒子数目取为300。
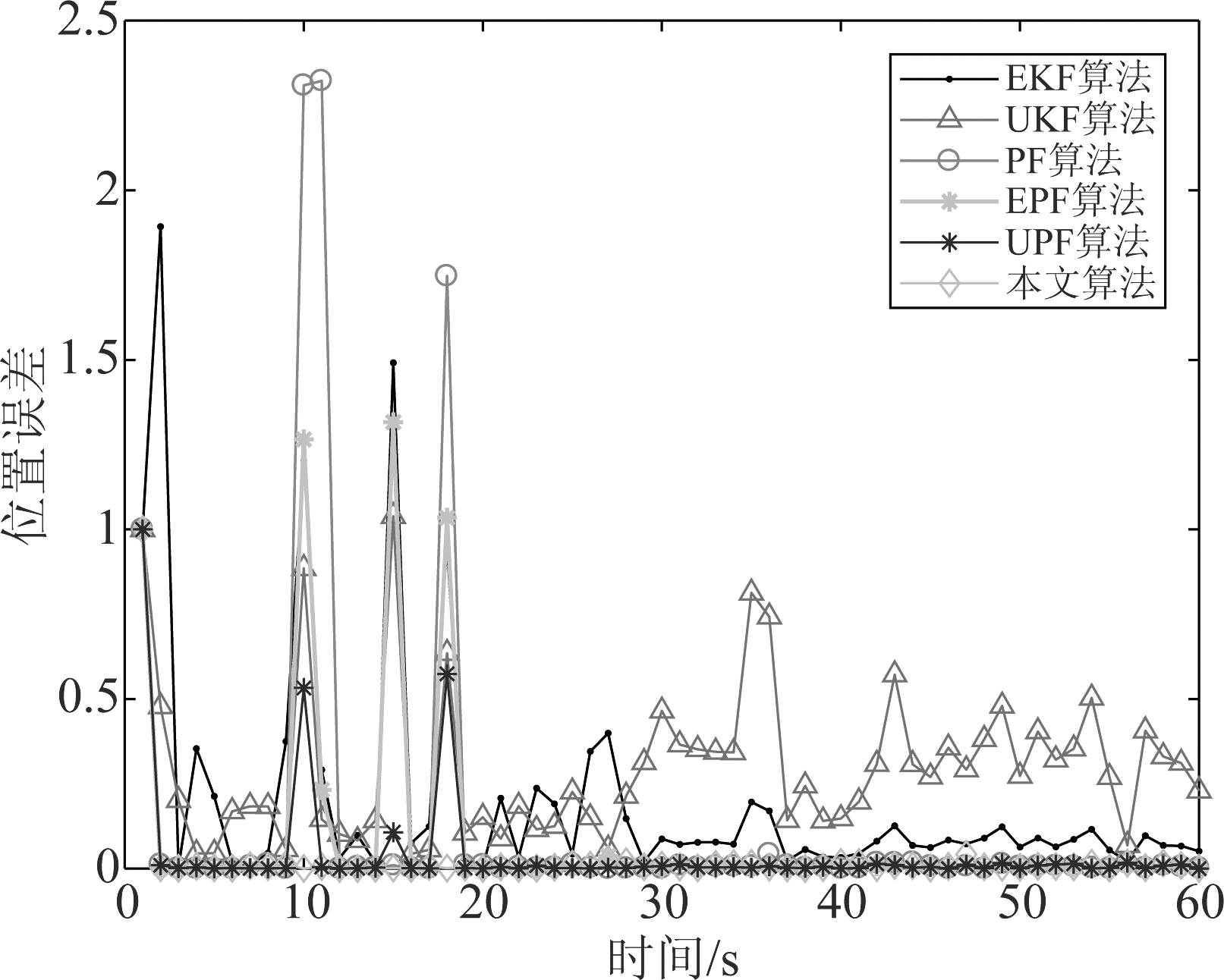
图1 不同滤波器的均方根对比
Fig.1 RMSE of different filters
图1定性分析比较了几种算法的均方根位置误差;表1定量总结了均值、方差及100次运行时间的比较结果。
表1 不同算法滤波性能对比
Tab.1 Statistics of different filters
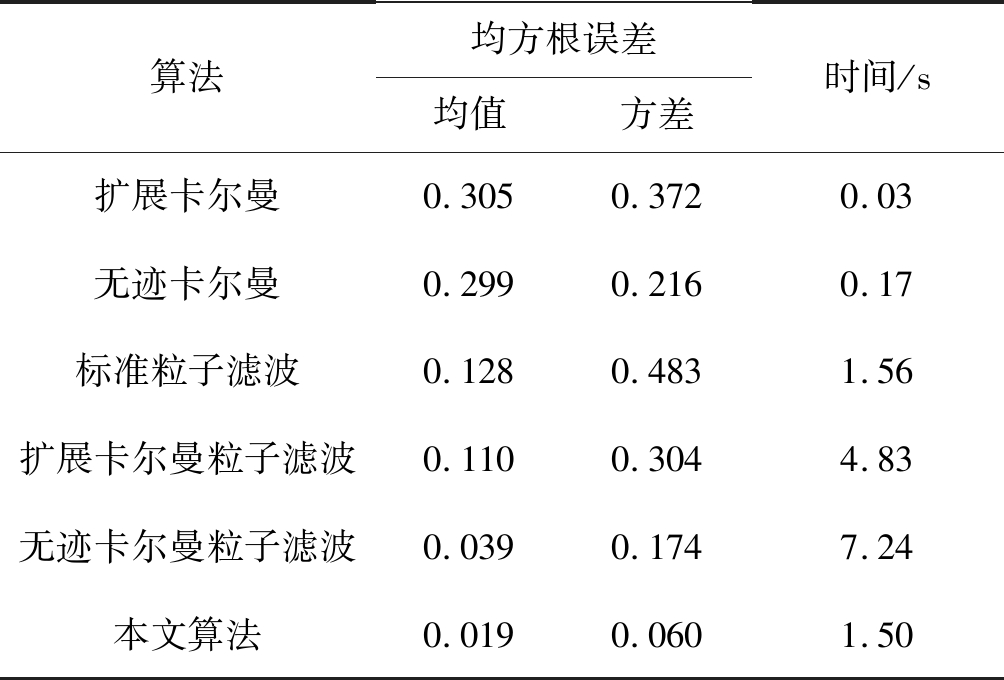
算法均方根误差均值方差时间/s扩展卡尔曼0.3050.3720.03无迹卡尔曼0.2990.2160.17标准粒子滤波0.1280.4831.56扩展卡尔曼粒子滤波0.1100.3044.83无迹卡尔曼粒子滤波0.0390.1747.24本文算法0.0190.0601.50
统计结果表明,均方根误差的均值及方差统计结果从大到小依次是扩展卡尔曼(EKF),无迹卡尔曼(UKF),标准粒子滤波(PF),扩展卡尔曼粒子滤波(EPF),无迹卡尔曼粒子滤波(UPF),平滑约束无迹卡尔曼(SCUKF)。在该实验条件下,所提算法的均方根误差最小,在准确性和鲁棒性方面具有优势。同时,实时性方面优于相关的粒子滤波算法。
4.2 纯方位机动目标跟踪
纯方位机动目标跟踪是典型的非线性估计问题,量测非线性和目标机动运动的不确定性是两个相互关联的主要挑战。在最近的工作[15]中,提出了约束多模型粒子滤波算法,该算法在非均匀稀疏采样环境下能够有效跟踪机动目标,不足之处是运算量过大,难以实现实时跟踪。本文所提算法,避免了模型细化以及雅可比计算,在保证准确性的同时有效提高了运算效率。
图2给出了不同观测噪声下的滤波误差分析。仿真轨迹设计可参考文献[15]。同时,和文献[12]中的截断无迹卡尔曼滤波算法以及克拉美罗界进行对比。随着观测噪声增大,滤波精度下降,而本文所提算法表现出稳定性。这主要是因为对观测噪声的约束截断,同时,通过数值优化近似全局最优解,误差可达到克拉美罗界值附近。
图2 不同量测噪声下的位置均方根误
Fig.2 The position root mean square error under the different measurement noise
5 结论
针对非线性动态系统中估计的观测非线性及不确定性问题,本文提出了平滑约束无迹卡尔曼滤波方法。采用数值优化近似求解修正先验概率统计量,以采样满足约束条件的西格玛点。从而,提高采样效率并有效抑制更新过程中可能产生的野值。仿真实验表明了该算法的有效性。
[1] Bar-Shalom Y, Kirubarajan T, Li X R. Estimation with Applications to Tracking and Navigation. Hoboken, NJ: Wiley, 2001.
[2] Li X R, Jilkov V P. A survey of maneuvering target tracking: approximation techniques for nonlinear filtering. Signal and Data Processing of Small Targets(Vol.5428), pp.537-550 Signal and Data Processing of Small Targets 2004.
[3] Merwe R V D, Doucet A, Freitas N D, et al. The unscented particle filter[C]∥International Conference on Neural Information Processing Systems, 2000.
[4] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401- 422.
[5] Doucet A, Freitas N D, Gordon N. An Introduction to Sequential Monte Carlo Methods[J]. Sequential Monte Carlo Methods in Practice, 2001, 18(1): 3-14.
[6] 王雪君, 孙进平, 张旭旺. 基于压缩感知的PD雷达序贯扩展卡尔曼滤波跟踪方法[J]. 信号处理, 2017, 33(4): 601- 606.
Wang Xuejun, Sun Jinping, Zhang Xuwang. New Sequential Extended Kalman Filter for Pulse Doppler Radar Tracker Based on Compressive Sensing[J]. Journal of Signal Processing, 2017, 33(4): 601- 606.(in Chinese)
[7] Zhao J, Netto M, Mili L. A Robust Iterated Extended Kalman Filter for Power System Dynamic State Estimation[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3205-3216.
[8] Tronarp F, Garcia-Fernandez A F, Sarkka S. Iterative Filtering and Smoothing In Non-Linear and Non-Gaussian Systems Using Conditional Moments[J]. IEEE Signal Processing Letters, 2018, (99): 1-1.
[9] Rouhani A, Abur A. Observability Analysis for Dynamic State Estimation of Synchronous Machines. IEEE Trans. Power Syst., Early access, 2016.
[10]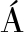 
ngel F. García-Fern
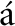ndez, Svensson L, Morelande M R, et al. Posterior Linearization Filter: Principles and Implementation Using Sigma Points[J]. IEEE Transactions on Signal Processing, 2015, 63(20): 5561-5573.
[11] Simon D. Kalman filtering with state constraints: a survey of linear and nonlinear algorithms, IET Control Theory and Applications, 2010, 4(8): 1303-1318.
[12] Garcia-Fernandez,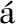 
. F, Morelande, R. M., Grajal. Truncated Unscented Kalman Filtering. IEEE Transactions on Signal Processing, 2012 , 60(7): 3372-3386.
[13] Rouhani A, Abur A. Constrained Iterated Unscented Kalman Filter for Dynamic State and Parameter Estimation[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2404-2414.
[14] Wächter A, Biegler L T. on the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming[J]. Mathematical Programming, 2006, 106(1): 25-57.
[15] Zhang H, Li L, Xie W. Constrained Multiple Model Particle Filtering for Bearings-Only Maneuvering Target Tracking. in IEEE Access, 2018, 6: 51721-51734.
