1 引言
心音分析是现阶段主流的心血管疾病诊断方法之一[1]。心音信号是人体心脏机械工作产生的振动经胸腔、胸壁等组织的传递到达胸部表层的信号,主要与人体心脏的心肌收缩、瓣膜关闭以及泵血等运动有关[2]。透过心音信号能够反映出人体心脏的工作状况,故心音信号中包含着大量的心血管生理信息与病理信息。在心血管疾病诊断中,心音信号因其独特的优势得到了广泛的研究与应用。相比现有的超声检查、冠状动脉CT、心机灌注同位素等方法,心音分析具备方便、快捷、完全无损等优势[3- 4];相比于心电分析,心音分析能够检测出早期心血管疾病,能够起到早检查、早预防、早治疗的关键性作用[4]。
心音分析的最终目的是通过对心音信号的特征分析检测出是否异常、是否患病,往往是通过心音分类器来实现该过程[5]。心音分析的主要方法为心音自动分析技术,主要包括分割与分类两个步骤[6]。分割的主要目的是将具备心音生理病理特征的部分(第一心音和第二心音)划分出来,使后续分类的特征参数更加准确。然而,在实际的研究处理中,又可将分割过程视作为对心音信号的状态分类过程。心音状态的分类中较困难的为基础心音信号的分类,可采用提取基础心音的特征参数进行训练来生成心音状态的分类器,通过提取输入信号的特征参数进行分类识别。其中,梅尔倒谱系数(Mel-frequency cepstral coefficients, MFCC)为心音信号分析中常用的特征参数之一[5]。MFCC是基于人耳感知特性提取的[7],虽然心音和语音存在一定的声学共性,但还是存在一些的差异,如频带分布不同。直接将MFCC用于心音信号的分割与分类识别其效果往往有限,因此需要进一步的研究与分析。
为了解决以上问题,本文对心音信号处理中的MFCC参数进行了优化,并将优化后的MFCC参数用于基础心音信号的状态识别中,验证优化方法的有效性。
2 心音信号的预处理
在对心音信号进行特征参数提取之前,一般都需要进行预处理操作。心音信号的预处理主要包括了趋势项消除、降噪、心动周期提取及基础心音分割等任务[8]。
2.1 基于最小二乘法的心音趋势项消除
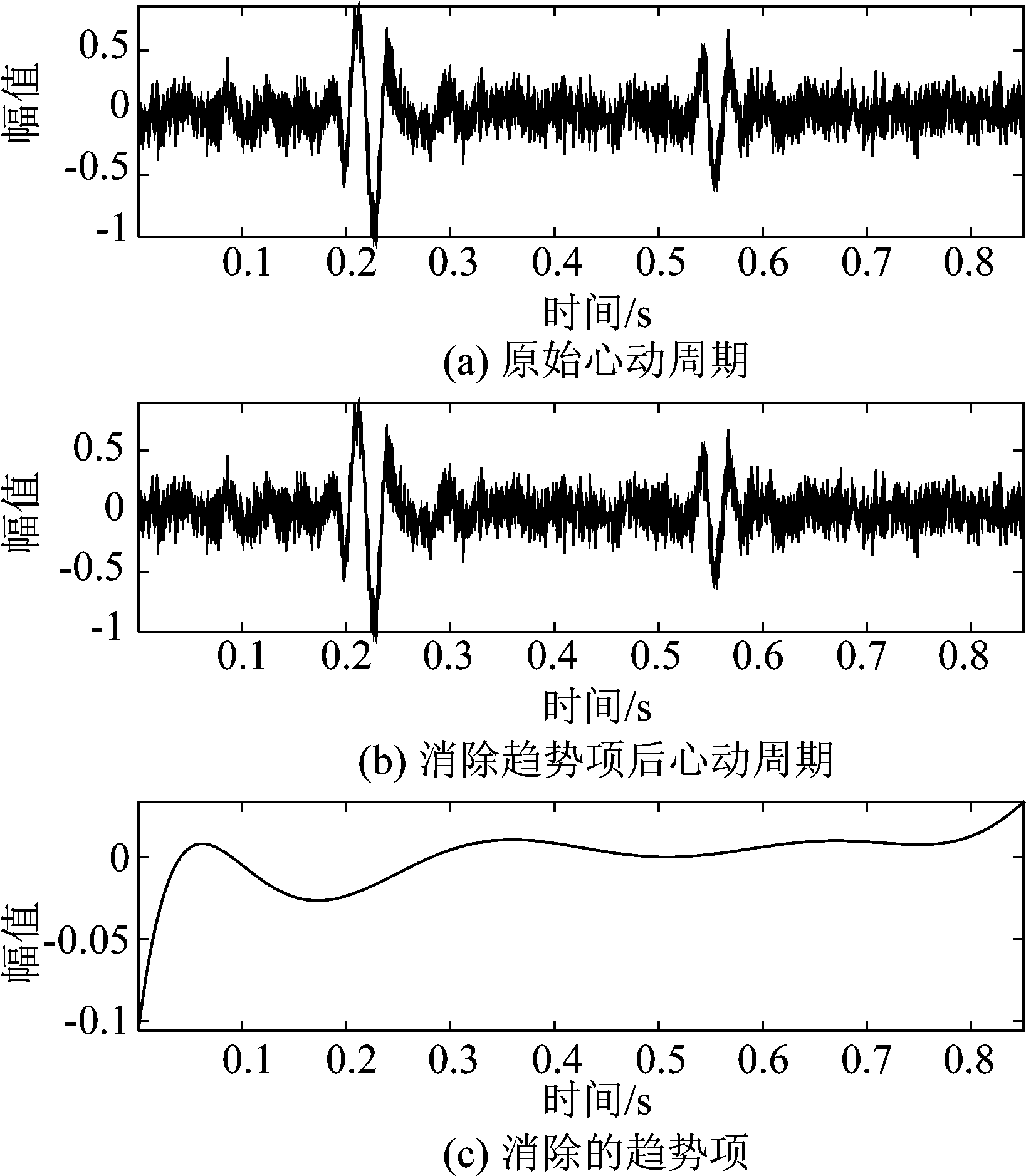
图1 趋势项消除结果
Fig.1 The result of trend items elimination
实际临床环境下,由于实验设备及受试者机体的不稳定性,容易使得采集到的心音信号产生一个线性的或者慢变的趋势误差,使得心音信号的零线偏离基线,如图1(a)所示。趋势项会给信号处理中带来一系列的问题,如会使相关法提取包络发生形变、使低频段的谱估计产生错误等[8-9]。因此,在对心音信号分析前需要先消除趋势项。消除趋势项的心音时域波形如图1(b)所示,消除的趋势项如图1(c)所示。
2.2 基于小波的心音降噪
在采集过程中,由于环境、采集设备、受试者机体状况等因素的干扰极易引入噪声,降低心音信号的可分析性。因此,降噪也是预处理中十分的重要步骤之一。在心音信号降噪中,小波降噪因其低频分辨率高的特点得到了广泛应用。
在心音信号的分割与识别过程中,处理或需求的对象往往是基础心音信号。与语音信号的频带范围不同,基础心音信号的频带范围在25 Hz~120 Hz 之间[10],因此心音信号的有效频带较窄。在降噪中只需将2 kHz采样率的心音信号采用coif5小波做5层分解,取第四、第五细节系数层即可获得31 Hz~125 Hz间的频带,占据约90%的基础心音频带分量,且基础心音成分主要都集中在该频带内,因此可丢弃其他频带系数。将保留的第四、第五细节系数层的系数通过阈值函数处理后进行重构,即可得到降噪后的心音信号。采用小波变换方法降噪后的心音如图2所示。
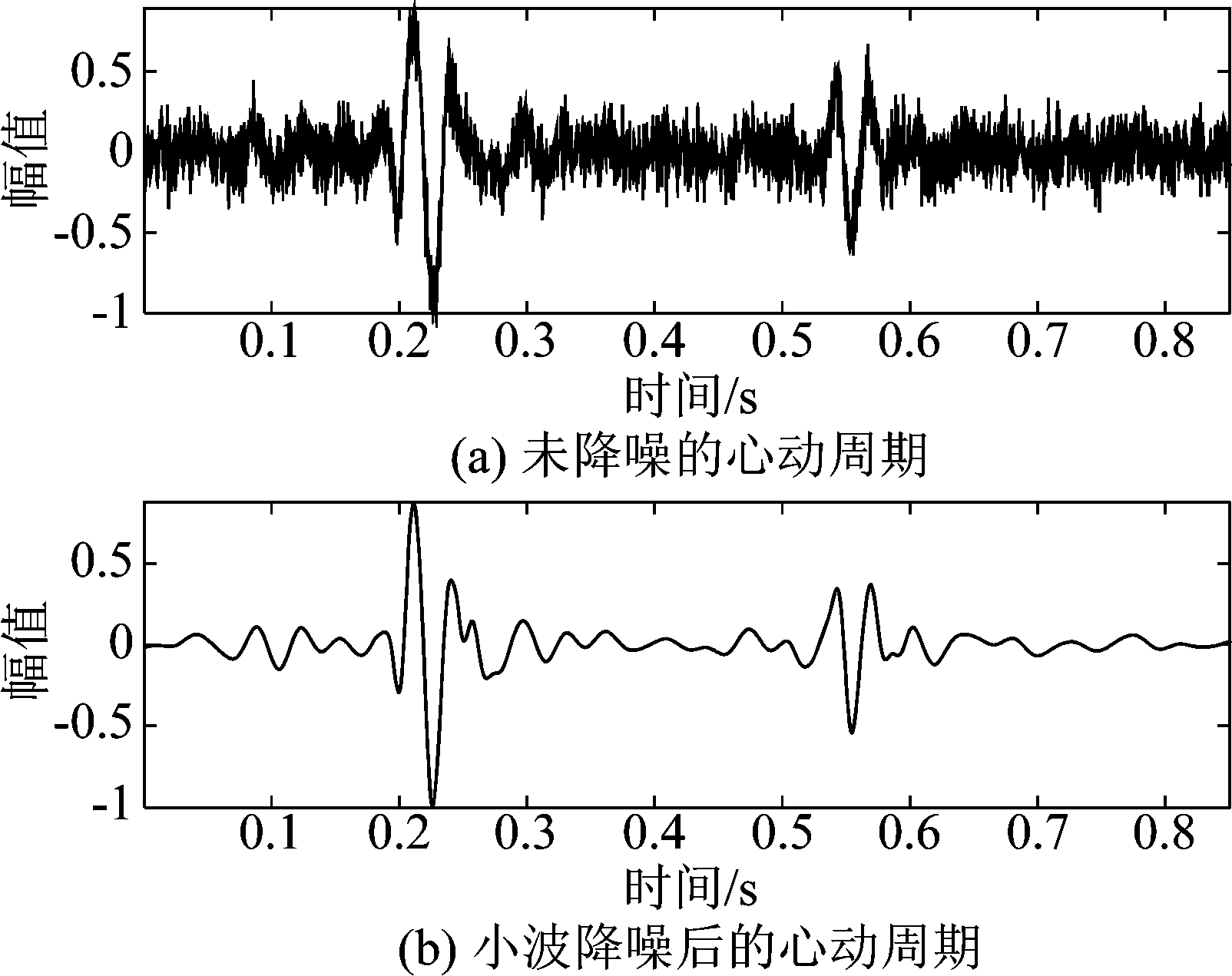
图2 小波降噪结果
Fig.2 The result of wavelet noise reduction
2.3 提取心动周期
除心率不齐的心音信号以外,心音信号几乎为一准周期信号[11],这也是心音与语音信号的差别之一。在心动周期的提取中,应用最多的为基于周期自相关函数的方法[11-12]。自相关函数法提取心动周期的过程可描述如下:
①按式(1)提取自相关包络
(1)
(2)
其中Se(n)为预处理的心音的第n帧信号的短时平均能量,p为心音信号总长度,Frame为帧长。
②提取的包络每间隔一段时间便会出现一个较高的极值波峰,每两个波峰间对应着一个相应的心动周期的长度,按波峰提取即可,如图3(a)所示。在获取心动周期的基础上,通过阈值分割较为容易获取基础心音,如图3(b)所示。
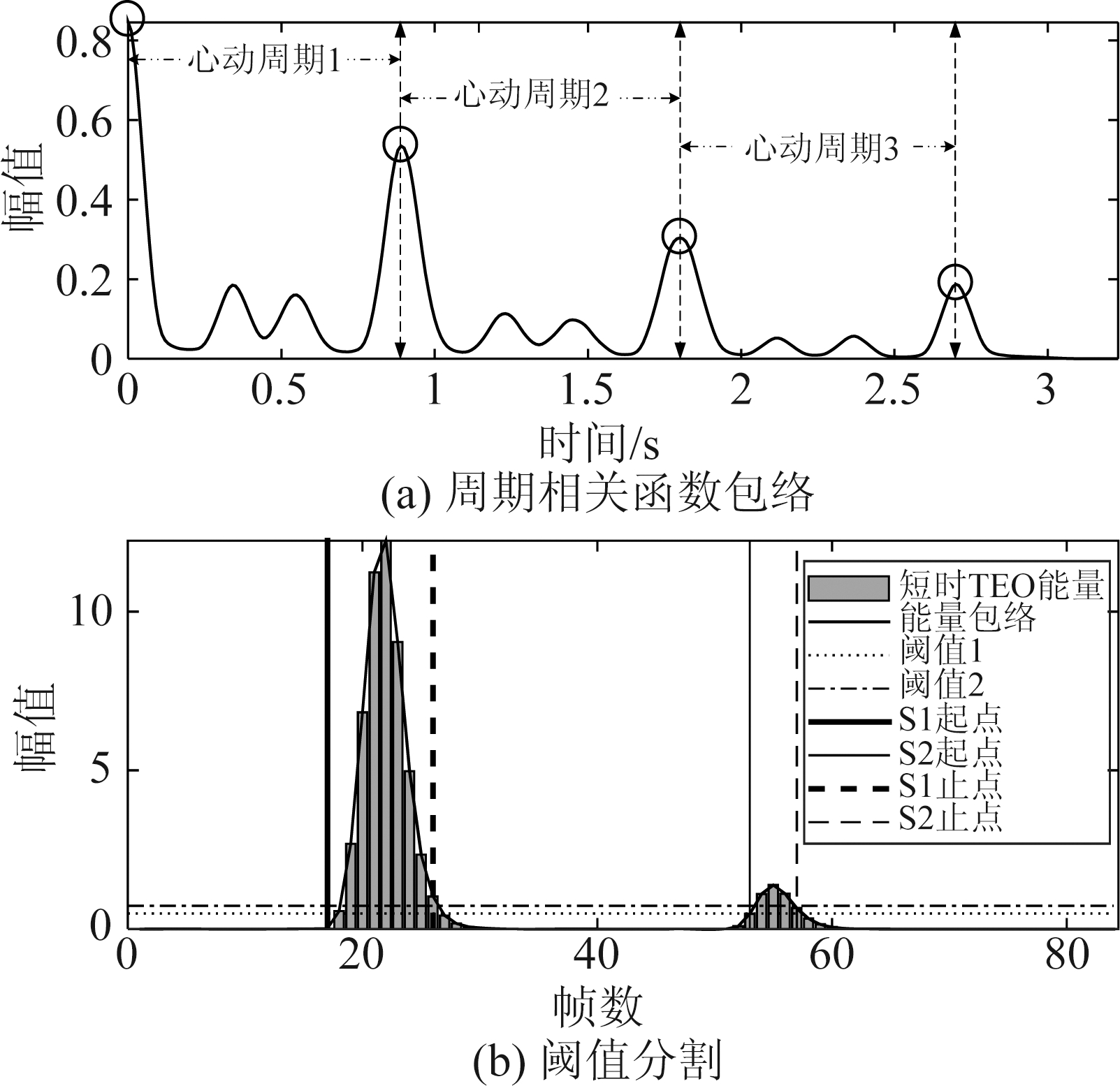
图3 心动周期的提取与分割
Fig.3 Extract the cardiac cycle and segment
3 MFCC特征向量的提取
在心音分类器的设计与识别中,特征参数提取的有效与否将直接影响到分类器的性能[5]及分类识别的结果。梅尔频率倒谱系数(Mel frequency cepstrum coefficient, MFCC)是根据人耳的听觉掩蔽效应提出来的[13],它能够反映出人耳耳蜗感知性能与声音频率呈非线性的关系,且在低频频带具有较高的分辨率[14-15],因此较为适用于心音信号的识别。MFCC是一组矢量序列,是将心音频谱变换到梅尔频率刻度下得到的。MFCC的线性频率转换关系如下[14,16]:
Mel(f)=C log10(1+f/p)
(3)
其中C和P均为常量参数,在处理语音信号中取值分别为2595和700。
基于语音信号中MFCC特征向量的提取方法,将心音信号的MFCC特征向量提取过程描述如下:
1) 基础心音的分帧与加窗。同语音信号相似,心音信号也具备短时平稳性,研究中一般认为心音信号在10 ms~30 ms内具备短时平稳性。在分帧与加窗处理中,帧长一般选取为20 ms,帧移选取为10 ms,窗函数选择长度为20 ms的Hamming窗,因为它可以在一定程度上克服频谱泄漏现象。
2) 快速傅里叶变换(FFT)。将分帧后的信号fm(n)逐帧做FFT,得到频域信号Xm(k):
(4)
其中m为帧数,L为帧长。
3) Mel频率刻度的变换。将Xm(k)经Mel滤波器组进行滤波和刻度转换,就可得到Mel频谱。Mel滤波器组由一组三角形滤波器构成,其个数一般与临界带宽有关[14-16]。实验中采用的心音信号采样率为2 kHz,选取三角滤波器的个数为N=12个,阶数为M=24。
4) 倒谱分析。倒谱分析主要包括取对数能量和逆变换。其中,取对数能量的作用是对频谱动态范围进行压缩;逆变换的作用是防止三角滤波器在频谱上叠加造成的干扰,即去除频谱成分间的相关性[14,16]。对数能量em及DCT变换可表述为:
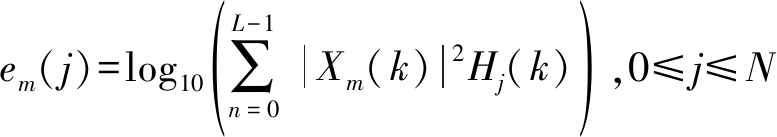
(5)
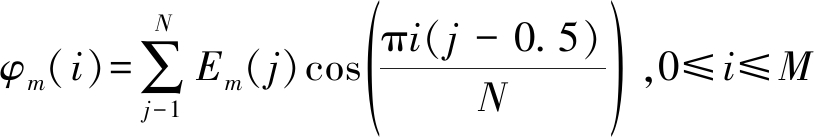
(6)
其中N为三角滤波器的个数,M为MFCC的阶数,φm即为提取到的特征向量。实验样本心动周期提取的MFCC特征向量如图4(a)、4(b)所示。
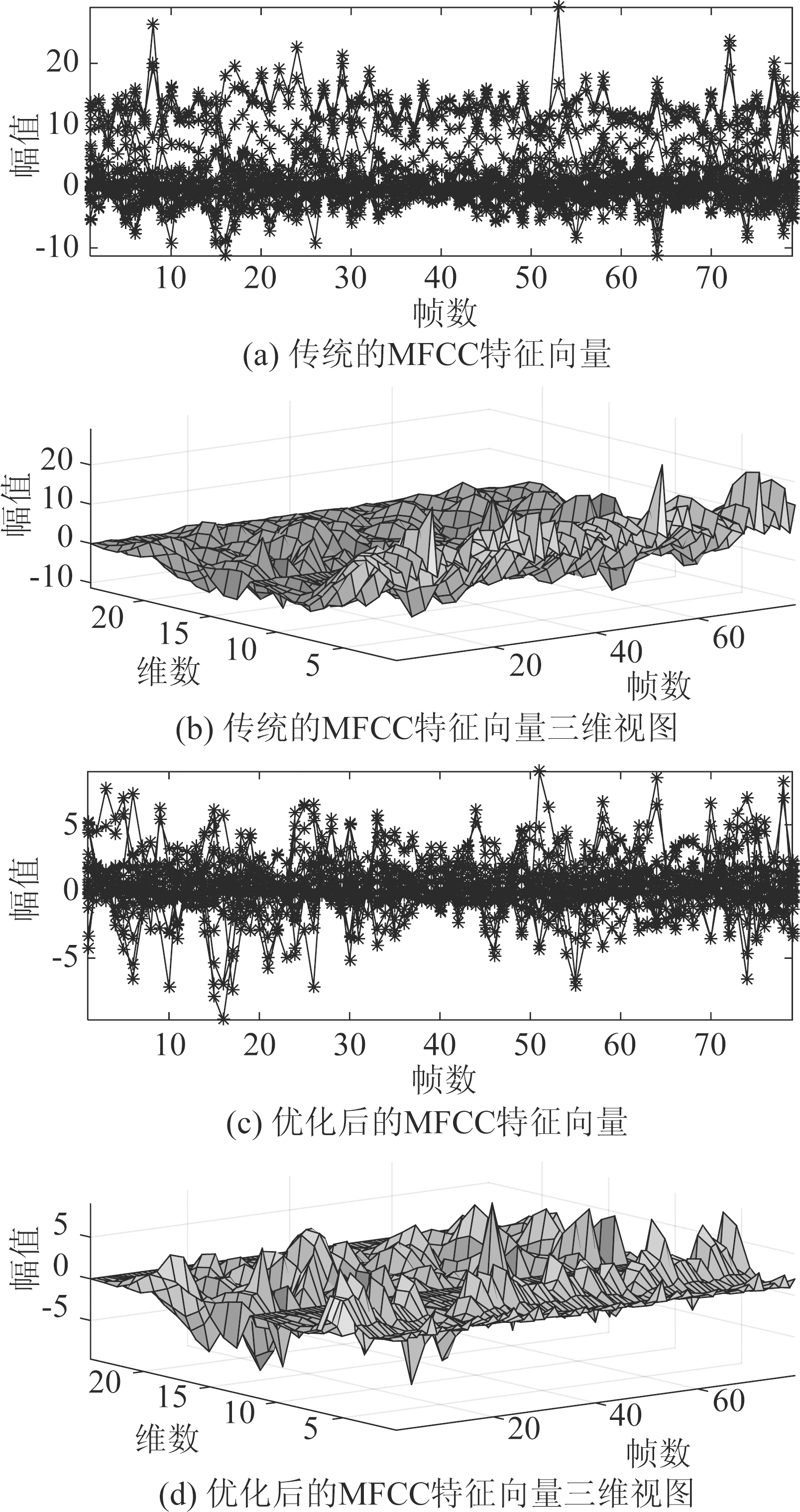
图4 传统的MFCC与优化后的MFCC
Fig.4 Traditional MFCC and optimized MFCC
4 MFCC的优化
在心音信号的特征向量提取中,传统的MFCC提取方法中存在两个问题,一是DCT变换无法做到高阶统计量的去相关[16],二是部分特征值对心音信号的特征表征贡献率不高[17]。基于以上两个问题,本文提出采用独立成分分析法(ICA)和权值优化相结合的方法来优化提取的MFCC特征向量。
4.1 ICA变换去相关
独立成分分析(Independent component analysis, ICA)算法是一种盲源分离的经典算法,其功能是将源信号从混合信号中分离开来,使所提取的各成分分量之间的相关性最小[17-18]。ICA算法中常用的为FastICA算法[14,19],但FastICA算法容易收敛不同的非高斯极值点,造成信号出现顺序不固定,使得心音鉴别器的识别结果严重偏离,且容易出现信号翻转。为了解决ICA算法中出现的难题,本文提出了一种解整体混合矩阵的方法。
解整体混合矩阵ICA变换提取特征向量主要增加了两个步骤[20]:一是获取样本整体的混合矩阵,二是解整体混合矩阵提取特征。获取统一解混合矩阵是在取对数能量后进行的,其方法是按三角滤波器的输出顺序将待解混合矩阵心音信号拼接起来生成统一待解混合矩阵;解混合矩阵特征提取中,首先通过ICA变换将待解混合矩阵的心音信号分离得到独立信号,然后按照方差排序选择较大的24个独立信号进行保留。其原理如下所述。
假定待分离的第m帧心音信号为em∈RN×1能够表示为d维位置独立变量sm,则em可表示为:
em=am*Sm+rm
(7)
其中am为第m帧心音混合矩阵,rm为第m帧心音的残差,am∈RN×d,rm∈RN×1。ICA的主要目的是通过em估计出am来获取独立信号分量sm。将所有的带分离三角滤波器输出心音样本按顺序排列成矩阵整体样本e∈RN×m,其中N为变量的维数,m为样本总数。因此整体混合矩阵的ICA变换可表示为:
e=As+r
(8)
其中A为整体混合矩阵,s为整体独立成分矩阵,r为整体残差矩阵。
设整体混合矩阵的逆为:
W=A-1
(9)
则解出的独立源信号为:
s=W*(e-r)
(10)
在寻找非高斯化极值时,最大化负熵目标函数为:
(11)
其中qi为正常数,u为标准高斯随机变量,G为非平方的非线性函数。其牛顿法求解的迭代公式为:
(12)
g=G′
(13)
按照式(12)重复迭代即可逐一分离出各分量。
4.2 MFCC的权值优化
文献[14]指出,并非所有的MFCC特征分量都对分类器的性能有很大贡献,因此需要通过一定的方法突出贡献大的特征分量,削弱贡献小的特征分量。为了衡量各心音特征分量的贡献大小,本文提出一种相关性权值指标优化混合矩阵,其定义如下:
(14)
其中Am,i为整体混合矩阵上第m个独立分量的第i个元素,1≤m≤N,1≤i≤d。
以上是对各维分量的独立权值优化,此外还需要衡量各维分量间的重要性。对于各维分量间的重要性衡量,我们提出采用F比进行考察。在信号的重要性、有效性的考察中,F比越大表明其贡献率越高[20]。心音信号中F比的计算如下:
Fcorr(j)=F1(j)/F2(j)
(15)
(16)
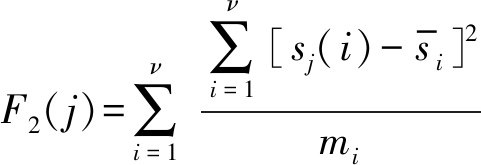
(17)
其中Fcorr(j)表示第j维的F比值,sj表示第j维特征向量,![]() 表示第j维特征向量的均值,
表示第j维特征向量的均值,![]() 表示第i帧特征向量的均值,mi表示第i个样本的总数。优化后的MFCC特征向量如图4(c)、4(d)所示。
表示第i帧特征向量的均值,mi表示第i个样本的总数。优化后的MFCC特征向量如图4(c)、4(d)所示。
5 实验方法及流程
实验所用的心音信号数据来源于“PhysioNet/Computing in Cardiology Challenge 2016”心音开源数据库及中国医学科学院阜外医院采集提供。其中,开源库中选取a~e五个库,去除部分较为杂乱、采集时长较短的信号,筛选出800条;中国医学科学院阜外医院采集提供400条,共计1200条心音。随机抽取800条作为训练集,共计35420个心动周期;200条作为验证集,共计7621个心动周期;剩余的200条心音作为测试集,共计8125个心动周期。三个数据集中均包含了正常与异常、不同年龄段、不同性别的受试者心音信号,且部分心音的采集设备和环境也不相同。所有心音均已降采样至2000 Hz,并已去除首尾两个心动周期避免采集设备不稳定带来的干扰,同时也去除首尾不完整的心动周期部分。对SVM分类器做迭代训练,第8次迭代后获得最佳结果:正确率80.12%,交叉熵损失值0.466。
为了验证第4节中提出的MFCC优化方法的有效性,实验中将采用SVM的方法检验MFCC特征向量优化前与优化后的整个处理系统对S1与S2分类识别的正确率[5]。实验算法分类正确率的结果为与人工标注结果对比获得。在心音信号标注中,可采用cool edit pro来完成,标注人员可结合心音信号的听诊、时域分布特征及能量频谱分布特征进行有效的判别,如图5所示。

图5 心音信号的能量频谱图
Fig.5 Energy spectrum of heart sound signal
实验的整个试算法流程可描述为3个步骤:
①预处理:首先,输入测试心音;接着,按最小二乘法去除趋势项;然后,经小波降噪方法处理获得降噪心音;最后,经周期相关函数获取心动周期,将信号分割为多个心动周期,获取基础心音。
②MFCC特征向量的提取。首先逐个输入各心动周期的基础心音,接着对基础心音加窗分帧并做FFT,然后将信号变换至Mel频率刻度下,最后经倒谱分析获得MFCC特征向量。在倒谱分析中,将DCT更改为ICA变换,同时采用相关系数优化混合矩阵,最后通过F比权值优化MFCC特征向量,获得最终结果。
③SVM分类器识别:将MFCC特征向量逐帧输入训练好的SVM分类器进行识别,识别的标记结果与手工标记进度对比,计算正确率并输出。
由于数据库中的部分数据采集的并不是很理想,为了验证不同类型噪声下MFCC特征向量优化的效果,实验中将白噪声、Babble类语音噪声、脉冲噪声和粉红噪声以0 dB、5 dB、10 dB、15 dB、20 dB的信噪比叠加到心音信号中,对SVM分类器识别正确率进行对比,测试优化方法的抗噪性能。
6 实验结果与分析
采用SVM分类器识别为加噪的心音数据的结果如表1所示。从表1中可以看出,将DCT替换为ICA后S1、S2的识别正确率均有提高,这也进一步验证了ICA变换较DCT变换能更有效的抑制三角滤波器带来的频率叠加问题。在传统的MFCC提取方法基础上增加权值优化处理,S1与S2的识别正确率与未做优化前相比有轻微提升。在ICA变换及权值优化共同作用下,S1和S2识别正确率得到了较为明显的提升,系统平均识别正确率较传统MFCC方法提升了1.5%左右。
叠加噪声后测试的部分分类正确率结果如表2所示,四类噪声下的分类正确率如图7所示。从表2及图7(a1)、(b1)、(c1)、(d1)结果可以看出,随着信噪比的降低,传统MFCC特征向量在SVM分类器中的分类结果正确率开始一定幅度下降;基于ICA和权值优化的MFCC特征向量用于SVM分类器中,随着信噪比降低,分类结果正确率虽然也呈现一定幅度的下降,但较传统MFCC特征向量分类结果的下降速度有了一定的减缓趋势;从(a2)、(b2)、(c2)、(d2)可以看出,随着信噪比的降低,优化前后平均正确率差值整体上存在一定的提升。可以得出结论,优化后的MFCC特征向量的提取方法具备一定的抗噪性能。
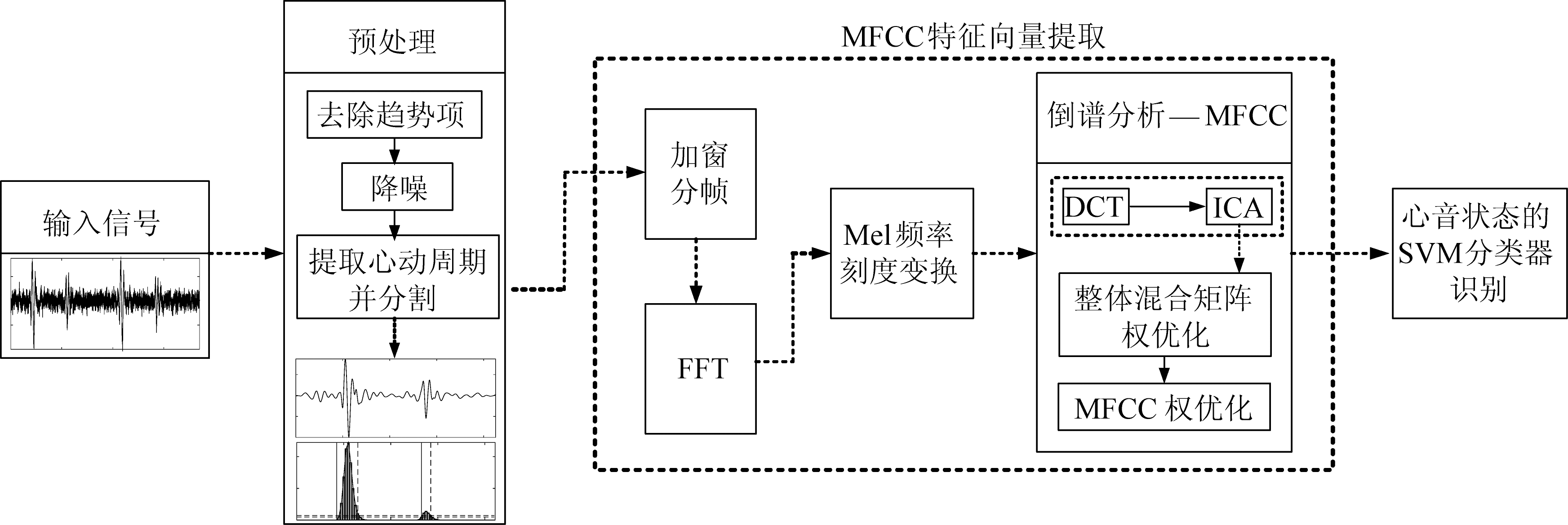
图6 MFCC特征向量提取及识别流程图
Fig.6 Flow chart of MFCC feature vector extraction and recognition
表1 测试集MFCC的分类结果
Tab.1 Classification results of test set by MFCC

传统的MFCCICA变换权值优化ICA变换+权值优化S1识别正确率/%84.1285.3184.2685.87S2识别正确率/%68.5769.2168.6369.68平均正确率/%76.3477.2676.4477.77
表2 不同信噪比噪声干扰下测试集的分类结果
Tab.2 Classification results of test set under different noise interferences and different SNR
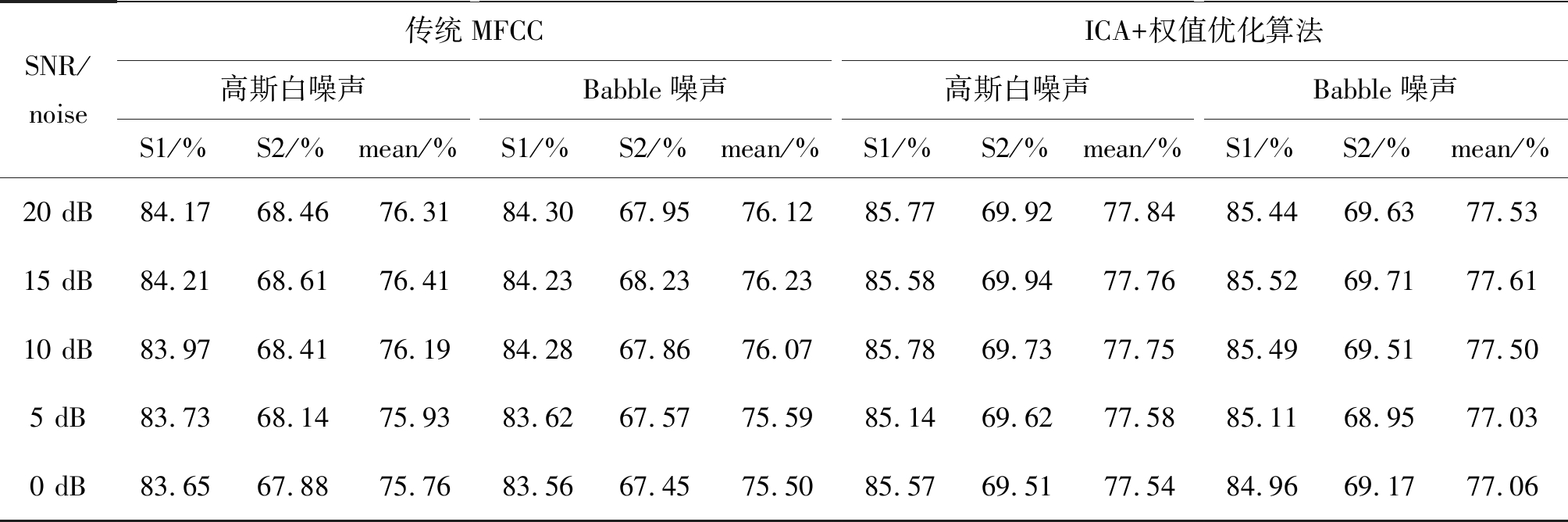
SNR/noise传统MFCC高斯白噪声Babble噪声S1/%S2/%mean/%S1/%S2/%mean/%ICA+权值优化算法高斯白噪声Babble噪声S1/%S2/%mean/%S1/%S2/%mean/%20 dB84.1768.4676.3184.3067.9576.1285.7769.9277.8485.4469.6377.5315 dB84.2168.6176.4184.2368.2376.2385.5869.9477.7685.5269.7177.6110 dB83.9768.4176.1984.2867.8676.0785.7869.7377.7585.4969.5177.505 dB83.7368.1475.9383.6267.5775.5985.1469.6277.5885.1168.9577.030 dB83.6567.8875.7683.5667.4575.5085.5769.5177.5484.9669.1777.06
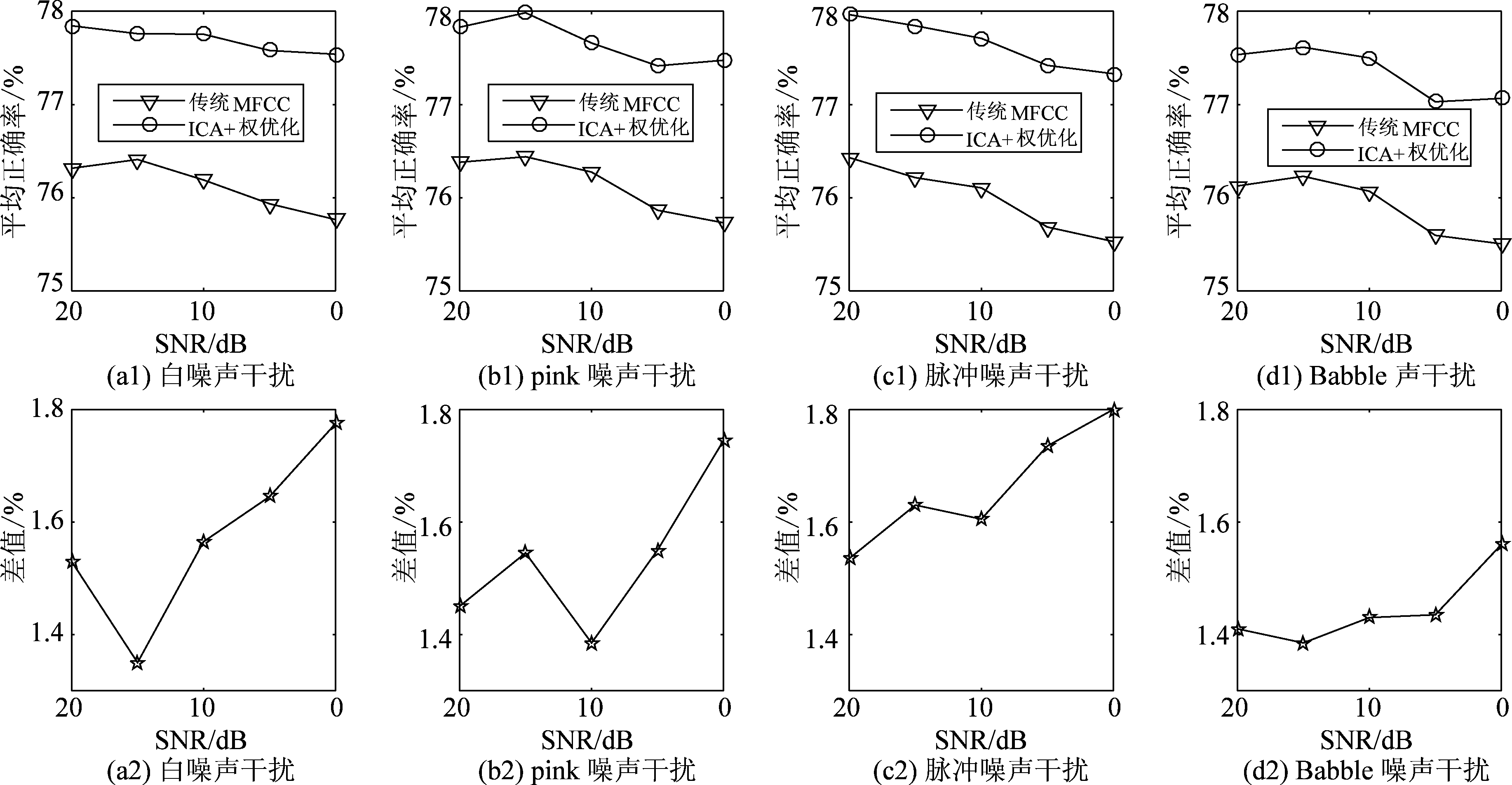
图7 不同SNR的不同噪声干扰下测试集分类结果
Fig.7 Classification results of test set under different noise interferences and different SNR
7 结论
本文在心音分析的基础上梳理了MFCC特征向量的提取流程,并对MFCC特征向量提取方法提出了优化。实验结果表明,在心音信号处理中,ICA变换较DCT变换能更为有效地去除频率叠加的高阶统计量的相关性;通过建立相关性指标、F比指标分别对混合矩阵及各维特征向量进行优化,突出有效性强、贡献率大的特征值及特征向量,能进一步强化特征向量,提高分类器的识别率;通过ICA变换及权值优化的方法能够有效的提高基础心音在SVM分类器中的识别正确率,提升了分割系统的性能,且算法具备一定的抗噪性能。
[1] 刘喻, 唐雪辉, 陈洪波, 等. 基于PCA-SOM的异常心音分类识别方法的研究[J]. 航天医学与医学工程, 2018, 31(1): 57- 61.
Liu Yu, Tang Xuehui, Chen Hongbo, et al. Clustering Recognition Method for Abnormal Heart Sounds Based on PCA-SOM[J]. Space Medicine & Medical Engineering, 2018, 31(1): 57- 61.(in Chinese)
[2] 成谢锋, 李允怡, 高珮熙, 等. 一种心音信号的源成分获取方法[J]. 南京邮电大学学报: 自然科学版, 2018, 38(1): 54-59.
Cheng Xiefeng, Li Yunyi, Gao Peixi, et al. New method for obtaining components of heart sound signal source[J]. Journal of Nanjing University of Posts and Telecommun-ications: Natural Science Edition, 2018, 38(1): 54-59.(in Chinese)
[3] 巩燕, 胡杰, 高彬, 等. 心血管疾病即时检测技术的研究进展[J]. 中国科学: 技术科学, 2016, 46(11): 1116-1134.
Gong Y, Hu J, Gao B, et al. Advances in monitoring of cardiovascular diseases at the point of care[J]. Sci Sin Tech, 2016, 46(11): 1116-1134.(in Chinese)
[4] Berkaya S K, Uysal A K, Gunal E S, et al. A survey on ECG analysis[J]. Biomedical Signal Processing & Control, 2018, 43: 216-235.
[5] 侯雷静, 应冬文, 国雁萌, 等. 基于心音分类的识别器分析[C]∥中国声学学会2017年全国声学学术会议. 中国声学学会, 2017.
Hou Leijing, Ying Dongwen, Guo Yanmeng, et al. Identifier analysis based on heart sound classification[C]∥2017 National Acoustic Conference of the Chinese Acoustic Society. Chinese Acoustic Society, 2017.(in Chinese)
[6] Puneet Kumar J, Anil Kumar T. Heart monitoring systems-a review[J]. Computers in Biology & Medicine, 2014, 54(C): 1-13.
[7] Rubin J, Rui A, Ganguli A, et al. Classifying heart sound recordings using deep convolutional neural networks and Mel: Frequency Cepstral Coefficients[C]∥2016 Computing in Cardiology Conference. IEEE, 2016.
[8] Zhang L, Tang R, Jiang J, et al. Research on pretreatment and envelope extraction algorithm of heart sound signal[J]. Journal of Biomedical Engineering, 2014, 31(4): 734-741.
[9] Lin Y, ChongYang W, ZhiCheng W. Research on the selection of wavelet bases for wavelet-based signal trend elimination[C]∥International Conference on Wavelet Active Media Technology & Information Processing. IEEE, 2013.
[10] Jain P K, Tiwari A K. An adaptive thresholding method for the wavelet based denoising of phonocardiogram signal[J]. Biomedical Signal Processing & Control, 2017, 38: 388-399.
[11] Whitaker B M, Suresha P B, Liu C, et al. Combining sparse coding and time-domain features for heart sound classification[J]. Physiological Measurement, 2017.
[12] Salman A H, Ahmadi N, Mengko R, et al. Automatic Segmentation and Detection of Heart Sound Components S1, S2, S3 and S4[C]∥International Conference on Instrumentation. IEEE, 2016.
[13] 马勇, 鲍长春. 基于高层信息特征的重叠语音检测[J]. 清华大学学报: 自然科学版, 2017, 57(1): 79- 83.
Ma Yong, Bao Changchun. Overlapping speech detection using high-level information features[J]. J Tsinghua Univ: Sci & Technol, 2017, 57(1): 79- 83.(in Chinese)
[14] 徐淑正, 孙忆南, 皇甫丽英, 等. 基于MFCC和时频图等多种特征的综合鸟声识别分类器设计[J]. 实验室研究与探索, 2018, 37(9): 81- 86, 91.
Xu Shuzheng, Sun Yinan, Huangfu Liying, et al. Design of Synthesized Bird Sounds Classifier Based on Multi Feature Extraction Classifiers and Time-frequency Chat[J]. Research and Exploration in Laboratory, 2018, 37(9): 81- 86, 91.(in Chinese)
[15] Dixit A, Vidwans A, Sharma P. Improved MFCC and LPC algorithm for bundelkhandi isolated digit speech recognition[C]∥2016 International Conference on Electrical, Electronics, and Optimization Techniques(ICEEOT). IEEE, 2016.
[16] Jancovic, Liu, Zou. The Effectiveness of ICA-based Representation: Application to Speech Feature Extraction for Noise Robust Speaker Recognition[C]∥European Signal Processing Conference. IEEE, 2006.
[17] 张健, 徐杰, 包秀国, 等. 应用于语种识别的加权音素对数似然比特征[J]. 清华大学学报: 自然科学版, 2017(10): 1038-1041.
Zhang Jian, Xu Jie, Bao Xiuguo, et al. Weighted phone log-likelihood ratio feature for spoken language recognition[J]. J Tsinghua Univ: Sci & Technol, 2017(10): 1038-1041.(in Chinese)
[18] 林秋华, 郑永瑞, 殷福亮. 基于参考独立分量分析的语音增强方法[J]. 大连理工大学学报, 2006, 46(6): 915-919.
Lin Qiuhua, Zheng Yongrui, Yin Fuliang. Speech enhancement method based on ICA-R[J]. Journal of Dalian University of Technology, 2006, 46(6): 915-919.(in Chinese)
[19] Zhang G, Harichandran R S, Ramuhalli P. Application of Noise Cancelling and Damage Detection Algorithms in NDE of Concrete Bridge Decks Using Impact Signals[J]. Journal of Nondestructive Evaluation, 2011, 30(4): 259-272.
[20] 胡炼. 基于NPC和改进的MFCC鲁棒语音特征提取研究[D]. 湖南: 湖南大学, 2011.
Hu Lian. The Research of Robust Speech Features Extraction Based on NPC and Improved MFCC[D]. Hunan: Hunan University, 2011.(in Chinese)



