1 引言
作为一种新的SAR成像体制,多角度SAR成像可获取观测对象的方位向非各向同性散射特征信息。自提出以来,研究人员纷纷针对其信号模型、成像方法、定标方法和干涉测量等方面开展了研究工作,以逐步提高其实用性。2008年德宇航利用ESAR进行了L波段全极化圆迹SAR机载实验[1],在高精度快速成像方面取得了突破,并首次对比了全极化圆迹SAR 图像和常规条带SAR对地物成像的特征差异,展现了在极化散射特征建模与分类应用方面的巨大研究价值。中科院电子所[2]、中科院空间中心[3]、北京航空航天大学[4]等也在近年来开展了圆迹SAR的理论和仿真研究。 其中中科院电子所微波成像技术国家级重点实验室于2011 年8 月在四川绵阳地区进行了P波段全极化圆迹SAR 机载实验,获取了高分辨率图像。不同子孔径间丰富的散射特征差异初步展示出圆周航迹多角度SAR在地物分类方面的应用潜力[2]。
在多角度观测SAR数据处理方面,现有研究以目标非各向同性散射中心检测为主。最初由Famil等人利用条带SAR子孔径图像对目标非稳定特征的分析方法[5],引入基于Wishart分布的似然比检测统计量及基于N-P 准则的恒虚警率门限估计,判决被观测对象是否满足各向同性散射假设。后续,Yang[6]等人解决了恒虚警率判决函数饱和等问题,将该方法改进后应用于圆迹观测模式,具备了对目标非各向同性散射中心检测的能力。
本文在该工作的基础上,针对多散射相位中心模型的极化特征变化机理提出分析及应用方法。下文首先建立基于似然比的多角度观测SAR极化散射特征模型,分析散射特征模型参数方位向变化与似然比变化之间的联系。其次,建立极化似然比序列、子孔径角度序列等特征。最后,通过SVM流程进行分类。通过机载P波段极化SAR开展圆迹观测试验及验证。
2 基于似然比的多角度观测SAR极化散射特征模型
基于似然比最大化条件的非各向同性散射消除机制在多散射相位中心检测框架中发挥关键作用[6]。一方面,该条件可以在处理过程中非监督地聚合各向同性散射孔径,另一方面可以获取特定的子孔径消除顺序。该顺序本身包含了观测对象的方位向多散射中心特征,且该特征与观测对象的朝向无关。将多角度观测与全极化测量相结合为分析观测对象的散射特征提供了一种可行的手段,可建立典型散射类型的多角度观测SAR极化散射特征模型。
为便于分析多角度观测条件下混合散射的变化规律,本文基于广义Freeman-Durden模型假设建立扩展的表面散射与二面角散射模型。根据特征值分解模型[7],小粗糙度表面散射的极化相干矩阵可以表示为:
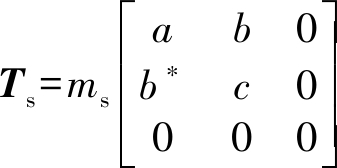
a=cos2α
b=-cos αsin α
c=sin2α
(1)
其中α是Bragg散射模型中与地表介电常数及入射角相关常数[7]。由二面角散射机理有αd=π/2-α,可得二面角散射的极化相干矩阵:
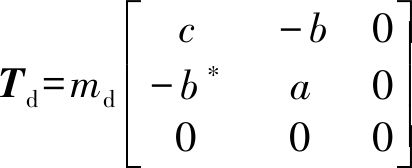
(2)
将表面散射及二面角散射扩展为包含去极化分量的形式,可表示为:
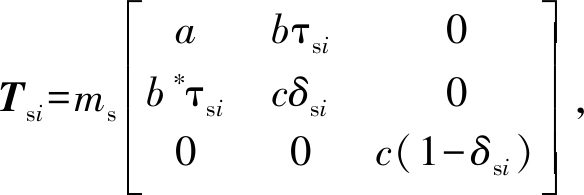

(3)
式中下标i代表方位向观测角度,可由方位向子孔径号表征。需要注意的是,表面散射中的极化方向角偏移函数δsi和τsi与地表局部坡度有关,而二面角散射的极化方向角偏移函数δdi和τdi只与雷达航迹和二面角轴向量的夹角有关,它们在物理含义上是有本质区别的。由于体散射为各向同性散射,因此其极化相干矩阵与广义Freeman-Durden模型中的体散射分量一致。
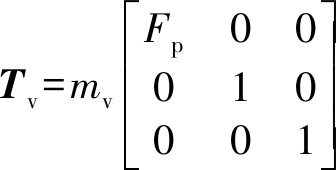
(4)
式中Fp=2对应于Freeman-Durden 模型。由三种散射之和可得扩展广义Freeman-Durden分解的混合散射模型:
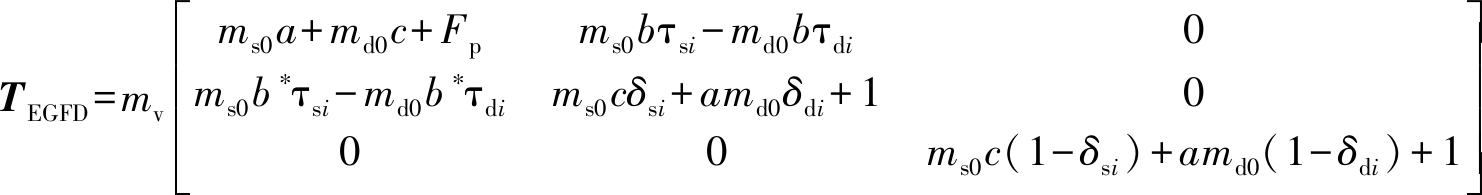
(5)
上式中
ms0=ms/mv
md0=md/mv
(6)
分别代表表面散射分量与体散射分量的比值,以及二次散射分量与体散射分量的比值。
通过该模型及极化似然比定义可推导基于广义Freeman-Durden模型的多角度观测似然比表达式,从而可从极化散射特型变化的角度帮助理解方位向多散射中心检测及重组过程内在的物理意义。若假设混合散射以表面散射与体散射为主,
(7)
上式中其他与观测角度无关的项包括体散射系数Fp及表面与体散射幅度比,因此它们不会影响总体变化规律。
同理可得混合散射以二次散射与体散射为主的情况,则有ms0≈0。似然比表达式为:
(8)
非各向同性散射中心序列重组过程与去极化规律之间不存在直接关系。去极化程度大小只与散射体的随机程度有关,而重组过程并不一定降低随机性。根据前文分析,多角度观测对表面散射以及二面角散射体散射的影响主要是通过表面坡度变化以及二面角轴线与航迹夹角的变化引起的。虽然上述变化都通过对极化相干矩阵两侧乘以旋转矩阵来实现,但在对极化相干矩阵特征值的影响上是有本质区别的。现有研究表明:在小粗糙度表面散射上叠加大粗糙度变化将导致极化熵增加,这是由于该过程假设大粗糙度具有随机性,而不同矢量方向的表面散射叠加在一起会引起极化熵增加,去极化程度变大。而二面角散射(例如房屋外墙)则是在小粗糙度表面上叠加一个平均值,因此不会改变小粗糙度表面的去极化程度,极化熵较低。如果它在多角度观测中与表面散射叠加在一起,那么按照功率加权原则,二面角散射应占主要贡献,极化熵较低。那么经过消除过程,若判断首先消除二面角散射,那么剩余的表面散射极化熵更高,因此消除过后的随机性反而增加了。
3 多角度极化SAR特征
基于方位向非各向同性多散射中心检测的处理方法不仅在保持多角度散射差异和相干班抑制两方面取得了平衡,而且对原始的子孔径序列进行了信息重组。以目标在方位向上的散射中心结构特征作为度量工具,来决定信息重组的结合顺序。其最大优势在于,该顺序与同类型目标的所处方位无关,而只与目标本身的散射结构特征有关。例如同样一栋房子,无论它是东西向还是南北向,Yang[6]提出的处理方法都会以同一个顺序来形成序列,其特征方向性散射特征,并依据方向性散射贡献强弱进行排序,有效避免了同物异谱现象(这里的谱是指特征)。基于以上思路,本节从重组后图像序列的似然比曲线、子孔径消除角度、极化熵、极化散射角以及极化各向异性度五个方面来构建极化多角度观测SAR的初级特征。
3.1 极化似然比序列
在第i次迭代循环计算周期中,R个子孔径的似然比值可通过下式计算。
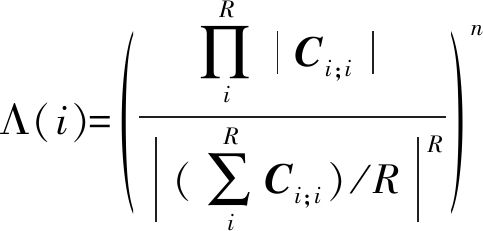
(9)
同一类散射目标的似然比曲线绝对值差异较大,这是由于似然比计算过程中主要依赖散射强度信息。而散射强度容易受到多种因素的影响,例如天线的散射方向图、地形坡度以及目标本身的介电常数和几何结构。由此可见,似然比曲线处理应以曲线特征提取及归一化为主。可结合似然比曲线的前向差分运算及状态编码来提取曲线特征并归一化。
3.2 子孔径角度序列
在求解极化似然比的迭代运算过程中可得到每个周期中对似然比贡献最大的主要散射方向,即孔径数Ap(i),其前向差分被定义为:
(10)
3.3 与极化特征相结合的似然比序列
通过Entropy-Alpha分解可获得极化熵、极化散射角及极化各向异性度,用于描述基本散射机理的随机性、散射类型及次要散射分布[8]。这里仍然采用前向差分形式来表达非各向同性散射中心检测及数据重组过程中的极化熵变化。
ΔH(i)=H(i+1)-H(i)
(11)
同理可得极化散射角及极化各向异性度变化:
(12)
ΔA(i)=A(i+1)-A(i)
(13)
4 SVM分类试验
4.1 支持向量机(SVM)
支持向量机(Support Vector Machine,SVM)[9]是一种有监督的分类器,该方法在小样本分类、非线性分类以及高维模式的数据分类方面有很好的效果,并且具有很强的泛化能力。支持向量机算法分类的核心思想是,利用核函数将输入从输入空间映射到一个高维空间得到特征向量之间的内积,不同的核函数对应不同的特征向量,通过合适的核函数学习非线性支持向量机,找到线性可分的最大间距作为最优的分类超平面。对于数据样本集(xi,yi),xi∈Rd,yi∈{-1,1},i=1,2,…,n,在满足条件
yi[(ω,xi)+b]≥1-ξi
(14)
的情况下,求解最优化
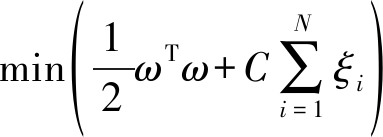
(15)
式中,ω为权重参数;b为偏移向量;ξi为松弛变量;C是惩罚因子,决定了不同类别样本的最大间距和最小分类误差。
目前常用的核函数主要有4类:线性核函数、径向基核函数、多项式核函数和Sigmoid核函数。本文通过实验对比,选择了分类效果更好的径向基核函数,
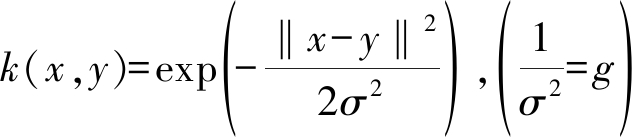
(16)
式中σ为径向基核函数的宽度。核函数中的参数g和惩罚因子C的确定对支持向量机系统的性能有着很大的影响[10],所以需要对参数进行选择。
4.2 网格搜索优化算法
在分类模型建立过程中,如果C过小或g过大,则可能会出现欠拟合的情况,如果g过小或C过大,则可能会出现过拟合的情况[11]。本文通过网格搜索算法[12]对SVM参数进行优化来提高检测准确度。网格搜索算法的基本原理是通过设定C和g的取值范围,建立以C和g为坐标的二维网格,对每个网格进行遍历,并利用对应的参数值训练SVM,最终取分类精度最高的C和g作为最优参数值。网格搜索算法与启发式或逼近式算法不同,其采用穷尽搜索,可以从所有可能解中找到最优解,且基本只涉及两个参数,寻优时间也和目前常见的几种算法差不多。此外,算法过程中的各组参数相互解耦,便于并行计算。
4.3 多角度极化SAR图像分类
多角度极化SAR图像分类流程图如图1所示。
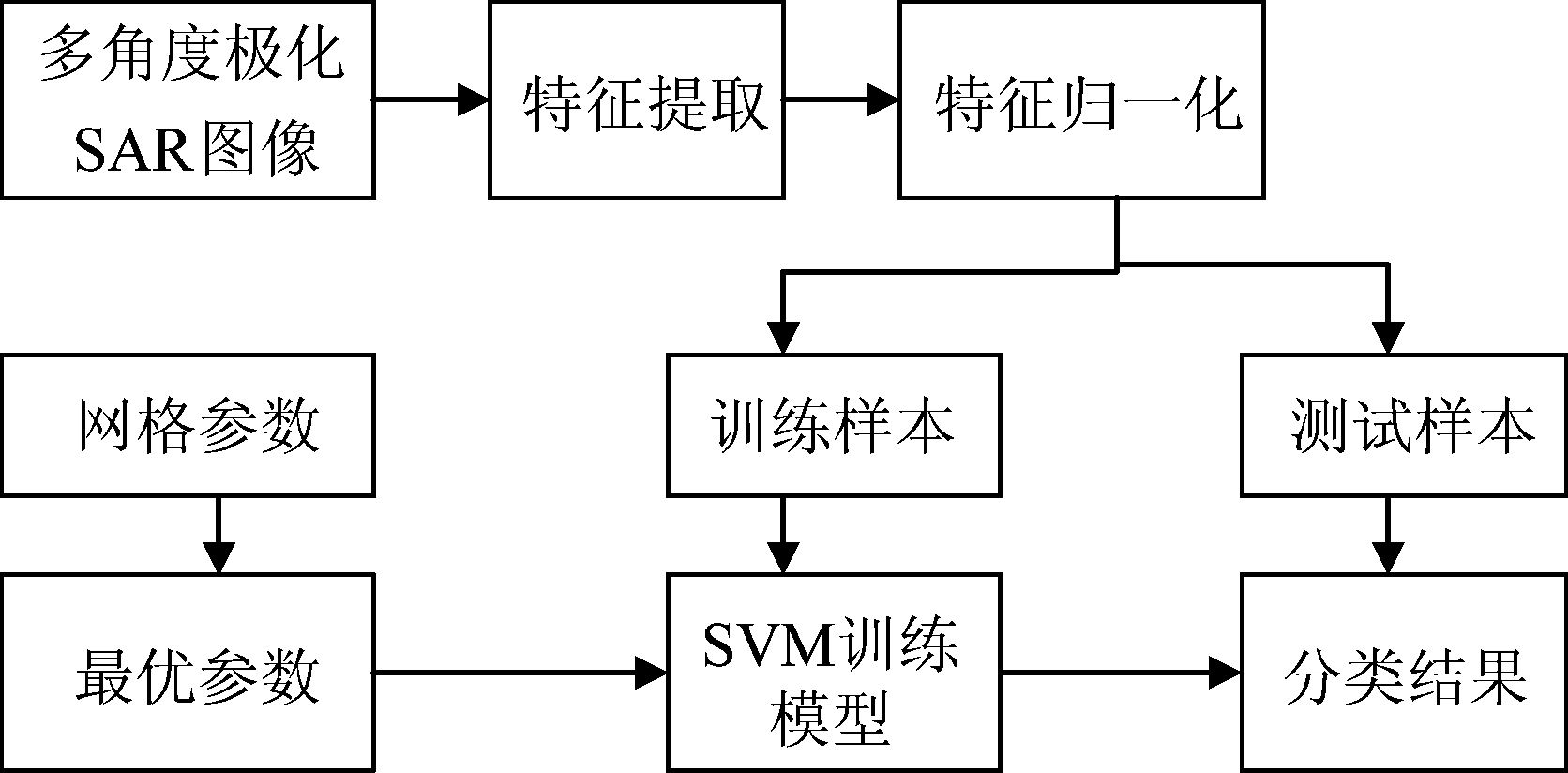
图1 多角度极化SAR图像分类流程图
Fig.1 Multi-angle polarization SAR image classification flow chart
流程图中提取的特征是基于前文从重组后图像序列的似然比曲线、子孔径消除角度、极化熵、极化散射角以及极化各向异性度五个方面构建的极化多角度观测SAR的初级特征,通过提取的五类特征进行归一化处理,其中每个特征都是实数,但是范围不同,于是进行归一化处理,将不同特征的值域范围规范到相同的区间[0-1],从而避免某个特征值域过大而掩盖了其他特征值域较小的特征参数变化的作用。然后通过网格搜索优化寻求最优参数C和g。最后通过SVM分类器进行分类。网格搜索优化的基本流程如下:
(1)初始化网格搜索中C、g的搜索范围,这里设置参数C的搜索范围为[-10,10],参数g的搜索范围为[-10,10];
(2)在选定的范围划分网格并遍历网格内所有点进行取值,最终选取使得训练集验证分类准确率最高的一组C和g作为最佳的参数。
选择网格搜索方法获得的最优参数C=1,g=0.001。
4.4 分类结果

图2(a)为训练区与测试区的分布,其中10组红色多边形区域为训练区,10组白色多边形区域为测试区,目前通过上文的方法对其中的四类进行分类,图2(b)为这四类的分类结果图,其分类精度为96.9%,分出的四个区域如图中的几个不同颜色的矩形块所示,绿色块区域表示山体叠掩区,蓝色块表示大桥区域,红色块表示农作物区域,黑色块表示房屋区域。
5 结论
通过构建基于极化似然比的多角度散射模型,可从物理及数据两个层面分析多角度观测方位向非各向同性极化散射过程。同时,提出了基于散射差异序列的特征提取方法,将模型内在的规律性信息转化为可应用与分类的形式。最后通过SVM方法对实际机载极化圆迹数据进行了分类处理,给出了初步的处理流程及结果,揭示了极化圆迹SAR数据在地物分类方面的应用价值。
[1] Ponce O, Pratsiraola P, Pinheiro M, et al. Fully Polarimetric High-Resolution 3-D Imaging With Circular SAR at L-Band[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(6): 3074-3090.
[2] 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135.
Hong W. Research progress of circular SAR imaging technology[J]. Journal of Radar, 2012, 1(2): 124-135.(in Chinese)
[3] Zhang X K, Zhang Y H, Jiang J S. Circular SAR imaging approximated by spotlight processing[C]∥International Symposium on Antennas, Propagation & Em Theory. IEEE, 2006.
[4] 唐智, 李景文, 王宝发. 曲线合成孔径雷达迭代算法[J]. 北京航空航天大学学报, 2007, 33(8): 882- 885.
Tang Z, Li J W, Wang B F. Iterative algorithm for curved synthetic aperture radar[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(8): 882- 885.(in Chinese)
[5] Ferro-Famil L, Reigber A, Pottier E, et al. Analysis of anisotropic behavior using sub-aperture polarimetric SAR data[C]∥IEEE International Geoscience & Remote Sensing Symposium. IEEE, 2003.
[6] Yang L, Qiang Y, Yun L, et al. Anisotropy Scattering Detection From Multiaspect Signatures of Circular Polarimetric SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2018: 1-5.
[7] Shane Cloude. Polarisation: Applications in Remote Sensing[M]. Oxford Scholarship Online: Shane Cloude,February 2010: 59-77.
[8] Cloude S R, Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience & Remote Sensing, 1996, 34(2): 498-518.
[9] Liu J W, Cui L P, Luo X L. MCR SVM classifier with group sparsity[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(17): 6915- 6926.
[10] 奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011, 47(3): 123-124.
Feng G H. SVM classification kernel function and parameter selection comparison[J]. Computer Engineering and Applications, 2011, 47(3): 123-124.(in Chinese)
[11] 宋永东. 支持向量机参数选择的研究[D]. 湖北武汉: 华中师范大学, 2013. 05.
Song Y D. Research on parameter selection of support vector machine[D]. Wuhan, Hubei: Huazhong Normal University, 2013. 05.(in Chinese)
[12] 王兴玲, 李占斌. 基于网格搜索的支持向量机核函数参数的确定[J]. 中国海洋大学学报: 自然科学版, 2005, 35(5): 859- 862.
Wang X L, Li Z B. Determination of kernel function parameters of support vector machine based on grid search[J]. Journal of Ocean University of China: Natural Science Edition, 2005, 35(5): 859- 862.(in Chinese)




