1 引言
目标跟踪是根据目标的过去状态和观测,精确地预测和估计目标的未来轨迹。为了获取目标的精确位置、速度和加速度,设计目标的精确模型是非常关键的。交互多模型[1-3](IMM)算法选择多个并行模型,并根据马尔可夫自动切换来有效地预测和估计目标的轨迹。然而,由于模型切换机制的存在,使得算法在切换过程中容易造成较大的估计误差。特别是对于不确定性模型的估计,标准的IMM算法更加降低了模型匹配和状态估计的精度。因此,IMM算法的关键是滤波方法的选择。
近年来,为了提高IMM算法的估计精度,基于非线性滤波[4-9]的多模型算法是目前应用最广泛的多模型算法,比较流行的非线性滤波方法是扩展卡尔曼滤波(EKF)。在序列乘性扩展卡尔曼滤波(EKF)[4]中,对每个矢量观测数据进行逐次处理以更新姿态,使测量模型线性化在下一次矢量观测更准确。然而,随着动态系统非线性的加剧,EKF的性能急剧下降。为了解决这个问题,Julier 和Uhlmann提出了无迹卡尔曼滤波(UKF)[8]算法。该算法是以无迹变换(UT)为基础获得一些精确的Sigma点,通过Kalman线性滤波的框架,抛弃了对非线性函数线性化的传统方法。在预测方程方面,在二阶泰勒展开时,通过迭代地传播一些精确的Sigma 点来获取精确的后验均值和协方差。和EKF相比,由于UKF滤波算法不需要在滤波过程中计算非线性函数的雅克比矩阵,所以对非线性环境没有任何限制要求,且具有更高的滤波跟踪精度。近几年来,学者们提出的许多改进UKF算法,其中包括截断无迹卡尔曼滤波算法[9]、迭代无迹卡尔曼滤波算法(IUKF)[10]、高斯和无迹卡尔曼滤波算法[11]等,使得UKF及相关算法得到广泛的应用。文献[12]将三种不同噪声协方差的无迹卡尔曼滤波器(UKF)引入交互多模型(IMM)算法框架中,形成IMM-UKF滤波器。针对模型不确定这一问题,文献[13]提出了一种基于交互多模型(IMM)估计的自适应鲁棒UKF算法。该方法综合了自适应衰落UKF和鲁棒UKF的优点。针对未知的连续系统参数非线性滤波问题,文献[14]提出了基于球形单纯形无迹卡尔曼滤波的跳静态IMM(SSUKF-JSIMM)方法。
为了获得精确的跟踪性能,上述方法需要精确的运动模型和自适应非线性滤波方法。然而,特别是在机动目标跟踪中,精确的运动建模几乎是不可能的。众所周知,由Zadeh提出的模糊逻辑办法是动态系统参数辨识和综合控制率的一种通用技术。模糊推理不仅涉及数值变量,也涉及语言变量,即定性变量(大、中、小等)。因此,当遇到难以建模或精确估计参数的系统时,这种方法是非常优越的。文献[15]提出了模糊交互多模型无迹卡尔曼滤波(FUZZY-IMMUKF)方法用于机动车辆组合导航,通过模糊推理系统确定系统噪声的上下界。此外,文献[16-17]的模糊建模方法在处理不确定问题方面也表现出了良好的性能。例如,由Takagi和Sugeno提出的T-S模糊模型[18-20],它能够以简单的方式引入关键性决定运动模型的模糊语义信息,并且这个模型可以逼近任意形状的非线性系统。实验结果证明,带反馈的T-S系统,系统能够收敛。
针对非线性系统中机动目标动态模型的不确定性问题,提出了基于UKF参数辨识的T-S模糊多模型目标跟踪算法。它主要包括以下两个方面的贡献:第一,由于目标动态模型的不确定性,该算法采用T-S模糊模型来融合目标的空间特征信息,从而引入空间特征信息,并用多个语义模糊集对其进行描述,能较高精度地逼近动态模型;第二,提出了一种模糊C回归聚类方法,并利用最优模糊隶属度自适应地辨识了T-S模糊模型的前件参数。同时,采用无迹卡尔曼滤波方法实现后件参数辨识过程。
2 提出的算法
T-S模糊模型已经广泛的应用于非线性系统的建模当中。已经证明,T-S模糊模型可以利用多个线性模型来表示任意精度的非线性系统。详细的T-S模糊模型可以参见文献[18-20],本节简单描述如下。根据前面的定义,对于加入目标特征信息的T-S模糊模型,其中状态方程被T-S模糊模型分成多个线性子模型,但观测方程还是非线性模型,每条模型规则定义如下:
(1)
其中,
表示k时刻目标的g个特征,
表示第g个目标特征的模糊隶属度函数,
为k时刻第i个模型的状态转移矩阵,
为k时刻第i个模型的观测函数,
分别为第i个模型过程噪声和观测噪声,
为k-1时刻第i个模型的状态。
在T-S模糊模型建模当中,最重要的就是模型前件参数
的隶属函数
和后件参数
和
的辨识问题。对于后件参数的辨识,传统的T-S模糊模型都采用最小二乘或加权最小二乘方法,因此对非线性非高斯系统的建模精度并不高。为此,在2.1节利用无迹卡尔曼滤波来实现后件参数的辨识,在2.2节利用模糊C均值回归聚类算法实现前件参数辨识过程。在本文中,将使用T-S模糊模型对目标的特征信息如距离、速度、新息或航向角差等进行建模,接着使用模糊C回归聚类算法实现对特征信息的模糊集隶属函数进行辨识,构建一个基于UKF参数辨识的T-S模糊多模型目标跟踪算法,框架如图1所示。从图1可以看出,提出的机动目标跟踪方法主要包括三大部分:1)基于无迹卡尔曼滤波的后件参数辨识;2)基于模糊C回归模型(FCRM:Fuzzy C-Recursive Model)[18]聚类的前件参数辨识;3)T-S模糊语义多模型融合。
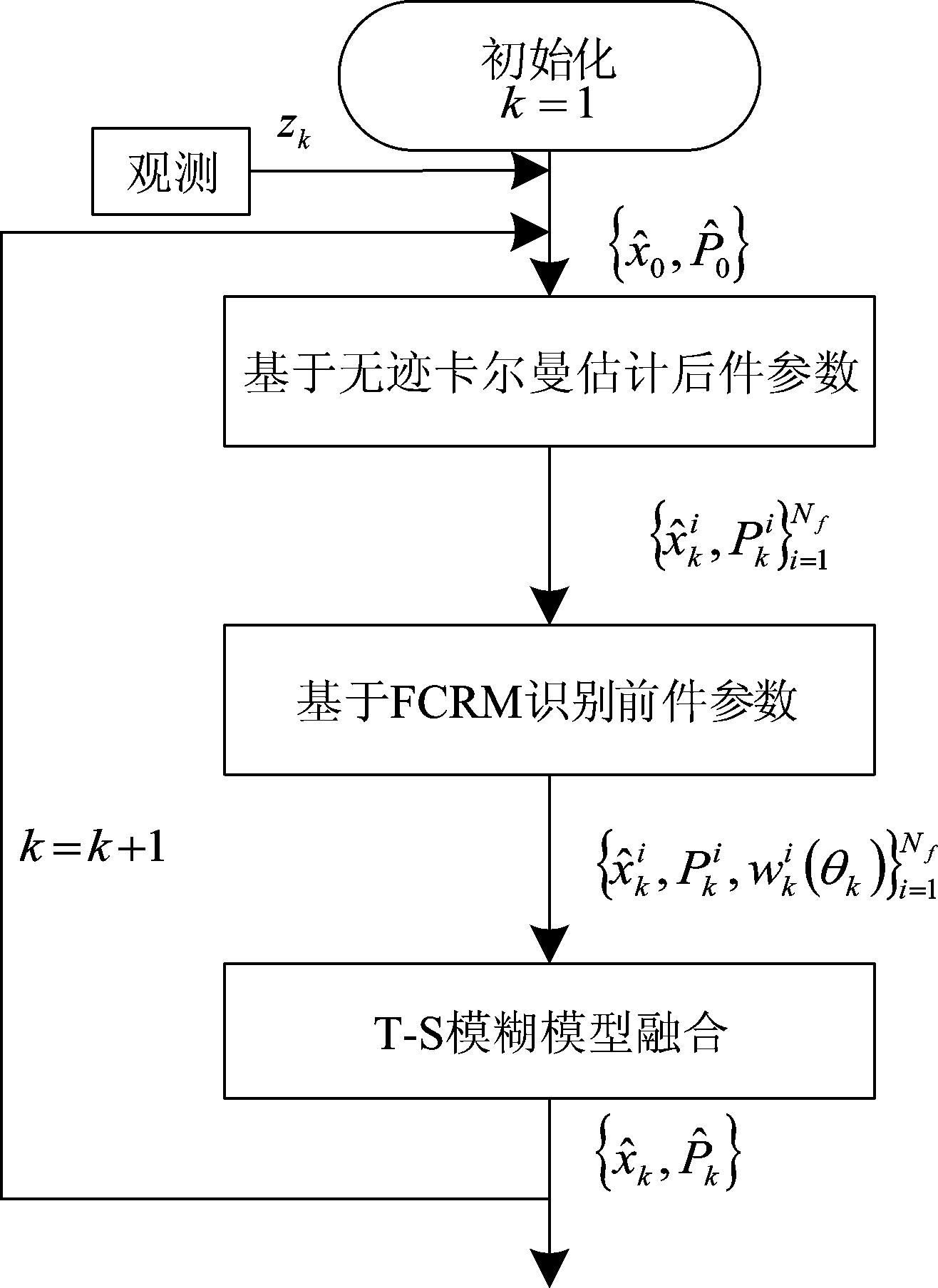
图1 基于UKF参数辨识的T-S模糊多模型算法框架
Fig.1 Block diagram of T-S Fuzzy multiple Model with UKF Parameter Identification
2.1 基于无迹卡尔曼滤波的后件参数辨识算法
无迹变换是通过对一定的已知随机变量统计特性后求其函数随机量的统计特性而得出。首先通过非线性状态方程来估算状态向量的概率密度函数,取出一组确定的采样点,然后根据无迹变换计算采样点,并通过非线性计算得到相应后验统计特征,最后用线性回归的方法得到后验统计。无迹卡尔曼滤波由于不需要对非线性系统进行线性化,并可以很容易地应用于非线性系统的状态估计,因此,UKF方法在许多方面得到应用。无迹卡尔曼(UKF)滤波主要是利用无迹变换获取带有不同权值的Sigma粒子,在本节中,使用无迹卡尔曼滤波法实现对T-S模糊语义多模型后件参数辨识过程。由此,根据式(1)定义的T-S模糊语义模型,UKF滤波算法的基本实现步骤如下所示:
考虑离散动态系统:
(2)
(3)
在式(2)、(3)中fk:Rnx×Rnν→Rnx和hk:Rnx×Rne→Rnz是一些已知的函数,
是系统在k时刻的状态,
是k时刻的测量矩阵,
和νk∈Rne表示过程噪声和测量噪声,它们的协方差分别为Q和R。
①根据采样规则,确定2nX+1个采样点以及相应的加权值。
(4)
(5)
其中,λ为尺度参数,可以为nX+λ≠0的任意值
为
均方根的第j列。nX为状态向量x的维数。
②一步预测
(6)
(7)
(8)
③预测的观测向量和观测向量的方差
再采样,确定2nX+1个采样点以及相应的加权值。
(9)
(10)
(11)
(12)
(13)
(14)
④状态更新
(15)
2.2 基于模糊C回归聚类的前件参数识别
更进一步,为了实现对前件参数的自适应辨识,前件参数的模糊隶属函数一般设定为高斯型函数:
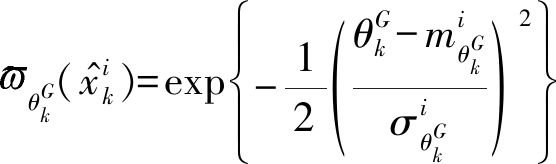
(16)
其中,
为高斯型前件参数隶属函数的均值,
为均方根误差。
式(1)表示的T-S模糊模型规则中,为了识别前件参数,模式识别中的无监督学习的聚类算法可解决该问题。模糊C均值聚类算法(FCM:Fuzzy C-Means)是最受欢迎的模糊聚类算法,但该算法只适用于超球面的数据分类中,而本文中T-S模糊规则对应超平面状态,常规超球面的FCM算法不再符合,本文使用了适用于超平面聚类算法的模糊C回归聚类算法。假设
是一个观测集,
是一个预测观测集,zk,l表示lth观测,同时
表示k时刻基于模糊规则ith的预测观测。与FCM算法一样,模糊C回归聚类算法的目标函数如下:
(17)
其中m是权重指数,一般情况下为
表示模糊规则ith的观测与输出之间的度量函数,隶属度函数满足下式:
(18)
结合式(18)约束条件,本文将目标函数定义如下:
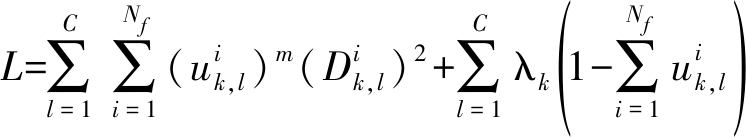
(19)
其中λk为拉格朗日乘子向量,(Dik)2为距离测量函数,它的表示如下:
(20)
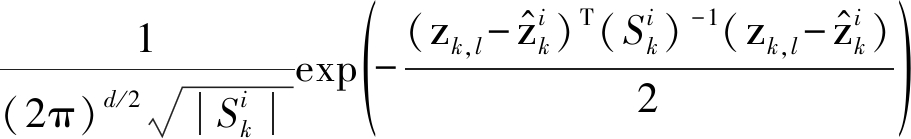
(21)
这里
称为给定目标状态
的观测zk,l似然函数
是新息协方差矩阵。
根据目标函数对
求偏导,得到隶属度更新表达式:
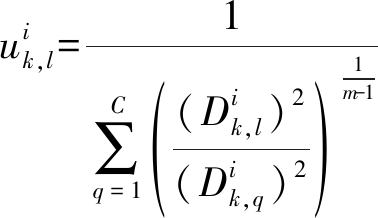
(22)
因此,对观测l在时间k上的模糊隶属度进行了如下计算:
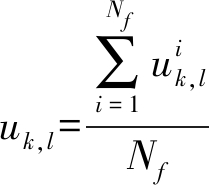
(23)
当隶属度矩阵U由式子(23)计算后,即可用到T-S模糊模型的参数识别的式(24)中。
(24)
2.3 算法总结
根据上述推理,基于UKF参数辨识的T-S模糊多模型目标跟踪算法总结如下:
算法1:基于UKF参数辨识的T-S模糊多模型目标跟踪算法(TS-UKF)1. 初始化k=0设定模型数为Nf。2. for k=1,2,…a) T-S模型模型参数辨识·基于UKF后件参数辨识,得到状态x^ik以及状态协方差Pik;·基于FCRM前件参数辨识,根据FCRM聚类算法得到的隶属度矩阵U自适应调整前件参数的隶属度函数θGk(x^ik);b) 模型概率更新·模型概率:w-ik(θk)=∏Gg=1θgk(x^ik)·标准化:wik(θk)=w-ik(θk)∑Nfj=1w-jk(θk)c) 状态更新及状态协方差估计:·输出状态估计:x^k=∑Nfi=1wik(θk)x^ik·输出协方差估计:P^k=∑Nfi=1wik(θk)(Pik+(x～k-xik)(x～k-xik)T)
3 实验结果
为了验证提出算法的跟踪性能,分析了一种仿真雷达机动目标跟踪问题,该问题对空防应用有一定的指导意义。同时对比于传统的交互多模型滤波算法(IMM: Interacting multiple model),交互多模型无迹卡尔曼滤波(IMM-UKF:Interacting multiple model unscented Kalman filtering),所有实验进行100次蒙特卡洛仿真。
在提出的算法中目标的状态方程和测量方程如下所示:
(25)
(26)
其中Nf表示模糊规则的总数目,
表示状态向量,xk表示目标x轴坐标,yk表示目标y轴坐标,
和
分别表示目标在x轴和y轴坐标对应的速度。假设过程噪声ek是服从零均值和均方根为σi,e的高斯噪声,其中过程噪声协方差矩阵Q是一个4×4矩阵(Qij=0,for i≠j,Q=diag(σi,e,σi,e))。本次实验中假设观测噪声νk为非高斯分布噪声,仿真中的非高斯噪声主要有两个高斯噪声叠加产生,其中R类似于高斯噪声的协方差矩阵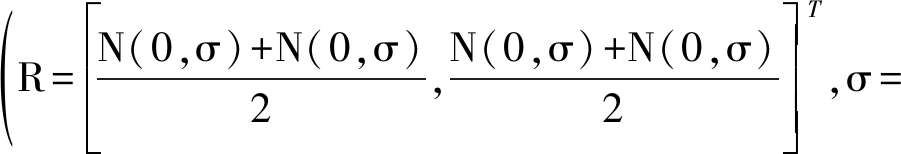
初始状态x0由目标初始位置决定x0=[2 km,0.15 km/s,8 km,0.26 km/s]T,主要描述目标的位置和速度,假设先验概率密度函数服从高斯分布,其x0|0=x0,P0|0=diag(0.152,0.01,0.152,0.01)。本文选择新息和航向角差作为语义信息是因为这些信息能够有效地体现出目标的运动状态,比如新息,它能够反映出目标运动模型是否合适,当新息较大时,说明目标运动模型不太符合当前的运动状态,我们就可以根据这个信息对每个模型的权值进行一定的调整,从而得到一个更加准确的运动模型。新息两个模糊集(Small, Large)和航向角差三个模糊集(Negative Large, Small, Positive Large)隶属函数的均值初始值分别为
2*0.15 
rad。初始的协方差为
同时传感器的位置在坐标原点
是状态转移矩阵,它的表示方法如下:
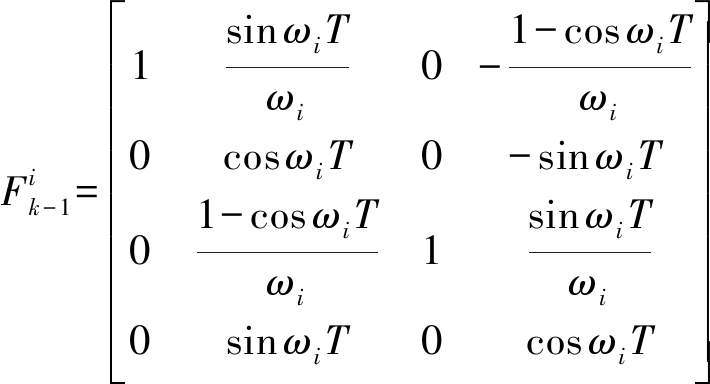
其中转弯率ωi由T-S模糊模型决定,表1给出了每条T-S模糊模型对应的转弯率和过程噪声标准差。过程噪声标准差设置为0时是一种理想状态,在实际情况下,过程噪声设置为0存在概率是非常低的,但是为了在实验中模拟更多的运动场景,因此将其考虑进来,如果在进行实验时,真正的实验环境噪声不为0,那么这条规则的权重就会很低。
表1 对于不同输入变量
和Δνk的转弯率ωi和过程噪声标准差
Tab.1 The angular rate ωi and the process noise standard deviation σi,e for different and Δνk
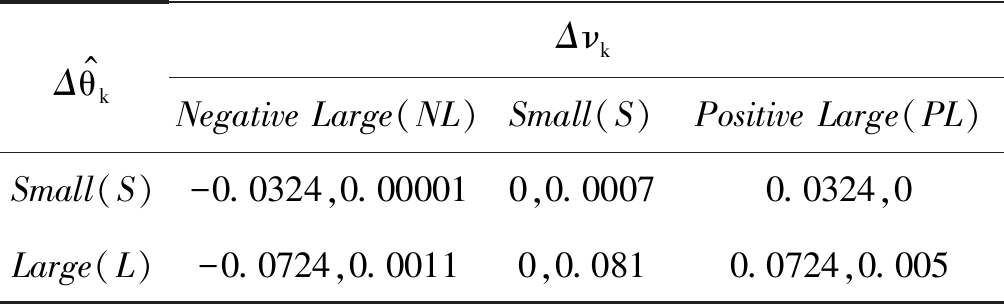
Δθ^kΔνkNegative Large(NL)Small(S)Positive Large(PL)Small(S)-0.0324,0.000010,0.00070.0324,0Large(L)-0.0724,0.00110,0.0810.0724,0.005
注意: 如果ωi=0,模糊线性模型就变成了常速度线性模型。
此外,对于IMM和IMM-UKF都采样三个运动模型:一个常速度运动模型和两个转弯模型(转弯率分别是w=0.0325 & -0.0325)。图2给出了目标运动轨迹和TS-UKF算法的估计轨迹图。从图中可以看出,本文提出算法跟踪效果和模拟仿真的轨迹基本一致,没有出现明显的跟丢现象,尤其是在目标机动的情况下,表现出很好的鲁棒性,说明该算法在非线性系统中能够高效地处理不确定信息。
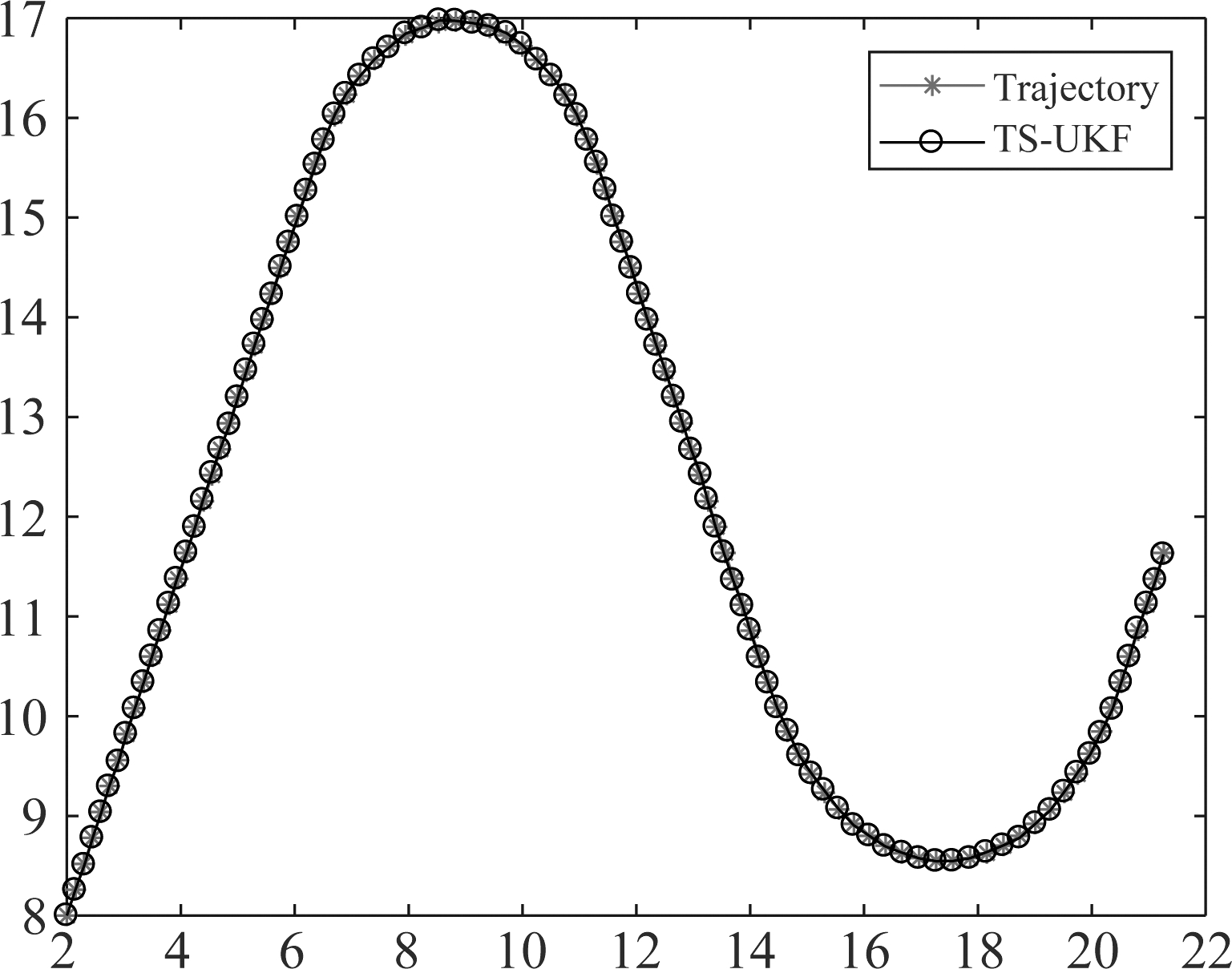
图2 真实和估计轨迹
Fig.2 Real and estimated trajectory
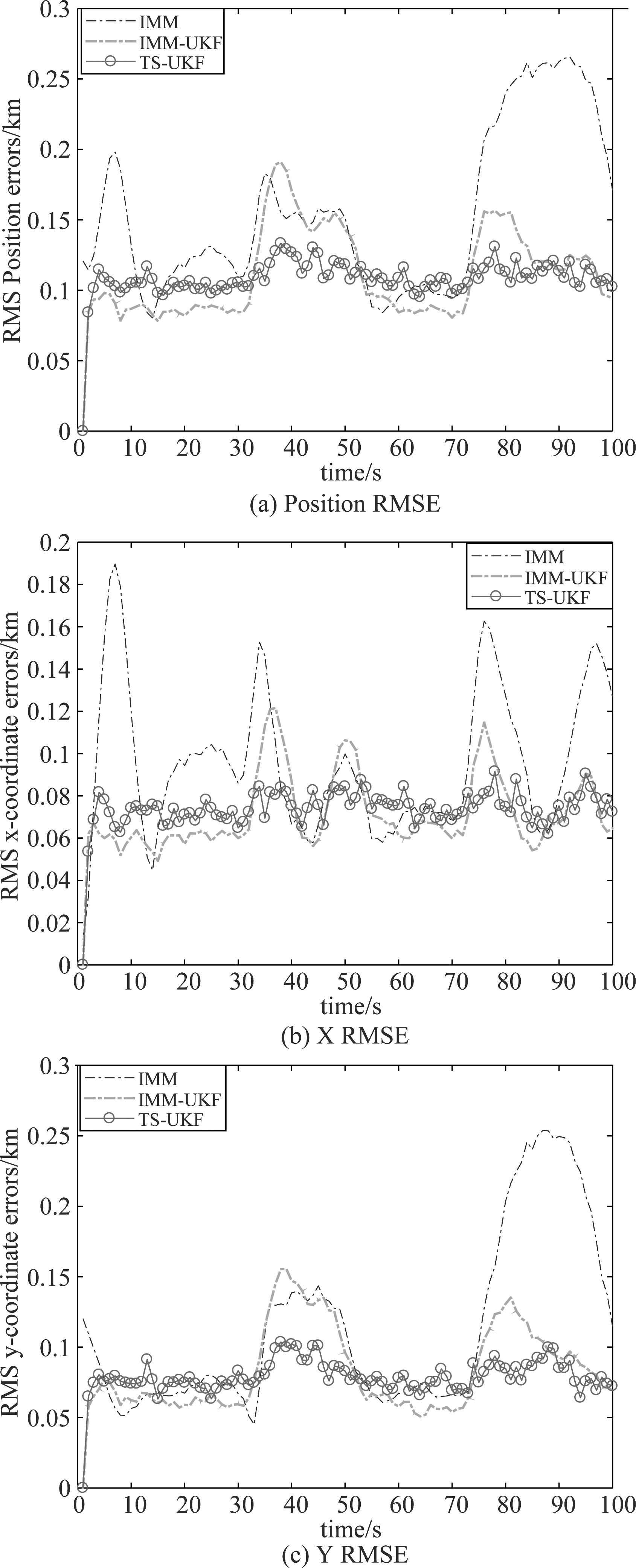
图3 均方根误差对比
Fig.3 Root mean square error comparison
图3(a)～(c)分别描述了目标的位置均方根误差,x轴方向的均方根误差和y轴方向的均方根误差,从图中可以看出,本文提出的算法在目标机动时跟踪效果优于其他两种算法,表现出相对稳定的跟踪性能。而IMM和IMM-UKF算法在目标转弯时误差较大,主要原因是IMM算法中使用的模型集可能不够大。当目标机动时,所选择的模型集不能有效地匹配目标的运动状态。而TS-UKF算法可以根据目标的空间特征信息多个语义信息构建目标运动模型,同时,利用T-S模糊模型中前件参数的隶属函数自适应地调整各规则的权重,最终目标运动模型的准确率得到更进一步的提升。并且使用无迹卡尔曼滤波算法对后件参数进行识别,提高了滤波精度。但是在目标直线运动阶段跟踪精度不如IMM-UKF方法,是因为IMM-UKF是从模型集中选出一个模型对目标进行滤波,IMM-UKF的模型集中主要选择了三个模型,分别是常速度运动模型和两个转弯模型,在IMM-UKF算法中模型的初始概率都是人为事先预设,直线模型初始概率赋值比其他模型大,使得IMM-UKF在每次运行前期阶段都是选中为直线模型,当目标作直线运动时,模型精确度相对较高。而本文的算法是多个模型集融合,所以在目标直线运动时运动模型精确度比IMM-UKF的模型差。
表2给出了三种算法的均方根误差统计结果。从表中数据得出,TS-UKF的跟踪精度在位置均方根误差上比IMM和IMM-UKF分别提高了30.32%和2.17%,体现了更精确的跟踪效果。
表2 均方根误差统计表
Tab.2 Root mean square error statistical table
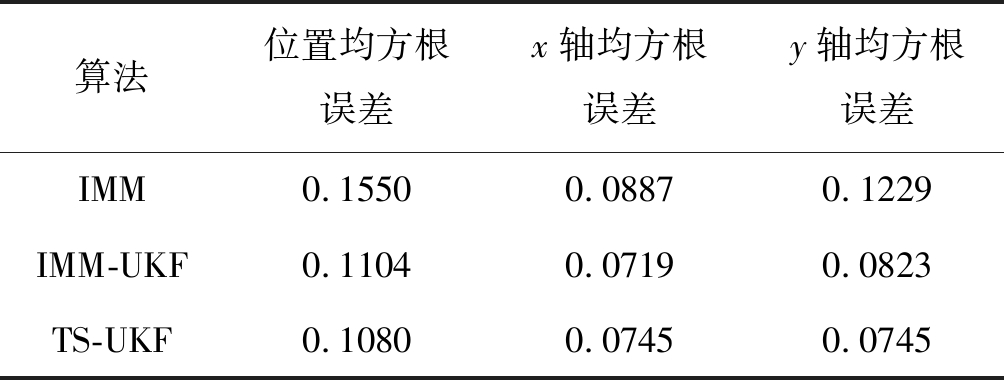
算法位置均方根误差x轴均方根误差y轴均方根误差IMM0.15500.08870.1229IMM-UKF0.11040.07190.0823TS-UKF0.10800.07450.0745
4 结论
本文提出了一种新的基于UKF参数辨识的T-S模糊多模型目标跟踪算法,用多个语义模糊集对目标特征信息进行模糊表示,构建一个通用的T-S模糊语义多模型框架。T-S模糊语义多模型的前件参数使用FCRM算法识别,而用无迹卡尔曼滤波算法实现对后件参数的辨识。当目标机动或者目标的运动状态不确定时,T-S模糊模型使用新息和航向角差这两个模糊语义信息自适应地调整目标最优的运动状态,使得在处理运动模型不确定问题方面比IMM和IMM-UKF算法更加精确稳定。
[1] Xie Guotao, Gao Hongbo, Qian Lijun, et al. Vehicle Trajectory Prediction by Integrating Physics- and Maneuver-Based Approaches Using Interactive Multiple Models[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5999- 6008.
[2] Khalid S S, Abrar S. A low-complexity interacting multiple model filter for maneuvering target tracking[J]. AEUE-International Journal of Electronics and Communications, 2017, 73(3): 157-164.
[3] Chen Xulong, Gao Jian, Han Xing. An algorithm based on interacting multiple models for maneuvering target tracking[C]∥Information Technology and Artificial Intelligence Conference. IEEE, 2015: 405- 408.
[4] Chang Lubin, Hu Baiqing, Li Kailong. Iterated multiplicative extended kalman filter for attitude estimation using vector observations[J]. Sensors, 2018, 18(5): 2053-2060.
[5] Kim B, Yi K, Yoo H, Chong H. An IMM/EKF Approach for Enhanced Multitarget State Estimation for Application to Integrated Risk Management System[J]. Vehicular Technology IEEE Transactions on, 2015, 64(3): 876- 889.
[6] Gao Bingbing, Hu Gaoge, Gao Shesheng, et al. Multi-sensor Optimal Data Fusion for INS/GNSS/CNS Integration Based on Unscented Kalman Filter[J]. International Journal of Control Automation & Systems, 2018, 16(1): 129-140.
[7] Qi Junjian, Sun Kai, Wang Jianhui, et al. Dynamic State Estimation for Multi-Machine Power System by Unscented Kalman Filter With Enhanced Numerical Stability[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1184-1196.
[8] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401- 422.
[9] 
ngel F. Garcia-Fernandez, Morelande M R, Grajal J. Truncated Unscented Kalman Filtering[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3372-3386.
[10] Zhan Ronghui, Wan Jianwei. Iterated Unscented Kalman Filter for Passive Target Tracking[J]. Aerospace & Electronic Systems IEEE Transactions on, 2007, 43(3): 1155-1163.
[11] Kottakki K K, Bhushan M, Bhartiya S. An Improved Gaussian Sum Unscented Kalman Filter[J]. IFAC Proceedings Volumes, 2014, 47(1): 355-362.
[12] Xu Qimin, Li Xu, Chan Chingyao. A Cost-Effective Vehicle Localization Solution Using an Interacting Multiple Model-Unscented Kalman Filters(IMM-UKF)Algorithm and Grey Neural Network[J]. Sensors, 2017, 17(6): 1431.
[13] Gao Bingbing, Gao Shesheng, Zhong Yongmin, et al. Interacting multiple model estimation-based adaptive robust unscented Kalman filter[J]. International Journal of Control Automation & Systems, 2017, 15(2): 1-13.
[14] Pan Yi, Ye Hui, He Keke. Spherical Simplex Unscented Kalman Filter-Based Jumping and Static Interacting Multiple Model[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2016, 32(4): 89-92.
[15] Jwo Dah-Jing, Tseng Chien-Hao. Fuzzy adaptive interacting multiple model unscented Kalman filter for integrated navigation[C]∥Control Applications. IEEE, 2009: 1684-1689.
[16] Hua Haochen, Cao Junwei, Yang Gang, et al. Voltage Control for Uncertain Stochastic Nonlinear System with Application to Energy Internet: Non-fragile Robust H ∞ Approach[J]. Journal of Mathematical Analysis & Applications, 2018, 463(1): 93-110.
[17] Mizumoto I, Kawabe N. Adaptive output feedback based output tracking control for uncertain nonlinear systems via T-S fuzzy model[C]∥IEEE, Conference on Decision and Control. IEEE, 2017: 891- 896.
[18] Chang Chia-Wen, Tao Chin-Wang: A Novel Approach to Implement Takagi-Sugeno Fuzzy Models[J]. IEEE Transactions on Cybernetics, 2017, 47(9): 2353-2361.
[19] Li Yanhui, Li Yulong. Robust L1 output tracking control for uncertain networked control systems described by T-S fuzzy model with distributed delays[J]. International Journal of Systems Science, 2017, 48(15): 1-9.
[20] Xie Xiaolong, Lin Lin, Zhong Shisheng. Process Takagi-Sugeno model: A novel approach for handling continuous input and output functions and its application to time series prediction[J]. Knowledge-Based Systems, 2014, 63(3): 46-58.
