1 引言
检测前跟踪(track-before-detect, TBD)[1]提供了检测和跟踪低信杂比(signal to clutter ratio, SCR)目标的一种有效途径。通过在目标可能的运动轨迹上对连续多帧观测数据进行积累,该方法能够检测信杂比很低的微弱目标,并在做出检测的同时提供目标航迹[2]。积累的关键在于对目标后验密度的准确表示。与常规的先检测后跟踪模式相比,TBD利用了传感器获得的原始测量数据,因而避免了信息损失[3]。目前,TBD技术有多种实现方法[1,4],包括动态规划(dynamic programming, DP)[5],霍夫变换(Hough transform, HT)[6],最大似然(maximum likelihood, ML)方法[7]和粒子滤波(particle filter, PF)[8-11]等。其中,PF由于在处理非线性观测模型方面的灵活性获得了快速发展。一种广泛应用的PF算法是序贯重要性采样(sequential importance sampling, SIS)粒子滤波器(SIS-PF)。但在SIS-PF中,当粒子在状态空间上分布很宽或量测的可信度很高时,量测更新后粒子权重的协方差很大,表现为大部分粒子的权重很低,只有少部分粒子权重比较高。这一现象称为权重退化[12]。权重退化会导致粒子对目标后验的表示不准确[13]。
目前已有多种途径解决权重退化问题。一种思路是改进建议密度。通过把最优重要性密度(optimal importance density, OID)作为建议密度,能够最小化权重的协方差,但OID通常没有解析形式。近年来一些粒子滤波器采用近似的OID构造建议密度,比如Rao-Blackwellised粒子滤波器[14],不敏粒子滤波器[15],但这些方法的效果并不总是很好。此外,一些方法利用量测信息构造建议密度,如辅助粒子滤波器[16]和基于马尔科夫链蒙特卡洛方法[17]的粒子滤波器等。但由于检测前跟踪处理的量测包括了所有单元的原始数据,因而难以确定哪个量测来自于目标,哪个量测来自于杂波。这种量测源的不确定性制约了该方法的应用。另一种思路是迁移式更新。其中一种方法称为步进贝叶斯更新[18],它使用一系列离散的介于先验分布和后验分布之间的桥式分布轮流采样粒子,使粒子从先验分布逐渐接近真实后验分布。而最新的两种采用迁移式更新的方法包括粒子流滤波器[19-21](particle flow filter, PFF)和最佳运输方法[22-23]。它们都从容易获得的先验分布采样粒子,然后根据某种微分方程建立的条件引导粒子从先验分布向后验分布流动。由于摒弃了重要性采样,它们能够避免权重退化。但由于粒子流执行过程中采用了大量近似计算,导致一些粒子无法迁移到量测附近,从而引起状态估计偏差。Kreucher首次将PFF用于雷达目标的TBD处理[24],但该方法过于依赖当前时刻的量测且忽视多帧积累,如果杂波的幅度高于目标幅度,粒子很可能向杂波迁移,从而造成错误检测和跟踪。为了消除PFF执行过程中各种近似计算造成的状态估计偏差,Bunch提出了粒子流重要性采样[25]的概念,将PFF的输出视为SIS-PF的重要性密度。Li继承了这一思想,提出了粒子流粒子滤波器(Particle flow particle filter, PFPF)[13],通过改造Exact Daum-Huang(EDH)[20]和Localized Exact Daum-Huang(LEDH)[21]滤波器以构成可逆映射,从而高效的估计粒子权重。PFPF结合了粒子流和粒子滤波的优点,因而提供了同时实现多帧量测积累和目标后验精确表示的一种可能方法。
本文提出一种在SIS-PF框架下采用LEDH的TBD方法。首先,针对TBD中量测源不确定的情况改造了LEDH滤波器,为每个粒子在其预测位置的邻域内通过最大似然估计确定最可能来自目标的量测,并通过LEDH滤波器将粒子向该量测迁移。然后,根据每个粒子在迁移前的状态计算权重并重采样,以实现目标量测的帧间积累。本文通过Rayleigh杂波中3种信杂比目标的检测和跟踪实验验证了所提算法的性能。
2 问题描述
2.1 目标运动模型
假设目标在x-y平面上近似匀速运动,定义目标状态为![]() 其中(xk,yk)和
其中(xk,yk)和![]() 分别为它在k时刻的位置和速度。目标状态的演化满足如下的线性马尔科夫模型
分别为它在k时刻的位置和速度。目标状态的演化满足如下的线性马尔科夫模型
xk=Fkxk-1+vk
(1)
其中vk~N(0,Qk)为白色高斯过程噪声,Qk为过程噪声协方差,Fk为状态转移矩阵,![]()
其中,T表示采样间隔,q为加速度噪声的功率谱密度。公式(1)还可以表示为函数形式,即xk=gk(xk-1,vk)。
2.2 雷达观测模型
假设目标在k时刻的量测幅度为Ak,则其复幅度为
(2)
其中φk表示k时刻的目标相位,通常认为在[0,2π)上均匀分布。如果量测幅度符合Swerling1型起伏模型,则其概率密度函数(probability density function, PDF)为
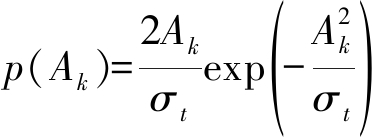
(3)
其中σt为目标幅度的均值。
定义Nr,Nd,Nb分别为雷达扫描一帧得到的距离、多普勒和方位单元的数量。当目标不存在(H0)时,观测域内任意一个距离-多普勒-方位单元{(m,n,l)|1≤m≤Nr,1≤n≤Nd,1≤l≤Nb}的幅度量测为
(4)
其中![]() 为k时刻单元(m,n,l)中的杂波。当目标存在(H1)时,单元(m,n,l)中的量测为
为k时刻单元(m,n,l)中的杂波。当目标存在(H1)时,单元(m,n,l)中的量测为
(5)
其中![]() 为如下的点扩散函数[8]
为如下的点扩散函数[8]
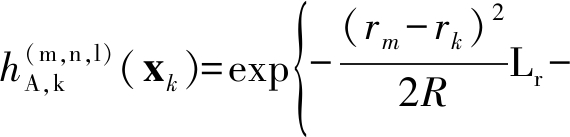
(6)
其中R,D,B分别表示距离单元、多普勒单元和方位单元的尺寸,Lr,Ld和Lb为损失常量,rk,dk和bk分别表示目标xk在量测空间上的距离、多普勒和方位坐标:
(7)
(8)

(9)
目标的位置量测为zp,k=[rk,dk,bk]′+wk,其中wk为3维量测噪声。xk向zp,k的映射可表示为zp,k=h(xk,wk)。
k时刻单元(m,n,l)中量测的似然比为
(10)
当各单元条件独立[8]时,整个区域的量测似然比为所有单元中似然比的乘积
(11)
其中zA,k为k时刻所有单元中幅度量测的集合。
3 粒子流滤波器
假设在k-1时刻用Np个粒子![]() 近似目标的后验分布,当利用运动模型预测粒子状态后,我们得到k时刻表示预测后验分布的粒子
近似目标的后验分布,当利用运动模型预测粒子状态后,我们得到k时刻表示预测后验分布的粒子![]() 之后,通过粒子流将这些粒子从先验(预测后验)分布平滑迁移到后验分布。我们用ηλ表示粒子流状态随伪时间步λ∈[0,1]的变化,用
之后,通过粒子流将这些粒子从先验(预测后验)分布平滑迁移到后验分布。我们用ηλ表示粒子流状态随伪时间步λ∈[0,1]的变化,用![]() 表示ηλ的第i种实现,并设置
表示ηλ的第i种实现,并设置![]() 将粒子流定义为粒子的条件概率密度函数
将粒子流定义为粒子的条件概率密度函数![]() 的对数形式的流动[26]
的对数形式的流动[26]
(12)
其中K(λ)为条件概率密度函数的归一化因子。
(13)
在公式(12)中,当λ从0连续变化到1时,粒子从先验分布同伦变换为后验分布。贝叶斯准则的粒子流服从如下的Ito随机微分方程[26]
(14)
其中![]() 为流函数,受Fokker-Planck方程控制。假设粒子流是零扩散的(即过程噪声为零),则有
为流函数,受Fokker-Planck方程控制。假设粒子流是零扩散的(即过程噪声为零),则有
(15)
零扩散的Fokker-Planck方程为
(16)
其中div为散度计算符。对粒子流施加不同的限制,(16)能生成多种粒子流滤波器。当g(·,·)和h(·)均为高斯概率密度时,可得到粒子流的精确解,相应的滤波器称为EDH滤波器[20]。但EDH依赖EKF/UKF计算粒子流的系数,当量测为高度非线性时EKF/UKF会失效,从而导致该滤波器性能不佳。Ding对EDH进行改进,提出了LEDH[21]滤波器。该滤波器对每个粒子分别求取流函数的参数。对第i个粒子,流函数为
(17)
其中
(18)
βi(λ)=(I+2λαi(λ))×
(19)
其中P为预测协方差,H为非线性函数h在![]() 处线性化的测量矩阵:
处线性化的测量矩阵:
4 采用LEDH流的粒子滤波检测前跟踪方法
本节首先给出了Rayleigh杂波的幅度似然比;然后改造了LEDH流以使其应用于检测前跟踪;最后从多帧积累的角度阐述了本文所提算法。
4.1 幅度似然比的计算
在TBD的量测更新部分,状态预测后粒子![]() 的权重
的权重![]() 正比于它对当前时刻量测zA,k的似然比
正比于它对当前时刻量测zA,k的似然比
(20)
其中,![]() 为k-1时刻该粒子的归一化权重。
为k-1时刻该粒子的归一化权重。
Rayleigh杂波nk的测量值![]() 的PDF为
的PDF为
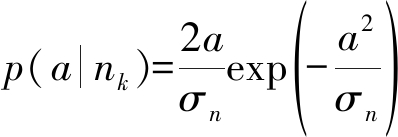
(21)
其中σn为杂波幅度的协方差。存在Swerling 1目标xk的情况下,量测的PDF[5]为
(22)
其中h为(6)中的点扩散函数。将(21)和(22)带入(20)可得k时刻Rayleigh杂波下的幅度似然比。
由于目标只影响与其邻近的单元,(20)可以近似计算[27]为
(23)
其中![]() 和
和![]() 分别为距离、多普勒和方位上受到
分别为距离、多普勒和方位上受到![]() 影响的单元。例如
影响的单元。例如![]() 可以选择为
可以选择为![]() 其中m0为粒子
其中m0为粒子![]() 所在的距离单元,q为邻域尺度参数。
所在的距离单元,q为邻域尺度参数。
4.2 LEDH流的应用
由公式(17)~(19)可知,在LEDH中每个粒子根据当前时刻的量测zp,k和![]() 计算对应的流参数。对目标滤波而言,每个时刻的量测是确定的,因而LEDH的实现比较容易。而对于TBD,由于没有检测和关联过程,当前时刻的量测包含了所有距离-多普勒-方位单元的测量值,因而无法直接确定哪个量测来自于目标。因此,在TBD中使用LEDH的前提是为每个粒子找到由目标产生的量测。
计算对应的流参数。对目标滤波而言,每个时刻的量测是确定的,因而LEDH的实现比较容易。而对于TBD,由于没有检测和关联过程,当前时刻的量测包含了所有距离-多普勒-方位单元的测量值,因而无法直接确定哪个量测来自于目标。因此,在TBD中使用LEDH的前提是为每个粒子找到由目标产生的量测。
为找到由目标产生的量测,通常的办法是对一帧中所有单元的量测进行最大似然估计,
(24)
其中Ω为包含所有距离-多普勒-方位单元的整个观测区域。
定义![]() 为
为![]() 的邻域,根据全概率公式有
的邻域,根据全概率公式有
当且仅当![]() 时等式成立。
时等式成立。
从单帧滤波的角度看,这种方法能得到目标最可能的量测。但由于实际应用中目标幅度经常起伏,在某些时刻目标幅度可能低于杂波幅度,因而式(24)估计出的量测有可能源于杂波而非目标。如果以该量测计算LEDH参数并迁移粒子,会造成严重的状态估计偏差。
出现上述问题的根本原因在于寻找目标量测时仅利用了当前时刻的观测数据。为解决这一问题,本文从长时间非相参积累的角度出发,结合多帧观测数据对目标量测进行搜索。
1)对每个粒子![]() 在该粒子的邻域内采用最大似然估计寻找最可能来自于该粒子的量测。即对于
在该粒子的邻域内采用最大似然估计寻找最可能来自于该粒子的量测。即对于![]() 的邻域
的邻域![]() 计算
计算![]() 对该邻域内所有距离-多普勒-方位单元中的量测
对该邻域内所有距离-多普勒-方位单元中的量测![]() 的似然函数。然后将似然函数最大值对应的量测作为目标产生的量测。
的似然函数。然后将似然函数最大值对应的量测作为目标产生的量测。
(25)
2)采用![]() 根据公式(17)~(19)计算LEDH的参数,并采用LEDH更新
根据公式(17)~(19)计算LEDH的参数,并采用LEDH更新![]() 的状态,得到
的状态,得到![]()
3)利用(20)计算![]() 的权重
的权重![]() 然后对所有粒子的权重进行归一化
然后对所有粒子的权重进行归一化![]() 和重采样。
和重采样。
通过第一步我们获得了最可能来自于目标的量测集![]() 如果当前时刻目标的幅度小于某个单元中杂波的幅度,只要将粒子邻域设置的足够小且粒子的分布足够宽广,则该量测集仍能以很高的概率覆盖真实目标量测,从而能够避免单帧最大似然估计造成的目标量测的遗漏。由于目标状态估计需要通过重采样获得,如果选择了目标真实量测的粒子能够获得足够高的权重,则可以避免高强度杂波造成的干扰。
如果当前时刻目标的幅度小于某个单元中杂波的幅度,只要将粒子邻域设置的足够小且粒子的分布足够宽广,则该量测集仍能以很高的概率覆盖真实目标量测,从而能够避免单帧最大似然估计造成的目标量测的遗漏。由于目标状态估计需要通过重采样获得,如果选择了目标真实量测的粒子能够获得足够高的权重,则可以避免高强度杂波造成的干扰。
5 数值仿真结果
5.1 仿真设置
为评价本文提出的粒子流粒子滤波TBD方法(PFPF-TBD)的性能,将其与传统的粒子滤波TBD方法(PF-TBD)和测地流(geodesic flow, GF)[24]TBD方法(GF-TBD)进行对比。考虑一部雷达对地面和低空小目标进行探测的场景,这类目标包括低空的鸟群和无人机,以及郊区行驶的车辆等。目标SCR定义为
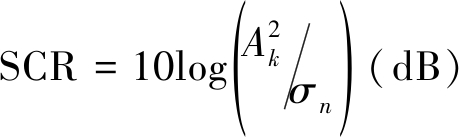
(26)
设置3个信杂比。设置Rayleigh杂波的功率为σn=1,根据(27)可以计算出目标在3种信杂比下的幅度,如表1中第2列所示。每个场景中目标的运动轨迹相同,如图1所示。雷达开始扫描时目标没有出现,第5帧时目标在距离雷达1500 m处出现,之后以10 m/s的速度朝雷达方向匀速运动,直到第51帧消失。目标真实运动状态如图1所示。雷达转速为20转/分,即扫描周期为3秒。考虑目标的状态空间为方位53°上 [0, 1500]m之间的距离单元,[-4,-20]m/s之间的多普勒单元。距离单元大小为15 m,单元数为100;多普勒单元大小为1 m/s,单元数为 16,方位单元数为1。在SCR=10 dB时,目标在距离-多普勒-幅度坐标系下的状态如图2所示。目标在第5帧的距离-多普勒-幅度量测如图3所示。对PF-TBD,设置总粒子数为1000,其中初始粒子数为900,在距离-多普勒空间中均匀分布;此外,在每一帧采样100个新生粒子,从超过量测门限的单元中均匀采样。不同场景下量测门限的设置如表1第3列所示。对GF-TBD和PFPF-TBD,设定总粒子数为500,其中初始粒子数为450,每一帧新生粒子数为50,采样方式与PF-TBD相同。
表1 仿真参数设置
Tab.1 Simulation parameters
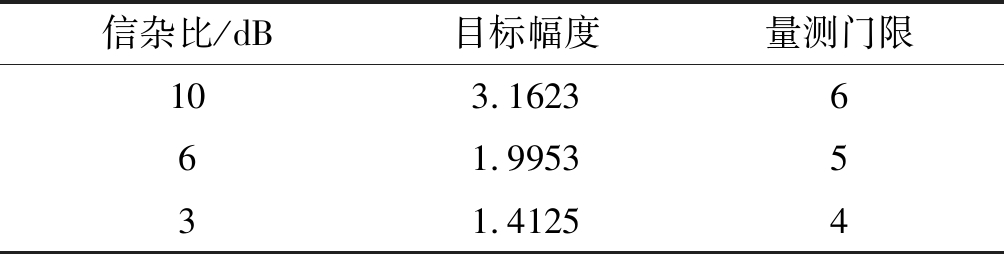
信杂比/dB目标幅度量测门限103.1623661.9953531.41254
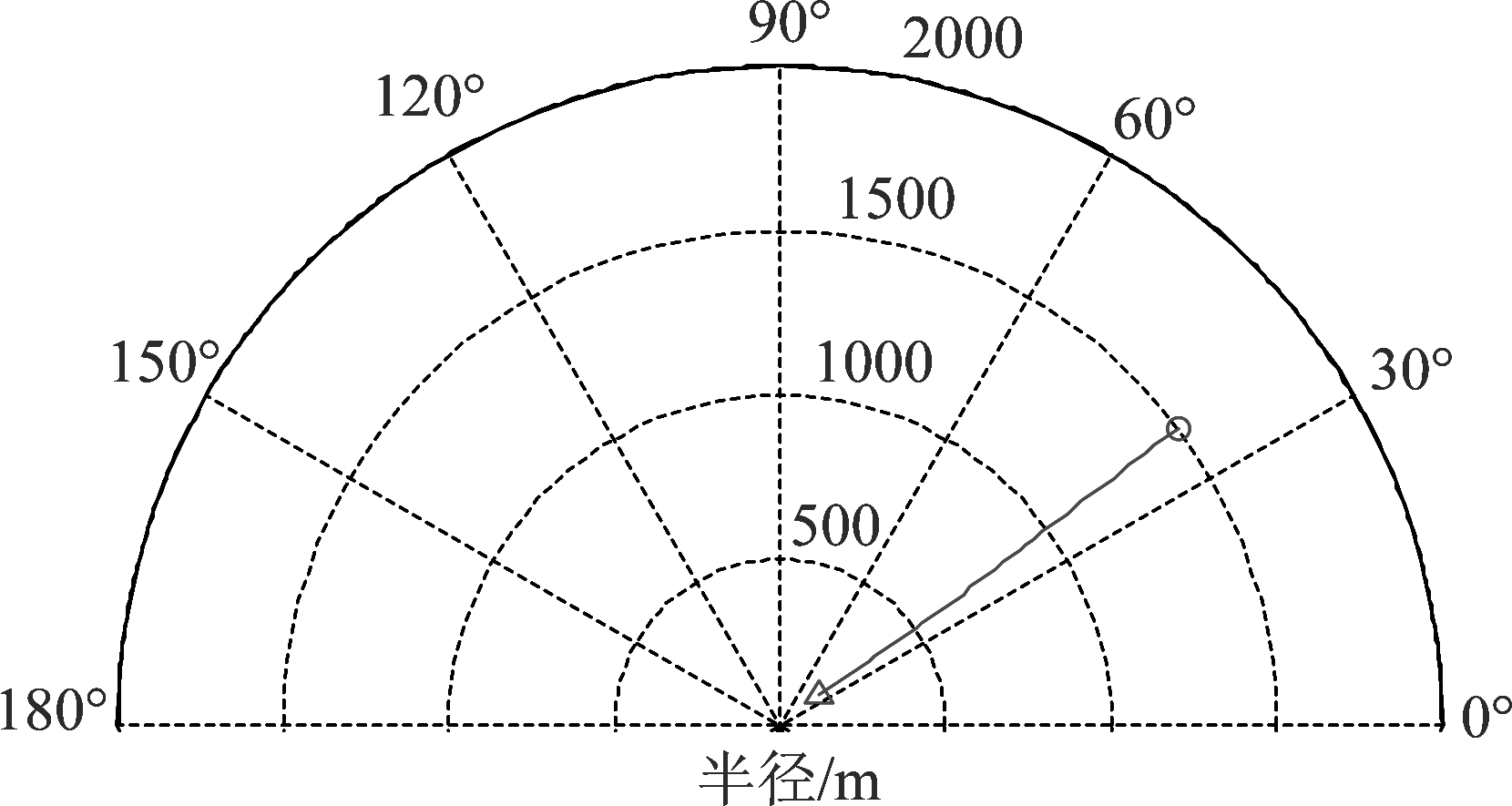
图1 极坐标系下目标真实运动轨迹
Fig.1 Ground truth trajectory in polar coordinates
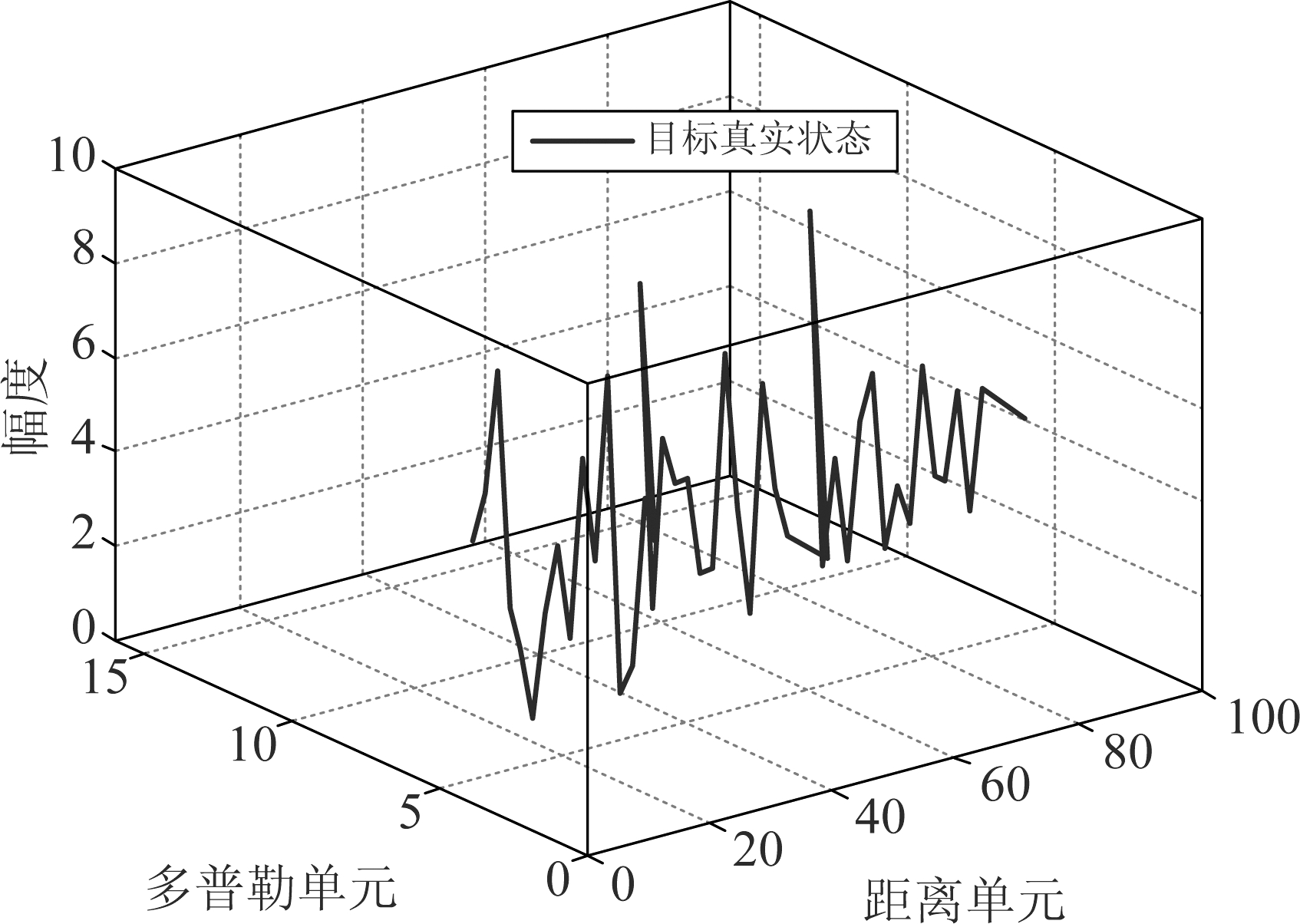
图2 距离-多普勒-幅度坐标系下目标真实航迹(SCR=10 dB)
Fig.2 Ground truth trajectory in range-Doppler-amplitude coordinates (SCR=10 dB)
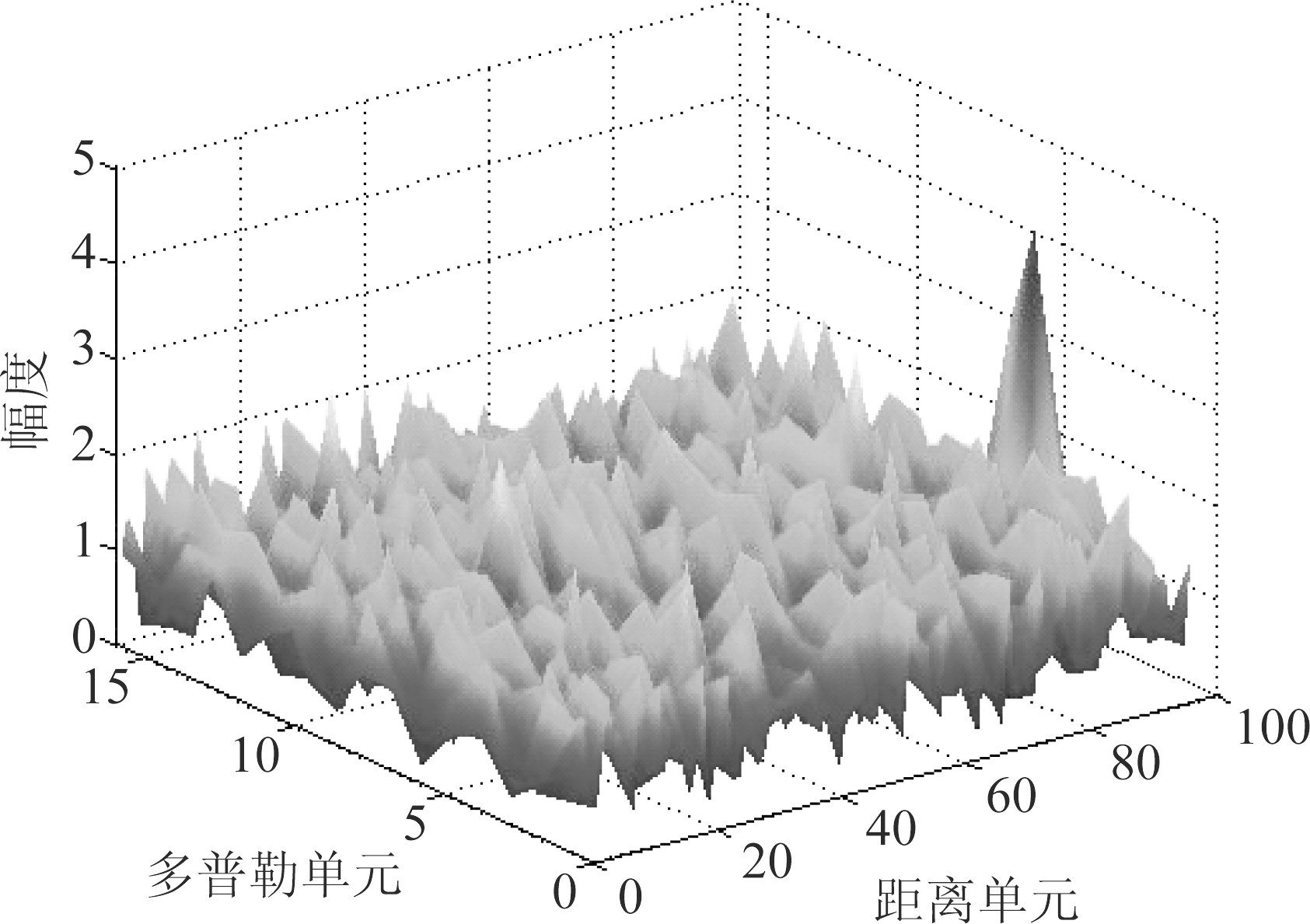
图3 第5帧中距离-多普勒-幅度量测(SNR=10 dB)
Fig.3 Range-Doppler-amplitude measurements in the 5th frame (SCR=10 dB)
一些PF-TBD方法通过粒子的存在概率考察算法的检测性能。但是,当杂波的幅度高于目标时,粒子有可能聚集到杂波附近,这时存在概率也很高,因此存在概率不能反映真实检测性能。本文中采用捕获概率(acquisition probability)这一新的指标。对于PFPF-TBD和PF-TBD,捕获概率为重采样后分布在受到目标影响的单元内的粒子数占全部粒子的比重;对于GF-TBD则是经过粒子流后分布在受到目标影响的单元内的粒子数占全部粒子的比重。k时刻的平均捕获概率可以表示为
其中![]() 为k时刻第i次试验中满足{(m,n,l)|m∈Cm(xk),n∈Cn(xk),l∈Cl(xk)}的后验粒子占全部采样粒子的比重。本文中计算捕获概率时设置邻域半径为3个单元。
为k时刻第i次试验中满足{(m,n,l)|m∈Cm(xk),n∈Cn(xk),l∈Cl(xk)}的后验粒子占全部采样粒子的比重。本文中计算捕获概率时设置邻域半径为3个单元。
5.2 仿真结果
图4~6为SCR=10 dB时PFPF-TBD, PF-TBD以及GF-TBD在某次试验中的跟踪结果。当目标在第5帧出现时,由于SCR比较高,PF-TBD和GF-TBD能及时探测到目标,PFPF-TBD对目标的探测有2帧延迟。从单次试验的跟踪效果看,PF-TBD出现比较明显的方位偏差,证明粒子的聚集效果不如采用粒子流的GF-TBD和PFPF-TBD。GF-TBD由于受到强杂波干扰,对目标的位置估计不准确。相比之下,PFPF-TBD的状态估计效果更加准确,从第7帧开始没有出现明显偏差。
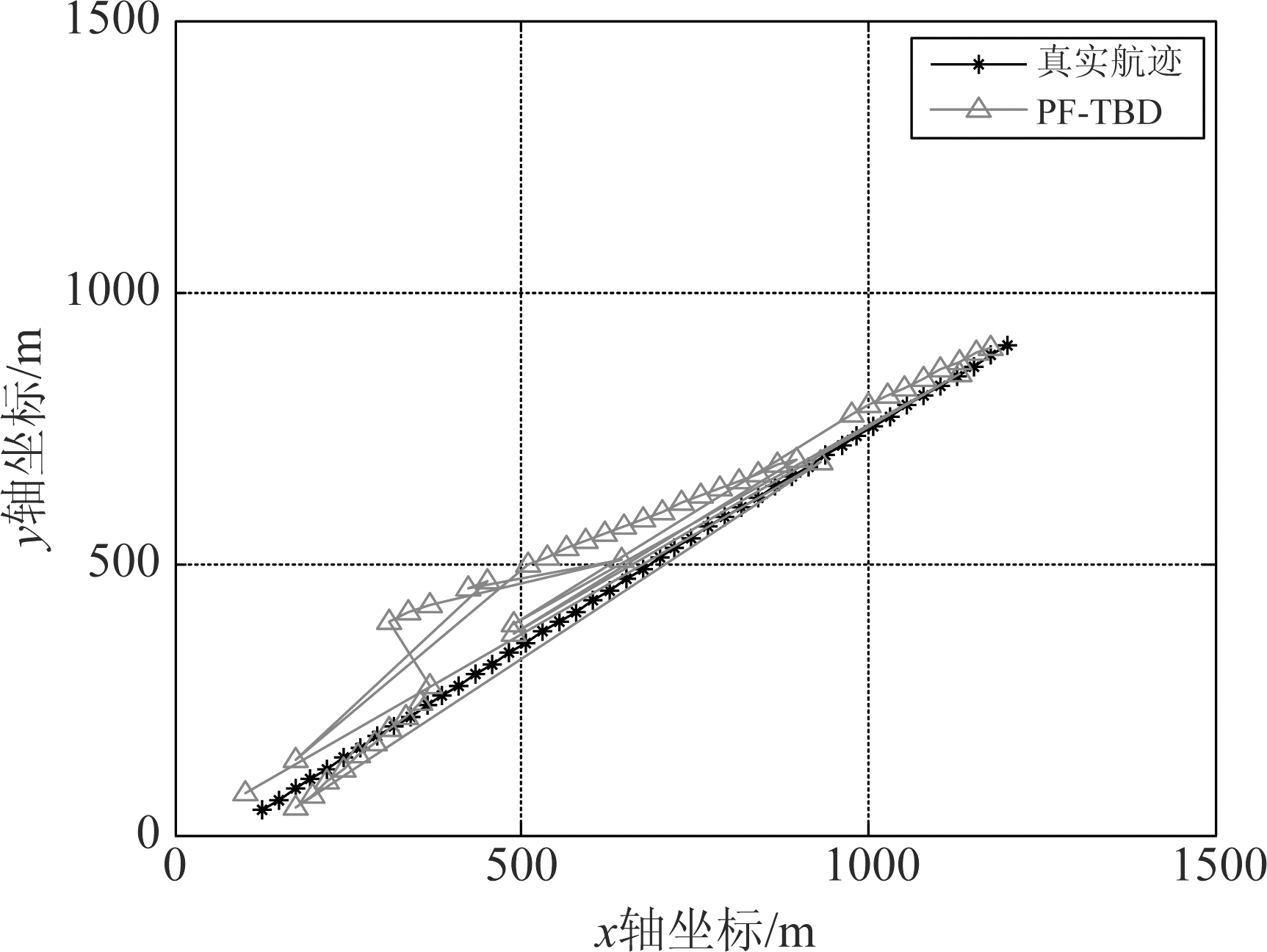
图4 PF-TBD跟踪结果(SCR=10 dB)
Fig.4 Tracking results of the PF-TBD (SCR=10 dB)
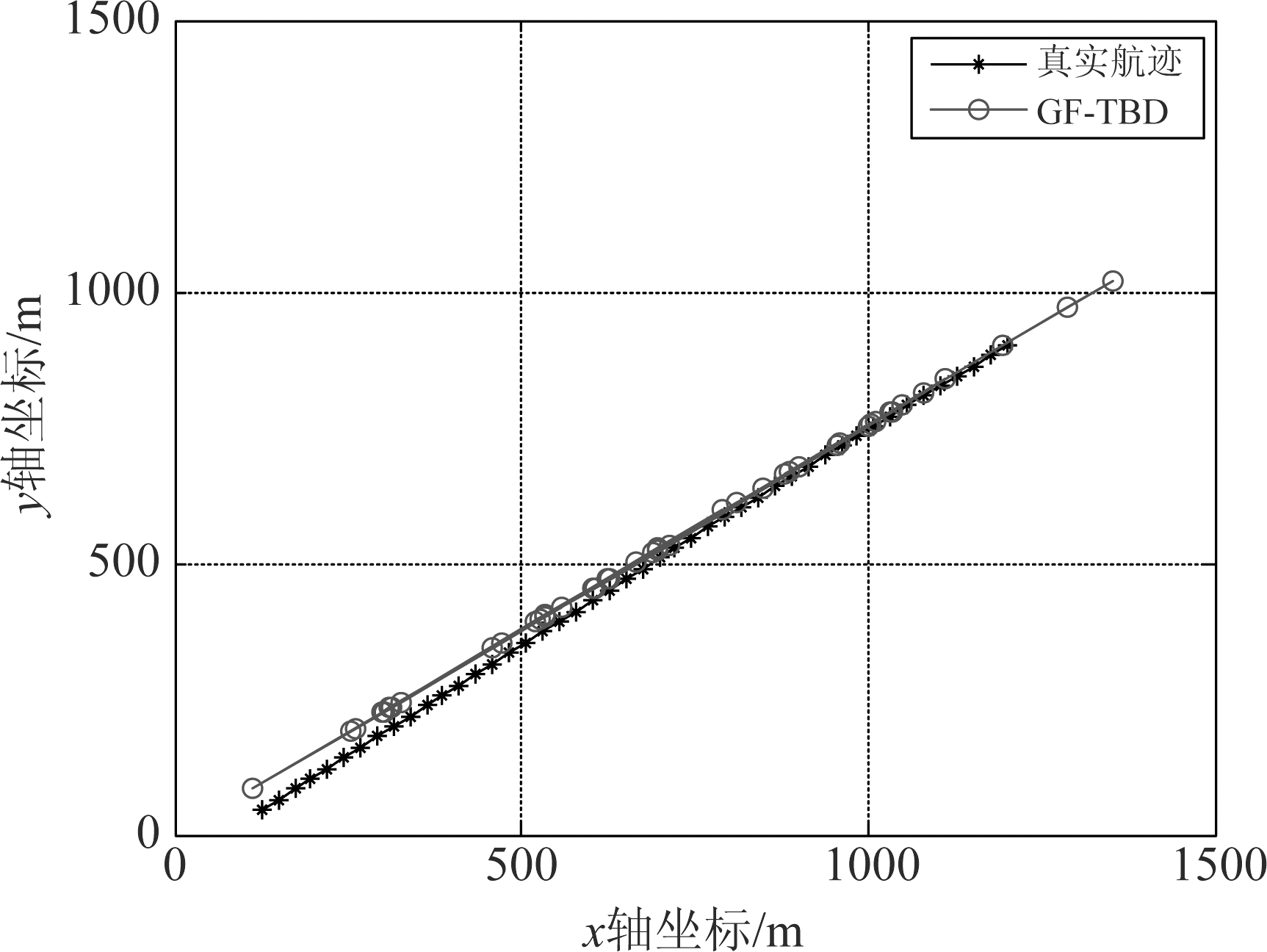
图5 GF-TBD跟踪结果(SCR=10 dB)
Fig.5 Tracking results of the GF-TBD (SCR=10 dB)
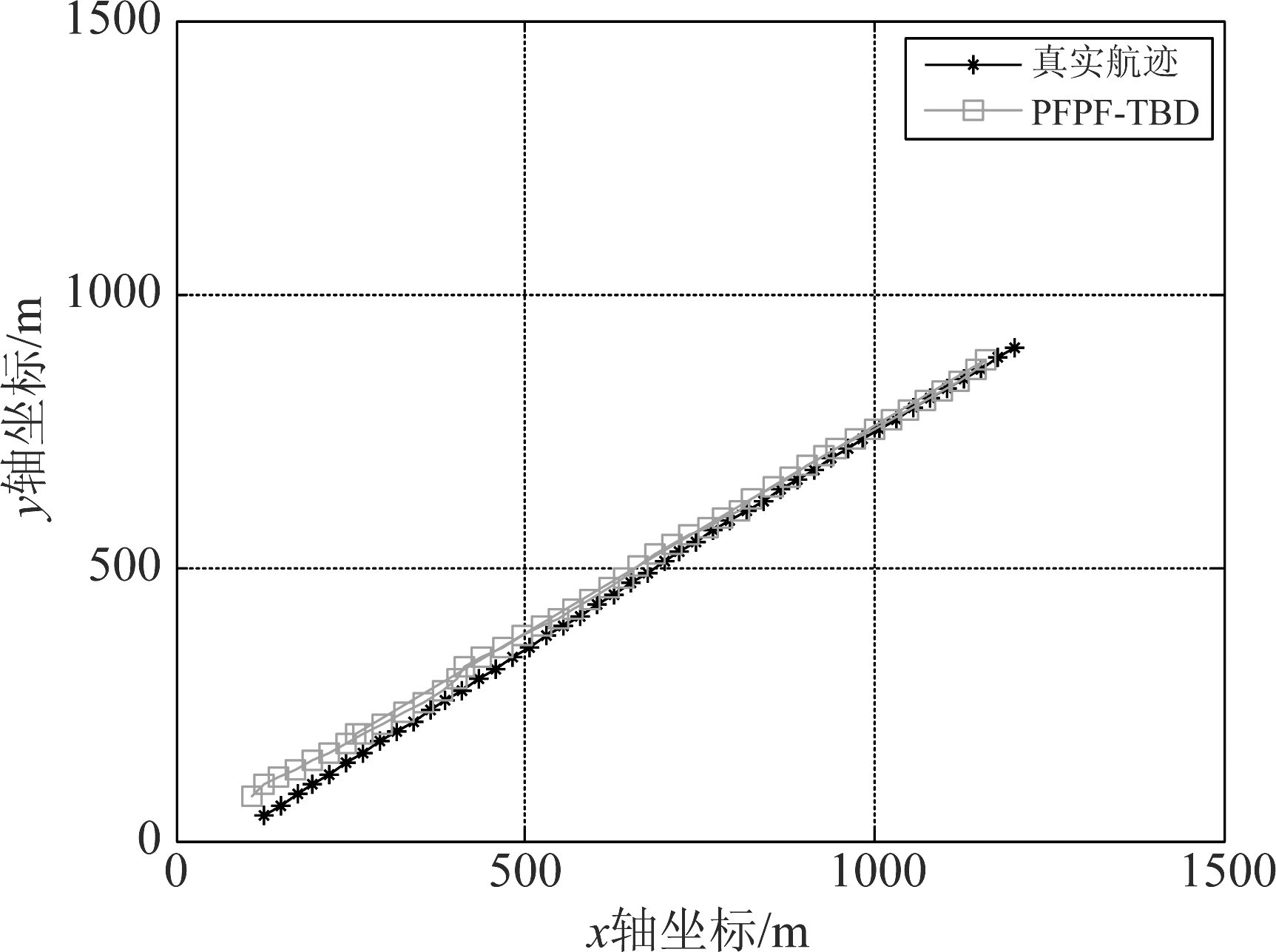
图6 PFPF-TBD跟踪结果(SCR=10 dB)
Fig.6 Tracking results of the PFPF-TBD (SCR=10 dB)
图7是PFPF-TBD, PF-TBD以及GF-TBD在SCR=10 dB时经50次试验得到的平均捕获概率。GF-TBD容易受到强杂波干扰,造成大量粒子向杂波迁移,因而捕获概率最低。PF-TBD的捕获概率明显高于GF-TBD,这是因为通过重采样PF-TBD可以迅速实现目标能量积累,从而提升信杂比,消除杂波干扰。在第5-13帧,PFPF-TBD的捕获概率增加迅速但是不如PF-TBD高,这是因为PFPF-TBD将粒子分散在多个可能的目标附近。但是从第14帧开始一直到目标消失PFPF-TBD的捕获概率明显高于PF-TBD,这是因为通过不断积累,真实目标周围的粒子的权重越来越高,粒子逐渐向真实目标聚集。由于滤波过程中累积的误差使粒子偏离了目标轨迹从而导致积累效果降低,PF-TBD在捕获概率达到最高点后(第16帧)开始下降。
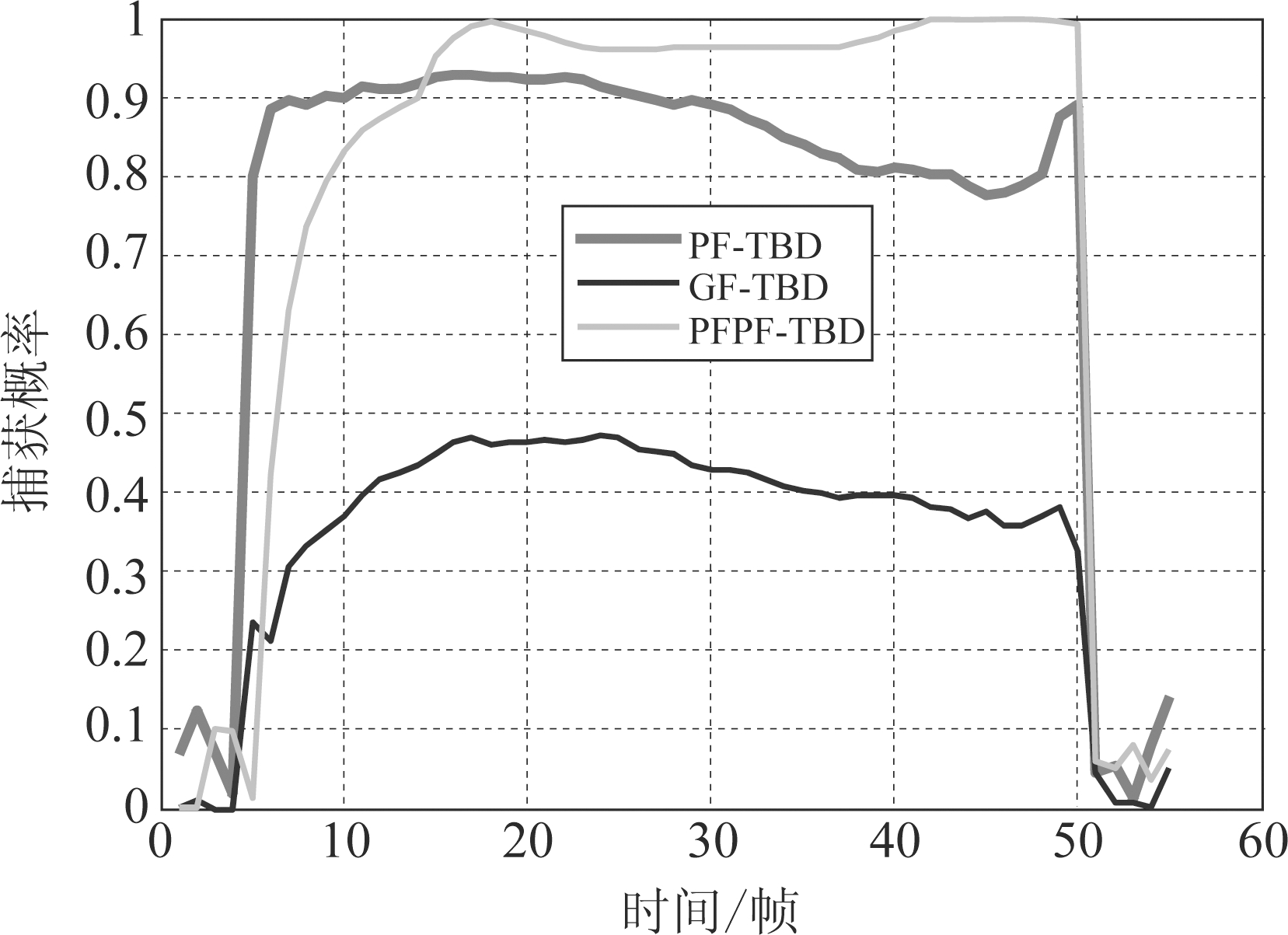
图7 50次仿真得到的平均捕获概率(SCR=10 dB)
Fig.7 Acquisition probability averaged over 50 runs (SCR=10 dB)
图8是SCR=10 dB时50次试验后得到的位置均方根误差。当目标出现后,PFPF-TBD, PF-TBD以及GF-TBD的跟踪误差迅速缩小。在第5- 8帧,PF-TBD以及GF-TBD的跟踪误差明显小于PFPF-TBD,这是因为PF-TBD通过重采样、GF-TBD通过粒子流将粒子迅速聚集到目标周围。而PFPF-TBD则是将粒子聚集到多个可能的目标处,并且由于目标运动时间较短积累效果不够好,真实目标周围的粒子所获权重不高。但是,随着时间增加积累的效果越来越好,真实目标周围的粒子所获权重逐渐增高,PFPF-TBD的状态估计效果也随之变好。从第9帧开始,PFPF-TBD的跟踪误差明显小于PF-TBD以及GF-TBD。
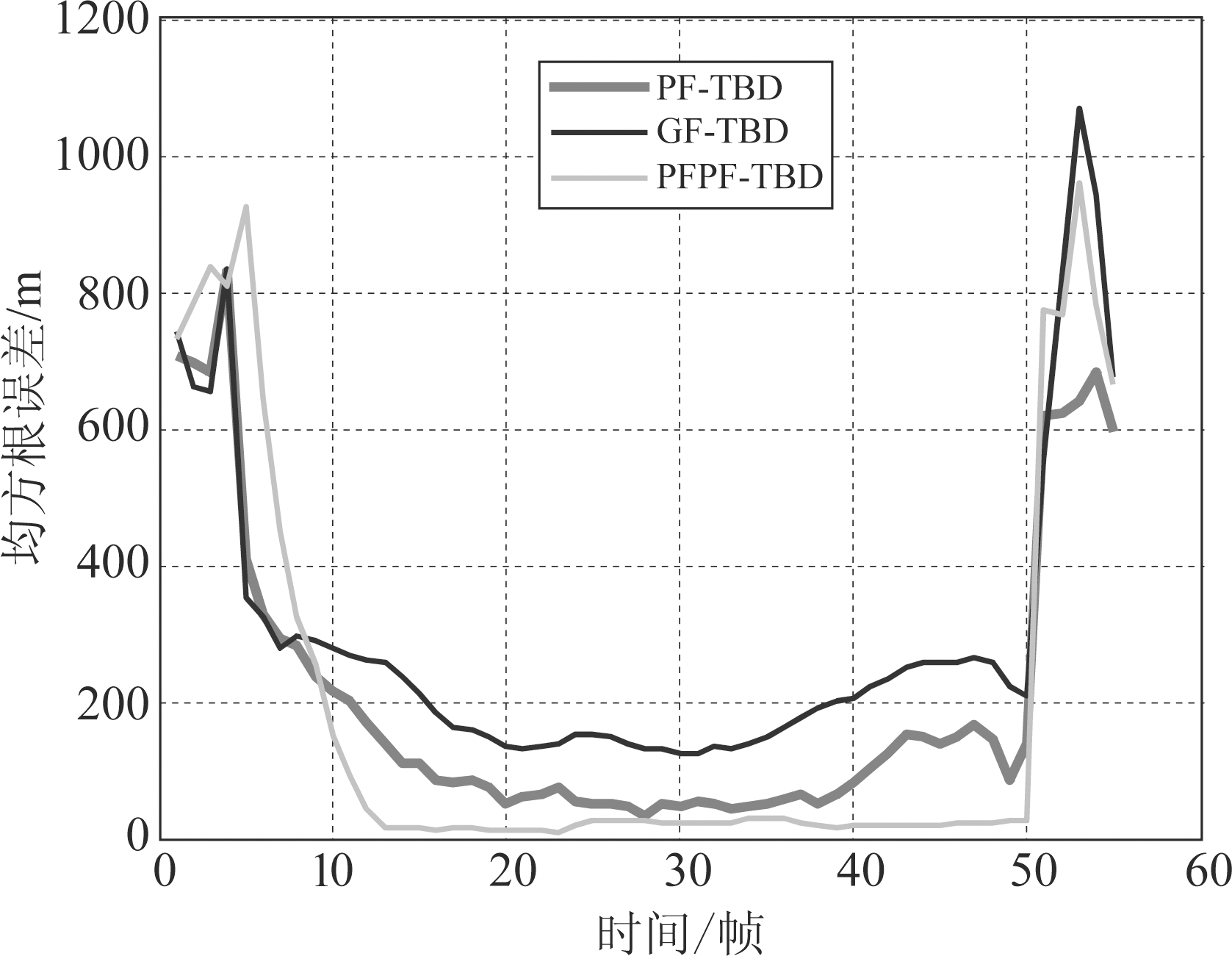
图8 50次仿真得到的RMSE(SCR=10 dB)
Fig.8 Root mean square error averaged over 50 runs (SCR=10 dB)
图9~10为PF-TBD、GF-TBD和PFPF-TBD在场景2和场景3得到的位置均方根误差。结合图7、9和10可以看到这3种算法的误差曲线基本呈现相同的特征。在刚开始跟踪的一段时间内PFPF-TBD的误差明显大于GF-TBD和PF-TBD,但随着跟踪时间的增加积累的效果逐渐显现,PFPF-TBD的误差会逐渐小于GF-TBD和PF-TBD。另外还可以看到,随着信杂比由10 dB逐渐下降到3 dB,三种算法的跟踪误差总体上都呈现变大的趋势。这是因为信杂比降低后,似然比也会降低,从而使粒子流和重采样的效果下降。并且信杂比越低,PFPF-TBD就需要越多的积累时间才能使其性能优于GF-TBD。
图11~12为PF-TBD、GF-TBD和PFPF-TBD在场景2和场景3的平均捕获概率。结合图7、11和12可以看到,随着信杂比下降三种算法的捕获概率都逐渐降低。总体上看PFPF-TBD的捕获概率更高更稳定。
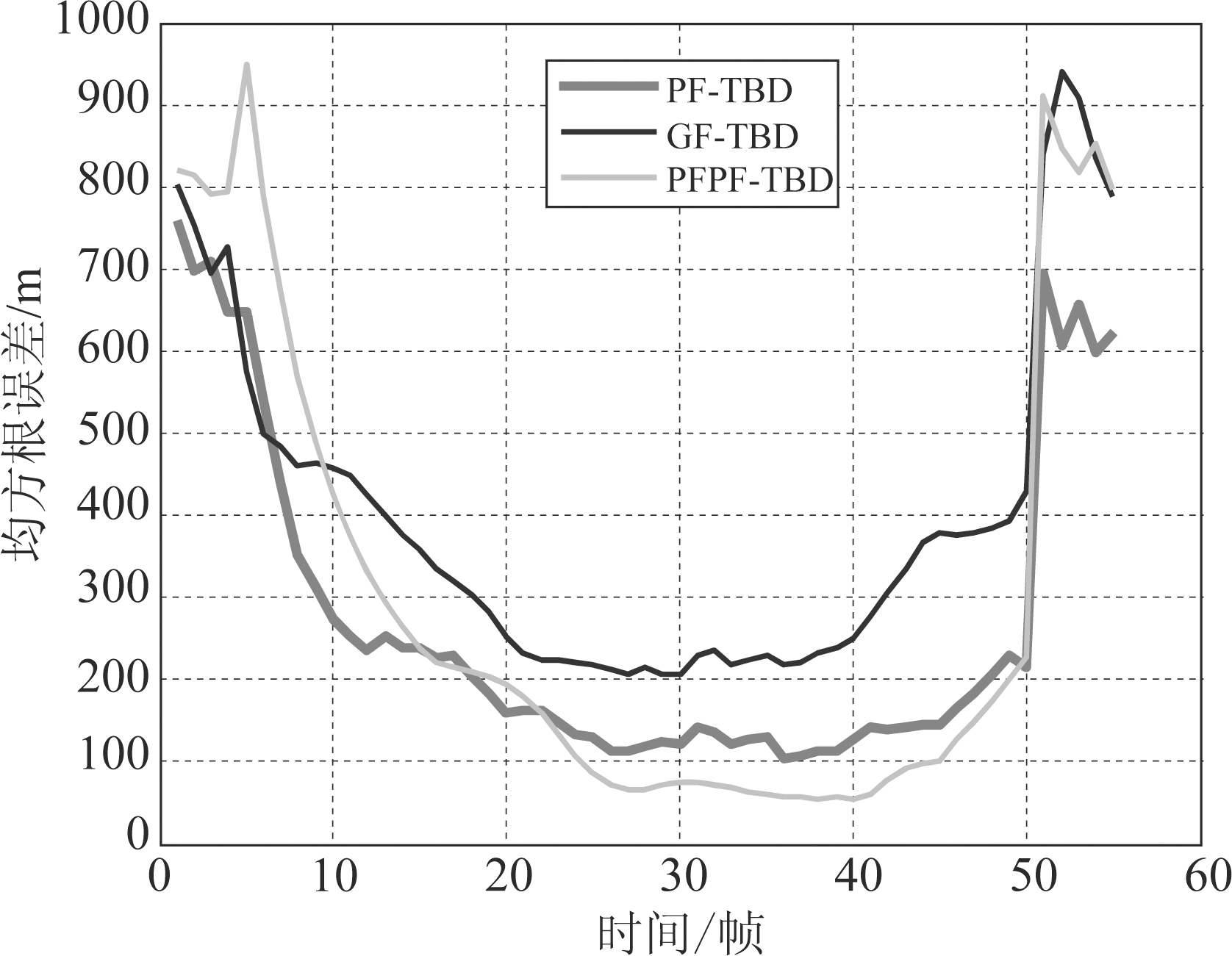
图9 50次仿真得到的RMSE(SCR=6 dB)
Fig.9 Root mean square error averaged over 50 runs (SCR=6 dB)
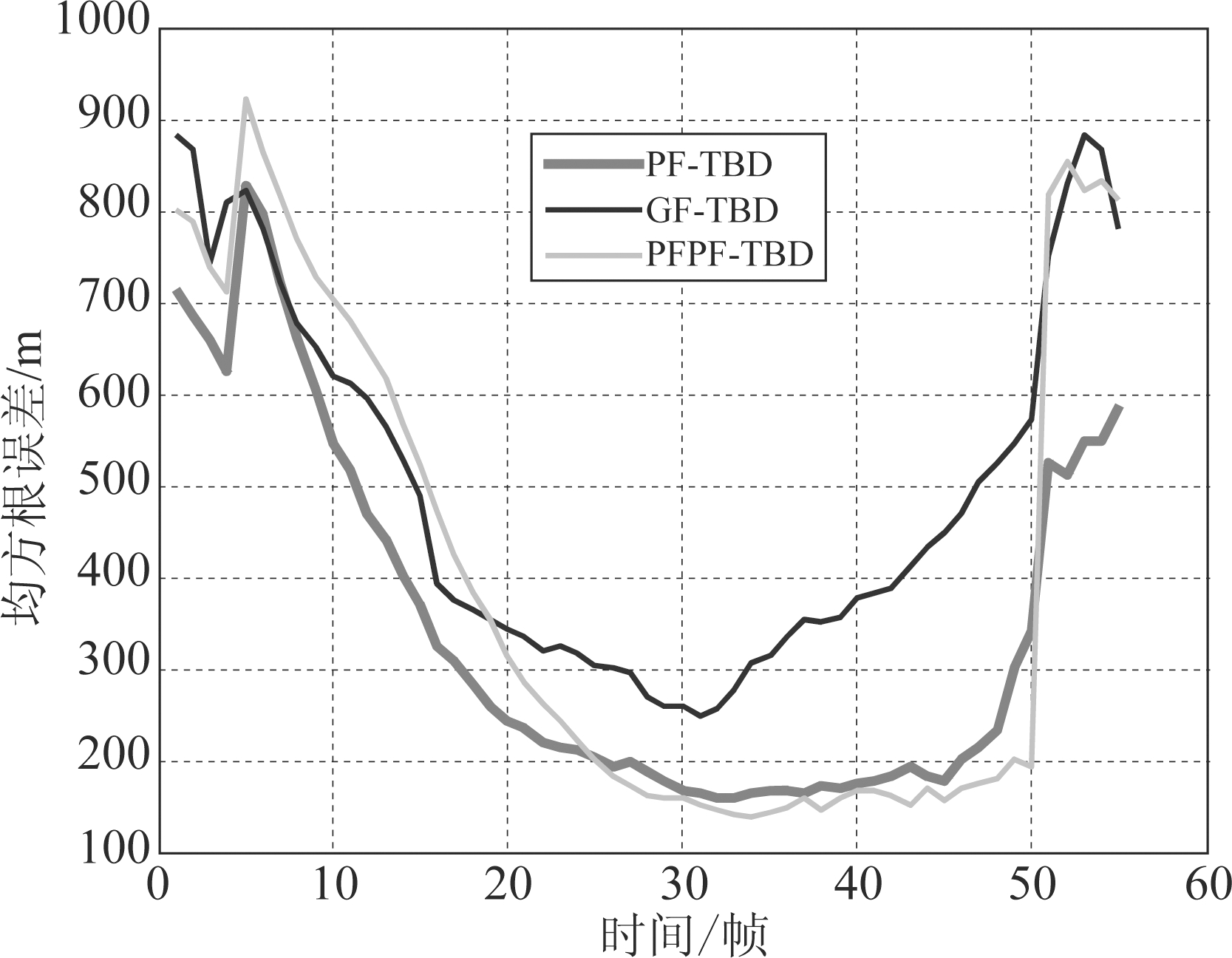
图10 50次仿真得到的RMSE(SCR=3 dB)
Fig.10 Root mean square error averaged over 50 runs (SCR=3 dB)
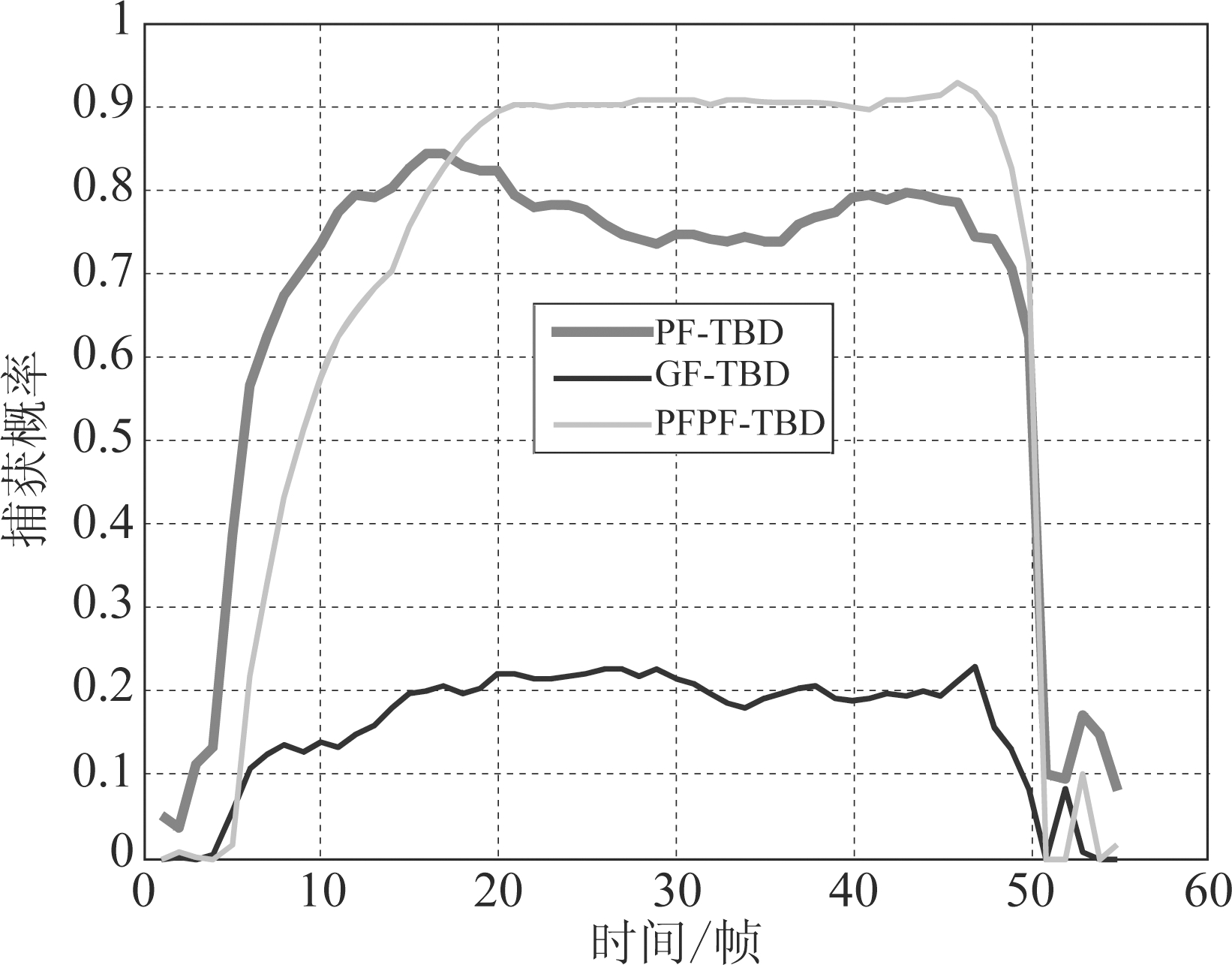
图11 50次仿真得到的平均捕获概率(SCR=6 dB)
Fig.11 Average acquisition probability averaged over 50 runs (SCR=6 dB)
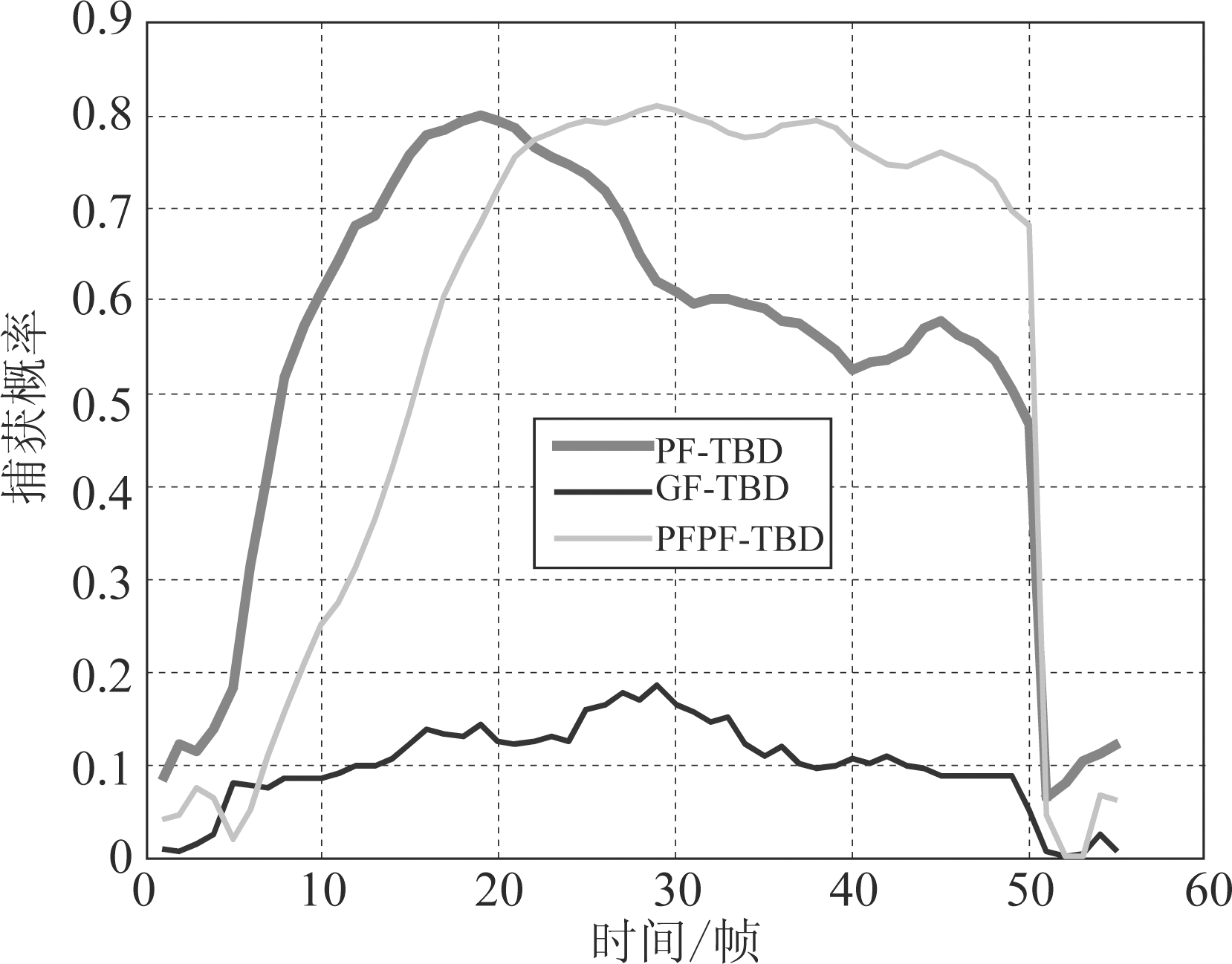
图12 50次仿真得到的平均捕获概率(SCR=3 dB)
Fig.12 Average acquisition probability averaged over 50 runs (SCR=3 dB)
6 结论
针对低空飞鸟和无人机,以及郊区行驶的地面车辆等低可观测目标的检测和跟踪问题,本文提出一种采用粒子流粒子滤波器的检测前跟踪方法。该方法的一个显著特点是结合了粒子滤波和粒子流的优点。与传统的粒子滤波检测前跟踪方法相比,其采用的粒子流可以更加精确的表示目标后验密度,从而提升量测积累效果。与采用测地粒子流的检测前跟踪方法相比,它实现了多帧观测数据的积累。通过瑞利杂波下3种低信杂比目标的检测和跟踪实验,我们证明经过若干扫描周期积累后该算法的性能明显优于粒子滤波检测前跟踪方法和测地粒子流检测前跟踪方法。
[1] Davey S J, Rutten M G, Gordon A N J. Track-before-detect techniques: integrated tracking, classification, and sensor management: theory and applications[M]. USA, John Wiley & Sons, 2013: 311-318.
[2] Berry P, Venkataraman K, Rosenberg L. Adaptive detection of low-observable targets in correlated sea clutter using Bayesian track-before-detect [C]∥in Proc. IEEE Radar Conf., Seattle, WA, USA, 2017: 398- 403.
[3] Northardt T, Nardone S C. Track-before-detect bearings-only localization performance in complex passive sonar scenarios: a case study[J]. IEEE Journ. Oceanic Engineer.(preprint).
[4] Davey S J, Rutten M G, Cheung B. A comparison of detection performance for several Track-before-detect algorithms[J]. Eura. Journ. Advan. Signal Process., 2007, 2008(1): 1-10.
[5] Jiang H, Yi W, Kirubarajan T, et al. Multi-frame radar detection of fluctuating targets using phase information[J]. IEEE Trans Aerosp. Electr. Syst, 2017, 53(2): 736-749.
[6] Sahin G, Demirekler M. A Multi-dimensional hough transform algorithm based on unscented transform as a track-before-detect method[C]∥in Proc. Int. Conf. Inf. Fusion. Salamanca, Spain, 2014: 1- 8.
[7] Ciuonzo D, Willett P K, Barshalom Y. Tracking the tracker from its passive sonar ML-PDA estimates [J]. IEEE Trans. Aerosp. Electron. Syst., 2014, 50(1): 573-590.
[8] Boers Y, Driessen J N. Multitarget particle filter track before detect application[J]. IEE Proc. Radar Sonar & Navig., 2004, 151(6): 351-357.
[9] Malcolm R, David S. Particle filter for track-before-detect of a target with unknown amplitude viewed against a structured scene[J]. IET Radar, Sonar & Navig., 2018, 12(6): 603- 609.
[10] 柳超, 李秀友, 黄勇. 优化的多模型粒子滤波机动微弱目标检测前跟踪方法[J]. 信号处理, 2015, 31(9): 1131-1137.
Liu Chao, Li Xiuyou, Huang Yong. Optimized multiple model particle filter track-before-detect algorithm for maneuvering weak target[J]. Journal of Signal Processing, 2015, 31(9): 1131-1137.(in Chinese)
[11] 王娜, 谭顺成, 王国宏. 目标数未知时基于粒子滤波的多目标TBD方法[J]. 信号处理, 2017, 33(9): 1248-1257.
Wang Na, Tan Shuncheng, Wang Guohong. Multitarget particle filter track-before-detect algorithm with unknown target number[J]. Journal of Signal Processing, 2017, 33(9): 1248-1257.(in Chinese)
[12] Daum F, Huang J. Particle degeneracy: root cause and solution [C]∥Proc. SPIE Conf. Signal Process., Sensor Fusion and Target Recog., Orlando, FL, 2011, 80500W.
[13] Li Y, Coates M. Particle filtering with invertible particle flow [J]. IEEE Trans. Signal Process., 2017, 65(15): 4102- 4116.
[14] Doucet A, De Freitas N, Murphy K, et al. Rao-Blackwellised particle filtering for dynamic Bayesian networks[C]∥Proc. Conf. Uncertainty Artif. Intell., San Francisco, CA, USA, 2000: 176-183.
[15] Doucet A, Freitas N D, Wan E. The unscented particle filter[C]∥in Proc. Neural Inf. Process. Syst., Denver, CO, USA, Dec. 2000: 584-590.
[16] Pitt M, Shephard N. Filtering via simulation: auxiliary particle filters[J]. Journ. Amer. Statist. Assoc., 1999, 94(446): 590-599.
[17] Septier F, Peters G W. Langevin and Hamiltonian based sequential MCMC for efficient Bayesian filtering in high-dimensional spaces[J]. IEEE Journ. Selec. Topics Signal Process., 2016, 10(2): 312-327.
[18] Hanebeck U D, Briechle K, Rauh A. Progressive Bayes: A new framework for nonlinear state estimation [C]∥in Proc. SPIE, 2003(5099): 256-267.
[19] Daum F, Huang J. Nonlinear filters with log-homotopy[C]∥in Proc. SPIE, vol. 6699, Sep. 2007, Art. no. 669918.
[20] Daum F, Huang J, Noushin A. Exact particle flow for nonlinear filters [J]∥in Proc. SPIE, vol. 7697, Apr. 2010: 769704.
[21] Ding T, Coates M. Implementation of the Daum-Huang exact flow particle filter[C]∥in Proc. IEEE Statist. Signal Process. Workshop, Ann Arbor, MI, USA, Aug. 2012: 257-260.
[22] Reich S. A dynamical systems framework for intermittent data assimilation[J]. Bit Numerical Mathematics, 2011, 51(1): 235-249.
[23] Reich S. A Gaussian-mixture ensemble transform filter[J]. Quarter. Journ. Royal Meteoro. Society, 2012, 138(662): 222-233.
[24] Kreucher C, Bell K. A Geodesic flow particle filter for non-thresholded measurements[C]∥in Proc. IEEE Radar Conf., Seattle, WA, USA, 2017: 891- 896.
[25] Bunch P, Godsill S. Approximations of the optimal importance density using Gaussian particle flow importance sampling[J]. Journ. Ame. Statist. Assoc., 2014, 111(514): 748-762.
[26] Daum F, Huang J. Particle flow for nonlinear filters, Bayesian decisions and transport[C]∥in Proc. IEEE Int. Conf. Inf. Fusion, Istanbul, Turkey, 2013: 1072-1079.
[27] Punithakumar K, Kirubarajan T, Sinha, A. A sequential Monte Carlo probability hypothesis density algorithm for multitarget track-before-detect[J]. Proc. SPIE-Int. Society Optical Engineer., 2005: 59131S-59131S- 8.
