1 引言
由于无线传输的广播特性,信息传输存在被恶意用户非法窃听的安全问题。在传统通信系统中,通信安全主要通过上层不同的加密算法实现,其安全性能的提高仅仅依赖于加密算法的复杂度[1]。随着加密算法的复杂度越来越高,通信系统的时间消耗主要在加解密的计算上。为了解决加密算法复杂度问题,无线物理层安全被提出来并被证明是一种有效加强无线通信安全传输的方法。主要思想是利用合法信道与窃听信道不同的信道特性实现信息的安全传输[2]。1975年,Wyner首次提出了窃听信道模型[3],并证明了当窃听信道是合法信道的一个弱化信道,即合法信道的信道质量优于窃听信道,完美的保密性是可以实现的。
为了进一步提高物理层的安全,提出的协作中继技术被证明可以有效提高系统安全性能以及增加系统的可靠性与吞吐量[4]。基于协作中继的思想,利用不同的中继选择策略可以有效阻止窃听者窃听中继转发信号[5-7]。其中,文献[5]分析了基于放大转发(Amplify and Forward, AF)和译码转发(Decode and Forward, DF)的最优中继选择,提出了一种多中继组合框架。文献[6]研究了具有保密约束的协作网络的中继选择,比较了三种基于不同信道状态信息选择中继来转发信息。文献[7]采用了波束成型技术实现信息的安全传输。
在中继协作过程中,为了消除多用户间的干扰,抵抗多径衰落的影响,多天线技术在无线通信系统中得到大量研究与应用[8-10]。在文献[8]中,研究天线相关性对具有Nakagami-m衰落的多输入多输出(Multiple-input Multiple-out, MIMO)窃听信道下保密性能的影响,并实现了多样性顺序和阵列增益。在文献[9]中,作者研究了在MIMO窃听信道下发送保密消息的问题,利用线性运算和连续干扰消除来获得有效的并行单天线窃听信道,并推导了窃听信道的容量表达式。在文献[10]中,作者研究了发射天线选择对大规模MIMO(Massive MIMO)系统保密性能的影响,考虑了一种窃听设置,并证明了有源天线数量将影响系统保密性能。在MIMO系统中通常在接收端或发送端使用天线选择策略提高系统性能[11-12]。文献[11]提出了一种新型的接收天线选择(Transmission Receive Antenna Selection, TRAS)策略,选择一对发送和接收的天线用户终端,用于全双工放大前向多输入多输出的双向中继网络,并讨论了四种不同的天线选择场景,仿真表明,通过在终端使用提供的TRAS策略,可以显着提高性能。文献[12]研究了在Nakagami-m衰落信道下双跳MIMO中继系统使用发射天线选择(Transmission Antenna Selection, TAS)和最大比合并(Maximum Receiver Combine, MRC)方案的安全协作传输,为了评估过时信道状态信息(Outdated Channel State Information, outdated CSI)对系统的影响,推导了准确遍历保密速率和准确安全中断概率闭合表达式。文献[13]基于AF模式协同系统,研究过时CSI下的反馈误差模型,但未对DF协议的过时CSI进行研究。文献[14]研究了安全的无线广播网络模型中时分方案与功率分配策略提高系统的安全性和可靠性性能,同时文献[15]利用机会中继选择策略实现信息安全传输,并提出了新的安全性与可靠性的折中性能(Security and Reliability Tradeoff, SRT)指标来描述系统的性能。
在文献[16]中,主要研究了过时信道状态信息下系统模型的性能,而在文献[17]提到了非可信中继对系统安全性能的影响。不同于文献[16]和[18],本文进一步研究了过时CSI以及多个窃听用户对系统的影响。对于接收用户,通过一般阶次选择策略来选择,实现信息的安全传输。采用一般阶次选择(General-order Selection)而不采用最佳选择的原因有两点:第一、由于不可靠的导频信道,发送信道的排序可能不准确;第二、最佳信道不可靠或被其他服务要求占用。为了使分析更加一般化,本文还考虑了接收用户在过时CSI的实际场景。利用在两种不同场景下的信道状态信息,本文提出了两种有效干扰策略提高系统SRT,并在此基础上分别推导了两种场景下两种干扰策略的中断概率与窃听概率来评估安全性与可靠性,以及二者的SRT关系。最后通过蒙特卡洛仿真来验证结果。
2 系统模型
图1给出了多用户选择机制实现物理层安全传输的系统模型。系统模型中包含一个发送用户(S)、一个可靠中继(R)、多个接收用户(Dn,n=1,2,…,N)和多个窃听用户(Ej, j=1,2,…,M)。所有用户和中继都配置单天线,且工作在半双工(Half-duplex, HD)模式。假设发送用户到目的用户及窃听用户的距离较远,且存在阴影衰落,因此不存在直接链路。假设中继已知接收用户的信道状态信息[1,19]。
图1 系统模型
Fig.1 System model
所有信道均服从准静态平坦Nakagami-m衰落信道。链路R→Dn、DJ→Dk、R→Ej和DJ→Ej的信道系数依次为hDk、gEj、hEj和gDk,分别具有Nakagami参数为m1、m2、m3和m4,其中Dn表示任意合法接收用户,Dk表示被选择来接收信号的接收用户,DJ表示干扰节点。平均信道功率增益依次为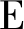
[|hDk|2]=Ω1、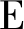[|gEj|2]=Ω2、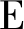[|hEj|2]=Ω3和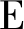[|gDk|2]=Ω4,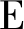[·]表示期望。因此合法信道和窃听信道的瞬时接收信噪比表示为
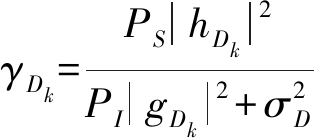
(1)
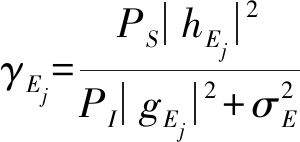
(2)
其中,PS和PI分别表示中继的发送功率以及干扰节点的发送功率,
和
分别表示目的用户与窃听用户的噪声,服从零均值高斯白噪声。
在实际传输过程中,由于从目的用户Dk向中继R反馈信道状态信息经历了延迟τ,导致反馈的信道状态信息因过时而不准确。为了考虑过时信道状态信息对目的用户选择的影响,建立反馈误差模型
(3)
其中,
表示R→Dn链路的过时信道增益,ω具有与随机变量hDk(t-τ)相同方差的循环对称复高斯随机变量。基于Jake自相关模型,ρ是和hDk(t-τ)的归一化相关系数,且ρ=[J0(2πfτ)]2, f表示最大多普勒衰落带宽,J0(·)表示第一类零阶贝塞尔函数[19]。
3 选择方案与性能分析
3.1 目的用户选择
本文考虑在多个合法接收用户中选择一个目的用户来接收中继转发的信息。假设第k个用户被选择,根据文献[20],目的用户选择准则表示为
(4)
其中,ktharg max(·)表示第k个最佳接收用户。
对于Nakagami-m衰落信道,信道系数的概率密度函数与累积分布函数分别表示为
(5)
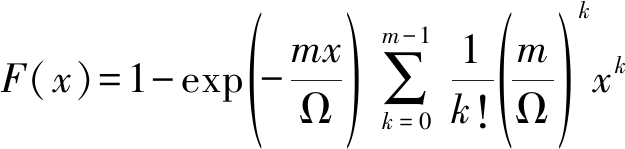
(6)
其中,衰落信道参数m∈{m1,m2,m3,m4},信道平均功率增益Ω∈{Ω1,Ω2,Ω3,Ω4}。
考虑过时信道的延迟以及和hDk之间的关系,的概率密度函数和累积分布函数表示如下:
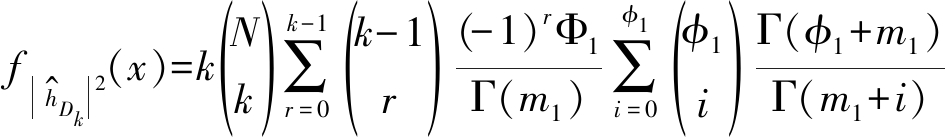
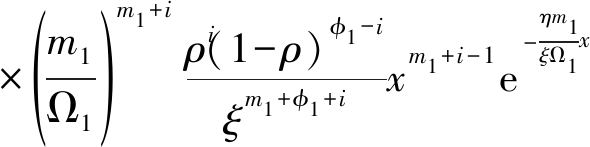
(7)
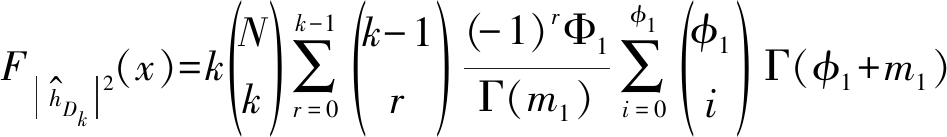
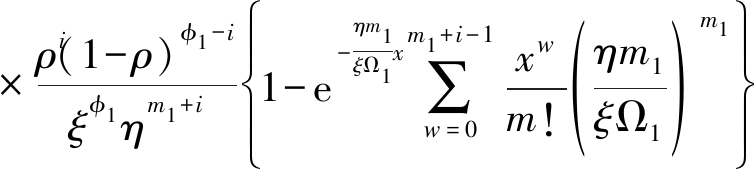
(8)
其中,
以及
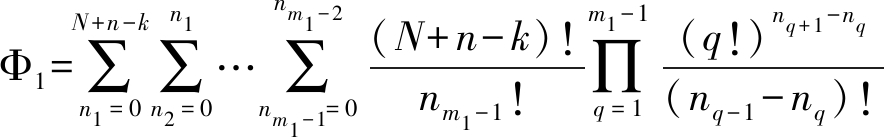
(9)
且n0=N+n-k,nm1=0。
以下是式(7)和式(8)的推导过程:
结合概率论及式(3)的反馈模型表达式,
的概率密度函数以及其条件分布函数表示为
(10)
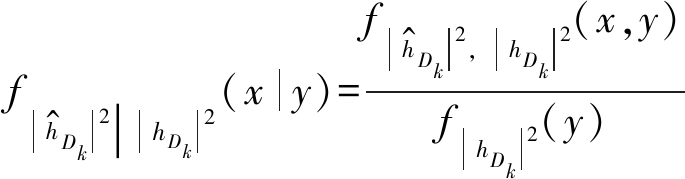
(11)
其中,
为
和|hDk|2的联合概率密度函数,由下式给出
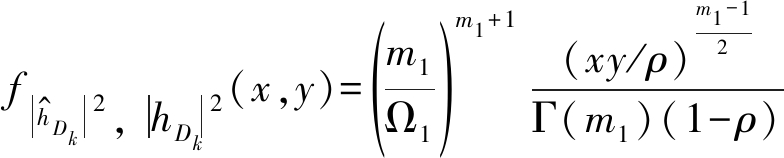
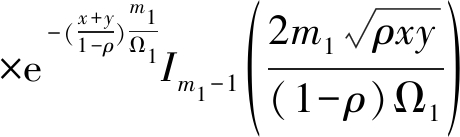
(12)
其中,In(·)表示n阶第一类修正贝塞尔函数,详见文献[19]中式(8.406.1)。由文献[20]中的式(2.1.6),得|hDk|2的联合概率密度函数表达式
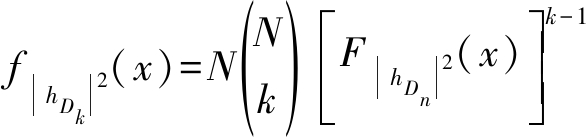
(13)
将m=m1、Ω=Ω1代入式(5)和式(6),求得|hDn|2的概率密度函数以及分布函数,再联合式(11)、式(12)和式(13),得到的概率密度表达式
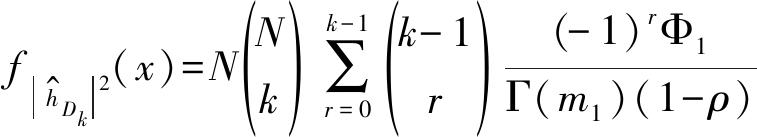
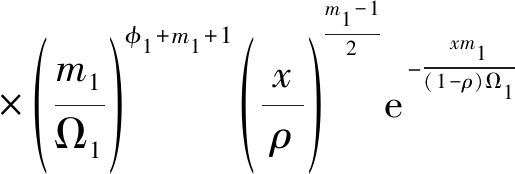
(14)
利用文献[19]中的式(6.643.2)以及一些简单的数学计算,得
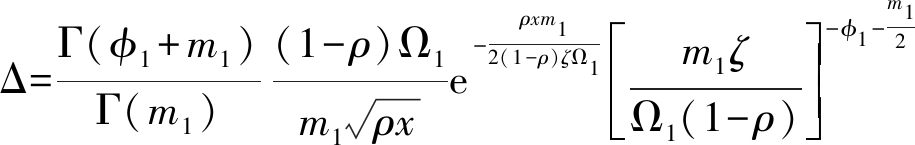
(15)
其中,Ma,b(·)是Whittaker-M函数,详见文献[19]中的式(9.220.2),多项式展开式为
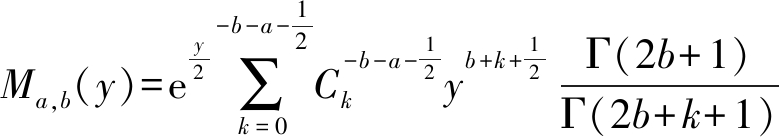
(16)
将式(15)和(16)代入式(14),整理得到式(7)表达式,再求积分即可得到式(8)。
3.2 干扰节点选择
为提高系统安全性能,根据窃听信道状态信息的两种不同情况,分别提出不同的干扰策略。
3.2.1 未知窃听信道状态信息
在信息接收阶段,从合法接收用户中选择了一个目的用户来接收中继转发的信息;在干扰选择阶段,系统无法获得窃听用户的信道状态信息,即未知窃听信道信息。但能够找到一个对目的用户干扰最小的一个接收用户作为干扰节点。因此,干扰节点J1的数学表达式为
(17)
其中,|gDn|2表示干扰节点到其他合法接收用户的信道增益,D表示所有合法接收用户的集合。
将m=m4和Ω=Ω4代入(5)和式(6),得|gEj|2的概率密度函数和累积分布函数。
利用式(17)以及阶量统计得
(18)
利用二项式展开定理以及平方和的推广公式,计算得到
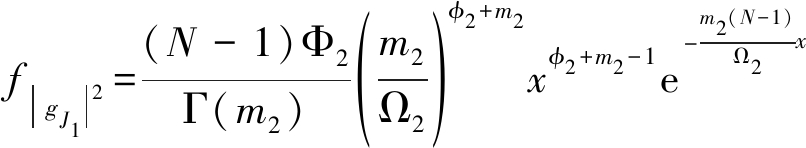
(19)
其中
以及
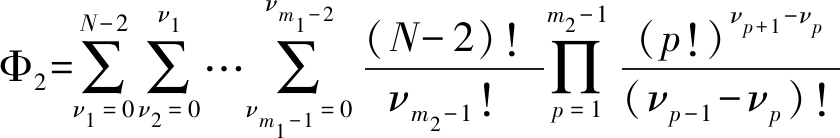
(20)
3.2.2 已知窃听信道状态信息
如果系统能够获取完全窃听信道状态信息,即已知窃听信道状态信息,可利用DJ→E的信道状态信息确定干扰节点。在确定目的用户后,选择对窃听用户影响较大的合法接收用户作为干扰用户,从而建立干扰用户J2的选择准则为
(21)
其中,|gJ2|2表示干扰节点到窃听用户的信道增益。将m=m4和Ω=Ω4代入(5)和式(6),得到|gJ2|2的概率密度函数。利用阶量统计理论及式(21)得到
(22)
利用二项式展开定理以及平方和的推广公式,计算得到
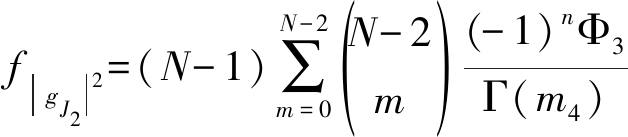
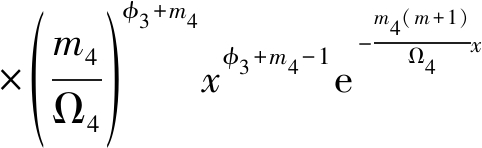
(23)
其中
以及
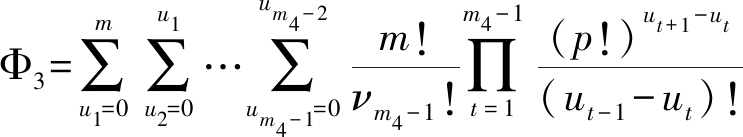
(24)
3.2.3 窃听用户选择
考虑非共谋窃听方式,即每个窃听用户独立窃听消息。从多个窃听用户中选择最大信噪比作为信息窃听的窃听用户,则窃听用户的信噪比
(25)
其中,γEj和γEm分别表示选择的窃听用户和任意一个窃听用户的瞬时接收信噪比。
3.3 系统性能分析
根据香农定理,合法信道与窃听信道的信道容量分别表示为
(26)
(27)
基于文献[16]的思想,当窃听信道容量高于数据传输速率RS,窃听节点能够解码源节点的信号,此时发生一个窃听事件,记为窃听概率Pint。当合法信道容量低于数据传输速率Rd,则发生一个中断事件,记为中断概率Pout。两个性能指标表示如下
Pout=P(CD<RS)
(28)
Pint=P(CE>RS)
(29)
其中,RS为预设的用户信息传输速率。
3.3.1 未知窃听信道状态信息
已知R→Dk与DJ→Dk信道相互独立,由联合分布函数,得累积分布函数为
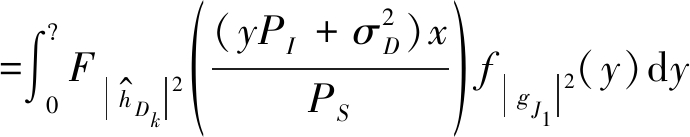
(30)
其中,
和|gJ1|2分别表示中继、干扰节点到目的用户的信道增益。
将式(6)及式(19)代入积分式,利用多项式定理、文献[19]中的式(3.351.3),得
的准确闭合表达式
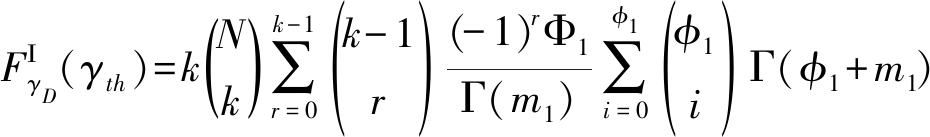
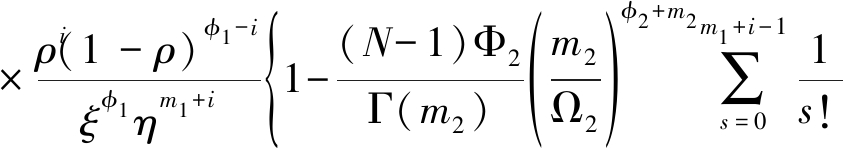
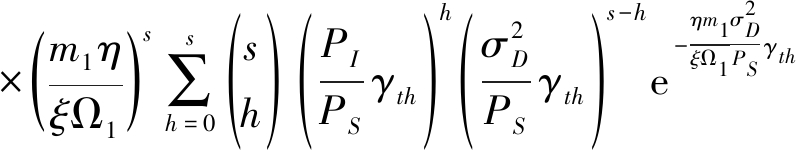
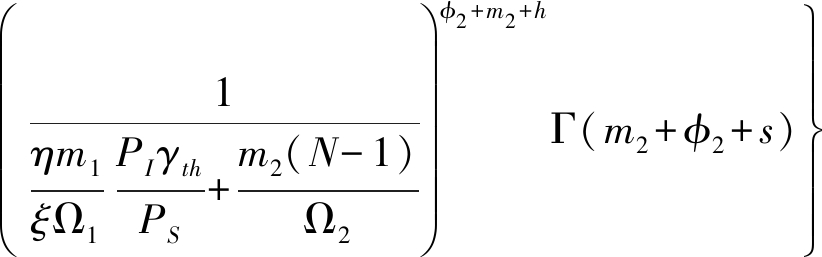
(31)
同理,可推导出
的准确闭合表达式
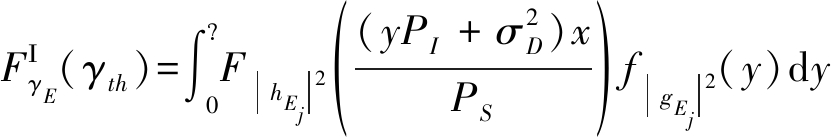
(32)
其中,|hEj|2和|gEj|2分别表示中继、干扰节点与窃听用户的信道增益。将m=m3和Ω=Ω3代入式(5)和式(6),得到|hEj|2的概率密度函数以及分布函数,代入(32)从而得到
的准确闭合表达式
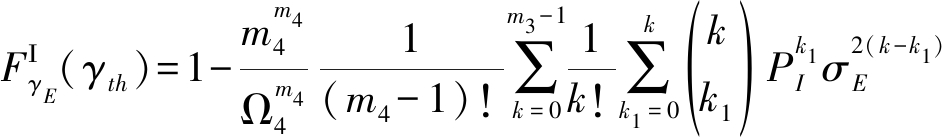
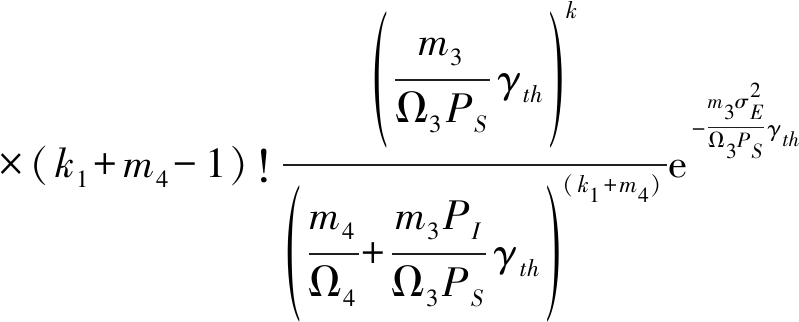
(33)
3.3.2 已知窃听信道状态信息
在已知窃听信道的信道状态信息的情况下,利用式(1)、式(2)及数学运算,简化得
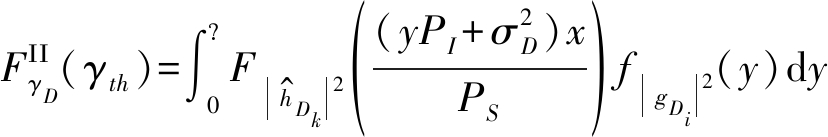
(34)
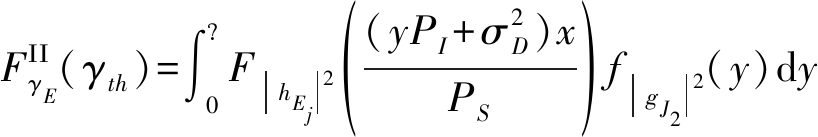
(35)
经过积分运算,整理得
和
准确闭合表达式
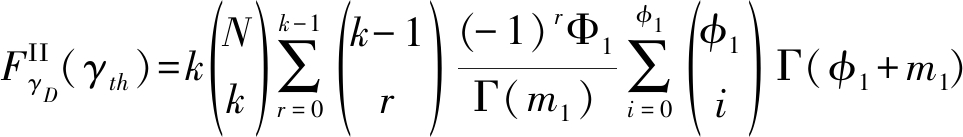
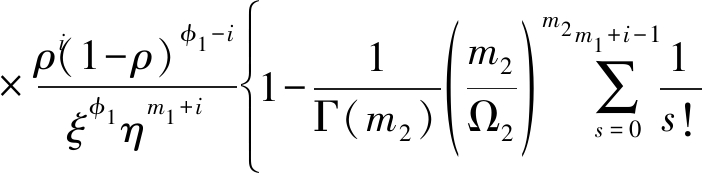
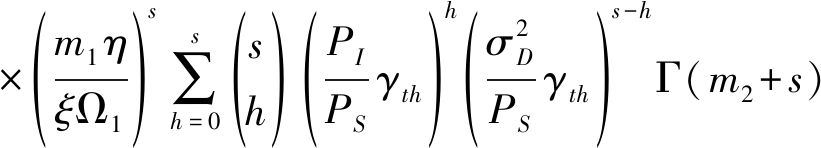
(36)
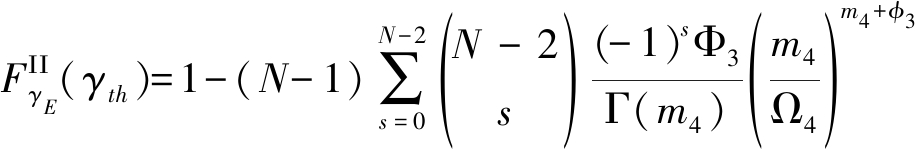
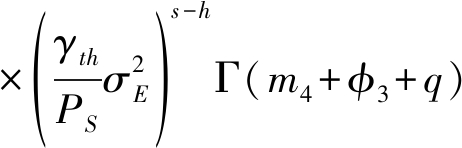
(37)
3.3.3 折中性能
根据上述推导的两种场景下FγD和FγE的准确闭合表达式,可得中断概率与窃听概率的表达式
(38)
(39)
根据文献[15]对折中性能的分析,知道窃听概率从窃听节点的角度出发,考虑这个节点能否窃听到信息的一个事件概率,度量的是系统安全性,而中断概率从目的节点角度出发,考虑这个节点传输过程中断事件发生得概率,体现的是系统的可靠性。中断概率越小,系统的可靠性就越高;窃听概率越小,系统的安全性就越强。因此,系统的总体安全传输性能可定义为SRT性能测度参数
Φ=Pint×Pout
(40)
很显然,该式实质上给出了系统可靠性与安全性的一种折中性能表示方法,Φ值越小,系统性能越佳。
4 实验仿真
针对多用户与协作干扰的系统模型在平坦Nakagami-m衰落信道下进行MATLAB仿真,对上述理论分析结果进行验证,其中仿真的参数设置如下:
和RS=0.5 bit/s/Hz。通过观察仿真结果,发现分析结果与蒙特卡洛仿真的结果一致。
图2表明在未知窃听信道的CSI情况下用户选择参数k、信道衰落参数m1与总功率P对SRT性能的影响。当k的值越高,对应的Φ值也越低,因为考虑的系统有更高的保密性能,且趋于平稳所需的总功率也将减小。当k一定时,Φ的值随m1增大减小,性能更佳。当k取得最大时,Φ的值不会随着m1改变,且趋于同一个值。随着总功率的增大,由于中断概率与窃听概率达到极限,SRT性能都将趋于平稳。
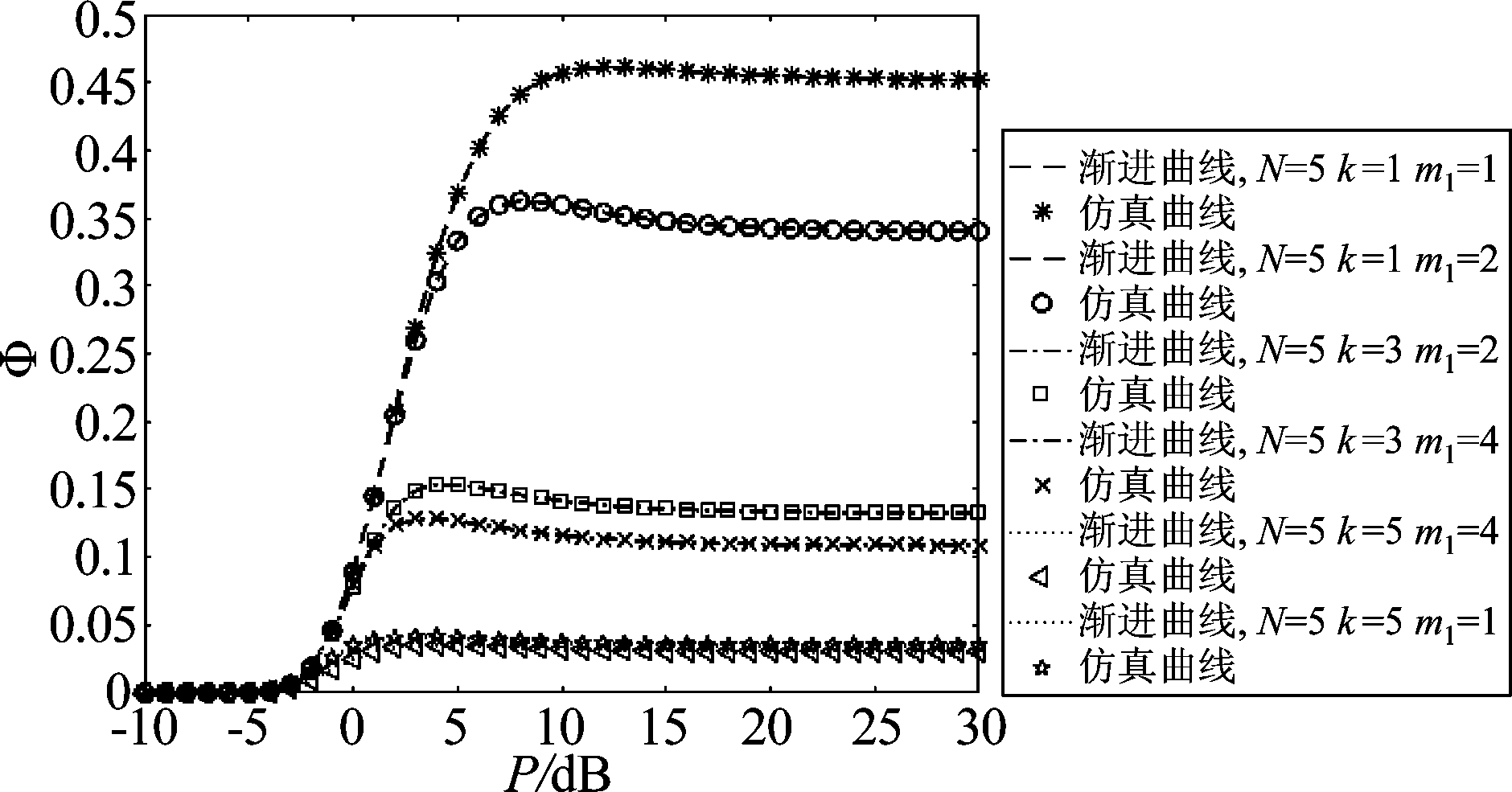
图2 总功率与SRT性能的关系
Fig.2 SRT performance versus total power
图3表明在未知窃听信道的CSI情况下中断概率与窃听概率呈负相关,随着k增大,中断概率逐渐减小,而窃听概率逐渐增大。当k一定时,m1越大,则中断概率与窃听概率取得折中后的最小值即为图2的SRT性能的峰值。
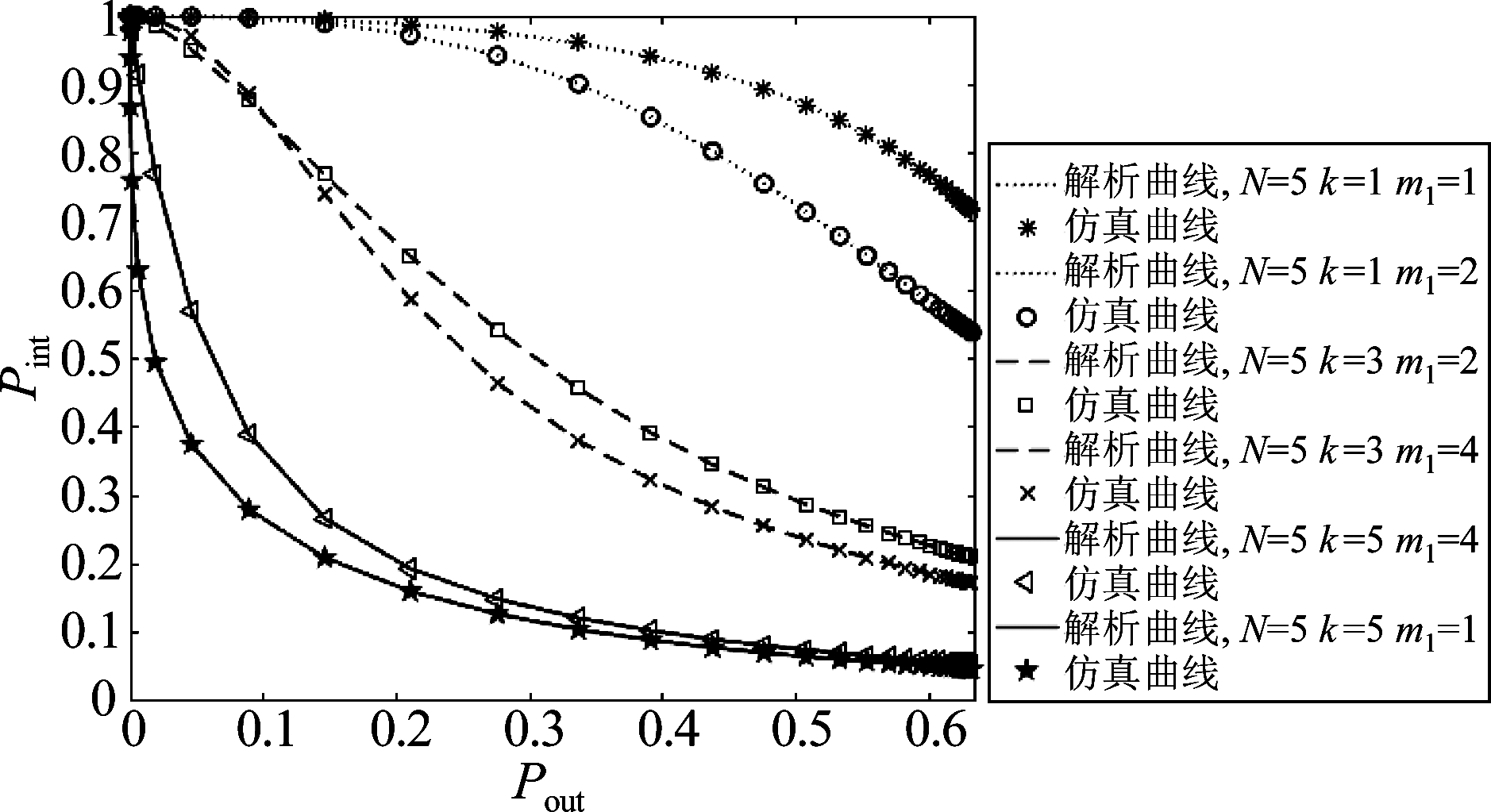
图3 CSI未知时中断概率与窃听概率关系
Fig.3 Intercept probability versus outage probability
对比图2和图4可知,当k的值越高,两种情况下对应的Φ值都较低。但在已知窃听信道的CSI情况下,随着窃听概率越来越小,其SRT性能在Φ达到峰值后也有所下降。随着功率的增大,由于中断概率与窃听概率达到极限,SRT性能将趋于平稳。
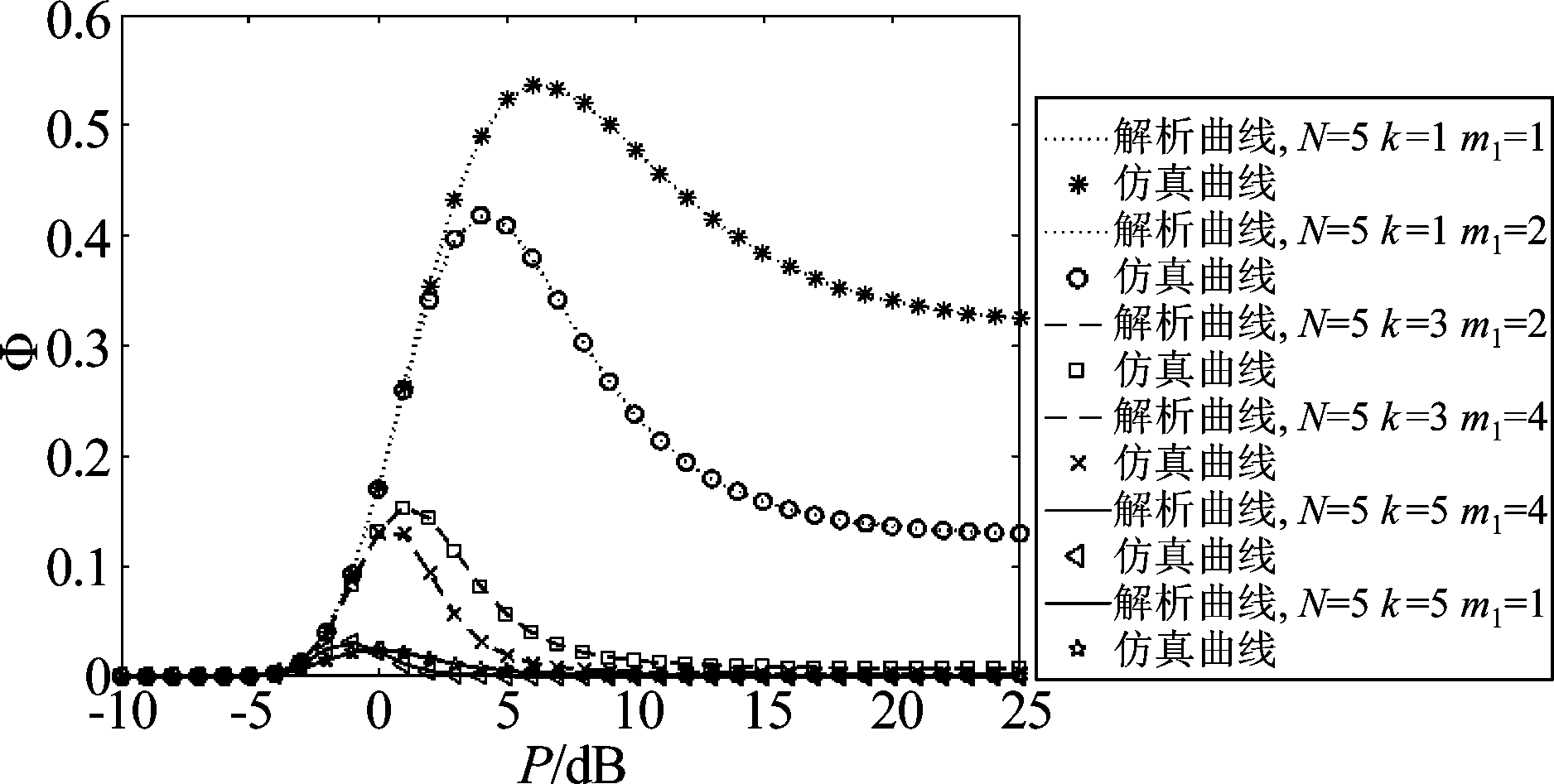
图4 总功率与SRT性能的关系
Fig.4 SRT performance versus total power
图5表明在窃听信道CSI已知情况下,中断概率与窃听概率仍然呈负相关,但由于窃听信道的CSI已知,使得窃听概率可以趋近于零,其趋势与窃听信道未知CSI的情况一致。
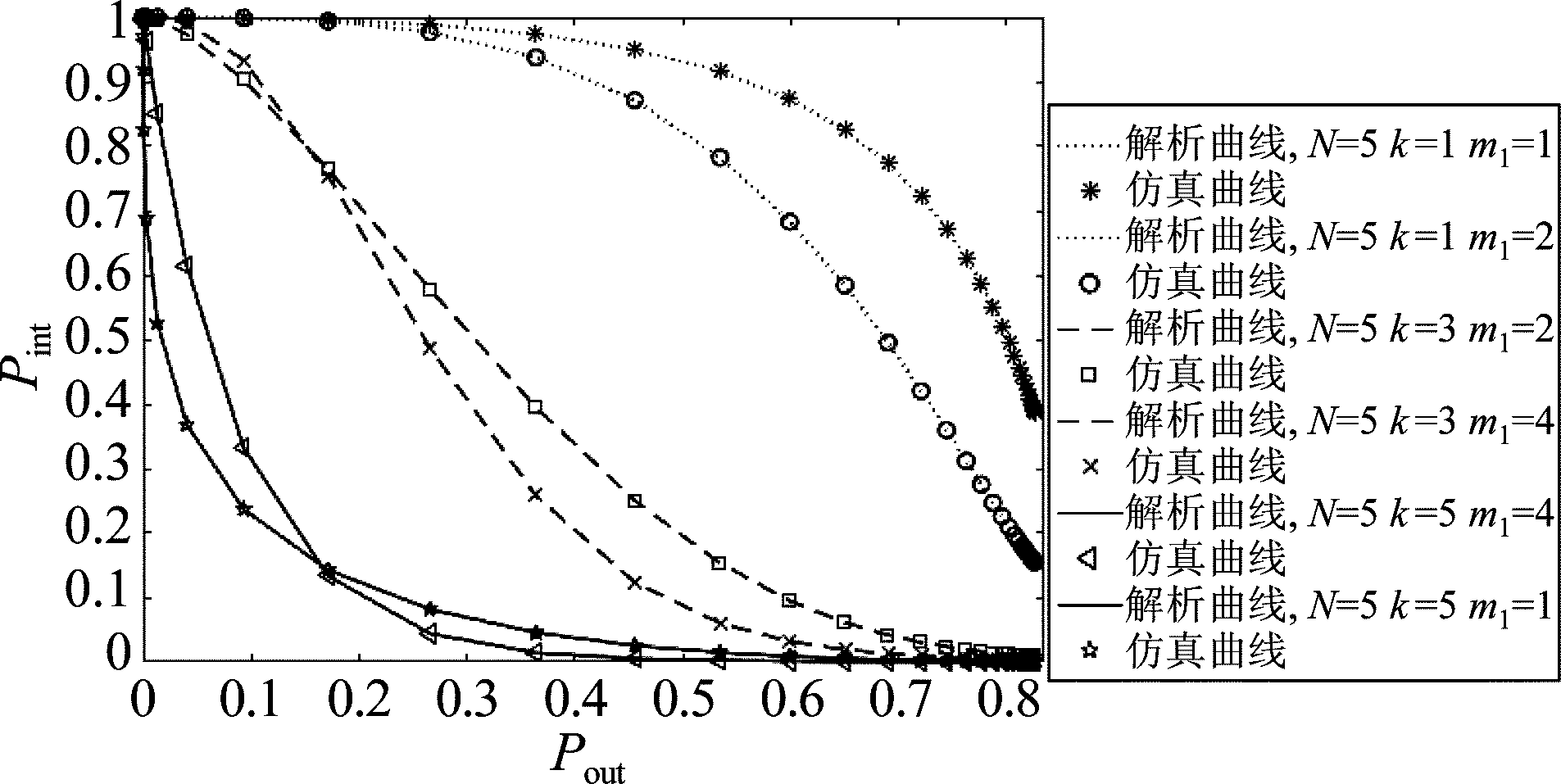
图5 中断概率与窃听概率关系
Fig.5 Intercept probability versus outage probability
图6可看出当过时信道的参数ρ越大,对应的SRT性能越好;当总功率P=4 dB时,不同延迟的Φ达到最大;当ρ=1时,表示系统不考虑反馈延迟。相比未知窃听信道的CSI,其所需要的总功率更大。
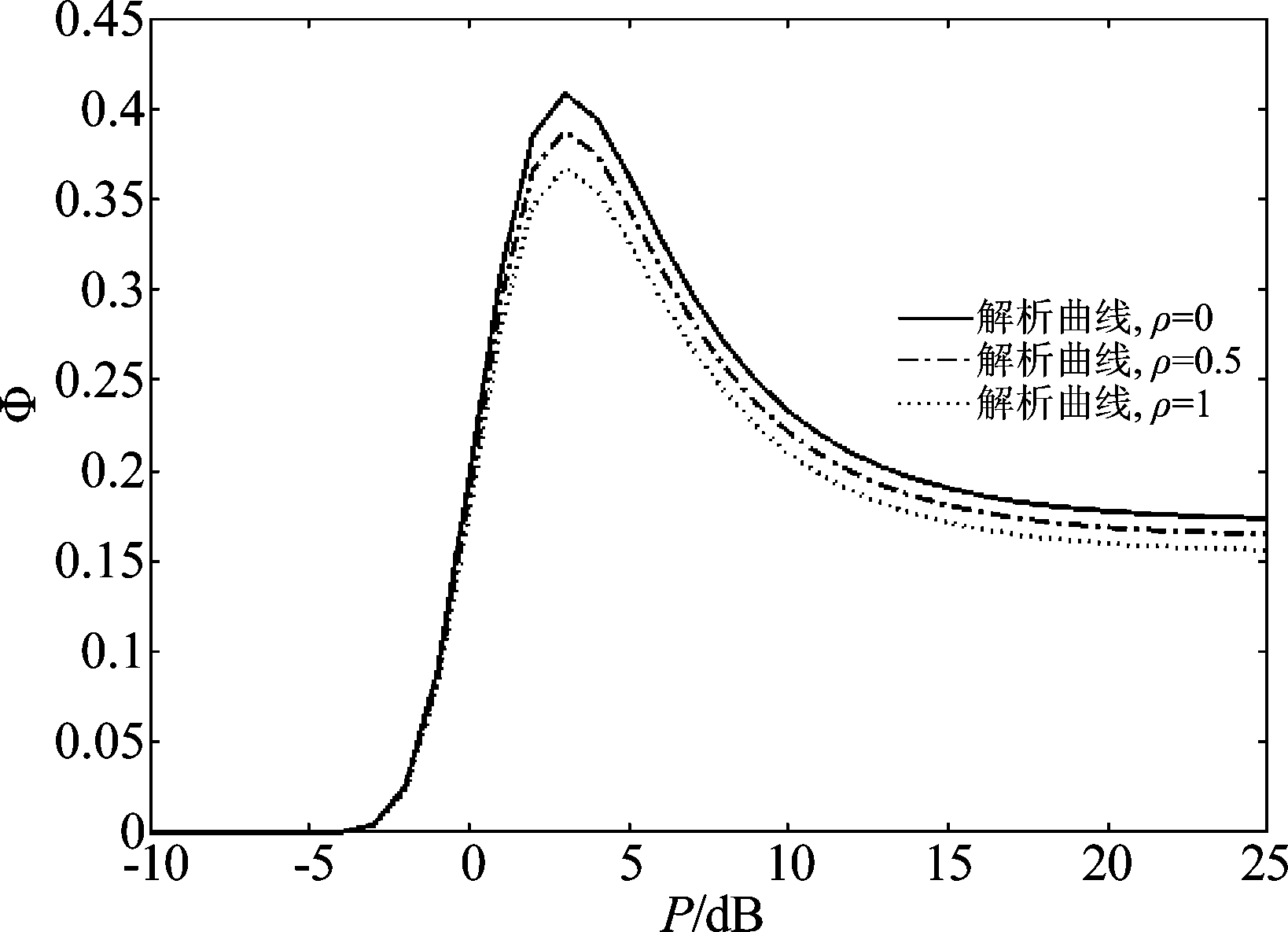
图6 过时信道下功率噪声与SRT性能的关系
Fig.6 SRT performance of outdated channel versus power noise
5 结论
分析了多用户选择与协作干扰的物理层安全传输性能。根据窃听信道状态信息已知与未知的两种条件,提出了不同的协作干扰传输方案。为了避免过时信道的不利影响,采用一般阶次选择策略选择目的用户。推导了Nakagami-m衰落信道下中断概率与窃听概率的准确表达式,对安全性与可靠性的进行了理论分析以及二者的折中关系。蒙特卡洛仿真表明,增加阶参数能够保证未知窃听信道状态信息条件下系统的安全性能,且在已知窃听信道时提升系统的安全性能。
[1] Shannon C E. Communication theory of secrecy systems[J]. Bell System Technical Journal, 1949, 28(4): 656-715.
[2] Poor H V. Information and inference in the wireless physical layer[J]. IEEE Wireless Communications, 2012, 19(1): 40- 47.
[3] Wyner A D. The wire-tap channel[J]. Bell System Technical Journal, 1975, 54(8): 1355-1387.
[4] Ding Zhiguo, Leung K K, Goeckel D L, et al. Opportunistic relaying for secrecy communications: cooperative jamming vs. relay chatting[J]. IEEE Transactions on Wireless Communications, 2011, 10(6): 1725-1729.
[5] Zou Yulong, Wang Xianbin, Shen Weiming. Optimal relay selection for physical layer security in cooperative wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(10): 2099-2111.
[6] Bao V N Q, Linh-Trung N, Debbah M. Relay selection schemes for dual-hop networks under security constraints with multiple eavesdroppers[J]. IEEE Transactions on Wireless Communications, 2013, 12(12): 6076- 6085.
[7] Feng Xiaofeng, Gao Xinbo, Zong Ru. Cooperative jamming for enhancing security of cognitive radio networks with multiple primary users[J]. China Communications, 2017, 14(7): 93-107.
[8] Sun Gangcan, Han Zhuo, Jiao Jinbo, et al. Physical layer security in MIMO wiretap channels with antenna correlation[J]. China Communications, 2017, 14(8): 149-156.
[9] Khina A, Kochman Y, Khisti A. The MIMO wiretap channel decomposed[J]. IEEE Transactions on Information Theory, 2018, 64(2): 1046-1063.
[10] Asaad S, Bereyhi A, Rabiei A M, et al. Optimal transmit antenna selection for massive MIMO wiretap channels[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(4): 817- 828.
[11] Fidan E, Kucur O. Performance of transceiver antenna selection in two way full-duplex relay networks over Rayleigh fading channels[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5909-5921.
[12] Zhao Rui, Lin Hongxin, He Yucheng, et al. Secrecy performance of transmit antenna selection for MIMO relay systems with outdated CSI[J]. IEEE Transactions on Communications, 2018, 66(2): 546-559.
[13] Michalopoulos D S, Suraweera H A, Karagiannidis G K, et al. Amplify-and-forward relay selection with outdated channel estimates[J]. IEEE Transactions on Communications, 2012, 60(5): 1278-1290.
[14] Liang Yingbin, Poor H V, Ying Lei. Wireless broadcast networks: Reliability, security, and stability[C]∥2008 Information Theory and Applications Workshop. San Diego, USA: IEEE Press, 2015: 249-255.
[15] Zou Yulong, Wang Xianbin, Shen Weiming, et al. Security versus reliability analysis of opportunistic relaying[J]. IEEE Transactions on Vehicular Technology, 2014, 63(6): 2653-2661.
[16] 林鸿鑫, 赵睿, 贺玉成, 等. 过时信道状态信息下的机会式中继选择系统的安全性能分析[J]. 信号处理, 2016, 32(7): 810- 818.
Lin Hongxin, Zhao Rui, He Yucheng. Secrecy performance analysis of opportunistic relay selection systems with outdated CSI[J]. Journal of Signal Processing, 2016, 32(7): 810- 818.(in Chinese)
[17] 谭星, 赵睿, 王聪, 等. 协作干扰下的非可信中继与全双工目的节点系统的遍历安全容量分析[J]. 信号处理, 2017, 33(5): 732-740.
Tan Xing, Zhao Rui, Wang Cong, et al. Ergodic secrecy capacity of untrusted relay and full duplex destination systems with cooperative jamming[J]. Journal of Signal Processing, 2017, 33(5): 732-740.(in Chinese)
[18] Yang Yijun, Chen Jin, Huang Yuzhen, et al. Secure transmission of wireless relaying systems with jammer and multiple-user selection[J]. IEEE Access, 2017, 5: 8771- 8779.
[19] Gradshteyn I S, Ryzhik I M. Table of integrals, series, and products, 7th ed[M]. New York: Academic Press, 2007: 1-1161.
[20] Hewhart, Walter A, Wilks S S. Order Statistics,3rd ed[M]. New Jersey: John Wiley and Sons. 2005: 1- 482.
