1 引言
云接入网络(Cloud Radio Access Network,Cloud-RAN),作为中国移动首先提出的技术,有希望是未来5G标准的候补[1]。在Cloud-RAN中,基带处理部分被聚集并且共享在一个虚拟的基带单元池(Base band unit pool,BBU Pool),这样可以有效的适应非均匀业务(例如数据的潮汐效应),并更有效利用资源。作为软中继的射频拉远头(Remote Radio Heads,RRHs),可以通过有线/无线前程连接,将移动用户设备(User,UE)接收来的信号压缩并转发至中央BBU Pool。比起全功能基站,RRHs仅拥有有限功能,包括:模拟/数字转换,数字/模拟转换,放大器,频率转换。比起传统的蜂窝结构,Cloud-RAN需要更少的基带单元,并能够有效减少网络运行成本。
与传统的网络结构[2- 4]与大规模天线系统[7]不同,在Cloud-RAN系统中,分布在RRHs与BBU池中间的前程链路容量是有限的。为了在前程容量约束的条件下提升Cloud-RAN性能,已有相关文献进行信号量化/压缩相关技术的研究[8-14]。但减轻前程链路负担的途径不止一条,通过设计带缓存功能RRHs,同样可以在前程链路容量受限的条件下,提升系统性能。
在带缓存的Cloud-RAN领域中,大多数工作集中于研究提升传统性能指标,如系统容量[15],能量效率[16]等。但随着5G技术的发展,传输时延作为一个重要指标,越来越受到业界关注。在现有的相关文献中,降低时延主要从三个方面进行技术优化:无线接入网[28-29](Radio access network,RAN);核心网络[30](Core Network);缓存[31-32](Caching)。以上的三种策略并不是完全独立的,实际通信中经常同时采用多种策略,本文研究工作属于云接入网络与缓存放置结合领域[17-23],共同实现通信的低时延传输。
在现有带缓存的Cloud-RAN文献中,TRAN Tuyen[17]与PARVEZ Imtiaz[18]从综述角度说明了未来网络中减少传输时延重要性,并介绍了相关领域应用背景;TANDON Ravil[19]首次从信息论角度建立传输时延的理论模型,提出并分析了衡量最差场景传输时延的性能指标;GIRGIS Antonious[20]针对所有RRHs与用户均带缓存场景设计了一种分布式编码缓存方案,利用离峰时间传输用户需求,减少系统时延;GOSELING Jasper[21]将用户规律请求内容场景拓展成更普遍的用户突发内容请求场景,并根据用户不同类型请求设计优化缓存方案;在假设所有节点已知完整信道状态信息的基础上,SENGUPTA Avik[22]从信息论角度推导了最小归一化传输时间的理论下界与理论上界;DAI Jianmei[23]考虑用户可移动性,基于视频片段受欢迎程度,研究了如何设计主动缓存策略减少系统时延。
在以上相关工作中,[19]发表在2016年,[17],[20]发表在2017年,[18],[23]是2018年刚被录用,但未正式发表的最新研究进展。本文工作延续了以上文献的研究思路,但希望解决已有工作的一些缺陷,比如未考虑具体传输机制,未考虑数据包传输成功概率,传统优化方法过于复杂等。
综上所述,本文的创新工作如下所示:
1)研究了具体传输机制(HARQ)下的时延优化问题。除了综述[17],大多数工作[19]侧重从信息论角度分析不同缓存方案对时延影响,传输时延上下界等,不涉及具体传输机制与算法设计。本文考虑将混合式自动重传请求(Hybrid Automatic Repeat Request, HARQ)的重传机制引入带缓存的Cloud-RAN,在具体机制下设计优化缓存算法减少传输时延,更具有实用性。
2)考虑数据包成功传输概率。大多数研究衡量传输时延是沿用TANDON Ravil[19]在2016年提出的归一化传输时间(Normalized Delivery Time, NDT),该概念是基于前程链路与RRHs下行链路的数据传输最坏场景提出的时延性能指标,与理想无干扰高信噪比场景下的最好时延相对,是最差时延(即最大时延)。本文考虑实际场景中传输时延应根据数据成功传输概率决定,即采用马尔可夫链分析理论建模,而不是仅研究最好时延或最差时延。
3)提出了一种适合复杂问题的优化算法,有效减少时延。现有大多数工作采用传统确定性算法[24]设计寻找最小化时延方案,但传统优化算法对目标函数与约束条件限制较高,且不适合解决复杂问题(具体见图4),因此头脑风暴优化(brain storm optimization,BSO)算法被引入解决本文优化问题,获得最优缓存方案。
因此,在采用HARQ的重传机制,考虑前程链路与下行链路频谱信道的正交性情形下,本文基于马尔可夫链理论建立了最小化系统传输时延的优化问题。考虑只能通过递归方式得到优化目标函数表达式,BSO算法被引入解决非凸问题,获得最优缓存方案。仿真结果表明,比起其他缓存方案,本文提出的优化算法可以有效地减少系统传输时延。
2 系统模型
如图1所示,本文提出基于缓存RRHs的Cloud-RAN三层架构。在Cloud-RAN单个聚类中,云中心通过网关与回程链路与上层核心网相连。在下层中,单个RRH通过无线前程链路与云中心相连,并通过频谱正交的无线信道(例如正交频分多址接入)与数量为K用户相连,用户集合定义为K={1,...,K}。整个网络的所有内容数目为T,定义为T={1,...,T},每个内容可细分为L数据包,确保每个数据包可以在一个独立帧内传输完毕。设定云中心已知所有被请求内容T,RRH的最大缓存容量为S。
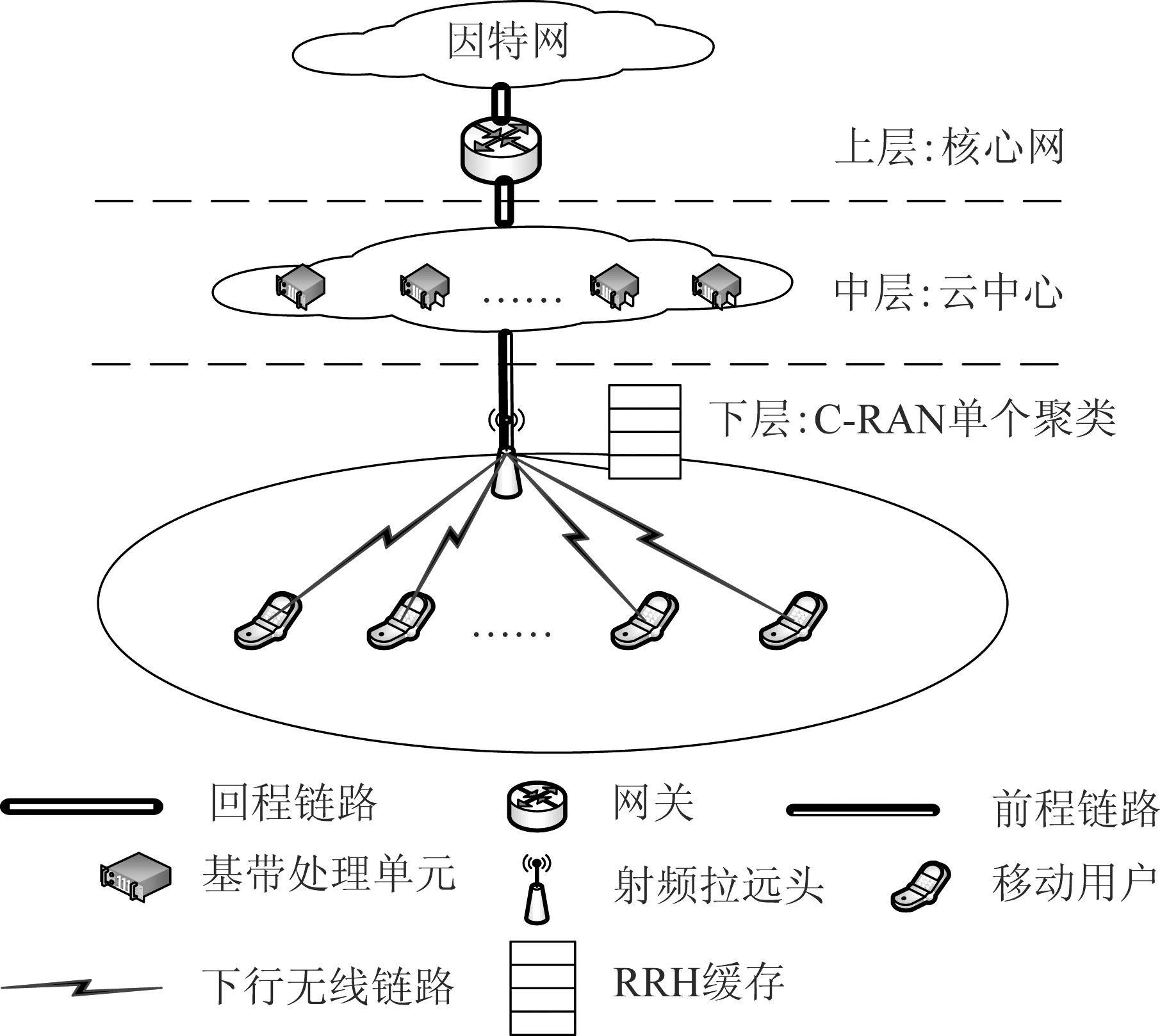
图1 带缓存Cloud-RAN下行传输结构图
Fig.1 The downlink transmission structure figure in cache-based Cloud-RAN
在缓存阶段,任何内容t的Lt数据包被缓存在RRH端,Lt∈{0,1,...,L},t∈{0,1,...,T}。因为RRH端最大缓存容量为S,所以存在以下关系:
(1)
在内容交付阶段,RRH一次同时服务一个用户。每个用户请求内容t的概率为τt,并满足
设定所有请求相互独立,其发生概率τt满足Zipf分布(齐普夫定律,含义是将请求内容的频率按由大到小的顺序排列,则每个内容出现的频率与它的名次的常数次幂存在简单的反比关系):
τt=ct-
,t∈{1,2,...,T}
(2)
式(2)中,c是归一化常数,{|0≤≤max}是内容流行指数。=0时,所有内容均匀分布,越大,内容分布越不均匀,内容t=1,2,...,T流行指数顺序降低。
设定前程链路与下行无线链路分别使用同样带宽,帧同步,但频率不同的两条信道,确保在每个传输时隙中同时容纳两个传输过程。两条链路分别建模为块衰落瑞利信道,具有独立零均值单位功率复高斯信道增益。信道增益在每次传输时隙中保持不变,并随着每次重新传输而独立变化。定义前程链路与下行链路的信噪比分别为γ1与γ2。数据包传输速率为R,单位为比特每秒每赫兹(bit/s/Hz)。本文考虑基于混合式自动重传请求(Hybrid Automatic Repeat Request, HARQ)的重传机制,即终端舍弃错误传输的数据包。所有信令信息,例如确认信息(Acknowledgement, ACK)与否定确认信息(Non-Acknowledgement,NACK),被认为帧长明显短于用户数据包长度,并且完全可靠传输。
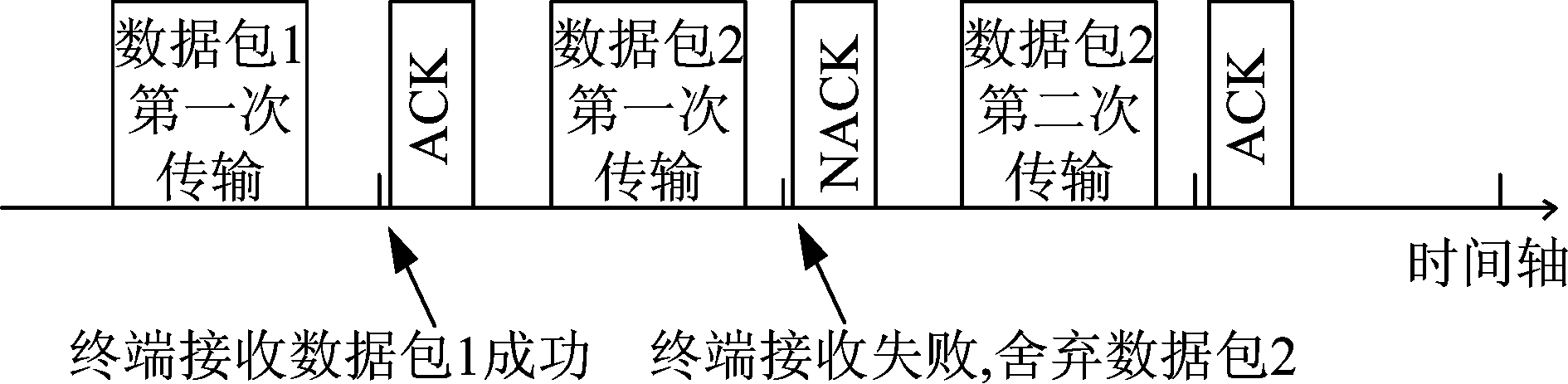
图2 本文的HARQ传输机制
Fig.2 The HARQ scheme in this paper
在系统中,设定圆形小区半径为Rrad,距离RRH距离为d的用户密度与距离d成正比,服从以下分布:
(3)
RRH与用户通信的下行链路信噪比与距离指数成反比,并满足以下路径损失模型:
γ2(d)=Π/dθ,0≤d≤Rrad
(4)
在(4)中,θ是传播损失指数,Π为一个常数,取决于RRH端下行功率值。
以单个请求数据的移动用户为例,当用户端请求数据全部存储在RRH端缓存端时,RRH通过下行链路将被请求数据直接发送给移动用户,传输时延仅为下行链路传输数据包的时间延迟;当用户端请求数据仅有部分在RRH端或者全部在云中心,则云中心先要通过前程链路将对应数据发送至RRH端,RRH再将请求数据发送至用户端,此时传输时延包括前程链路与下行链路共同传输数据包的时间延迟。总体而言,端到端时延是指:传输完用户所需求的所有数据包所需时隙的平均值,端到端指的是云中心至移动用户端。本文采用端到端平均延迟作为传输时延的性能指标,即传输完所有L个数据包所需时隙的平均值。本文中的“传输时延”与以往文献定义相关时延的主要有两个不同之处:考虑具体重传机制(混合式自动重传请求),考虑数据包传输成功概率(马尔可夫链分析理论建模)。
3 优化缓存策略设计
本节首先针对单用户请求文件t的Lt缓存数据包传输时延进行分析,再将其扩展至多用户场景,建立通优化缓存策略,最小化传输时延的优化问题。
3.1 对于给定内容的时延分析
从上文可知,传输时延是一个关于缓存数据包数目Lt的函数,基于文献[27],数据包成功传输的概率取决于信道容量适应传输速率R的概率,并满足以下等式:
ηj=e-(2R-1)/2γj, j∈{1,2}
(5)
等式(5)中,η1,η2分别是前程链路与下行无线链路成功传输概率,γ1,γ2分别是两条链路的信噪比。
为了定义端到端平均时延,本章采用马尔可夫链分析,定义马尔可夫链分析的状态为(α,β)。α∈{0,1,...,L}, β∈{0,1,...,L}分别是RRH端未发送至用户数据包的个数与已发送至用户数据包个数,并满足不等式Lt≤α+β≤L。初始状态为(Lt,0),表示RRH端有未完成传输的Lt数据包,已传输完成0个数据包;最终状态为(0,L),表示RRH端未发送数据包数目是0,所有L数据包全部传输至用户端。任何非最终状态(α,β)≠(0,L)的状态转移概率如图3所示。
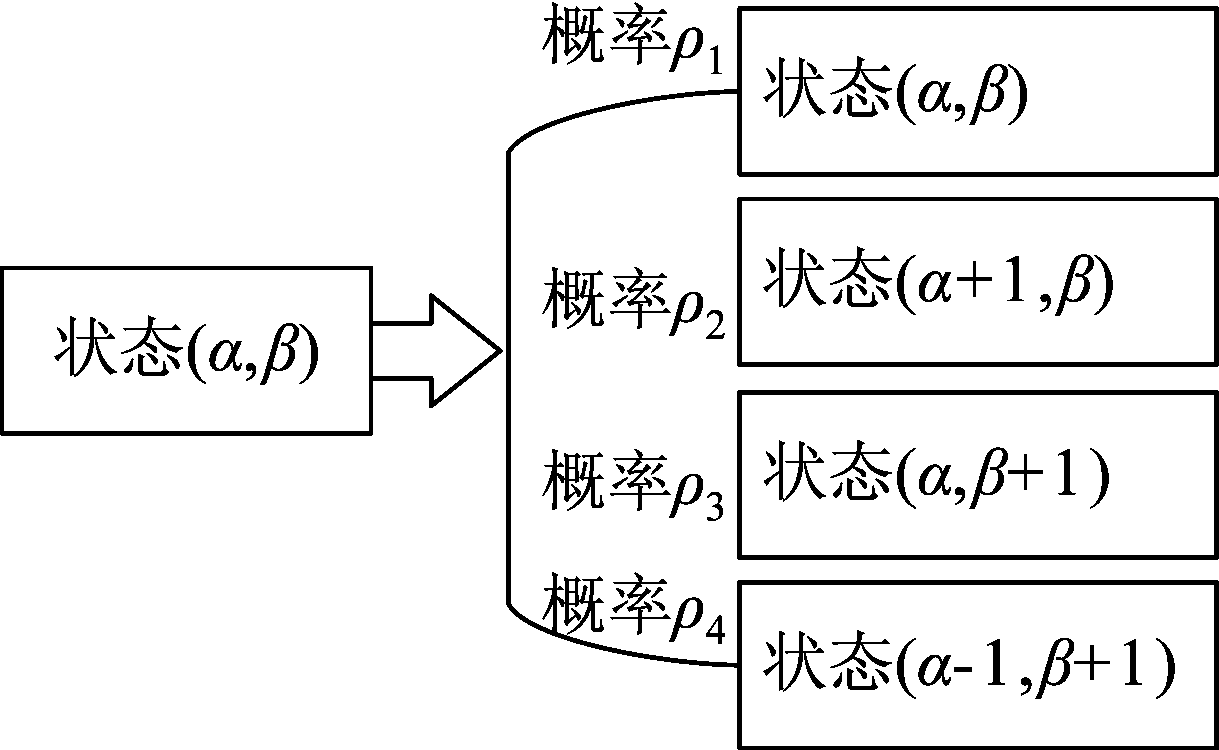
图3 内容传输状态转移图
Fig.3 The state transition diagram of content transmission
在图3中,根据系统模型定义,不同状态转移概率由推论3.1给出。
推论3.1 已知η1,η2分别是前程链路与下行无线链路成功传输概率,马尔可夫链分析的状态为(α,β),所有内容数据包总数为L,图3中的不同状态转移概率如下所示:
ρ1=(1-η1)A1(1-η2)B1,
A1=sign|α+β-L|,B1=sign|α|
(6)
ρ2=A1η1(1-η2)B1
(7)
ρ3=A1B1η1η2
(8)
ρ4=B1η2(1-η1)A1
(9)
证明:
(1)状态(α,β)转移至(α,β),即不存在任何成功数据包传输,有以下三种情况:
1) 所有数据包均在RRH端缓存或已发送至用户端,此时α+β=L,前程链路传输状态无意义,下行传输失败,状态转移概率ρ1=1-η2;
2) RRH端没有缓存数据,此时α=0,前程链路传输失败,下行链路传输状态无意义,状态转移概率ρ1=1-η1;
3) 以上两种情况均不是,RRH端存在缓存数据,传输过程也没有结束,则是前程链路与下行链路传输同时失败,状态没有转移,状态转移概率ρ1=(1-η1)(1-η2)。
综合三种情况,可知状态转移概率ρ1可表示为:
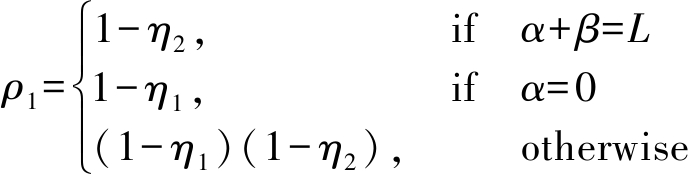
(10)
定义A1=sign|α+β-L|,B1=sign|α|,(10)可缩写如(6)所示,公式(6)得证。
(2)公式(7～9)证明方法与(6)相同,这里不再赘述。
在推论3.1中,α+β=L时,所有数据包均在RRH端或用户端,前程链路上没有任何传输过程,因此前程链路传输状态无意义,α=0时,RRH端没有缓存数据,下行链路上没有任何传输过程,因此下行链路传输状态无意义。
基于带激励的马尔可夫链理论,定义从状态(α,β)至最终状态传输时隙(或马尔可夫链的步长数目)为λ(α,β)。根据图3与推论3.1,λ(α,β)的具体值由推论3.2给出。
推论3.2 已知ρ1,ρ2,ρ3,ρ4分别是图3中不同状态转移概率,马尔可夫链分析的状态为(α,β),所有内容数据包总数为L,从状态(α,β)至最终状态传输时隙λ(α,β)如下所示:
λ(α,β)=A2+A2(1-ρ1)B2(1-ρ2)C2λ(α,β)
(11)
(12)
基于推论3.2,进一步给出传输时隙λ(α,β)与其他不同状态传输时隙λ(α+1,β),λ(α,β+1),λ(α-1,β+1)关系表示式推论3.3。
推论3.3 已知ρ1,ρ2,ρ3,ρ4分别是图3中不同状态转移概率,马尔可夫链分析的状态为(α,β),所有内容数据包总数为L,传输时隙λ(α,β)与其他不同状态传输时隙λ(α+1,β),λ(α,β+1),λ(α-1,β+1)关系表示式如下所示:
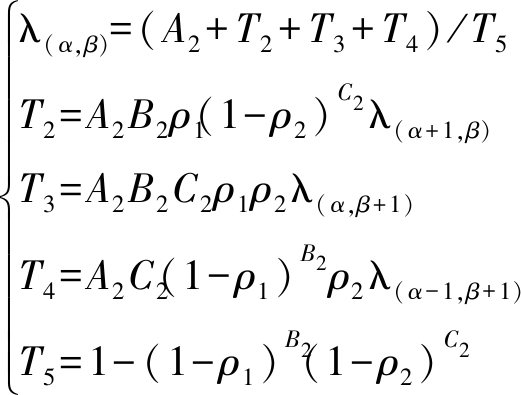
(13)
(13)中,A2,B2,C2相关定义与(12)中一致。
推论3.3中,所有状态(α,β)中,初始状态为(Lt,0),最终状态为(0,L)。定义平均端到端时延等于从初始状态(Lt,0)到最终状态(0,L)步长的平均数,如下所示:
DLt(γ2)=λ(Lt,0)
(14)
公式(14)中,时延长度取决于给定需求内容t的数据包个数Lt与下行链路的平均信噪比γ2。
3.2 缓存优化问题建立
基于(14),本节将讨论缓存分配变量是Lt,t∈{1,2,...,T}的优化问题。建立RRH至用户之间距离的离散模型dy=Rrady/Y,y=1,2,...,Y。假设在一个圆形小区用户随机均匀分布,距离dy上的用户密度如下所示:
...,Y
(15)
将(15)对RRH与用户距离取平均值,并考虑内容流行分布,可得平均端到端时延表达式:
(16)
本文的目的是通过优化缓存策略(例如变量Lt,t∈{1,2,...,T})最小化(16)中的平均时延D。为了使优化问题便于处理,定义每个内容t的二进制指示优化变量σtl,l∈{0,1,...,L}表达式:
(17)
基于定义(17),缓存数据包个数Lt与时延DLt可写作
综上所述,最小化时延的优化问题可表示为:
(18)
...,T}
(19)
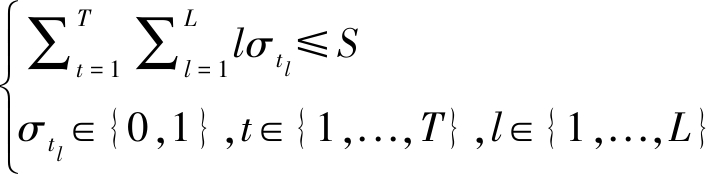
(20)
0≤≤max
(21)
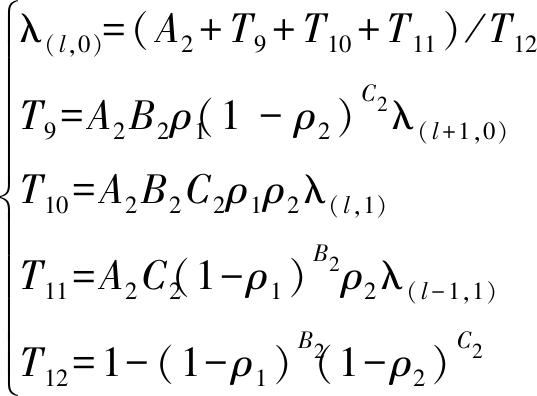
(22)
A2=max(sign|l|,sign|-L|),
B2=sign|l-L|,C2=sign|l|
(23)
优化问题(18)中,2y/Y(1+Y)是(15)中定义不同距离的用户密度;ct-是(2)中齐普夫定律定义的相关概率;σtl是(17)中定义的二进制指示优化变量,用于取代Lt;λ(l,0)是将(14)代入(16)中整理得到的单个时延表达式,实际应用中可以递归得到;约束(19)、(20)分别是σtl的定义范围与RRH端缓存最大值约束,对于一个特定内容t,仅有一个指示变量σtl为1,其他值为0;约束(21)是公式(2)中内容流行指数定义范围;约束(22)、(23)是将推论3,公式(14)代入(16)得到的等式约束。在所有约束中,并没有直接出现前程链路的容量约束,这是因为前程约束已经包括在传输成功概率ρ1的定义中,具体可见公式(5)。
4 优化问题解决方案
问题(18)是一个线性整数二次优化问题,考虑到λ(l,0)单个时延表达式只能通过递归方式得到,因此使用传统优化方法(如拉格朗日对偶分解等)解决问题比较困难。为了适应未来算法鲁棒性,运行并行性与实现简洁性的趋势,本文采用一种新的群智能优化算法——头脑风暴优化(Brain Storm Optimization, BSO)算法来解决优化问题。
4.1 BSO算法相关背景知识
BSO算法是史玉回教授在2011年提出的一种基于人类头脑风暴创新思维过程的新型群智能算法[25-26]。与传统的群智能优化算法不同,BSO算法中的个体是具有逻辑推理与思维创新能力的人类。当人们在遇到较难解决的复杂问题时,往往会将几个不同专业背景的人聚在一起,进行头脑风暴活动,通过各自对问题认知的讨论与交谈,产生新的思路和想法。BSO优化算法是模拟头脑风暴产生新见解的流程,将整个新方案产生过程抽象为具有聚集功能的聚类操作、新个体产生的交互操作,以及实现局部搜索过程的随机变异。在交互过程中,对个体的更新设置了不同的交互规则与原理,充分增强了算法的全局搜索功能。图4列出了传统确定性优化算法与BSO算法的特性对比。
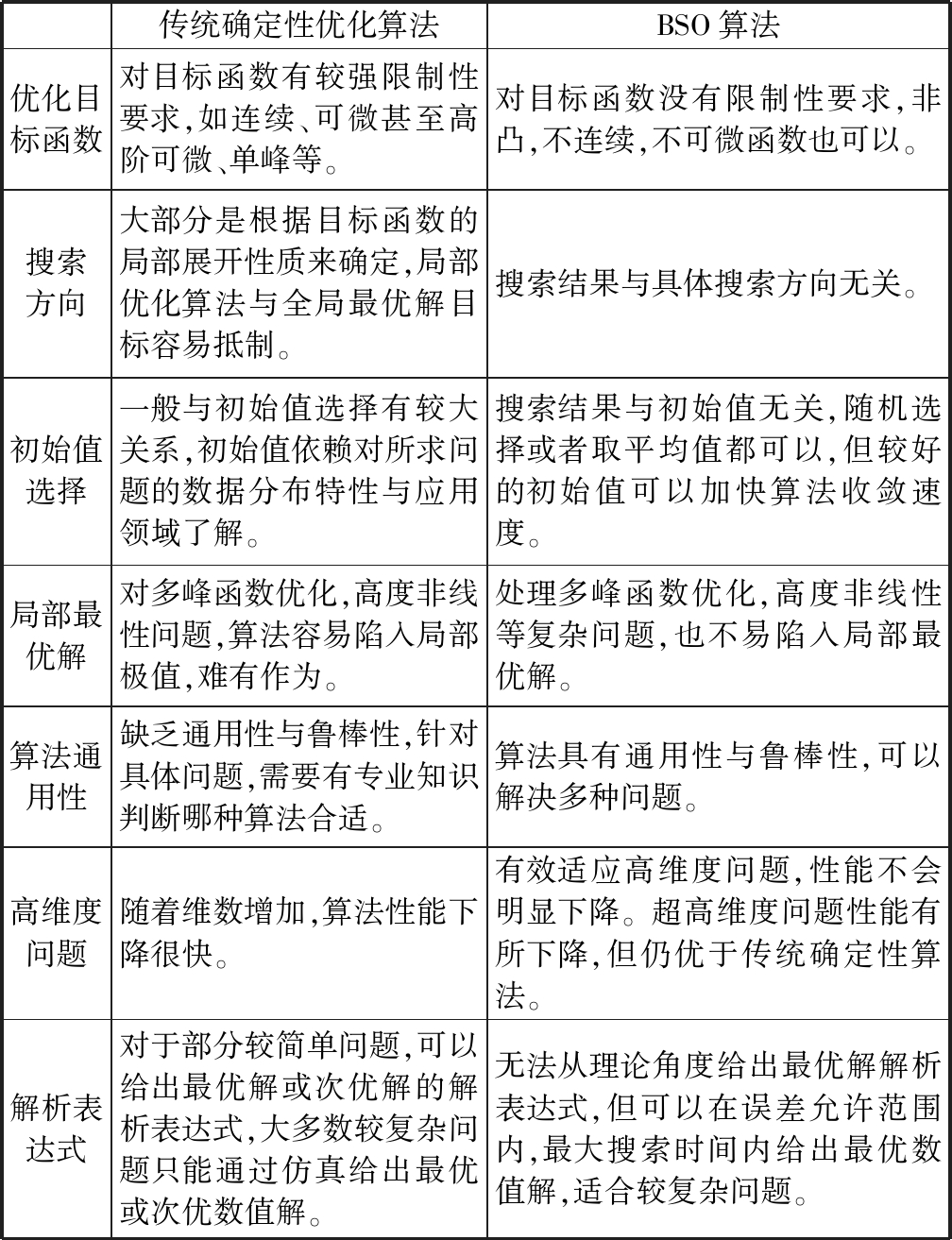
传统确定性优化算法BSO算法优化目标函数对目标函数有较强限制性要求,如连续、可微甚至高阶可微、单峰等。对目标函数没有限制性要求,非凸,不连续,不可微函数也可以。搜索方向大部分是根据目标函数的局部展开性质来确定,局部优化算法与全局最优解目标容易抵制。搜索结果与具体搜索方向无关。初始值选择一般与初始值选择有较大关系,初始值依赖对所求问题的数据分布特性与应用领域了解。搜索结果与初始值无关,随机选择或者取平均值都可以,但较好的初始值可以加快算法收敛速度。局部最优解对多峰函数优化,高度非线性问题,算法容易陷入局部极值,难有作为。处理多峰函数优化,高度非线性等复杂问题,也不易陷入局部最优解。算法通用性缺乏通用性与鲁棒性,针对具体问题,需要有专业知识判断哪种算法合适。算法具有通用性与鲁棒性,可以解决多种问题。高维度问题随着维数增加,算法性能下降很快。有效适应高维度问题,性能不会明显下降。超高维度问题性能有所下降,但仍优于传统确定性算法。解析表达式对于部分较简单问题,可以给出最优解或次优解的解析表达式,大多数较复杂问题只能通过仿真给出最优或次优数值解。无法从理论角度给出最优解解析表达式,但可以在误差允许范围内,最大搜索时间内给出最优数值解,适合较复杂问题。
图4 传统确定性优化算法与BSO算法对比图
Fig.4 The Comparison diagram between traditional deterministic optimization algorithms and BSO algorithms
4.2 最小化时延的BSO算法设计
基于BSO算法解决(18)中的优化问题的基本步骤如算法1所示。
算法1 问题(18)最小化时延的BSO算法设计
步骤1 相关参数初始化,设置最大迭代次数Imax等,随机生成Θ个初始解集合{σtl,};
步骤2 按照相关原则(如K-means聚类方法[25]),将Θ个解集分成Ξ个聚类;
步骤3 将Θ个解集代入(18)目标函数,按照得到时延大小评价Θ个解集;
步骤4 将每个聚类中的解集进行排序,得到Ξ个聚类中心;
步骤5 以很小的概率用变异解集(如高斯函数变异发散方法[26])替代聚类中心的解集;
步骤6 按照一定的规则(如多个类中心产生新个体方法[26])生成新的解集,并进行整体解集的更新;
步骤7 如果解集的个数达到最大值Θ,转步骤8,否则转步骤6;
步骤8 如果达到最大迭代次数或者算法已经收敛,则转步骤9,否则转步骤2;
步骤9 输出最优解{σtl,}与最小时延值,算法结束。
通过分析,可知该算法计算复杂度最小值为C1*
最大值为C1*O
其中C1为考虑已经递归得到优化目标的常数,Θ为初始解集解的个数,Ξ是聚类的个数,Γ是优化变量的个数(本文是常数2),ζϑ是每个聚类中解集的个数。比起传统算法,算法暂未得到广泛应用的最大的限制是无法从理论角度给出最优解/次优解的解析表达式,只能在误差允许范围内给出最优数值解。
算法1中,步骤1是解集初始化过程;步骤2～4是BSO算法“聚类”过程,即找出几个潜在的最优解集;步骤5～7是BSO算法“发散”的过程,即产生更多解集,防止陷入局部最优解集,BSO算法的核心是如何设计优化“聚类”与“发散”的过程。由于篇幅限制,本文主要关注如何使用BSO算法解决优化问题,因此均采用经典方法(例如K-means聚类方法,高斯函数变异发散方法, 多个类中心产生新个体方法)。
算法1中,步骤1中解集初始化,步骤3中解集评价是BSO算法与其他群智能算法类似之处,但步骤2中解集聚类,步骤5中聚类中心加扰动,步骤6中解集更新是BSO算法特有的操作,也是BSO算法优于其他受动物群体行为启发的群智能算法之处。
5 仿真结果与分析
本章节将通过仿真实验,分析算法1不同缓存优化变量对总时延的影响。根据(17)可知,指示变量σtl与缓存数据包个数Lt存在等式映射,为了更好的分析结果,仿真将着重研究总时延与缓存数据包个数Lt,齐普夫定律中内容流行指数变量之间的关系。设定数据包个数L=30,数据包传输速率R=3 bit/s/hz,其他仿真参数根据不同仿真图具体设定。
在仿真中,除了本文提出的算法1,还涉及以下对比方案:
方案1 平均分配。RRHs端所有缓存参数平均设置,不进行任何优化。
方案2 无缓存。RRHs没有缓存功能,用户请求任何数据,均需要通过前程链路向BBU Pool请求。
方案3 整体内容缓存。RRHs端仅能缓存某个请求内容整体,不能将内容细分数据包分别缓存。
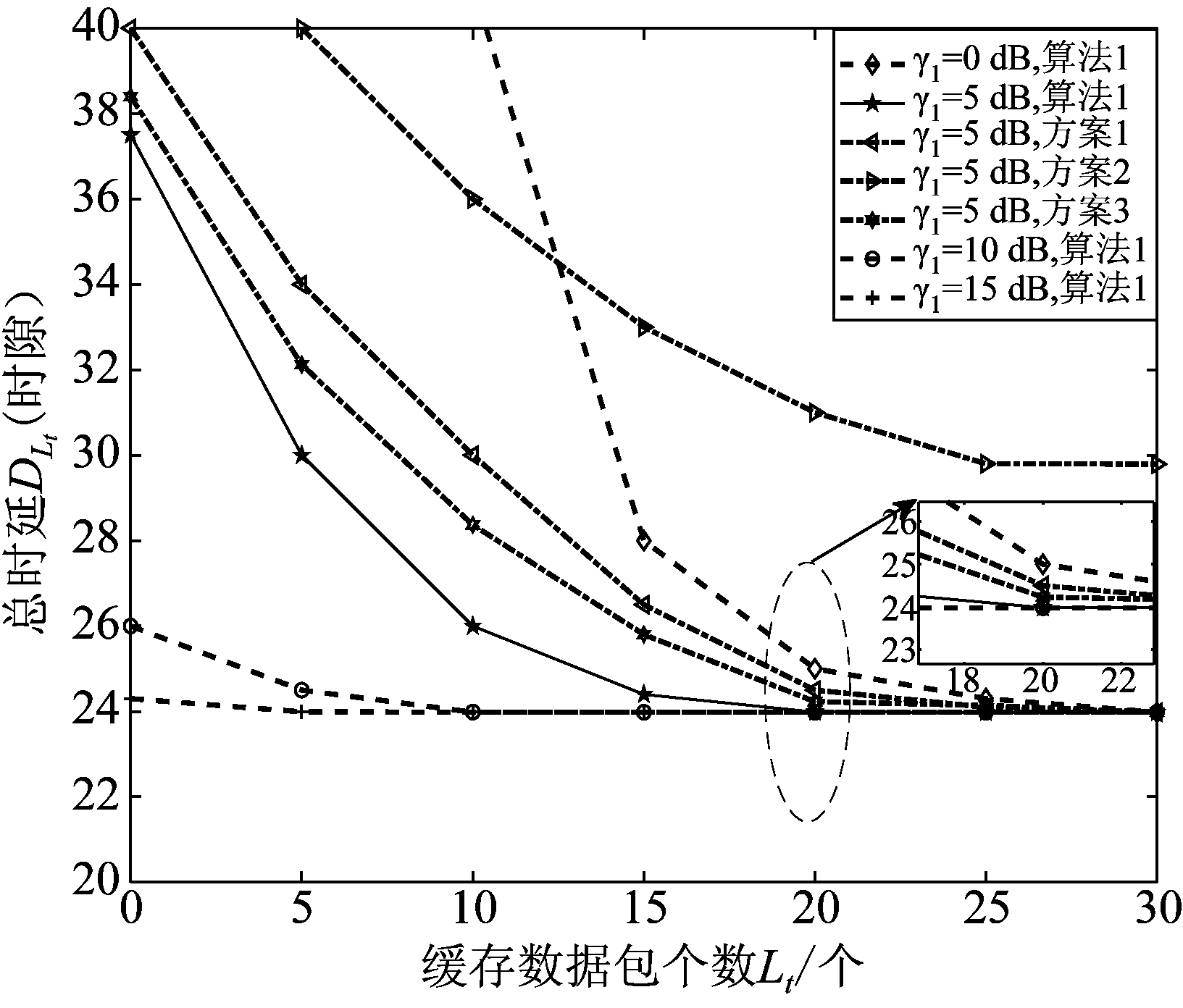
图5 不同方案总时延对比图,,γ2固定,Lt,γ1变化
Fig.5 Comparison diagram of total transmission delay between different schemes, and γ2 are fixed, Lt and γ1 change
在图5中,内容流行指数为固定值5,下行链路信噪比γ2为固定值10 dB,数据包个数L最大值为30,前程链路信噪比γ1变化,缓存数据包个数Lt逐渐递增时,不同方案的总时延呈下降趋势。由图5可知,当其他参数固定时,前程链路信噪比γ1越大,系统总时延越小,但这种变化趋势并不是无限的,例如当γ1=10 dB时,时延曲线将短暂下降,但很快趋向稳定值。因为当前程链路信噪比增长到一定数值时,数据传输成功率将接近100%,此时总时延受γ1影响很小,而受别的参数影响,保持一个最小值以上。比起平均分配参数的方案1与无缓存的方案2,算法1可以有效减少总时延,且这种性能优势在缓存数目Lt较小,前程信噪比γ1较小时更明显。
在图6中,内容流行指数为固定值5,前程链路信噪比γ1为固定值0 dB,数据包个数L最大值为30,下行链路信噪比γ2变化,缓存数据包个数Lt逐渐递增时,不同方案的总时延数值下降趋势变缓。当其他参数固定时,下行链路信噪比γ2越大,系统总时延越小,并趋向稳定值。在图6中,可知方案3对应的总时延略优于方案1,但仍大幅落后于算法1。与其他方案相比,算法1可以明显减少总时延,提升系统运行效率,该结论与图5中结论一致。
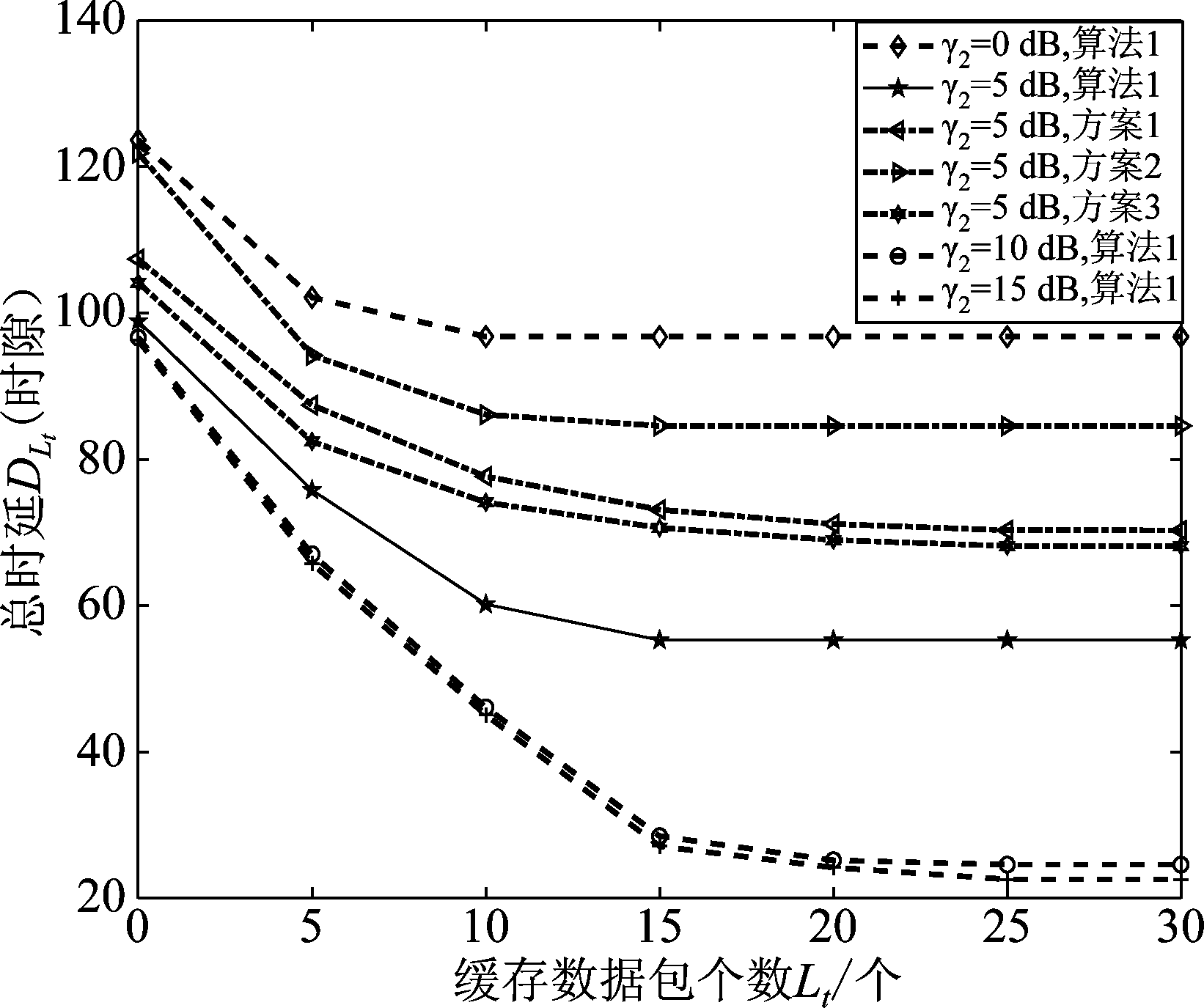
图6 不同方案总时延对比图,,γ1固定,Lt,γ2变化
Fig.6 Comparison diagram of total transmission delay between different schemes, and γ1 are fixed, Lt and γ2 change
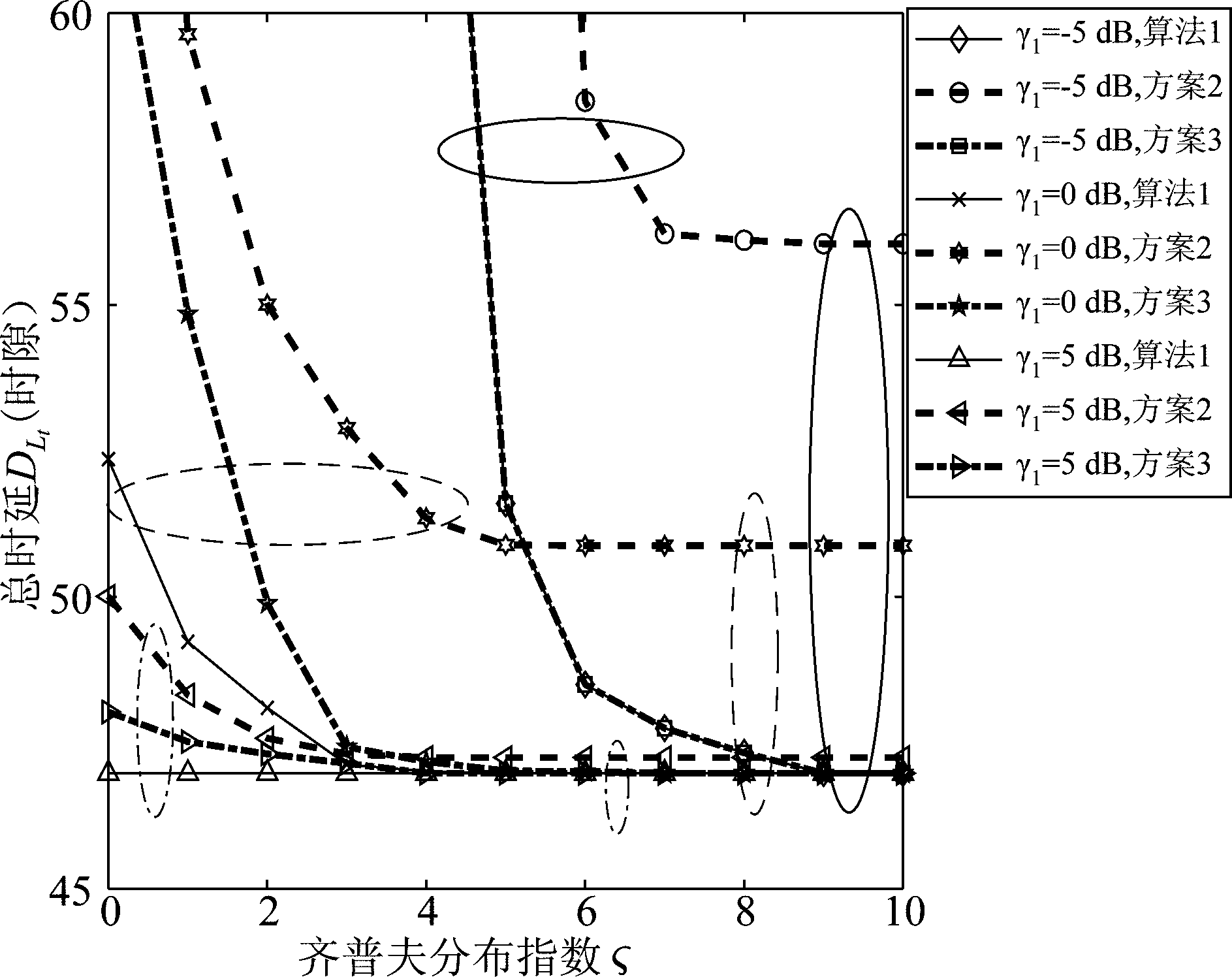
图7 不同方案总时延对比图,Lt,γ2固定,,γ1变化
Fig.7 Comparison diagram of total transmission delay between different schemes, Lt and γ2 are fixed, and γ1 change
在图7中,RRH的最大缓存容量S为固定值90,数据包个数L最大值为30,请求内容数目T=5,传播损失指数θ=2,小区半径Rrad=100 m,小区半径距离等分参数Y=1000,下行链路信噪比γ2为固定值10 dB,前程链路信噪比γ1取值为-5 dB,0 dB,5 dB,齐普夫分布指数逐渐递增时,不同方案的总时延数值变化不同。由图7可知,无论γ1如何取值,比起其他方案,方案2始终实现最大总时延,即性能最差。当γ1=-5 dB时,算法1与方案3性能曲线几乎重合,γ1=0 dB时,算法1明显优于方案3,γ1=5 dB时,算法1总时延几乎不随变化,保持恒定,但仍优于方案3。这是因为前程链路信噪比过低时,数据传输失败率过高,整体内容缓存(方案3)与数据包细分缓存(算法1)均会导致很大的时延,性能曲线重合度较高;信噪比γ1=0 dB,算法1总时延较小,性能优势明显;γ1=5 dB时,数据传输成功率过高,总时延受γ1影响很小,将很快收敛到一个最小值上,此时算法1仍保持最小时延,但性能优势有所减少。
在图8中,前程链路信噪比γ1为固定值0 dB,下行链路信噪比γ2取值为-5 dB,0 dB,5 dB,其他参数与图7保持一致,齐普夫分布指数逐渐递增时,不同方案的总时延数值依次变化。当齐普夫分布指数逐渐递增时,所有方案总时延逐渐递减,但趋势逐渐减小,最终保持在最小值以上,而算法1始终能实现最小时延。下行链路信噪比γ2递增时,算法1实现时延逐渐减小,最终收敛到一个稳定值,这说明不能通过增长γ2实现时延的无限制减少,需要综合考虑其他因素。
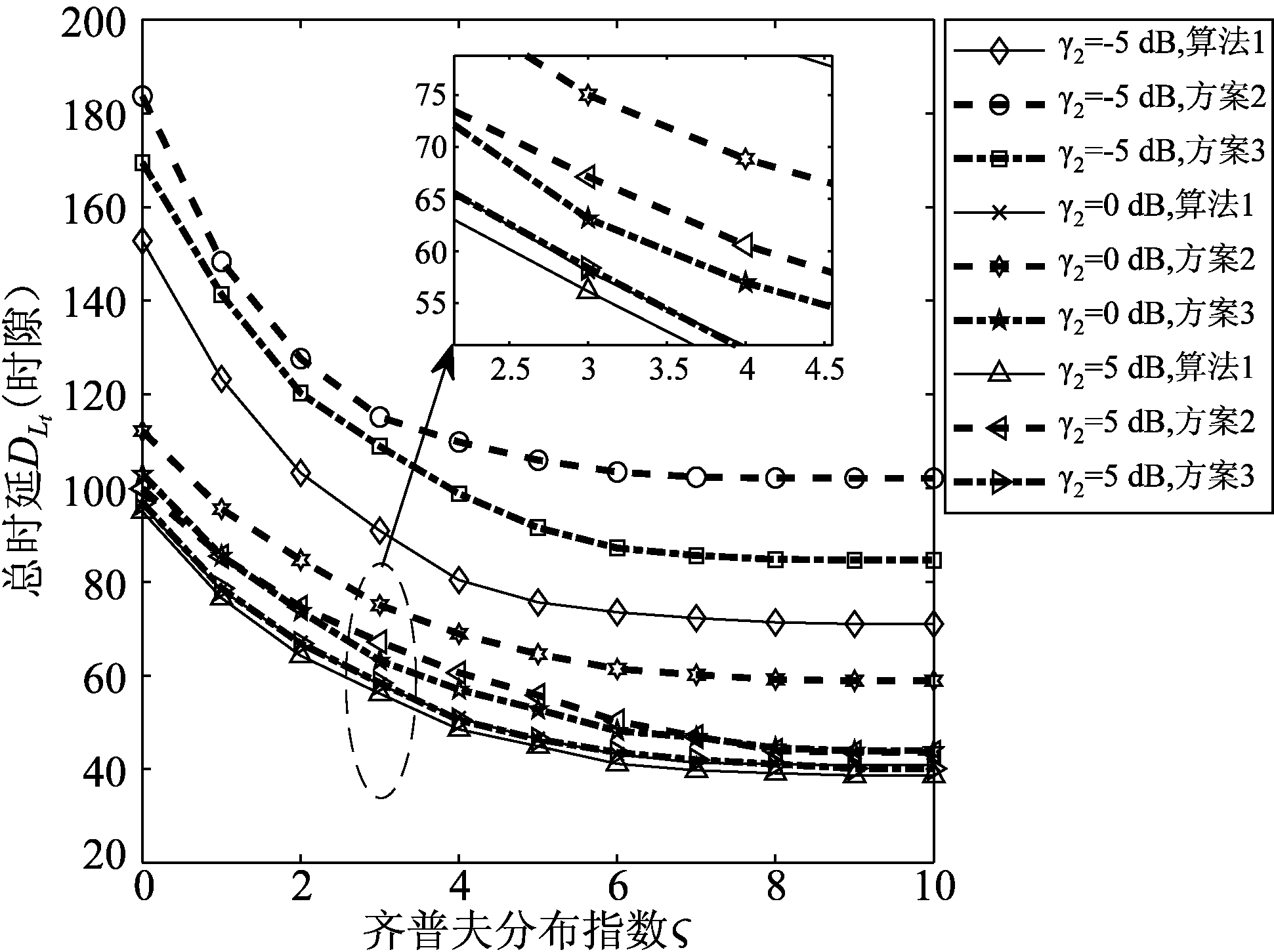
图8 不同方案总时延对比图,Lt,γ1固定,,γ2变化
Fig.8 Comparison diagram of total transmission delay between different schemes, Lt and γ1 are fixed, and γ2 change
综上所述,本文的仿真部分主要研究总时延DLt(时隙)与几个重要变量(缓存包个数Lt,齐普夫定律中内容流行指数变量,前程链路信噪比γ1,下行链路信噪比γ2)之间的变化对应关系,与本文提出算法1与其他三种方案(平均分配,无缓存,整体内容缓存)的性能对比。
从以上分析中,可总结得知:
1)比起其他三种方案,算法1始终实现最小时延,但这种性能优势会随着几个变量的变化扩大或缩小;
2)为了尽可能减少总时延,需要增加缓存包个数,提升前程链路信噪比,提升下行链路信噪比,增加齐普夫定律中内容流行指数变量。随着各种变量数值增长,总时延不会无限降低,而是收敛到一个稳定最小值,各种变化趋势可详见仿真图。
6 结论
本文针对带缓存的Cloud-RAN,以最小化传输时延为目标,利用BSO算法对缓存方案进行了优化设计。基于HARQ机制与马尔可夫链理论,系统建立最小化系统传输时延的优化问题,并引入BSO算法解决无明确目标函数的优化问题。仿真结果验证了所提算法可以有效地降低传统时延,符合未来通信的需求。本文仅考虑单RRH场景下最小化时延方案研究,未考虑多RRHs场景下的相关问题,未来工作中需要进一步研究。
附录
附录1 推论3.2证明过程
证明 同推论3.1的证明相似,根据α,β不同取值,有以下四种情况:
1)RRH端没有数据包,用户端已成功接收L数据包,此时α=0,β=L,A2=0,λ(α,β)=0;
2)RRH端有缓存数据包,用户端已成功接收部分数据包,满足α+β=L,A2=1,B2=0,C2=1,λ(α,β)=1+(1-ρ2)λ(α,β)+ρ2λ(α-1,β+1);
3)RRH端没有数据包,此时α=0,A2=1,B2=1,C2=0,λ(α,β)=1+(1-ρ1)λ(α,β)+ρ1λ(α,β+1);
4)RRH端有部分缓存数据包,用户端已成功接收部分数据包,并满足α≠0,α+β≠L,此时A2=1,B2=1,C2=1,传输时隙λ(α,β)如下所示:
λ(α,β)=1+ρ1ρ2λ(α,β+1)+(1-ρ1)ρ2λ(α-1,β+1)
(1-ρ1)(1-ρ2)λ(α,β)+ρ1(1-ρ2)λ(α+1,β)
(24)
将四种情况中的结论合并,可得公式(11),推论3.2得证。
附录2 推论3.3证明过程
证明 同推论3.1的证明相似,根据α,β不同取值,有以下四种情况:
1)RRH端没有数据包,用户端已成功接收L数据包,此时α=0,β=L,A2=0,B2=0,C2=0,可得传输时隙λ(α,β)表达式:
λ(α,β)=0
(25)
这与推论3.2中情况1)中结论一致。
2)RRH端有缓存数据包,用户端已成功接收部分数据包,满足α+β=L,A2=1,B2=0,C2=1, 从推论3.2中情况2)可知:λ(α,β)=1+(1-ρ2)λ(α,β)+ρ2λ(α-1,β+1),将(1-ρ2)λ(α,β)移至等式左侧,解方程可得传输时隙λ(α,β)表达式:
λ(α,β)=(1+ρ2λ(α-1,β+1))/ρ2
(26)
3)RRH端没有数据包,此时α=0,A2=1,B2=1,C2=0,从推论3.2中情况3)可知:λ(α,β)=1+(1-ρ1)λ(α,β)+ρ1λ(α,β+1),将(1-ρ2)λ(α,β)移至等式左侧,解方程可得传输时隙λ(α,β)表达式:
λ(α,β)=(1+ρ1λ(α+1,β))/ρ1
(27)
4)RRH端有部分缓存数据包,用户端已成功接收部分数据包,并满足α≠0,α+β≠L,此时A2=1,B2=1,C2=1,从推论3.2中情况可知:
λ(α,β)=1+(1-ρ1)(1-ρ2)λ(α,β)+ρ1(1-ρ2)λ(α+1,β)
+ρ1ρ2λ(α,β+1)+(1-ρ1)ρ2λ(α-1,β+1)
(28)
将(1-ρ1)(1-ρ2)λ(α,β)移至等式左侧,解方程可得传输时隙λ(α,β)表达式:
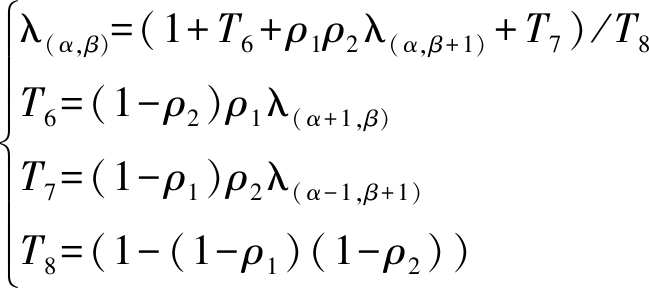
(29)
将四种情况中的结论合并,可得公式(13),推论3.3得证。
[1] Checko A, Christiansen H L, Yan Y, et al. Cloud RAN for Mobile Networks—A Technology Overview[J]. IEEE Communications Surveys & Tutorials, 2015, 17(1): 405- 426.
[2] You X H, Wang D M, Sheng B, et al. Cooperative distributed antenna systems for mobile communications[Coordinated and Distributed MIMO][J]. IEEE Wireless Communications, 2010, 17(3): 35- 43.
[3] Wang D M, Wang J Z, You X H, et al. Spectral Efficiency of Distributed MIMO Systems[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(10): 2112-2127.
[4] Li C G, Song K, Li Y S, et al. Energy efficient design for multiuser downlink energy and uplink information transfer in 5G[J]. Science China Information Sciences, 2016, 59(2): 74- 81.
[5] Xin Y X, Wang D M, Li J M, et al. Area Spectral Efficiency and Area Energy Efficiency of Massive MIMO Cellular Systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(5): 3243-3254.
[6] He S W, Huang Y M, Yang L X, et al. Energy Efficient Coordinated Beamforming for Multicell System: Duality-Based Algorithm Design and Massive MIMO Transition[J]. IEEE Transactions on Communications, 2015, 63(12): 4920- 4935.
[7] Wang Y, Li C G, Huang Y M, et al. Energy-Efficient Optimization for Downlink Massive MIMO FDD Systems With Transmit-Side Channel[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7228-7243.
[8] Liu L, Bi S Z, Zhang R. Joint Power Control and Fronthaul Rate Allocation for Throughput Maximization in OFDMA-Based Cloud Radio Access Network[J]. IEEE Transactions on Communications, 2015, 63(11): 4097- 4110.
[9] Sun Y, Li C G, Huang Y M, et al. Energy-efficient resource allocation in C-RAN with fronthaul rate constraints[C]∥IEEE International Conference on Wireless Communications & Signal Processing, Yangzhou, 2016: 1- 6.
[10] Park S H, Simeone O, Sahin O, et al. Joint Decompression and Decoding for Cloud Radio Access Networks[J]. IEEE Signal Processing Letters, 2013, 20(5): 503-506.
[11] Sun Y, Li S D, Yang L X. Green fronthaul allocation and power management in Cloud-RAN[J]. EURASIP Journal on Wireless Communications and Networking, 2018, 2018(1): 188.
[12] Zhou Y H, Yu W. Optimized Backhaul Compression for Uplink Cloud Radio Access Network[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1295-1307.
[13] Sun Y, Li C G, Huang Y M, et al. Joint Fronthaul Rate Allocation and Power Control in OFDMA-based C-RANs: Multi-Objective Approach[J]. Ad Hoc & Sensor Wireless Networks, 2017, 37(1- 4): 197-229.
[14] Li C G, Song K, Wang D M, et al. Optimal remote radio head selection for cloud radio access networks[J]. Science China Information Sciences, 59(10): 1-12.
[15] Tao M X, Chen E, Zhou H, et al. Content-Centric Sparse Multicast Beamforming for Cache-Enabled Cloud RAN[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6118- 6131.
[16] Zhao Z Y, Peng M G, Ding Z G, et al. Cluster Content Caching: An Energy-Efficient Approach to Improve Quality of Service in Cloud Radio Access Networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(6): 1207-1221.
[17] Tran T X, Hajisami A, Pandey P, et al. Collaborative Mobile Edge Computing in 5G Networks: New Paradigms, Scenarios, and Challenges[J]. IEEE Communications Magazine, 2017, 55(4): 54- 61.
[18] Parvez I, Rahmati A, Guvenc I, et al. A Survey on Low Latency Towards 5G: RAN, Core Network and Caching Solutions[J]. IEEE Communications Surveys & Tutorials, 2018, accepted for publication.
[19] Tandon R, Simeone O. Cloud-aided wireless networks with edge caching: Fundamental latency trade-offs in fog Radio Access Networks[C]∥IEEE International Symposium on Information Theory, Barcelona, 2016: 2029-2033.
[20] Girgis A M, Ercetin O, Nafie M, et al. Decentralized coded caching in wireless networks: Trade-off between storage and latency[C]∥IEEE International Symposium on Information Theory, Aachen, 2017: 2443-2447.
[21] Goseling J, Simeone O, Popovski P, et al. Delivery Latency Trade-Offs of Heterogeneous Contents in Fog Radio Access Networks[C]∥IEEE Global Communications Conference, Singapore, 2017: 1- 6.
[22] Sengupta A, Tandon R, Simeone O. Fog-Aided Wireless Networks for Content Delivery: Fundamental Latency Tradeoffs[J]. IEEE Transactions on Information Theory, 2017, 63(10): 6650- 6678.
[23] Dai J M, Zhang Z L, Liu D P. Proactive Caching over Cloud Radio Access Network with User Mobility and Video Segment Popularity Awared[J]. IEEE Access, 2018, accepted for publication.
[24] Boyd S, Vandenberghe L. Convex Optimization[M]. New York: Cambridge University Press, 2004: 32- 40.
[25] Shi Y H. An optimization algorithm based on brainstorming process[J]. International Journal of Swarm Intelligence Reseach, 2011, 2(4): 36- 62.
[26] Shi Y H. Brain storm optimization algorithm[C]∥International Conference in Swarm Intelligence, Berlin, 2011: 303-309.
[27] Stanvjev I, Simeonr O, Bar-ness Y, et al. Energy efficiency of non-collaborative and collaborative Hybrid-ARQ protocols[J]. IEEE Transactions on Wireless Communications, 2009, 8(1): 326-335.
[28] Mao C N, Huang M H, Padhy S, et al. Minimizing Latency of Real-Time Container Cloud for Software Radio Access Networks[C]∥IEEE International Conference on Cloud Computing Technology and Science, Vancouver, 2015: 611- 616.
[29] Mountaser G, Rosas M L, Mahmoodi T, et al. On the Feasibility of MAC and PHY Split in Cloud RAN[C]∥IEEE Wireless Communications and Networking Conference, San Francisco, 2017: 1- 6.
[30] Ioannou A, Weber S. A Survey of Caching Policies and Forwarding Mechanisms in Information-Centric Networking[J]. IEEE Communications Surveys & Tutorials, 2016, 18(4): 2847-2886.
[31] Shanmugam K, Dimakis A G, Caire G. FemtoCaching: Wireless Content Delivery Through Distributed Caching Helpers[J]. IEEE Transactions on Information Theory, 2013, 59(12): 8402- 8413.
[32] Hsu H, Chen K. A Resource Allocation Perspective on Caching to Achieve Low Latency[J]. IEEE Communications Letters, 2016, 20(1): 145-148.
