1 引言
非线性滤波是目标跟踪研究的热点问题。已取得的研究成果可分为两类:(1)基于采样的非线性滤波,代表性方法有无味滤波[1](UKF: Unscented Kalman Filter)、容积卡尔曼滤波[2](CKF: Cubature Kalman Filter)、粒子滤波[3](PF: Particle Filter)等。这些方法估计性能好,但计算量偏大;(2)基于非线性变换的方法,代表性算法有扩展卡尔曼滤波(EKF: Extended Kalman Filter)和量测转换卡尔曼滤波(CMKF: Converted Measurement Kalman Filter)。这类方法实现容易,实时性好,但性能一般。基于非线性变换的跟踪方法中,CMKF出现较晚,该方法自提出以来,针对目标跟踪产生诸多成果:Lerro等首先发现CMKF在非线性变换过程中,有一个加性量测转换偏差,需做去偏处理,并给出处理方法。文献[4]推导出量测转换偏差的实质是乘性的,进一步将算法扩展到量测噪声符合对称非高斯分布的情况,使其更具有普适性。文献[5]研究发现文献[4]的方法存在转换兼容性问题,提出以量测为条件来计算转换误差统计特性的方法,称为无偏量测转换,并仿真验证其优越性。文献[6]对前述方法进行概括,指出其存在三个缺陷与Kalman滤波前提相冲突,因此尽管能够在转换后完成滤波,但估计值绝非最优,提出最佳无偏滤波方法(BLUE),修正了CMKF的缺陷,提高了性能。文献[7]对CMKF的几类典型方法进行比较后,认为BLUE滤波方法在实时性、一致性和精确性都是最优。量测转换[8-13]已被用于测角定位、测量距离变化率定位、机动目标跟踪、多普勒跟踪、塔康系统中。
作为量测转换中性能最优的一种方法,经典BLUE滤波的性能不如基于采样的非线性滤波器,以塔康系统[14]中的目标跟踪为例,目标距离中心站较近时,斜距和高程大小相近,受量测噪声影响,斜距在地面的投影误差会急剧增大,甚至出现虚数解的情况,称为“共线”效应。“共线”效应会导致滤波误差增大甚至发散。为解决此问题,基于非线性量测和状态预测的融合估计,提出改进的量测转换模型,通过减小非线性参数误差,抑制“共线”效应。参数误差减小后,基于改进模型的BLUE滤波器能精确估计转换量测统计特性,提高对近距离目标的估计精度,且计算量较小。
2 量测预测融合估计的BLUE
本节简述BLUE算法流程,给出塔康系统中的量测转换模型。分析该模型不足后,提出改进的量测转换模型,产生一种自适应BLUE滤波方法。
2.1 BLUE算法原理
假设目标状态满足式(1)的线性关系。
xk=Fk/k-1xk-1+wk
(1)
xk是k时刻目标状态,wk～N(0,Qk)是高斯观测白噪声,Fk/k-1是状态转移矩阵。
基于式(1)的BLUE滤波器具有递归结构。已知目标状态先验估计
和误差协方差阵P0,第1步预测目标状态。
(2)
是k-1时刻状态估计,
是k时刻状态预测。
第2步计算状态预测协方差阵。
(3)
Pk-1是k-1时刻的状态估计协方差阵,
是k时刻状态预测协方差阵。
第3步是计算转换量测误差
是k时刻转换量测,
是对zk的预测。
(4)
第4步计算k时刻滤波增益因子Kk。
(5)
是k时刻状态预测误差
和
的协方差阵,Sk是的协方差阵。
第5步状态估计。
(6)
第6步计算估计误差的协方差阵。
(7)
可见BLUE递归滤波的关键是构建转换量测zk,并在线估计
和
下面分析原有量测转换模型的缺陷,提出改进的量测转换模型,并推导滤波参数。
2.2 改进量测转换模型
(1)原有量测转换模型
塔康系统定位模型如图1所示。中心站位于原点,目标位于T处。目标到中心的斜距为r、方位角θ,高程为h,量测误差
和
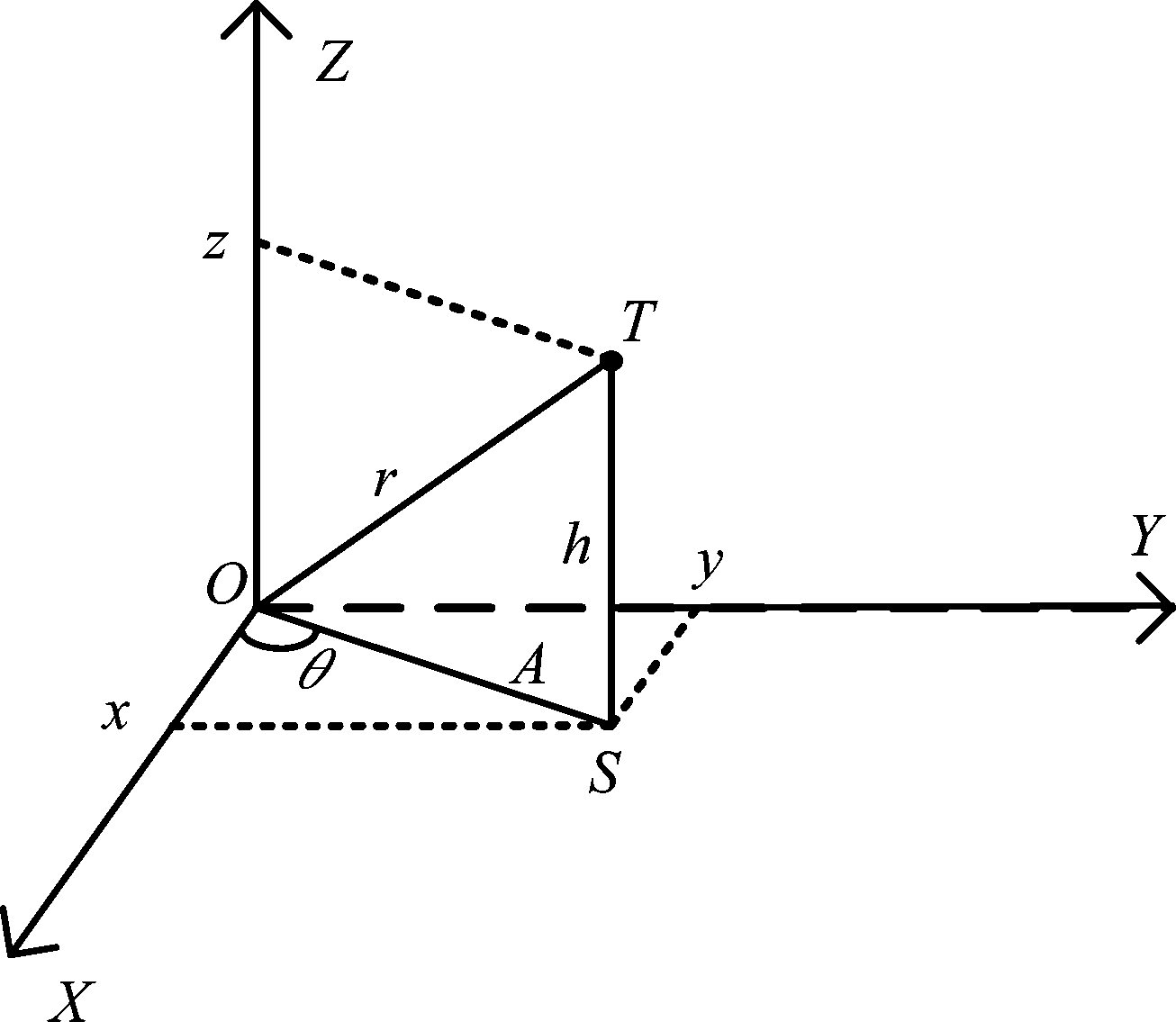
图1 塔康系统定位示意图
Fig. 1 Location diagram of TACON system
由非线性量测可以得到直角坐标系的量测转换模型。
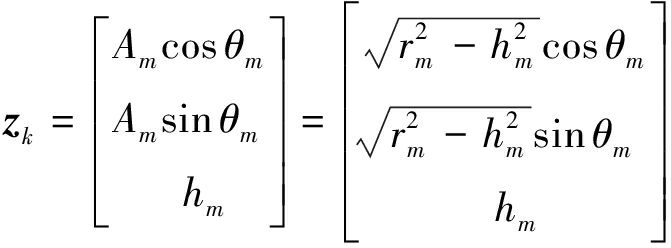
(8)
如图2,Am为rm在XOY平面的投影。基于该模型的BLUE滤波对近程目标跟踪性能较差,原因在于:斜距和高程大小相近时,很小的斜距或高程误差都会使Am误差增大,甚至出现虚数解(比如真实斜距和高程分别为2000 m和1900 m,斜距误差-50 m,高程误差60 m,则Am为虚数解)。为解决此问题,需要减小斜距和高程误差,克服“共线”效应和虚数解出现,因此在量测转换模型中引入量测和预测的融合估计,通过减小参数误差,抑制非线性影响。
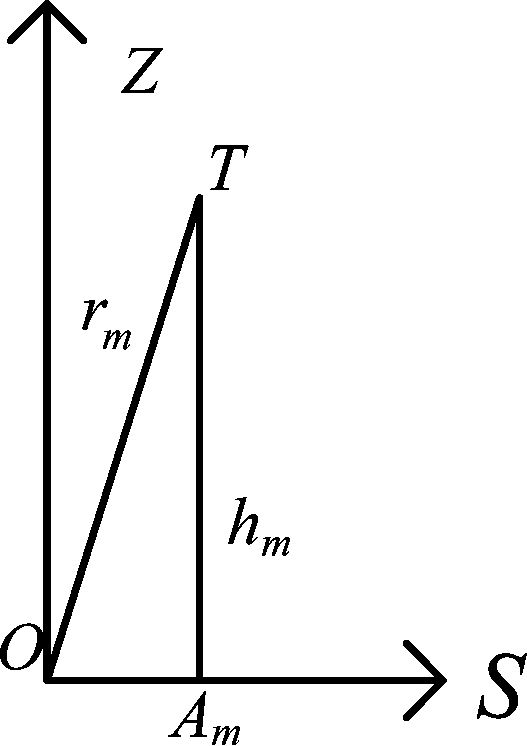
图2 “共线”效应说明
Fig.2 Diagram of collinear effect
(2)改进量测转换模型
已知k时刻真实状态
状态预测
根据位置预测构造斜距预测rp。
(9)
其中
斜距预测误差为
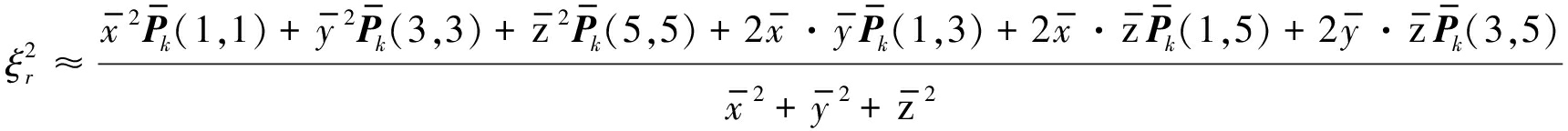
表示xk的预测协方差阵
第i行第j列的元素。由斜距量测和预测构造出斜距估计rf,αk为k时刻斜距权值。
rf=αkrm+(1-αk)rp
(10)
类似的可构造高程估计hf,βk为k时刻高程权值。
(11)
斜距、高程估计构建的量测转换模型可以提高BLUE滤波性能,原因在于:1)rf和hf的误差小于rm和hm,可降低虚数解出现概率,抑制滤波发散。2)参数误差的减小使得
的均方差小于
目标位于中心站顶部时,rf有小于hf的可能。为此在斜距和高程中加入偏置rb和hb,进一步降低虚数解出现概率。最终构建斜距在XOY面投影的融合估计Af,其估计误差
(12)
构建Af后需解决两个问题:①αk和βk取值多少？②偏置rb和hb如何设置？
Af的估计精度与斜距、高程误差相关
和
越小,对Af估计越准确,下面基于加权估计误差最小原则推导出αk和βk表达式。
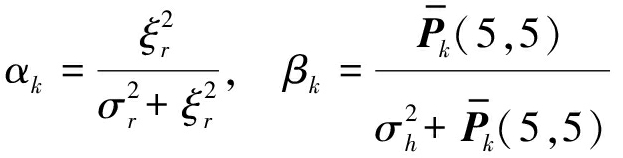
(13)
得到αk和βk后,可求解斜距、高程估计方差和互协方差。
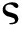
(14)
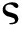
(15)
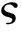
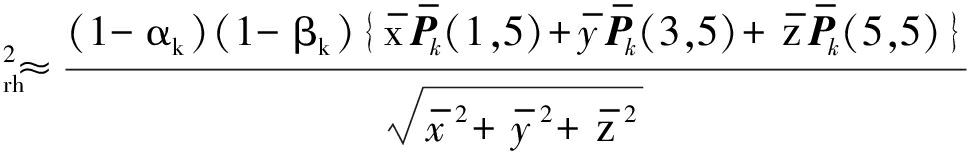
(16)
下面求解rb和hb。引入偏置是为了降低虚数解出现概率,即rf+rb以较大概率高于hf+hb。
Pr{rf+rb≥hf+hb}=
(17)
PT是概率门限。假设
和
为高斯分布,则
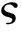
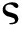
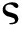
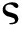
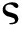
(18)
PT=97.72%时,有以下关系。
r-h+rb-hb≥2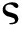
(19)
即在式(19)的条件下,rf+rb≥hf+hb可能性超过 97.72%,rb和hb之间关系为
(20)
下面讨论在式(20)的约束下,如何使rb和hb最佳:rb相对r的比例越小,rb对斜距投影误差的影响越小;同理hb相对h的比例越小越好。据此建立目标函数(21)。
(21)
在式(20)的约束下,使f(rb,hb)最小化,可以得到rb和hb。
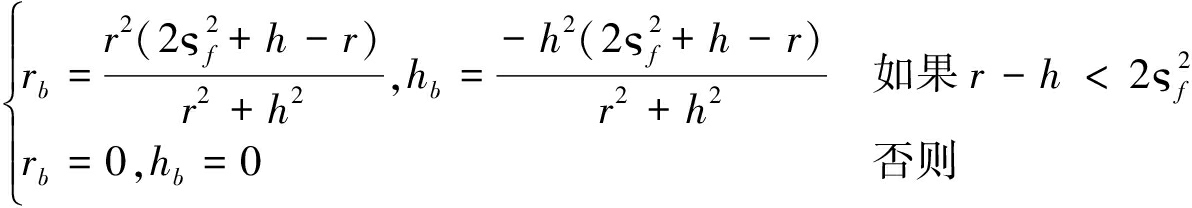
(22)
得到斜距、高程估计的权值和偏置后,可以计算Af的方差
和均值πA。
量测转换模型的最终形式为公式(23)。
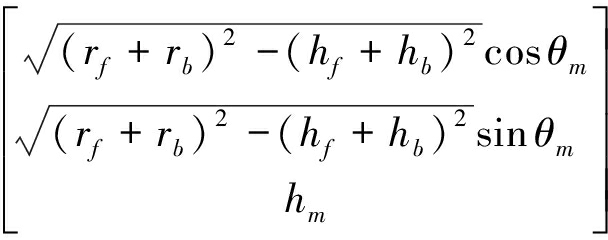
(23)
2.3 参数解算和滤波流程
前面提出改进转换量测模型,并分析模型参数和误差统计特性。下面基于此模型推导BLUE滤波器参数。由式(12)的量测转换模型得到量测预测
其中
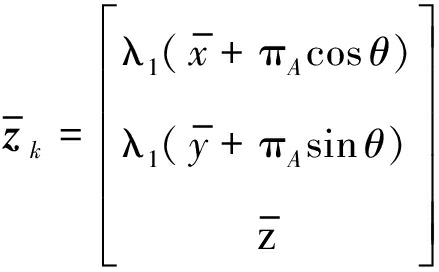
(24)
其中
转换量测误差表达式如式(25)所示。
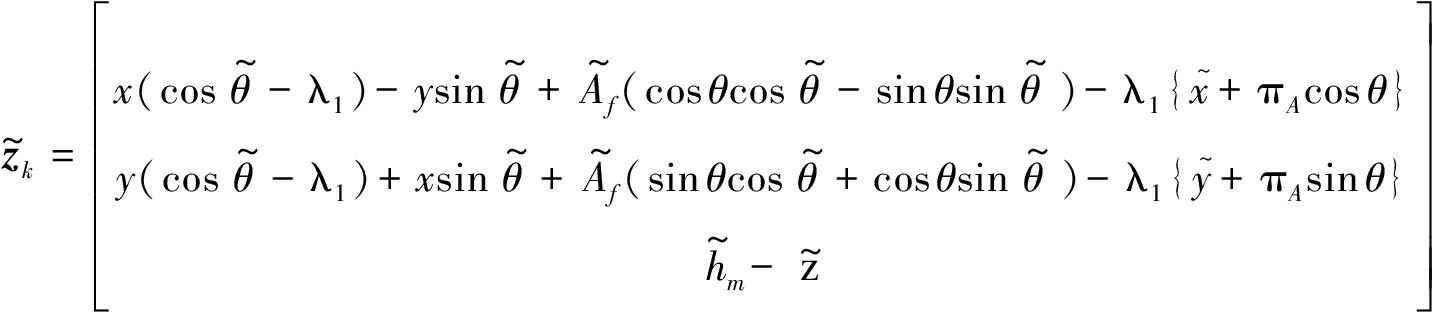
(25)
预测误差与量测误差的互协方差矩阵
如式(26)所示。
(26)
其中
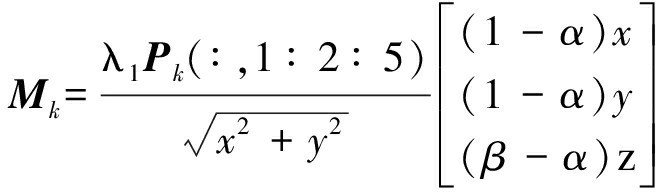[cos θ sin θ 0]
最后求解Sk,其元素如式(27)所示。
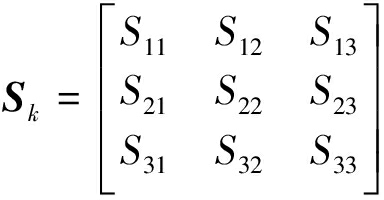
(27)
Sk矩阵中相关参数表达式如下。其中
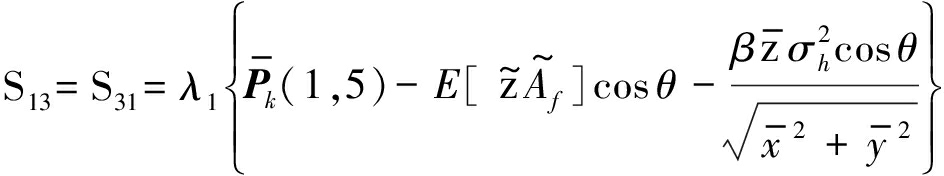
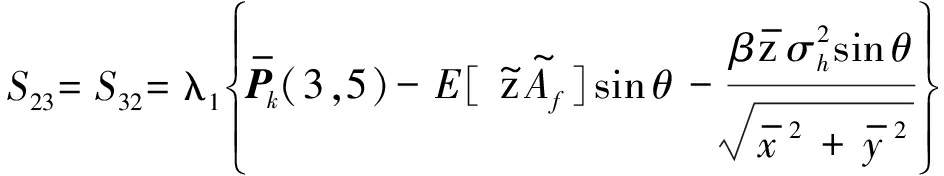
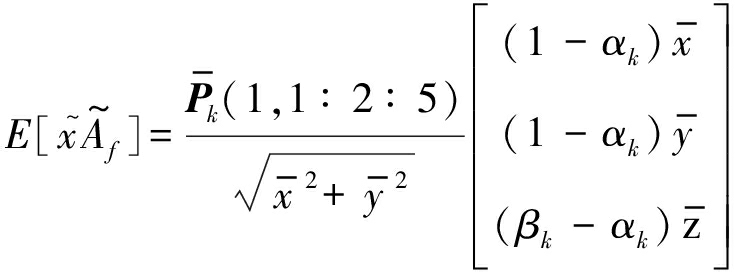
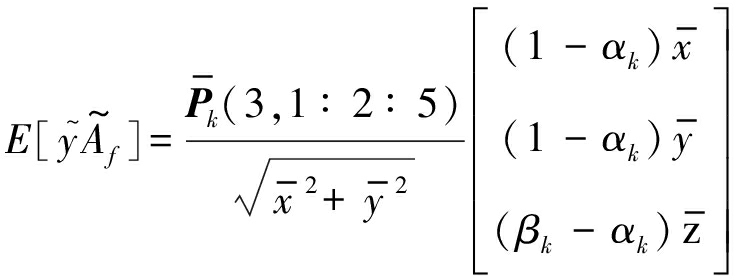
改进BLUE滤波流程如图3所示。
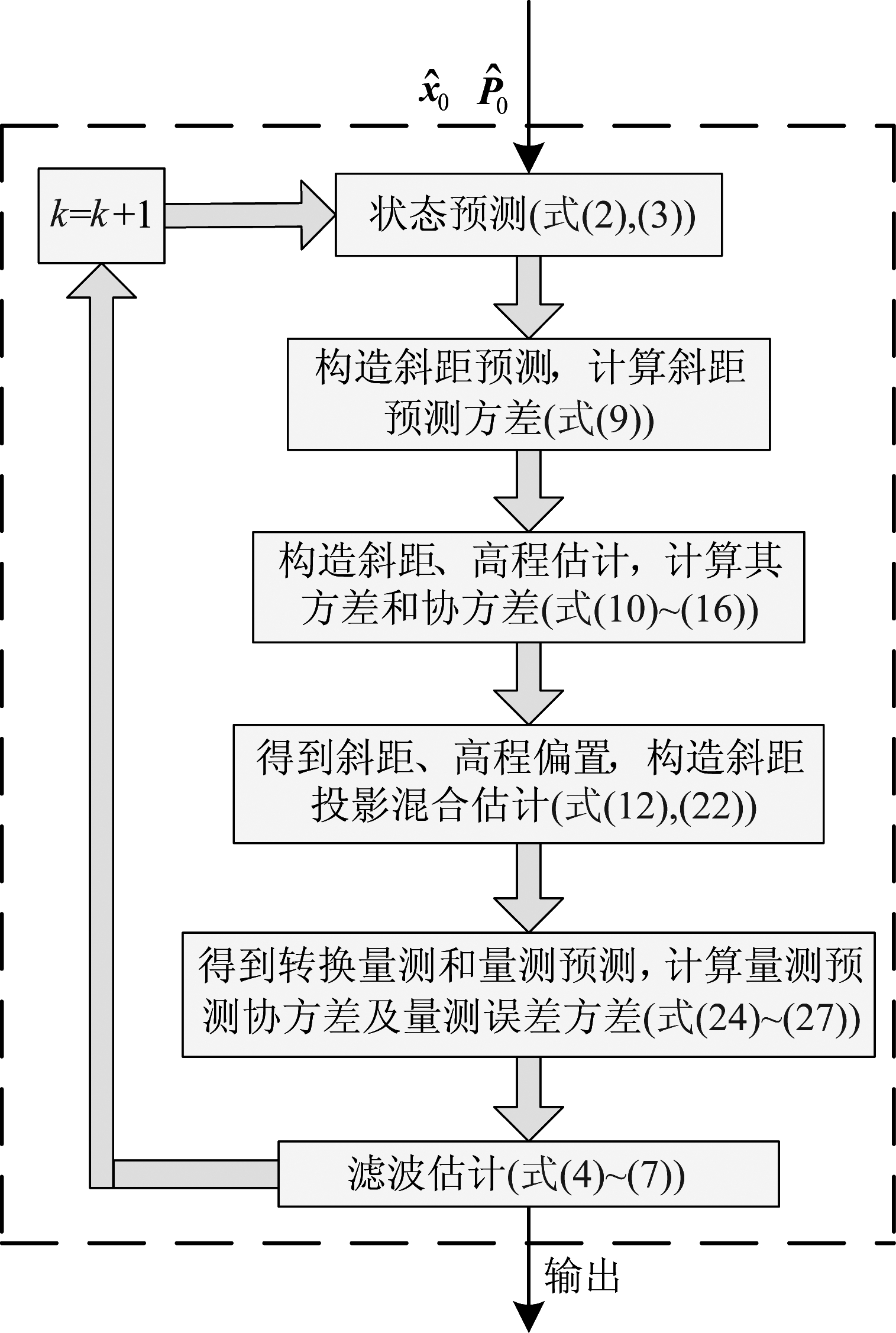
图3 自适应BLUE算法流程
Fig.3 Flow of adaptive BLUE algorithm
3 仿真与分析
EKF跟踪近程目标时数值稳定性较差,因此将所提自适应算法与基于高程补偿的BLUE[10]和CKF[2]比对,具体设置如下:中心站位于原点,目标起始位置均值(-5,0,5)km,标准差(10,10,10)m,起始速度均值(50,0,0)m/s,标准差(1,1,1)m/s。斜距精度30 m,高程精度60 m,方位精度0.1度。各坐标轴位置噪声独立无关,标准差0.1 m;速度噪声独立无关,标准差0.1 m/s。概率阈值PT=97.72%。采样周期1 s,仿真时长200 s。
评估指标包括位置RMSE(Root Mean Square Error)、ANEES(Average Normalized Estimation Error Square),ANEES为1时滤波置信度最高[6]。为便于分析问题,提出归一化转换量测误差均方ANCMES(Average Normalized Converted Measurement Error Squared),定义如下。
(28)
和Si是第i次仿真中的转换量测误差和协方差阵,N是仿真次数,n是转换量测维数。ANCMES用于检验转换量测的二阶特性,接近1时表明能够精确估计转换量测二阶矩。
仿真200次的结果如图4所示。由仿真结果有以下分析:
(1)图4(a)可见在“共线”情况下(100 s附近),单纯对高程偏差进行补偿的方法不足以有效减小参数误差,抑制斜距和高程量测之间的强非线性,因此基于高程补偿的BLUE算法精度很差;而自适应BLUE对斜距和高程同时做融合估计和偏差补偿,能有效减小参数误差,抑制“共线”效应,取得了和CKF相当的精度。
(2)图4(b)表明在“共线”情况下,自适应BLUE和CKF滤波器置信度最优,而高程补偿的BLUE则出现下降。
(3)图4(c)揭示自适应BLUE性能稳定的原因:目标位于中心站顶空时,非线性增强,较大的斜距和高程误差会导致对转换量测的估计精度下降;自适应BLUE通过引入斜距和高程预测,减小参数误差,克服了对转换量测估计不准的问题,因此性能较好。
(4)图4(d)是自适应BLUE跟踪中斜距和高程权值的变化,目标接近中心站时,斜距和高程预测精度提高,而斜距、高程观测精度保持不变,由式(13)可知斜距和高程权值会下降;远离中心时,预测精度降低,相应的斜距、高程权值增大。
场景2中,其他条件不变,提高各轴的状态噪声。假设位置噪声标准差1 m,速度噪声标准差1 m/s,相关跟踪结果如图5所示。
由图5的仿真结果有以下分析:
(1)目标状态噪声导致算法跟踪误差变大,但自适应BLUE方法性能依然较好(图5(a))。
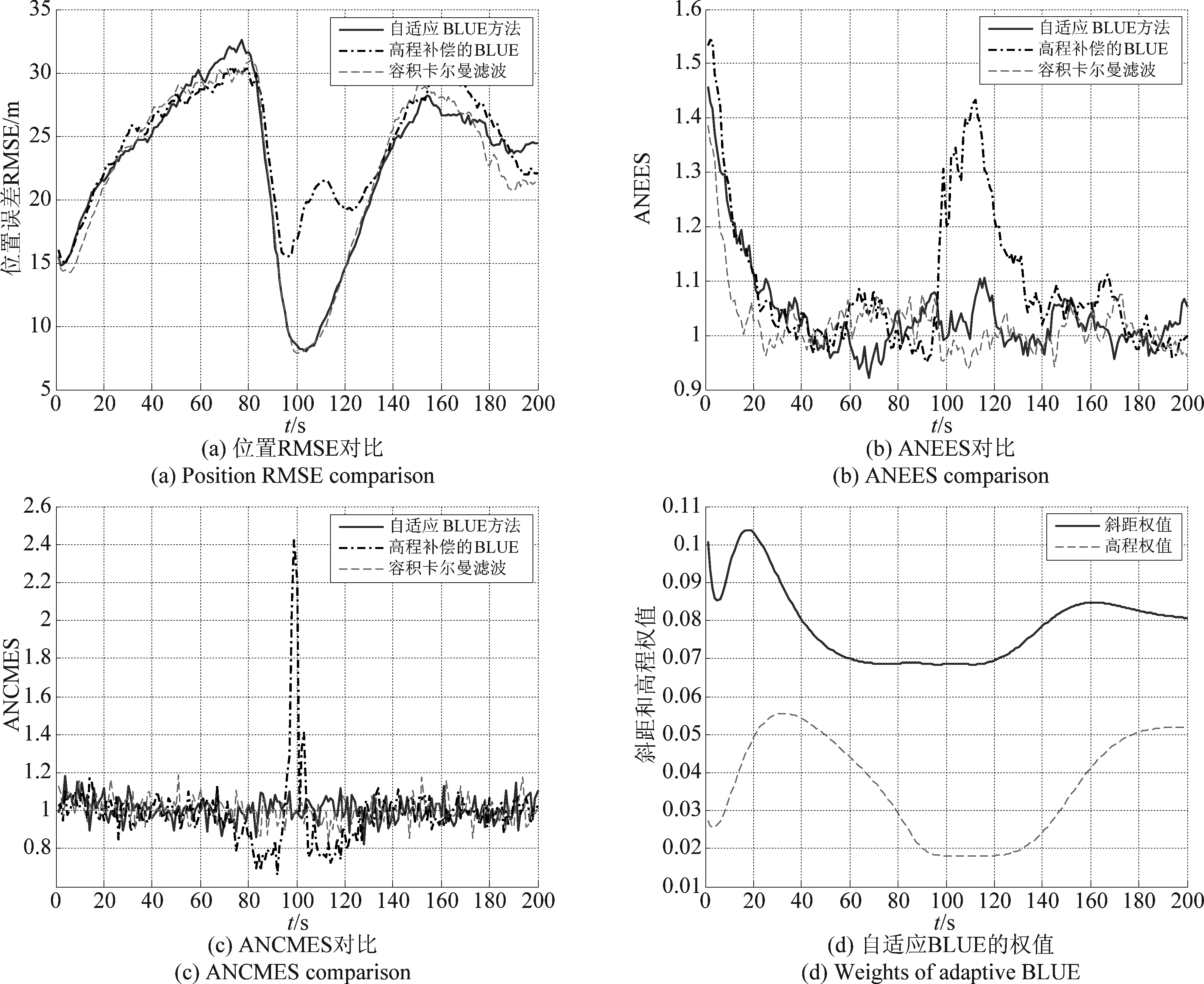
图4 场景1的跟踪性能
Fig.4 Tracking performance for scenario 1
图5 场景2的跟踪性能
Fig.5 Tracking performance for scenario 2
(2)目标接近中心站时,受“共线”效应影响,基于高程补偿的BLUE滤波不能精确估计转换量测序列统计特性,导致ANEES增大(图5(b));自适应方法能精确估计转换量测统计特性(图5(c)),因此滤波置信度接近最优。
(3)场景2的状态噪声相对场景1有数量级的增大,因此目标跟踪的预测精度下降,而量测精度不变,由公式(13)可知斜距、高程的权值会相对场景1有所增大,图5(d)的仿真结果验证了这一推理。
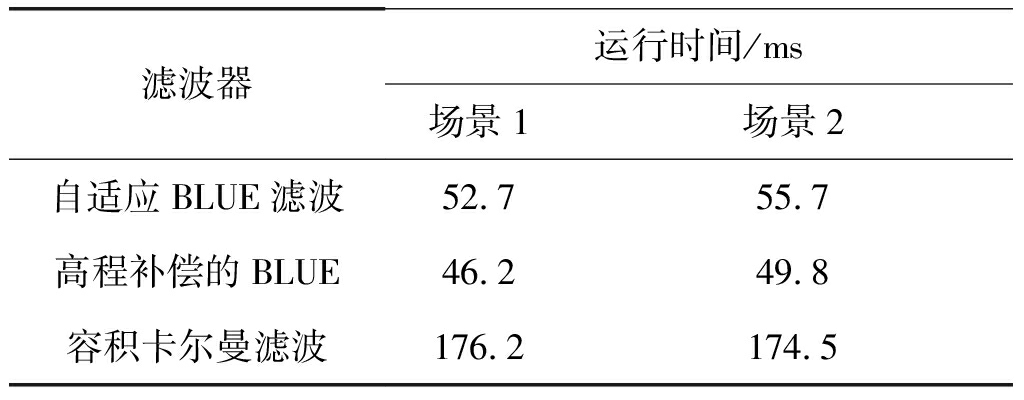
除了估计精度和稳健性,实时滤波是目标跟踪的基本要求,三种算法在奔腾双核4 GHz计算机上,Matlab 7.11中完成一次跟踪的运行时间如表1所示。三种方法中CKF的计算量最大,两种BLUE方法的计算量相当,只有CKF的30%左右,可见自适应BLUE估计精度较高,且能满足跟踪实时性要求。
表1 一次完整跟踪过程所需时间对比
Tab.1 Comparison of running time for a single iteration
滤波器运行时间/ms场景1场景2自适应BLUE滤波52.755.7高程补偿的BLUE46.249.8容积卡尔曼滤波176.2174.5
4 结论
BLUE算法跟踪近程目标时,斜距、高程间的“共线”效应影响对转换量测的估计精度,导致性能下降。提出量测和预测融合估计概念,通过减小参数误差,克服非线性变换不利影响,并引入斜距和高程偏置降低无效量测出现概率,提高了算法性能。仿真实验表明:改进算法能精确估计出转换量测的统计特性,因此性能与采样类滤波方法相当,而计算量较小。算法在不同状态噪声下的滤波性能良好,是一种很有价值的自适应跟踪方法。
[1] Julier S J,Uhlmann J K. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations[C]∥Proceeding of the American Control Conference,2002: 887-892.
[2] Ienkaran A,Simon H. Cubature Kalman filters[J]. IEEE Trans. on Automatic Control,2009,54(6): 1254-1269.
[3] 程水英,张剑云. 粒子滤波评述[J]. 宇航学报,2008,29(4): 1099-1111.
Cheng Shuiying,Zhang Jianyun. Commentaries of particle filter[J]. Journal of Astronautics,2008,29(4): 1099-1111.(in Chinese)
[4] Mo Longbin,Song Xiaoquan,Zhou Yiyu,et al. Unbiased converted measurements for tracking[J]. IEEE Trans. on AES,1998,34(3): 1023-1027.
[5] Duan Zhansheng,Han Chongzhao,Li Xiaorong. Comments on “Unbiased converted measurements for tracking”[J]. IEEE Trans. on AES,2004,40(4): 1374-1377.
[6] Zhao Zhanlue. Best linear unbiased filtering with nonlinear measurements for target tracking[J]. IEEE Trans. on AES,2004,40(4): 1324-1336.
[7] Katkuri J R,Jilkov V P. A comparative study of nonlinear filters for target tracking in mixed coordinates[C]∥2010 42nd Southeastern Symposium on System Theory,2010: 202-207.
[8] Jiao Lianmeng,Pan Quan,Liang Yan.Nonlinear tracking algorithm with range-rate measurements based on unbiased measurement conversion[C]∥2012 15th International Conference on Information Fusion,2012: 1400-1405.
[9] Zhang Yunjun,Geng Zhi.Detection of target maneuver from bearings-only measurements[J]. IEEE Trans. on AES,2013,49(3): 2028-2034.
[10] 盛琥,王金根,陈治平,等. 基于高程补偿的BLUE算法在塔康中的应用研究[J]. 系统工程与电子技术,2016,36(8): 1752-1757.
Sheng Hu,Wang Jingen,Chen Zhiping,et al. Application research of altitude compensation based BLUE algorithm in TACON[J]. Systems Engineering and Electronics,2016,36(8): 1752-1757.(in Chinese)
[11] 王炜,李丹,姜礼平,等.可处理多普勒量测的最佳线性无偏估计算法[J]. 电子与信息学报,2015,37(6): 1336-1342.
Wang Wei,Li Dan,Jiang Lipin,et al. The Best Linear Unbiased Estimation Algorithm with Doppler Measurements[J]. Journal of Electronics & Information Technology,2015,37(6): 1336-1342.(in Chinese)
[12] 李为,李一平,封锡盛. 基于卡尔曼滤波预测的无偏量测转换方法[J]. 控制与决策,2015,30(2): 229-235.
Li Wei,Li Yipin,Feng Xisheng. Tracking with prediction-conditioned unbiased converted measurements[J]. Control and Decision,2015,30(2): 229-235.(in Chinese)
[13] Sheng Hu,Zhao Wenbo,Wang Jingen. Interacting multiple model tracking algorithm fusing input estimation and best linear unbiased estimation filter[J]. IET Radar,Sonar & Navigation,2017,11(1): 70-77.
[14] 盛琥,王金根,王立明,等. 量测转换卡尔曼滤波在塔康导航中的应用[J]. 信号处理,2015,31(1): 34-38.
Sheng Hu,Wang Jingen,Wang Liming,et al. Application of Converted Measurements Kalman Filter for TACAN Navigation[J]. Journal of Signal Processing,2015,31(1): 34-38.(in Chinese)
