随着移动智能设备的急剧增长,下一代无线网络将面临着数据业务需求的激增。根据思科报告[1]的最新预测,现有150多亿设备接入互联网,预计到2020年这一数字将增加至当前的三倍。无线接入的持续增长对当前移动通信的基础设施带来了巨大的挑战。为此,研究人员提出了异构网络(heterogeneous networks,HetNets)架构,其中不同类型的基站(base station,BS)部署在一个多级分层结构中,以提高网络的频谱效率[2- 4]。对于一个多层HetNets,其通常部署在常规的宏小区中,其中高性能的宏基站覆盖范围为一千米或者两千米,宏小区一般与小小区、微小区相结合。小小区BS通常用于减轻宏基站负载,实现负载平衡并提高服务质量。因此,HetNets的概念在未来的无线网络中十分重要,用来满足持续增长的移动通信量需求[5-7]。然而,为了充分发掘它的潜力,必须解决在异构部署中产生的一些挑战。
HetNets的主要挑战之一是用户级联(user association,UA)问题,即用户如何选择级联至不同层网络中的BS。UA方案不仅影响当前用户使用的物理资源块,而且还影响与同一BS级联的其他用户。同时,一旦某些BS被关闭,最初与其通信的移动终端需要与其他BS重新级联,这也极大地影响了网络性能。因此,如何解决UA问题在HetNets中至关重要。
通常,下行链路接收信号功率和信号与干扰加噪声比(signal-to-interference-noise ratio,SINR)是UA方案中两个主要的性能标准[8]。在4G网络中,下行链路接收信号功率主要用于实现UA。文献[9]中采用了一种基于SINR的UA规则,并获得了更高的用户吞吐量。然而,这两种传统的UA方案并不适合于HetNets。其原因在于,HetNets中不同小区的发送功率不同,小小区通常被高功率宏小区所覆盖。这种严重的负载不平衡将导致性能的损失。为了克服这个问题,文献[10]提出了小区范围扩展的概念,其基本思想是通过增加偏置因子来控制小小区用户的接收功率,实现最近小区UA来减轻宏小区负载,该方法也称为平均偏置接收功率(average biased received power,ABRP)方案。然而,这种UA方案的缺点是用户遭受到附近宏小区的强烈干扰。为了解决基于偏置的UA问题,提出了基于资源划分的干扰抑制方案。其中一种方法是增强小区内干扰协调,另一种方法是双连接[11]。在上述文献中,UA的选择取决于下行链路信号,并且一个用户的上行链路(uplink,UL)和下行链路(downlink,DL)均接入同一个BS。然而,在HetNets中,耦合的UL/DL访问模式效果不佳。其原因是,在HetNets中不同层BS的发送功率、网络架构等各不相同,加剧了UL和DL之间传输的不对称性。为此,文献[12-13]提出了解耦UL-DL用户级联方案。
虽然上述文章提出了各种有效的UA方案,但至今一些关键问题仍未得到解决。特别是在现有的文献中,广泛地使用了最佳UA方案。在该方案中,一个给定用户总是与提供最强接收信号功率(或SINR)的BS相级联。然而,在某些情况下,由于调度或负载平衡问题,提供最强信号(或SINR)的BS不可用。例如,一种情况是由于功率约束,最佳BS无法提供服务。此外,当BS级联的用户数达到上限时,即使BS能够提供最强的信号功率,用户也无法级联至该BS。例如,由于延迟约束,最佳BS受到限制。再者,频谱资源也是影响最佳BS选择的主要因素。为了解决此问题,将一个给定用户与非最佳BS相级联是一个很好的选择。另一种情况是,由于反馈延迟,系统仅获得了过时的信道状态信息,这导致系统做出一个错误选择,并且用户可能与非最佳BS(或层)相级联。这种情况下,急需提供一种有效的方案来评估由服务BS的错误选择而引起的性能损失。然而,据我们所知,上述问题迄今尚未得到解决。
受上述文献的启发,本文提出了K层HetNets非最佳UA方案,即第m阶ABRP UA方案,一个用户与具有第m个最强ABRP的BS相级联。即第k层网络BS的ABRP是第m个次序统计量。显然,最佳UA方案属于本文所提方案的特殊情况。对于提出的第m阶ABRP UA方案,通过随机几何建模,网络元素的位置服从齐次泊松点过程(Poisson point process,PPP),研究了一个给定用户与第m个最强ABRP的BS相级联的概率以及相应的下行链路SINR覆盖概率。研究发现,对于给定网络层k,当采用传统的最佳UA方案时,一个给定用户与该层相级联的概率随着当前层BS的发送功率单调增加。然而,采用本文所提出的非最佳UA方案,当BS的发送功率或强度相对较小时,UA概率增大;而当BS的发送功率或强度较大时,UA概率降低。由于非最佳BS的选择将导致网络平均性能的下降,但是该方案解决了最佳级联BS受限情况下,用户的级联问题,即使得用户设备选择次优的BS以保证通信。
考虑一个K层HetNets,以空间强度、发射功率、路径损耗指数和偏置因子等参数来区分各层。为了平衡网络负载,同时提高网络吞吐量,每层的覆盖区域可能重叠。第k层BS的空间位置满足强度为λk的PPP Φk,其中k=1,2,...,K表示第几层网络。此外,小区用户位置满足强度为λU的独立PPP ΦU。为了便于研究,假设第k层网络中每个BS都有相同的发送功率Pk,k=1,2,...,K,偏置因子βk。因此,每个网络层可由一个三元组(λk,Pk,βk)作唯一描述。在不考虑阴影衰落的情况下,此K层HetNets布局类似于加权Voronoi多边形[14]。图1给出了K=3时由宏小区,小小区和微小区组成的HetNets结构。
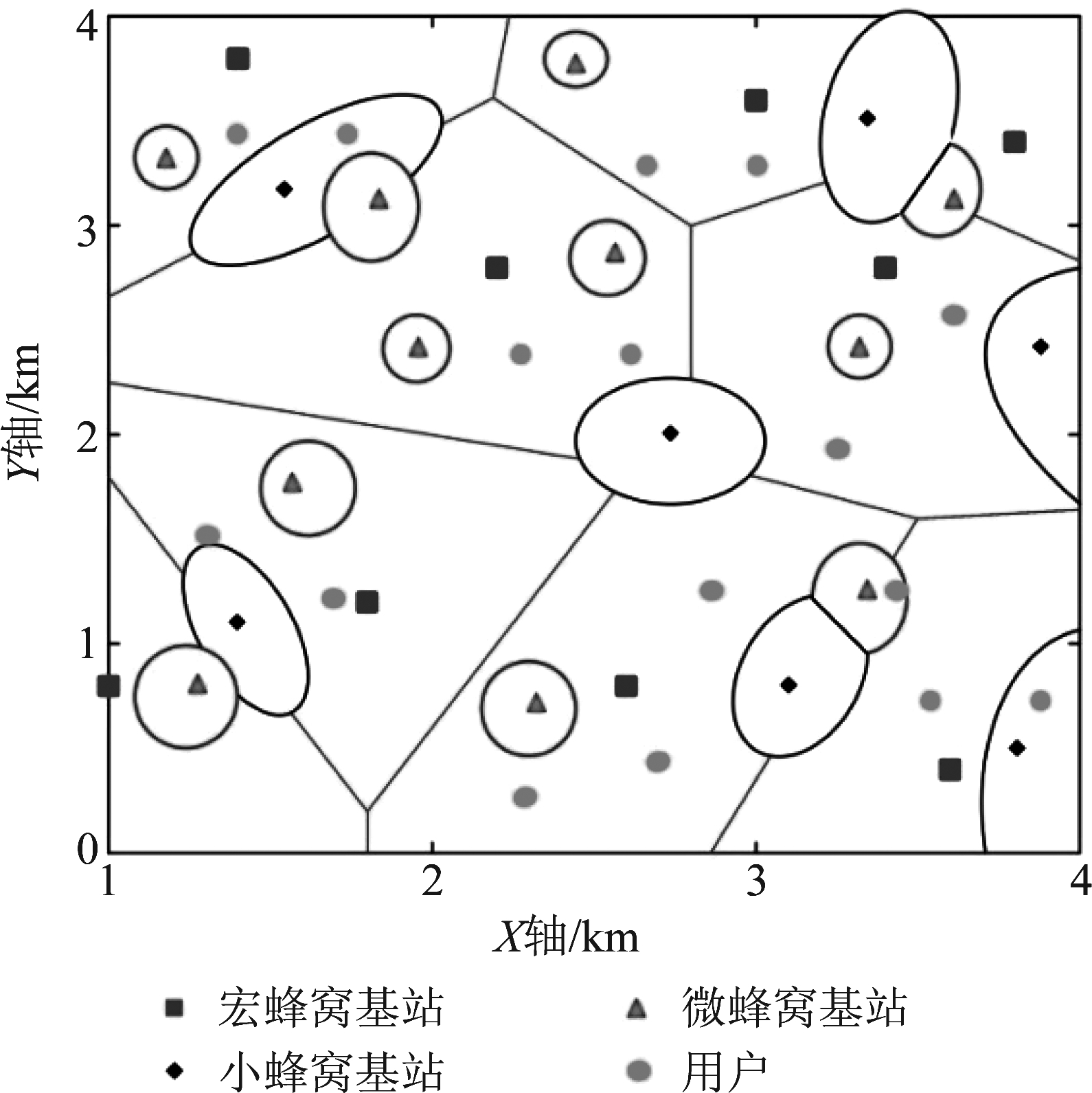
图1 3层HetNets示意图
Fig.1 Illustration of one realization of 3-tier HetNets
本文考虑一个位于原点给定用户的下行链路传输。对于所考虑的链路,给定用户为接收机,与其相级联的BS为信号发射机,而其他BS为干扰源。基于Silvngak理论,在满足PPP的HetNets中随机选择用户作为给定用户,即原来的PPP的分布相当于简化的Palm分布。即用于传输的PPP属性不变[15],且潜在干扰BS的分布仍服从具有相同强度的PPP。其中,用Yki表示BS i∈Φk到原点(即给定用户)的距离,用{Rj},j=1,2,...,K表示为第j层网络中给定用户与最近BS的距离。假设第k层网络的路径损耗指数相同,记为αk>2,k=1,2,...,K。信道模型满足瑞利衰落,在每个接收机处的加性高斯噪声为一恒定值W。
根据上述网络模型和假设,考虑基于ABRP方案的用户级联。在此方案中,对于原点处的一个给定用户,来自最近第k层网络BS的平均偏置接收功率Prk是K个独立的随机变量(random variables,RVs)。其表达如下
Prk=PkL0(Rk/r0)-αkβk
(1)
其中,L0是参考距离r0处的路径损耗(一般地r0=1时,L0=(4λ/ν)-2,其中ν为波长)。
考虑到在实际情况中,由于系统调度、负载平衡和资源约束等影响,HetNets网络中信道资源往往受限,这种情况下用户设备连接到提供最强ABRP的第k层网络的BS是困难的,在文献[18]中给出了相关的用户随机接入概率。为此,本文提出了一种更广义的UA方案,即一个给定用户与非最佳BS相级联。非最佳UA的核心思想是,当最佳BS不可用时,用户选择位于第k层网络中的第m个最强ABRP且位置最近的BS进行级联,m=1,2,...,K表示具有最强ABRP的BS的次序。假设K个RVs Prk,k=1,2,...,K的相应次序统计量可以通过对非增次序![]() ...,
...,![]() 取平均来获得,其中,m1,m2,...,mK∈k表示第mk层网络,是集合k∈{1,2,...,K}的一组序列。显然,
取平均来获得,其中,m1,m2,...,mK∈k表示第mk层网络,是集合k∈{1,2,...,K}的一组序列。显然,![]() 表示第m1层网络具有最强ABRP的最近
表示第m1层网络具有最强ABRP的最近![]() 表示第mK层网络中ABRP最弱的最近BS,则称
表示第mK层网络中ABRP最弱的最近BS,则称![]() 为第m个次序统计量[16]。因此,根据上述定义有
为第m个次序统计量[16]。因此,根据上述定义有
(2)
根据上述次序统计量的定义[16],这里定义![]() 为一个给定用户与第k层网络最近的BS相级联的概率,其中BS的ABRP是第m个次序统计量。那么就有
为一个给定用户与第k层网络最近的BS相级联的概率,其中BS的ABRP是第m个次序统计量。那么就有![]() 以图1的三层网络为例,
以图1的三层网络为例,![]() 表示在每一层选择一个具有最强ABRP的BS,则第m1层网络具有最强ABRP的BS,其中m1∈{1,2,3}。因此,根据次序统计[16],UA概率
表示在每一层选择一个具有最强ABRP的BS,则第m1层网络具有最强ABRP的BS,其中m1∈{1,2,3}。因此,根据次序统计[16],UA概率![]() 给出如下
给出如下
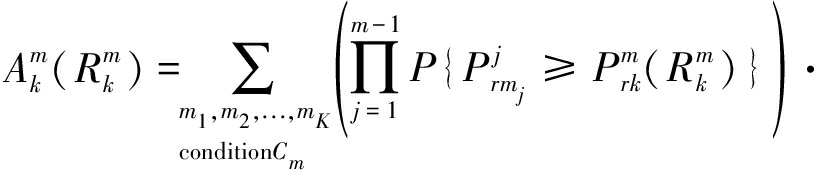
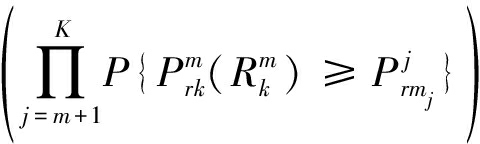
(3)
其中,条件Cm定义为:m1,m2,...,mm-1∈{1,2,...,K}-k,m1≠m2≠…≠mm-1,mm+1,mm+2,...,mK∈{1,2,...,K}-k,mm+1≠mm+2≠…≠mK,P{·}表示概率,这里的求和是对集合{1,2,...,k-1,k+1,...,K}的所有序列进行求和,![]() 是给定用户与其连接的最近第k层网络BS之间的距离。则平均UA概率可以表示为
是给定用户与其连接的最近第k层网络BS之间的距离。则平均UA概率可以表示为
(4)
其中,![]() 表示对
表示对![]() 求其期望。因此,将式(1)代入式(3),结合式(4),可得定理1,即平均UA概率
求其期望。因此,将式(1)代入式(3),结合式(4),可得定理1,即平均UA概率![]()
定理 1 对于K层HetNets的下行链路传输,一个给定用户与第k层网络最近BS连接的概率为![]() 其中用户的ABRP是第m个最大次序统计量,那么UA概率可以表示为
其中用户的ABRP是第m个最大次序统计量,那么UA概率可以表示为
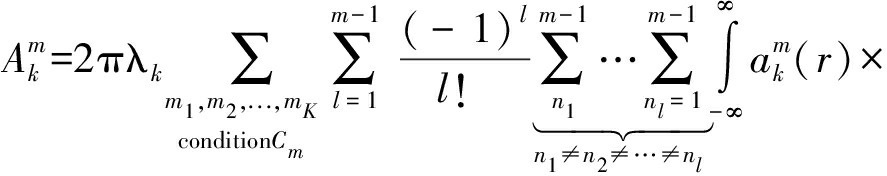
r×exp(-πλkr2)dr
(5)
其中,![]() 定义为
定义为
(6)
(7)
证明 见附录A。
根据定理1,当系统采用第m阶ABRP UA方案时,相应的UA概率![]() 在很大程度上取决于m。显然,随着m的增大,用户级联概率
在很大程度上取决于m。显然,随着m的增大,用户级联概率![]() 减小。观察表明,非最佳UA方案对UA概率
减小。观察表明,非最佳UA方案对UA概率![]() 产生了很大的影响。为了便于研究,且不失其一般性,考虑α1=α2=…=αK=α这一特殊情况。推论1给出了
产生了很大的影响。为了便于研究,且不失其一般性,考虑α1=α2=…=αK=α这一特殊情况。推论1给出了![]() 的闭式表达式。
的闭式表达式。
推论 1 在条件α1=α2=…=αK=α下,基于提出的第m阶ABRP UA方案,UA概率![]() 可以写成
可以写成
(8)
尽管式(8)给出了![]() 的闭式表达式,但由于其复杂的求和操作,很难得到Pj和λj等网络参数对UA概率的影响。为此,取K=3,m=2和k=1,在这种情况下,利用式(8),将UA概率
的闭式表达式,但由于其复杂的求和操作,很难得到Pj和λj等网络参数对UA概率的影响。为此,取K=3,m=2和k=1,在这种情况下,利用式(8),将UA概率![]() 表示为
表示为
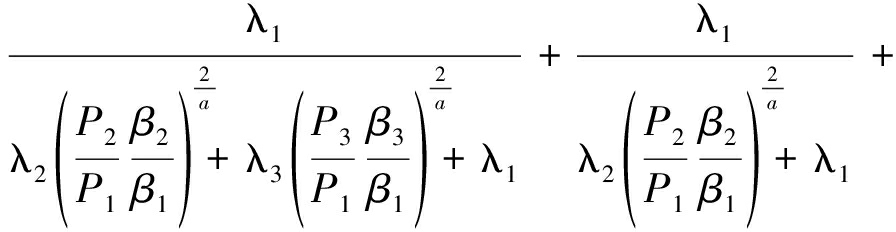

(9)
令![]() 和
和![]() 式(9)可写为
式(9)可写为
(10)
其中,E1,E2和E3为网络部署因子。尽管文献[10]表明,在最佳ABRP的UA方案中,UA概率![]() 随当前网络部署因子Ek增大,随着Ej,j≠k而减小。然而,当采用所提出的第m阶ABRP的UA方案时,由式(10)可以清晰地看出上述结果不成立。因此,为了研究式(10)中网络部署因子E1、E2和E3对
随当前网络部署因子Ek增大,随着Ej,j≠k而减小。然而,当采用所提出的第m阶ABRP的UA方案时,由式(10)可以清晰地看出上述结果不成立。因此,为了研究式(10)中网络部署因子E1、E2和E3对![]() 单调性的影响,借助数学工具,我们得出了推论2。
单调性的影响,借助数学工具,我们得出了推论2。
推论 2 对于第m阶ABRP的UA方案,考虑特殊情况K=3,m=2和k=1时,有以下两种情况:
(1)若E1和E3(或E2)固定,当![]() 时,UA概率
时,UA概率![]() 随着网络部署因子E2(或E3)减小;当
随着网络部署因子E2(或E3)减小;当![]() 时,UA概率
时,UA概率![]() 随E2(E3)增大。
随E2(E3)增大。
(2)若E2和E3固定,当![]() 时,UA概率
时,UA概率![]() 随E1增大;当
随E1增大;当![]() 时,UA概率
时,UA概率![]() 随E1减小。其中
随E1减小。其中![]() 由下式确定
由下式确定
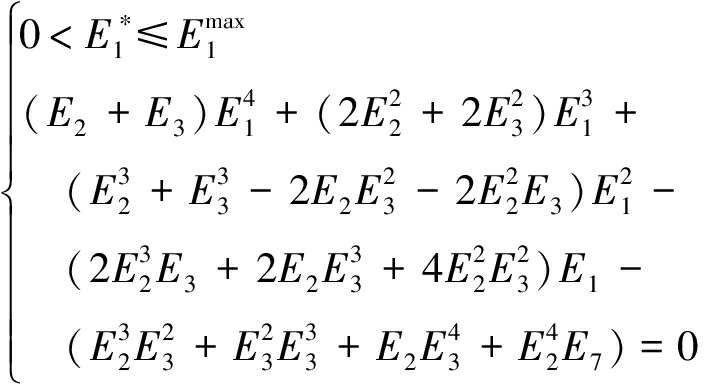
(11)
其中,![]() 是E1的最大值。由于E1=P1λ1,显然
是E1的最大值。由于E1=P1λ1,显然![]() 由λ1和P1的最大值决定。其证明过程参见附录B。
由λ1和P1的最大值决定。其证明过程参见附录B。
此外,式(8)表明,当m=1时,UA概率![]() 随着λk,Pk和βk的增大而增大。然而,当m>1时,结果并不总是如此。特别地,当Pk相对较小时,增大Pk将导致
随着λk,Pk和βk的增大而增大。然而,当m>1时,结果并不总是如此。特别地,当Pk相对较小时,增大Pk将导致![]() 的增大;当Pk较大时,UA概率
的增大;当Pk较大时,UA概率![]() 随着Pk而减小。对于λk和βk的影响,也可以得到类似的结论。
随着Pk而减小。对于λk和βk的影响,也可以得到类似的结论。
根据UA概率,很容易得出第k层网络中每个BS级联的平均用户数,一个给定用户的ABRP是第m个次序统计量。当采用非最佳UA方案时,用![]() 表示与第k层网络中的BS相级联的平均数用户数,则有
表示与第k层网络中的BS相级联的平均数用户数,则有
(12)
其中,![]() 和
和![]() 分别是第k层网络中用户和BS的平均数。因此,根据定理1,可得定理2。
分别是第k层网络中用户和BS的平均数。因此,根据定理1,可得定理2。
定理 2 当采用非最佳UA方案,与第k层网络中的一个BS相级联用户的平均数量可以表示为
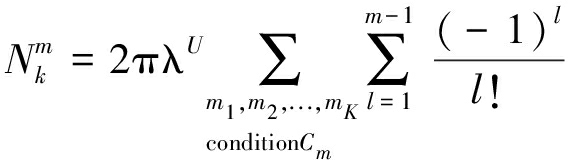
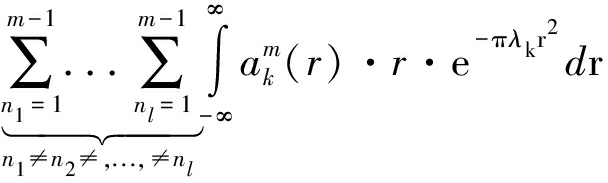
(13)
其中,![]() 在式(6)中给出。类似地,当满足条件α1=α2=...=αK=α时,得出推论3,给出
在式(6)中给出。类似地,当满足条件α1=α2=...=αK=α时,得出推论3,给出![]() 的闭式表达式。
的闭式表达式。
推论 3 当采用非最佳UA方案时,路径损耗指数满足α1=α2=...=αK=α,与第k层网络中的一个BS相级联的用户平均数![]() 给出如下
给出如下
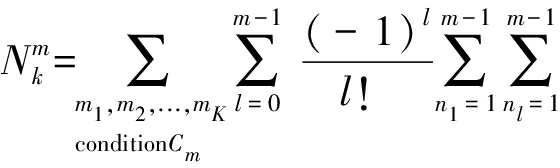
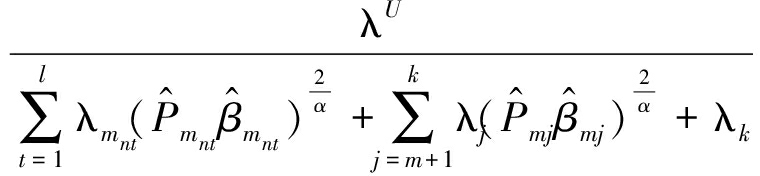
(14)
从定理2和推论3不难发现,级联至第k层网络中BS的用户平均数量与用户强度λU成比例,这与实际网络模型相一致。同时,级联用户平均数![]() 随
随![]() 增大。根据定理1的结果,可以发现当发送功率相对较小时,增大发送功率可以增大相应层的级联用户数,同时减少其他层的级联用户数。然而,当发送功率相对较大时,结果相反。显然,在非最佳UA方案下所得出的结果不同于最佳UA方案。
增大。根据定理1的结果,可以发现当发送功率相对较小时,增大发送功率可以增大相应层的级联用户数,同时减少其他层的级联用户数。然而,当发送功率相对较大时,结果相反。显然,在非最佳UA方案下所得出的结果不同于最佳UA方案。
这部分考虑当采用所提出的第m阶ABRP UA时,第k层网络中的一个给定用户与为其服务BS之间的距离![]() 的统计描述。因为网络中的BS空间位置满足PPP,所以
的统计描述。因为网络中的BS空间位置满足PPP,所以![]() 是关于概率密度函数(probability density function,PDF)
是关于概率密度函数(probability density function,PDF)![]() 的RV。要得到PDF
的RV。要得到PDF ![]() 首先要计算累积分布函数
首先要计算累积分布函数![]() 其定义为
其定义为
(15)
由于事件![]() 等同于事件
等同于事件![]() 当一个给定用户与采用第m个最强ABRP的第k层网络BS级联时,可以表示出事件
当一个给定用户与采用第m个最强ABRP的第k层网络BS级联时,可以表示出事件![]() 的概率为
的概率为
(16)
其中,n表示采用第m阶ABRP方案时,一个给定用户所级联网络层的序数,![]() 表示在给定用户与最近的第k个BS相级联的情况下的事件
表示在给定用户与最近的第k个BS相级联的情况下的事件![]() 发生的概率,且ABRP是第m个次序统计量,(a)满足条件概率。UA概率
发生的概率,且ABRP是第m个次序统计量,(a)满足条件概率。UA概率![]() 已在定理1中给出,式(16)分子中概率
已在定理1中给出,式(16)分子中概率![]() 计算如下
计算如下
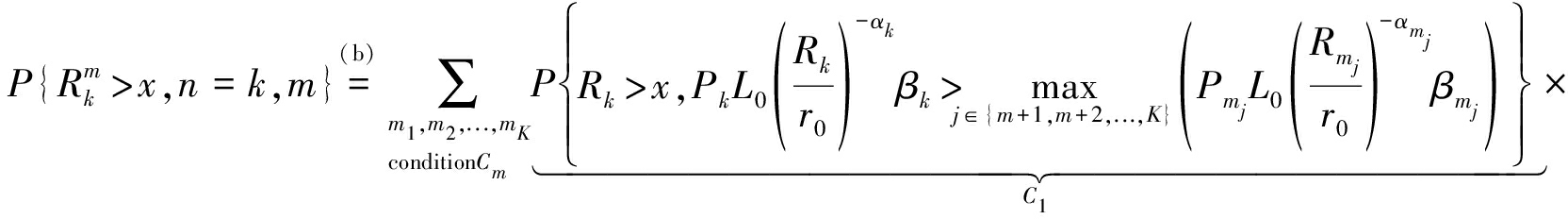
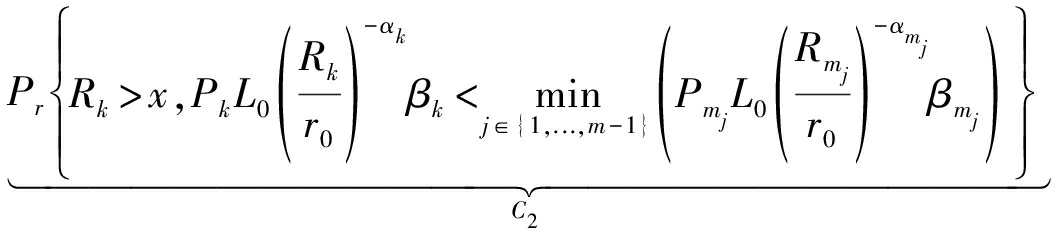
(17)
其中(b)来自独立性假设。在式(17)中,使用了文献[17]中的结果,A1可由下式给出
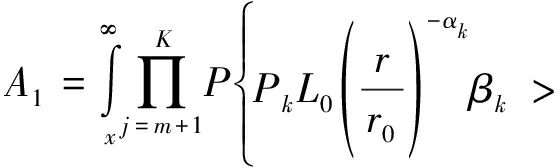
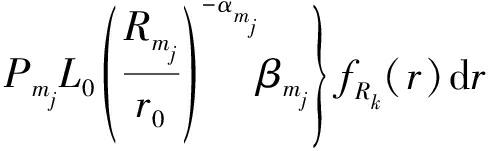
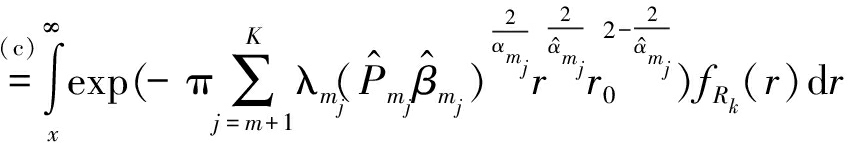
(18)
其中(c)来自FRk(x)=1-e-πlkx2。类似地,式(17)中A2给出如下
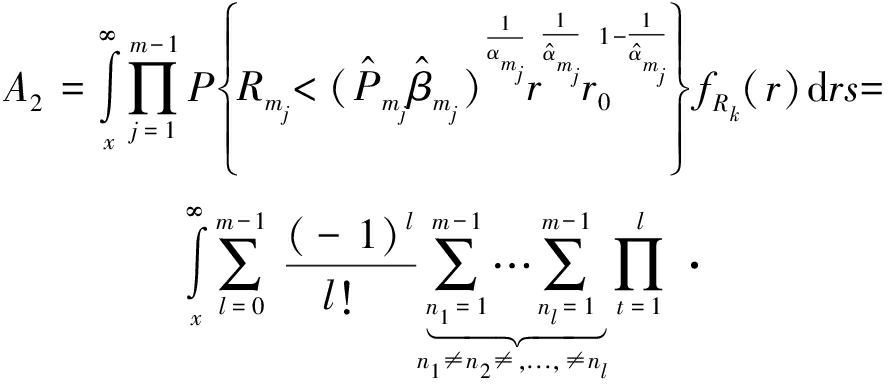
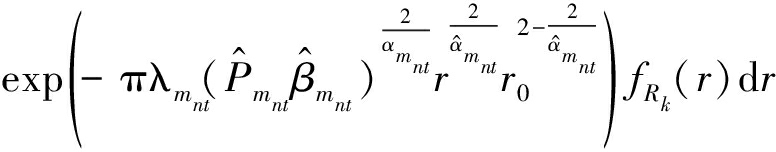
(19)
最后,将式(16)、(17)、(18)、(19)代入式(15)并取![]() 关于x的导数,可得定理3。
关于x的导数,可得定理3。
定理 3 对于多层HetNets,当采用所提出的第m阶ABRP方案选择BS服务时,一个给定用户与为其服务BS之间的距离![]() 的PDF由下式给出
的PDF由下式给出
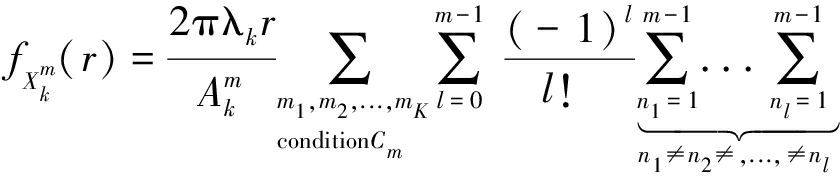
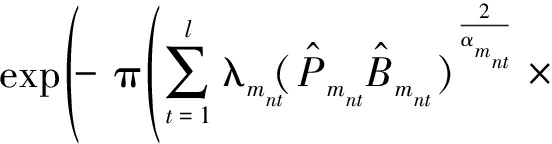
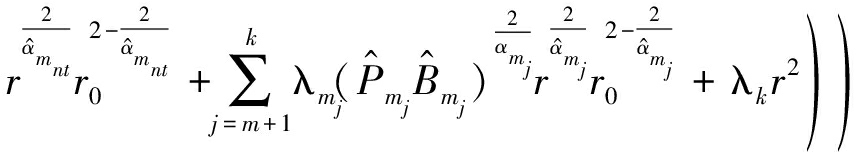
(20)
基于上述分析,本节给出了仿真和数值结果,验证了之前的推导。在本部分,考虑一个3层HetNets,其路径损耗为L0=-36.5 dB/m,热噪声功率W=-104 dB。同时,路径损耗指数分别为α1=3.8,α2=3.5,α3=4;密度分别为λ 1=1/5002π,λ 2=2λ 1,λ 3=20λ 1;发送功率分别为P1=53 dBm,P2=33 dBm和P3=23 dBm。
在图2中,首先给出了最佳ABRP与第m阶ABRP方案之间的UA概率和发送功率P1的比较分析。从图2(a)很容易看出,推导结果与仿真结果高度拟合,且满足![]() 这验证了推导的正确性。同时,当采用所提出的第m阶ABRP UA方案时,UA概率与文献[10]中提出的最佳ABRP方案有很大不同。文献[10]中的结果表明,UA概率
这验证了推导的正确性。同时,当采用所提出的第m阶ABRP UA方案时,UA概率与文献[10]中提出的最佳ABRP方案有很大不同。文献[10]中的结果表明,UA概率![]() 随功率P1增大,而
随功率P1增大,而![]() 和
和![]() 减小。然而,当采用第m阶ABRP方案时,在功率P1相对较小,且P1<P2,P1<P3时,
减小。然而,当采用第m阶ABRP方案时,在功率P1相对较小,且P1<P2,P1<P3时,![]() 随P1增大;而在功率P1相对较大,且P1>P2,P1>P3时,
随P1增大;而在功率P1相对较大,且P1>P2,P1>P3时,![]() 减小。相反,当P1相对较小时,UA概率
减小。相反,当P1相对较小时,UA概率![]() 和
和![]() 减小;当P1相对较大时,UA概率
减小;当P1相对较大时,UA概率![]() 和
和![]() 增大。此外,当P1小时,UA概率还满足
增大。此外,当P1小时,UA概率还满足![]() 和
和![]() 所有这些观察结果表明,非最佳UA方案对HetNets性能有很大影响。对此,有如下解释:当同时满足条件P1<P2和P1<P3时,给定用户从第1层所获得的接收信号功率为第二个最强次序统计量的概率大于其最强的概率。然而,在条件P1>P2和P1>P3下,随着P1的增加,给定用户的接收功率Pr2和Pr3是增大的二阶统计量。这导致
所有这些观察结果表明,非最佳UA方案对HetNets性能有很大影响。对此,有如下解释:当同时满足条件P1<P2和P1<P3时,给定用户从第1层所获得的接收信号功率为第二个最强次序统计量的概率大于其最强的概率。然而,在条件P1>P2和P1>P3下,随着P1的增加,给定用户的接收功率Pr2和Pr3是增大的二阶统计量。这导致![]() 随着P1而减小。显然,
随着P1而减小。显然,![]() 的拐点取决于P2和P3。为了进一步验证所得结果,图2(b)中分别显示了不同P2和P3下
的拐点取决于P2和P3。为了进一步验证所得结果,图2(b)中分别显示了不同P2和P3下![]() 与
与![]() 的比较。通过观察,可以清楚地看到,
的比较。通过观察,可以清楚地看到,![]() 的拐点随着P2和P3的减小向左移动。上述结果验证了定理1~3的正确性。
的拐点随着P2和P3的减小向左移动。上述结果验证了定理1~3的正确性。

图2 用户级联概率与发送功率P1的关系
Fig.2 User association probabilities versus transmission power P1
上文定义了网络各层部署因子![]() 并指出参数λ1和Pk对UA概率有同样的影响。为了说明结果,图3研究了UA概率
并指出参数λ1和Pk对UA概率有同样的影响。为了说明结果,图3研究了UA概率![]() 与λ 1的关系。研究表明在使用ABRP方案时,UA概率
与λ 1的关系。研究表明在使用ABRP方案时,UA概率![]() 随λ1增大,而
随λ1增大,而![]() 和
和![]() 减小。然而,当使用本文提出的非最佳ABRP方案时,非最佳服务BS对UA概率影响极大。根据图2和图3的观察结果,可以发现在第m阶ABRP UA方案中,UA概率由部署因子Ek决定。此外,在图4给出了λ1和P1对UA概率
减小。然而,当使用本文提出的非最佳ABRP方案时,非最佳服务BS对UA概率影响极大。根据图2和图3的观察结果,可以发现在第m阶ABRP UA方案中,UA概率由部署因子Ek决定。此外,在图4给出了λ1和P1对UA概率![]() 的联合影响。
的联合影响。
图5研究了级联用户数与发送功率P1的关系。
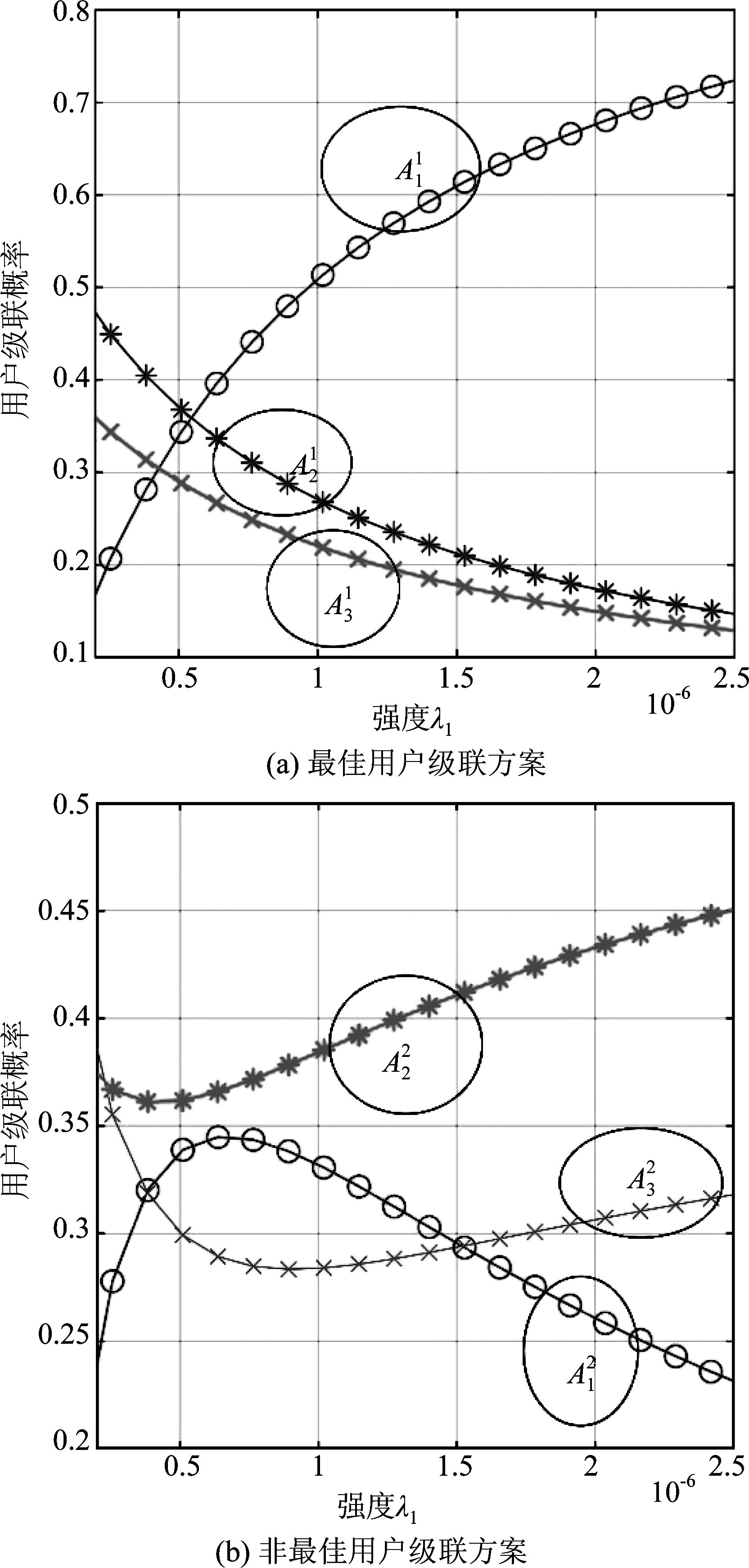
图3 用户级联概率与强度λ 1的关系
Fig.3 User association probability versus density λ 1
为了方便起见,在图5中取λ 3=5λ 1。除了与图2~图4有相似结果外,该图还直观地显示了非最佳UA方案对网络性能的影响。显然,第2佳ABRP方案的总级联用户数![]() 小于最佳ABRP方案。同时,在传统的最佳ABRP方案中,尽管总平均级联用户数
小于最佳ABRP方案。同时,在传统的最佳ABRP方案中,尽管总平均级联用户数![]() 并不总是随着发送功率P1增大,但当发送功率P1相对较大时,
并不总是随着发送功率P1增大,但当发送功率P1相对较大时,![]() 单调增大。然而,在第m阶ABRP方案中,观察图5(b)可以看出,当发送功率P1相对较大时,P1的增加将导致
单调增大。然而,在第m阶ABRP方案中,观察图5(b)可以看出,当发送功率P1相对较大时,P1的增加将导致![]() 的减小,这是本文的重要发现。此外,类似于UA概率,发送功率P1的增加并不总是对
的减小,这是本文的重要发现。此外,类似于UA概率,发送功率P1的增加并不总是对![]() 有益。
有益。
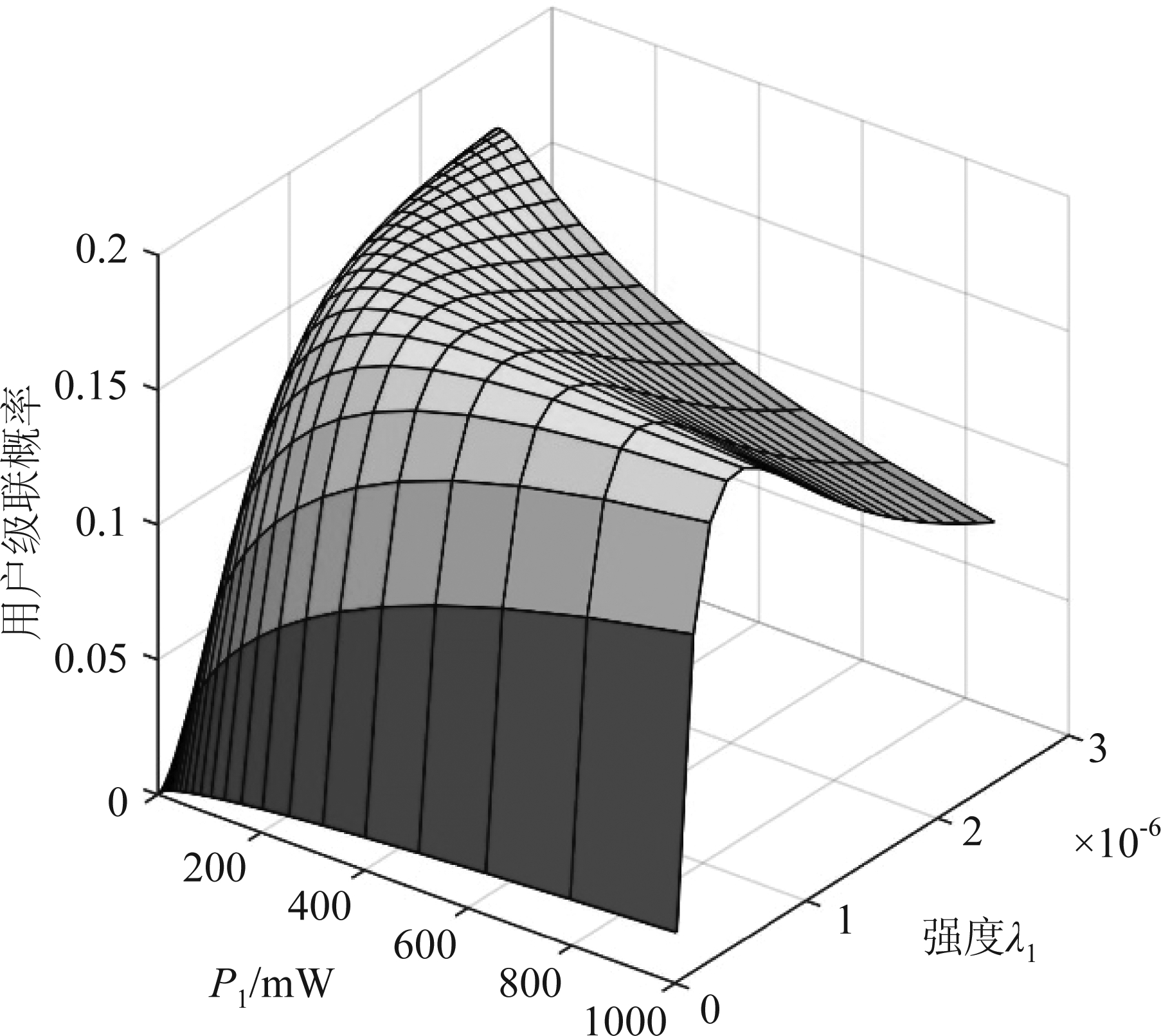
图4 用户级联概率![]() 与功率P1 和λ 1的关系
与功率P1 和λ 1的关系
Fig.4 User association probability ![]() versus power P1 and density λ 1
versus power P1 and density λ 1
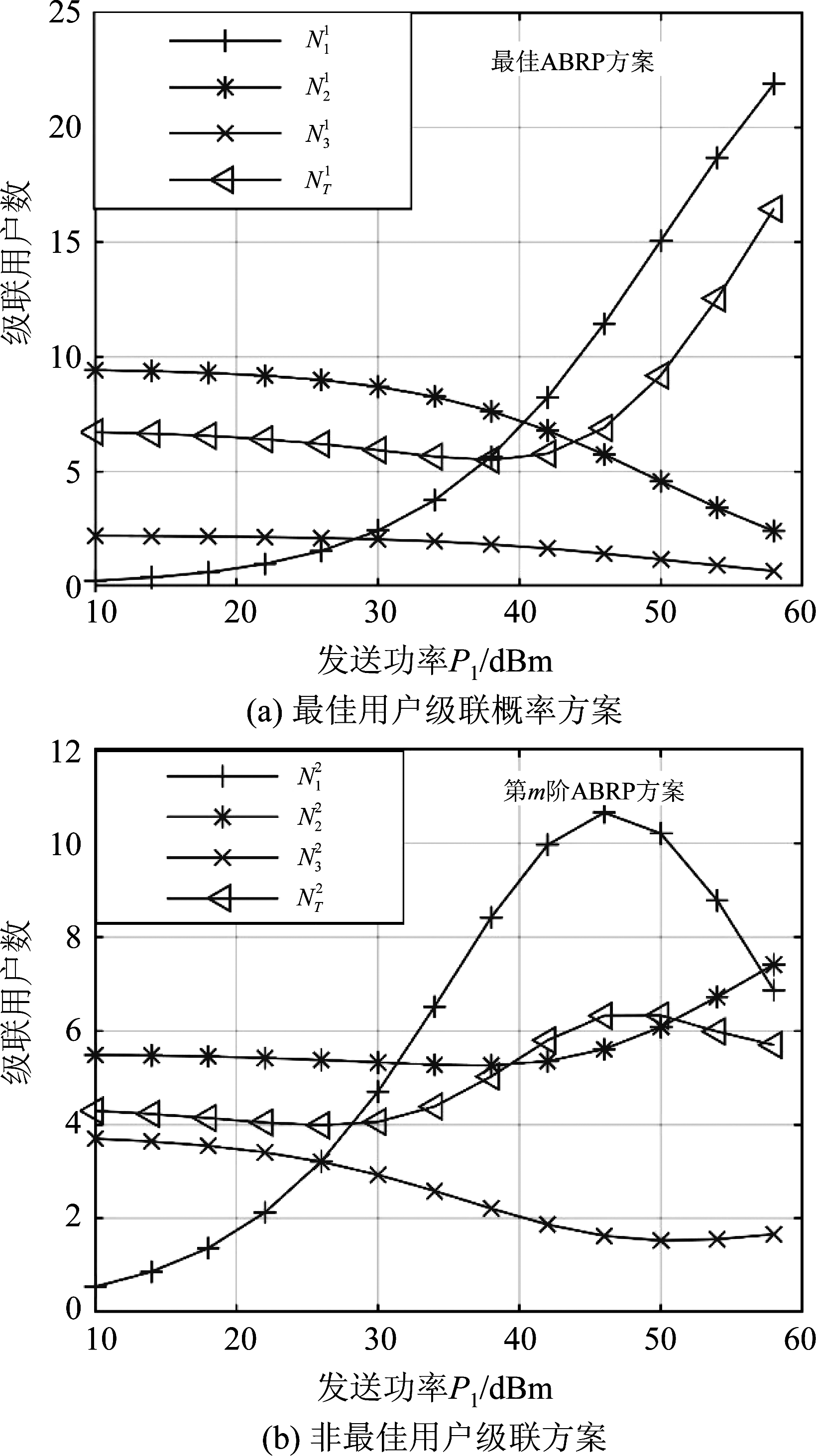
图5 级联用户数与功率P1的关系
Fig.5 Associated user number versus transmission P1
考虑到在实际情况中,由于调度、负载均衡等条件的约束,最佳服务BS有时不可用。本文基于HetNets中的ABRP,提出了一种新颖的非最佳UA方案。在通信过程中,通信端首先需要进行信道估计等协调工作。在这一过程中,通信端即可获得对方的信道质量信息,在得到此信息后,本地通信端即可进行排序、选择级联BS等工作。在非最佳UA方案中,一个给定用户与第m阶ABRP的BS相级联,也是一个通信端对BS进行排序与选择的过程。即,选择每一层中最强ABRP 的BS,对所有BS根据ABRP进行排序,如若最佳BS无法接入,为了保障通信,遂选择次优的BS,依次向后选择直至连接到第m个BS。在该方案中,一个给定用户与第m阶ABRP的BS相级联。对于所提出的第m阶ABRP UA方案,研究了UA概率,并给出了解析表达式。此外,在所有路径损耗指数完全相同的特殊情况下,研究了系统的UA概率和级联用户数。结果表明,对于给定的第k层BS,其发送功率为Pk。当Pk相对较小时,相应的UA概率![]() 随Pk增大;当Pk相对较大时,相应的UA概率
随Pk增大;当Pk相对较大时,相应的UA概率![]() 随Pk减小。同时,UA概率
随Pk减小。同时,UA概率![]() 与Pk没有一致单调性。而在最佳UA方案中
与Pk没有一致单调性。而在最佳UA方案中![]() 随Pk增大,
随Pk增大,![]() 单调递减,显然与本文所提方案具有很大不同。本文提出的第m阶ABRP UA方案有两个方面的意义。首先,通过选择非最佳BS来解决由实际约束导致的最佳BS不可靠的问题。其次,不完全信道状态信息评估将导致UA误差决策,从而引起网络容量和覆盖概率等性能损失,利用所提出的方案,可以对此性能损失进行评估。
单调递减,显然与本文所提方案具有很大不同。本文提出的第m阶ABRP UA方案有两个方面的意义。首先,通过选择非最佳BS来解决由实际约束导致的最佳BS不可靠的问题。其次,不完全信道状态信息评估将导致UA误差决策,从而引起网络容量和覆盖概率等性能损失,利用所提出的方案,可以对此性能损失进行评估。
首先考虑![]() 将式(1)中定义的Prk代入式(3),可得
将式(1)中定义的Prk代入式(3),可得
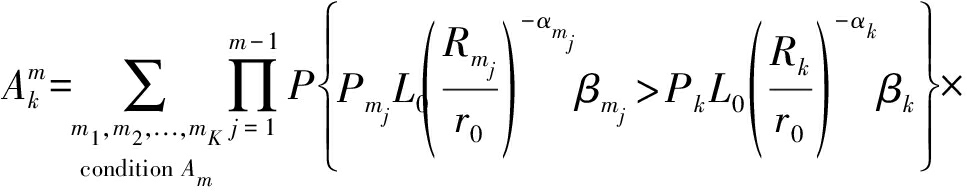

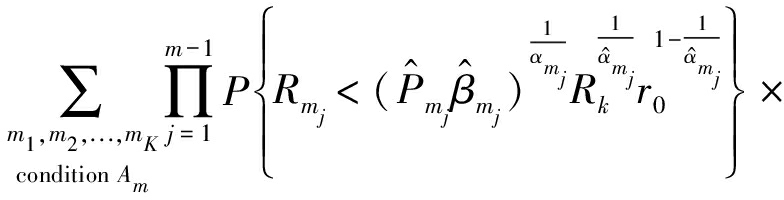
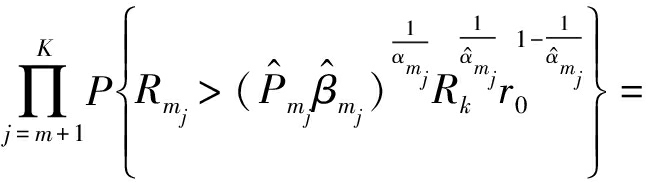
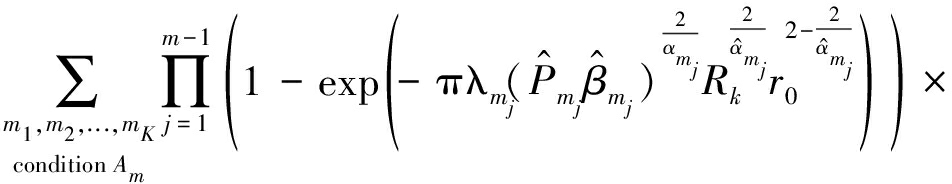
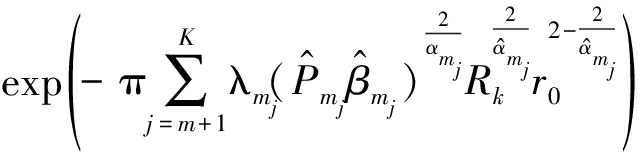
(21)
其中,FRk(x)=1-e-πlkx2。为了便于处理式(21),这里利用定义
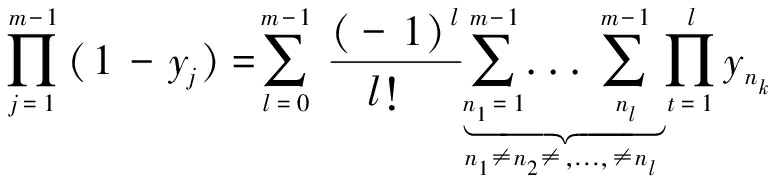
(22)
则(21)可进一步写为
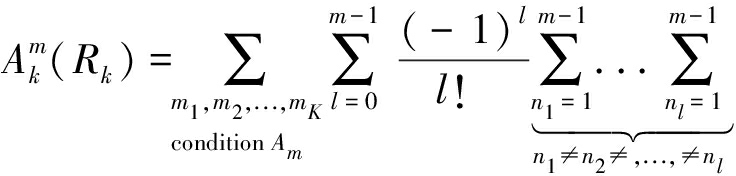
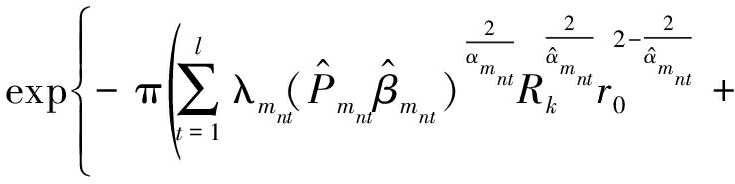
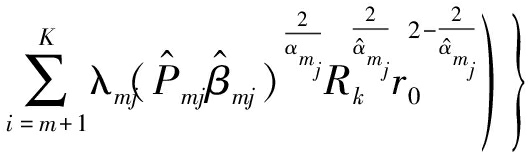
(23)
然后,用式(4)和fRk(r)=2πλkrexp(-πλkr2),可得式(5),即可得定理1。
1)首先取E1和E2为固定值,研究![]() 和E2之间的关系。为此,取
和E2之间的关系。为此,取![]() 关于E2的导数,可得
关于E2的导数,可得
(24)
考虑到E1≠0,令式(24)为零,可得
(25)
由E2>0,得到
(26)
对于![]() 和E3之间的关系,有类似的结果。
和E3之间的关系,有类似的结果。
2)类似地,通过求A1关于E1的导数即可求得![]() 和E1之间的关系,经过数学运算,可得
和E1之间的关系,经过数学运算,可得
(27)
显然,式(35)是RV E1的四阶方程。通过解方程式,得到式(11)。
[1] Cisco Visual Networking Index: Global Mobile Data Traffic Forecast Update(2014-2019)[R]. Cisco Publication Information,2015: 1-26.
[2] 尤肖虎,潘志文,高西奇,等. 5G移动通信发展趋势与若干关键技术[J]. 中国科学: 信息科学,2014,44(5): 551-563.
You Xiaohu,Pan Zhiwen,Gao Xiqi,et al. The 5G Mobile Communication: The Development Trends and Its Emerging Key Techniques[J]. Science China: Information Sciences,2014,44(5): 551-563.(in Chinese)
[3] Jia Xiangdong,Deng Pengfei,Yang Longxiang,et al. Spectrum and Energy Efficiencies for Multiuser Pairs Massive MIMO Systems With Full-Duplex Amplify-and-Forward Relay[J]. IEEE Access,2015,3: 1907-1918.
[4] Hao Peng,Yan Xiao,Yu-Ngok Ruyue,et al. Ultra Dense Network: Challenges,Enabling Technologies and New Trends[J]. China Communications,2016,13(2): 30- 40.
[5] 周猛,贾向东,颉满刚. 基于随机几何的大规模MIMO中继异构网络性能分析[J]. 计算机工程与科学,2018,40(6): 1037-1044.
Zhou Meng,Jia Xiangdong,Xie Mangang. Performance Analysis for HetNets with Massive MIMO Relay Based on Stochastic Geometry[J]. Computer Engineering and Science,2018,40(6): 1037-1044.(in Chinese)
[6] 刘文佳,杨晨阳,李琪. Massive MIMO异构网的高能效资源分配[J]. 信号处理,2017,33(7): 901-910.
Liu Wenjia,Yang Chenyang,Li Qi. Energy Efficient Resource Allocation in Heterogeneous Network with Massive MIMO[J]. Journal of Signal Processing,2017,33(7): 901-910.(in Chinese)
[7] Andrews J G,Buzzi S,Wan C,et al. What Will 5G Be?[J]. IEEE Journal on Selected Areas in Communications,2014,32(6): 1065-1082.
[8] Andrews J,Singh S,Ye Q,et al. An Overview of Load Balancing in HetNets: Old Myths and Open Problems[J]. IEEE Wireless Communications,2013,21(2): 18-25.
[9] Dhillon H S,Ganti R K,Baccelli F,et al. Modeling and Analysis of k-tier Downlink Heterogeneous Cellular Networks[J]. IEEE Journal on Selected Areas in Communications,2012,30(3): 550-560.
[10] Jo H S,Sang Y J,Xia P,et al. Heterogeneous Cellular Networks with Flexible Cell Association: A Comprehensive Downlink SINR Analysis[J]. IEEE Transactions on Wireless Communications,2011,11(10): 3484-3495.
[11] Ahmad S A,Datla D. Distributed Power Allocations in Heterogeneous Networks with Dual Connectivity Using Backhaul State Information[J]. IEEE Transactions on Wireless Communications,2015,14(8): 4574- 4581.
[12] Sekander S,Tabassum H,Hossain E.Decoupled Uplink-downlink User Association in Multi-tier Full-duplex Cellular Networks: A Two-sided Matching Game[J]. IEEE Transactions on Mobile Computing,2017,PP(99): 1-1.
[13] Semiari O,Saad W,Valentin S,et al. Matching Theory for Priority-based Cell Association in The Downlink of Wireless Small Cell Networks[C]∥2014 IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP). Florence,Italy: IEEE,2014: 444- 448.
[14] Cao Dong Xu,Zhou Sheng,Niu Zhi Sheng. Optimal Combination of Base Station Densities for Energy-efficient Two-tier Heterogeneous Cellular Networks[J]. IEEE Transactions on Wireless Communications,2013,12(9): 4350- 4362.
[15] Haenggi M,Andrews J G,Baccelli F,et al. Stochastic Geometry and Random Graphs for The Analysis and Design of Wireless Networks[J]. IEEE Journal on Selected Areas in Communications,2009,27(7): 1029-1046.
[16] David H A,Nagaraja H N. Order Statistics[M]. 3rd ed. New York: Wiley,2003: 23- 42.
[17] Gradshteyn I S,Ryzhik I M. Table of Integrals,Series,and Products[M]. 7th ed. Acdemic: San Diego,CA,2007: 12-30.
[18] Sakr A H,Hossain E. Cognitive and Energy Harvesting-Based D2D Communication in Cellular Networks: Stochastic Geometry Modeling and Analysis[J]. IEEE Transactions on Communications,2015,63(5): 1867-1880.

徐文娟 女,1994年生,甘肃兰州人。西北师范大学计算机科学与工程学院硕士研究生。研究方向为5G异构网络致密化技术、NOMA技术、毫米波技术。
E-mail: 1154987160@qq.com

贾向东 男,1971年生,甘肃渭源人。西北师范大学计算机科学与工程学院教授,南京邮电大学博士、博士后,甘肃省杰出青年基金获得者。研究方向为移动与无线通信关键理论与技术,主要包括下一代无线网络、5G技术、协作通信、压缩感知协作、网络编码、物联网技术等。
E-mail: jiaxd@nwnu.edu.cn

杨小蓉 女,1993年生,甘肃华亭人。西北师范大学计算机科学与工程学院硕士研究生,研究方向为5G及其关键技术。
E-mail: 954016199@qq.com

纪珊珊 女,1994年生,江苏盱眙人。西北师范大学计算机科学与工程学院硕士研究生。研究方向为5G技术、异构网络。
E-mail: 1347920139@qq.com