1 引言
随着近年来智能移动化设备的爆炸式增长以及人们对各种各样多媒体应用的需求不断增加,传统蜂窝网络受到了极大的挑战。NOMA(Non-Orthogonal Multiple Access,NOMA)技术作为第五代移动通信的关键技术之一[1],它能够通过功率分配和串行干扰消除(Successive Interference Cancellation,SIC)技术使得多个用户共享同一资源,如时间、频率等资源,从而使得系统的吞吐量和能量效率得到极大的提升[2-3]。
如何协调用户之间的资源是应用NOMA技术系统中亟待解决的关键问题之一。文献[4]针对多用户复用同一信道资源的情况,提出了动态分数规划的方法来最大化系统能效。文献[5]给出了NOMA模式下最优用户的解码顺序,并证明了在用户QoS(Quality of Service)约束下系统速率最大化问题是凸的,保证了全局最优解的存在。文献[6]针对NOMA下行链路现有功率分配算法中存在的局部最优问题,提出了一种利用共轭梯度法的最优功率分配方案,可以收敛到全局最优解。文献[7]研究了多子带多用户情况下的资源分配情况,提出了多对多用户子带匹配方法和一种基于梯度辅助二分法的次优功率分配算法,有效提高了系统能效值。然而以上文献均是单一的应用NOMA技术进行的资源分配方式,未与其他先进技术相结合。
D2D(Device-to-Device)与辅助中继(Cooperative Relaying)技术是5G系统中的关键技术,已有学者开始研究NOMA技术与D2D和中继技术相结合的场景。文献[8]研究了在采用NOMA技术的“D2D组”场景中,每个D2D组中作为D2D发射端的用户可采用NOMA技术同时与另外两个D2D接收端进行通信,进一步增加了系统容量。文献[9]针对基于能量采集的译码转发中继蜂窝异构网络,提出了一种系统容量最大化的功率分配算法,与受限于中继和用户采集能量因果性的用户平均功率算法相比,可以显著提高系统平均容量。
文献[10]将NOMA与D2D和辅助中继技术(NOMA-DC)结合,提出了一种两阶段NOMA-DC场景,并在此基础上推导了系统各态历经容量,证明了此方案较单一NOMA方式能显著提高系统各态历经容量,但是论文没有对中断概率进行分析,也没有对功率进行优化分配。文献[11]针对基于NOMA的D2D异构网络场景,研究了包括功率分配、接入点选择和传输模式切换的问题,但是文章没有考虑子信道分配、用户调度和中继选择等方面的问题。文献[12]提出了一个两时隙的NOMA中继辅助频谱共享方案,利用最大比合并推导了用户功率分配方案并证明了其有效性,但是没有考虑通过中继转发信号时涉及用户的公平性问题。
本文针对两阶段NOMA-D2D辅助中继场景提出了一种功率优化算法并推导分析了各用户的中断概率。该算法首先简化了原目标函数,鉴于基站和D2D发射端发送功率的差异,本文的优化重点为第一阶段的功率分配因子,为了解决该问题,本文将原优化问题分为两部分解决,然后分阶段对目标函数求导并利用凸函数性质优化了功率分配因子,并在此基础上推导分析了用户中断概率的变化情况。
本文接下来的内容安排如下:第2节给出了本文的系统模型;第3节提出的第一阶段功率分配算法;第4节对用户中断概率进行分析;第5节对提出的算法进行仿真分析;第6节是结论。
2 系统模型
如图1所示[10],本文的场景中包括一个基站(BS),三个蜂窝用户UE1、UE2、UE3,其中UE2离基站最近,信道条件最好,UE1位于小区边缘,信道条件最差。在两阶段NOMA-DC模型中,UE2可以充当UE1的中继,同时UE2可以作为D2D发射端与UE3直接进行通信。第一阶段,BS以NOMA方式发送信号给UE1和UE2;第二阶段,UE2作为中继和D2D发射端也以NOMA方式发送信号给UE1和UE3。本文假设接收用户可以利用完全SIC且所有衰落信道为独立瑞利衰落模型。
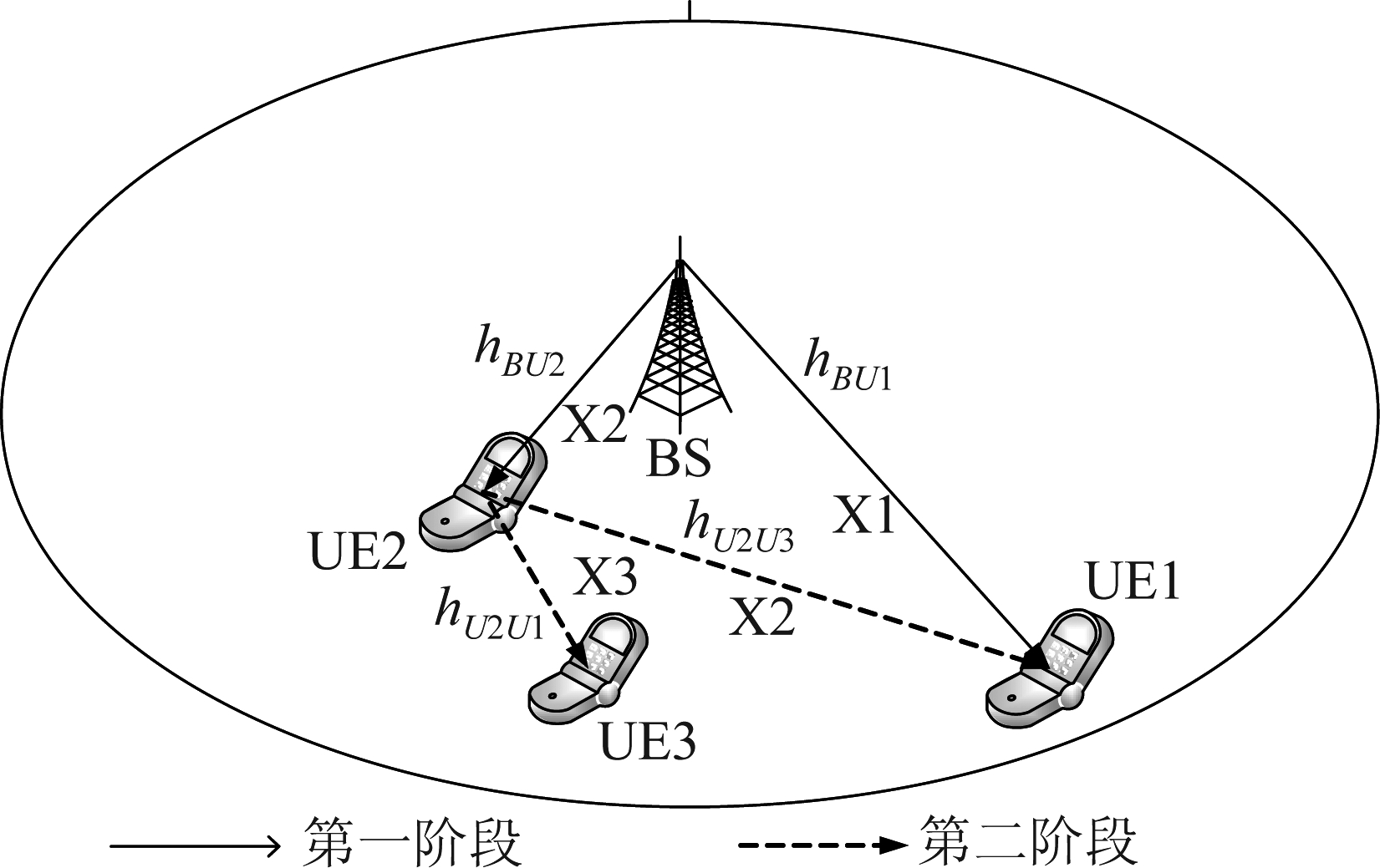
图1 系统模型
Fig.1 System model
第一阶段,BS以NOMA方式发送信号给UE1和UE2,则BS发送的信号y和UE1、UE2接收信号y1、y2分别为:
(1)
(2)
(3)
其中PB为基站发送功率,a1为基站发送给UE1的功率分配因子,a2为基站发送给UE2的功率分配因子,且
和nU2分别表示UE1、UE2到接收端的加性高斯白噪声,t1为第一阶段持续时间。
在第一阶段中,UE2首先解码X1,然后利用SIC去掉X1并获得X2,因此在UE2端接收到的X1和X2的SINRs(Signal to Interference plus Noise Ratio,SINR)分别表示为:
(4)
(5)
在UE1端直接解码X1,这里X2为干扰信号,则UE1的SINR为:
(6)
在第二阶段,UE2作为中继发送信号X2给UE1,同时以D2D形式发送信号X3给UE3,这个阶段也是以NOMA方式发送信号的。则UE2发送的信号y′和UE1、UE3接收的信号
分别为:
(7)
(8)
(9)
其中P2为UE2的发送功率,b1为发送给UE1的功率分配因子,b2为发送给UE3的功率分配因子,且b1>b2,b1+b2=1,t2为第二阶段持续时间。同理在第二阶段,UE3作为强用户先解码X2并利用SIC去掉然后获得X3,则在UE3端解码X2和X3的SINRs分别为:
(10)
(11)
在UE1端,获得信号X2的SINR为:
(12)
假设无线信道为块衰落信道,并且hXY～Nc(0,βXY)代表X∈{B,U2}和Y∈{U1,U2,U3}之间的信道系数,其中hXY～Nc(0,βXY)表示hXY服从均值为0方差为βXY的复高斯分布,不失一般性假设βBU2>βBU1,βU2U3>βU2U1。
综上,因为UE2作为中继需要先利用SIC解码X1,则根据文献[10]由式(4)和(6)可得X1的可实现速率表示为:
(13)
同理,X2的可现实速率由式(5)、(10)和(12)可得:
(14)
X3的可实现的速率由式(11)可得:
(15)
其中各式中的1/2表示两个阶段持续时间t1、t2相等。
3 系统容量
3.1 系统各态历经容量
系统的各态历经容量可以定义为[10 ]:
(16)
其中E[X]表示随机变量X的期望(均值),令ρB=PB/σ2,ρ2=P2/σ2,则由文献[10]和[13]得用户各态历经容量分别为:
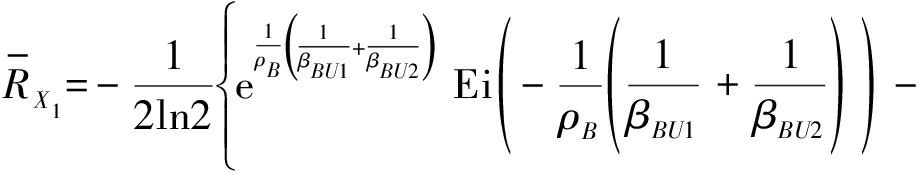
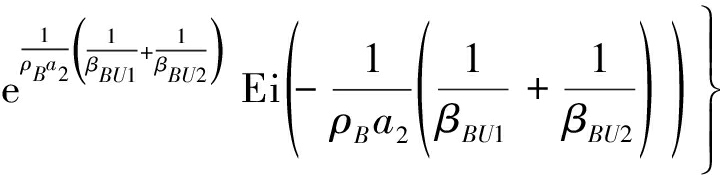
(17)
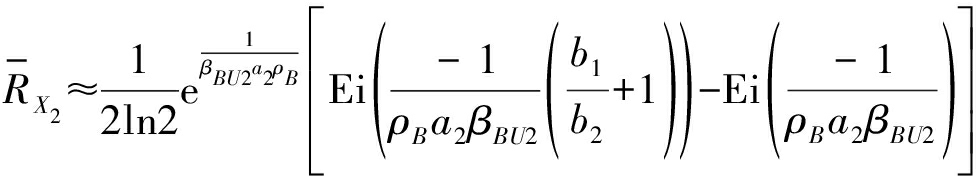
(18)
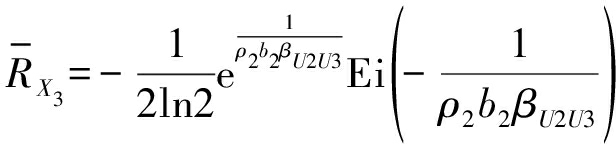
(19)
其中Ei为指数积分函数,且满足
3.2 功率分配因子优化算法
本文的目标是最大化系统各态历经容量,故优化问题为:
(20)
为了最大化系统各态历经容量,需要对功率分配因子进行优化。由公式(17)、(18)和(19)可以看出,
与第一阶段功率分配因子a2有关,
与两阶段功率分配因子a2、b2有关,而
与第二阶段分配因子b2有关,故可将
改写为:
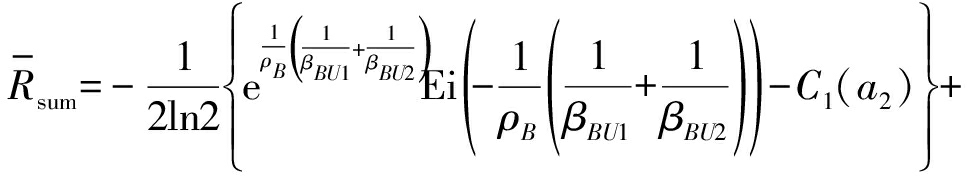
(21)
其中C1(a2)、C2(a2,b2)、C3(b2)和C4分别代表:
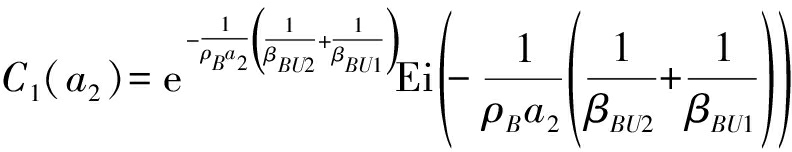
(22)
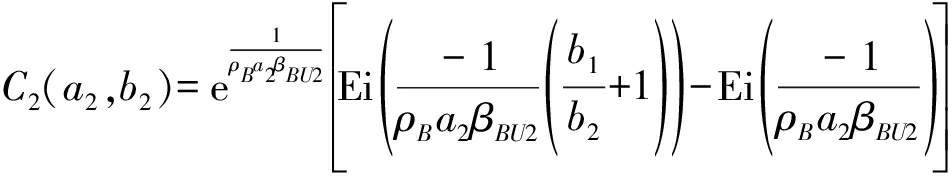
(23)
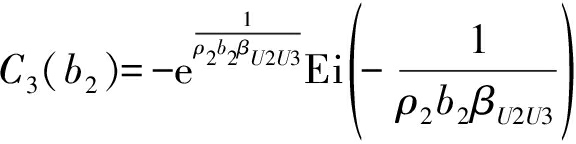
(24)
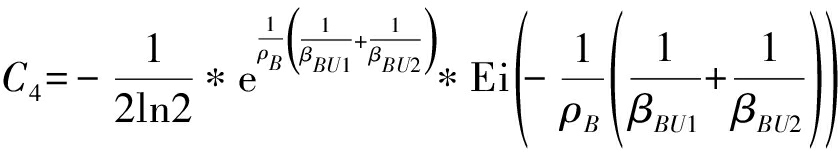
(25)
因为C4为定值,故求解原优化问题等价于先求解C1(a2)+C2(a2,b2)+C3(b2)的最大值,即转换优化问题为:
(26)
P2为一个复杂的非凸优化问题,又因为两阶段发送功率相差较大(中继发送功率为基站发送功率的十分之一),故将优化问题分成两部分求解,即重点优化对系统容量的提高起决定作用的第一阶段功率分配因子a2而将第二阶段功率分配因子b2视为定值,以下为详细求解的过程。首先将第二阶段的功率分配因子b1、b2设为定值,求解第一阶段的功率分配因子a2,令f(a2)=C1(a2)+C2(a2)。令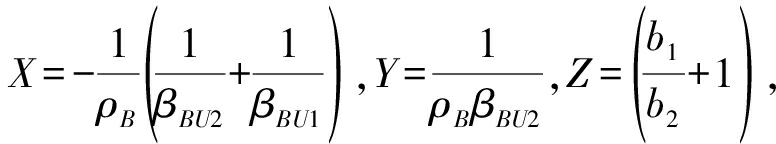
则f(a2)可以化简为:
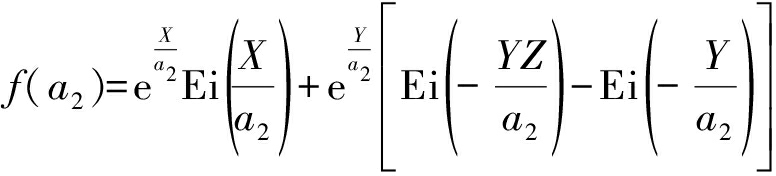
(27)
由Ei(-x)≈Ec+lnx,ex≈1+x(当x较小时满足,且Ec为欧拉常数),所以函数改写为:
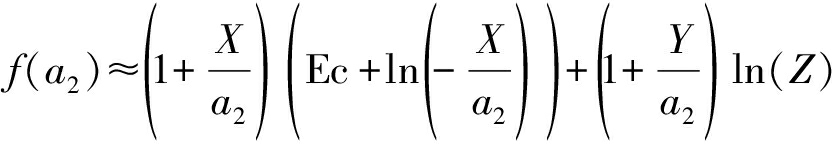
(28)
对f(a2)求导得:
(29)
可以看出,f(a2)导数是a2的减函数,故f(a2)的二阶导数为:
(30)
由X、Y和Z的取值得f ″(a2)<0,故f(a2)存在最值点,令导数为零得:
a2=-XEc-Xln(-X)+Xln(a2)-X-Yln(Z)
(31)
令ζ=lna2,则改写为:
eζ=-XEc-Xln(-X)+Xζ-X-Yln(Z)
(32)
则:
(33)
即得:
(34)
其中
令
由朗伯W函数的定义[14]得W(w)eW(w)=W,则:
(35)
即
所以ζ=-W(w)+Ec+ψ,又由朗伯W函数的性质[14]得:
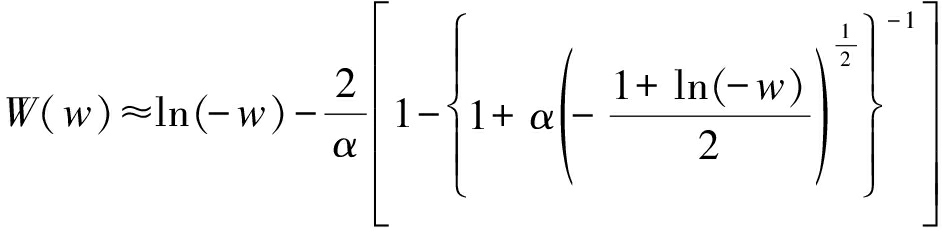
(36)
其中α=0.3205。
综上,联立式子(33)、(34)和(35)可得第一阶段最优功率分配因子为:
(37)
由于第一阶段的基站发送功率PB远大于第二阶段中继的发送功率P2,故
对系统总容量起决定作用,所以第二阶段的功率分配因子采用固定功率分配算法,又根据NOMA功率分配原理,强用户功率分配因子应小于0.5。详细功率分配算法步骤如表1所示。
表1 功率分配算法
Tab.1 Power allocation algorithm
算法:功率分配算法1. 初始化:第二阶段功率分配因子b2;由式(26)初始化X、Y和Z;集合A,用来存放每次迭代生成的最优功率分配因子a2;最大迭代次数K。2. For i =1:K do3. 将b2代入式(27),得f(a∗2)=C1(a∗2)+C2(a∗2,b∗2);4. 根据式(34)、(35)和(36)分别计算得ψ、w、W(w)和ξ;5. 根据式(37)计算a2=eξ;6. If a2<0.5 then7. A(i)=a2;8. 将A(i)、b2代入式(17)、(18)和(19)中得R-sum(i)=R-1+R-2+R-3;9. End if10. R-∗sum=mean(R-sum);11. End for12. Output: 系统最大各态历经容量R-∗sum。
4 中断概率分析
假设UE1、UE2和UE3的最小速率限制分别
且令
和
分别代表三个用户容量门限值,定义当瞬时信道SINR小于归一化用户容量门限U时产生通信中断。本文的中断概率定义为当且仅当用户所有链路都发生通信中断时的概率,则各用户发生中断的详细情况分析如下。
UE1在两阶段都接收信号,即从两条链路接收信号,所以当且仅当两条链路都发生中断时UE1才发生中断,令事件A1表示在第一阶段UE1不能正确解码信号X1,事件A2表示在第二阶段UE1不能正确解码信号X2(A′表示事件A的对立事件),则UE1的中断概率可以表示为:
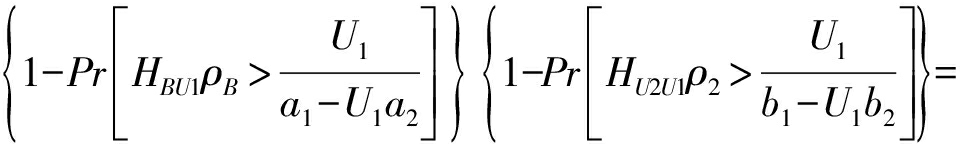
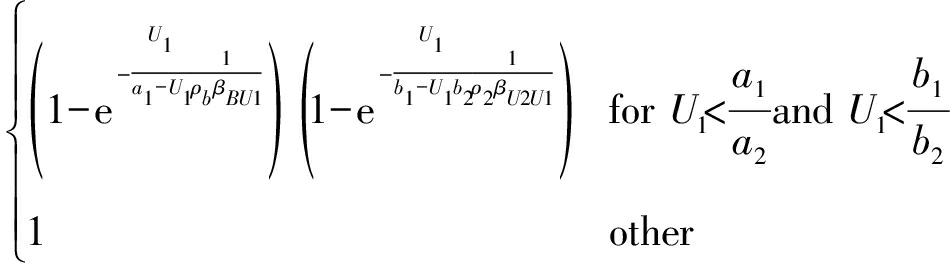
(38)
UE2从基站接收信号时,必须先解码X1,再利用SIC获得X2,令事件A3表示在第一阶段UE2不能正确解码信号X1,令事件A4表示在第一阶段UE2不能正确解码信号X2。则UE2中断概率可以表示为:
Pout,2=Pr[A3∩A4]=Pr[A3]Pr[A4A3]+
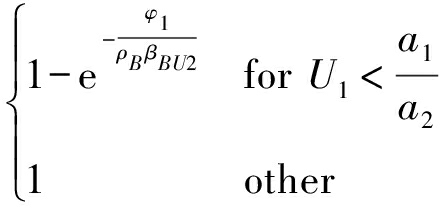
(39)
其中
同理UE3从UE2接受信号时必须先解码X2,然后利用SIC获得X3,令事件A5表示在第二阶段UE3不能正确解码信号X2,令事件A6表示在第二阶段UE3不能正确解码信号X3。则UE3的中断概率可以表示为:
Pout,3=Pr[A5∩A6]=Pr[A5]Pr[A6A5]+
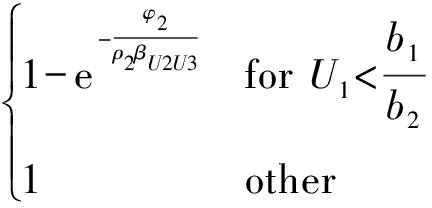
(40)
其中
5 仿真结果与分析
本节采用MATLAB对提出的功率优化算法进行了仿真,并且分析了各用户的中断概率随基站发送功率的变化情况。假设小区半径为500 m,蜂窝用户个数为3个,分别为UE1、UE2和UE3,用户最小速率限制为
设中继或D2D发送端发送功率P2是基站发送功率PB的十分之一,且假设所有接收端噪声都一样。信道均为独立分布瑞利衰落的小尺度衰落,不失一般性,假设各瑞利衰落信道方差为βBU1=0.1、βBU2=1.5、βU2U3=0.5和βU2U1=2。
图2给出了随基站发送功率的变化三个蜂窝用户中断概率的变化情况。从图中可以看出,用户中断概率的仿真值与理论值完全一致,验证了本文理论推导的正确性。三个用户中,UE1的中断性能最好,这是因为它从两条链路接收信号,当且仅当两条链路都发生中断时UE1才中断。UE2和UE3在低信噪比(SNR<35 dB)时中断概率相差不大,而在高信噪比时,UE3的中断概率继续下降,UE2的中断概率基本不变,这是因为为了最大化系统容量,将更多的功率分配给了UE1,故UE2接收到的功率基本不随SNR的变化而变化,所以中断概率基本不变。
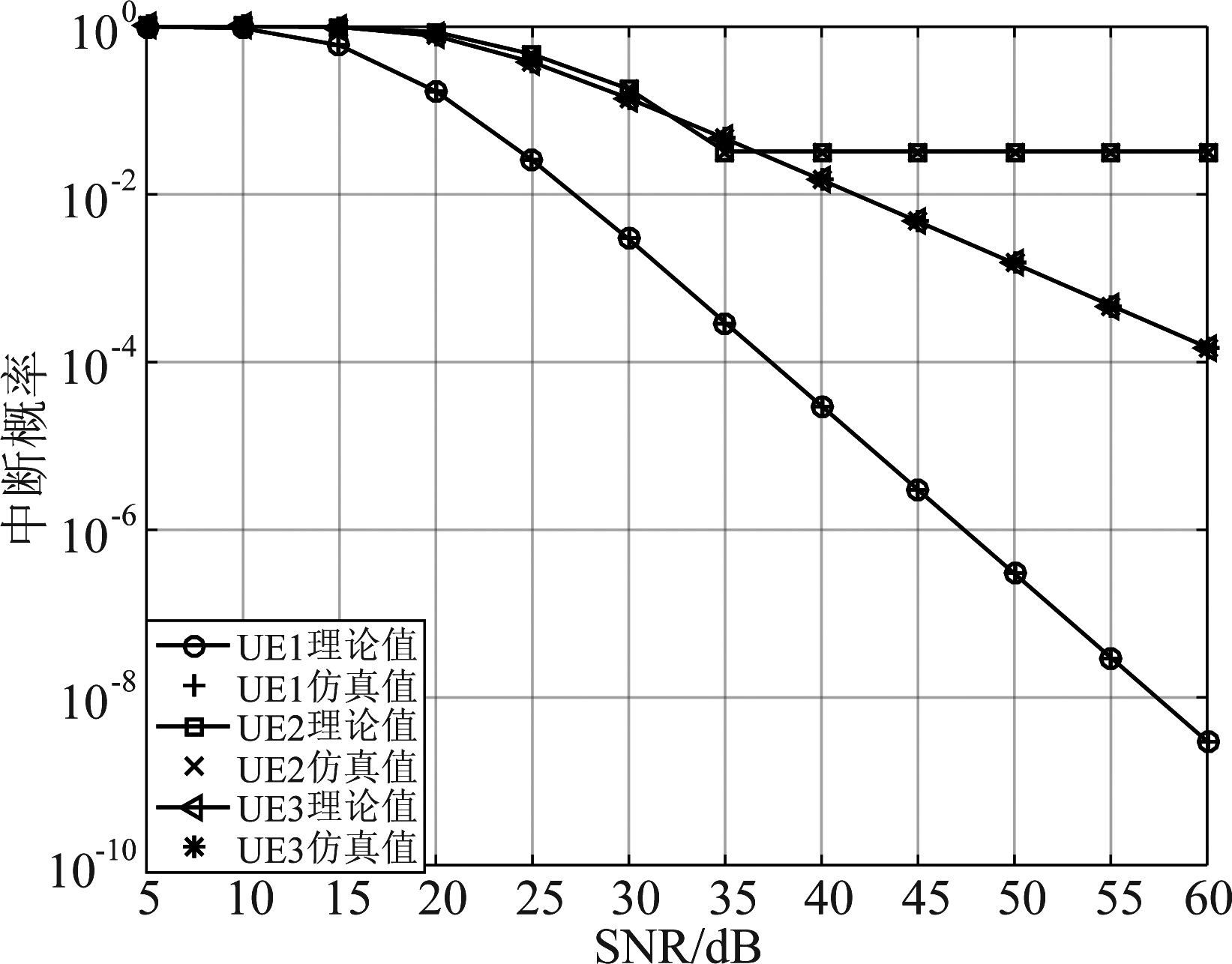
图2 用户中断概率随发送功率变化图
Fig.2 The variance of outage probability as a
function of BS transmitter power
图3给出了随基站发送功率的变化系统各态历经容量的变化情况。从图中可以看出,系统各态历经容量随着基站发送功率的增大而增大。当高SNR(SNR>35 dB)时,本文算法优于文献[10]的算法,能显著提高系统容量,这是因为文献[10]的两阶段功率分配因子均为固定值a2=min(0.01,1/ρB)和b2=0.2,而高SNR时本文算法得到的一阶段功率分配因子a2大于文献[10]算法,使得UE2获得了更高的功率,作为强用户的UE2给系统带来了更高的容量。例如当SNR为35 dB时,本文算法得到的容量比文献[10]的容量高17.6%,当SNR为50 dB时高18.7%。
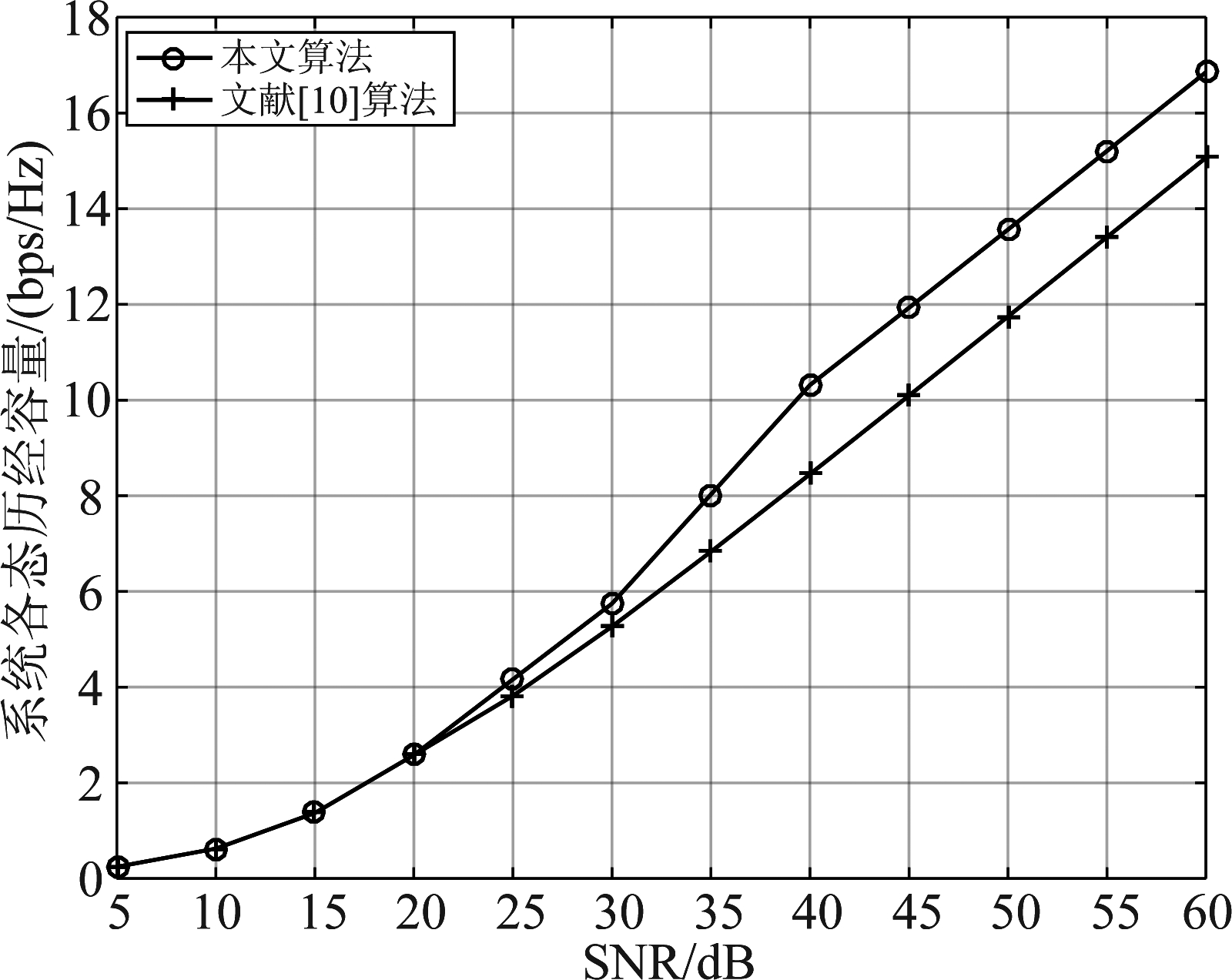
图3 系统各态历经容量的比较图
Fig.3 Comparisons of ergodic sum capacity
图4给出了本文算法中UE2和文献[10]中UE2的中断概率对比图。从图中可以看出,UE2的中断概率都随着发送功率的增大而减小,在文献[10]中,因为UE2的功率分配因子在SNR大于20 dB之后就急剧下降,故此后中断概率基本持平。而在本文算法中,UE2的功率分配因子在大于35 dB之后才急剧下降,且始终大于文献[10]中的功率分配因子,故本文算法中UE2能获得更多的功率,所以中断性能优于文献[10]中UE2的中断性能。例如当SNR大于35 dB时,本文得到的中断概率相比文献[10]降低了大约81.3%。
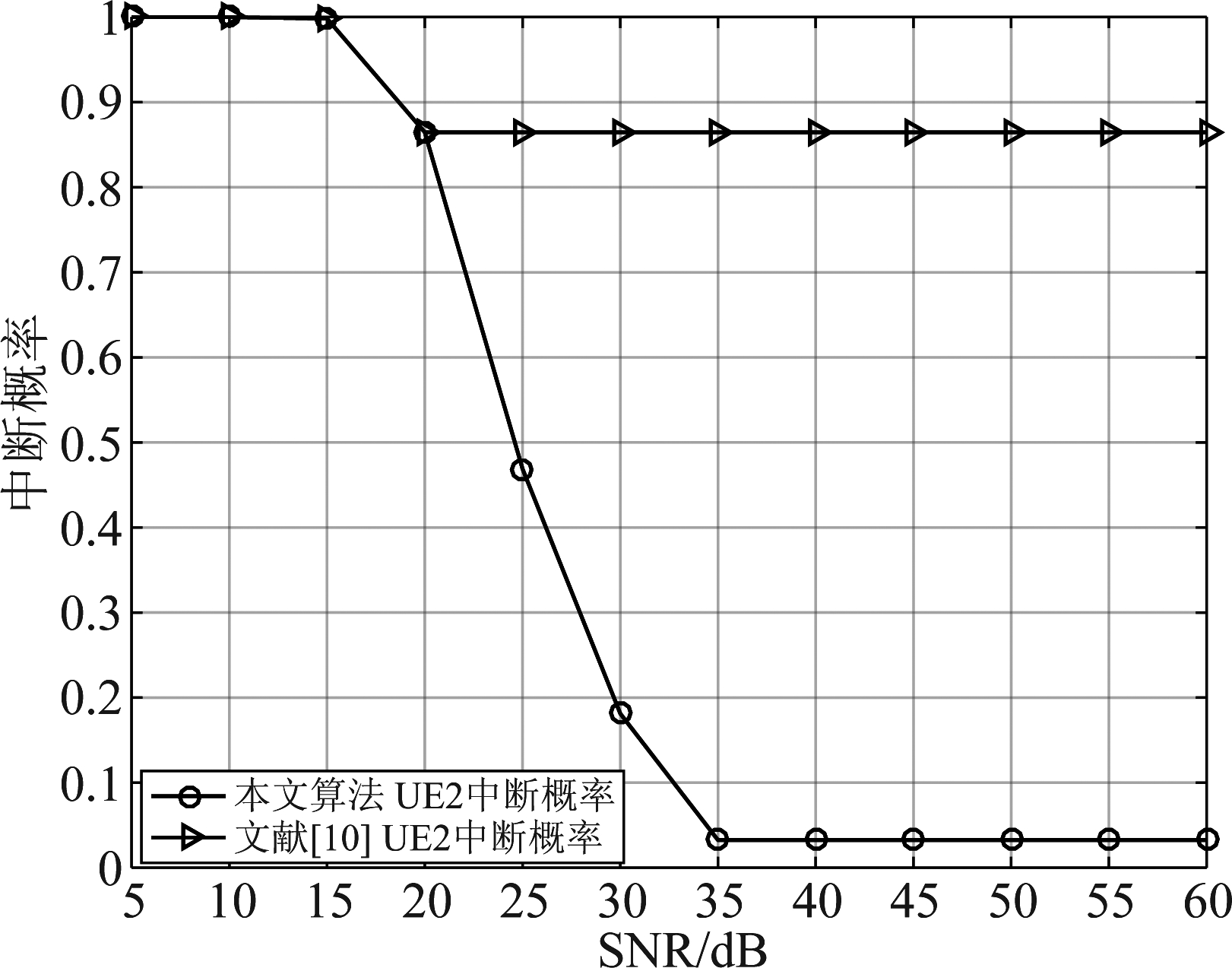
图4 UE2中断概率的比较图
Fig.4 Comparisons of outage probability
图5给出了第二阶段取不同的b2值时的系统各态历经容量变化情况。从图中可以看出,随着b2的增加系统容量只在低SNR时有少量增加,而在高SNR时容量基本不变。
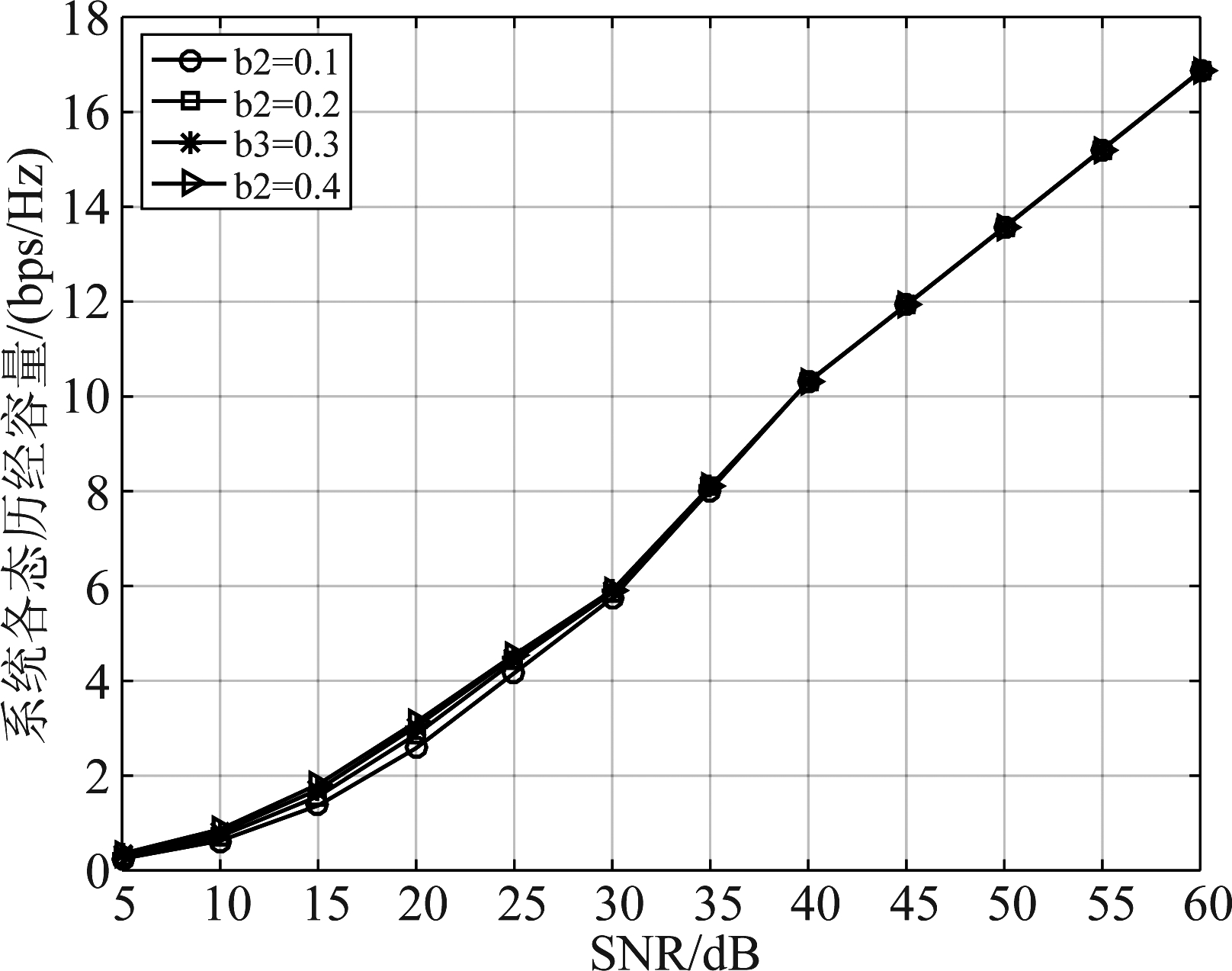
图5 不同b2值下的系统容量对比图
Fig.5 Comparisons of system capacity under different b2 values
6 结论
本文研究了在两阶段NOMA-D2D和辅助中继(NOMA-DC)场景中,提出了一种功率分配因子优化算法,最大化系统各态历经容量。该算法将两阶段优化问题分成两部分解决,且着重解决了起决定作用的第一阶段功率分配因子,简化了目标函数,利用凸函数性质和朗伯W函数,得到第一阶段最优功率分配因子,并在此基础上分析了各用户中断概率性能变化情况。仿真结果表明,本文提出算法能显著提高系统容量,且降低了UE2的中断概率。
[1] Dai Linglong,Wang Bichai,Yuan Yifei,et al. Non-Orthogonal Multiple Access for 5G: Solutions,Challenges,Opportunities,and Future Research Trends[J]. IEEE Communications Magazine,2015,53(9): 74- 81.
[2] Saito Y,Kishiyama Y,Benjebbour A,et al. Non-Orthogonal Multiple Access(NOMA) for Cellular Future Radio Access[C]∥IEEE 77th Vehicular Technology Conference. IEEE,2013: 1-5.
[3] Li Anxin,Yang Lan,Chen Xianhang,et al. Non-Orthogonal Multiple Access(NOMA) for Future Downlink Radio Access of 5G[C]∥China Communications,2015: 28-37.
[4] Zhang Yi,Wang Huiming,Zheng Tongxing,et al. Energy-Efficient Transmission Design in Non-orthogonal Multiple Access[J]. IEEE Transactions on Vehicular Technology,2017,66(3): 2852-2857.
[5] Yang Zhaohui,Xu Wei,Pan Cunhua,et al. On the Optimality of Power Allocation for NOMA Downlinks with Individual QoS Constraints[J]. IEEE Communication Letters,2017,21(7): 1649-1652.
[6] 王歌,赵知劲. NOMA系统中利用共轭梯度法的功率分配方案[J]. 信号处理,2018,34(9): 1124-1129.
Wang Ge,Zhao Zhijin. A Power Allocation Scheme Based on Conjugate Gradient Method in NOMA System[J]. Journal of Signal Processing,2018,34(9): 1124-1129.(in Chinese)
[7] Timotheou S,Krikidis I. Fairness for Non-Orthogonal Multiple Access in 5G Systems[J]. IEEE Signal Processing Letters,2015,22(10): 1647-1651.
[8] Fang Fang,Zhang Haijun,Chen Julian,et al. Energy-Efficient Resource Scheduling for NOMA Systems With Imperfect Channel State Information[C]∥IEEE ICC 2017 Mobile and Wireless Networking. IEEE,2017: 1-5.
[9] 谭锴,朱琦. 基于能量采集的译码转发中继系统功率分配算法[J]. 信号处理,2017,33(6): 887- 893.
Tan Kai,Zhu Qi. The Algorithm of Power Allocation in Decode-and-Forword Relaying System with Energy Harvesting[J]. Journal of Signal Processing,2017,33(6): 887- 893.(in Chinese)
[10] Kim J B,Lee I H,Lee J. Capacity Scaling for D2D Aided Cooperative Relaying Systems Using NOMA[J]. IEEE Wireless Communications Letters,2018,7(1): 42- 45.
[11] Liu Jiaqi,Xiao Sa,Geoffrey Y L,et al. Optimal Mobile Association and Power Allocation in Device-to-Device-enable Heterogeneous Networks with Non-Orthogonal Multiple Access Protocol[C]∥IEEE International Conference on Communications. IEEE,2018:1- 6.
[12] Chen Bingcai,Chen Yu,Chen Yunfei,et al. A Novel Spectrum Sharing Scheme Assisted by Secondary NOMA Relay[J]. IEEE Wireless Communications Letters,2018,7(5): 732-735.
[13] Kim J B,Lee I H. Capacity Analysis of Cooperative Relaying Systems Using Non-Orthogonal Multiple Access[J]. IEEE Communications Letters,2015,19(11): 1949-1953.
[14] Chatzigeorgiou I. Bounds on the Lambert Function and Their Application to the Outage Analysis of User Cooperation[J]. IEEE Communications Letters,2013,17(8): 1505-1508.
