1 引言
为了满足无线数据业务的指数级增长需求,未来第五代移动通信系统(5th Generation Mobile Communication System,5G)需要提供千倍以上的容量提升[1]。而在5G系统的众多备选关键技术中,大规模多输入多输出技术(Massive MIMO)通过深入挖掘丰富的天线阵列空间资源,在无需额外时频资源的条件下,其在系统吞吐量、频谱效率、能效、信号处理复杂度以及上层调度等方面取得了显著地性能优势[2]。该项技术是通过在基站部署比现有MIMO系统(如4G LTE-A)天线数高若干数量级的天线阵列(几十到几百甚至上千根天线)来同时服务数量相对较小的多个用户,由此获得了许多与传统MIMO系统完全不同的传输特性[3- 4]。正因为如此,该技术自提出以来便受到了业内众多机构和学者的关注,也被普遍认为是未来5G系统的核心技术之一[5]。
目前,针对大规模MIMO系统的研究主要沿着两条路径:(1)集中式大规模MIMO[6-9],即在基站集中部署大规模天线阵列来服务小区内多个用户,该方案也是早期大规模MIMO技术的主要研究内容;(2)分布式大规模MIMO[10],将配备大规模天线阵列的多个射频拉远头(Remote Radio Head,RRH)放置在小区的不同位置,拉近用户的接入距离,再通过骨干网(如光纤或微波回程链路)将各RRH连接至基带处理单元(Base-Band Unit,BBU),该思想也为后续的云无线接入网(Cloud Radio Access Network,CRAN)奠定了研究基础。两者的区别主要在于,在分布式MIMO系统中,同一用户到各RRH的大尺度衰落系数将不同,BBU端最终的复合信道形式将比集中式MIMO系统更加复杂,这对于研究其系统性能和方案设计带来了更大的困难。
然而,随着技术的发展,研究人员发现分布式MIMO系统在提升覆盖范围、增强边缘用户速率以及消除室内盲区等方面,可以获得较之集中式MIMO系统更多的性能优势[11-12]。因此,分布式大规模MIMO系统逐渐成为了又一热点研究方向。文献[10]基于5G场景下分析对比了集中式大规模MIMO和分布式大规模MIMO两种传输方案的性能,给出了两种系统的区域平均频谱效率和能效指标,研究结果也表明分布式大规模MIMO系统可以获得更优的性能提升。
根据文献[2]和文献[4]可知,大规模MIMO系统所能获得性能增益或优势主要依赖于理想的信道传播条件,而实际系统受制于各种因素通常无法获得满足要求的理想信道状态,因此,针对非理想信道传播条件下的大规模MIMO系统性能分析与方案设计将是非常重要的。文献[13]研究了单小区多用户分布式大规模MIMO系统中存在信道估计误差条件下的系统上行与下行可达速率性能。文献[14]将文献[13]扩展至多小区多用户场景中,研究了存在导频污染时的下行链路可达速率性能。文献[15]则在文献[14]的基础上,考虑了多小区分布式大规模MIMO系统中存在信道空间相关性条件下的系统传输速率性能。文献[16]研究集中式大规模MIMO系统中相位噪声因素对系统上行可达速率的性能影响。文献[17]研究了非理想的电路硬件损伤对集中式大规模MIMO系统的能效和容量性能影响。
值得注意的是,目前针对分布式大规模MIMO系统的研究,大都只考虑了信道估计误差、导频污染或发送端天线空间相关性等非理想信道传播条件对系统性能所造成的影响,而对于实际系统中经常出现的时变信道因素却未有充分考虑。特别是在移动场景中,由于用户与基站之间的相对移动性,会导致多普勒频偏的出现,进而无线信道呈现出时变特性,即信道系数随着时间的变化发生改变,加之实际系统中运算处理延时等因素,使得估计出的当前时刻信道状态信息(Channel State Information,CSI)用于下一时刻的波束赋形发送或检测接收时,与真实的CSI发生偏差,即信道估计值与当前信道系数失配[18]。对于时变信道条件下大规模MIMO系统的性能分析最早见于文献[18],该文针对集中式大规模MIMO系统分析了基站采用最大比合并和最大比发送条件下的上下行可达速率性能。而对于分布式大规模MIMO系统中信道时变特性的研究较为少见。最近的研究结果[19]针对时变信道下单小区分布式大规模MIMO系统的频谱效率进行了初步研究,也仅是考虑了信道估计误差与时变信道特性的双重作用。但实际蜂窝系统中常采用多小区工作,此时多小区分布式大规模MIMO系统会遭受导频污染现象,在这种情况下,时变信道对系统性能产生的影响可能会发生变化。因此,研究信道时变性对多小区多用户分布式大规模MIMO系统所带来的影响将是十分重要的,并且对于指导系统设计也具有很好的工程意义。
本文将针对蜂窝多小区多用户分布式大规模MIMO上行系统,综合考虑多小区导频污染、信道估计误差和时变信道等多种因素,分析这些因素对于上行可达速率和发送功率效率所带来的影响,借助高斯马尔科夫过程对时变信道进行建模,以信道时间相关性系数作为时变信道的重要参量,描述时变信道的变化快慢程度。利用大维随机矩阵理论中的相关定理以及Gamma随机变量的统计特性,推导得出了包含上述三种因素的上行可达速率解析表达式,明确了时变信道参量与系统可达速率的数量变化关系。进一步,当基站总发送天线趋于无穷大时,给出了可达速率的渐进性能与时变信道参量的关系,以及此时用户所能获得发射功率缩放增益。最后,利用计算机仿真验证了分析得出的各种结论。
文中符号说明:(·)T和(·)H分别表示转置与共轭转置运算;C表示复数集合;IK表示K×K维单位阵;Tr{·}表示矩阵的迹;diag(a)表示以向量a为主对角线元素生成的对角阵;E{·}和Var{·}分别表示期望运算和方差运算;CN(n,R)表示均值向量为n、协方差阵为R的循环对称复高斯分布;·和‖·‖分别表示取模运算和Frobenius范数;Γ(α,β)表示服从形状参数α和尺度参数β的Gamma分布;⊗表示克罗内克乘积。
2 系统模型
考虑S个相邻正六边形小区所组成的多小区多用户分布式大规模MIMO上行链路蜂窝系统,如图1所示。每个小区由一个位于中心的基带处理单元(Base-Band Unit,BBU)、M个随机均匀部署的射频拉远头(Remote Radio Head,RRH)和K个随机均匀分布的单天线移动用户(Mobile User,MU)所组成。每个RRH配备N根天线,并通过光纤或微波中继链路与本小区的BBU连接。假设该蜂窝系统采用时分双工(Time Division Duplexing,TDD),根据TDD传输特性,系统的上行信道与下行信道满足互易性。
假设无线信道满足瑞利平衰落,信道系数在一个符号间隔内保持静态不变,且随着时间变化而逐渐变化。因此,第i个小区中第k个MU到第j个小区内所有RRH的NM×1维上行信道向量在第t个符号间隔内可以表示为如下形式:
(1)
式中:Dj,i,k∈CNM×NM表示大尺度衰落系数矩阵(对角阵),该参量在相对较长的时间内是保持不变的[13-14],gj,i,k[t]∈CNM×1表示小尺度快衰落系数向量,且二者的具体形式如下:
Dj,i,k=diag([βj,1,i,k,...,βj,m,i,k,...,βj,M,i,k])⊗IN
(2)
(3)
gj,i,k[t]=![]() ...,
...,![]() ...,
...,![]() T
T
(4)
式中:βj,m,i,k用于描述第i个小区中第k个MU到第j个小区中第m个RRH之间的路径传播损耗和阴影衰落影响[11-14];ξj,m,i,k表示第i个小区中第k个MU到第j个小区中第m个RRH之间的距离;τ表示传播损耗的指数衰减因子(典型取值范围为3.0~5.0);μ表示当参考距离ξj,m,i,k为1 km时的平均路径增益中值;δj,m,i,k表示对数正态阴影衰落变量;gj,m,i,k[t]∈CN×1~CN(0,IN)表示第i个小区中第k个MU到第j个小区中第m个RRH之间的瑞利衰落系数。
因此,第t个符号时刻内,第j个小区的BBU收到的本小区和其他小区的MU发送的上行信号向量可以表示为
(5)
式中:xul,i[t]=[xul,i,1[t],...,xul,i,k[t],...,xul,i,K[t]]T表示第i小区中所有MU在第t个符号时刻内的发送数据符号向量,且每个MU的发射符号满足功率归一化,即E{xul,i[t](xul,i[t])H}=IK;pul表示MU的上行信号平均发射功率[13-14],此处意味着假设所有MU具有相同的上行发射功率;Hj,i=[hj,i,1[t],...,hj,i,k[t],...,hj,i,K[t]]∈CNM×K表示第t个符号时刻内第i小区所有MU到第j小区所有RRH的信道矩阵;zul,j[t]∈CNM×1表示第t个符号时刻内加性复高斯白噪声向量,且具有零均值和单位方差。由于每个MU是随机分布在每个小区的不同位置。因此,不同MU到每个RRH的信道向量满足统计独立性。

图1 多小区多用户分布式大规模MIMO系统
Fig.1 Multi-cell multi-user distributed massive MIMO system
3 信道信息获取与时变信道建模
3.1 考虑导频污染条件下的信道信息获取
在TDD制式下,可利用上下行信道互易性,通过用户发送上行导频序列,在BBU端进行信道估计,从而直接获得上下行信道状态信息(Channel State Information,CSI)用于下行波束赋形和上行接收检测。采用上行信道估计方案,既可以降低正交导频开销(与传统的频分双工(Frequency Division Duplexing,FDD)系统比较而言,由于TDD系统中正交导频长度与用户数成正比,与BBU端巨大的天线数无关,用户数相对于天线数而言,其数量级小很多),也可以降低用户端的信道估计运算开销,因而,该方案是大规模MIMO TDD系统中常用的CSI获取方法。但是,与单小区场景不同的是,随着多小区蜂窝系统的拓展,用户数大量增加,而在一定的信道相干时间和相干带宽条件下,正交导频的资源又是十分有限的,因此,无法保证所有小区中的用户都能使用正交导频,势必需要采用导频复用。因而,此处为了降低导频开销,考虑最差条件下的导频复用场景,即同一小区内的所有用户采用正交导频组,在其他所有小区复用该正交导频组。因此,在各小区的上行信道估计阶段,会受到来自其他小区的导频污染影响。
假设第j个小区内的K个MU使用正交导频序列用于上行信道估计,导频序列符号长度为L(≥K) [13-15],则导频序列矩阵![]() ∈CL×K满足条件:
∈CL×K满足条件:![]() H
H![]() =IK,此处的导频序列功率已进行归一化。为了简化后续分析并不失一般性,假设信道系数在信道估计阶段是不变的或极为缓慢的,可忽略由于信道变化所带来的信道估计误差[18,21]。因此,第j个小区的BBU收到的导频信号可以表示为
=IK,此处的导频序列功率已进行归一化。为了简化后续分析并不失一般性,假设信道系数在信道估计阶段是不变的或极为缓慢的,可忽略由于信道变化所带来的信道估计误差[18,21]。因此,第j个小区的BBU收到的导频信号可以表示为
![]() H+Zp,j[t]
H+Zp,j[t]
(6)
式中: pp=Lpul表示每个小区中MU的导频序列发射功率[6,14];Zp,j[t]∈CNM×L表示信道估计阶段受到的零均值单位方差的加性复高斯白噪声干扰矩阵。
接着,BBU对接收信号Yp,j[t]进行去相关运算[6,20],即Yp,j[t]·(![]()
![]() 得到如下信号:
得到如下信号:
(7)
式中:![]() 即为正交导频组复用后,其他小区使用相同导频的用户所带来的导频污染干扰项;
即为正交导频组复用后,其他小区使用相同导频的用户所带来的导频污染干扰项;![]()
![]()
![]() 表示去相关后的噪声分量。
表示去相关后的噪声分量。
最终,第j小区中的BBU将基于如下信号估计本小区第k个MU到本小区各RRH的信道向量hj,j,k[t]:
(8)
式中:![]() 表示
表示![]() 的列向量;
的列向量;![]() 表示
表示![]() 的列向量。由于
的列向量。由于![]() H
H![]() =IK,因此
=IK,因此![]() 具有独立同分布元素,且各元素服从
具有独立同分布元素,且各元素服从![]() 分布。
分布。
假设BBU使用最小均方误差(Minimum Mean Squared Error,MMSE)估计器,根据文献[6]和文献[20]中的推导方法,可以得到hj,j,k[t]的估计向量为
![]()
(9)
根据式(1)~式(4)可知,hj,j,k[t]服从CN(0,Dj,j,k)分布。对式(9)化简可以得到![]() 其中,
其中,![]() 又由于hj,j,k[t]、hj,i,k[t]和
又由于hj,j,k[t]、hj,i,k[t]和![]() 三者相互独立,根据式(9),可进一步得到
三者相互独立,根据式(9),可进一步得到![]()
令![]() 则可以发现
则可以发现![]() 服从CN(0,IMN)分布。为了后续分析与推导时符号简洁,定义参数αj,m,j,k如下所示:
服从CN(0,IMN)分布。为了后续分析与推导时符号简洁,定义参数αj,m,j,k如下所示:
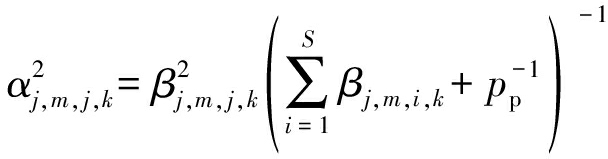
(10)
此时,估计向量![]() 可进一步表示为
可进一步表示为
![]() ...,
...,![]() ...,
...,![]() T
T
(11)
式中:![]() 表示第j个小区内第k个MU到第j个小区内第m个RRH之间的等价大尺度衰落因子,
表示第j个小区内第k个MU到第j个小区内第m个RRH之间的等价大尺度衰落因子,![]() 可视为等效的瑞利快衰落系数,式(11)中的信道估计等价模型将在后续的理论分析中带来有效的简化。
可视为等效的瑞利快衰落系数,式(11)中的信道估计等价模型将在后续的理论分析中带来有效的简化。
利用最小均方误差估计的正交性原理[6,20],可将hj,j,k[t]分解为如下两项和的形式:
(12)
式中:![]() 表示信道估计过程中出现的误差项,且服从
表示信道估计过程中出现的误差项,且服从![]() 分布,同时且
分布,同时且![]() 与
与![]() 是统计独立的[6,20]。
是统计独立的[6,20]。
下面来分析导频污染对于信道估计所产生的影响。由式(9)可知,信道估计向量![]() 和
和![]() 具有如下相关阵:
具有如下相关阵:
(13)
式中:![]() 进一步可以发现,各MU的信道估计误差向量具有如下相关特性:
进一步可以发现,各MU的信道估计误差向量具有如下相关特性:
(14)
通过式(13)和式(14)可以看出,多小区中的导频污染对于信道估计所产生的影响与单小区中各用户使用完全正交导频下的情况是不同的,主要反映在以下几点:
1)在不同小区中,使用相同导频的MU到同一小区BBU的信道估计向量的等效瑞利衰落系数是相同的,即![]() 和
和![]() 在式(11)中的等效瑞利衰落系数相同;
在式(11)中的等效瑞利衰落系数相同;
2)使用相同导频的MU到同一小区BBU的信道估计向量具有相关性,即![]() 和
和![]() 具有统计相关性;
具有统计相关性;
3)使用相同导频的MU到同一小区BBU的信道估计误差向量具有相关性,即![]() 和
和![]() 具有统计相关性。
具有统计相关性。
假设各小区的BBU通过骨干网相互连接,小区之间可以共享各个MU的大尺度衰落信息,因而,对于第j个小区,除了可以估计得出本小区第k个MU的信道向量外,也可以得到其他小区中使用相同导频序列的MU到第j小区的上行信道系数,即第j个小区BBU可以估计得到第i小区第k个MU到其的信道估计向量![]()
3.2 时变信道建模
除了上面章节中讨论的多小区导频污染和信道估计误差影响外,用户的随机移动性将会导致多普勒频移的出现,特别是高速移动场景中,这将使得用户到RRH之间的无线信道呈现时变特性。换句话说,当BBU估计出第t个符号时刻的CSI后,将其用于第t+1时刻的下行波束赋形或上行信号检测时,第t+1时刻的信道系数已经随时间发生了变化,而前后时刻信道系数变化的剧烈或快慢程度与用户的相对移动速度有着直接关系。在以往的研究中,大都假定用户静止或慢速移动,由此认为信道在较长的相干时间内是静止不变的,且在该相干时间内,只进行有限的信道估计,而并非频繁地发送导频信号用于信道估计,从而忽略了时变特性影响。
为了描述时变信道中信道系数随时间的变化情况,我们采用一阶高斯马尔科夫过程来对时变信道进行建模[18,21-23],通过引入时间相关性系数来定量刻画不同时刻信道系数之间的关系。因此,第t+1个符号时刻的信道系数向量可以表示为
hj,i,k[t+1]=ηhj,i,k[t]+ej,i,k[t+1]
(15)
式中:ej,i,k[t+1]服从CN(0,(1-η2)Dj,i,k)分布,它表示第t+1时刻的信道系数中所引入的与第t时刻信道系数不相关的高斯更新过程;η表示信道的时间相关性系数,用以表征前后两个符号时间内信道系数的相关程度,即信道系数随时间变化的快慢程度。对于系数η,通常采用Jakes模型进行建模[18,21-23],即
η=J0(2πfDTs)
(16)
式中:J0(·)表示第一类零阶贝塞尔函数,Ts表示信道采样间隔,fD表示最大多普勒频移(与用户的移动速度和工作频率成正比)。根据文献[18]和文献[21]可知,时间相关性系数的取值范围为0≤η≤1。η越小,表明前后两个时刻的信道系数相关性越小,即信道随时间变化越剧烈(越快),反之,η越大则表明信道的时变性越慢,前后时刻的信道系数相关性就越强。显然,当η=0时,前后两个时刻的信道系数完全独立。也就是说,在这种情况下获得的当前时刻的CSI已经完全不适用于下一时刻的波束赋形设计或检测接收。当η=1时,表明信道完全没有时变性影响。
结合式(12)和式(15),可以得到第t+1个时刻内包含信道估计误差和信道时变双重影响的信道向量为
hj,i,k[t+1]=ηhj,i,k[t]+ej,i,k[t+1]=
(17)
式中:![]() 表示信道失配项。利用ej,i,k[t+1]、
表示信道失配项。利用ej,i,k[t+1]、![]() 和
和![]() 的复高斯分布特性和相互统计独立性可以进一步得到,
的复高斯分布特性和相互统计独立性可以进一步得到,![]() 也服从复高斯分布,且具有零均值和如下协方差矩阵:
也服从复高斯分布,且具有零均值和如下协方差矩阵:
(18)
基于式(17),将在下一节中详细分析导频污染、信道估计误差以及信道时变性等因素对系统上行可达速率和用户功率效率所带来的影响。
4 上行可达速率和功率效率分析
由式(5)可得,第j个小区内的BBU所接收到的第t+1时刻的上行信号向量为
yul,j[t+1]=
(19)
假设各小区BBU事先已知各用户的信道大尺度衰落和信道时间相关性系数信息[20-21],则第j个小区BBU可获得的本小区第k个用户在第t+1时刻的信道信息为
(20)
假设各小区BBU使用MRC接收机,则第j小区BBU的检测处理矩阵Fj[t+1]为
![]() ...,
...,![]() ...,
...,![]() H
H
(21)
将接收信号yul,j[t+1]乘以检测矩阵Fj[t+1]可得
(22)
最终,经过接收机检测滤波处理后,第j小区BBU得到的本小区第k个MU的信号可以表示为
(23)
根据文献[6,20,24]中的最差情况不相干加性噪声理论,可从式(23)中接收信号rj,k[t+1]得到第j小区内第k个MU的上行遍历可达速率为
Rul,j,k=E{log2(1+γul,j,k)}
(24)
式中:γul,j,k表示第j小区第k个MU的上行等效接收信干噪比(Signal-to-Interference Noise Ratio,SINR),且具有如下表达式:
γul,j,k=
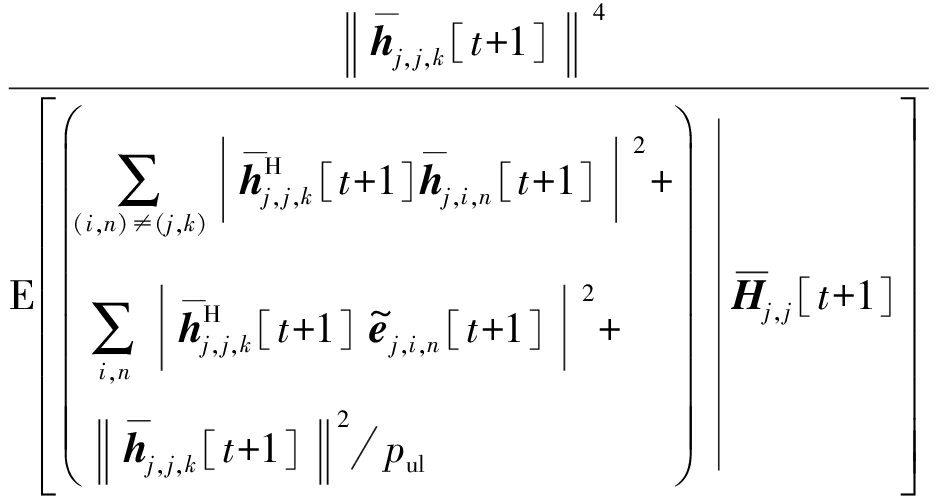
(25)
此处,γul,j,k是将式(21)中的所有干扰项和加性噪声项统一看作与有效信号项不相关的等效“白噪声”,且该“白噪声”具有与这些干扰项叠加后的相同功率,由此可以计算得到式(25)所示的等效信干噪比。
通常情况下,式(24)中的可达速率解析表达式是无法精确推导的。为了能够获得有效的闭合表达式,我们借助于Jensen不等式,并利用确定性等价原理和Gamma随机变量的各阶矩,对式(24)进行简化,有如下定理。
定理1 当信道存在导频污染与时变特性时,在BBU采用MMSE信道估计和MRC检测接收的条件下,第j个小区内第k个MU的上行可达速率具有如下所示的下界闭合表达式:
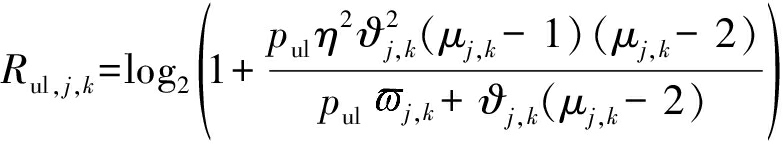
(26)
式中:![]() j,k、μj,k和ϑj,k具有如下表达式:
j,k、μj,k和ϑj,k具有如下表达式:
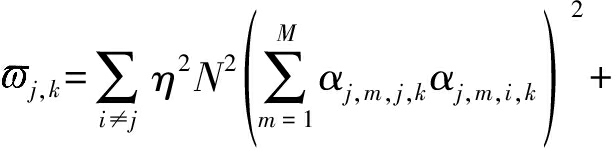

(27)
证明过程见附录A。
从式(26)中可以看到,用户上行可达速率主要由信道统计量(信道大尺度衰落系数和信道时间相关性系数)和系统参数(每个RRH的天线数、数据发送功率、导频功率等)直接决定,而不再与瞬时信道信息有关。同时还可以看到,上行可达速率值随η的增加而单调增加,这一现象与先前的理解是一致的,即信道随时间变化越快,则前一时刻估计出的信道信息与后一时刻的实际信道系数的背离程度就会越大,从而导致严重的检测失真。在后面的仿真章节中也会发现,定理1中所提供的可达速率下界是一种紧致的下界,对于可达速率理论值具有很好的近似效果。
从式(26)中看到可达速率与天线数有关,因而,下面将分析当小区内天线总数NM→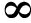 且用户数固定(或增长速率小于NM)时,可达速率的渐进极限性能,有如下推论。
且用户数固定(或增长速率小于NM)时,可达速率的渐进极限性能,有如下推论。
推论1 当NM/K→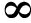 ,则第j个小区的第k个MU的上行可达速率极限值为
,则第j个小区的第k个MU的上行可达速率极限值为
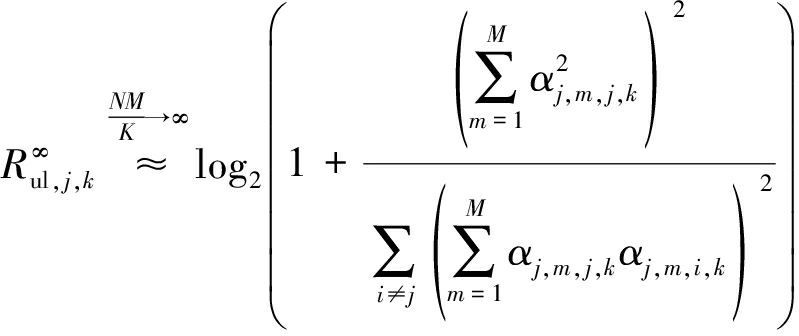
(28)
证明过程参见附录B。
结合式(10)和式(28)可以看到,在多小区分布式大规模MIMO系统中,当总天线数与用户数之比趋于无穷大时,上行可达速率极限值将只由信道大尺度衰落系数和导频功率所决定,数据发送功率将不再起作用。进一步,令导频功率pp趋于无穷大,可以发现,可达速率的极限值将只与用户的大尺度衰落因子有关,即只由导频污染项所决定,而不再受到导频功率的影响,这也再次印证了多小区大规模MIMO系统中导频污染现象对于系统性能的制约影响。同时,时变信道的影响也最终消失了,即![]() 中不再包含有信道时变系数η。从另一角度来理解,大规模天线阵列的使用可有效对抗信道的信道时变性,从而可以使其较好的应用于高速移动等场景中,而避免时变信道的影响。其主要原因在于,多小区系统中的导频污染现象使得本小区基站对本小区用户的CSI估计值中始终含有其他小区使用相同导频的用户信道信息干扰(式(28)中的分母项正是导频污染所带来的干扰)。因此,导频污染带来的小区间用户干扰成为了制约分布式大规模MIMO上行可达速率的主要因素,从而使得信道的时变特性不再成为主导因素,而这是与单小区场景中所不同的。在单小区中,其可达速率极限值将随天线总数的增加持续增加,并且可达速率极限值受到信道时变系数η的影响[19]。
中不再包含有信道时变系数η。从另一角度来理解,大规模天线阵列的使用可有效对抗信道的信道时变性,从而可以使其较好的应用于高速移动等场景中,而避免时变信道的影响。其主要原因在于,多小区系统中的导频污染现象使得本小区基站对本小区用户的CSI估计值中始终含有其他小区使用相同导频的用户信道信息干扰(式(28)中的分母项正是导频污染所带来的干扰)。因此,导频污染带来的小区间用户干扰成为了制约分布式大规模MIMO上行可达速率的主要因素,从而使得信道的时变特性不再成为主导因素,而这是与单小区场景中所不同的。在单小区中,其可达速率极限值将随天线总数的增加持续增加,并且可达速率极限值受到信道时变系数η的影响[19]。
随着小区内总天线数的增加,不单会对系统的可达速率产生影响,也会影响上行用户的发射功率增益[6]。下面将考虑时变信道条件下,多小区多用户分布式大规模MIMO系统中发射功率缩放增益变化情况,有如下推论。
推论2 假设用户平均发射功率![]() 其中Eul和M固定(与N无关)。当NM→
其中Eul和M固定(与N无关)。当NM→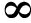 时,第j个小区中第k个MU的上行可达速率极限值为
时,第j个小区中第k个MU的上行可达速率极限值为
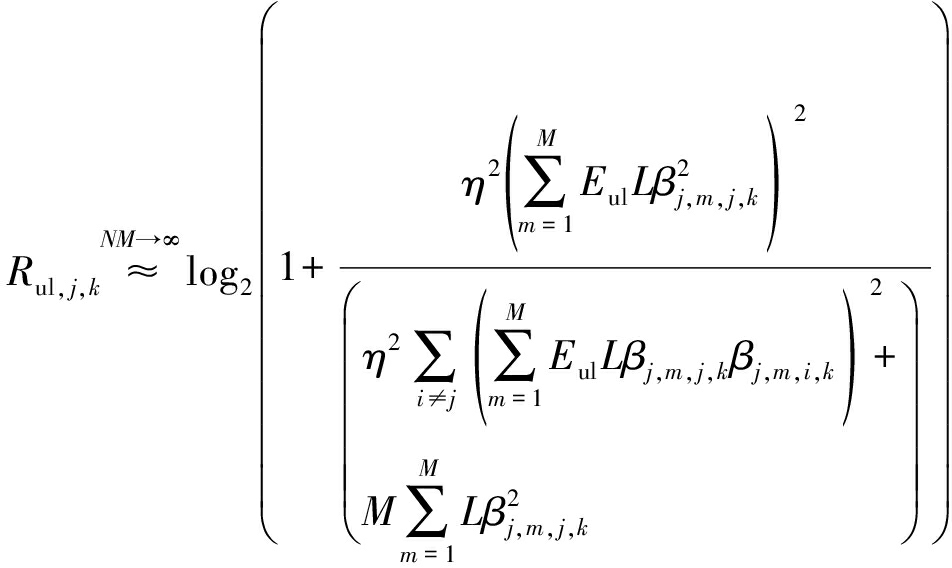
(29)
证明过程参见附录C。
从推论2中可以看到,同时存在导频污染和信道时变影响时,用户上行发射功率可以获得![]() 倍的缩放增益,同时可达速率将趋近于一个稳定值,该值与信道大尺度衰落系数、RRH个数、导频长度以及信道相关性系数有关,并且该可达速率极限值与时间相关性系数η呈单调递增关系。该功率缩放增益的物理意义在于:随着小区天线总数的增加,每个用户的实际发射功率将以
倍的缩放增益,同时可达速率将趋近于一个稳定值,该值与信道大尺度衰落系数、RRH个数、导频长度以及信道相关性系数有关,并且该可达速率极限值与时间相关性系数η呈单调递增关系。该功率缩放增益的物理意义在于:随着小区天线总数的增加,每个用户的实际发射功率将以![]() 倍持续线性降低,然而系统的可达速率将维持在极限值,而不受用户实际发射功率降低的影响。这也表明,随着天线总数的增加,用户可以获得
倍持续线性降低,然而系统的可达速率将维持在极限值,而不受用户实际发射功率降低的影响。这也表明,随着天线总数的增加,用户可以获得![]() 倍的功率效率增益。另一方面,从式(29)中可以看到,时变信道变化的快慢程度,即η值的大小,只会影响可达速率极限值的大小,而不会影响用户所能获得的发射功率缩放增益。
倍的功率效率增益。另一方面,从式(29)中可以看到,时变信道变化的快慢程度,即η值的大小,只会影响可达速率极限值的大小,而不会影响用户所能获得的发射功率缩放增益。
5 仿真结果与分析
本节将利用蒙特卡洛数值仿真对图1所示的多小区多用户分布式大规模MIMO系统在时变信道下的可达速率性能进行验证,仿真参数设置如下表1所示。关于每个小区中各RRH的部署位置,借鉴文献[13,14]中的仿真条件,7个RRH在各小区中位置如下图2所示。考虑信道时间相关性系数的设置范围时,以载波频率fc=2 GHz和信道采样间隔Ts=5 ms为例,当用户速率ν=5 km/h时,对应相关系数η=0.9790;当用户速率ν=200 km/h时,对应η=0.0364。用户移动速度越快则表示多普勒频偏越严重,信道的时变特性也就越强,前后时刻的信道时间相关性越弱。仿真中采用的时间相关性系数典型值[0.2,0.5,0.8],用于表征用户速度从高到低变化的移动场景。
每次仿真的蒙特卡洛数值结果都是基于10000次的独立信道取平均得到。不考虑各小区的导频分配策略,采用随机的方法给本小区内各用户分配正交导频。为了便于比较,在仿真中集中式大规模MIMO系统的基站部署于各小区中心位置,且每个小区基站天线总数与分布式MIMO系统的天线总数相同,关于集中式大规模MIMO系统在时变信道下的性能将根据文献[21]中得到。
表1 仿真参数设置
Tab.1 Simulation parameters setting

小区个数S=7每小区RRH个数M=7每小区内用户数K=4小区内用户分布方式随机均匀分布相邻小区距离d=3 km小区半径(中心到顶点距离)r=1 km平均路径增益中值μ=1路径损耗衰减因子τ=3.7阴影衰落因子δj,m,i,k=1加性高斯白噪声功率1 w导频长度L=K(最小长度)[6]信道时间相关性系数η=[0.2,0.5,0.8]
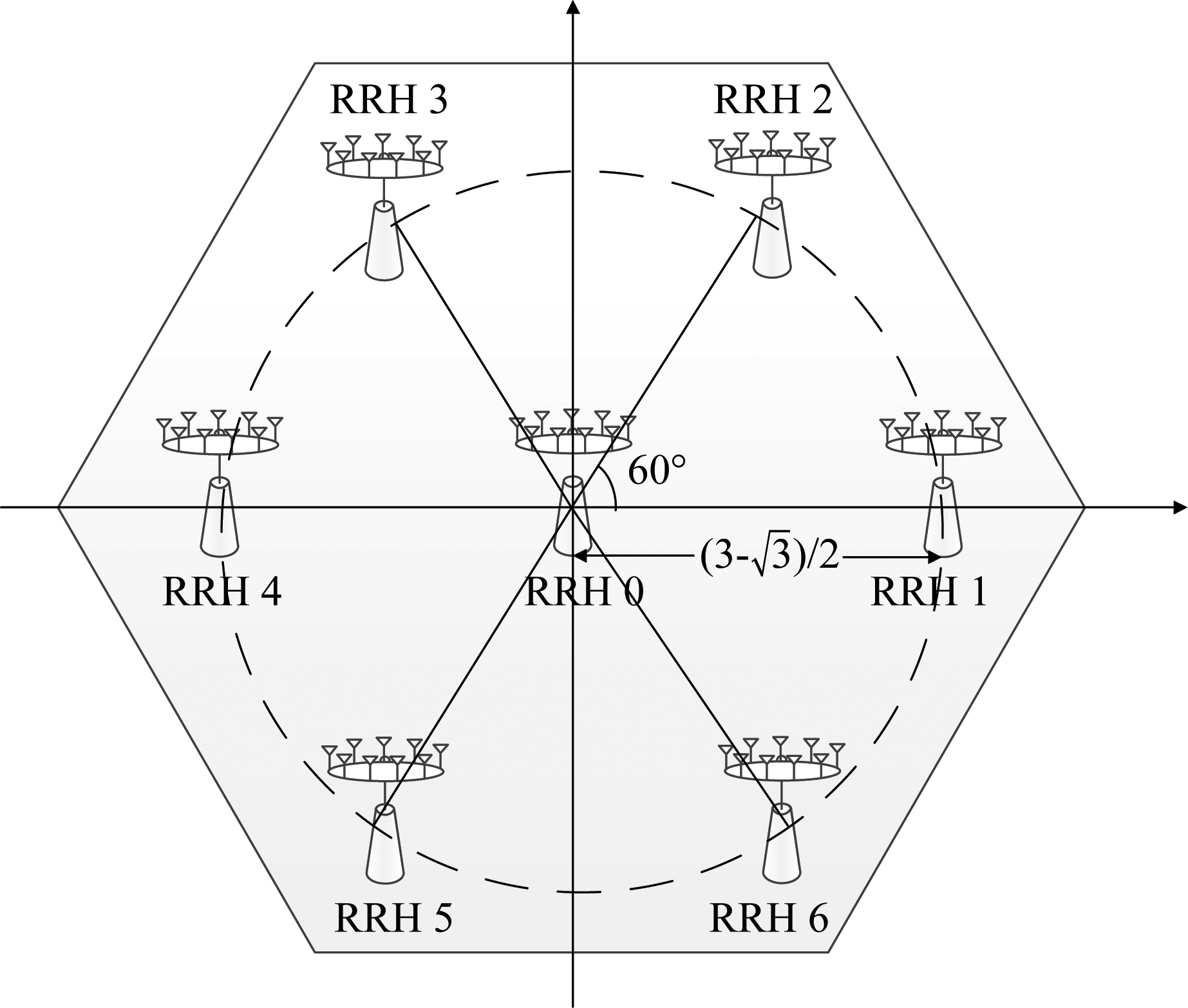
图2 每个小区内RRH的位置分布示意图
Fig.2 Diagram of RRH location distribution in each cell
图3给出了多小区多用户存在导频污染时,在有功率缩放和无功率缩放两种条件下,上行可达速率性能随总天线数与用户数比值的变化趋势。首先从图3中的两幅子图中可以看到,定理1中所给出的多小区上行可达速率解析形式与数值仿真结果具有较好的近似特性,特别是随着总天线数的增加,其近似程度也越来越精确。从(a)图所示的无发射功率缩放的性能中看到,随着时间相关性系数η的增加,可达速率是逐渐增加的,这与之前的分析结果类似,即η增加,则信道时变性越弱,前后两个时刻的信道系数误差就越小,从而性能越好。当η=1时,则表明信道无时变性。同时,从(a)图中也可以看到,在多小区场景下,由于导频污染现象的存在,随着总天线数趋近于无穷大,信道的时间相关性影响将不再存在。在不同的η取值下,最终的可达速率都将趋近于同一个极限值,这主要是由于导频污染是影响接收信干噪比的主要因素,使得时间相关性的影响趋于消失。从(b)图中则可以看到,当发射功率存在![]() 的缩放增益时,随着时间相关性系数η的变化,可达速率将收敛到不同的极限值,这与推论2中的结论是一致的。同时,对比子图(a)和子图(b)可以发现,存在发射功率缩放时的可达速率性能要稍低于无发射功率缩放的性能,也印证了在发射功率与可达速率之间的性能折中,即天线数的增加,空间资源既可以选择用于提升系统可达速率,也可以选择用来降低发射功率。
的缩放增益时,随着时间相关性系数η的变化,可达速率将收敛到不同的极限值,这与推论2中的结论是一致的。同时,对比子图(a)和子图(b)可以发现,存在发射功率缩放时的可达速率性能要稍低于无发射功率缩放的性能,也印证了在发射功率与可达速率之间的性能折中,即天线数的增加,空间资源既可以选择用于提升系统可达速率,也可以选择用来降低发射功率。
最后,考察小区边缘用户场景下分布式大规模MIMO和集中式大规模MIMO的在同时考虑导频污染和信道时变条件下的频谱有效性。此处,定义小区边缘为正六边形的内切圆[15],假设K=4个用户随机均匀分布在小区边缘上。图4显示了小区边界用户的平均可达速率在总天线数与用户数之比等于不同值时的变化关系,其中信道时变系数η=0.8。从图中可以发现,分布式大规模MIMO和集中式大规模MIMO都趋近于干扰受限,即受到导频污染的影响,可达速率趋近于饱和值。此外,我们也可以发现,即使在信道存在时变特性下,分布式大规模MIMO系统相较集中式大规模MIMO系统在边缘用户处仍然获得了较好的性能增益。
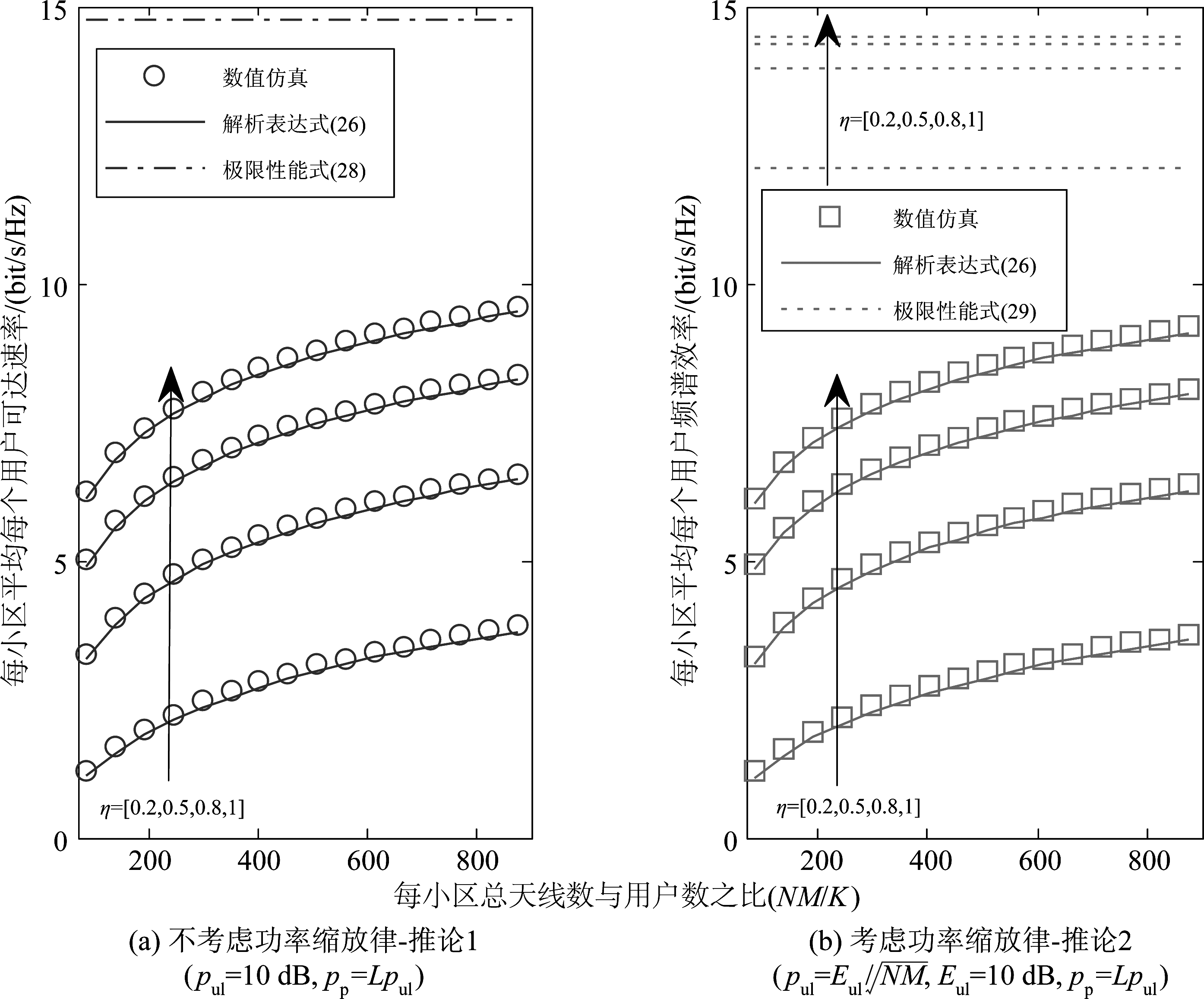
图3 多小区分布式大规模MIMO系统上行可达速率在不同信道时变程度下随总天线数的变化趋势及极限值
Fig.3 Under different degrees of time-varying channel,the trend and limiting performance of uplink achievable rate of multi-cell distributed massive MIMO system against the total number of BS antennas
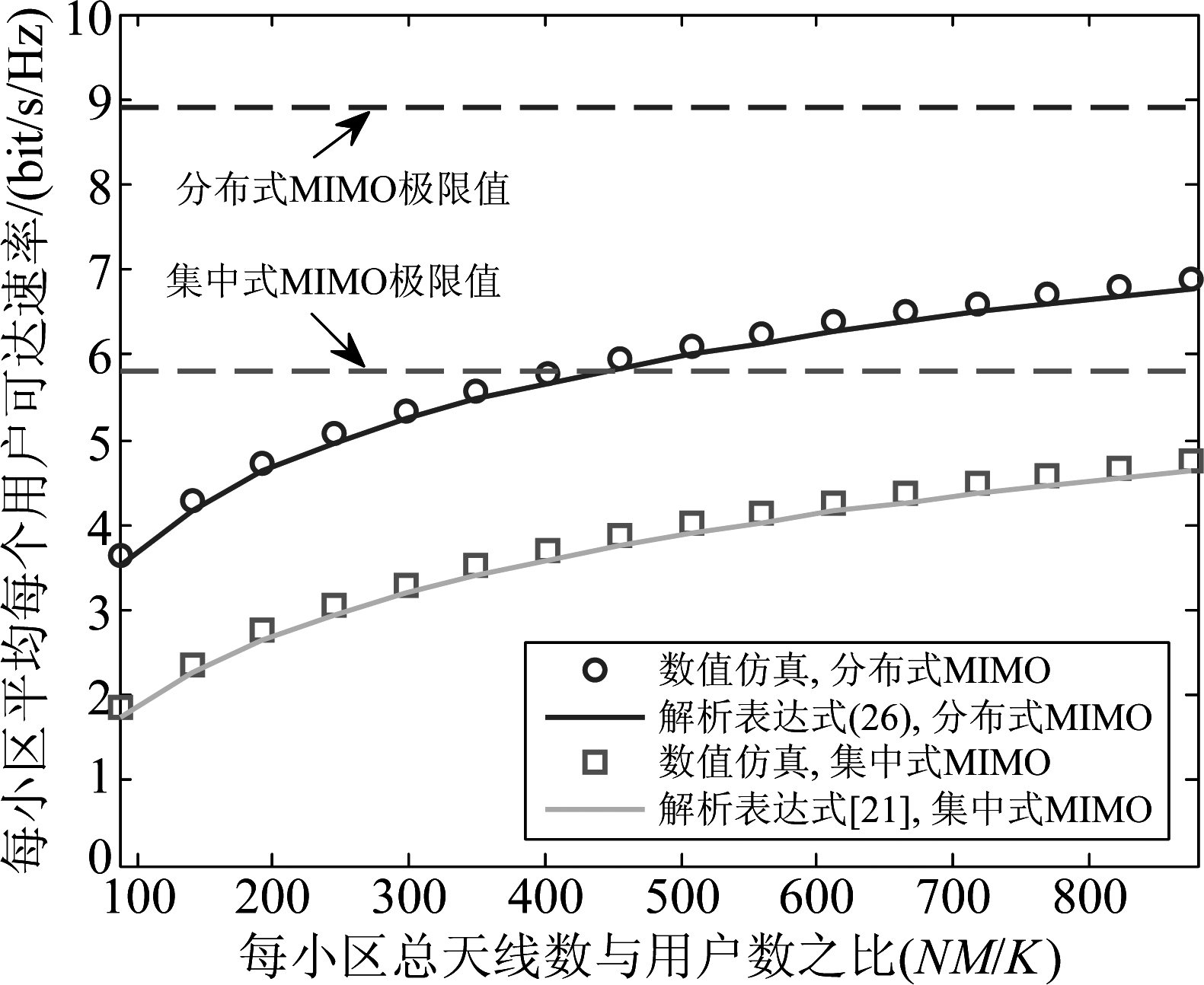
图4 多小区分布式大规模MIMO 与集中式大规模MIMO系统边缘用户的上行可达速率性能比较
(pul=10 dB,pp=Lpul,η=0.8)
Fig.4 Comparisons of uplink achievable rates of cell edge users between multi-cell distributed massive MIMO system and centralized massive MIMO system(pul=10 dB,pp=Lpul,η=0.8)
6 结论
本文基于时变信道,并结合多小区导频污染现象和信道估计误差条件,研究分析这些因素对蜂窝多小区多用户大规模MIMO上行链路可达速率和功率效率的性能影响。通过高斯马尔科夫过程对信道系数随时间变化的快慢程度进行建模,在小区基站采用最大比合并接收机的情况下,推导得出了包含时变信道参量的可达速率解析表达式,并且发现可达速率值随时变信道参量增加而增加。同时,当小区总天线数无限增加时,推导得出了上行系统可达速率极限值和用户所能获得的发射功率缩放增益。分析发现,当不考虑用户发射功率缩放时,上行可达速率随总天线数的增加将趋于一个与时变信道参量无关的极限值,即时变信道将不再影响系统性能,而该极限值主要受到多小区导频污染制约。当考虑发射功率缩放增益时,时变信道参量仅会影响系统的可达速率绝对值,而不会对用户发射功率增益产生影响。最后,通过蒙特卡洛数值仿真验证了所推导的理论结果的有效性和正确性。在未来研究中,将着重考虑电路硬件损伤、TDD系统上下行信道校准等因素所带来信道失配对于系统可达速率及功率缩放律的影响。
附 录
A.定理1证明
因为式(24)中的γul,j,k项表达式过于复杂,无法直接求解其期望运算。为了能够获得可达速率的有效闭合形式,考虑到函数log2(1+1/x)关于x的凸性,根据Jensen不等式[6],式(24)中的可达速率有如下所示下界形式:
(30)
根据条件期望的性质,可将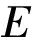
![]() 化简为
化简为

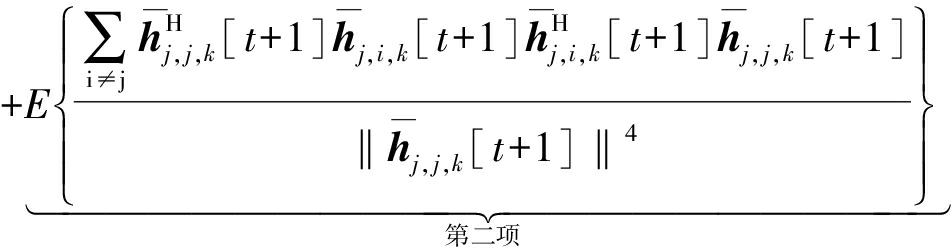

(31)
由式(31)可知,下界闭合表达式的求解关键在于计算式(31)等号右边四项。下面将借助于大维随机矩阵理论中的确定性等价原理[20]和Gamma分布随机变量的统计特性[13]来依次求解各项,先将第一项进行化简后可以得到:
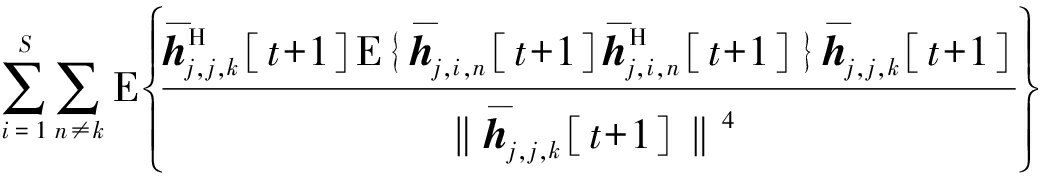
![]()
![]()
![]()
(32)
式中:步骤(1)是根据文献[20]中引理4(ii)推导得到,步骤(2)是由于随机向量![]() 服从CN(0,IN)的分布特性直接计算得到。
服从CN(0,IN)的分布特性直接计算得到。
对于式(31)中第二项,化简后可以得到:
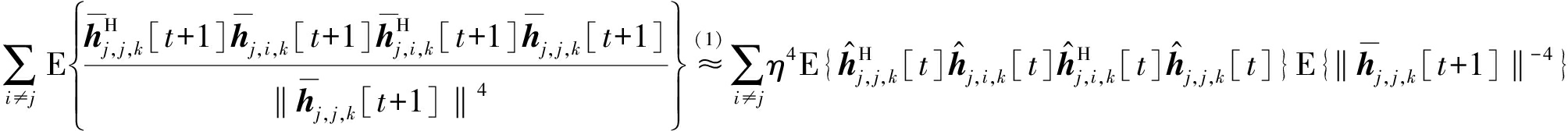
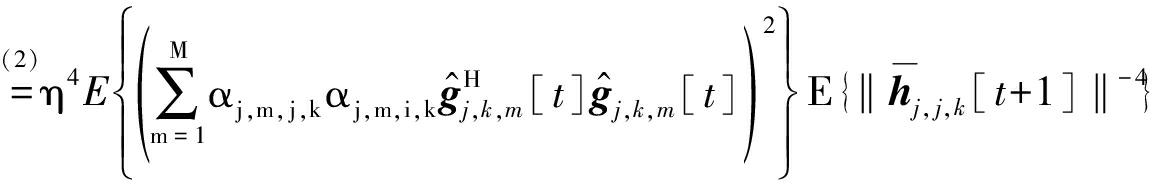
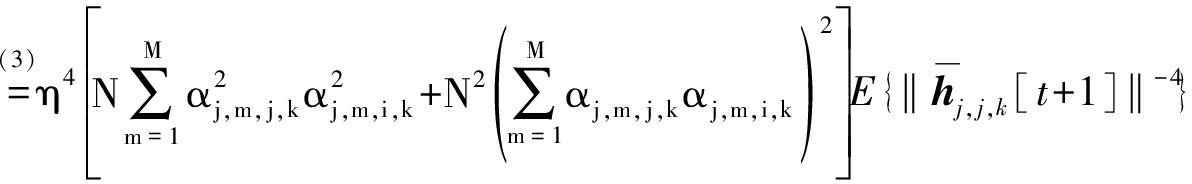
(33)
式中:步骤(1)是利用式(20)并根据文献[20]中引理4(ii)得到,步骤(2)是通过代入![]() 和
和![]() 得到,步骤(3)是先根据文献[13]中引理1~3得到随机变量χm
得到,步骤(3)是先根据文献[13]中引理1~3得到随机变量χm![]() 再利用文献[13]中引理4进行化简后得到。
再利用文献[13]中引理4进行化简后得到。
对于式(31)中第三项,则利用类似第一项的推导方法可以得到
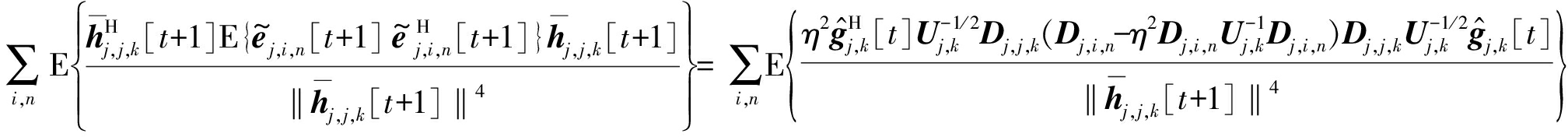
(34)
式中:![]() 步骤(1)是利用文献[20]中引理4(ii),步骤(2)利用
步骤(1)是利用文献[20]中引理4(ii),步骤(2)利用![]() 的分布特性以及文献[13]中引理1和引理4得到。
的分布特性以及文献[13]中引理1和引理4得到。
对于式(32)~式(33)中的公共项![]() 可计算如下:
可计算如下:
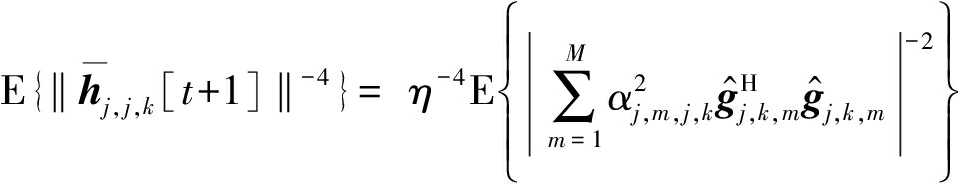
(35)
式中: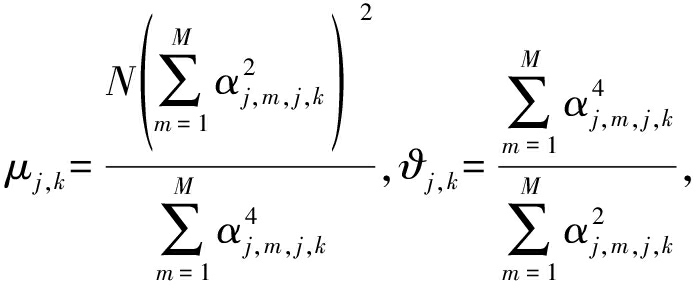 步骤(1)是先定义变量
步骤(1)是先定义变量![]() 进而根据文献[13]中Gamma随机变量的定义和各阶矩性质(引理1~引理3)得到
进而根据文献[13]中Gamma随机变量的定义和各阶矩性质(引理1~引理3)得到![]() 最后利用文献[13]中引理5计算得到,步骤(2)是通过查询积分表后得到[25]。
最后利用文献[13]中引理5计算得到,步骤(2)是通过查询积分表后得到[25]。
对于式(31)中的第四项,可采用类似式(35)的推导过程,直接得到如下形式:
(36)
最后,将式(32)~式(36)代入式(30),进行经过简单的合并简化即可得到定理1中结论。证毕。
B.推论1证明
当![]()
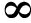 时,可以得到式(26)中上行可达速率极限值为
时,可以得到式(26)中上行可达速率极限值为
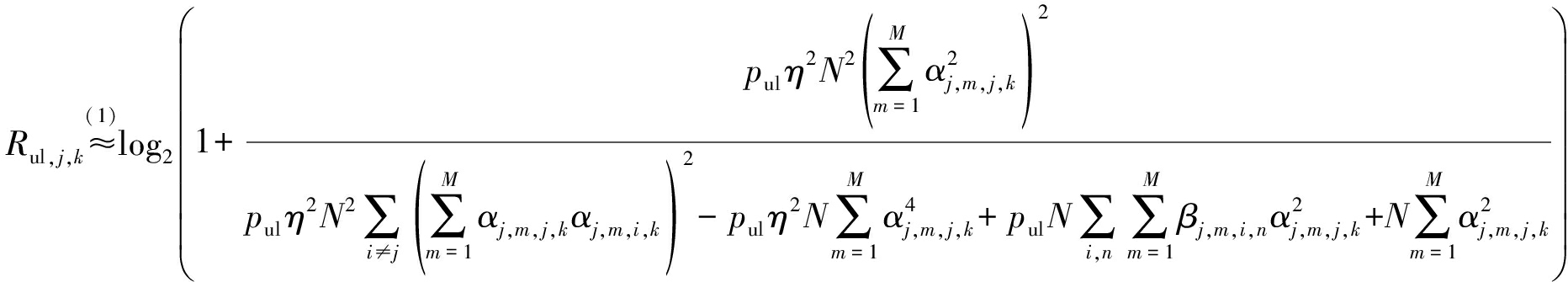

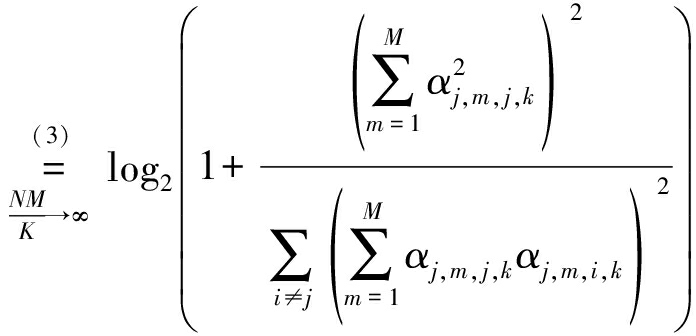
(37)
式中:步骤(1)是当![]()
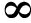 时,利用μj,k-1≈μj,k-2≈μj,k化简得到,步骤(2)则是将分子分母同除以MNK后化简得到,步骤(3)则是当
时,利用μj,k-1≈μj,k-2≈μj,k化简得到,步骤(2)则是将分子分母同除以MNK后化简得到,步骤(3)则是当![]()
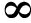 时,
时,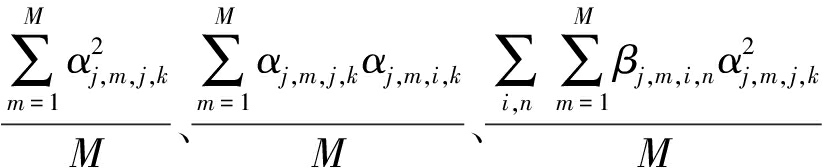 和
和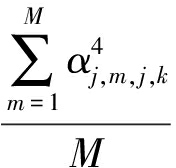 是对应
是对应![]() 和
和![]() 四项的均值,因此都为有限值。从而,分母中第二项、第三项和第四项都趋于0,最终化简得到。证毕。
四项的均值,因此都为有限值。从而,分母中第二项、第三项和第四项都趋于0,最终化简得到。证毕。
C.推论2证明
令小区中各用户发射功率![]() 即实际发射功率随天线数增加而线性降低,其中,Eul和M是固定的(与N无关),再结合导频功率条件pp=Lpul。当NM→
即实际发射功率随天线数增加而线性降低,其中,Eul和M是固定的(与N无关),再结合导频功率条件pp=Lpul。当NM→ 时,可以得到式(26)中可达速率的极限值如下:
时,可以得到式(26)中可达速率的极限值如下:

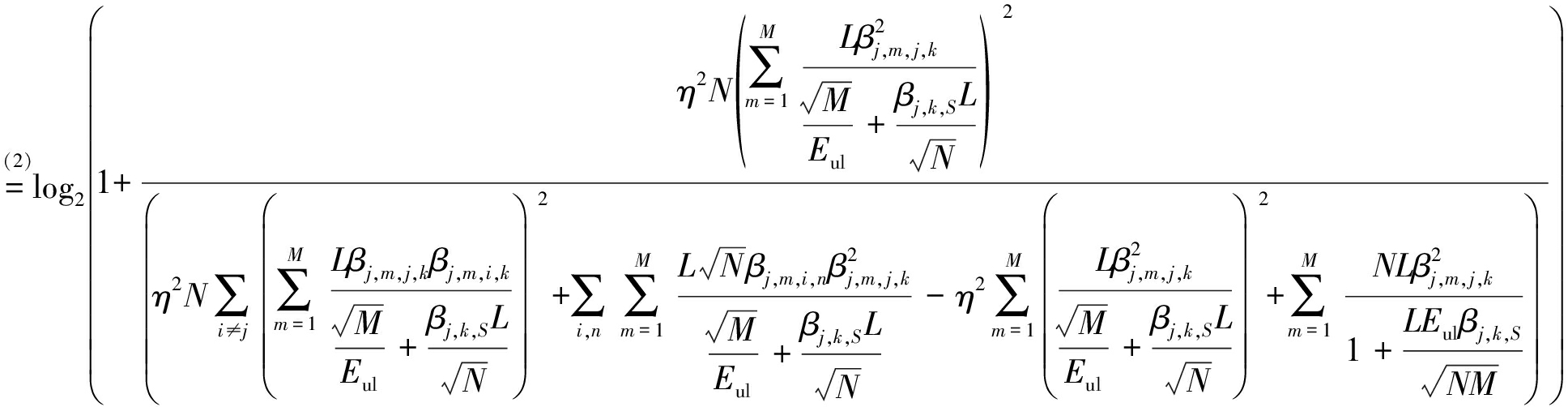
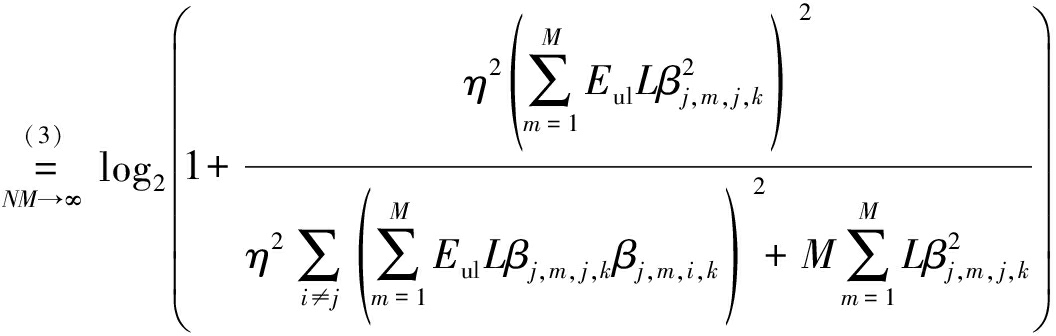
(38)
式中:![]() 步骤(1)是当N→
步骤(1)是当N→ 时,μj,k-1≈μj,k-2≈μj,k,同时代入αj,m,j,k、
时,μj,k-1≈μj,k-2≈μj,k,同时代入αj,m,j,k、![]() j,k、μj,k和ϑj,k的具体表达式后化简得到,步骤(2)是代入
j,k、μj,k和ϑj,k的具体表达式后化简得到,步骤(2)是代入![]() 和pp=Lpul后,并在分子分母上各项同乘以
和pp=Lpul后,并在分子分母上各项同乘以![]() 后化简得到,步骤(3)是当N→
后化简得到,步骤(3)是当N→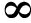 时,
时,![]() 且分母中的第二项和第三项也将趋于0,由此简化后所得到的极限可达速率表达式。证毕。
且分母中的第二项和第三项也将趋于0,由此简化后所得到的极限可达速率表达式。证毕。
[1] Andrews J G,Buzzi S,Choi W,et al. What will 5G be?[J]. IEEE Journal on Selected Areas In Communications,2014,32(6): 1065-1082.
[2] Larsson E,Edfors O,Tufvesson F,et al. Massive MIMO for next generation wireless systems[J]. IEEE Communications Magazine,2014,52(2): 186-195.
[3] Bjornson E. Massive MIMO for 5G[C]∥2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications,2015: 1-58.
[4] 张平,陶运铮,张治. 5G 若干关键技术评述[J]. 通信学报,2016,37(7): 15-29.
Zhang P,Tao Y Z,Zhang Z. Survey of several key technologies for 5G[J]. Journal on Communications,2016,37(7): 15-29.(in Chinese)
[5] Wang C X,Haider F,Gao X,et al. Cellular architecture and key technologies for 5G wireless communication networks[J]. IEEE Communications Magazine,2014,52(2): 122-130.
[6] Ngo H Q,Larsson E G,Marzetta T L. Energy and spectral efficiency of very large multiuser MIMO systems[J]. IEEE Transactions on Communications,2013,61(4): 1436-1449.
[7] Jin S,Li M,Huang Y,et al. Pilot scheduling schemes for multi-cell massive multiple-input-multiple-output transmission[J]. IET Communications,2015,9(5): 689-700.
[8] Björnson E,Matthaiou M,Debbah M. Massive MIMO with non-ideal arbitrary arrays: Hardware scaling laws and circuit-aware design[J]. IEEE Transactions on Wireless Communications,2015,14(8): 4353- 4368.
[9] Wang Y,Li C,Huang Y,et al. Energy-efficient optimization for downlink massive MIMO FDD systems with transmit-side channel correlation[J]. IEEE Transactions on Vehicular Technology,2016,65(9): 7228-7243.
[10] Qiao D,Wu Y,Chen Y. Massive MIMO architecture for 5G networks: Co-located,or distributed? [C]∥IEEE International Symposium on Wireless Communications Systems,2014: 192-197.
[11] Lee S R,Moon S H,Kim J S,et al. Capacity analysis of distributed antenna systems in a composite fading channel[J]. IEEE Transactions on Wireless Communications,2012,11(3): 1076-1086.
[12] Wang D,Wang J,You X,et al. Spectral efficiency of distributed MIMO systems[J]. IEEE Journal on Selected Areas in Communications,2013,31(10): 2112-2127.
[13] Li J,Wang D,Zhu P,et al. Spectral efficiency analysis of single-cell multi-user large-scale distributed antenna system[J]. IET Communications,2014,8(12): 2213-2221.
[14] Li J,Wang D,Zhu P,et al. Downlink spectral efficiency of multi-cell multi-user large-scale DAS with pilot contamination[C]∥2015 IEEE International Conference on Communications,2015: 2011-2016.
[15] Li J,Wang D,Zhu P,et al. Spectral efficiency analysis of large-scale distributed antenna system in a composite correlated Rayleigh fading channel[J]. IET Communications,2015,9(5): 681- 688.
[16] Pitarokoilis A,Mohammed S K,Larsson E G. Uplink performance of time-reversal MRC in massive MIMO systems subject to phase noise[J]. IEEE Transactions on Wireless Communications,2015,14(2): 711-723.
[17] Björnson E,Hoydis J,Kountouris M,et al. Massive MIMO systems with non-ideal hardware: Energy efficiency,estimation,and capacity limits[J]. IEEE Transactions on Information Theory,2014,60(11): 7112-7139.
[18] Truong K T,Heath R W. Effects of channel aging in massive MIMO systems[J]. Journal of Communications and Networks,2013,15(4): 338-351.
[19] 王毅,钱叶旺,林艳,等. 时间相关信道下分布式大规模 MIMO 系统频谱效率分析[J]. 信号处理,2016,32(11): 1269-1282.
Wang Y,Qian Y W,Lin Y,et al. Analysis over Spectral Efficiency for Distributed Massive MIMO Systems with Temporally Correlated Channel[J]. Journal of Signal Processing,2016,32(11): 1269-1282.(in Chinese)
[20] Hoydis J,Brink S T,Debbah M. Massive MIMO in the UL/DL of cellular networks: How many antennas do we need?[J]. IEEE Journal on Selected Areas in Communications,2013,31(2): 160-171.
[21] Kong C,Zhong C,Papazafeiropoulos A K,et al. Sum-Rate and Power Scaling of Massive MIMO Systems With Channel Aging[J]. IEEE Transactions on Communications,2015,63(12): 4879- 4893.
[22] Papazafeiropoulos A K. Impact of general channel aging conditions on the downlink performance of massive MIMO[J]. IEEE Transactions on Vehicular Technology,2017,66(2): 1428-1442.
[23] Love D J,Choi J,Bidigare P. A closed-loop training approach for massive MIMO beamforming systems[C]∥2013 47th Annual Conference on Information Sciences and Systems,2013: 1-5.
[24] Jose J,Ashikhmin A,Marzetta T L,et al. Pilot contamination and precoding in multi-cell TDD systems[J]. IEEE Transactions on Wireless Communications,2011,10(8): 2640-2651.
[25] Jeffrey A,Zwillinger D. Table of integrals,series,and products [M]. Academic Press,Burlington,2007.





