1 引言
随着智能终端的普及,移动宽带业务迅速增长。据预测,未来10年移动流量将增加1000倍,为了满足急剧增长的流量需求,第5代移动通信系统技术相比现有系统技术的容量预计也将增长1000倍[1]。非正交多址NOMA是5G中比较有前景的技术之一,比传统的正交多址接入(OMA,orthogonal multiple access)具有更高的频谱效率。NOMA允许多个用户同时共用同一个频谱资源,给不同信道条件的用户分配不同的功率,通过发送端的重叠编码(SC,superposition coding)和接收端的连续干扰抵消(SIC,successive interference cancellation)技术分离不同用户,实现资源复用,可以显著提高频谱利用率[1-3]。除此之外,NOMA还具有用户公平性较高、传输时延和信号成本较低、可以接入的设备量更大等优点[3],可以显著地提高系统容量,满足5G急剧增长的流量需求。
近年来有很多工作致力于下行NOMA系统的研究,文献[4]从优化的角度理论证明了NOMA系统的性能优于传统OMA系统。文献[5]研究了下行NOMA系统的中断性能,证明了用户目标速率的设置和功率的分配对中断性能的提升至关重要。文献[6]通过协作全双工中继提高了下行NOMA系统的总速率。文献[7]分析了下行NOMA系统中中断概率对系统容量和信源失真的影响,并发现系统不能同时获得最大中断容量和最小失真。除了对下行NOMA系统的研究,还有一些工作致力于上行NOMA系统。文献[8]详细研究了上行场景中的SIC解码顺序、子载波分配、功率分配问题。文献[9]研究了上行NOMA系统的最优用户配对问题。文献[10]提出了一种基于NOMA上行链路的先进的SIC解码方法,即基站将没有成功解码的用户信号当作后面用户的干扰信号。
在上行NOMA系统中,基站使用SIC技术先将功率小的用户信号当作噪声,解调出信号功率较大的用户,然后再解功率小的用户信号。实际情况中解码顺序不是固定的,因为用户的位置变化、信道状态的随机性等都会导致到达接收端的用户信号功率的大小关系发生变化。文献[11]在给定的上行NOMA场景中,采用了动态顺序的SIC解码。文献[12]在[11]的基础上考虑了有信道估计误差的情况,分析了额外的干扰信号和错误的解码顺序对系统中断性能的影响。
但是上面的文章大都考虑的是用户位置固定时的情况,基站需要将用户到基站间的具体距离反馈给相应的用户。但是在实际场景中,用户都是在一定区域内运动的,在基于动态用户的系统中,如果基站仍然将具体的距离实时地反馈给用户,势必会增加系统开销。
在本文给出的上行NOMA系统中,用户是动态分布的,基站将距离的统计特性反馈给用户,用户在后面的信息传输中,根据之前得到的统计特性确定发射功率,相比于传统NOMA系统,可以减少实时地反馈具体距离的开销。基站根据接收到的不同用户的信号瞬时功率实时地确定解码顺序,进行动态的SIC解码。仿真表明了当平均距离与具体距离相差较小时,利用距离的统计特性和利用具体距离确定发射功率可以获得几乎相同的中断性能。
文章的后续内容概述如下:第2部分给出了系统模型;第3部分介绍了动态SIC解码方法,并给出了任一用户中断概率的理论表达式;第4部分对两用户上行NOMA系统的中断概率进行了求解;第5部分给出了理论推导结果和蒙特卡罗仿真结果,同时对仿真结果进行分析;最后总结全文。
2 系统模型
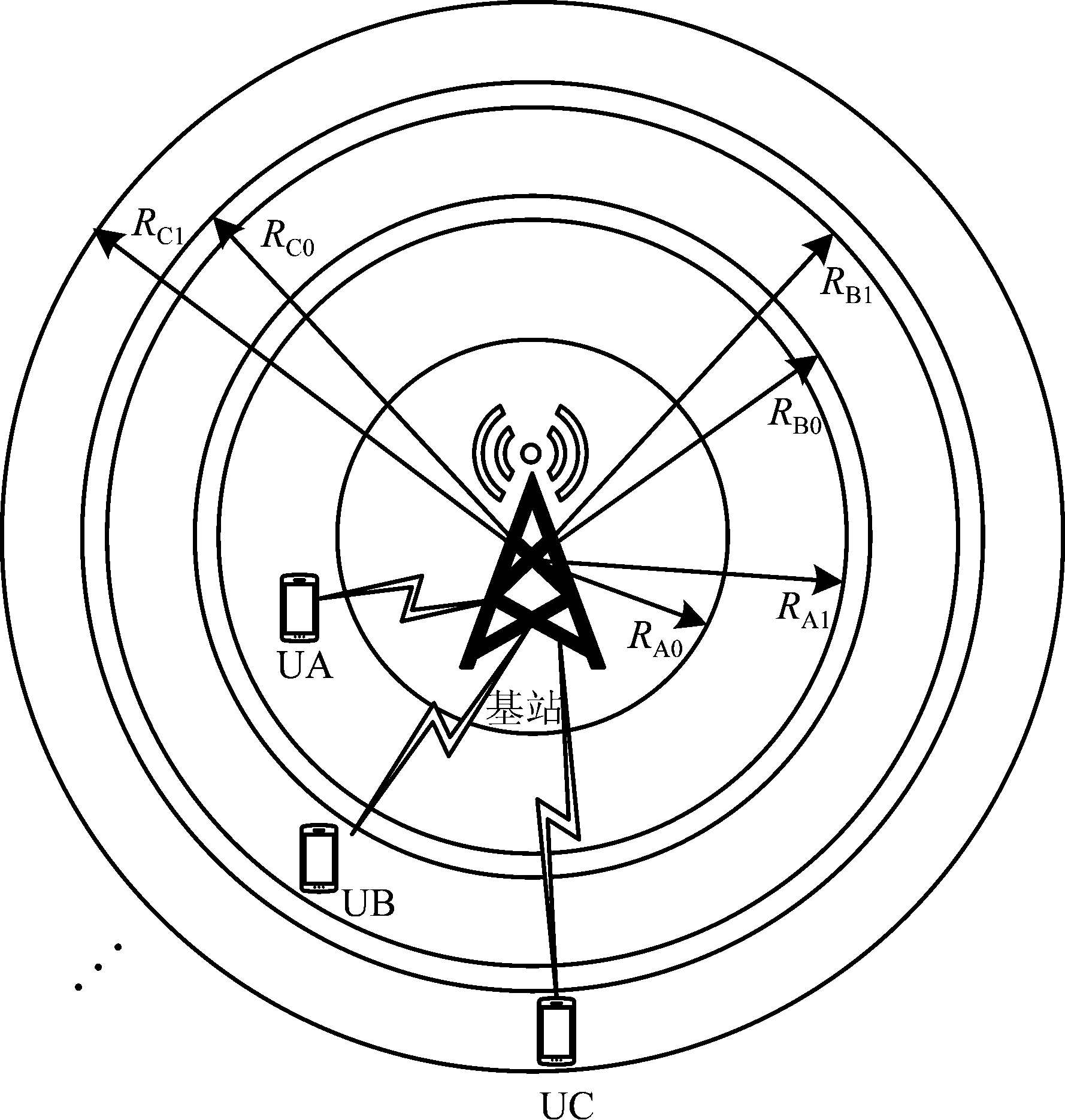
图1 系统模型
Fig.1 System model
系统模型如图1所示,基站位于圆形区域的中心且基站可以准确地获得用户的信道状态信息。所有用户位于同一小区内,Π为包含所有用户的集合,用户A,B,C...∈Π分布在从基站向外扩散的一个个圆环区域内,某一时刻某一用户出现在其圆环区域内的每个位置的概率均相等。假设用户π到基站的距离表示为rπ,则这个距离的概率密度函数为
(1)
考虑到实际场景中用户大都在办公室、教室、家等地点活动,所以本文仅分析各用户的分布区域内外边界值相差不大(Rπ 1-Rπ 0<10)时的情况,因此距离的平均值与具体值相差不大。在OFDMA系统中,每个载波频谱资源最多能被一个用户使用,系统通过不同用户所在频谱的正交关系来区分不同的用户;而NOMA系统允许多个用户共享同一时频资源块,通过给不同的用户分配不同的功率将用户区分开。用户A,B,C...复用在一个NOMA系统中,为了推导方便,频带带宽归一化为1,每个用户配有一个单天线。
假定信道模型由瑞利衰落和路径损耗组成[13],路径损耗与用户到基站间的具体距离有关,且各用户信道是相互独立的,那么用户π到基站的信道参数可以表示为
(2)
其中π=A,B,C...∈Π,gπ2表示瑞利衰落信道增益,服从参数为1的指数分布,rπ为用户π到基站间的距离,α是信道衰落指数。
用户根据基站反馈的用户到基站距离的统计特性,计算出rπ的平均值
进而确定发射功率,基站不需要实时地向用户反馈具体的距离信息。本文研究的是在某一时间段内所有用户的分布都不发生变化时的情况,因此不需要考虑基站多久反馈一次对系统性能的影响。在上行链路NOMA系统中使用功率控制技术,即给不同位置的用户提供不同的发射功率,距基站近的用户发射功率小、距基站远的用户发射功率大，可以减少小区间干扰,使用功率控制后,用户π的发射功率为[14]
(3)
其中β为功率控制参数,用于补偿用户的路径损耗。注意到β∈[0,1],β越大,发射功率对路径损耗的补偿越大。当β=0时,系统中不同用户的发射功率相同,用户没有对路径损耗进行补偿;当β∈(0,1)时,发射功率对路径损耗进行部分补偿;当β=1时,发射功率与路径损耗相差不大,基站接收到的不同用户的功率几乎服从相同的分布。基站处用户π的信号瞬时功率可以表示为
(4)
各用户发射功率以及信道参数的随机性,使基站处不同时刻各个用户信号功率的大小关系不是固定的,所以基站在进行 SIC解码时,要根据瞬时功率的大小关系实时地确定解码顺序。
NOMA系统中不同用户共用同一频谱资源同时向基站发送信号,因此基站接收到的瞬时信号为多个用户的混合信号,可以表示为
(5)
其中sπ表示用户π发送过来的信息,且E[sπ2]=1,n表示均值为0,方差为σ2的加性高斯白噪声。
3 动态SIC 解码
在下行链路NOMA系统中基站向不同的用户发送相同的信号,用户π收到的叠加信号来自单个链路,每个用户进行SIC解码;上行链路中,每个用户具有单独的发射功率,基站收到的是来自不同链路的混合信号,基站对混合信号进行SIC解码。本文中基站对不同用户的信号按接收功率降序排序并按该顺序进行解码。在没有差错传播的情况下,升序和降序时的系统总吞吐量一样,但在有差错的实际系统中,最佳SIC解码顺序是接收功率递减的顺序[15]。
发射功率以及信道参数的随机性使不同时刻的解码顺序不一定相同。用Ω表示所有可能的解码顺序的集合,ω1,ω2,ω3...∈Ω。在特定的解码顺序ωm中,当基站解第i个用户的信号时,先解码并重建前面(i-1)个用户的信号,然后从混合信号中减去它们,最后将剩余用户的信号当作干扰对第i个用户进行解码。
当解码顺序为ωm时,根据香农公式可得用户π的可获得速率为
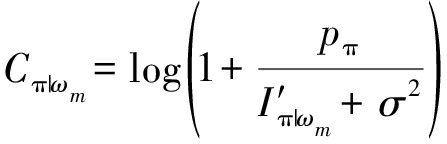
(6)
其中
为干扰信号,即在用户π之后解码的所有用户的信号功率总和。记Cπ|ωm大于等于用户π的预设速率
为事件
其概率可以表示为
(7)
在某一次解码过程中,假设用户π第i个解码,如果用户π解码成功,前面(i-1)个用户都应解码成功,所以当解码顺序为ωm时用户π的中断概率可以表示为[13]
...
(8)
其中事件
和事件
相互独立。
某一用户的中断概率为其在所有解码顺序时的中断概率的加权平均和[11],则用户π的中断概率为
(9)
4 两用户系统的中断概率求解
在NOMA系统中,子载波上的用户数为2与OMA系统相比可以使系统容量显著提升,用户数过多会使系统复杂度过大[8]。在两用户NOMA系统中,假设用户A的活动区域比用户B的活动区域距基站更近一些。基站对接收到的混合信号进行SIC解码,当用户A到达基站的信号瞬时功率大于用户B到达基站的信号瞬时功率时,基站先将用户B的信号当作干扰信号来解用户A,如果用户A被成功解码,基站将用户A的信号从混合信号中去除,再解用户B的信号,此时用户B没有干扰信号(不考虑信道固有白噪声的话)。
下面对本文提出的动态场景中用户数为2时的中断概率进行理论分析与求解。某一用户的中断概率可由式(9)得出,需要求出每种解码顺序发生的概率以及该用户在每种解码顺序下的中断概率。在推导这些概率时都需要进行可获得速率与预设速率间的比较,而速率间的比较可以转化为功率间的比较,所以需要求出基站接收到的任一用户的信号瞬时功率pπ的概率密度函数,
的累积分布函数与瑞利衰落和用户π到基站的距离分布有关。具体求解过程如下:
瑞利衰落信道增益服从参数为1的指数分布,所以对于用户A,gA2的概率密度函数为
fgA2(x)=e-x
(10)
上式为关于自变量的减函数并且随着自变量的增加函数值趋于零,为了推导方便,记fgA2(x)小于一定值时的自变量为XA,则0
由rA的概率密度函数可得
的概率密度函数为
(11)
基站接收到的用户A的信号瞬时功率
的累积分布函数推导如下
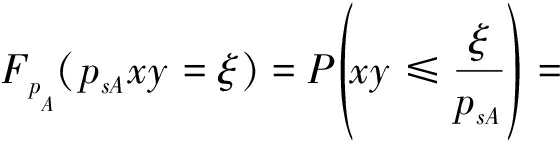
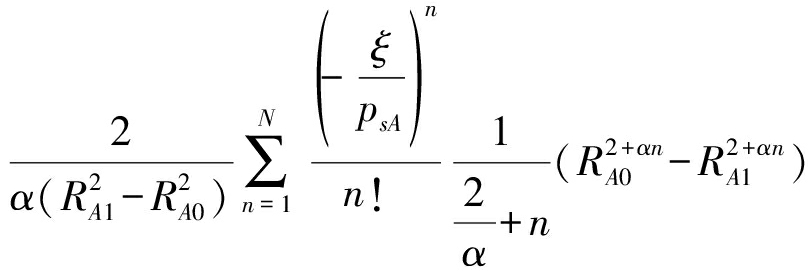
(12)
累积分布函数对自变量求导可得pA的概率密度函数
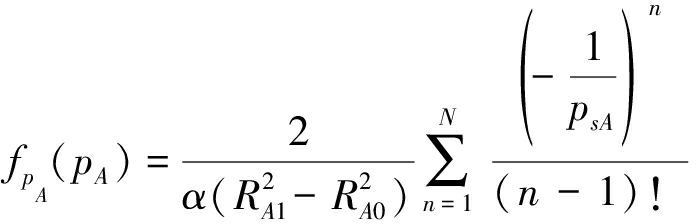
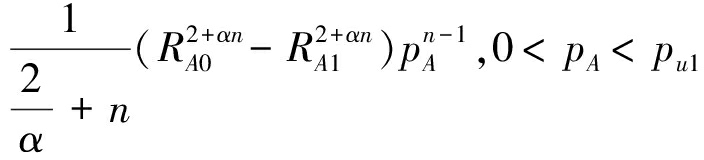
(13)
其中
为pA能取到的最大值。同理可得pB的概率密度函数
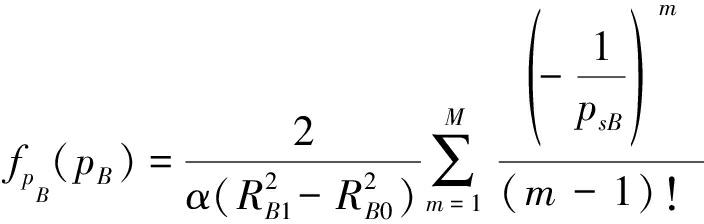
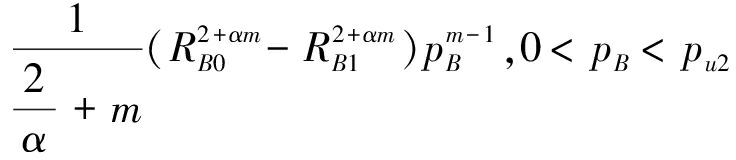
(14)
其中
为pB能取到的最大值。
两用户的NOMA系统,基站有两种解码顺序,即ω1:先解用户A再解用户B(用户A到达基站时的信号瞬时功率大于等于用户B的功率),和ω2:先解用户B再解用户A(用户A到达基站时的信号瞬时功率小于用户B的功率)。ω1发生的概率可以表示为
fpB(pB)dpB
fpA(pA)dpA=
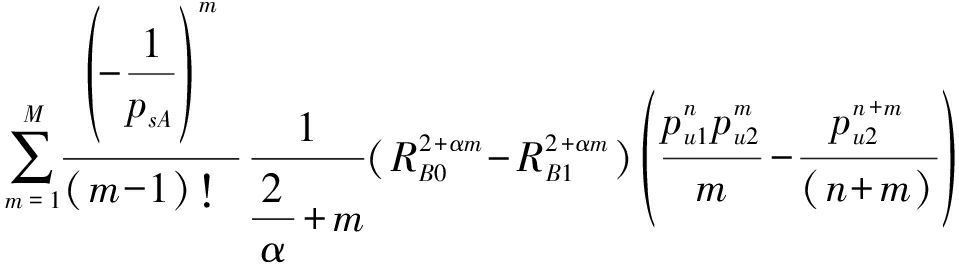
(15)
由P(ω1)+P(ω2)=1可得P(ω2)的表达式。
根据式(9)可得用户数为2时,用户A和用户B的中断概率表达式为
(16)
其中
(17)
令
将用户可获得速率与预设速率之间的比较转化为功率关系的比较。Iπ|ωm表示当解码顺序为ωm时,用户π的干扰信号和噪声信号的总功率。
当解码顺序为ω1时:
1)由贝叶斯公式可得CA大于
的概率可以表示为
(18)
为了确定上式分子中两概率的积分上下限,需要对τA进行讨论。
当τA≥1时,可以得到
P(pA≥τA(pB+σ2)≥pB)=
fpB(pB)dpB
fpA(pA)dpA=
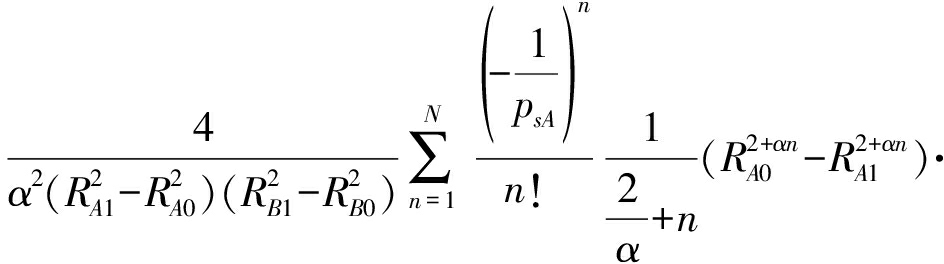
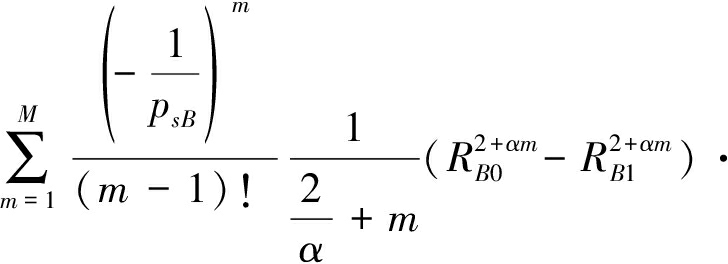
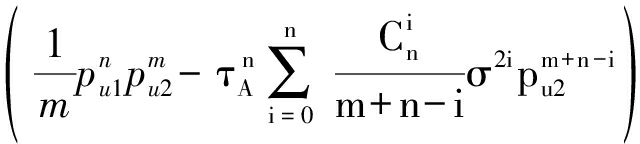
(19)
由τA≥1知τA(pB+σ2)一定大于pB,所以在对上式进行积分计算的时候只考虑了P(pA≥τA(pB+σ2)),同时可以看出P(pA≥pB≥τA(pB+σ2))=0。
当τA≤1时,可以得到
P(pA≥τA(pB+σ2)≥pB)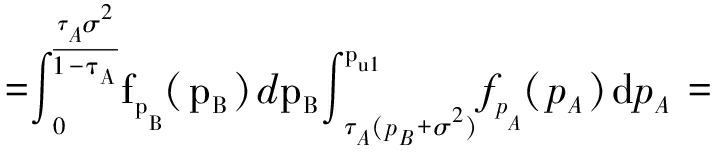
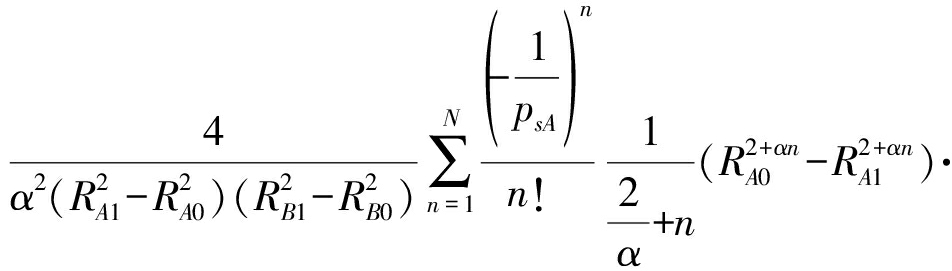
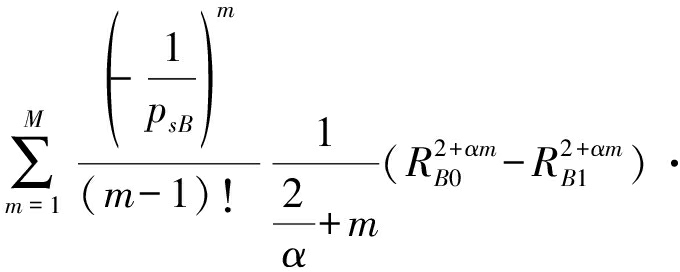
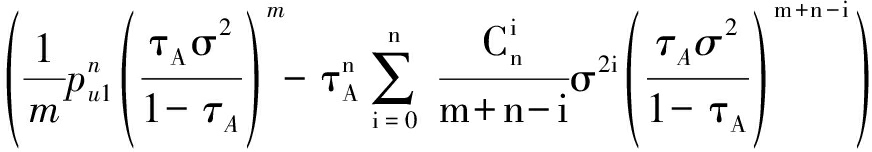
(20)
且
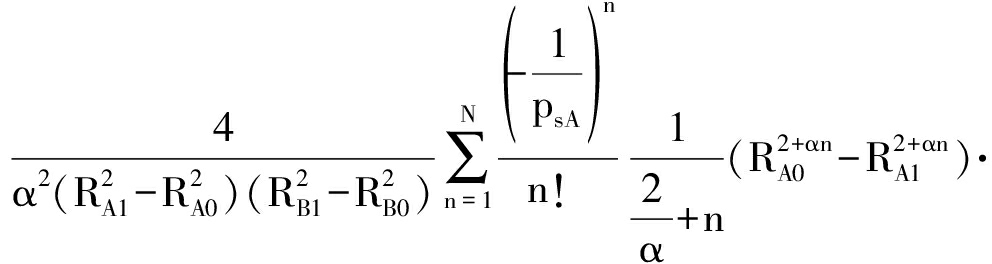
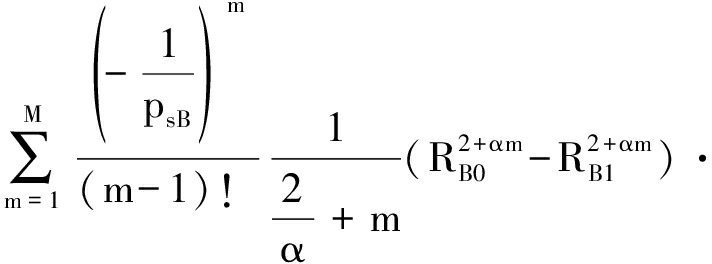
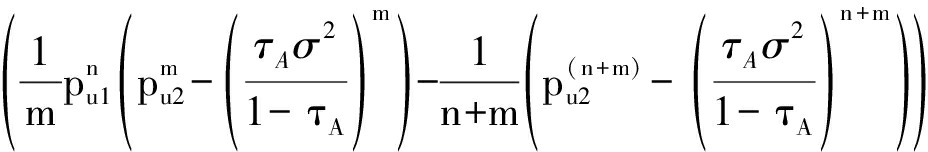
(21)
上式中pB的积分下界
由pB≥τA(pB+σ2)解出。
2)CB大于
的概率可以表示为
(22)
其中在求P(pA≥pB≥τBσ2)的值时不需要对τB进行讨论,结果如下
P(pA≥pB≥τBσ2)=
fpB(pB)dpB
fpA(pA)dpA=
(23)
当解码顺序为ω2时,CA大于的概率、CB大于的概率分别如式(24)、(25)所示,具体求解过程与解码顺序为ω1时的情况类似。
(24)
(25)
将上述两种解码顺序时的结果代入式(16)、(17)中可得到用户A、B的中断概率。
5 仿真结果分析
本文使用matlab软件对两用户NOMA系统的用户中断概率进行蒙特卡罗仿真。如果没有特殊说明,RA0=40,RA1=45,RB1=60,令用户B和用户A的活动区域面积相同得到RB0的值,信道衰落指数α设置为2,功率控制参数β的取值为0.8。考虑到许多场景如物联网在上行链路NOMA系统中所需的数据速率通常是固定且较小的,令用户A、用户B的预设数据速率分别为0.8 bps/Hz,0.3 bps/Hz。信噪比定义为
其中
为基站接收到的用户A和用户B的信号平均功率。
从图2可以看出用户中断概率的理论推导结果曲线、蒙特卡罗仿真结果曲线几乎重合,理论推导正确。随着SNR的提高,两个用户的中断性能都大幅提高,远高于固定解码顺序即先解用户A再解用户B时的情况,这是因为即使在用户A距基站比用户B近的情况下,功率控制使到基站平均距离较小的用户发射功率较小,两个用户在一定区域范围内的移动使得信道参数的分布也在发生变化,基站处各用户信号的功率大小关系不是固定的。因此接收端必须使用动态的SIC解码。
令SNR=15、用户B的分布不变
固定为42、RA1不断扩大,则RA0相应减小。表1示出了用户A通过两种方式确定发射功率时(也即基站反馈不同内容时)的中断概率。可以看出,当中断概率的数量级为10-2时,两中断概率差值的数量级大约在10-6到10-4(当Rπ 1-Rπ 0<10时),随着用户区域的不断扩大,中断概率的差值也越来越大。结合图2和表1可以得出结论:当用户的分布区域内外边界值相差不大,即平均距离与具体距离相差较小时,通过具体距离和距离的统计特性(基站反馈的不同内容)确定发射功率获得的中断性能差异可以忽略。
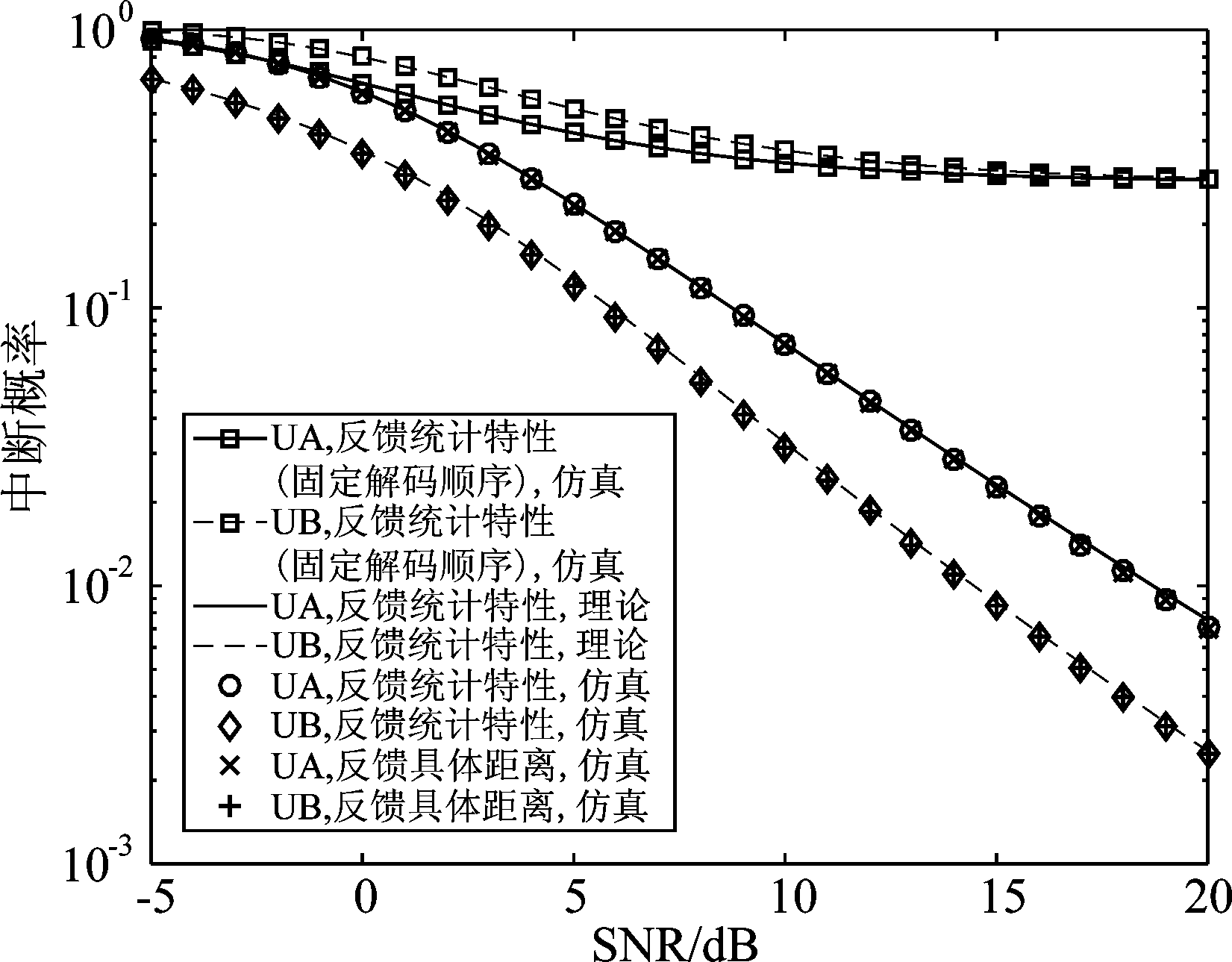
图2 反馈不同内容时的中断概率
Fig.2 Outage probability of feeding back different contents
表1 用户A分布区域扩大,中断概率的变化
Tab.1 Change of outage probability as the user A’s distribution area expands
RA1确定发射 功率的方式 42434445465055具体距离0.0224810.0224550.0224900.0225010.0224880.0224960.022549距离的统计特性0.0224810.0224600.0225710.0225820.0227060.0233090.025080
图3对比了不同β值时的中断概率,在同样的噪声环境下,功率控制参数越大,发射功率对用户路径损耗的补偿越大,中断性能越好。从图中可以看出在本文的场景下,不同β值时,两个用户之间的中断概率差异几乎一样,中断性能得到平衡。
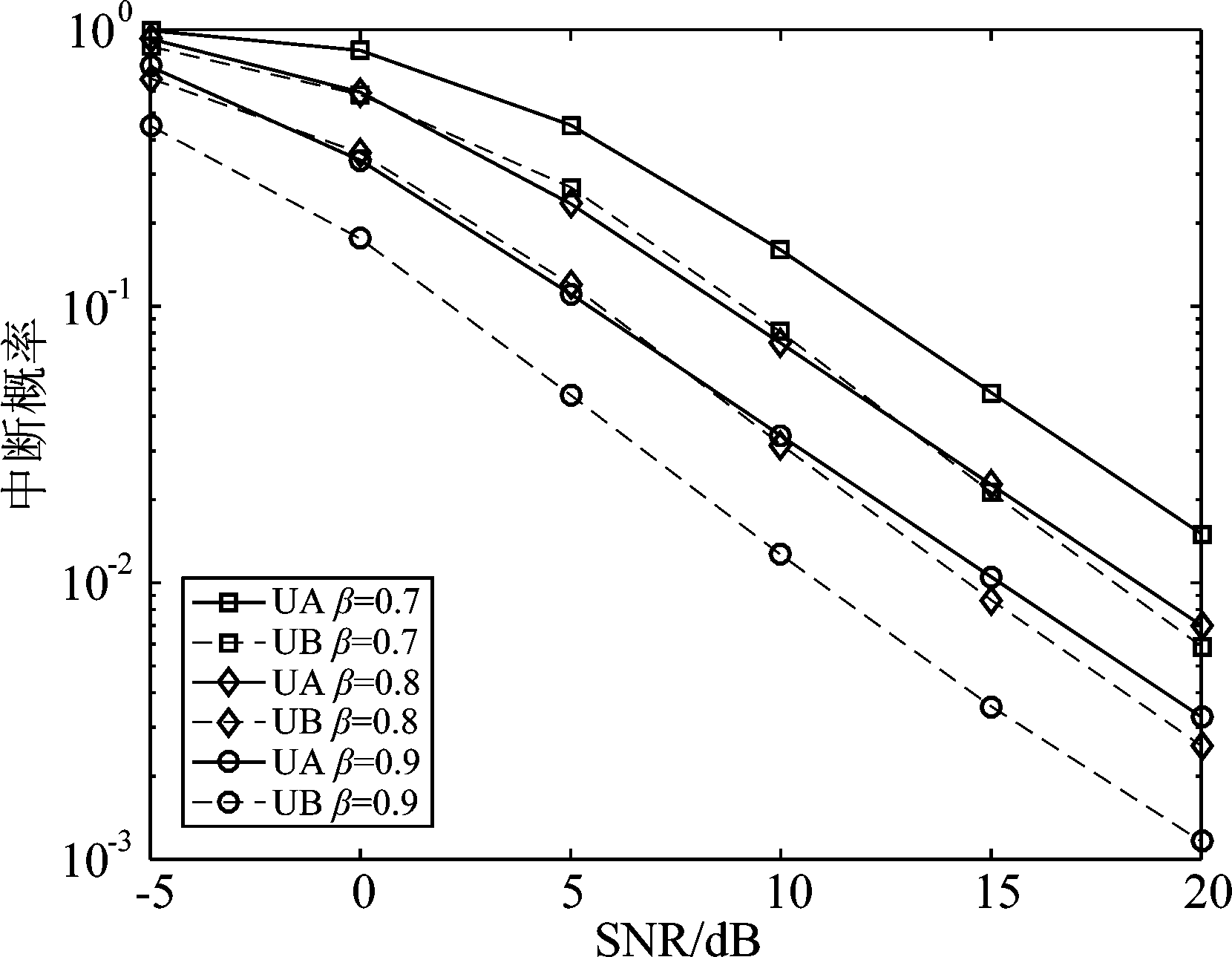
图3 不同功率控制参数时的中断概率
Fig.3 Outage probability of different power control parameters
图4对比了不同预设速率时的中断概率。从图中可以看出当用户A的预设速率
大于1时,两个用户的中断概率都远大于
均小于1时的情况,这是因为用户A和用户B的分布区域相距较近且发射功率对路径损耗进行了部分补偿,两个用户到达基站时的功率相差不大,由香农公式可知可获得速率CA、CB的值大概率小于1。因此如果某一用户的预设速率超过1,两个用户的中断性能将大幅降低。当SNR较大时,噪声的影响可以忽略,中断概率收敛;当
相等时,用户A的中断性能优于用户B,因为用户A的分布区域离基站更近一些,先解码的概率更大,受另一用户的影响更小;当
提高时,对于用户B,即使预设速率不变,其中断性能也会降低,这是因为当用户B后解码时,用户A的中断会使用户B也中断,从而降低用户B的中断性能。
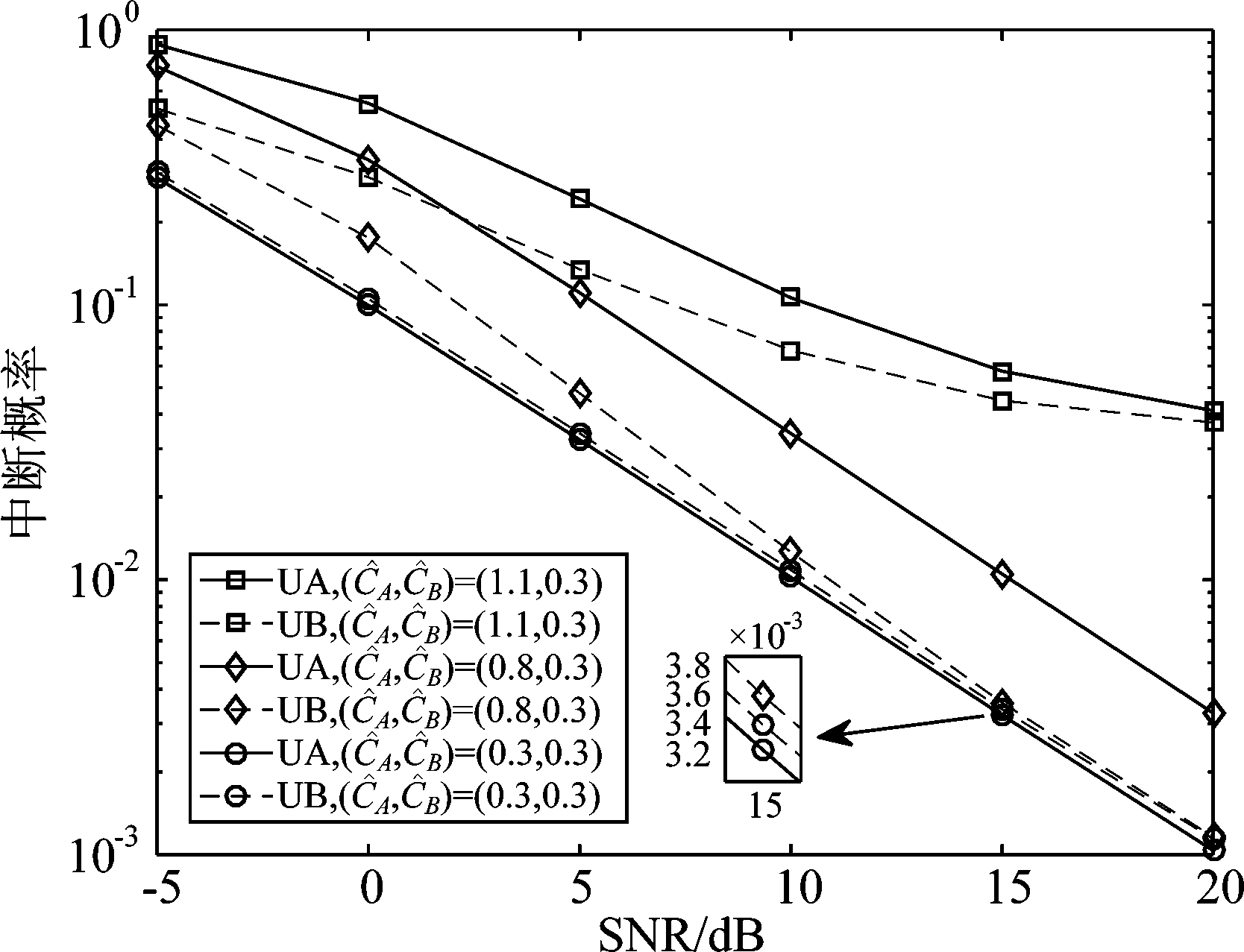
图4 不同预设速率时的中断概率
Fig.4 Outage probability of different preset speeds
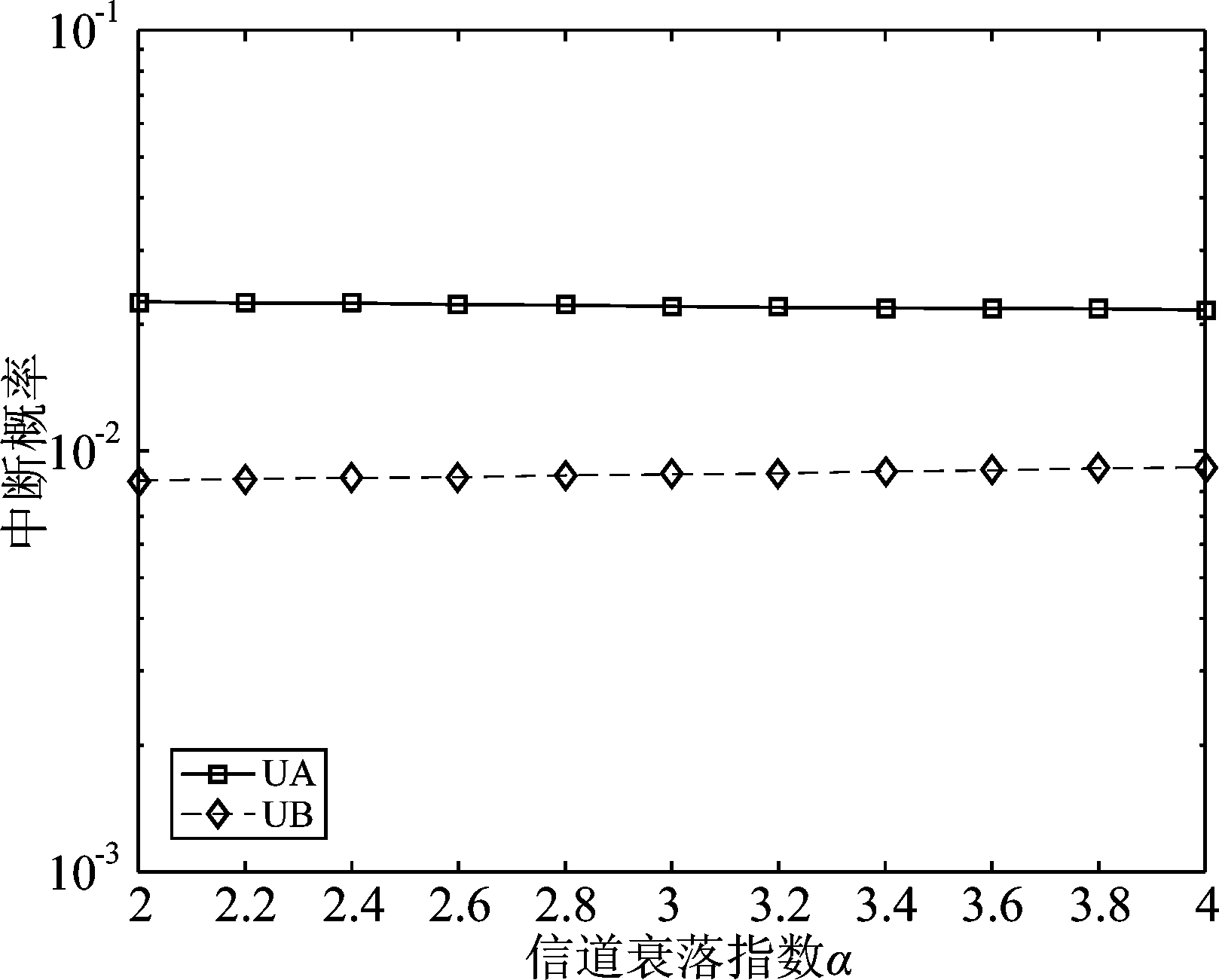
图5 不同信道衰落指数时的中断概率
Fig.5 Outage probability of different channel fading parameters
令SNR=15,图5对比了不同信道衰落指数时的中断概率,可以看出,随着信道衰落指数的增加,用户A的中断概率略微下降,用户B的中断概率略微升高。根据基站接收到的某一用户的信号功率
其中用户π的发射功率为
可以看出,在其他参数固定的情况下,α设置的越大,各个用户到达基站时的功率也就越小,同时用户A和用户B功率的比值也就越大,由公式(6)可知,相应地,用户A可获得的速率增加,中断概率降低;用户B可获得的速率减小,中断概率增加。由于用户的发射功率对信道衰落进行了部分补偿,所以随着信道衰落指数的变化,两用户的中断概率只是略微变化。
6 结论
在本文提出的针对动态用户的NOMA系统中,基站只向用户反馈用户到基站间距离的统计特性,而不是实时地反馈具体距离,减少系统开销的同时保证了中断性能。但是本文只考虑了平均距离与具体距离相差较小且所有用户的统计特性不发生变化时的情况,在后面的研究中,应进一步分析用户位置及位置的变化、基站多久反馈一次等因素对系统性能的影响。
[1] Li Q C,Niu H,Papathanassiou A T,et al. 5G Network Capacity: Key Elements and Technologies[J]. IEEE Vehicular Technology Magazine,2014,9(1): 71-78.
[2] Islam S M R,Avazov N,Dobre O A,et al. Power-Domain Non-Orthogonal Multiple Access(NOMA) in 5G Systems: Potentials and Challenges[J]. IEEE Communications Surveys & Tutorials,2017,19(2): 721-742.
[3] Dai L,Wang B,Yuan Y,et al. Non-Orthogonal Multiple Access for 5G: Solutions,Challenges,Opportunities,and Future Research Trends[J]. IEEE Communications Magazine,2015,53(9): 74- 81.
[4] Chen Z,Ding Z,Dai X,et al. An Optimization Perspective of the Superiority of NOMA Compared to Conventional OMA[J]. IEEE Transactions on Signal Processing,2017,65(19): 5191-5202.
[5] Ding Z,Yang Z,Fan P,et al. On the Performance of Non-Orthogonal Multiple Access in 5G Systems with Randomly Deployed Users[J]. IEEE Signal Processing Letters,2014,21(12): 1501-1505.
[6] Zhang L,Liu J,Xiao M,et al. Performance Analysis and Optimization in Downlink NOMA Systems with Cooperative Full-Duplex Relaying[J]. IEEE Journal on Selected Areas in Communications,2017,35(10): 2398-2412.
[7] Islam S M R,Kwak K S. Outage Capacity and Source Distortion Analysis for NOMA Users in 5G Systems[J]. Electronics Letters,2016,52(15): 1344-1345.
[8] Lv G,Li X,Shang R,et al. Dynamic Resource Allocation for Uplink Non-Orthogonal Multiple Access Systems[J]. Iet Communications,2018,12(6): 649- 655.
[9] Sedaghat M A,Müller R R. On User Pairing in Uplink NOMA[J]. IEEE Transactions on Wireless Communications,2018,17(5): 3474-3486.
[10] Xia B,Wang J,Xiao K,et al. Outage Performance Analysis for the Advanced SIC Receiver in Wireless NOMA Systems[J]. IEEE Transactions on Vehicular Technology,2018,67(7): 6711- 6715.
[11] Gao Y,Xia B,Xiao K,et al. Theoretical Analysis of the Dynamic Decode Ordering SIC Receiver for Uplink NOMA Systems[J]. IEEE Communications Letters,2017,21(10): 2246-2249.
[12] Gao Y,Xia B,Liu Y,et al. Analysis of the Dynamic Ordered Decoding for Uplink NOMA Systems with Imperfect CSI[J]. IEEE Transactions on Vehicular Technology,2018,67(7): 6647- 6651.
[13] Zhang N,Wang J,Kang G,et al. Uplink Nonorthogonal Multiple Access in 5G Systems[J]. IEEE Communications Letters,2016,20(3): 458- 461.
[14] Zhang Z,Hu R Q. Uplink Non-Orthogonal Multiple Access with Fractional Power Control[C]∥Wireless Communications and Networking Conference. IEEE,2017: 1- 6.
[15] Anass B. An Overview of Non-Orthogonal Multiple Access[J]. ZTE Communications,2017,15(S1): 21-30.
