1 引言
在实际海杂波干扰环境中,雷达面临的干扰复杂多变,海杂波干扰强度较大,且频谱中心频率变化大,非高斯、非平稳特性显著[1-2]。传统基于频域滤波器的杂波抑制方法,如两脉冲对消、三脉冲对消等方法,很难有效抑制海杂波[3]。Sira等提出了基于子空间方法的海杂波抑制技术,通过估计海杂波子空间来进行海杂波抑制[4]。Rafaat Khan等提出基于奇异值分解的海杂波抑制技术[5]。该算法在海杂波Bragg峰不显著情况下,很难有效抑制掉海杂波。Salvatore等研究了高频雷达海杂波的时变特性,使用线性预测或者AR模型的方法来进行海杂波抑制[6]。A.Yasotharan等对海杂波的时频特性进行了分析,利用时频滤波的方法抑制海杂波[7]。有学者研究了分数阶傅里叶变换在海面环境下动目标检测中的应用,通过分析海杂波的FRFT谱特性,提升雷达目标检测性能[8-10]。在时频滤波方面,部分学者研究了基于直方图统计的时频滤波方法,该方法能够自适应进行时频滤波,在滤除干扰信号的同时能减少有效信号的损失[11-12]。
由此,本文将基于时频谱能量分布的时频滤波方法应用于海杂波抑制中,通过分析海杂波时频分布特性,提出了基于时频谱能量分布的改进型时频滤波方法。
2 基于时频谱能量分布的时频滤波方法
对非平稳信号,通过时频分析方法研究其在不同时刻的频率分布具有重要意义。短时傅里叶变换(STFT)是常用的时频分析方法之一,其原理是设置一个随着时间移动的窗对信号进行截取,认为窗内信号是平稳的,对其进行傅里叶变换,便得到了该信号的时频分布[13]。
在实际应用中,常用到的短时傅里叶变换为离散形式,即对STFTz(t,f)在(mT,nF)处进行采样,其中m、n为整数,T>0为时间采样周期,F>0为频率采样周期。记STFTz(m,n)=STFTz(mT,nF),则短时傅里叶变换的离散形式为:
(1)
式中,z(k)为原始信号,g(m)为窗函数。
信号z(k)可以由STFTz(m,n)完全重构出来,STFT的反变换形式为:
(2)
基于信号时频谱能量分布的时频滤波算法流程如下:
(1)对有杂波干扰的信号进行STFT,得到该信号的时频谱并计算时频谱的每一点的瞬时能量E(i,j):
E(i,j)=STFT(ti,fi)2
i=1,2,…,n;j=1,2,…,m
(3)
(2)将时频谱的频率区间等分为N个小区间,每个小区间有m/N个频率点,则第k个子区间的能量为:
(4)
(3)计算第i时间点第k个子区间的在总区间能量的占比![]()
(5)
式中Ei表示时频谱第i时间点的总能量。
(4)选择第i时间点能量占比最大的频率区间,认为该区间为受强干扰信号干扰严重的区间,计算该区间幅度的均值作为滤波阈值。
(5)比较第i时间的每个频率点的幅值与阈值,若幅值大于阈值,则滤除该频率点信号,即时频滤波因子w(ti,fi)设为0;否则,保留该信号,即时频滤波因子w(ti,fi)设为1。
STFT′(ti,fi)=STFT(ti,fi)*w(ti,fi)
(6)
(6)重复步骤(4)、(5),遍历时频谱所有时间点,若滤波后时频谱仍存在干扰,重复步骤(2)~(5)直到干扰信号基本被滤除,对滤波后的时频谱,通过公式(2)进行逆短时傅里叶变换得到滤波后时域信号。
在该算法中滤波阈值的选择受频率区间的大小影响,当等分的频率子区间较大且超过杂波谱宽时,阈值会偏小,滤波后会造成低速目标信号能量损失;当等分的频率子区间较小,阈值偏大,滤波后会造成杂波未被完全抑制。因此,根据各种杂波频谱宽度合理划分频率区间具有重要作用。
3 针对海杂波的基于时频谱能量分布的时频滤波方法
海杂波和目标回波的时频分布有明显的区别,海杂波的非平稳性较大,这里采用IPIX雷达(Ice Multiparameter Imaging X-Band Radar)实测海杂波数据进行分析,探测目标为漂浮在海面上的直径约1 m的球,球表面包裹铝箔[14]。对IPIX雷达17号数据高信杂比数据段中的海杂波单元和目标单元数据进行时频分析,如图1、图2所示。
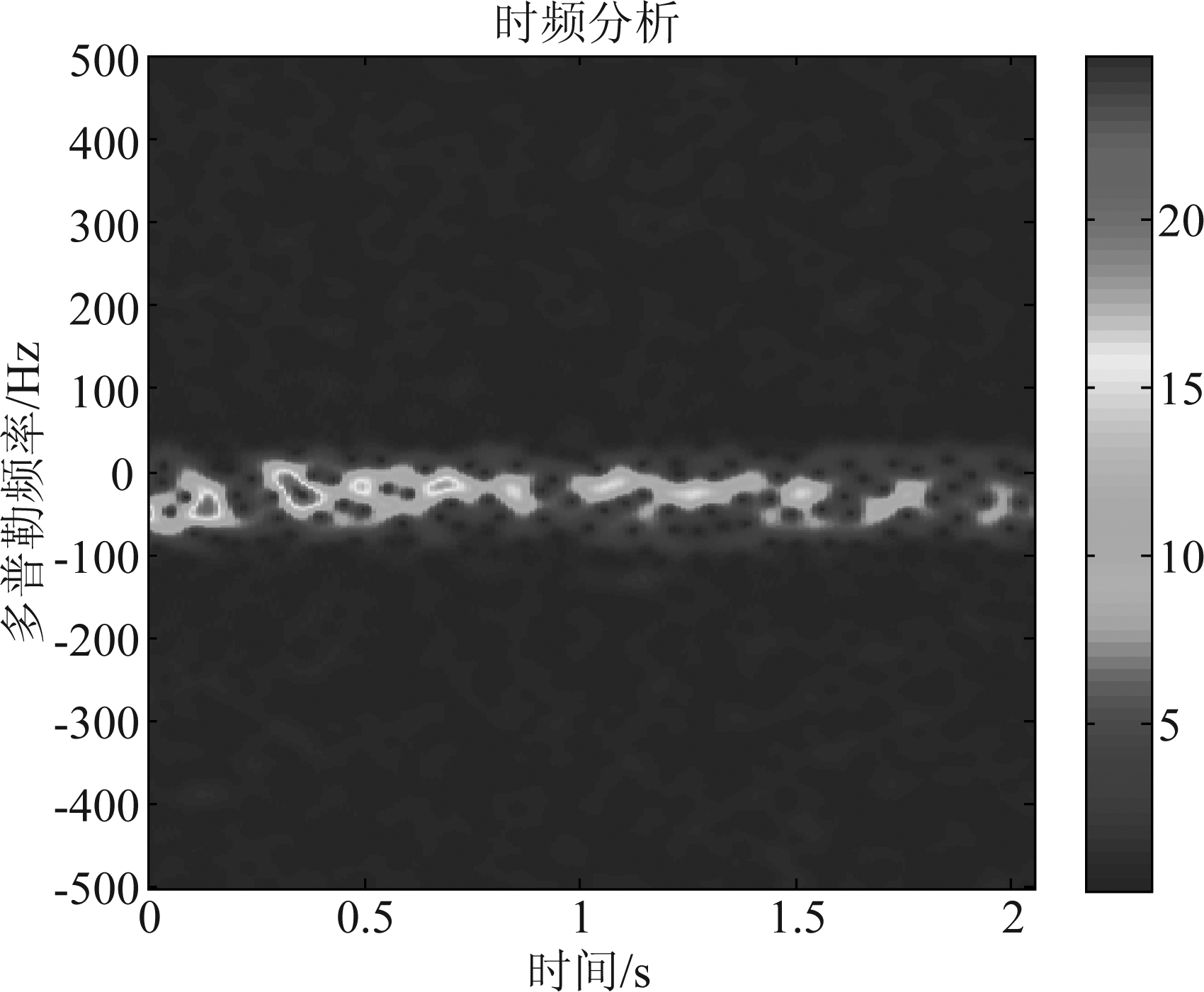
图1 海杂波单元的时频图
Fig.1 Time-frequency diagram of sea clutter unit
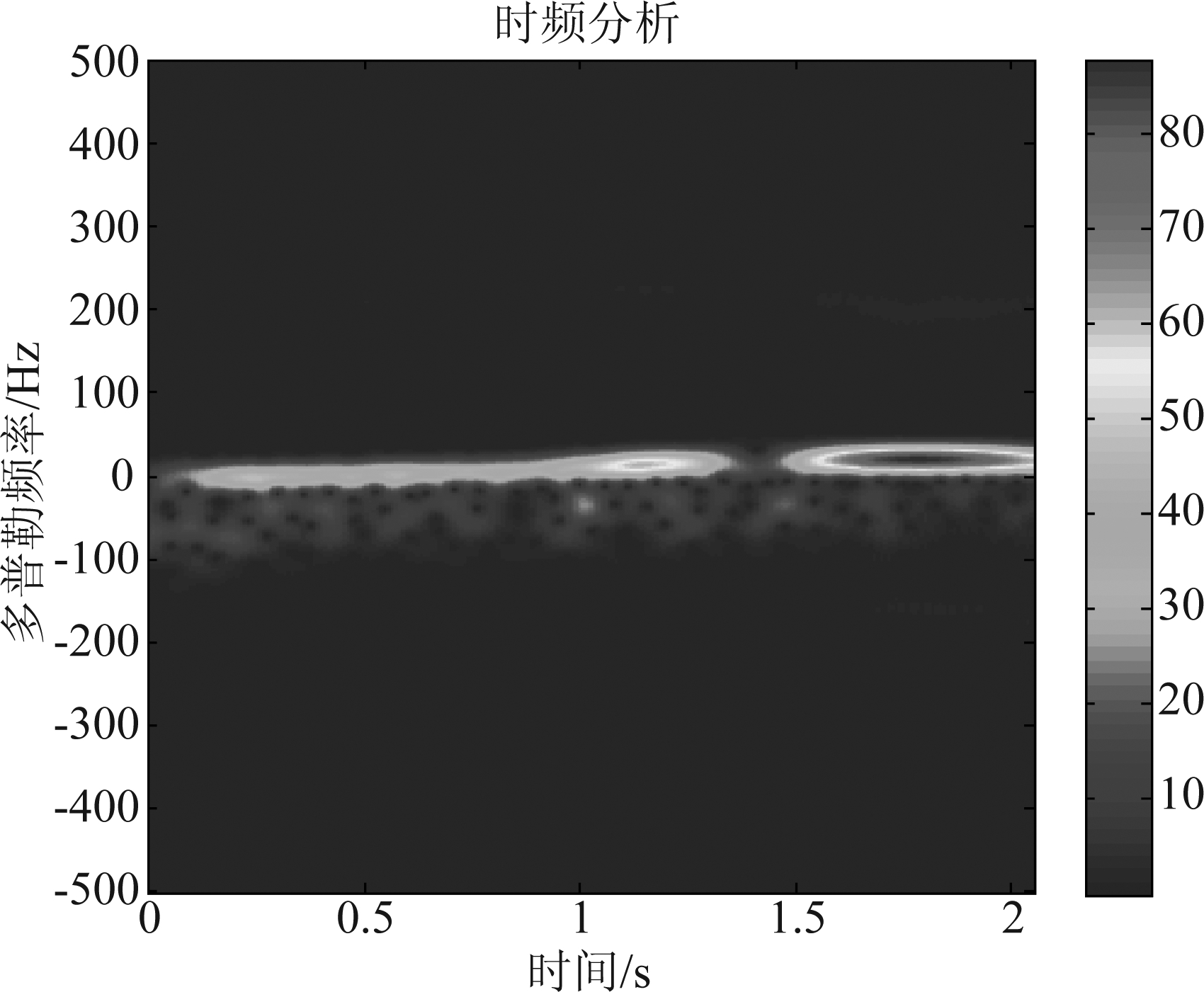
图2 目标单元的时频图
Fig.2 Time-frequency diagram of target unit
由图1、图2可知,对短时间内的雷达回波进行时频分析,目标信号频率变化小,而海杂波的非平稳性较大,中心频率发生非线性偏移。针对此特征,本文通过计算中心频率平滑度来定量分析时频谱中的信号的平稳性。
由于在很短的脉冲积累时间内,目标信号在时频图上表现为线性变化,且频率变化率较小。而海杂波单元的时频谱,中心频率非线性和线性的变化量同时存在。根据这一特征,本文算法对时频谱进行预处理,对时频谱中心频率变化率进行统计,确定时频谱中心频率变化是否趋于线性变化。依次在不同时刻计算能量分布最大的频率区间的阈值T,选择该时刻幅值超过阈值T的最大值频率,由此得到随时间变化的幅值最大的频率值,本文称之为时频谱脊线[15]。海杂波单元脊线、目标单元脊线分别如图3、图4所示。
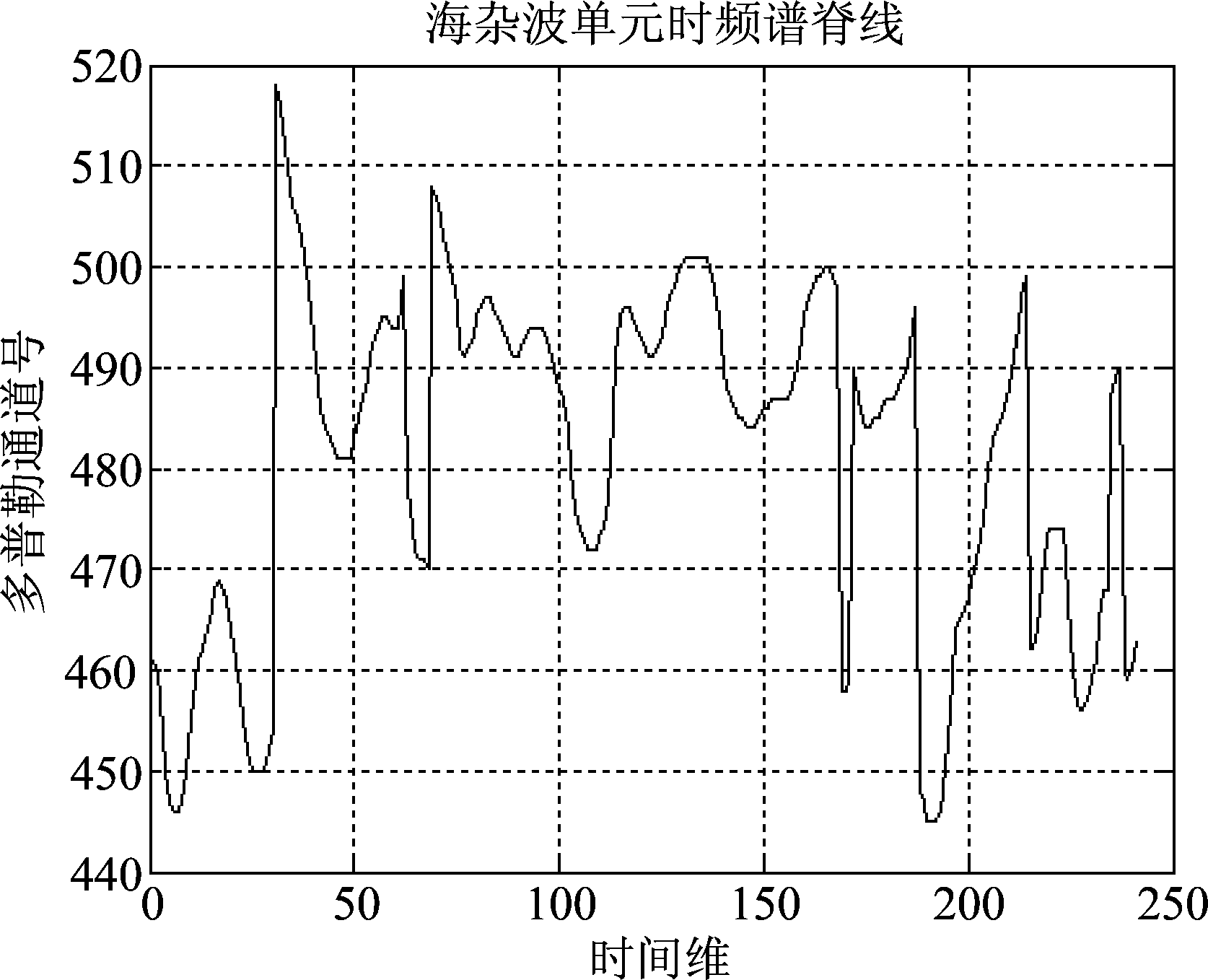
图3 海杂波单元时频谱脊线
Fig.3 The ridge line of time-frequency spectrum in sea clutter unit
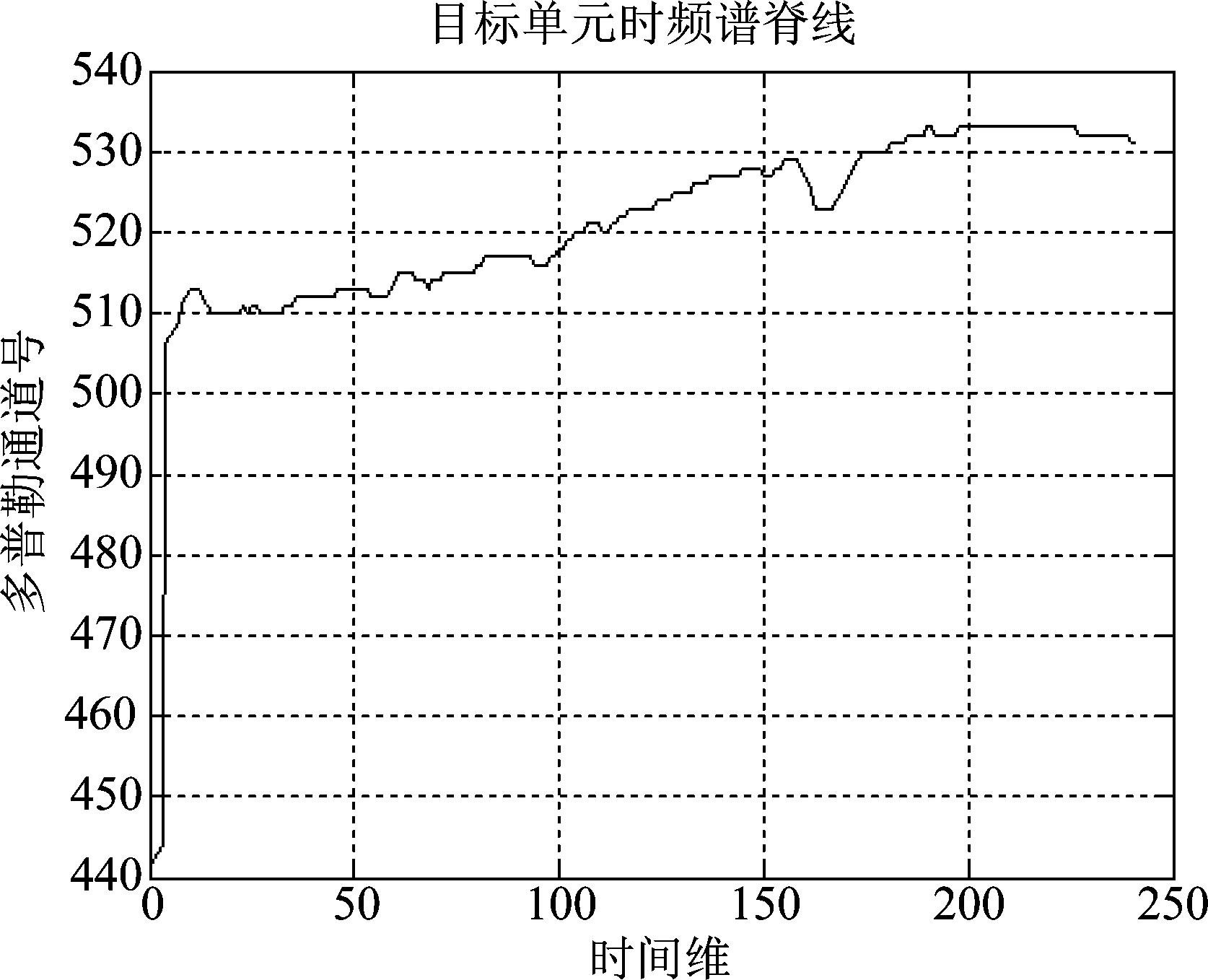
图4 目标单元时频谱脊线
Fig.4 The ridge line of time-frequency spectrum in target unit
如图3所示,海杂波单元脊线频率变化较大;如图4所示,目标单元脊线较平滑,本文通过采用对脊线求一阶导数的方法,分析时频谱脊线频率的变化率。
由图5海杂波单元时频谱脊线的一阶导数值较大;由图6可知,目标单元时频谱脊线的一阶导数除个别较大值以外,大部分值较小,表明目标单元的中心频率变化率较小。
由以上分析可知,目标单元与海杂波单元时频谱的一阶导数值有明显差异,对小于2的一阶导数值进行统计,统计结果定义为中心频率平滑度,对各单元中心频率平滑度进行分析,结果如图7所示。
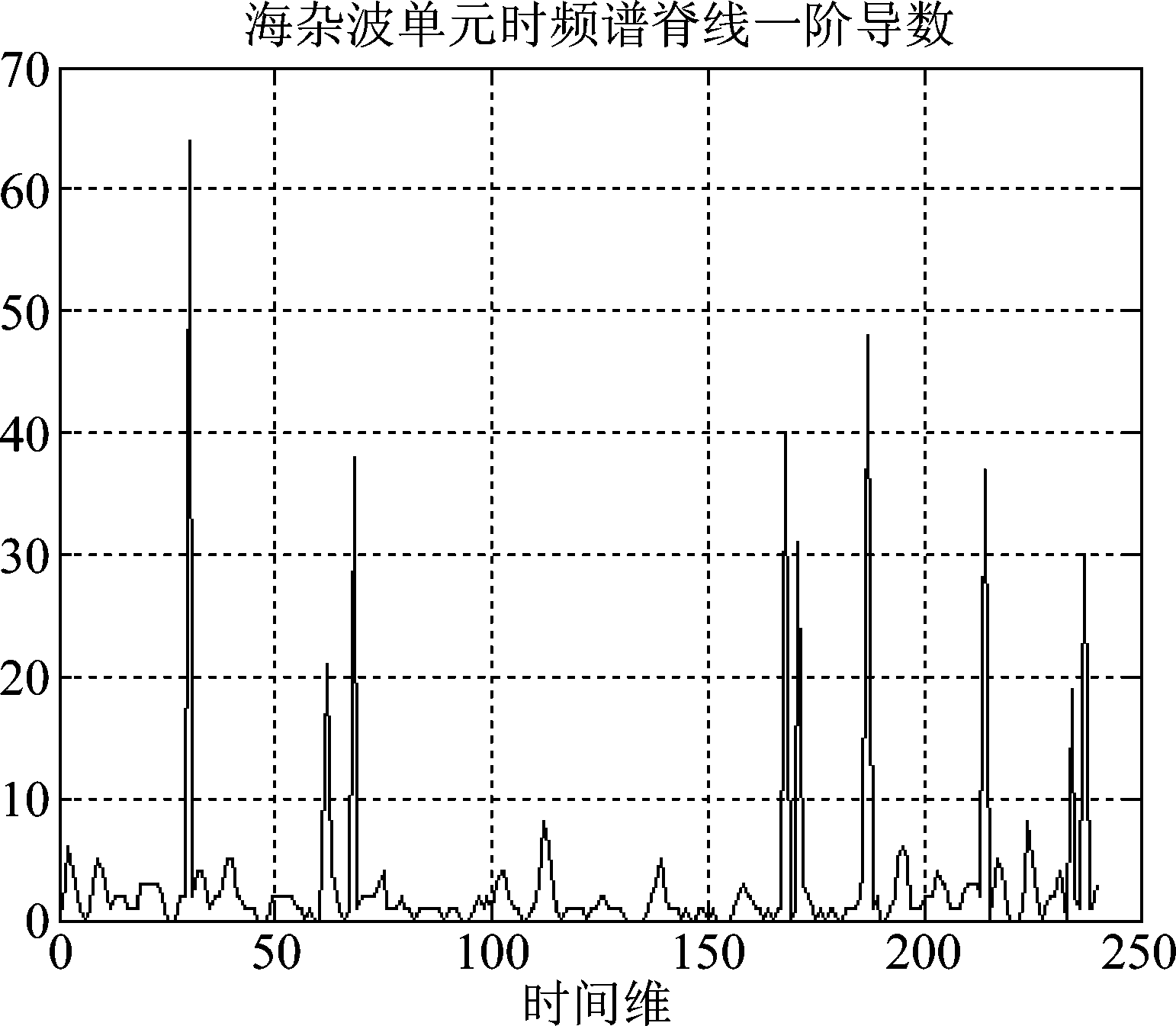
图5 海杂波单元时频谱脊线导数
Fig.5 The derivative of time-frequency spectrum’s ridge line in sea clutter unit
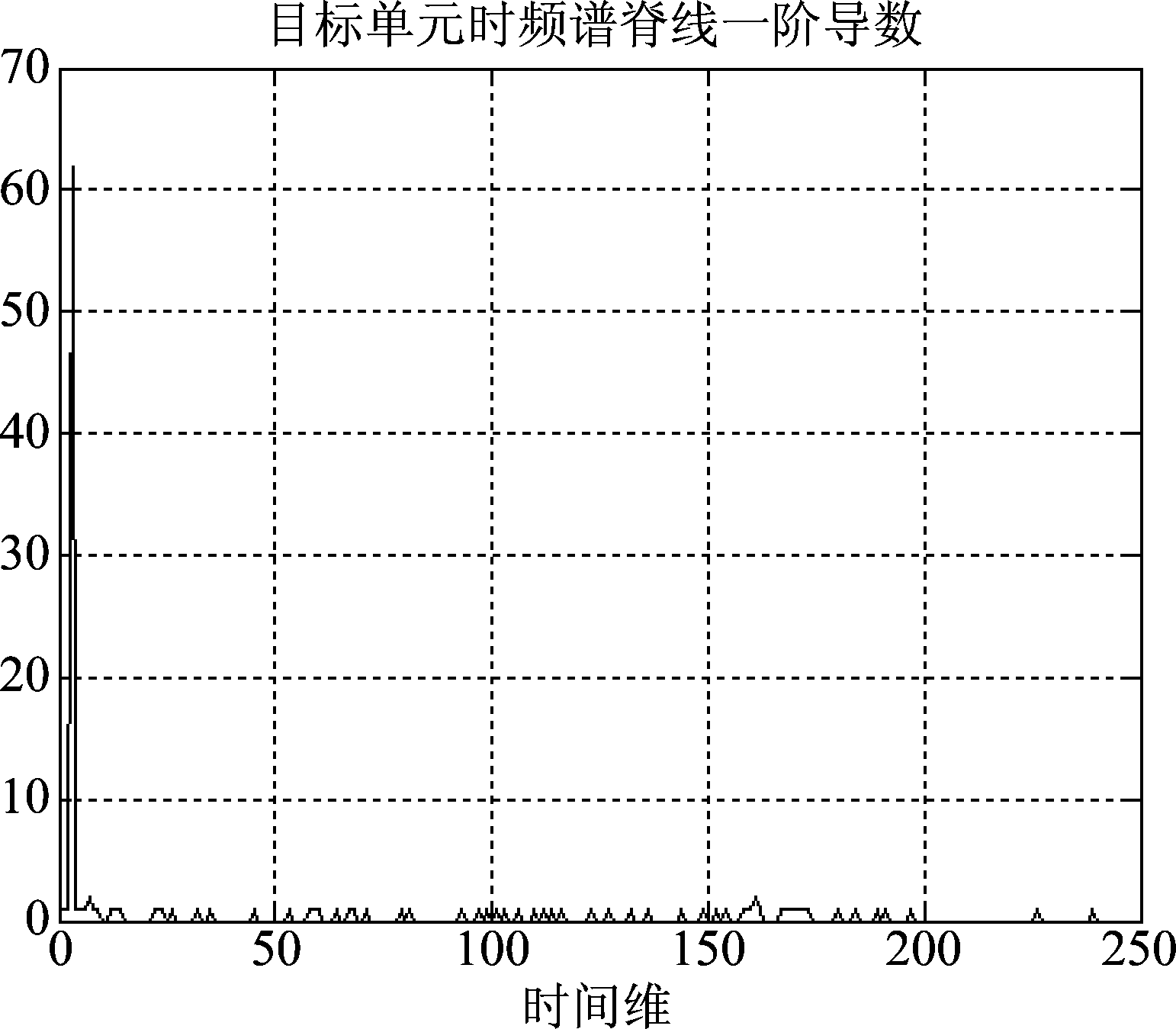
图6 目标单元时频谱脊线导数
Fig.6 The derivative of time-frequency spectrum’s ridge line in target unit
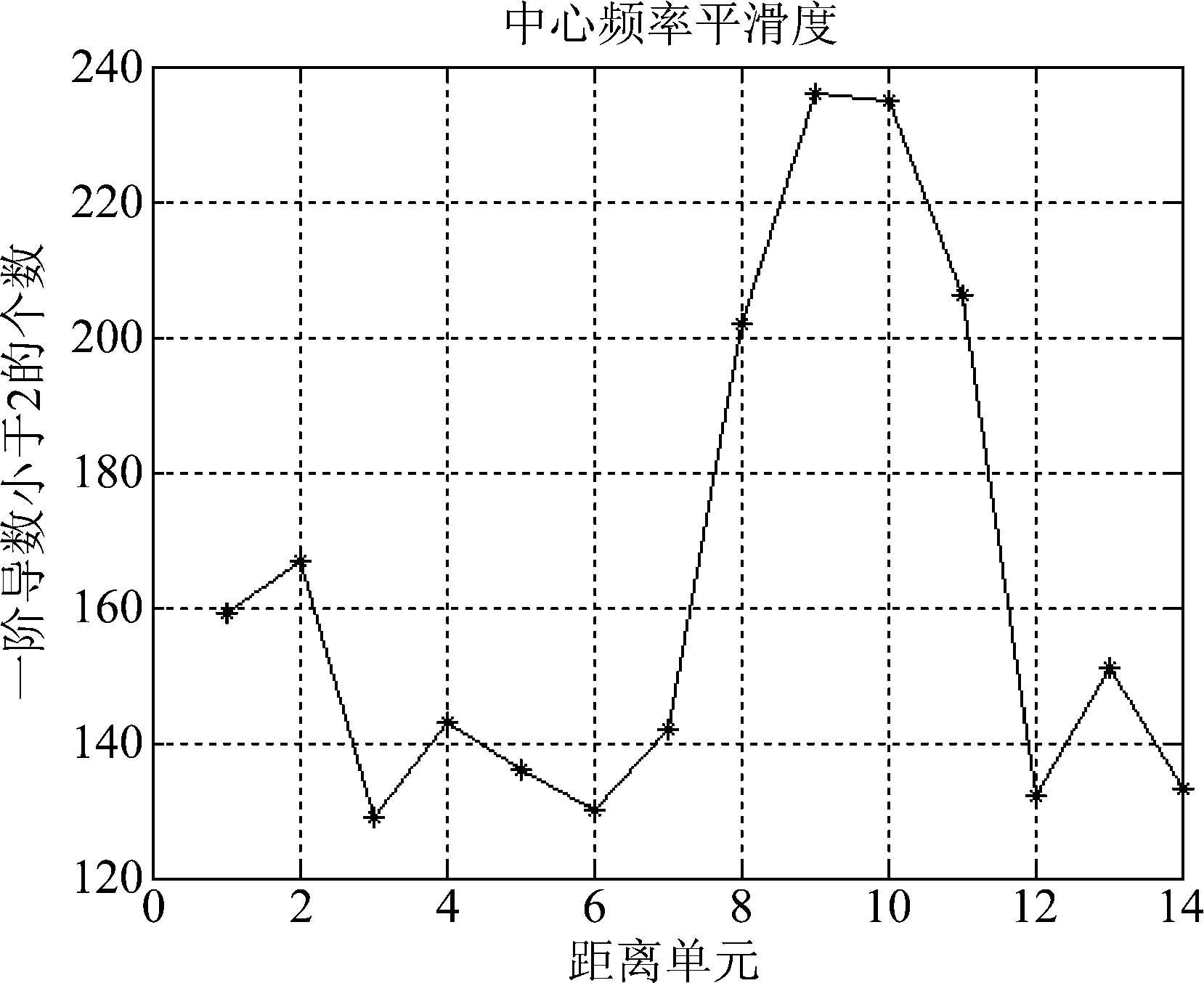
图7 中心频率平滑度
Fig.7 The smoothness of center frequency
如图7中的第9、第10距离单元,在含有目标的距离单元,该单元得到的时频谱中心频率平滑度较大,其余只有海杂波的单元,中心频率平滑度较小。对平滑度较大的单元视为有目标信号混在海杂波频谱中且目标信号强度大于海杂波,对平滑度较小的单元,说明海杂波较强,需滤除较强的杂波。定义各单元中心频率平滑度的自适应门限为在一定虚警概率下,通过恒虚警检测的方法计算中心频率平滑度得到的门限值。据此判断该单元是否具有频率线性变化的较强信号。
基于以上实测数据定量分析结果,本文提出了适用于海杂波抑制的基于能量分布的改进型时频滤波方法,如图8所示为基于能量分布的改进型时频滤波方法的整体流程。
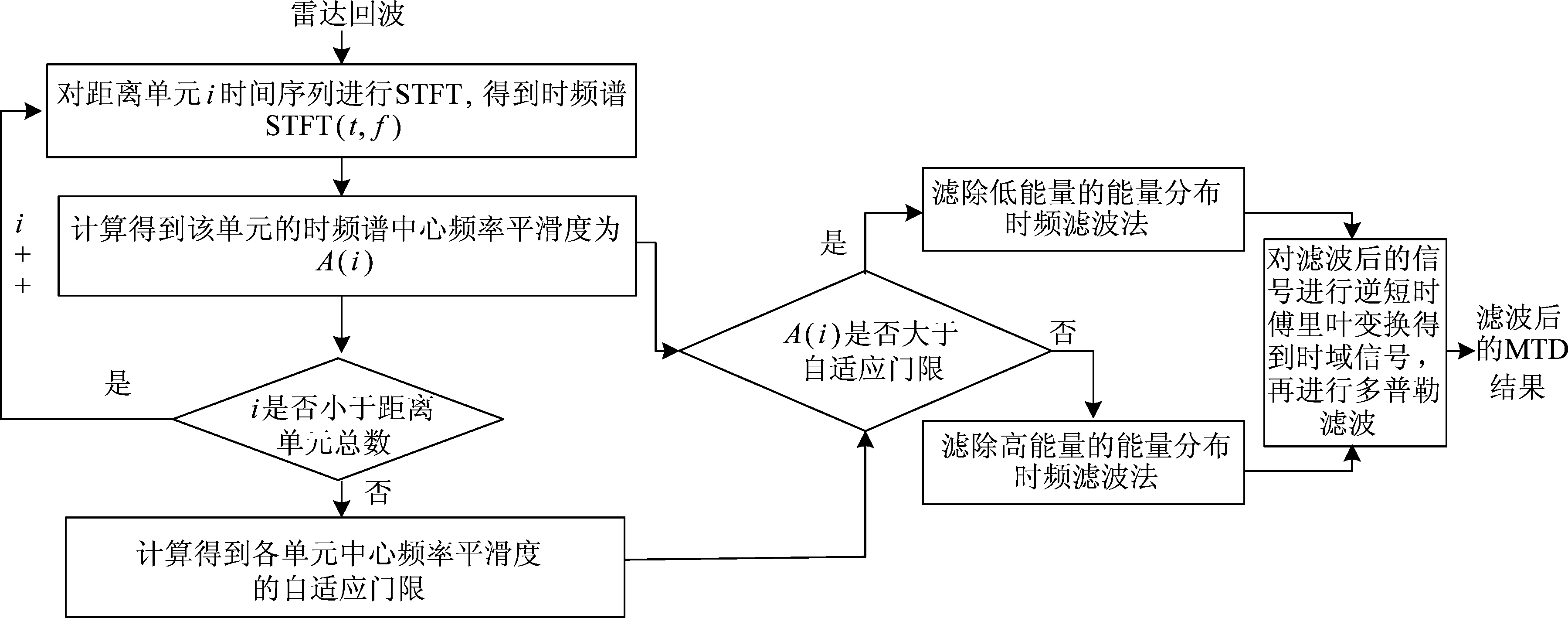
图8 基于时频谱能量分布的改进型时频滤波算法流程图
Fig.8 Flow chart of improved time-frequency filtering method based on energy distribution
本文算法对雷达回波各个距离单元数据做短时傅里叶变换得到各单元信号的时频谱,对各单元时频谱的中心频率变化率进行统计,即得到各单元中心频率的平滑度。计算各单元中心频率平滑度的自适应门限,对各单元中心频率平滑度与自适应门限进行比较,选择相应的滤波方法。
当某单元的中心频率平滑度低于门限时,即该距离单元的时频谱中具有非线性变化的频率占主要成分,此时采用滤除高能量的基于能量分布的时频滤波方法。由公式(3)~(5)计算该单元的时频谱各区间的能量占比,选择能量占比最大的区间,计算该区间的幅度的均值作为阈值。在能量占比最大的区间及其相邻区间进行滤波,滤除高于该阈值的信号,保留低于该阈值的信号,以达到滤除强海杂波的目的。
当某单元的中心频率平滑度高于门限时,即该距离单元时频谱中的信号主要呈线性变化,此时采用滤除低能量的基于能量分布的时频滤波方法。该方法与前文滤除高能量的方法类似,区别只在滤波部分,滤除低能量的信号,保留高能量的信号。以达到当慢速目标混在海杂波中,能够有效抑制杂波而不造成目标信号严重损失的目的。
对滤波后的信号做逆短时傅里叶变换得到该单元的时域信号,再对各单元时域信号做相参积累得到多普勒滤波结果,即滤波后距离-多普勒结果。
当目标信号位于海杂波频带以外,即中心频率复杂度小于自适应门限时,采用滤除高能量的能量分布时频滤波方法进行滤波。在此种情况下,由于杂波中心频率和频谱展宽不固定,给设计频域滤波器带来困难;采用经典的基于AR模型的线性预测的滤波方法,由于过渡带较宽,会造成低速目标能量的损失。本文方法将滤波范围设定在能量占比大的频率区间附近,在时频谱沿杂波边缘自适应的滤除高于阈值的信号,形成的滤波器过渡带窄,能减少目标能量损失,具有良好的滤波性能。
针对强目标信号混在海杂波频带内的情况,采用滤除低能量的能量分布时频滤波方法。在能量占比最大的区间,滤除低于阈值的信号,保留高于该阈值的信号。
4 实测海杂波数据验证
4.1 本文算法与AR线性预测算法的对比
海杂波在短时间内可以看作线性、平稳的过程,采用基于AR模型线性预测的海杂波抑制方法进行杂波抑制是较为经典的抑制方法[16]。本文采用实测海杂波数据,在其上添加海杂波频带外的仿真目标信号,对同一距离单元的1024个脉冲进行处理,对比两种算法的滤波性能。
采用基于AR线性预测的海杂波抑制方法,其中模型参数为6阶,对数据时间序列前1000点进行AR模型训练,对含仿真目标信号的1024点时间序列进行线性预测滤波。滤波结果如图9所示,海杂波信号基本被滤除,能够良好的匹配海杂波的带宽,但目标信号损失了约18.8 dB。滤波前后信号损失严重。
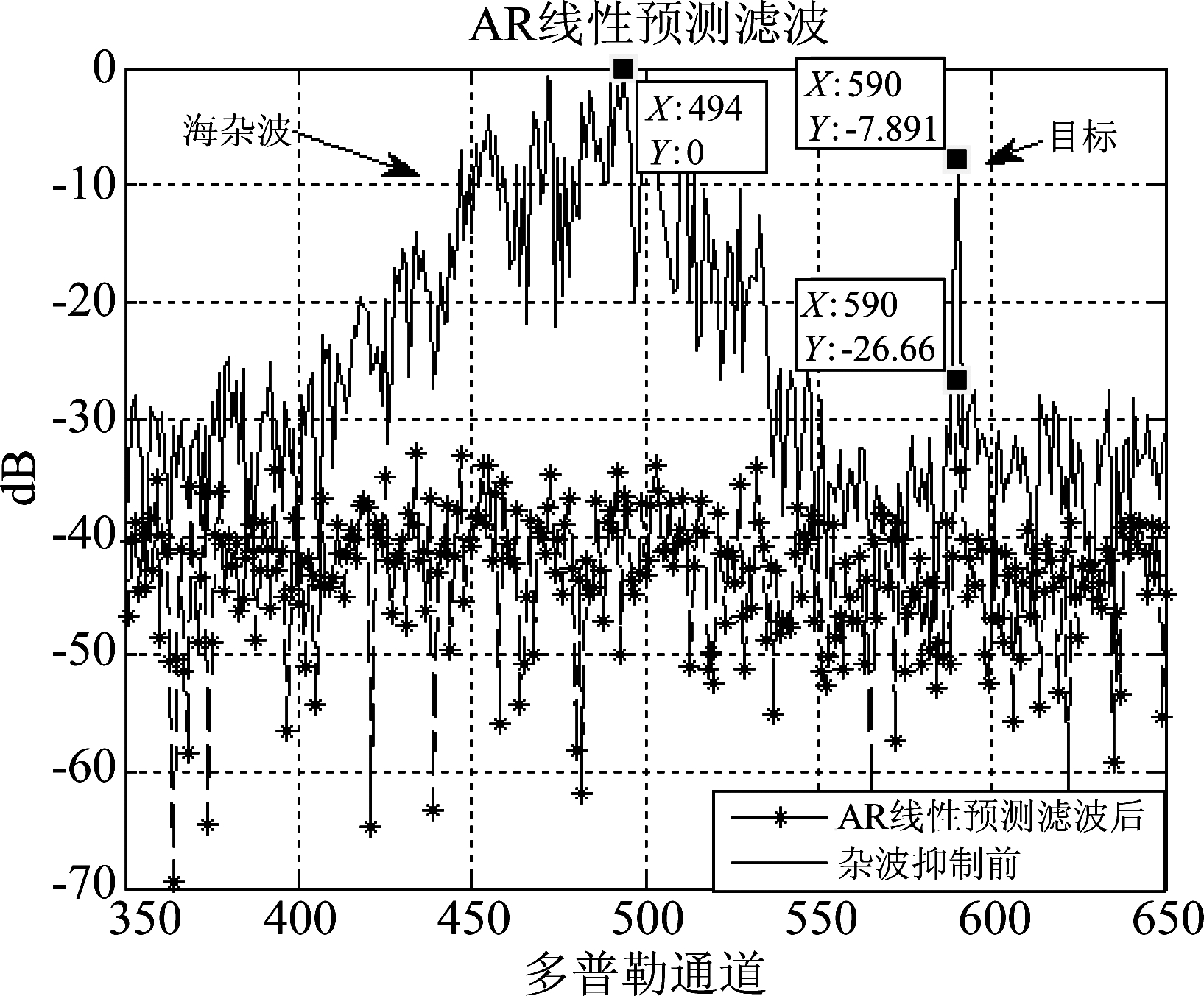
图9 AR线性预测滤波效果图
Fig.9 Effect diagram after filtering based on AR linear prediction
如图10所示为采用基于时频谱能量分布的改进型时频滤波方法结果,将时频谱频率区间等分为30段,滤波后,对信号做FFT进行相参积累,可有效提高目标信号的信噪比。
由图10可见,采用基于能量分布的时频滤波方法滤波后,海杂波信号被滤除,目标信号仅损失0.6 dB,滤波前后信杂比改善明显。
综上,本文所采用算法能够自适应抑制谱宽不固定的海杂波,在能量占比最大的频率区间附近进行滤波,易于保护低速目标信号能量。滤波性能比基于AR线性预测的海杂波抑制方法要好。

图10 基于能量分布的时频滤波后FFT效果图
Fig.10 FFT effect diagram after time-frequency filtering based on energy distribution
4.2 本文算法在整个距离段中海杂波的抑制性能
本文采用实测海杂波数据进行算法验证。以下数据1表示IPIX雷达17号数据,海情为1;数据2表示IPIX雷达320号数据,海情为3;数据3表示南非某海杂波数据,具有31个距离单元,目标为船只。本文算法时频谱频率维等分为30段频率区间,在能量分布最大的区间附近3段区间内进行滤波。
4.2.1 不同信杂比下,基于时频谱能量分布的时频滤波性能
对数据1低信杂比下的数据段,脉冲积累数为1024,采用本文算法进行海杂波抑制,效果如图11所示,本文算法在时频域能够沿着海杂波时频分布对海杂波进行有效抑制,且过渡带较窄。本文算法形成的滤波器是自适应的,克服了传统滤波器固定通带难以对谱宽变化的复杂海杂波进行抑制的缺点。
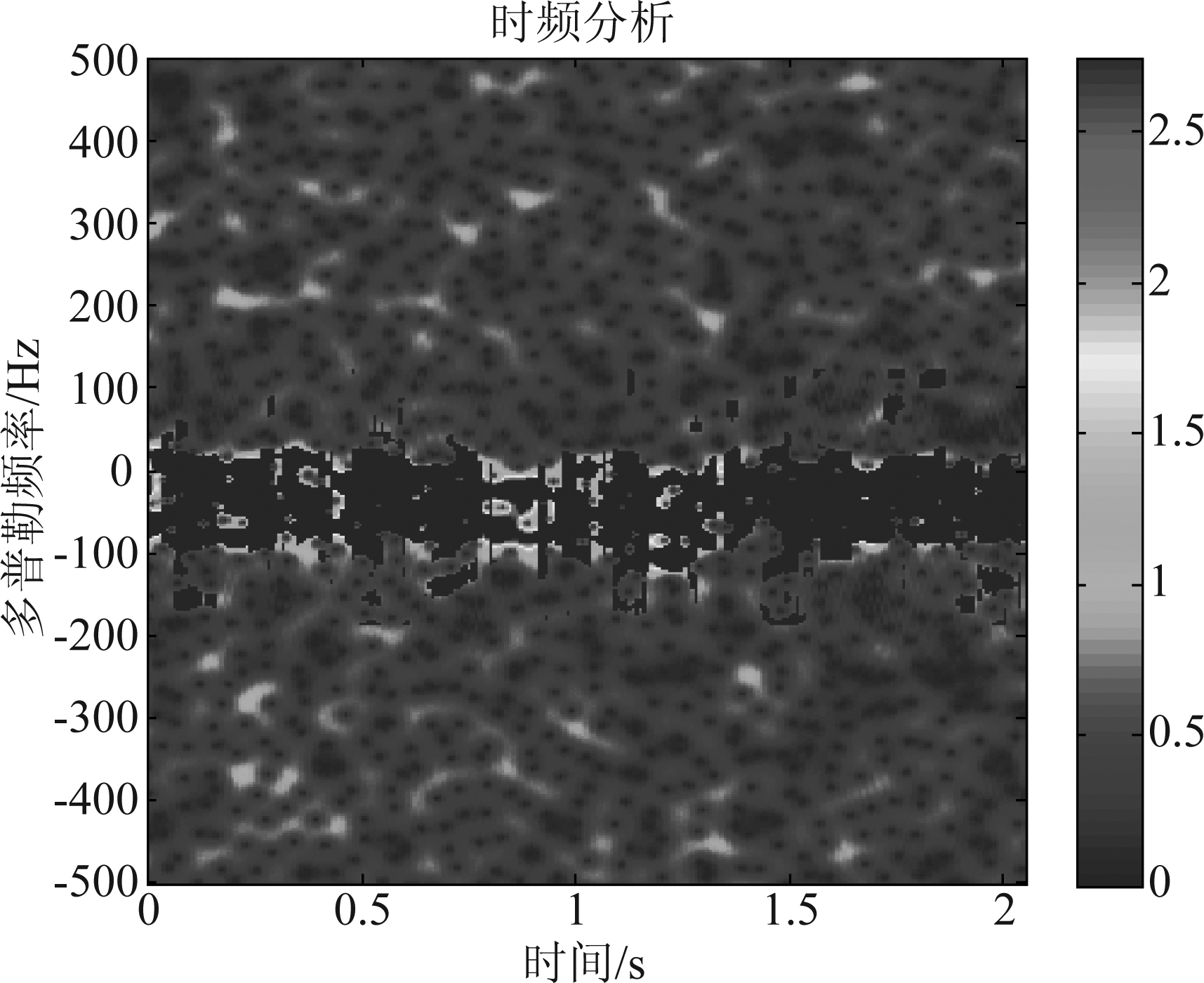
图11 海杂波单元滤波后的时频图
Fig.11 The time-frequency diagram after filtering in sea clutter unit
采用本文算法对目标单元的海杂波抑制效果如图12所示,该算法有效保护了目标能量,抑制了周围海杂波干扰。

图12 目标单元滤波后的时频图
Fig.12 The time-frequency diagram after filtering in target unit
采用本文算法对全距离段进行时频滤波,检测整个算法的滤波效果。对雷达回波数据进行多普勒滤波,动目标显示(MTI)和动目标检测(MTD)得到如图13、图14所示结果。
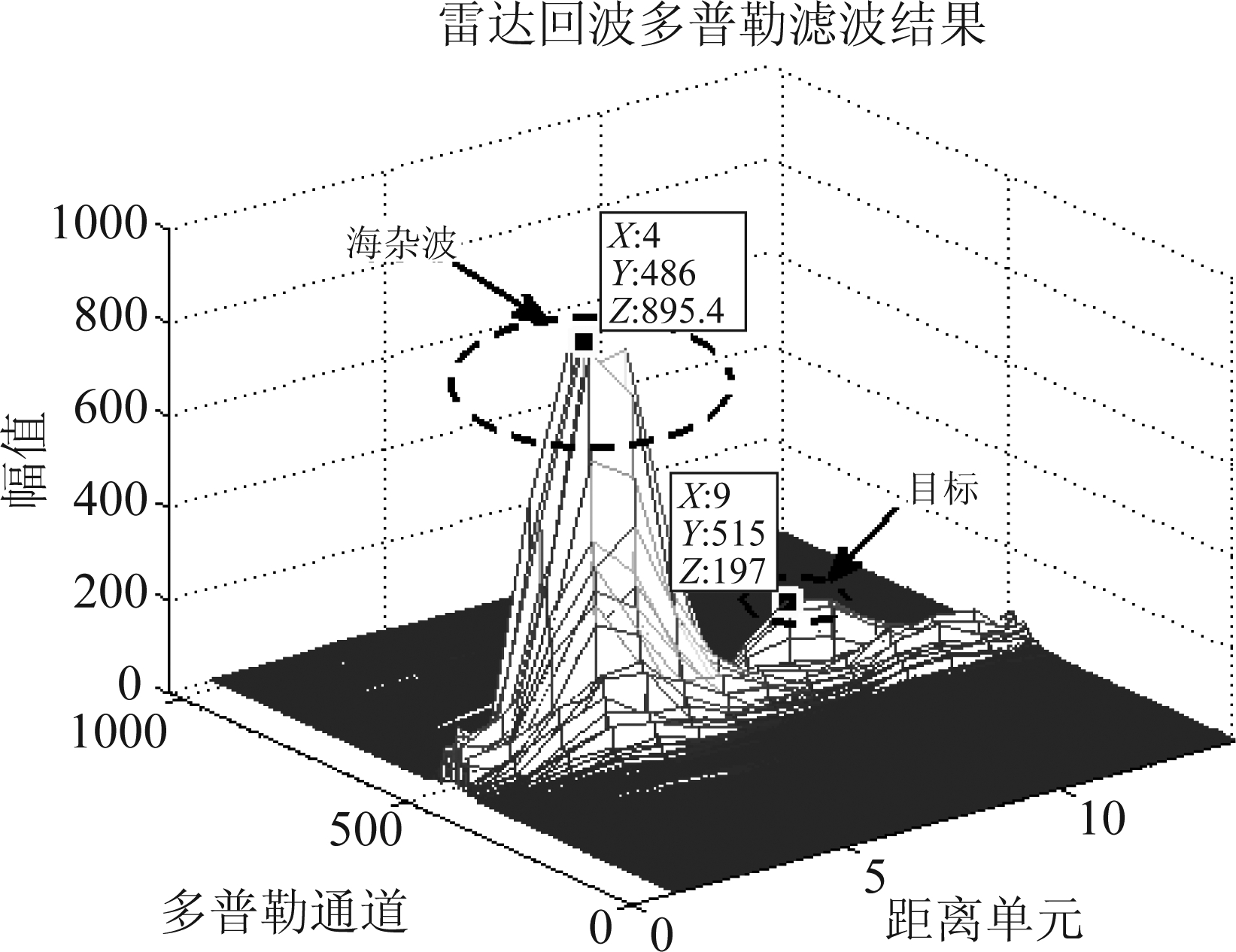
图13 雷达回波多普勒滤波结果
Fig.13 Radar echo Doppler filtering result
图13所示为雷达回波多普勒滤波结果,第9单元的目标信号幅值小于第4单元的海杂波,如果直接沿距离维进行目标检测,会造成很高的虚警率。采用传统两脉冲对消方法进行杂波抑制结果如图14所示,该方法对中心频率偏离零频的海杂波信号抑制效果较差。对消前后,靠近零频的目标信号损失严重,频谱展宽的海杂波并未被完全抑制,其残余仍比目标信号强,严重影响目标检测。
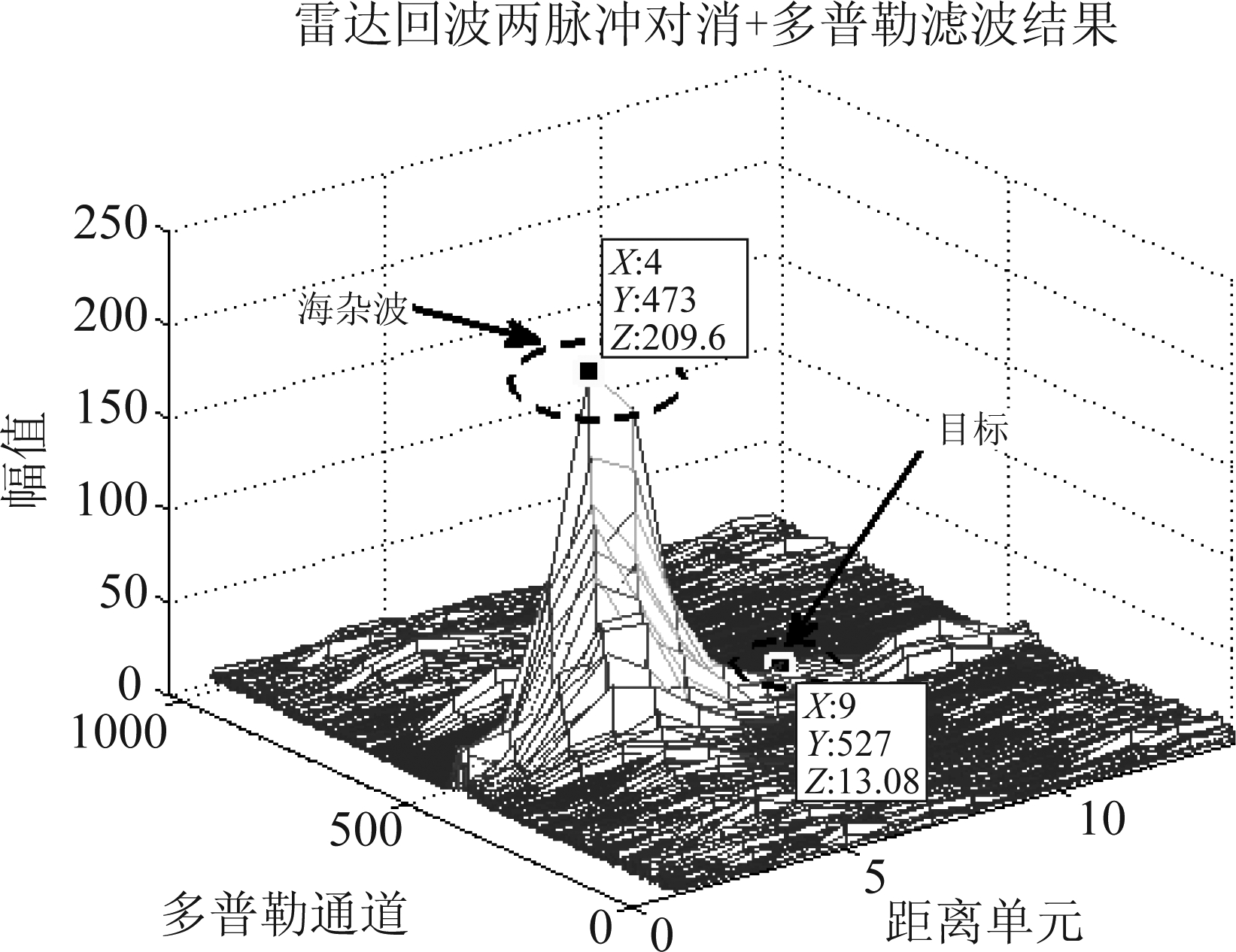
图14 雷达回波两脉冲对消+多普勒滤波结果
Fig.14 Radar echo two-pulse canceller +Doppler filtering result
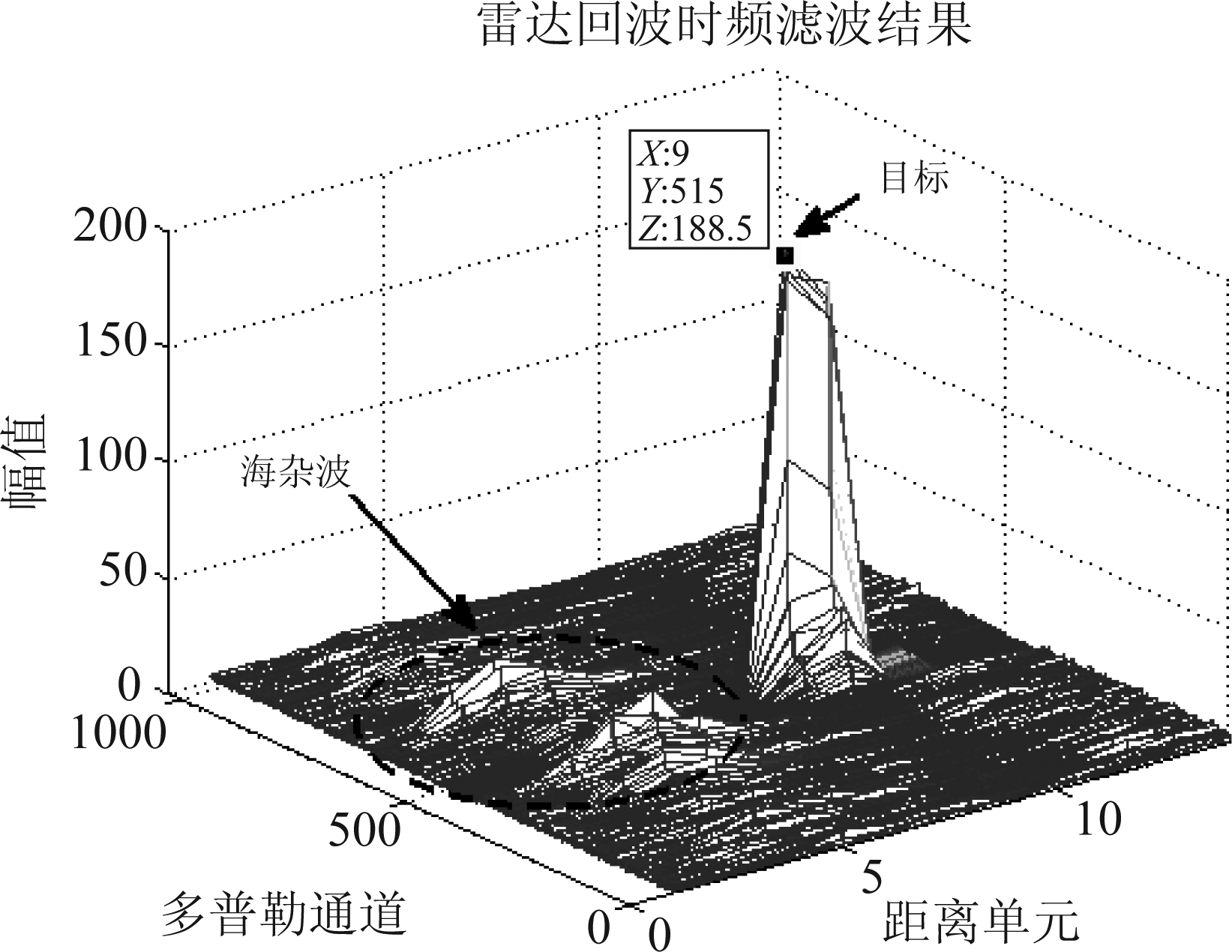
图15 雷达回波时频滤波后多普勒滤波结果
Fig.15 Radar echo Doppler filtering result after time-frequency filtering
表1 基于时频谱能量分布的改进型自适应时频滤波算法滤波性能
Tab.1 Filtering performance of improved adaptive time-frequency filtering algorithm based on energy distribution

数据段滤波前信杂比/dB滤波前SNR/dB滤波后信杂比/dB滤波后SNR/dB信杂比改善/dBSNR改善/dB数据1高信杂比段数据1低信杂比段数据2低信杂比段2.05-13.13-15.4850.436140.004334.673131.1617.3310.7650.448140.936.417329.1130.4626.240.0120.89571.7442
如图15所示,经本文算法滤波后,海杂波得到抑制,低速目标信号得到保留,此时信杂比得到很大改善,信噪比损失较小。
本文对数据1和数据2应用基于时频谱能量分布的改进型时频滤波方法进行杂波抑制分析,对不同数据段、不同信杂比下的滤波性能如表1所示。
由表1可知,基于时频谱能量分布的改进型自适应时频滤波算法在不同海情下、不同信杂比下都具有很优的杂波抑制性能,信杂比改善在26 dB以上。同时保护了目标信号能量,滤波前后信噪比并未损失。
4.2.2 采用其他雷达海杂波数据进行验证
由于本算法中心频率平滑度特征是根据IPIX雷达实测数据分析得到的,其他情景下的海杂波特性是否符合该特征仍需验证。
本节采用南非某海杂波数据进行滤波性能测试,统计数据3各距离单元的中心频率平滑度的结果如图16所示。
由图16所示,非目标单元的中心频率平滑度较小,与本文分析雷达海杂波时频谱中心频率非平稳性特征相符。采用基于时频谱能量分布的改进型时频滤波方法进行杂波抑制。
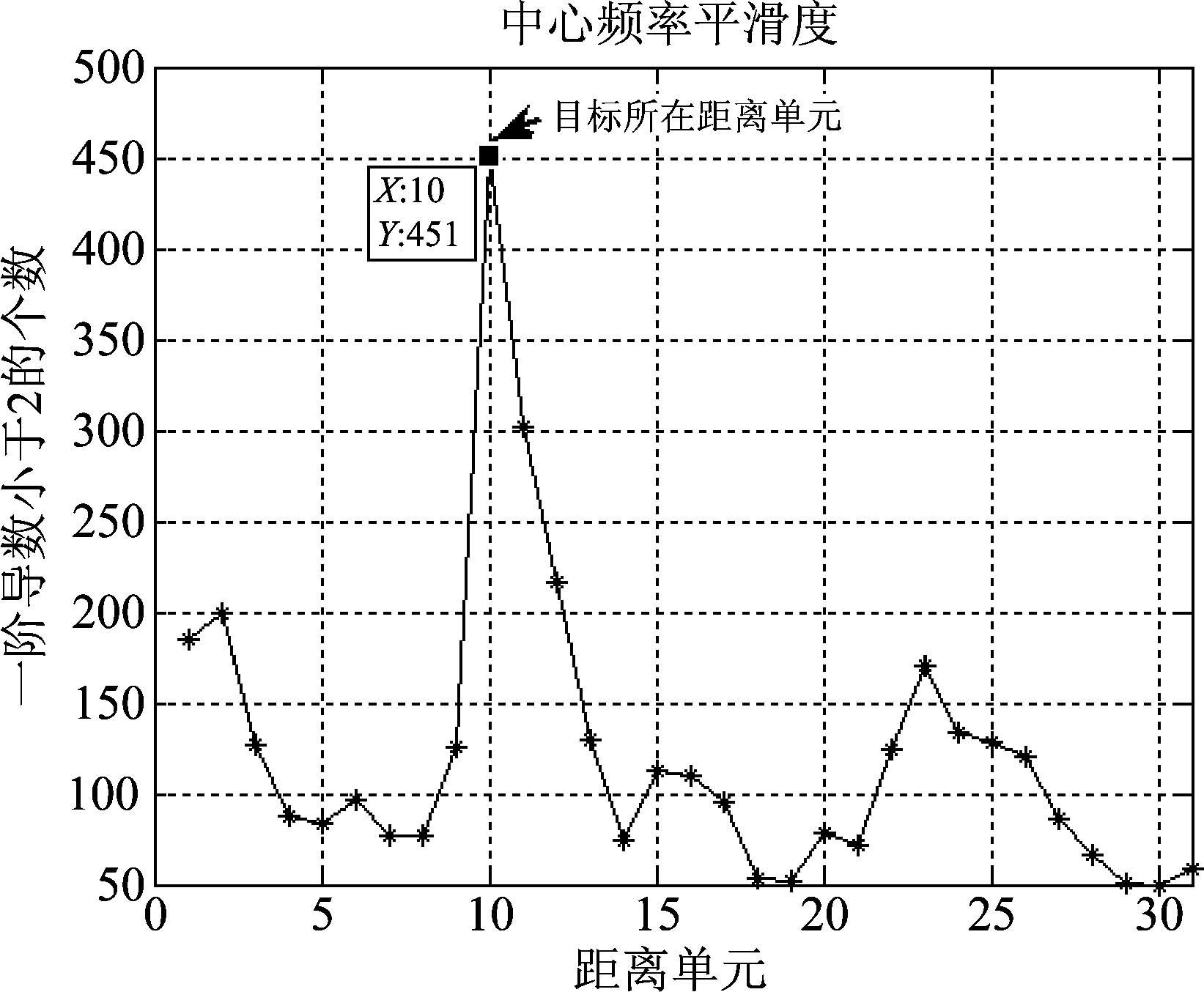
图16 数据3时频谱中心频率平滑度
Fig.16 Time-frequency spectrum center frequency smoothness of Data 3
图17为雷达回波的多普勒滤波结果,目标位于10距离单元处,其他单元存在较强的海杂波干扰信号。图18为雷达回波经本文算法滤波后的多普勒滤波结果,由图18可知,基于时频谱能量分布的改进型自适应时频滤波方法能有效抑制数据3中的海杂波,并非只适用于IPIX雷达海杂波数据。
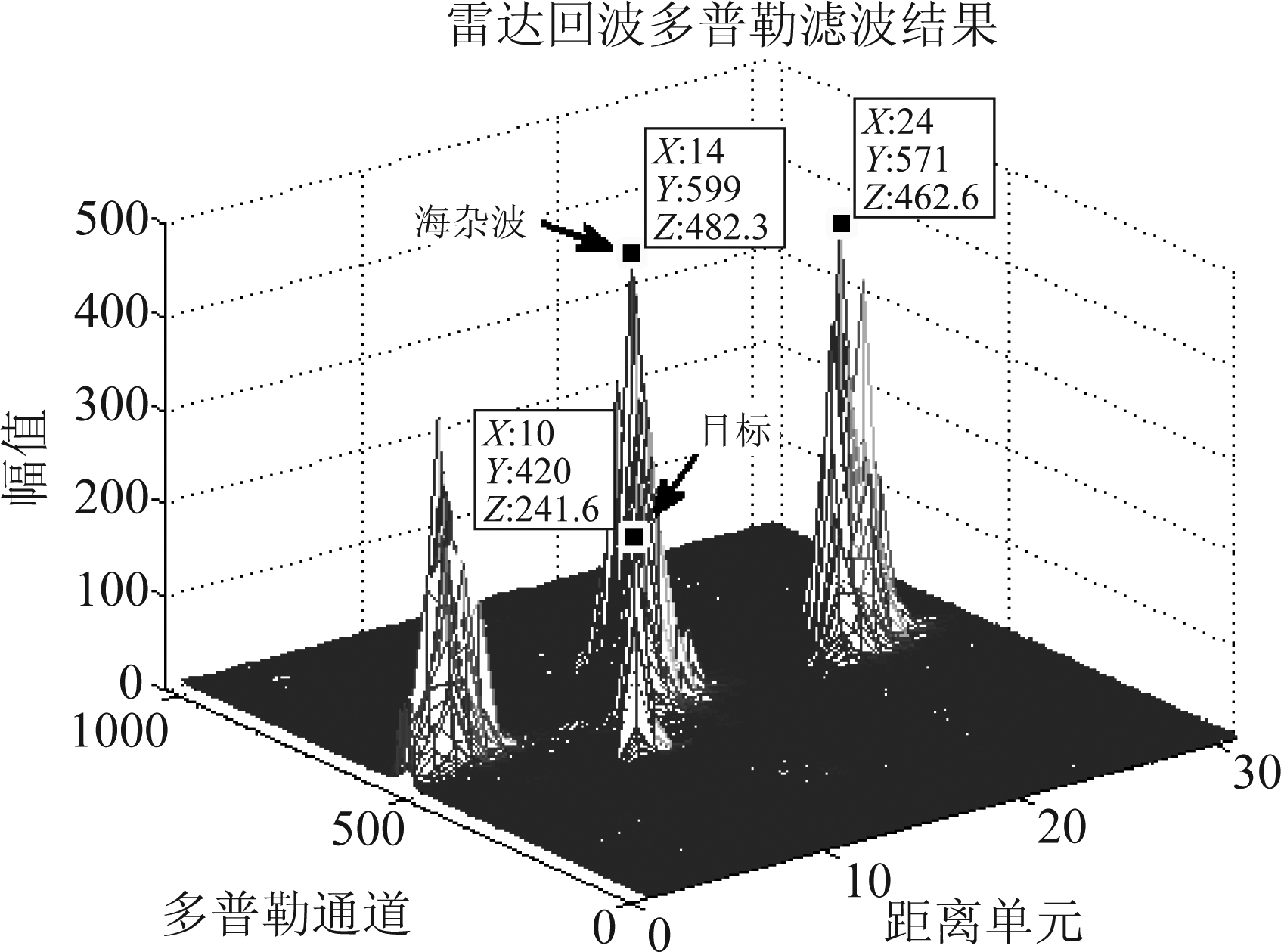
图17 雷达回波多普勒滤波结果
Fig.17 Radar echo Doppler filtering result
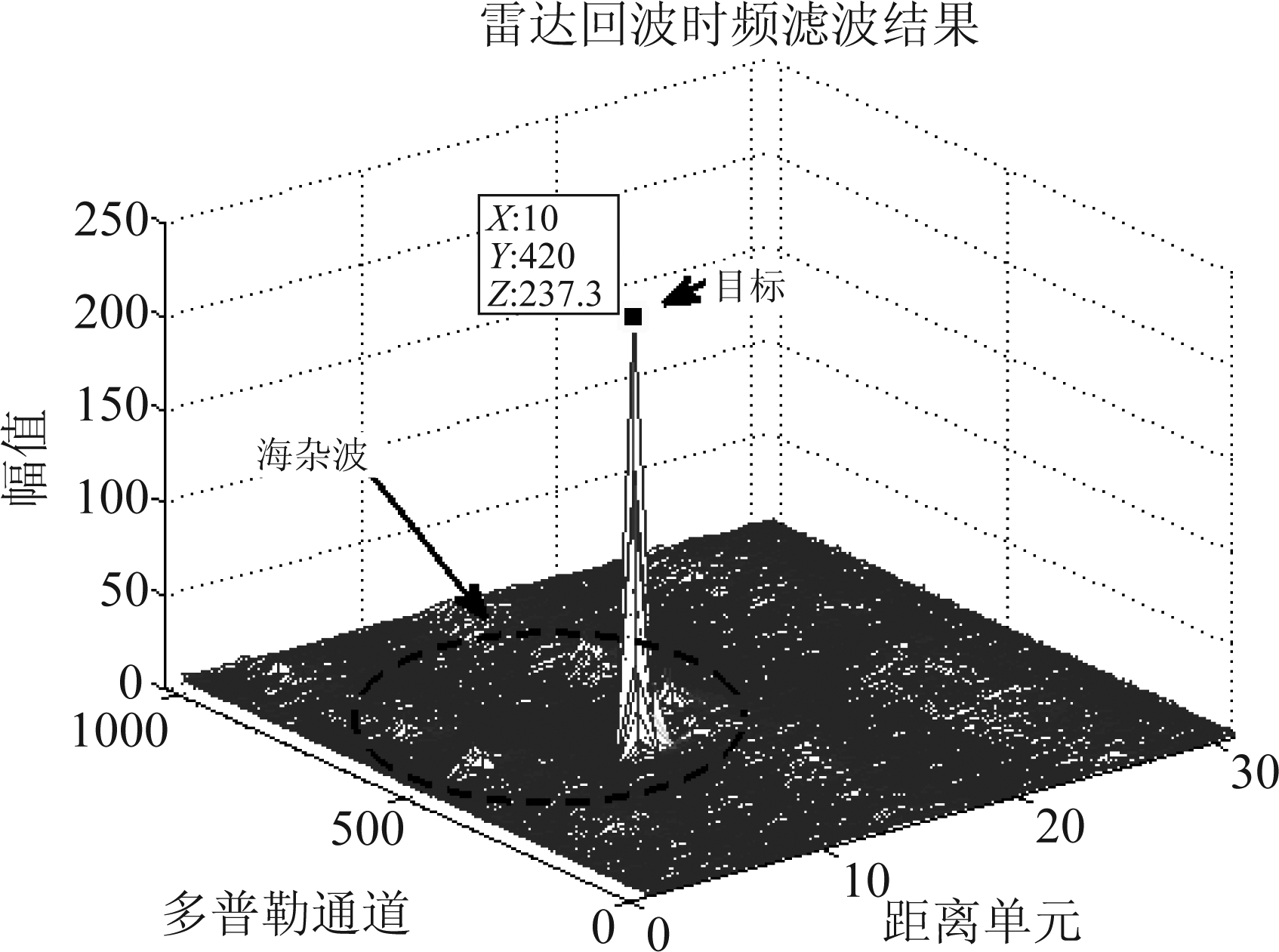
图18 雷达回波时频滤波后结果
Fig.18 Radar echo Doppler filtering result after time-frequency filtering
综上所述,本文所采用的基于时频谱能量分布的改进型时频滤波方法在不同信杂比下的海杂波干扰下,均具有很好的滤波性能,具有很好的实用性。
5 结论
本文通过研究海杂波时频特性,定量分析海杂波时频谱脊线的平滑程度,提出了基于时频谱能量分布的改进型时频滤波方法,弥补了原算法只滤除高能量杂波的缺点,能够保护混在海杂波频带内的低速目标能量。通过与基于AR线性预测的海杂波抑制方法的对比,验证了本文算法能够在有效抑制海杂波的同时避免了目标能量的损失。通过对不同信杂比的实测海杂波数据进行滤波性能分析,验证了本文算法能有效的应用在海杂波抑制方面,具有很好的实用价值。
[1] 李重威,杨勇,李永祯,等. 基于实测数据的分时全极化雷达海杂波分布研究[J]. 电波科学学报,2017,32(3): 253-260.
Li Zhongwei,Yang Yong,Li Yongzhen,et al. Time-sharing fully polarimetric radar sea clutter distribution based on real measured data[J]. Chinese Journal of Radio Science,2017,32(3): 253-260.(in Chinese)
[2] 周超,刘泉华. Ku波段实验雷达海杂波实测数据分析[J]. 信号处理,2015,31(12): 1573-1578.
Zhou chao,Liu Quanhua. Analysis of field sea clutter data of Ku band[J]. Journal of Signal Processing,2015,31(12): 1573-1578.(in Chinese)
[3] 吴鹏. 某雷达杂波的实测数据分析及其抑制技术研究[D]. 西安: 西安电子科技大学,2017.
Wu Peng. Research on clutter analysis and suppression technology of real data in radar[D]. Xi’an: Xidian University,2017.(in Chinese)
[4] Sira S P,Cochran D,Papandrcou-Suppappola A,et al. A subspace-based approach to sea clutter suppression for improved target detection[C]∥2006 Fortieth Asilomar Conference on Signals,Systems and Computers,2006: 752-756.
[5] Khan R,Power D,Walsh J. Ocean clutter suppression for an HF ground wave radar[C]∥CCECE’97. Canadian Conference on Electrical and Computer Engineering. Engineering Innovation: Voyage of Discovery. Conference Proceedings,1997(2): 512-515.
[6] Maresca S,Greco M,Grasso R,et al. The HF surface Wave Radar WERA. Part Ⅱ:Spectral Analysis of Recorded data[C]∥2010 IEEE Radar Conference,2010: 969-974.
[7] Yasotharan A,Thayaparan T. Time-frequency method for detecting an accelerating target in sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems,2006,42(4): 1289-1310.
[8] Guan Jian,Chen Xiaolong,Huang Yong,et al. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter[J]. IET Radar,Sonar and Navigation,2012,6(5): 389- 401.
[9] 陈小龙,关键,黄勇,等. 分数阶Fourier变换在动目标检测和识别中的应用: 回顾与展望[J]. 信号处理,2013,29(1): 85-97.
Chen Xiaolong,Guan Jian,Huang Yong,et al. Application of Fractional Fourier Transform in Moving Target Detection and Recognition: Development and Prospect[J]. Journal of Signal Processing,2013,29(1): 85-97.(in Chinese)
[10] Chen Xiaolong,Huang Yong,Guan Jian,et al. Radar micro-Doppler signal detection and extraction via short-time sparse fractional fourier transform[C]∥International Conference on Radar Systems(Radar 2017),2017: 1- 4.
[11] Zuo Lei,Li Ming,Xia Xianggen. New Smoothed Time-Frequency Rate Representations for Suppressing Cross Terms[J]. IEEE Transactions on Signal Processing,2017,65(3): 733-747.
[12] Zhang Rui,Li Gang,Zhang Yimin. Micro-doppler interference removal via histogram analysis in time-frequency domain[J]. IEEE Transactions on Aerospace and Electronic Systems,2016,52(2): 755-768.
[13] 马忠超. 基于时频变换的时变滤波器性能仿真与优化[D]. 哈尔滨: 哈尔滨工业大学,2017.
Ma Zhongchao. Performance simulation and optimization of time-varying filter based on time-frequency transform[D]. Harbin: Harbin Institute of Technology,2017.(in Chinese)
[14] 苏晓宏. 海杂波的特性分析与目标检测处理[D]. 大连: 大连海事大学,2010.
Su Xiaohong. Analysis of sea clutter characteristics and processing of target detection[D]. Dalian: Dalian Maritime University,2010.(in Chinese)
[15] 包文杰,毛成龙,胡越,等. 基于Crazy Climber的时频分析方法与应用[J]. 噪声与振动控制,2018,38(Z1): 669- 672.
Bao Wenjie,Mao Chenglong,Hu Yue,et al. The Time-frequency Analysis based on Crazy Climber Algorithm and its Application[J]. Noise and Vibration Control,2018,38(Z1): 669- 672.(in Chinese)
[16] 赵翠. 海杂波特性及抑制技术研究[D]. 成都: 电子科技大学,2014.
Zhao Cui. Research on characteristics and suppression technology of sea clutter[D]. Chengdu: University of Electronic Science and Technology of China,2014.(in Chinese)


