1 引言
干扰信道指具有多个收发对的通信场景,例如无线电网络、点对点无线通信网络以及其他具有广播特性的通信系统[1]。具体而言,系统中存在多个收发对同时地发送独立信号,而每个接收机只对来自成对发射机的信号感兴趣,并将来自其他发射机的信号视为干扰。由于干扰信道具有广播特性,即信号在网络中以广播的形式传播且可被任意节点接收,若不加以有效防护,保密信息极易遭到窃听。当发射机和接收机之间距离较远时,为了保证通信质量,需要使用中继对信号进行放大和转发,而中继环节的引入进一步增大了信息泄露的风险。
以往,传统的保密手段主要依赖于网络层以上的密码学技术,但随着计算机性能的迅速发展,一旦量子计算机投入使用,其可以对密码本进行暴力破解,使传统的加密方式面临严重的挑战[2-3]。因此,物理层安全(physical layer security,PLS)作为一种定义在物理层上的新式保密手段,引起了众多学者的兴趣,并被认为可以补充其他层级安全性方面的不足。PLS通过对发送信号进行预编码,在增大合法用户的信道容量的同时劣化窃听者的信道容量,由于其编码基于信道参数,即使编码方式遭到泄露,仍能保证信道容量的差异,可以抵御量子攻击,是一种稳定性较好的保密手段[4-5]。
在干扰信道网络中,常应用多输入多输出技术(Multiple-Input Multiple-Output,MIMO)来提高通信速率,在丰富物理层资源的同时,也为物理层编码提供了便利。针对不含中继的简单干扰信道,文献[6-7]建立了双用户窃听信道模型,并以增大窃听者与合法用户估计目标信息的均方误差为目的设计了波束成形方案。在此基础上,文献[8]将其扩展到多用户场景,并提出MT-MSE算法求解各用户的联合收发机的最优编码。但是,在干扰信道系统中加入中继节点之后,其物理层编码复杂度急剧上升,相关研究局限于降低收发对之间的互相干扰。文献[9]和[10]分别针对单中继和多中继干扰信道网络,以最小化总体MSE为目的设计了收发机和中继的联合编码。然而,上述文献的系统模型不包含窃听者,在编码设计时也没有考虑安全性能,针对这一空缺,本文以最大化窃听者和合法收发对的MSE之差为目的,设计了一种发射机、中继和接收机的联合编码方案,并提出一种异步迭代算法对其进行求解。
2 系统模型
如图1所示,假设一个干扰信道网络中含有K个收发对,每个发射机与配对的接收机之间进行通信,但由于广播特性,收发对之间互相干扰。由于发射机和接收机的距离较远,采用M个半双工中继对信号进行放大和转发(Amplify-and-forward,AF)。为了降低干扰,各发射机、中继和接收机之间可以通过发送训练序列估计彼此间的信道状态信息(channel state information,CSI),再依此进行物理层编码。与文献[8,11]类似,本文假设网络中存在一个窃听者(eavesdropper,Eve),其并非外来的敌对节点,而是网络中的某个固有接收机,却试图窃听来自非成对发射机的信息,所以其同样获知上述CSI。假设发射机k、中继m、接收机k和窃听者的天线数量分别为Nt,k、Nf,m、Nr,k和Ne。工作于AF模式的中继需要通过两个时隙来完成通信。以中继m为例,第一时隙中,所有发射机向其发送信号如下:
(1)
其中,Hkm为发射机k和中继m之间的信道矩阵;Tk为发射机k的预编码矩阵;sk为发射机k发送的保密数据,且假设其服从
其中(·)和I分别为期望运算符和对应维度的单位矩阵;nr,m为中继m接收到的噪声,且假设其方差为
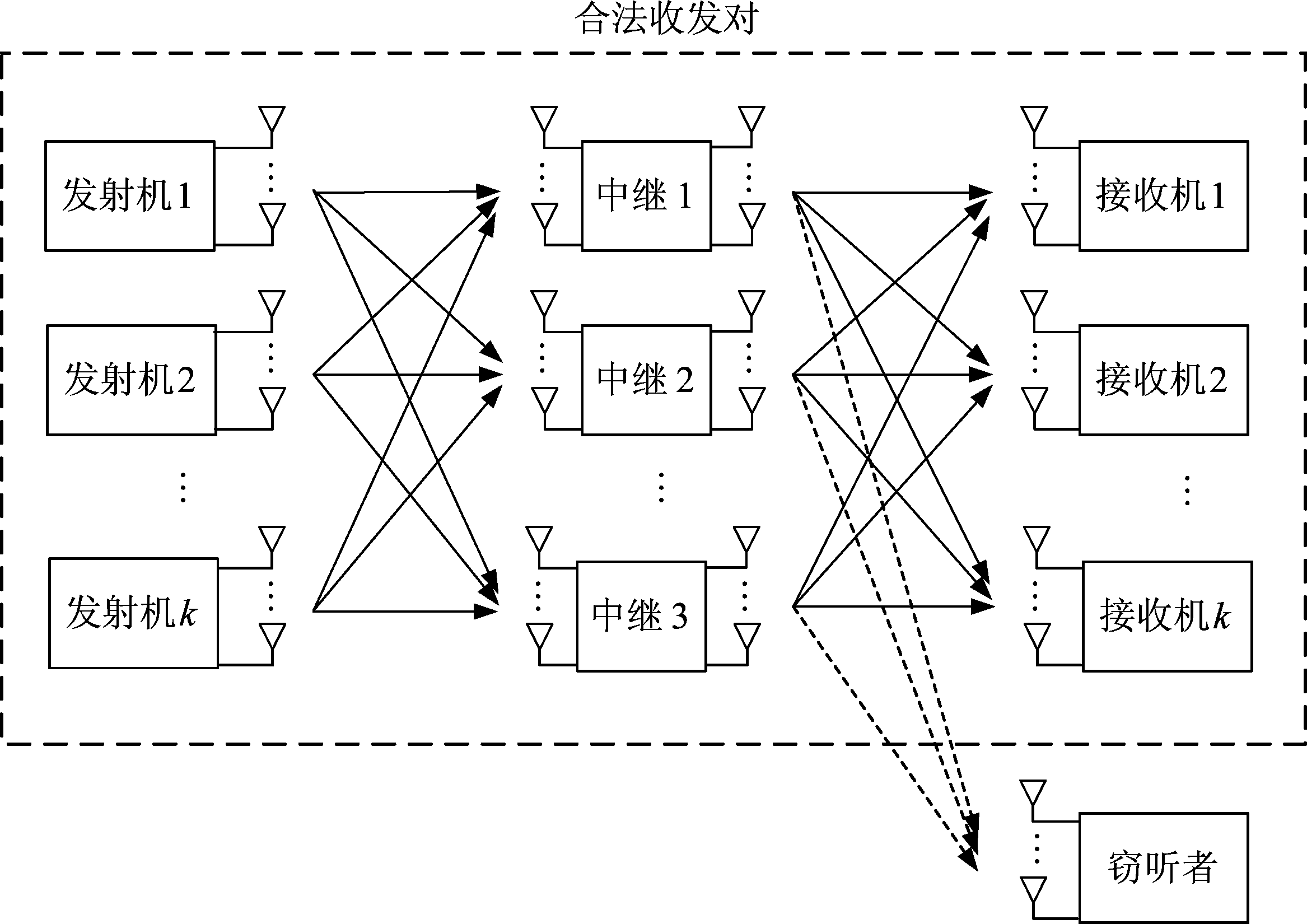
图1 含有K个收发对、M个中继和1个潜在窃听者的MIMO干扰信道网络
Fig.1 A MIMO interference network consists of K transmitter-receiver pairs,M relays and a potential eavesdropper
第二时隙中,m个中继向k个接收机转发放大过的信号,假设Eve试图窃听收发对k,接收机k和Eve接收到来自发射机k的信号分别如下:
(2)
(3)
其中,Gmk和Gme分别为中继m和接收机k之间以及中继m和Eve之间的信道矩阵;Fm为中继m的编码矩阵;nd,k和ne,k分别为接收机k和Eve接收到的噪声,假设其方差分别为
和
在接收端,接收机k和Eve分别采用解码矩阵Rk和Re,k对保密数据sk进行如下估计:
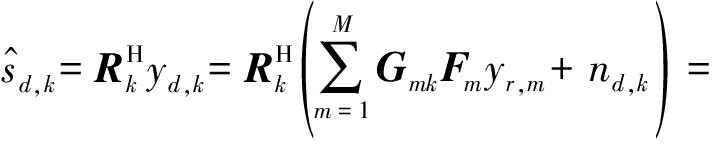
(4)
(5)
本文采用MSE作为通信质量的指标,依据式(4)和(5),可以分别计算出接收机k和Eve估计保密数据sk的MSE,其表达式如下:
MSEk=tr{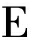
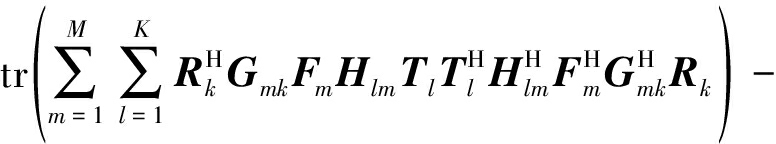
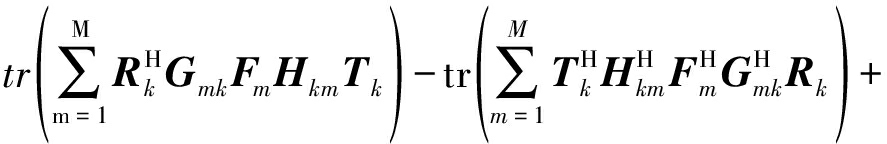
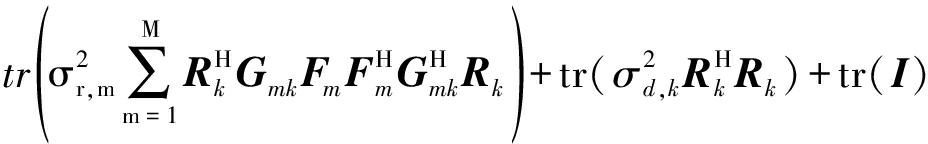
(6)
MSEe,k=tr{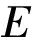
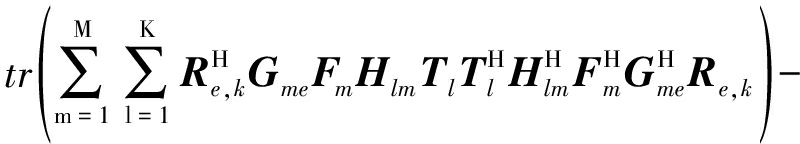
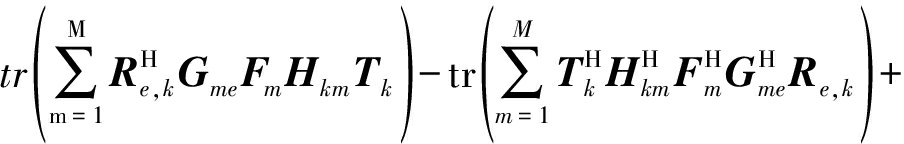
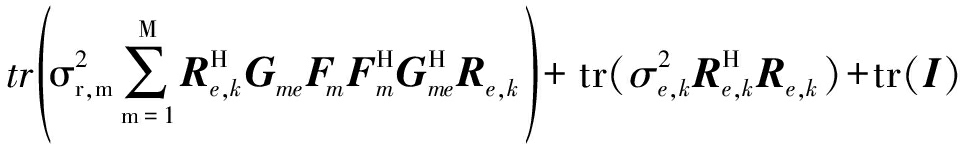
(7)
其中,tr(·)表示求迹运算符。
3 SMSE安全算法
为了提高安全性,我们希望在优化合法收发对的通信质量的同时恶化Eve的通信质量,即尽可能地增大二者的MSE之差。从网络中所有用户的利益出发,我们约束Eve对各收发对的窃听,使其MSE大于一个可以接受的数值,在此基础上最小化所有合法收发对的MSE之和(sum mean square error,SMSE),该策略可以表述为以下最优化问题:
s.t. MSEe,k≥εk,∀k∈{1,2,...,K},
∀k∈{1,2,...,K}
∀m∈{1,2,...,M}
(8)
其中,
分别为发射机k、中继m和接收机k的最优编码矩阵。εk为Eve窃听来自发射机k信号的最小MSE;pt,k和pr,m分别为发射机k和中继m的最大功率。
最优化问题(8)中的目标函数包含三个变量集:发射机的预编码矩阵{Tk}、中继的编码矩阵{Fm}和接收机的解码矩阵{Rk}。同时求解以上三个变量集复杂度较高,且目标函数非凸,不便于求解。但通过观察式(6)可知,如果假设任意两个变量集已知,目标函数可以化为仅包含一个变量集的凸函数,其最优解可以通过梯度下降法得到。因此,以化简最优化问题(8)为目的,本章提出一种异步迭代算法,将其拆分为三个单一变量集的子优化问题,再依次进行求解,逐步逼近其最优解。由于子优化问题为凸,迭代过程中目标函数始终减小,该算法是收敛的,其详细证明如附录所示。
3.1 接收机的解码矩阵求解
为最小化MSE,接收端采用线性MMSE接收机[12],其表达式可以通过对式(6)求导得到:
k
(9)
其中,
假设{Tk}和{Fm}已知,{Rk}可以通过式(9)求解。公平起见,假设Eve也采用MMSE接收机,可以用同样的方法求得其表达式如下:
e,k
(10)
其中,
3.2 发射机的预编码矩阵求解
将式(6)代入式(8),得到所有收发对的MSE之和SMSE如下:
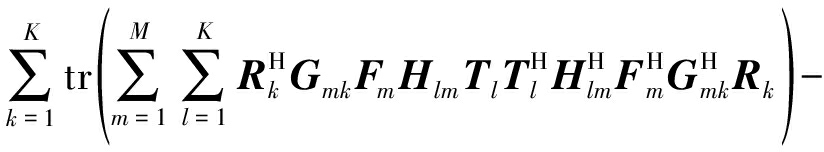
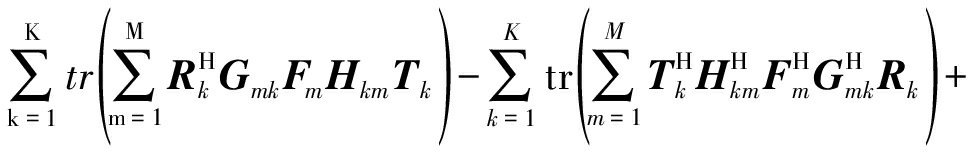
(11)
假设{Fm}和{Rk}已知,式(11)以{Tk}为自变量,但其表达式仍然十分复杂,为了将其化简,引入以下矩阵:
T=blkdiag(T1,T2,…,Tk)
(12)
(13)
(14)
v=[I1,I2,…,Ik]
(15)
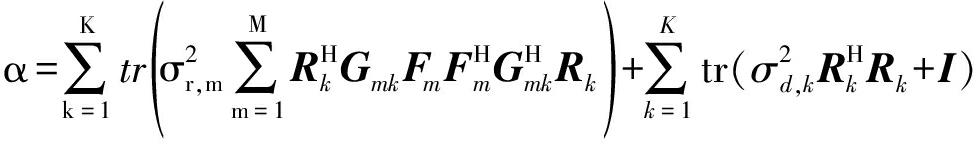
(16)
将式(12)、(13)、(14)和(15)代入(11),可以将其化简为:
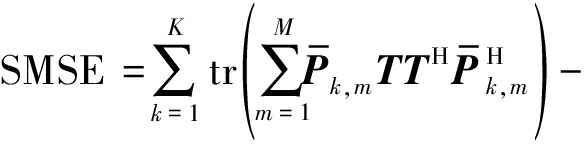
(17)
式(17)仍然非凸,为了将其化为凸函数,需要引入变量t=vec(T),并利用以下求迹公式[13]:
(18)
其中,vec(·)为向量化运算符。
将式(18)代入式(17),将其可以变化为:
⊗
⊗
)t-
⊗)t)H+α=
tHΩt-θt-tHθH+α
(19)
其中,
⊗
⊗);α不包含{Tk}。
类似地,Eve估计sk的MSE为:
(20)
其中,
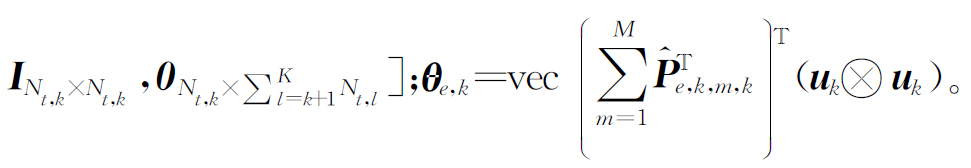
至此,式(8)中的最优化问题转化为以下标准凸二次型,其最优解可以利用梯度下降法得到。
∀k∈{1,2,...,K},
tHDkt≤pt,k,∀k∈{1,2,...,K}
(21)
其中,
⊗
3.3 中继的编码码矩阵求解
假设{Tk}和{Rk}已知,式(11)以{Fm}为自变量,但其表达式仍然十分复杂,为了将其化简,引入以下矩阵:
F=blkdiag(F1,F2,…,Fm)
(22)
(23)
(24)
(25)
(26)
将式(22)、(23)、(24)、(25)和(26)代入(11),可以将其化简为:
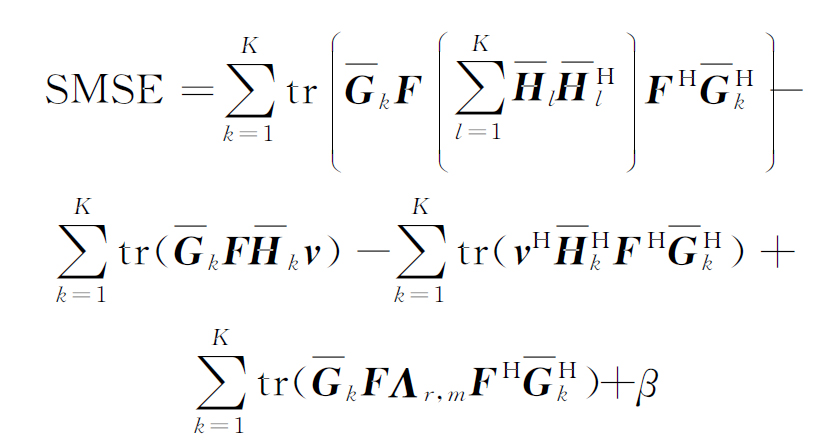
(27)
式(27)仍然非凸,为了将其化为凸函数,引入变量f=vec(F),并利用求迹公式(18),可得:
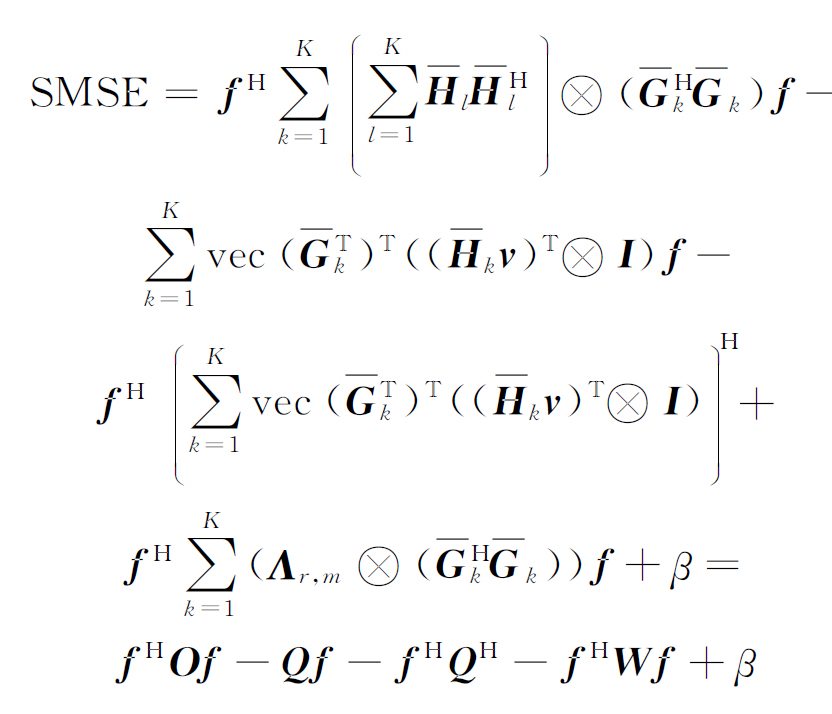
(28)
其中,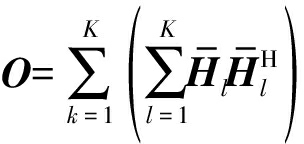
⊗
⊗
⊗
不包含{Fm}。
类似地,Eve估计sk的MSE为:
(29)
其中,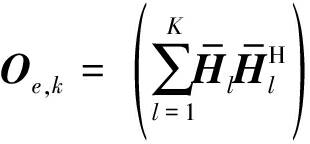
⊗
⊗
⊗
至此,式(8)中的优化问题转化为以下标准凸二次型,其最优解可以利用梯度下降法得到。
fHWe,k f+βe,k≥εk,∀k∈{1,2,...,K},
fHCmf≤pr,m,∀m∈{1,2,...,M}
(30)
其中,
⊗
⊗
综上,式(8)被拆分为三个子最优化问题,且三者都为凸优化问题。因此,本文提出一种异步迭代算法,联合求解发射机、中继和收发机的编码矩阵的最优解,其步骤如表1所示。
表1 迭代算法
Tab.1 Iterated algorithm
1.初始化:令迭代计数器n=0,随机生成矩阵{T(0)k}和{F(0)m}。2.开始迭代:利用{T(n)k}和{F(n)m},依据式(9)和(10)计算{R(n+1)k}和{R(n+1)e,k}。 3.利用{F(n)m}、{R(n+1)k}和{R(n+1)e,k},依据式(21)计算{T(n+1)k}。4.利用{T(n+1)k}、{R(n+1)k}和{R(n+1)e,k},依据式(30)计算{F(n+1)m}。n=n+1。5. 重复步骤2和4,直至效用函数SMSE收敛。
接下来,对该算法的复杂度进行讨论。在每一次迭代中,需要依次求解式(9)、(21)和(30),式(9)中对MMSE接收机的求解较为简单,因此算法的复杂度主要来源于对式(21)和(30)的求解。式(21)和(30)都为凸二次型,假设采用内点法对其进行求解,二者的复杂度分别为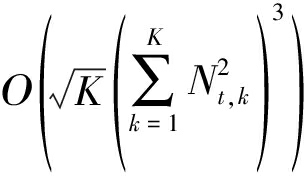
和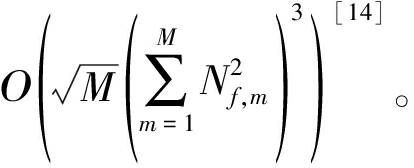
为了便于分析,此处假设所有发射机配备同样数目的天线,即Nt,1=Nt,2=…=Nt,k=Nt,∀k∈{1,2,...,K};所有中继配备同样数目的天线,即Nf,1=Nf,2=…=Nf,m=Nf,∀m∈{1,2,...,M}。综上,在最坏的情况下,每一步迭代中,本文所提出算法的复杂度为
4 仿真实验
本章对上文提出的算法进行一系列仿真实验。不失一般性,我们作如下假设:所有发射机、中继和接收机都配备3根天线;所有背景噪声方差都为1,即
信道矩阵{Hkm}和{Gmk}皆服从高斯分布;约束Eve窃听每个收发对的MSE都为3,即MSEe,k=3;发射机和中继拥有同样的功率,即pt,k=pr,m。依据上述参数,我们为下文所讨论的每个场景都随机生成了500组信道实例,以下结论均为基于500组实例仿真实验的统计结果。
4.1 收敛性分析
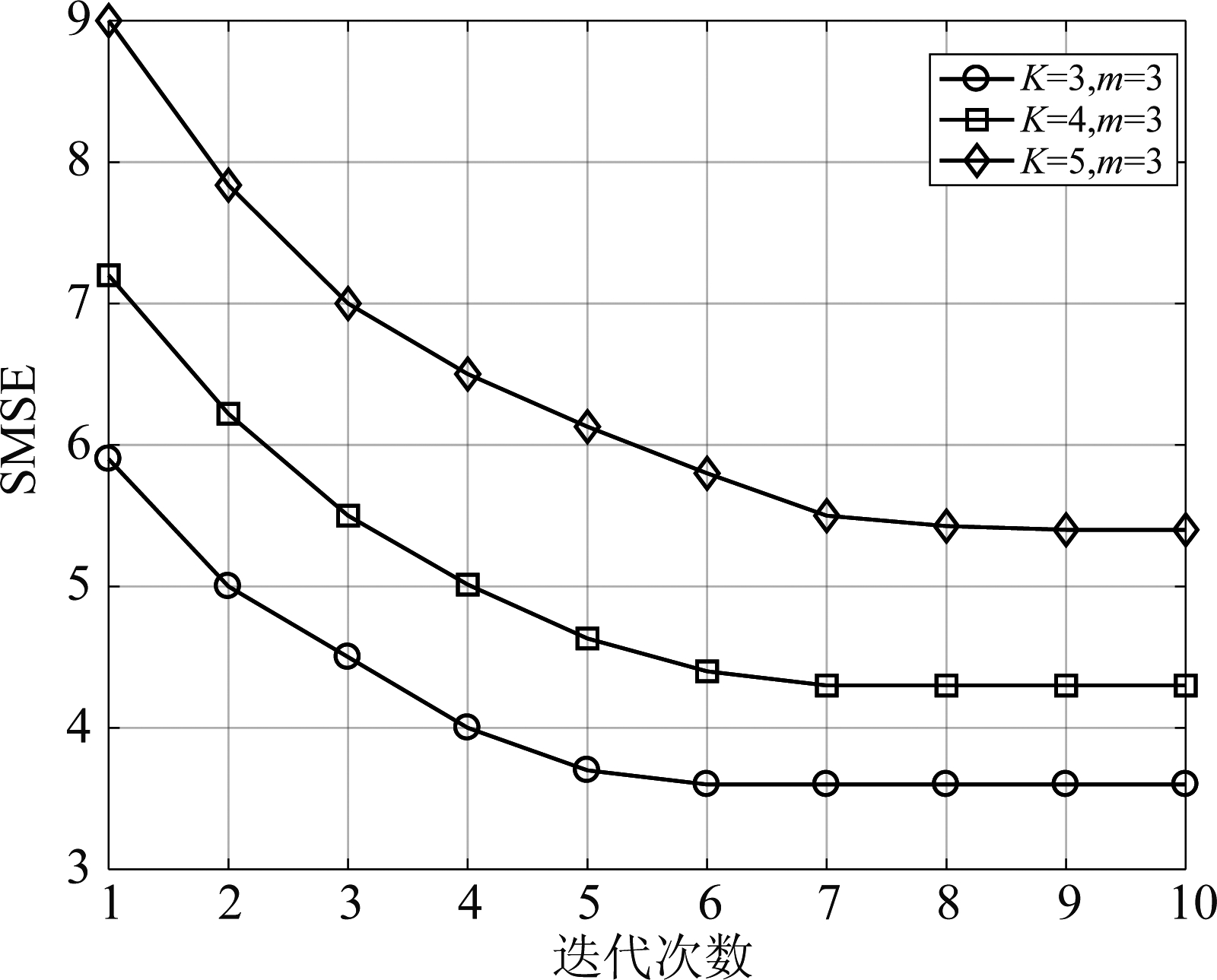
图2 算法收敛性能表现
Fig.2 Convergence behaviour of the proposed algorithms
使用第3章的算法,分别对含有3个中继和3～5个收发对的系统在功率约束为20 dB时进行了仿真,其SMSE表现如图2所示。显然,在3种系统中,随着迭代次数的增加,SMSE都逐渐下降且均能收敛。此外,当系统中的收发对增加时,收敛所需要的迭代次数和合法收发对的SMSE总和都呈上升趋势,其原因如下:由于迭代的初始值是随机的,当收发对数量增加时,网络的复杂度随之上升,在逼近最优解时需要更多的迭代次数。此外,当收发对数量增加,每个收发对受到其他收发对的干扰也随之上升,表现为MSE的增大,最终导致了SMSE增大。
4.2 安全性能分析
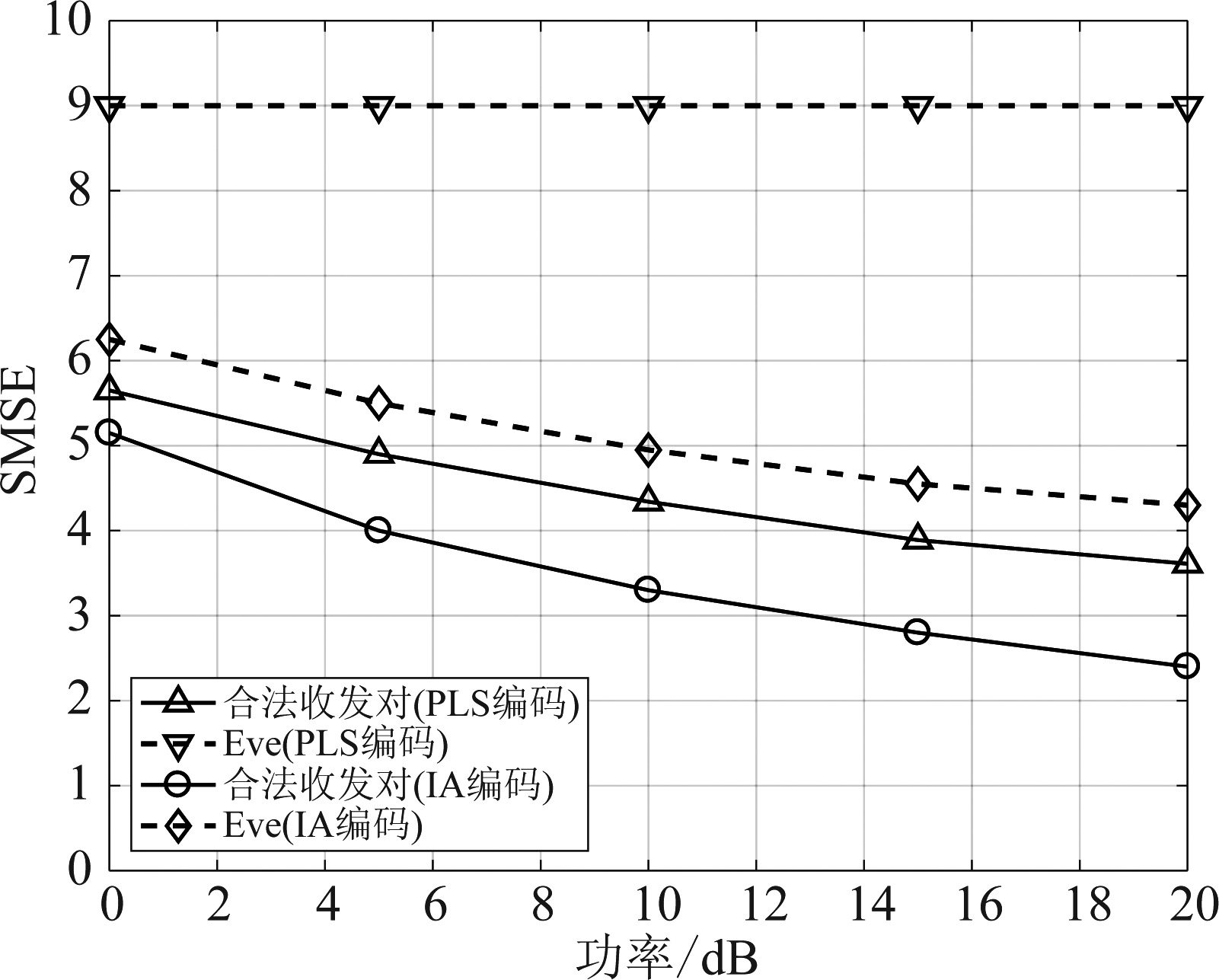
图3 算法SMSE表现
Fig.3 SMSE performance of the proposed algorithms
为了验证算法的安全性能,现以含有3个收发对和3个中继的网络为例,运用所提出的算法生成物理层编码,其SMSE表现如图3所示。同时,我们也选择传统干扰对齐(interference alignment,IA)编码作为比较[15-16],该算法旨在降低各收发对之间的干扰,并未考虑安全因素。可以看出,由于IA算法在优化时利用了合法收发对的CSI,使得合法收发对与Eve相比具有一定优势,其SMSE更小,但是二者仍然很接近,安全性不强。采用PLS编码后,合法收发对的SMSE相较于IA编码略有增大,而Eve的SMSE急剧增大,这说明PLS编码能在保证合法收发对通信质量的同时,极大地恶化Eve的通信质量,从而防止信息泄漏,保证通信安全。此外,虽然本算法设计基于最小化SMSE,但其优化同样体现在安全速率方面。图4展示了在使用所提出算法进行编码后,系统内各收发对的安全速率。在物理层安全中,安全速率定义为合法收发信道与窃听信道的通信速率之差,由于传统编码未考虑系统安全性,从统计上可以认为其安全速率为零[17]。而如图4所示,本文所提出算法能为各收发对提供正的安全速率,同时随着通信功率的增加,安全速率逐渐增加,系统安全性能随之增强。
图4 算法安全速率表现
Fig.4 secrecy rate performance of the proposed algorithms
值得注意的是,PLS编码的SMSE高于IA编码,其通信质量较IA编码有所降低,说明该编码是安全性和通信质量之间的一种折衷方案,牺牲了一部分通信质量换取必要的安全性能。在实际应用中,针对不同安全性能需求的场景,可以通过调整安全约束条件εk实现安全性能和通信质量的平衡。
5 结论
为了提高中继辅助的MIMO干扰信道网络的安全性能,本文设计了一种发射机、中继和收发机的物理层联合编码方案。具体而言,该方案将窃听者对保密信号估计的MSE约束在一个可以接受的范围内,其后最小化合法用户的MSE之和,在提高合法收发对通信质量的同时劣化了窃听者对保密信号的估计。为了获得最优解,本文利用数学变换,将非凸的最优化问题化为三个标准凸二次型的子问题,使其可以通过梯度下降法快速求解,再使用迭代算法,逐步逼近其最优解。仿真结果表明,所提出算法收敛,且能使中继辅助的MIMO干扰信道网络的SMSE表现得到大幅提高,防止了信息泄漏,保证了通信安全。
附录 算法收敛性证明
证明:
设
和
为第n步迭代所得最优解,由于子优化问题(9)、(21)和(30)皆为凸,在每一步迭代中,其梯度都小于零,即:
tr(
(31)
tr(
(32)
tr(
(33)
引入新变量X=[T1,T2,...,Tk,F1,F2,...,Fm,R1,R2,...,Rk],有
tr(X(n)SMSE(X(n))T(X(n+1)-X(n)))≤0
(34)
即在每一步迭代中,目标函数SMSE对变量X而言总是递减的。算法收敛性得证。
[1] Diana M,Daniela T,Natasha D. Multi-user Cognitive Interference Channels: A Survey and New Capacity Results[J]. IEEE Transactions on Cognitive Communications & Networking,2015,1(1): 29- 44. DOI: 10.1109/TCCN.2015.2488633.
[2] 徐鑫,金梁. NOMA系统中基于协作干扰的物理层安全方案[J]. 信号处理,2017,33(6): 836- 844. DOI: 10.16798/j.issn.1003-0530.2017.06.009.
Xu Xin,Jin Liang. Physical Layer Security Schemes Based on Cooperative Jamming for Non-Orthogonal Multiple Access System[J]. Journal of Signal Processing,2017,33(6): 836- 844. DOI: 10.16798/j.issn.1003- 0530.2017.06.009.(in Chinese)
[3] Harrison W K,Almeida J,Bloch M R,et al. Coding for Secrecy: An Overview of Error-Control Coding Techniques for Physical-Layer Security[J]. IEEE Signal Processing Magazine,2013,30(5): 41-50. DOI: 10.1109/MSP.2013.2265141.
[4] Bloch M,Hayashi M,Thangaraj A. Error-Control Coding for Physical-Layer Secrecy[J]. Proceedings of the IEEE,2015,103(10): 1725-1746. DOI: 10.1109/JPROC.2015.2463678.
[5] 罗屹洁,崔丽,杨旸. D2D使能蜂窝网络中存在主动窃听者的物理层安全研究[J]. 信号处理,2018,34(1): 119-125. DOI: 10.16798/j.issn.1003-0530.2018.01.015.
Luo Yijie,Cui Li,Yang Yang. Research on Physical Layer Security in D2D Enabled Cellular Networks with an Active Eavesdropper[J]. Journal of Signal Processing,2018,34(1): 119-125. DOI: 10.16798/j.issn.1003- 0530.2018.01.015.(in Chinese)
[6] Li Lingxiang,Huang Chuan,Chen Zhi. Cooperative Secrecy Beamforming in Wiretap Interference Channels[J]. IEEE Signal Processing Letters,2015,22(12): 2435-2439. DOI: 10.1109/LSP.2015.2490602.
[7] Fakoorian S A A,Swindlehurst A L. Competing for Secrecy in the MISO Interference Channel[J]. IEEE Transactions on Signal Processing,2013,61(1): 170-181. DOI: 10.1109/TSP.2012.2223689.
[8] Kong Zhengmin,Yang Shaoshi,Wu Feilong,et al. Iterative Distributed Minimum Total MSE Approach for Secure Communications in MIMO Interference Channels[J]. IEEE Transactions on Information Forensics & Security,2015,3(11): 594- 608. DOI: 10.1109/TIFS.2015.2493888.
[9] Nguyen K X,Rong Yue,Nordholm S. Simplified MMSE Precoding Design in Interference Two-Way MIMO Relay Systems[J]. IEEE Signal Processing Letters,2016,23(2): 262-266. DOI: 10.1109/LSP.2015.2513482.
[10] Singh V P,Chaturvedi A K. Statistically Robust Transceiver Design Algorithms for Relay aided MIMO Interference Systems[J]. IET Signal Processing,2018,12(1): 51- 63. DOI: 10.1049/iet-spr.2017.0054.
[11] Kalantari A,Maleki S,Zheng Gan,et al. Joint Power Control in Wiretap Interference Channels[J]. IEEE Transactions on Wireless Communications,2015,14(7): 3810-3823. DOI: 10.1109/TWC.2015.2412531.
[12] Zhong Caijun,Ratnarajah T,Zhang Zhaoyang,et al. Performance of Rayleigh-Product MIMO Channels with Linear Receivers[J]. IEEE Transactions on Wireless Communications,2014,13(4): 2270-2281. DOI: 10.1109/TWC.2014.031314.131478.
[13] Rong Yue. Linear Non-Regenerative Multicarrier MIMO Relay Communications Based on MMSE Criterion[J]. IEEE Transactions on Communications,2010,58(7): 1918-1923. DOI: 10.1109/TCOMM.2010.07.090056.
[14] Boyd S,Vandenberghe L. Convex Optimization[M]. Cambridge,U.K.: Cambridge University Press,2004.
[15] Maddah-Ali M A,Motahari A S,Khandani A K. Communication Over MIMO X Channels: Interference Alignment,Decomposition,and Performance Analysis[J]. IEEE Transactions on Information Theory,2008,54(8): 3457-3470. DOI: 10.1109/TIT.2008.926460.
[16] Cadambe V R,Jafar S A. Interference Alignment and Degrees of Freedom of the K-user Interference Channel[J]. IEEE Transactions on Information Theory,2008,54(8): 3425-3441. DOI: 10.1109/TIT.2008.926344.
[17] Chu Zheng,Cumanan K,Ding Zhiguo,et al. Robust Outage Secrecy Rate Optimizations for a MIMO Secrecy Channel[J]. IEEE Wireless Communications Letters. 2015,4(1): 86- 89. DOI: 10.1109/LWC.2014.2374611.
