1 引言
基于阵列处理的信源波达方向(Direction Of Arrival,DOA)估计已在雷达、声纳、无线通信、无源定位等领域得到了广泛应用[1-2]。传统的高分辨空间谱估计方法,如多重信号分类(Multiple Signal Classification,MUSIC)法[3]、旋转不变子空间技术(Estimation of Signal Parameter via Rotational Invariance Techniques,ESPRIT)[4]等均假定背景噪声是统计独立的白高斯噪声,且信源相互独立。然而实际测向环境中,一方面,由于天线阵列未校准或接收通道的硬件组成存在差异,此时各个阵元噪声相互统计独立且功率互不相同,即为非均匀噪声；另一方面,由于多径信号广泛存在,入射信号环境通常是非相关信号与相干信源同时存在,非均匀噪声和相干信源均会导致常规子空间类测向算法性能下降。
为了克服非均匀噪声对子空间类测向性能的影响,文献[5]提出了基于分步迭代最大似然法,将噪声协方差矩阵和DOA均作为未知参数,利用分步迭代最大似然法获得噪声协方差矩阵和DOA的联合估计,该方法求解需要迭代进行,计算量较大；文献[6]提出了基于数据协方差矩阵分块的噪声协方差估计方法,避免了迭代处理,计算量相对较小,但存在阵列自由度损失,估计信源数有限等不足。Liao等人提出了基于迭代最小二乘DOA估计[7- 8],但均假设信源相互独立,若信源存在相干信号,此时算法性能严重下降。
为了解决相干信号测向估计问题[9],学者们提出了许多算法,一般可分为两大类:第一类是空间平滑类算法,包括前向平滑[10],前后向平滑[11]。另一类是矩阵重构法[12-14],包括Toeplize矩阵重构法[12]、ESPRIT-Like法[13-14]。上述方法均以牺牲有效阵元来恢复相干信号协方差矩阵秩,且无法区分相干和非相干源。Ye 等人提出了基于空间差分矩阵重构的混合信源DOA估计方法[15-17],利用空间差分算法将非相关信源剔除,实现混合信号DOA估计。但该方法假设噪声为高斯白噪声,若阵元噪声为非均匀噪声白噪声,此时空间差分平滑无法消除噪声影响,DOA估计将出现较大误差。
针对以上问题,本文提出了非均匀噪声背景下非相关信源与相干信源共存时混合信号DOA估计算法。该算法首先利用迭代最小二乘方法得到噪声协方差矩阵估计,利用ESPRIT实现非相关信源DOA估计；其次基于空间差分法消除非相关信号并构造新矩阵,利用前后向空间平滑技术实现对相干信源解相干；最后利用求根MUSIC法估计相干信源DOA。所提算法实现了非均匀噪声混合信号DOA估计。
2 信号模型
假设K个远场窄带信号入射到M元均匀线阵上,阵元间距为半波长。不失一般性,假定共有D组相干信号,第k(k=1,...,D)个相干信源组的基准信号为sk(t),信号功率为
...,D,其组间的第p(p=1,2,...,Pk)个信号的来波方向为θkp,其中Pk为第k组相干信源包含多径信号源数,即满足
且相干信源组彼此相互统计独立；其余Ku=K-Kc个信源是非相关的,以角度θk入射,信号波形为sk(t),信号功率为
...,
为相干信源组基准波形矢量,su(t)=[sKc+1(t),...,sK(t)]T为非相关信源波形矢量,则阵列接收信号x(t)可表示为
(1)
式中:a(θ)是方向矢量,
为信源导向矢量矩阵；
...,Ac,DρD]为相干信源导向矢量矩阵,Ac,k=[a(θk1),...,a(θkPk)]；ρk=[ρk1,...,ρkPk]T,ρkp表示第k组第p个相干信号相对于第一个信号的衰落系数；Au=[a(θKc+1),...,a(θK)]为非相关信源导向矢量矩阵,n(t)为零均值高斯非均匀噪声,且与信号不相关。则x(t)协方差矩阵为
Rx=E{x(t)xH(t)}=ARsAH+Q
(2)
式中:Rs=E{s(t)sH(t)}=diag{Ru,Rc}为信号s(t)的协方差矩阵；
...,
...,
分别为sc(t)、su(t)的协方差矩阵；
非均匀噪声协方差矩阵为Q。
全文中,符号(·)T、(·)*、(·)H、(·)†和E{·}分别表示转置、共轭、共轭转置、求Moore-Penrose逆矩阵和求期望,diag{α1,...,αk}为由对角元素α1,...,αk组成的对角矩阵,blkdiag{Z1,Z2}表示由矩阵Z1,Z2组成的块对角矩阵,A(a∶b,c∶d)表示矩阵A的a～b行和c～d列元素构成子矩阵,rank(·)表示矩阵秩,IM为M×M维单位矩阵,‖·‖F表示对矩阵求Frobenius范数,符号DM×M表示M×M对角矩阵集,angle(·)表示取相位操作,⎣·」表示向下取整。
3 非均匀噪声背景下混合信号DOA估计
3.1 噪声协方差矩阵估计
若噪声为空间白噪声,即Q=σ2IM。其中σ2表示噪声功率；若噪声为空间色噪声,即各阵元噪声互不相关,功率不同,
...,
其中
表示第m个阵元上噪声功率。
由于信号s(t)彼此统计独立,则协方差矩阵Rs为满秩矩阵,对Rs进行矩阵分解,可得
Rs=BBH
(3)
其中B是维数为(D+Ku)的非奇异方阵。
将式(3)代入式(2)可得
Rx=ABBHAH+Q=CCH+Q
(4)
其中C=AB∈CM×(D+Ku)。
由于B为非奇异矩阵,则C列向量与A列向量张成为同一空间。考虑到Q对角矩阵,因此若能得到C和Q估计值,则对数据“去噪”,再利用子空间类算法实现DOA估计。
基于以上分析,可得如下约束优化问题[8]
(5)
任意正交矩阵T,满足TTH=IM,则
CCH=CTTHCH=C′C′H
(6)
其中C′=CT,因此若(C,Q)是式(5)解,则(C′,Q)也是式(5)解。为了避免求解C的多值性,对C进行约束,即
s.t Q∈DM×M,CCH∈DM×M
(7)
利用最小二乘法可得式(7)的解为
Q=D(Rx-CCH)
(8)
C=U
1/2
(9)
其中U、分别为R-Q的Ku+D个主特征值对应的特征值矩阵和特性矢量矩阵。D(A)表示取矩阵A的主对角线元素组成对角矩阵。
通过观察式(8)、式(9)可知,矩阵Q与C求解存在耦合,因此考虑采用迭代最小二乘方法求解Q,该方法在每次迭代过程中将前一次Q迭代值作为当前值,直到前后两次迭代估计值误差小于ε时停止迭代,其中ε为设置的误差容忍度,实现流程如表1所示。
表1 噪声协方差矩阵计算流程
Tab.1 Computational procedure for noise covariance matrix
(1)初始化。计算R^x=1N∑Nt=1x(t)xH(t),N为采样点数,迭代次数i=0,Q(0)=(D(R^x-1))-1,设置ε和最大迭代次数NImax。(2)迭代过程。利用式(9)、式(8)分别计算C(i+1)、Q(i+1)更新i=i+1。(3)判决。若‖Qi+1-Qi‖F≤ε,或i=NImax,则认为Q^=Q(i) 并退出迭代,否则返回(2)。
3.2 非相关信源DOA估计
定义无噪阵列接收数据z(t)可表示为
z(t)=x(t)-n(t)=[Au,AcΓ]s(t)
(10)
式中Γ=blkdiag{ρ1,...,ρD},Ac=[Ac,1,...,Ac,D]。
若将阵列分解为两个子阵,子阵间距为阵元间距,则第i(i=1,2)个子阵数据zi(t)=[zi(t),...,zM+i-2(t)]T可表示为
(11)
其中
Bu=diag{ejπsin θ1,...,ejπsin θKu}
(12)
Bc=blkdiag{Bc,Ku+1,...,Bc,Ku+D}
(13)
Bc,Ku+k=diag{ejπsin θk1,...,ejπsin θkPk}
(14)
A1u=Au(1∶M-1,∶)、A1c=Ac(1∶M-1,∶)。
将两个子阵数据联合可得
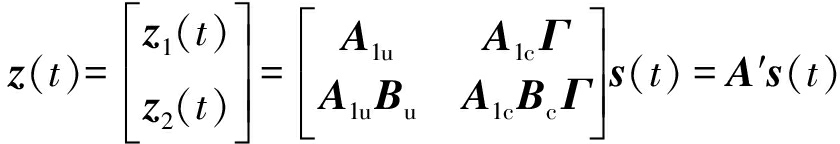
(15)
其中
若矩阵Q已知或估计得到,则“去噪”后数据协方差矩阵为
R=Rx-Q=ARsAH
(16)
假定z(t)的协方差矩阵为Rz=E{z(t)zH(t)},将Rz的行、列按(M-1,M-1)其表示为分块矩阵形式为
(17)
其中Rij=Rz(Li,Lj)i,j=1,2,Lk=((k-1)(M-1)+1):k(M-1),k=1,2。
由式(16)、式(17)可得:
假定M≥Ku+D+1,对Rz特征分解可得
(18)
其中Us=[u1,...,uKu+D],s=diag{λ1,...,λKu+D}、Un=[uKu+D+1,...,u2(M-1)],n=diag{λKu+D+1,...,λ2(M-1)}、λ1≥λ2…≥λKu+D>λKu+D+1=…=λ2(M-1)=0。
联合式(16)、(18)可知Us与A′列向量张成空间为同一空间,即span{Us}=span{A′},此时存在唯一的非奇异矩阵G∈C(Ku+D)×(Ku+D),使得
Us=A′G
(19)
若将信号子空间Us拆分成两个维度均为(M-1)×(Ku+D)的子矩阵U1s、U2s,即
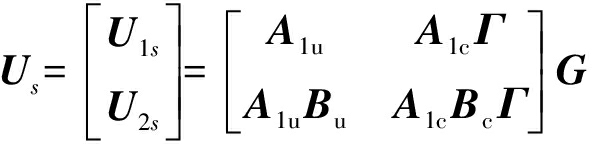
(20)
假定Kc≤M-1,则
为列满秩矩阵,同时考虑到相干信源DOA各不相同,因此A1cΓ的列向量与A1cBcΓ的列向量相互独立,因此rank[U1sU2s]=min(M-1,2(Ku+D)),则存在维数为2(Ku+D)×Ku的列满矩阵E满足如下等式
=[A1u,A1cΓ]GE1+[A1uBu,A1cBcΓ]GE2=0(M-1)×Ku
(21)
E1、E2维数均为
由式(22)可知,E为矩阵[U1sU2s]H[U1sU2s]的Ku最小特征值对应特征向量矩阵。
假定
其中F11、F21的维数均为Ku×Ku、F12、F22的维数均为D×Ku,则可得
(22)
式(21)、式(22)证明见文献[16]。
由(22)可知,Ω的特征值δk,k=1,...,Ku对应Bu的对角线元素,即可得非相关信源的DOA估计为
...,Ku
(23)
3.3 相干信源DOA估计
考虑RT为Toeplitz矩阵,即满足
为置换矩阵,则对矩阵R进行空间差分可得
Rd=R-JRTJ=RNT-JRNTJ=
(24)
式中
...,
若对Rd特征分解,可得
(25)
则Ud与Ac的列向量张成空间为同一空间,即存在列满秩矩阵T′∈C2Kc×2,使得Ud=AcT′。
利用Rd构造新的矩阵Rnew为[16]
(26)
式中:
...,
为列满秩矩阵；
...,
为第k组相干信源的正特征值；H为满秩矩阵,满足HWHH=W,W=diag{1,-1,...,1,-1}。
对矩阵Rnew进行空间平滑即可实现解相干,利用Root-MUSIC算法求解相干信源DOA。
3.4 阵元需求分析
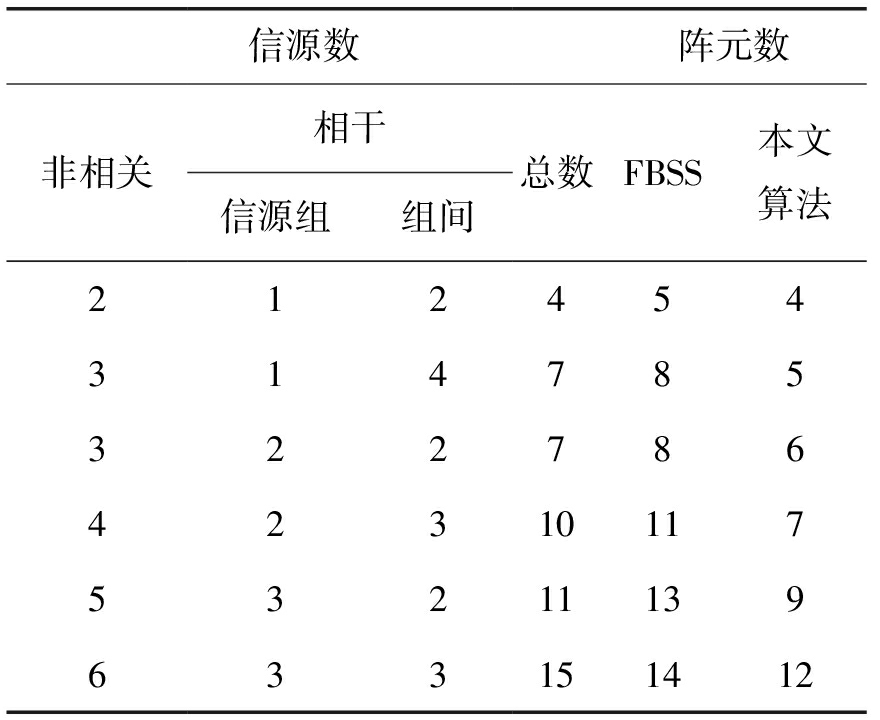
本文算法需要Ku+D+1个阵元分辨非相关信源、Kc+「Pmax/2⎤个阵元分辨相干信源,Pmax为所有相干信源组中最大信源数,最少阵元数为max{(Ku+D+1),「Pmax/2⎤+Kc},而FBSS算法需要Ku+Kc+「Pmax/2⎤分辨所有信号。表1为两种算法分辨所有信源最少阵元数。
由表2可知,本文算法分辨信源数可以超过阵元数,而FBSS算法由于无法对非相关信源与相干信源分开处理,因此空间平滑后阵列孔径损失最大。
表2 分辨信源所需最少阵元数
Tab.2 Number of sensors necessary for resolving the signals
信源数阵元数非相关相干信源组组间总数FBSS本文算法2124543147853227864231011753211139633151412
4 仿真实验与分析
假定M元均匀线阵,间距为半波长,入射信号为等功率信号,其功率为
...,
...,M)为第m个阵元的噪声功率。平均信噪比(Signal to Noise Ration,SNR)定义为
分别表示第k个信号DOA的真实值和估计值
则表示为有效估计。Monte Carlo实验次数为200。DOA估计均方根误差定义为
其中θk(n)表示第k个信号角度的第n次估计值。噪声功率估计均方根误差RMSE采用类似定义。误差ε取0.01。
为了验证算法有效性,在非均匀噪声协方差估计方面,比较本文方法(记为迭代法)与文献[6]法(记为直接法)；在混合信号DOA估计方面,比较本文方法(记为IterLS)、FBSS法,文献[16]法(记为YZF)。
实验1 非均匀噪声协方差矩阵估计
假定M=10,非相关信号DOA为10°,1组相干信号DOA分别为[-12°18°],噪声协方差矩阵Q=diag{10,2,1.5,2.5,5,1,1.5,3,5,2}。采样快拍数为1000。图1是SNR为0 dB时各阵元噪声功率估计值,图2是不同SNR条件下阵元噪声功率估计RMSE。
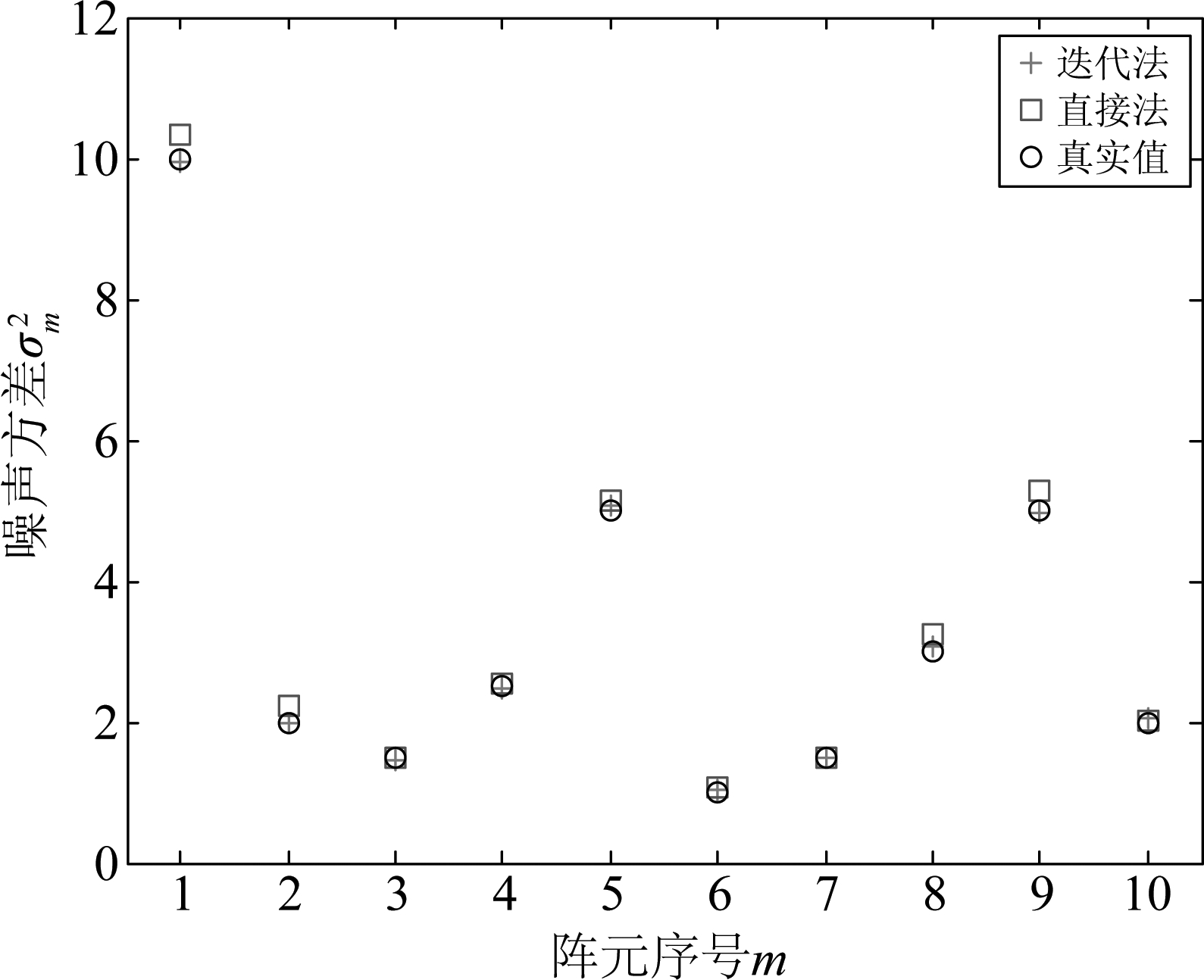
图1 不同阵元噪声功率估计
Fig.1 Noise variance estimation for different array element
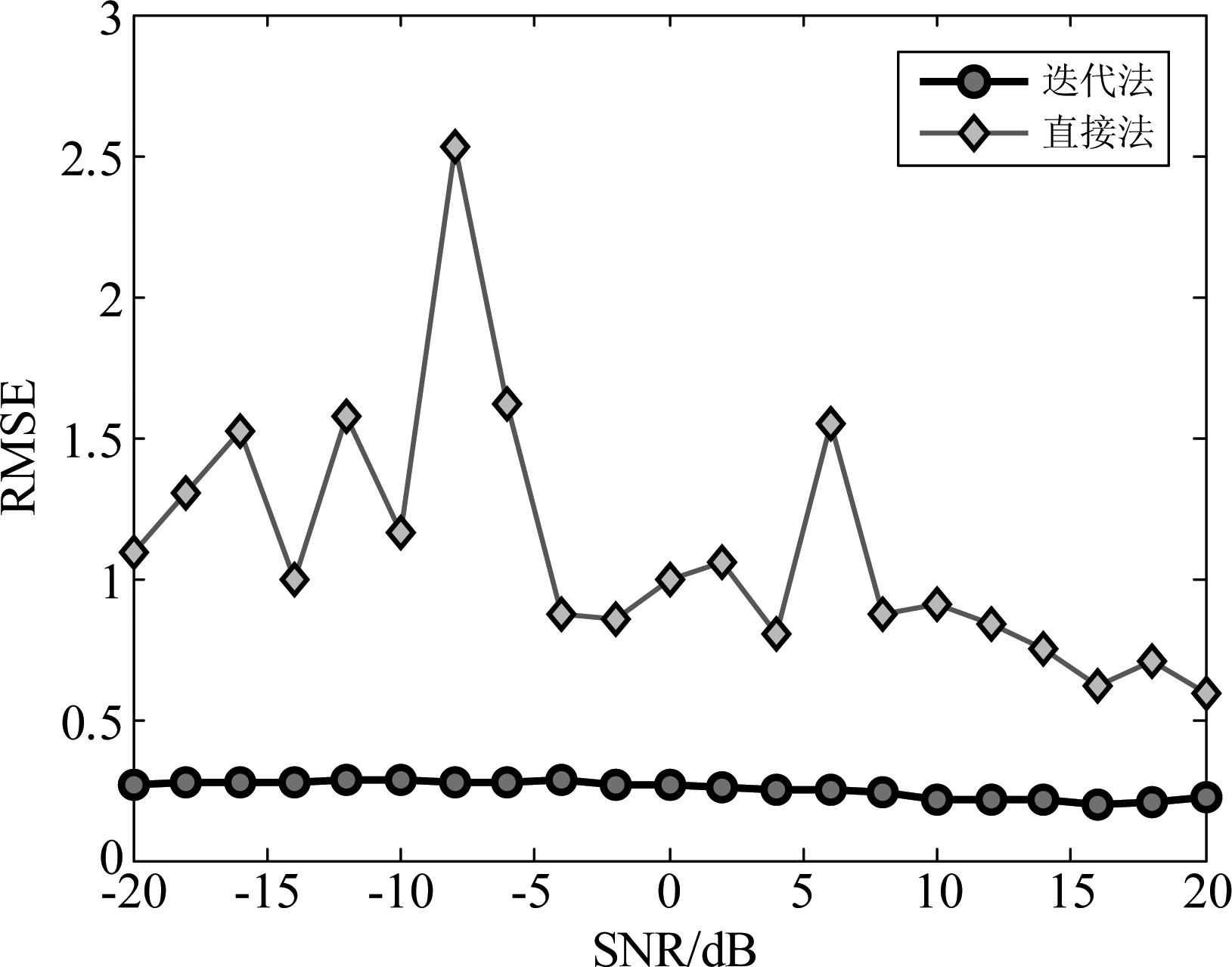
图2 不同SNR时噪声协方差估计RMSE
Fig.2 RMSE of noise variance versus SNR
从图1、图2可知,在SNR为0 dB时,文献[6]直接法基本实现噪声协方差矩阵估计,但存在一定误差,在不同SNR时RMSE值出现波动,尤其是当某阵元噪声功率较大时,其误差值相对较大,且最多只能处理⎣M/3」个相干信源；本文方法能实现各阵元噪声功率准确估计,随SNR变化,其RMSE性能基本保持一致,其RMSE性能更优,噪声协方差矩阵估计更为准确。
实验2 不同SNR时算法RMSE与有效估计概率
考虑M=12,非相关信号DOA分别为[-13°-2°42°],2组相干信号DOA分别为[-19°15°]、[29°56°],FBSS的平滑子阵数为3,阵元数为10,采样快拍数为1000。图3为不同SNR时测向RMSE；图4为不同SNR时有效估计概率。图例中“Un”对应非相关信源,“Co”对应相干信源。
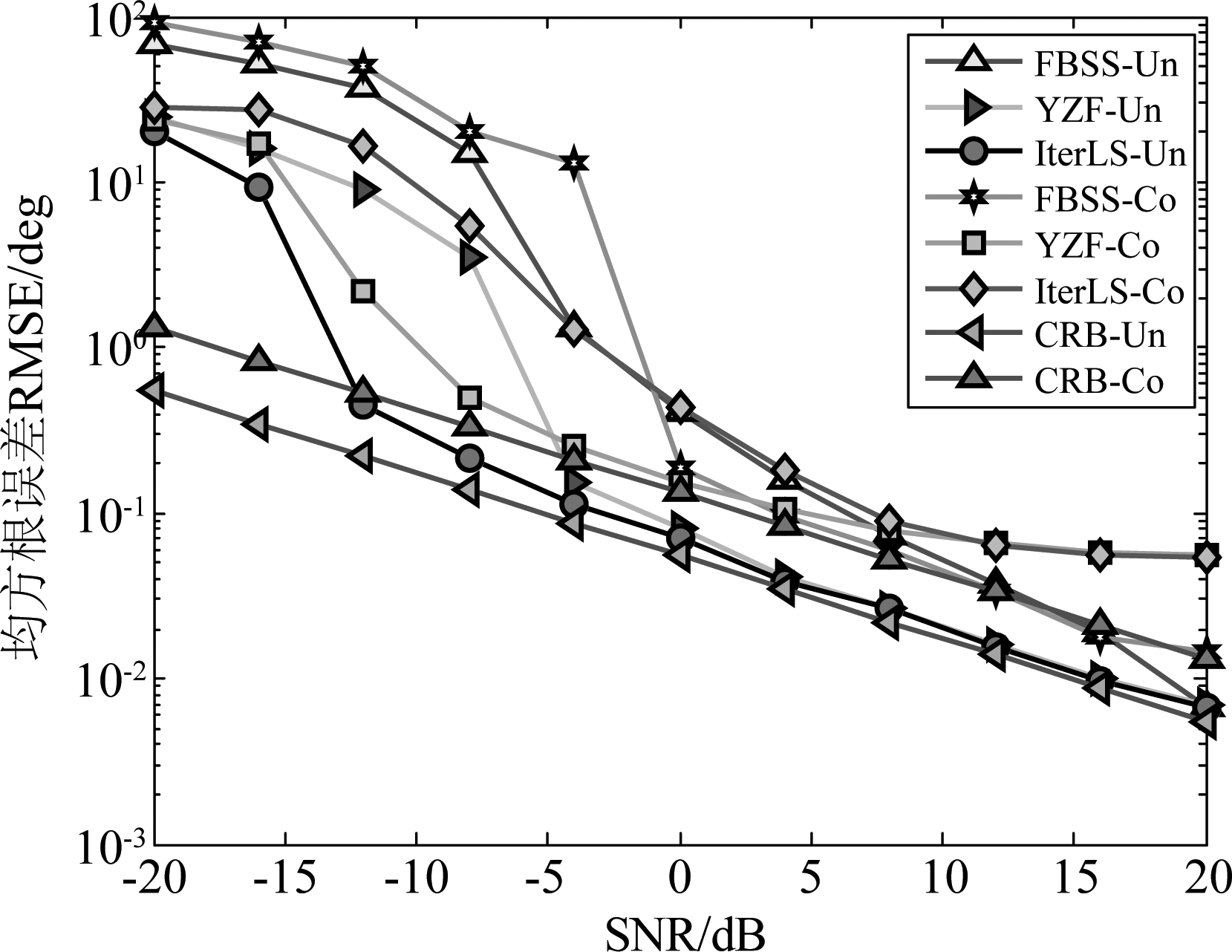
图3 不同SNR时均方根误差RMSE
Fig.3 RMSE curves of the DOA estimates versus SNR
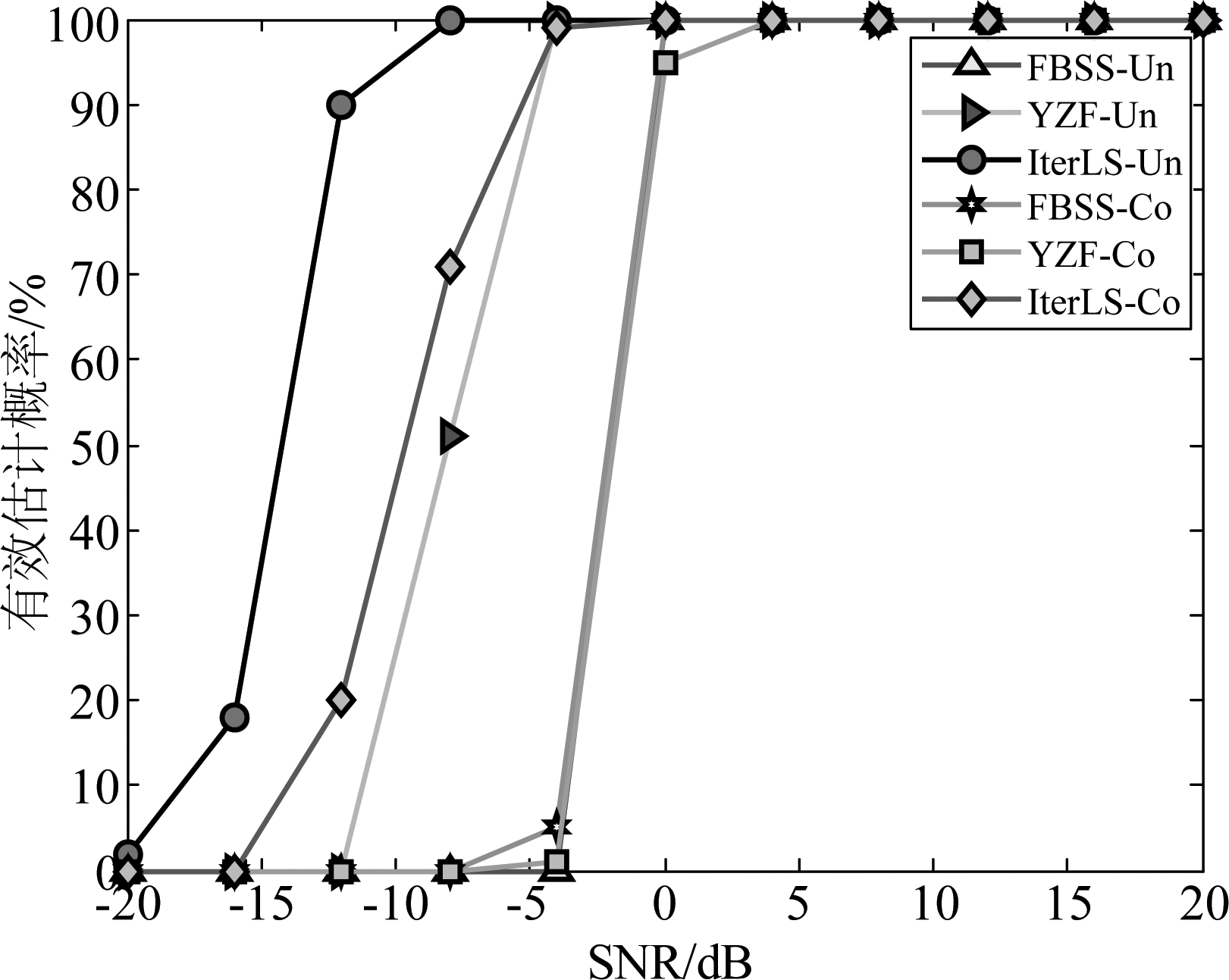
图4 不同SNR时有效估计概率
Fig.4 Probabilities of effective estimation versus SNR
从图3、图4可以看出,FBSS、YZF以及本文算法均能实现对混合信号DOA估计。在DOA估计RMSE和有效估计概率方面,本文算法在低SNR时优于FBSS算法和YZF算法,DOA估计的RMSE性能逼近克拉美罗界(Cramer-Rao Bound,CRB)。在高SNR时YZF与本文算法测向性能接近,FBSS算法RMSE性能相对最差。在低SNR时本文算法准确估计噪声协方差矩阵后,剔除了噪声的影响,而FBSS算法、YZF算法无法剔除非均匀噪声影响,因此其测向RMSE性能比本文算法差。
实验3 不同快拍时算法RMSE与有效估计概率
假定SNR为0 dB,其他仿真条件与实验2相同。图5为不同快拍数时测向RMSE；图6为不同快拍数时有效估计概率。
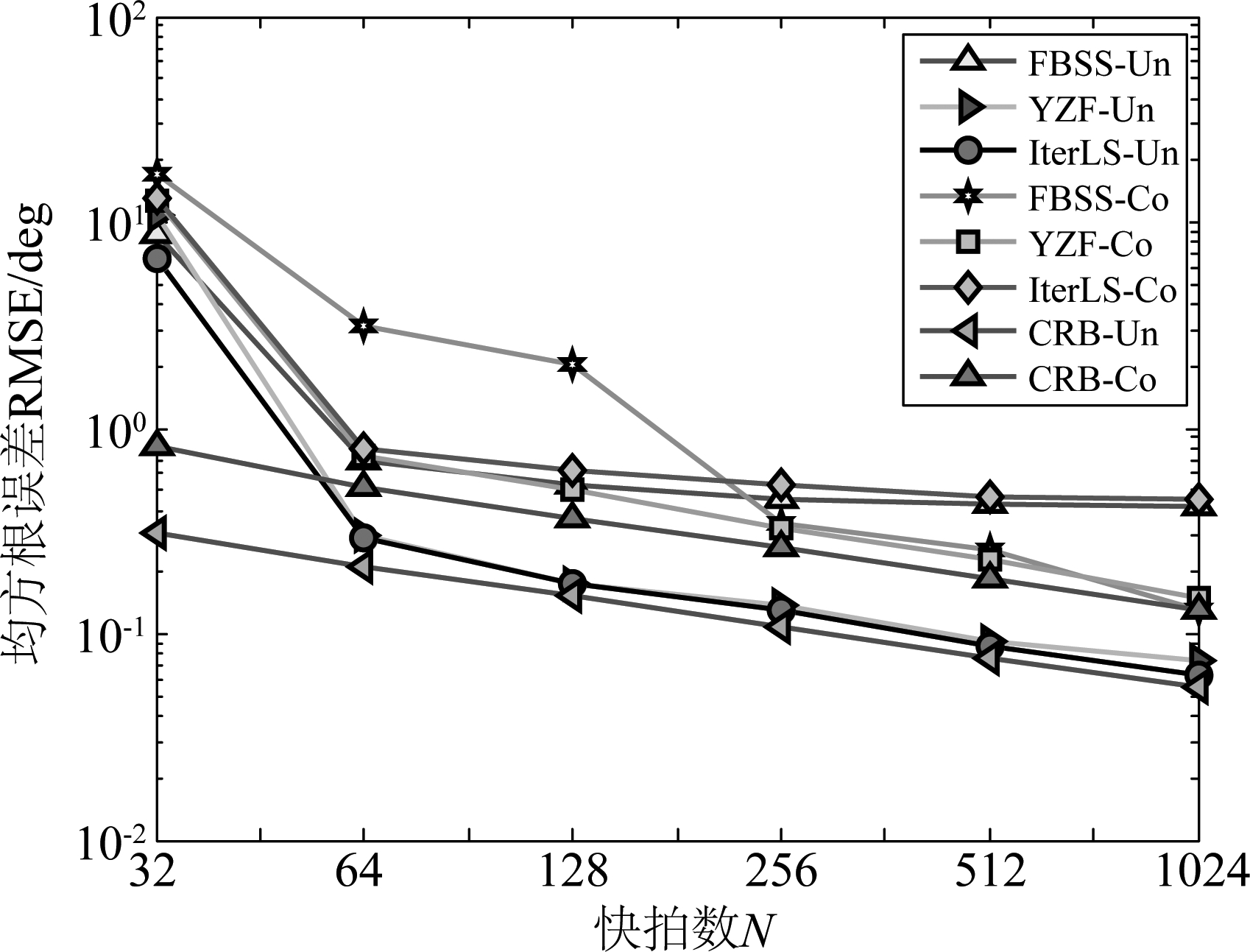
图5 不同快拍数N时均方根误差RMSE
Fig.5 RMSE of the DOA estimates versus snapshots
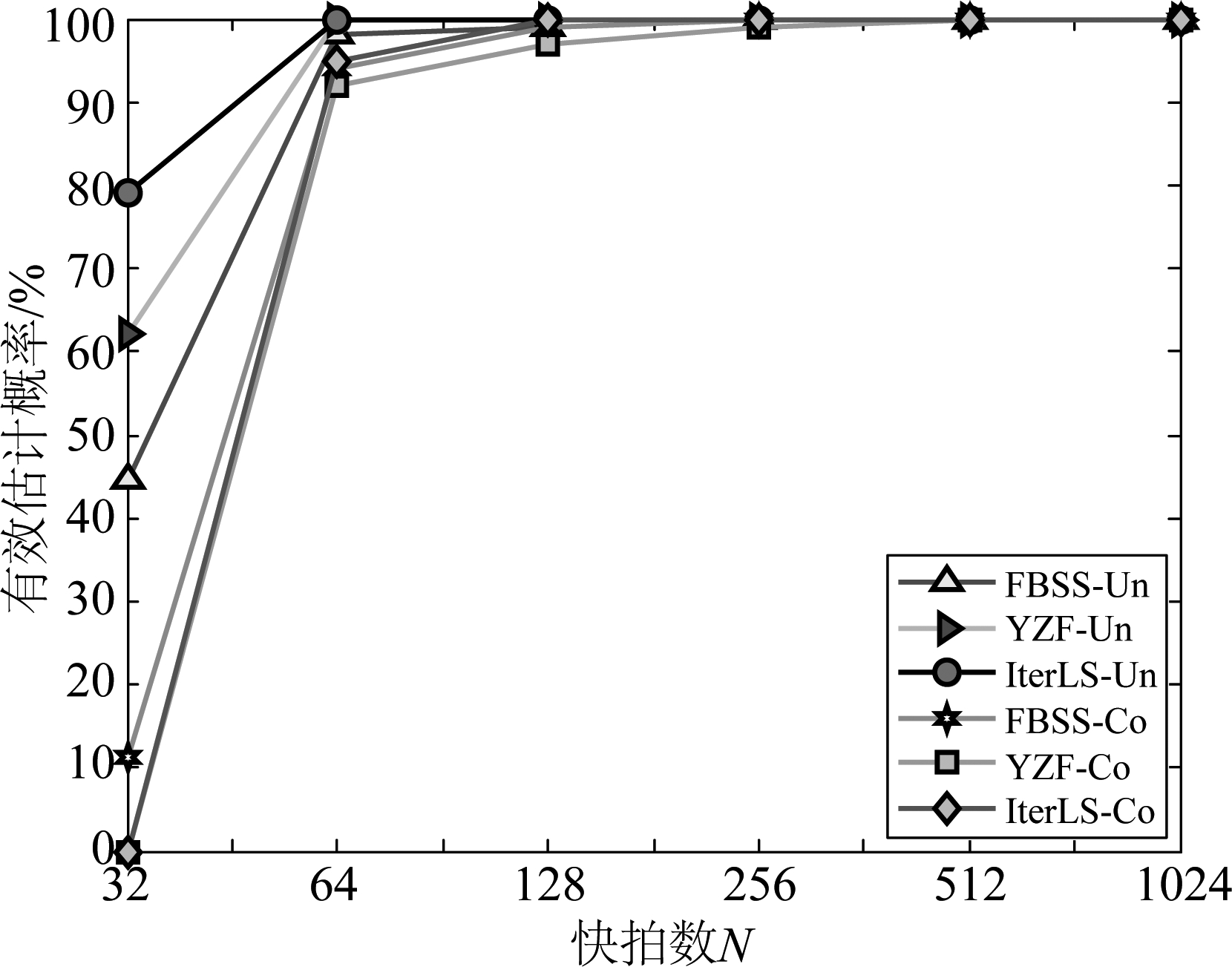
图6 不同快拍数N时有效估计概率
Fig.6 Probabilities of effective estimation versus snapshots
由图5、图6可知:在SNR为0 dB时对于非相关信源测向,YZF算法与本文算法在快拍数大于64时算法RMSE性能迅速接近CRB值,且本文算法略优于YZF算法,有效估计概率接近100%,且两者性能相差较小,而FBSS算法有效估计概率虽然接近100%,但RMSE性能要劣于YZF算法和本文算法。
实验4 非均匀背景下算法RMSE与WNPR关系
假定SNR为0 dB,快拍数为1000,其他仿真条件与实验2相同。定义阵元噪声功率最大值与最小值之比为
...,M,表征了非均匀噪声功率的动态范围。
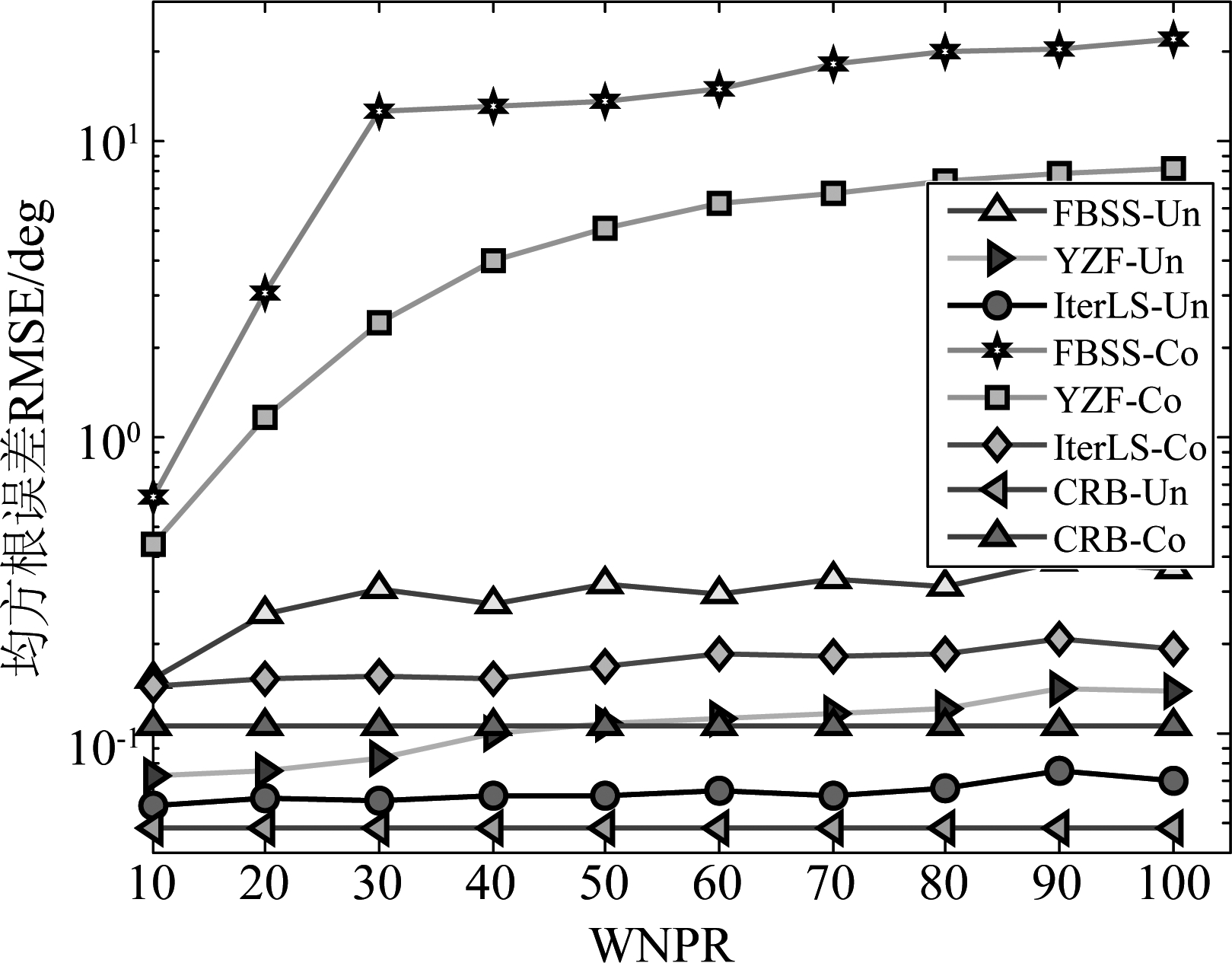
图7 不同WNPR时均方根误差RMSE
Fig.7 RMSE of the DOA estimates versus WNPR
由图7可知,FBSS法、YZF法算法对WNPR值较为敏感,尤其是相干信号测向,随着WNPR增大,测向RMSE值逐渐增大。本文算法对WNPR变化不敏感,即对非均匀噪声具有一定稳健性。
5 结论
针对非相关和相干信源共存时DOA估计问题,本文提出了一种基于迭代最小二乘和空间差分平滑测向算法。该算法利用迭代最小二乘和ESPRIT算法实现非均匀噪声协方差矩阵和非相关信源DOA联合估计；然后基于空间差分平滑技术,利用矩阵重构实现相干信源DOA估计。本文算法具有如下优点:能够实现非均匀噪声背景下混合信号DOA估计,提高了算法在低SNR时DOA估计性能。
[1] Wang J,Xu H,Leus G J T,et al. Experimental assessment of the co-array concept for DOA estimation in wireless communications[J]. IEEE Transactions on Antennas & Propagation,2018,66(6): 3064-3075.
[2] 吴仁斌,井亚鹊,刘展,等.接收多径相干信号的鲁棒自适应波束形成算法[J]. 信号处理,2014,30(4): 470- 476.
Wu Renbin,Jing Yaque,Liu Zhan,et al.Robust adaptive beamforming algorithm for multiplecoherent signals reception[J]. Journal of Signal Precessing,2014,30(4): 470- 476.(in Chinese)
[3] Liu G,Chen H,Sun X,et al.Modified MUSIC algorithm for DOA estimation with nyström approximation[J]. IEEE Sensors Journal,2016,16(12): 4673- 4674.
[4] Chen H,Hou C,Zhu W P,et al. ESPRIT-like two-dimensional direction finding for mixed circular and strictly noncircular sources based on joint diagonalization[J]. Signal Processing,2017,141: 48-56.
[5] Pesavento M,Gershman A B. Maximum-likelihood direction-of-arrival estimation in the presence of unknown nonuniform noise[J]. IEEE Transactions on Signal Processing,2002,49(7): 1310-1324.
[6] Wu Y,Hou C,Liao G,et al. Direction-of-arrival estimation in the presence of unknown nonuniform noise fields[J]. IEEE Journal of Oceanic Engineering,2006,31(2): 504-510.
[7] Liao B,Chan S C. A simple method for DOA estimation in the presence of unknown nonuniform noise[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing.(ICASSP) Brisbane,Australia,Apr,2015: 2789-2793.
[8] Liao B,Chan S C,Huang L,et al. Iterative methods for subspace and DOA estimation in nonuniform noise[J]. IEEE Transactions on Signal Processing,2016,64(12): 3008-3020.
[9] 李小波,张正言,王珽,等. 双基地MIMO雷达相干目标的角度快速估计算法[J]. 信号处理,2016,32(3): 370-377.
Li Xiaobo,Zhang Zhengyan,Wang Ting,et al. DOA estimation of correlated signals based on Rarget rapid location of coherent target for bistatic mimo radar[J]. Journal of Signal Processing,2016,32(3): 370-377.(in Chinese)
[10] Wei J Q,Xu X,Luo D W,et al. Sequential DOA estimation method for multi-group coherent signals[J]. Signal Processing,2017,130: 169-174.
[11] Wen J,Liao B,Guo C. Spatial smoothing based methods for direction-of-arrival estimation of coherent signals in nonuniform noise[J]. Digital Signal Processing,2017,67: 116-122.
[12] Wang Y,Trinkle M,Ng W H. Efficient DOA estimation of noncircular signals in the presence of multipath propagation[J]. Signal Processing,2018,149: 14-26.
[13] Wu X,Zhu W P,Yan J.A toeplitz covariance matrix reconstruction approach for direction of arrival estimation[J].IEEE Transactions on Vehicular Technology,2017,66(9): 8233- 8237.
[14] Han F M,Zhang X D. An ESPRIT-like algorithm for coherent DOA estimation[J]. IEEE Antennas & Wireless Propagation Letters,2005,4(1): 443- 446.
[15] Ye Z F,Xu X. DOA Estimation by exploiting the symmetric configuration of uniform linear array[J]. IEEE Transactions on Antennas & Propagation,2007,55(12): 3716-3720.
[16] Ye Z F,Zhang Y,Xu X,et al. Direction of arrival estimation for uncorrelated and coherent signals with uniform linear array[J]. IET Radar Sonar & Navigation,2009,3(2): 144-154.
[17] Zhang Y,Ye Z,Liu C. Direction-of-arrival estimation for uncorrelated and coherent signals with fewer sensors[J]. Iet Microwaves Antennas & Propagation,2009,3(3):473- 482.
