1 引言
随着无线通信技术的广泛应用,频谱资源日益紧张,而固定的频谱分配方式已很难满足当前无线通信技术发展的需要,因此出现了能够动态使用空闲频谱的认知无线电技术[1]。频谱感知是确保认知无线电系统能够正常应用的关键技术之一,其检测性能的优劣直接影响了电磁频谱的使用效率。
经典的频谱感知方法包括能量检测算法、匹配滤波器检测算法、循环平稳检测算法[2]。能量检测算法计算量小、实现简单、不需要主用户的先验知识,但由于其易受噪声不确定度影响,在低信噪比时检测性能急剧下降。
近年来基于随机矩阵理论的方法逐渐应用于频谱感知。这种方法将协方差矩阵的特征值作为信号的检验统计量,再利用统计特征与门限比较从而实现频谱感知[3]。但是这种方法需要计算特征值及对门限的准确估计[4-5],而门限估计值的精度严重影响着频谱感知的效果。因此,基于机器学习的频谱感知算法逐渐成为了研究的焦点。Yingqi Lu等人[6]首先将原始的N维向量降维到2维,再将其作为K均值聚类(K-means)和SVM算法的输入进行训练,最后利用训练好的分类器进行频谱感知;Xue H等人[7]将协方差矩阵的最大最小特征值之差(DMM)作为特征向量,利用有监督学习中的SVM算法进行频谱感知;Yu-Di Huang等人[8]将次级用户接受到的信号组合成特征向量,利用非平行超平面支持向量机(NP-FSVM)算法进行频谱感知;Thilina,K.M等人[9]提出使用K-means和混合高斯模型(Gaussian Mixture Model,GMM)的非监督学习框架进行频谱感知;Yonghua Wang等人[10]先对接收信号矩阵进行切分与重组,利用新的矩阵构造出不同的特征值用于训练K-means分类器,最终用训练好的分类器进行频谱感知;Vaibhav Kumar等人[11]基于K均值聚类的无监督学习方法,对广义κ-μ衰落信道中协作频谱感知的性能进行了改进。Yi Chen等人[12]首先构造出置信参数,利用人工神经网络预测下一感知周期内各个次级用户的检测概率作为权重,最终利用能量检测算法在决策中心对各个次级用户的感知结果进行加权求和完成感知。但以上机器学习的方法均需构造特征向量,这在一定程度上会造成接收信号原有结构信息的丢失,影响算法性能。
本文针对传统方法中检测门限难以准确估计且在低信噪比时检测性能急剧下降问题,以及机器学习算法需要人为构造特征向量且其构造方式将影响频谱感知的性能的问题,对接收信号进行采样使用长短期记忆网络(Long Short-Term Memory,LSTM)进行学习,提取深层特征,实现频谱感知。该方法无需建立检测统计量以及相应的检测阈值,无需构造特征向量,充分地利用了信号原始信息,仿真结果证明在采样点及次级用户数更少的情况下本文算法性能仍优于对比算法。
2 频谱感知
频谱感知的目的是对频段进行监控,然后通过对接收端信号的成分分析,从而确定该频段是否被主用户(Primary User,PU)占用。从数学角度来看,频谱感知本质上是一个二元分类问题,即:H0情况,检验统计量小于检测门限,认为PU不存在,次级用户(Second User,SU)可以接入授权频段;H1情况,当检验统计量大于检测门限时,判定PU存在,SU不可接入授权频段。其数学模型如下所示:
(1)
其中,s(n)为主用户信号,x(n)表示次用户接收接信号(n=1,2,...,N)在时间n处的采样值,w(n)表示噪声信号,h(n)表示信道增益。
3 数据集
对接收端接收到的原始时间序列x(n)采样,得到N个采样点的序列Xi=[xi1 xi2 ... xiN]1×N(i=1,2,...,M)。为了保留原始数据的时域相关性,按时间对接收信号进行M次的顺序采样,得到数据矩阵(即数据集)X及其对应的标签集Y。于是数据集表示为:

(2)
X对应的标签集为![]() 在下面研究的基于LSTM感知算法中,将得到的数据集X按照7∶2∶1的比例划分为训练数据集、验证数据集、测试数据集。本文仿真所用数据集参考文献[10],参数如表1所示。
在下面研究的基于LSTM感知算法中,将得到的数据集X按照7∶2∶1的比例划分为训练数据集、验证数据集、测试数据集。本文仿真所用数据集参考文献[10],参数如表1所示。
表1 数据集参数
Tab.1 Parameters of data set
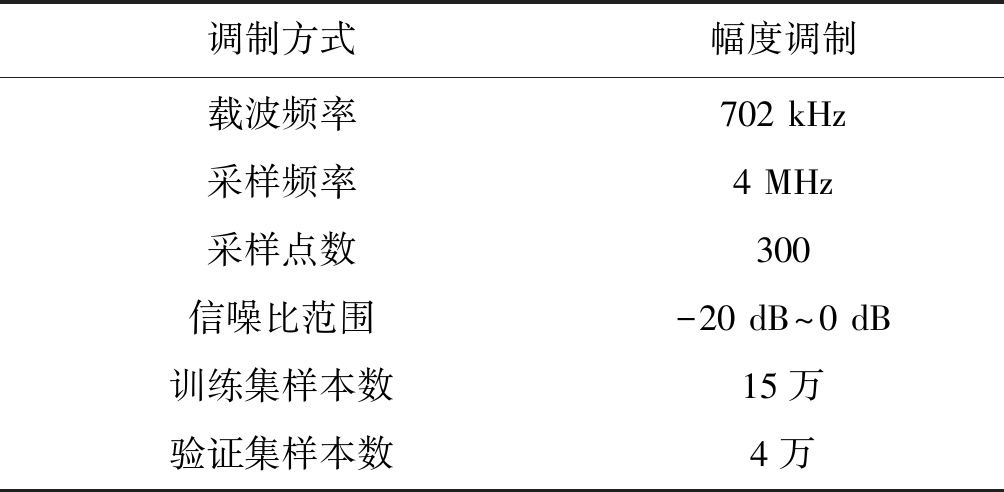
调制方式幅度调制载波频率采样频率采样点数信噪比范围训练集样本数验证集样本数702 kHz4 MHz300-20 dB~0 dB15万4万
4 频谱感知模型
4.1 LSTM神经网络
循环神经网络(Recurrent Neural Network,RNN)为包含循环的网络(如图1),其中循环指图1中对隐藏层A的循环[13],U、W、V分别表示输入层到隐藏层、隐藏层之间以及隐藏层到输出层的权重矩阵。在RNN中当前时刻的信息可以传递给相邻的下一时刻,相比于人工神经网络能更加充分利用到时序信号之间的信息。可见RNN主要有三个特征:
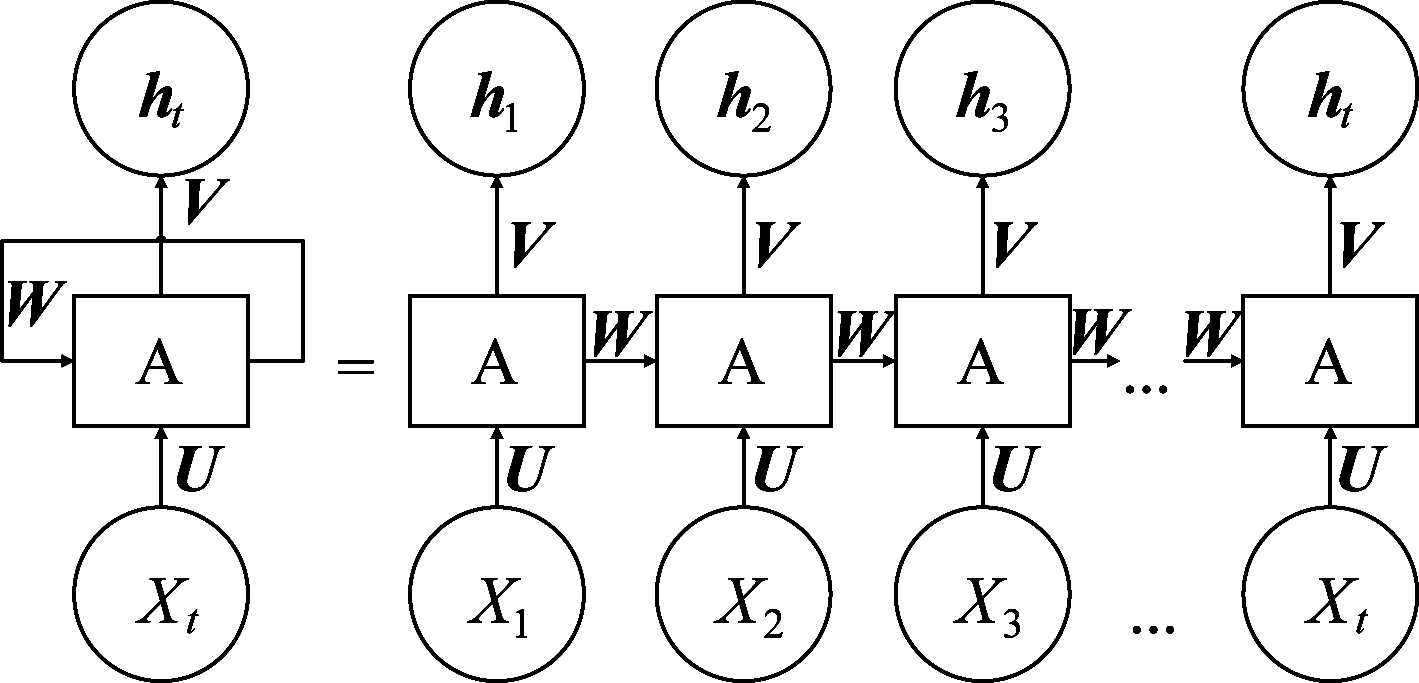
图1 RNN沿时间轴展开
Fig.1 RNN expanded along the time axis
a)时序长度可变。由于计算所用到的权重U、V、W都是共享的,故RNN可以处理任意长度的时间序列,而频谱感知即是对接收端时间序列的处理。
b)考虑时间依赖。计算当前时刻t的隐藏层状态需要当前时刻的输入以及t-1时刻的隐藏层状态,而t-1隐藏层的状态又与t-2时刻有关,以此类推,意味着循环神经网络对过去所有状态都存在着依赖关系,这有利于从接收端序列中提取高维特征进行频谱感知。
c)参数更少。由于RNN的权重是共享的,相比于ANN(Artificial Neutral Network),其参数有了数量级的下降,因此训练时间也更短。
然而,当目标输出与相关输入相隔太长时,网络在训练时就会产生梯度消失或者梯度爆炸问题,使得网络无法利用到很长间隔之前的信息为当前输出做出贡献,即RNN的长时记忆失效。这个问题被称为长期依赖问题[14]。
为了解决长期依赖问题Hochreiter S设计出了LSTM神经网络[15],与普通的RNN相比,LSTM是在标准的RNN的基础上装备了若干个控制级数的门。相当于神经网络(RNN整体)中加入了其他神经网络(门),而这些门只控制级数和信息流动量。图2中LSTM网络中的重复单元A包含四个交互层,以特别的方式进行交互[16]。其中,门本身可以看成一个有物理意义的神经网络,输入是控制依据(如当前时刻的输入xt、上一时刻的隐藏层状态ht-1及上一时刻的记忆细胞状态Ct-1),输出是(0,1)之间的数值,表示该如何调节其他数据的数级的控制方式。门产生的输出会控制其他数据的数级,本质相当于一个过滤器。
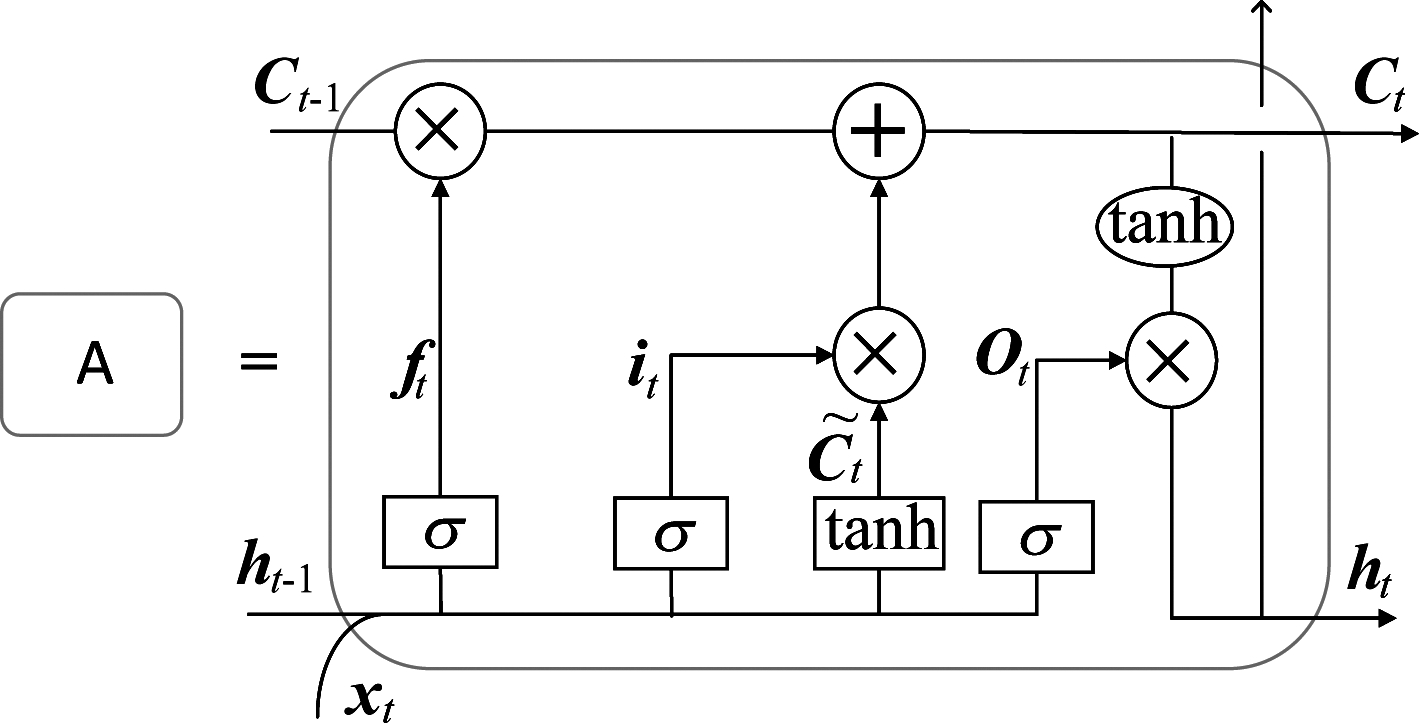
图2 LSTM重复的四个交互层
Fig.2 Four interactive layers of LSTM repeat units
4.2 模型训练
模型的前向传播过程如图3所示。将预处理后的数据作为模型的输入,经过隐藏层提取高维特征,再经过全连接层和Softmax层将模型的输出映射为频谱感知的结果,其中P0表示当前输入样本属于H0的概率,P1表示当前输入样本属于H1的概率。

图3 前向传播流程
Fig.3 The flow of forward propagation
在LSTM中,网络先构建了三个门控制信息的流通量(各自有不同的权重矩阵和偏置),再利用它装备在RNN上控制信息流,根据控制信息流通的地点的不同,它们被分为:
输入门it:控制有多少信息可以流入记忆细胞Ct中。
遗忘门ft:控制着有多少上一时刻记忆细胞Ct-1中的信息可以累积到当前时刻的Ct中。
输出门Ot:控制有多少当前时刻记忆细胞的信息可以流入到当前隐藏层状态ht中。
于是,LSTM单元的数学表达式如下:
门
ft=sigmoid(Wf[ht-1,xt]+bf)
(3)
it=sigmoid(Wi[ht-1,xt]+bi)
(4)
Ot=sigmoid(WO[ht-1,xt]+bO)
(5)
输入转换
(6)
状态更新
(7)
ht=Ot*tanh(Ct)
(8)
式中,*表示向量点乘,[ht-1,xt]表示向量ht-1和xt的拼接,Wf、Wi、WC、WO分别表示不同门中的权重矩阵。
现有n对训练数据{(x(1),y(1)),(x(2),y(2)),...,(x(n),y(n))},前向传播从输入层开始,经过隐藏层、全连接层和Softmax层,将神经网络的输出映射成分类结果,得到最终的映射关系:
(9)
其中,W和b是LSTM中需要训练的参数,分别表示权值和偏置值,![]() 表示x(n)经过LSTM映射后的输出。
表示x(n)经过LSTM映射后的输出。
由于前向传播所得到的结果![]() 与所期望的结果标签y(n)存在误差,本文采用交叉熵作为误差损失函数,其可表示为:
与所期望的结果标签y(n)存在误差,本文采用交叉熵作为误差损失函数,其可表示为:
(10)
为了降低最终预测值与实际值之间的误差损失函数Loss值,利用反向传播算法,逐层优化LSTM中的参数值。在训练时,根据损失曲线以及验证数据集上的准确率来调整当前模型的超参数。
本文所提算法流程如下表2。
表2 算法流程
Tab.2 Algorithm flow

算法1 基于LSTM神经网络的频谱感知算法1.搭建模型并初始化结构参数,设置迭代次数及其他优化超参数。2.输入训练集、验证集,前向传播,计算Loss。3.利用梯度下降法反向传播,计算梯度更新参数,直到迭代结束。4.观察损失曲线、验证集准确率曲线,若不收敛,适当调整模型超参数转向步骤2,若收敛转向步骤5。5.输入测试集,得到频谱感知结果。
5 实验分析
5.1 LSTM结构参数对频谱感知性能影响
本小节旨在通过实验仿真得到LSTM模型中结构参数及学习率(learning rate,lr)对性能的影响来指导后续工作。主用户信号为正弦信号,噪声是均值为0、方差为1的高斯白噪声。通过Matlab仿真生成21万条数据,信噪比为-20 dB~0 dB,正负样本1∶1。将数据集按照7∶2∶1的比例划分为训练集、验证集、测试集。
对输入层神经元节点数(等价于采样点N)、隐藏层层数、隐藏层神经元节点数以及学习率对模型的复杂度以及模型性能的影响进行实验分析。本节迭代次数为2000,学习率采用指数衰减学习率,正则化系数为0.0001,batch_size为256,在验证集、测试集上计算平均准确率,同时对SNR=-10 dB的测试数据计算其检测概率(Detection Probability,Pd)、虚警概率(False Alarm Probability,Pf)。各个参数对频谱感知性能的影响如表3所示。
a)输入层节点数对频谱感知性能的影响
观察表3,对比模型1和2、模型3和4可知,当固定隐藏层层数以及隐藏层节点数时,模型输入层节点数越多,即采样点N越大时,模型准确率和检测概率越高,虚警概率降低。这是由于采样点越多,训练数据集含有越多的原始时间序列的信息,使得模型学习到更好的特征,但输入层节点也不宜过多,否则模型太大难以训练(如模型13,它与模型12相比结构更加复杂但性能相差无几)。
表3 LSTM结构参数对频谱感知性能的影响
Tab.3 The influence of LSTM structural parameters on spectrum sensing performance
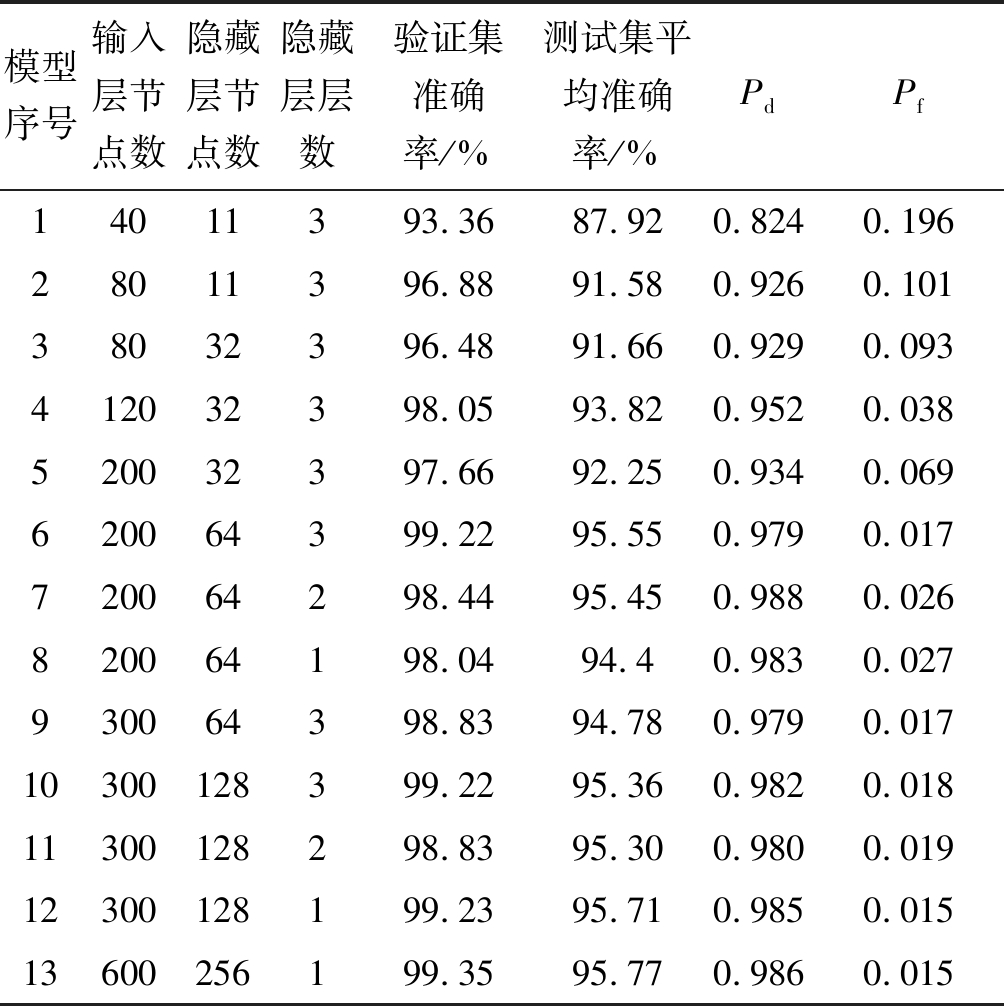
模型序号输入层节点数隐藏层节点数隐藏层层数验证集准确率/%测试集平均准确率/%PdPf14011393.3687.920.8240.19628011396.8891.580.9260.10138032396.4891.660.9290.093412032398.0593.820.9520.038520032397.6692.250.9340.069620064399.2295.550.9790.017720064298.4495.450.9880.026820064198.0494.40.9830.027930064398.8394.780.9790.01710300128399.2295.360.9820.01811300128298.8395.300.9800.01912300128199.2395.710.9850.01513600256199.3595.770.9860.015
b)隐藏层节点数对频谱感知性能的影响
由表3,对比模型4和5、6和9可知,当模型隐藏层节点数‘不合适’时,即使增大了输入层节点数,模型的效果也不会提升,通过模型5和6、9和10的对比进一步说明了模型隐藏层节点数要‘适合’于其他结构参数才有助于模型效果的提升。经过实验,隐藏层节点数在输入层节点数一半附近且为2的整数幂时较为合适。
c)隐藏层层数对频谱感知性能的影响
当固定输入层节点数、隐藏层节点数时,对比编号为6、7、8的模型可知,随着模型隐藏层层数的增多,模型愈加复杂,但是模型的平均准确率、检测概率、虚警概率变化并不明显。增加模型的隐藏层层数模型的拟合能力增强,但是频谱感知的负样本为噪声,增加隐藏层层数会使得模型过拟合训练集中的噪声,在测试集上准确率甚至会降低(如编号为10、11、12的模型)。
d)学习率对频谱感知性能的影响
固定输入层节点数300、隐藏层节点数128、隐藏层层数1、学习衰减率0.96,每迭代20次在验证集上验证一次准确率,不同初始学习率对模型误差及性能影响如图4、图5。
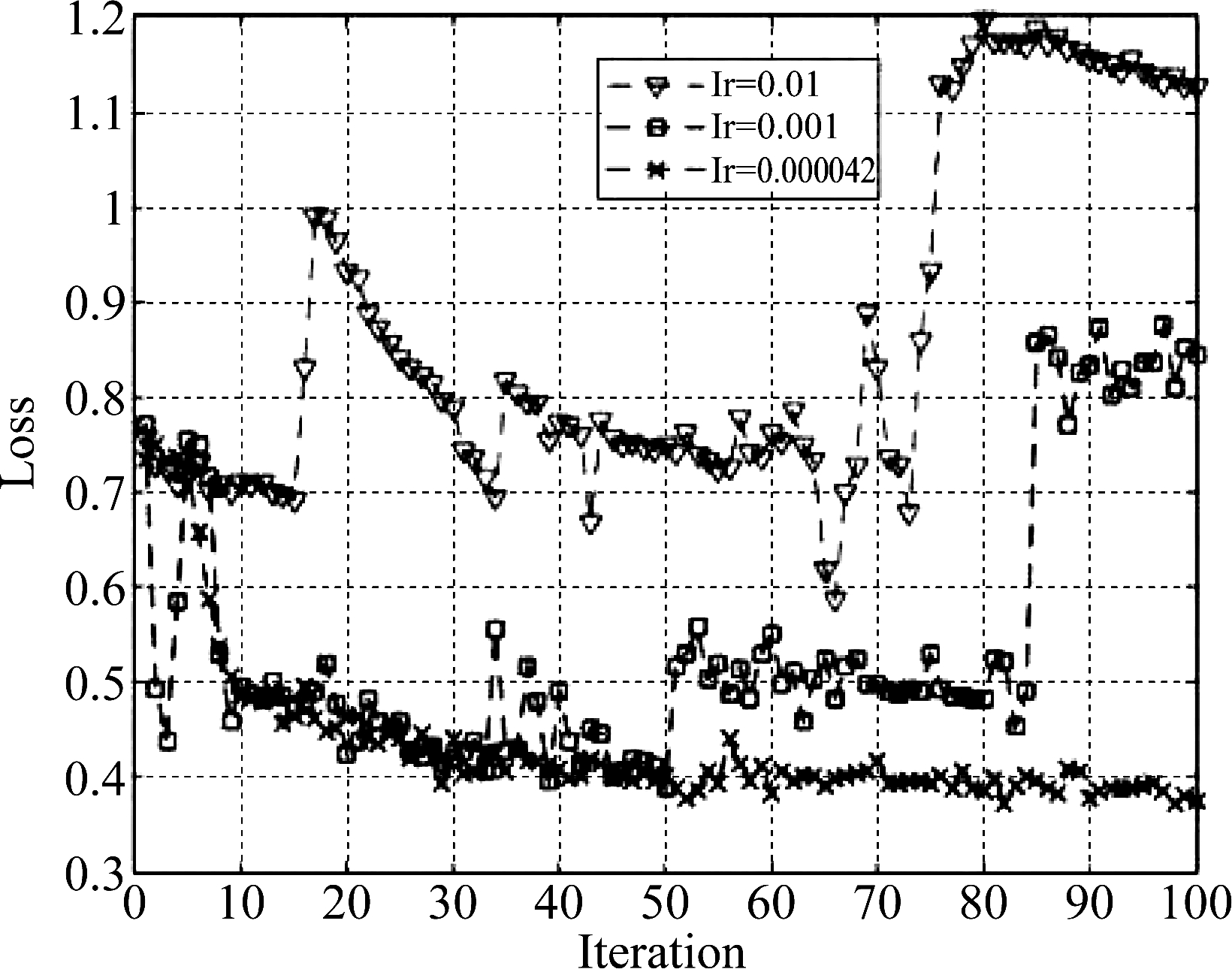
图4 学习率对损失函数曲线的影响
Fig.4 The effect of learning rate on loss function curve

图5 学习率对验证集平均准确率曲线的影响
Fig.5 The influence of learning rate on the average accuracy curve on verification data set
由图4可知,当初始学习率为0.01、0.001时,误差不收敛,相应图5中验证集上的准确率也在震荡;当学习率为42e-6时,图4中模型在迭代600次左右时误差已趋于平稳,相应的图5中准确率收敛在0.95附近。可见,适合于当前模型的学习率不仅能让模型快速收敛,也能让模型达到一个较高的准确率。
e)模型结构对训练时间及测试时间的影响
表4为模型结构参数对训练时间及测试时间的影响,训练数据15万条,测试数据5000条,硬件采用i7- 4790 CPU。由表4可知随着模型隐藏层节点数或隐藏层层数的增加,模型愈加复杂,相应的训练时间及测试时间也随之增加。
表4 模型结构对训练时间及测试时间的影响 Tab.4 The influence of model structure on training time and test time
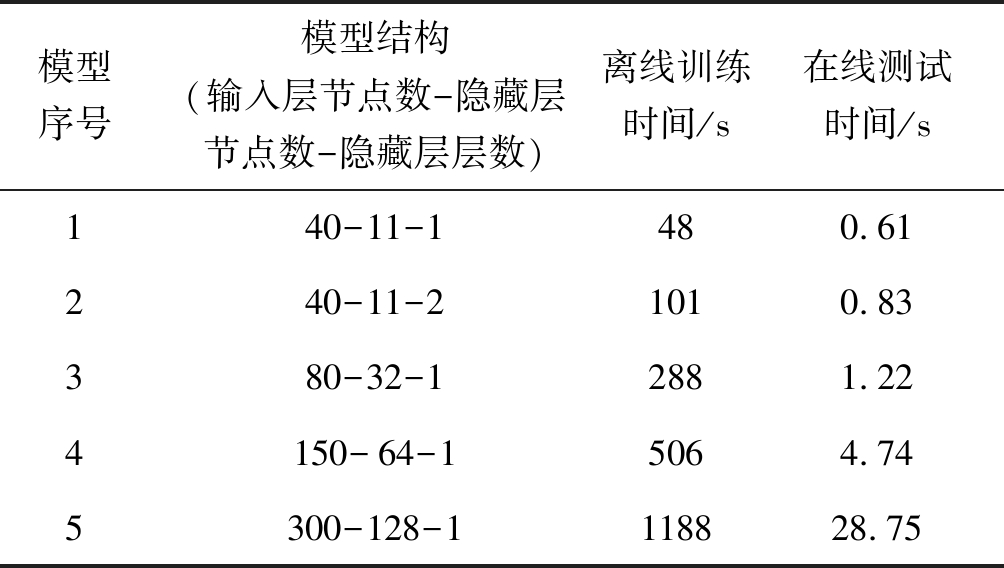
模型序号模型结构(输入层节点数-隐藏层节点数-隐藏层层数)离线训练时间/s在线测试时间/s140-11-1480.61240-11-21010.83380-32-12881.224150-64-15064.745300-128-1118828.75
5.2 算法性能对比
本小节利用5.1节分析结果对所提方法进行仿真,并与文献[10]所提方法、人工神经网络(Back Propagation Neural Network,BPNN)和传统的ED方法进行比较。仿真数据参考文献[10],主用户信号为Matlab仿真生成的幅度调制信号,其载波频率为702 kHz,采样频率4 MHz,不同点在于本文算法及BPNN的采样点和次级用户分别为300和1,文献[10](DAR MSE、DAR MME、DAR DMM、DAR RMET)和ED算法为1000和2。
图6、图7分别为SNR=-11 dB和SNR=-13 dB本文算法与对比算法的ROC(Receiver Operating Characteristic)曲线对比图。从图中可以看出本文算法、文献[10]、BPNN的性能均优于传统的ED算法。在采样点及次级用户数少于对比算法的情况下本文算法的性能仍优于文献[10]中的4种算法,同时文献[10]中4条曲线的性能差异也说明了基于机器学习的算法性能受到特征向量构造的影响。同时在同等条件下本文算法性能也优于BPNN,这是由于LSTM神经网络能更加充分利用时序信号之间的信息,证明了LSTM神经网络在时序信号处理问题上的优势。当信噪比为-11 dB、虚警概率为0.1时,本文算法的检测概率为0.985,而文献[10]的4种算法中最大值为0.934,BPNN为0.8,ED仅为0.565。
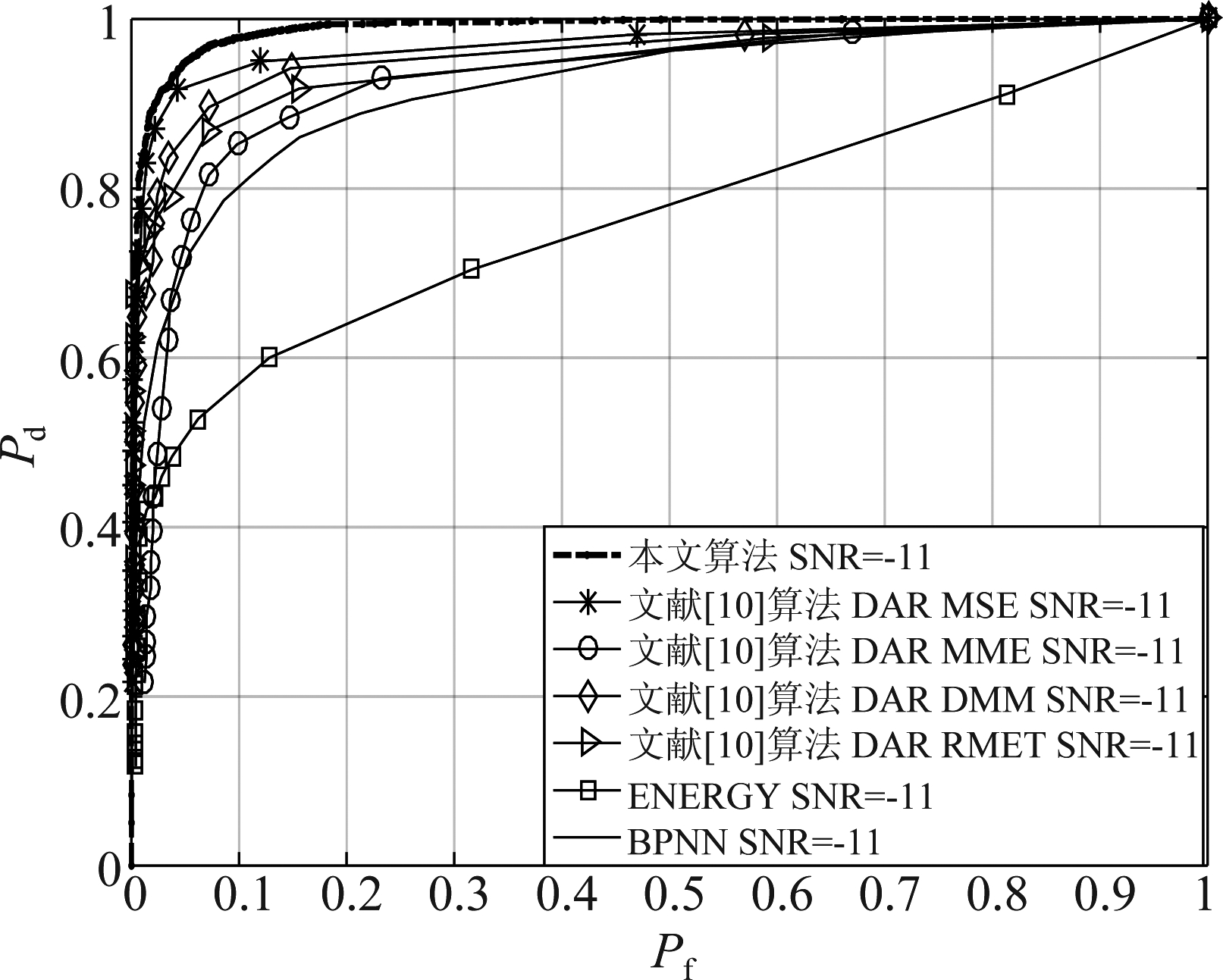
图6 SNR=-11 dB算法性能对比
Fig.6 Comparison of algorithm performance when SNR=-11 dB
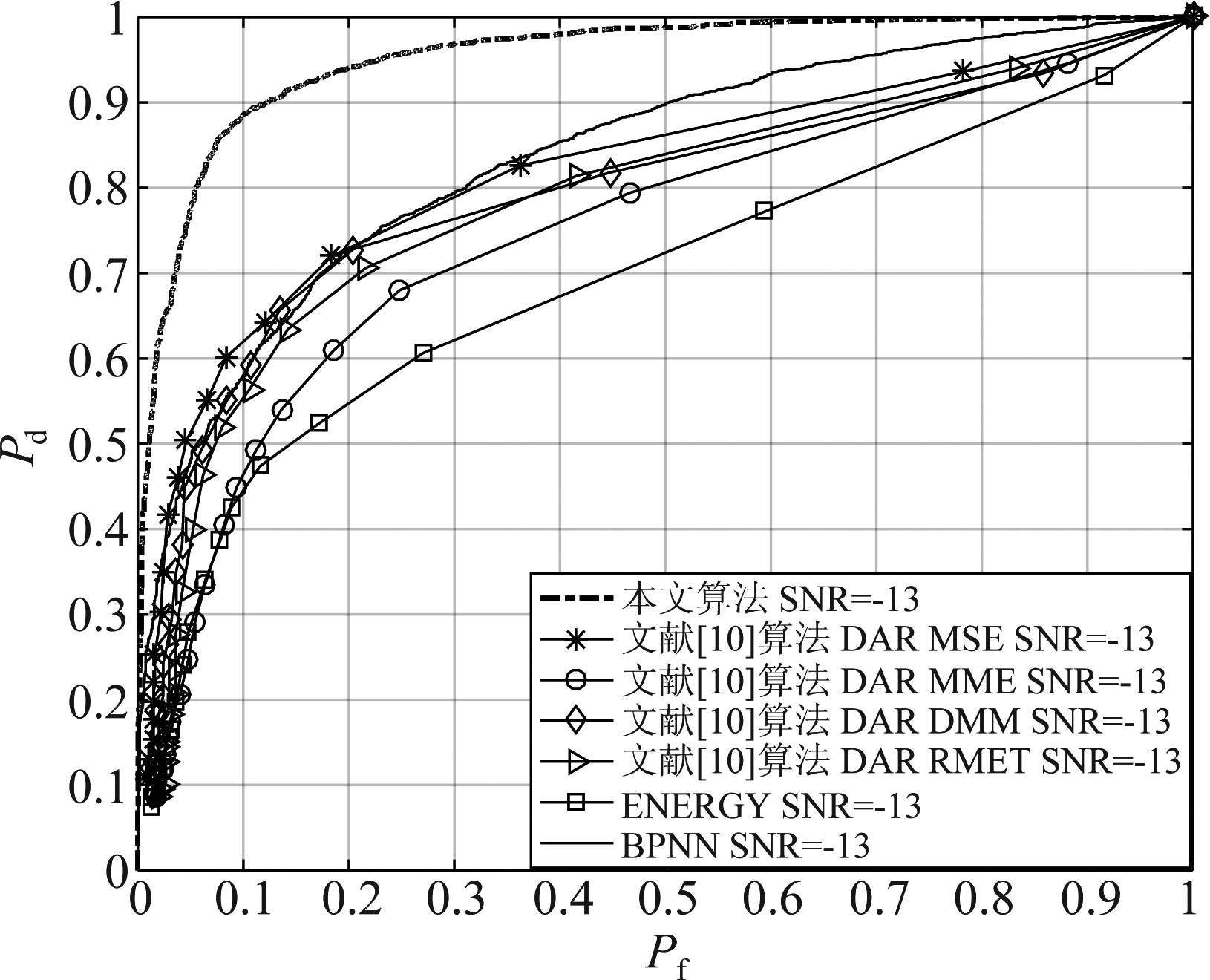
图7 SNR=-13 dB算法性能对比
Fig.7 Comparison of algorithm performance when SNR=-13 dB
图8为主用户信号为BPSK、QPSK时随信噪比变化检测概率的变化曲线,可看出随信噪比的增高检测性能逐步提升。在-10 dB时,本文算法检测概率达到0.9916,同时虚警概率低于0.02,而BPNN及ED算法的检测概率分别为0.8834、0.542。
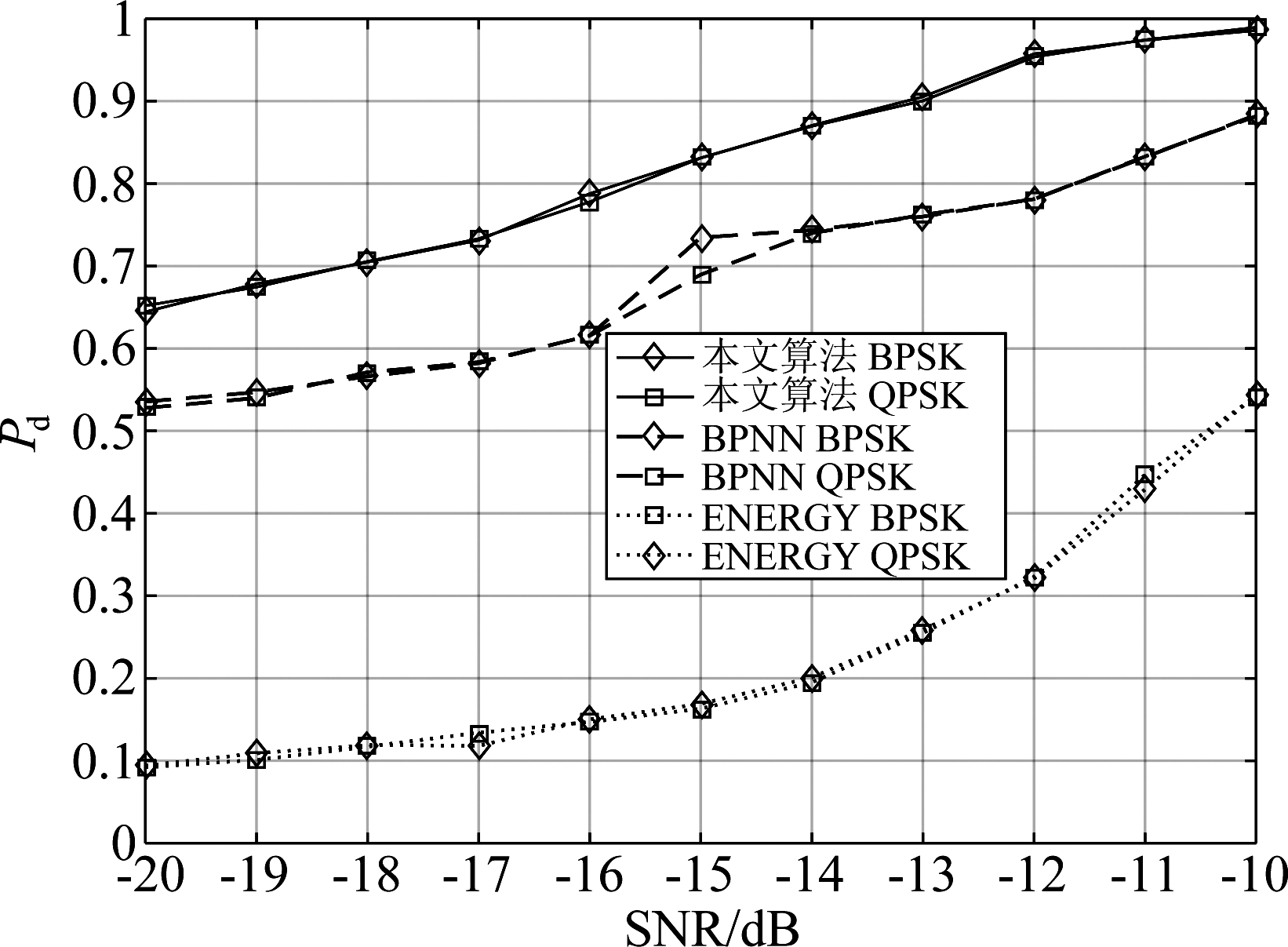
图8 主信号为BPSK/QPSK时检测概率曲线
Fig.8 Detection probability curve when the primary signal is BPSK/QPSK
图9是在SNR=-13 dB时文中所提算法的ROC曲线。不同采样点N算法性能对比。仿真结果证明随着采样点增加检测性能逐步提升。当虚警概率为0.2时,采样点N为40、80、150、300对应的检测概率分别为0.425、0.619、0.802、0.929。
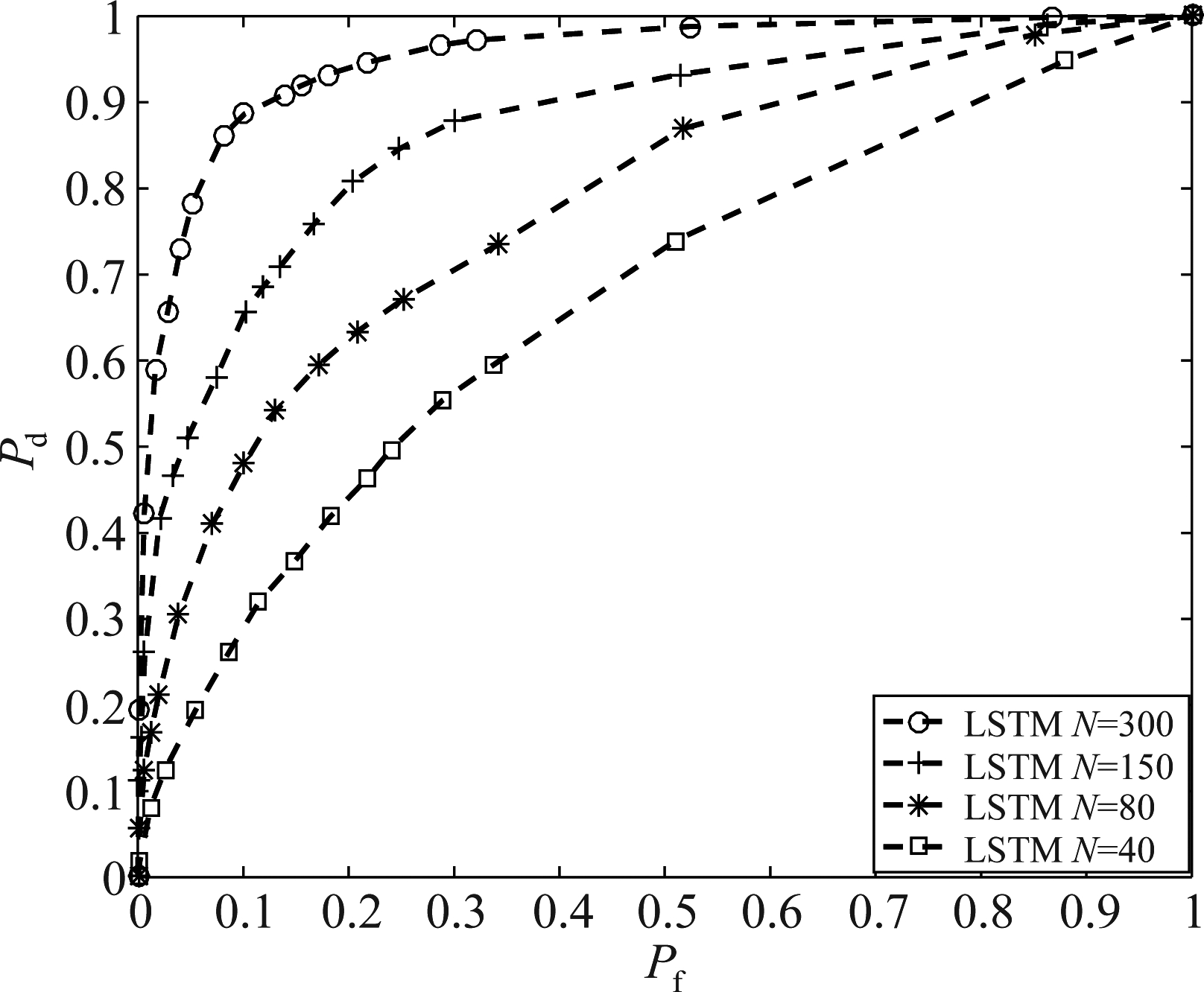
图9 不同采样点N的ROC曲线
Fig.9 ROC curves of different sampling points N
6 结论
本文利用LSTM神经网络在时间序列信号上的天然优势进行建模,从而进行频谱感知。首先将接收信号按时间顺序进行采样,然后通过隐藏层提取高维特征训练LSTM神经网络,最后用训练好的网络进行频谱感知。在仿真和结果分析部分,对文中提出的方法进行了详细的分析,证明了该方法具有较好的性能。
[1] Zhou Xiangwei, Sun Mingxuan, Li Ye, et al. Intelligent wireless communications enabled by cognitive radio and machine learning[J]. China Communications, 2018, 15(12): 16- 48.
[2] Alom M Z, Godder T K, Morshed M N. A survey of spectrum sensing techniques in cognitive radio network[C]∥Proc of 3rd International Conference on Advances in Electrical Engineering. Piscataway, NJ: IEEE Press, 2015: 161-164.
[3] Wael C B A, Armi N, Rohman B P A. Spectrum sensing for low SNR environment using maximum-minimum eigenvalue (MME) detection[C]∥Proc of IEEE ISITIA 2016. Piscataway, NJ: IEEE Press, 2016: 435- 438.
[4] Cardoso L S, Debbah M, Bianchi P, et al. Cooperative spectrum sensing using random matrix theory[C]∥Proc of 3rd International Symposium on Wireless Pervasive Computing. Piscataway, NJ: IEEE Press, 2008: 334-338.
[5] Tulino A M, Verdú S. Random matrix theory and wireless communications[J]. Foundations and Trends® in Communications and Information Theory, 2004, 1(1): 1-182.
[6] Lu Y, Zhu P, Wang D, et al. Machine learning techniques with probability vector for cooperative spectrum sensing in cognitive radio networks[C]∥Proc of IEEE WCNC 2016. Piscataway, NJ: IEEE Press, 2016: 1- 6.
[7] Xue H, Gao F. A machine learning based spectrum-sensing algorithm using sample covariance matrix[C]∥Proc of 10th International Conference on Communications and Networking in China. Piscataway, NJ: IEEE Press, 2015: 476- 480.
[8] Huang Y D, Liang Y C, Yang G. A fuzzy support vector machine algorithm for cooperative spectrum sensing with noise uncertainty[C]∥Proc of IEEE GLOBECOM 2016. Piscataway, NJ: IEEE Press, 2016: 1- 6.
[9] Thilina K M, Choi K W, Saquib N, et al. Machine learning techniques for cooperative spectrum sensing in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(11): 2209-2221.
[10] Wang Y, Zhang Y, Zhang S, et al. A Cooperative Spectrum Sensing Method Based on a Feature and Clustering Algorithm[C]∥Proc of IEEE CAC 2018. Piscataway, NJ: IEEE Press, 2018: 1029-1033.
[11] Kumar V, Kandpal D C, Jain M, et al. K-mean clustering based cooperative spectrum sensing in generalized K-μ fading channels[C]∥Proc of IEEE NCC 2016. Piscataway, NJ: IEEE Press, 2016: 1-5.
[12] Chen Y, Zhang H, Hu H, et al. An Efficient Cooperative Spectrum Sensing Algorithm Based on BP Neural Network[C]∥International Conference on Wireless Communication & Sensor Network. Piscataway, NJ: IEEE Press, 2014: 297-301.
[13] Jin L, Li S, Hu B. RNN models for dynamic matrix inversion: A control-theoretical perspective[J]. IEEE Trans on Industrial Informatics, 2017, 14(1): 189-199.
[14] Kong W, Dong Z Y, Jia Y, et al. Short-term residential load forecasting based on LSTM recurrent neural network[J]. IEEE Transactions on Smart Grid, 2017, 10(1): 841- 851.
[15] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[16] Zhang Z, Yang R, Fang Y. LSTM Network Based on on Antlion Optimization and its Application in Flight Trajectory Prediction[C]∥Proc of 2nd Advanced Information Management, Communicates, Electronic and Automation Control Conference. Piscataway, NJ: IEEE Press, 2018: 1658-1662.



