1 引言
近年来,卷积神经网络(Convolutional Neural Network,CNN)成为计算机视觉领域最流行的技术,它在图像分类问题中发挥着重要的作用[1]。卷积神经网络作为深度学习中一种代表性的算法,具有出色的特征提取能力,已经在多个领域取得了可观的成果,包括人脸识别[2-3],目标检测[4],图像分类[5-7]等。
目前,研究者们针对应用中的实际问题对卷积神经网络做出各种改进,主要包括两种类型,一种是对网络本身的优化。其中,吴慧华[2]等基于传统的softmax损失函数和Island损失函数提出了一种新的基于余弦距离损失函数来指导深度卷积神经网络的学习;郭继昌[5]等提出了基于残差连接卷积神经网络的图像超分辨率重构算法;赵京霞[7]等采用Dropout技术提出一种基于改进的卷积神经网络的乳腺疾病诊断方法有效地防止过拟合现象。另一种是将网络与其他方法结合。其中,付炜[8]等采用随机森林替换卷积神经网络中的softmax层;张辉[8]等将决策树放置到全连接层之后进行精细化数据分类;胡晓依[10]等将卷积神经网络结合SVM搭建适于滚动轴承故障诊断的深度卷积神经网络模型;汪鸿翔[13]等引入高斯核函数提出一种无需训练的简化卷积神经网络跟踪算法。上述方法均在具体问题中展现出优异效果,但第一种类型局限在对模型的优化方面,没有改变网络的传统结构,第二种类型将网络与其他方法训练过程割裂开,没有实现两种方法紧耦合。在前人的研究中,针对核函数与卷积的研究不多,文献[13]虽然提高了效率,但需要提前对样本预处理提取滤波器模板。
鉴于此,本文提出一种核卷积神经网络(Kernel-Convolutional Neural Network, Kernel-CNN)模型,将非线性变换引入卷积过程构成核卷积操作,利用核函数来简化该操作,进一步增强模型特征提取的能力。
2 算法理论
2.1 核函数
分类问题主要表现为非线性模式,线性分类研究大多存在于理论分析中。为解决非线性问题,常需要引入非线性的映射,使映射后的空间出现线性的规律,从而应用线性的理论解决问题。然而,非线性映射的形式较复杂,无法直观地理解,导致分析以及计算难度的增加。
核函数方法是解决非线性模式分析问题的一种有效的方法,在支持向量机中,核函数的使用将低维空间不可分数据映射到高维使得数据线性可分,很多复杂问题分析得以简化。常用的核函数有:线性核函数、多项式核函数、径向基(RBF)核函数以及sigmoid核函数等,这些核函数均在不同应用中取得了较好的效果。通过引入核函数,简化了非线性映射,只需要对核函数进行调整和选择则可以对映射后的空间进行调整。核函数的选取需要满足Mercer定理,不同的核函数以及不同参数的同种核函数都对应着不同的映射空间,决定着不同的非线性问题解决能力[14]。
RBF核函数是所有核函数中应用最广泛的一种,如式(1)所示。
(1)
其中,σ是核半径且σ>0,在实际应用中发现,对于数据没有先验知识的情况,在参数选取合适的情况下,RBF核函数总会取得较好的结果。
2.2 卷积神经网络
卷积神经网络方面的研究经历了相关理论的提出,模型的基本实现以及广泛的应用种种阶段,卷积神经网络是一种前馈型神经网络,主要包括输入层、卷积层、池化层、全连接层和输出层。它目前在图像分类、目标检测等领域取得了较好的应用效果,同时也是学术界关注的焦点之一。卷积层是利用卷积核提取特征,得到特征图,池化层对特征图按照特定的方式降采样处理,减少复杂度同时保留有用的信息,提高网络的鲁棒性,全连接层对前面得到的特征进行分类回归处理,得到分类输出[15]。
3 本文网络模型Kernel-CNN
3.1 网络模型Kernel-CNN
卷积操作在卷积神经网络中扮演着提取特征的功能,会直接影响网络整体性能。核函数在非线性映射中具有重要的作用,避免了维数灾难,不需清楚特征空间中坐标形式,只通过点间的内积便可实现特征空间的映射。其中,RBF核函数是一种作用局部的核函数,特别在参数选取恰当时具有较好的效果,本文通过将非线性映射引入卷积操作构建一种新型的网络模型Kernel-CNN,该网络模型核卷积部分如图1所示。
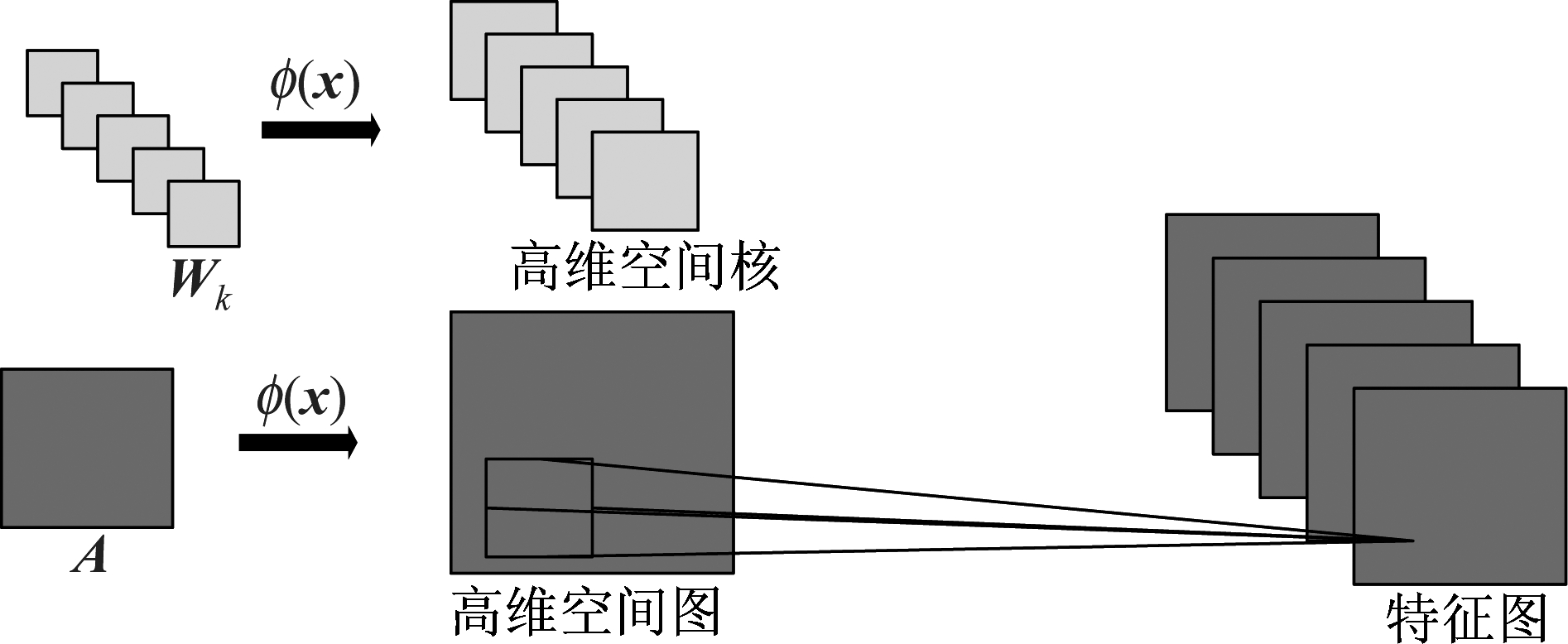
图1 核卷积过程
Fig.1 Kernel convolution process
一些线性不可分的问题可能是非线性可分的,即在特征空间存在超曲面将正负类之间分开。非线性函数可以将非线性可分问题从原始的特征空间映射到高维的希尔伯特空间,从而可转换为线性可分问题[16]。因为映射函数具有复杂的形式,难以计算内积,所以可用核方法,通过核函数以回避内积的显式计算,如式(2)所示。
K(x1,x2)=φ(x1)Τφ(x2)
(2)
核卷积操作是本文提出的一种结合核函数和卷积过程的方法,通过非线性函数实现对原始数据以及核卷积核的映射,提高模型的识别性能。为描述核卷积操作,假设输入数据为矩阵A,其中一个核卷积核为矩阵Wk,k为核卷积核索引号,可将核卷积操作实现过程描述如下:
(1)首先将输入数据按照核卷积核的大小以固定步长划分为m×n个矩阵,划分完矩阵如式(3)所示。

(3)
(2)其次,实现输入矩阵中每个矩阵Aij和核卷积核的点乘和加和运算。将矩阵Aij与核卷积核运算结果表示为cij,如式(4)所示。
(4)
输入数据运算后的结果,如式(5)所示。
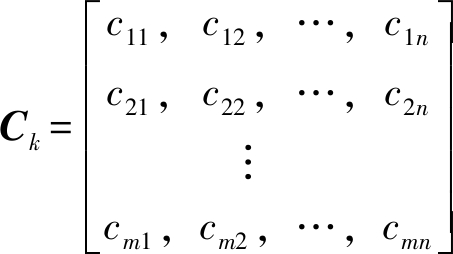
(5)
(3)利用核技巧得到核卷积结果,如式(6)所示。
(6)
然后对核卷积结果进行池化操作,实现特征的降维,再经过全连接层将核卷积层所提取到的特征综合,最终通过softmax函数得到分类模型的概率。
3.2 Kernel-CNN反向传播和参数更新3.2.1 Kernel-CNN反向传播
Kernel-CNN和BP网络一样,均是通过反向传播去调节参数的,最常使用的方法为梯度下降法。反向传播的步骤简单归纳如下:
(1)实现网络的前向传播运算,并且得到每一层每一个节点的输出值;
(2)确定出该网络的损失函数;
(3)在输出层计算出输出和样本值的残差δnl;
(4)分别计算出其他各层各节点的残差δl;
(5)分别求出损失函数对于权值和偏置的偏导数,![]() 和
和![]()
(6)根据梯度下降法更新权值W和偏置b。
3.2.2 Kernel-CNN参数更新
利用网络中各层的残差,使用梯度下降法进行权重和偏置的更新以及调整,多次进行训练后网络的效果便可以达到最优。
根据后层得到的残差,可以推出损失函数对于权重W和偏置b的偏导数计算公式,如式(7)和式(8)所示。
(7)
(8)
在网络的迭代训练过程中,本文使用梯度下降法最小化损失函数,达到对权值W和偏置b的优化,公式如式(9)和式(10)所示。
(9)
(10)
式中,![]() 表示第l层中第i个输入的特征图计算时所使用核变换核,bl为计算第l层特征图时使用的偏置,η为学习率,
表示第l层中第i个输入的特征图计算时所使用核变换核,bl为计算第l层特征图时使用的偏置,η为学习率,![]() 和
和![]() 表示损失函数的偏导数。
表示损失函数的偏导数。
4 实验结果与分析
4.1 实验环境及实验数据
本文实验平台为Intel Core(TM) i5- 3337U CPU @1.80 GHz,内存为8 GB,仿真软件为Matlab R2014b。本文采用包含一个核变换卷积层的Kernel-CNN与含有一个卷积层的卷积神经网络进行对比实验,具体网络结构为输入层,卷积层(核卷积层),池化层,全连接层和输出层。两种对比网络卷积核的尺寸,数量、池化层步长、全连接层神经元数量、激活函数类型以及网络学习率均保持一致。
为验证Kernel-CNN的效果,选用两组官方数据集,第一组数据来自美国麻省理工学院提供的MIT-BIH 心律失常数据库,该数据库包含从47个研究对象采集的共48组双导联记录,本组所有数据均取自MLII导联,信号采样频率为360 Hz,设置心拍模板长度为250个采样点,以R波为中心,向前截取40%RR间期长度,向后截取45%RR间期长度。如果截取点数大于250个采样点,则两边均匀剔除至总数为250个采样点,否则两边均匀补端点值至250个采样点。分别截取了正常搏动、左束支传导阻滞、右束支传导阻滞、室性早搏以及房性早搏五种类型心拍数据,该组数据随机选取心拍共5000个(每种类型心拍1000个),4000个作为训练集(每种类型心拍800个),1000个作为测试集(每种类型心拍200个)。第二组数据MNIST手写数字数据库由250不同人手写数字构成,每张像素均为28×28,数字标签为0到9之间的数,用来描述给定图像里表示的数字,是最流行的深度学习分类数据库之一。该组数据随机选择图像7300张,6000张作为训练集(每类数字600张),1300张作为测试集(每类数字130张)。
4.2 实验评价指标
实验分别选用正确率和迭代过程中的LOSS值作为评价模型的指标。正确率表示预测正确的个数占总预测个数的比率,如式(11)所示。
(11)
式中accuary为正确率,n为该组心拍(数字)预测正确的个数,N为心拍(数字)总预测的个数。
LOSS值表示每次迭代时每个数据预测概率值的对数值的和,如式(12)所示。
LOSS=∑-log(p)
(12)
式中,p为当前数据的预测概率值。LOSS值反映了预测概率值的变化情况,当LOSS值越小时,说明模型预测的越准确。
4.3 实验模型分析
在本文提出的核卷积过程中,使用非线性函数实现了数据从原始的特征空间至高维的希尔伯特空间映射,通过这种非线性变换可得到数据高维的表征。如图2所示,在二维平面上无法线性分类的数据,映射到三维空间可通过一平面将其分开。
通过非线性映射,可直观的理解数据的分类效果。本文模型通过将非线性映射引入卷积操作,利用核技巧简化映射过程,增强了模型的识别性能。因此,本文模型在分类任务中会发挥较好的作用。
4.4 实验结果
(1)第一组数据集实验
第一组数据集中,心拍长度为250个采样点,设置卷积核长度为31个点,卷积核个数为20,隐藏层设为每层50个全连接神经元,学习率为0.001。根据实验确定第二组数据集中Kernel-CNN模型中核变换时σ的取值,不同σ值下预测正确率以及150次迭代后的LOSS值如表1所示。
实验表明,σ逐渐增大,预测正确率均为0.97,测试集上的LOSS值有变化,当σ取值为3.27时,训练集的LOSS值达到最小。因此,第一组数据集在Kernel-CNN中参数σ设置为3.27。
为验证所提模型有效性,使用卷积神经网络和支持向量机两种模型与本文提出模型Kernel-CNN进行对比,支持向量机使用RBF核函数。则卷积神经网络、支持向量机以及本文模型在第一组数据集上的LOSS值和正确率如表2所示。
实验表明,在第一组数据集中本文模型Kernel-CNNσ取值为3.27时,本文模型较好于卷积神经网络和支持向量机。
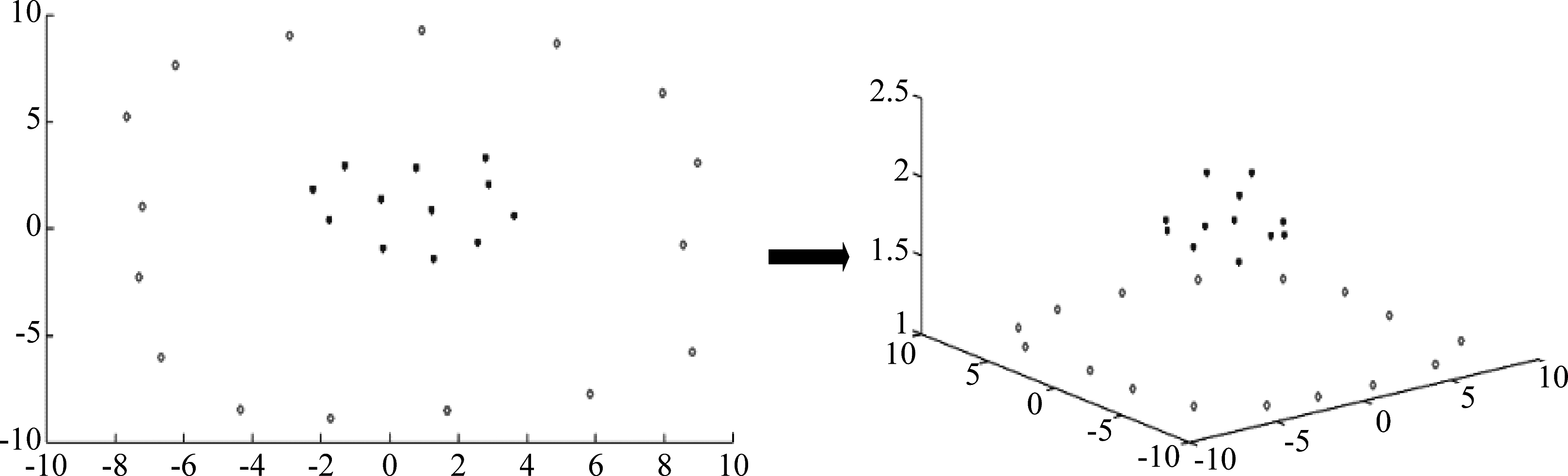
图2 数据高维映射
Fig.2 Data high-dimensional mapping
表1 不同参数σ下Kernel-CNN模型预测正确率和LOSS值
Tab.1 Prediction of correct rate and LOSS value of Kernel-CNN model under different parameters σ
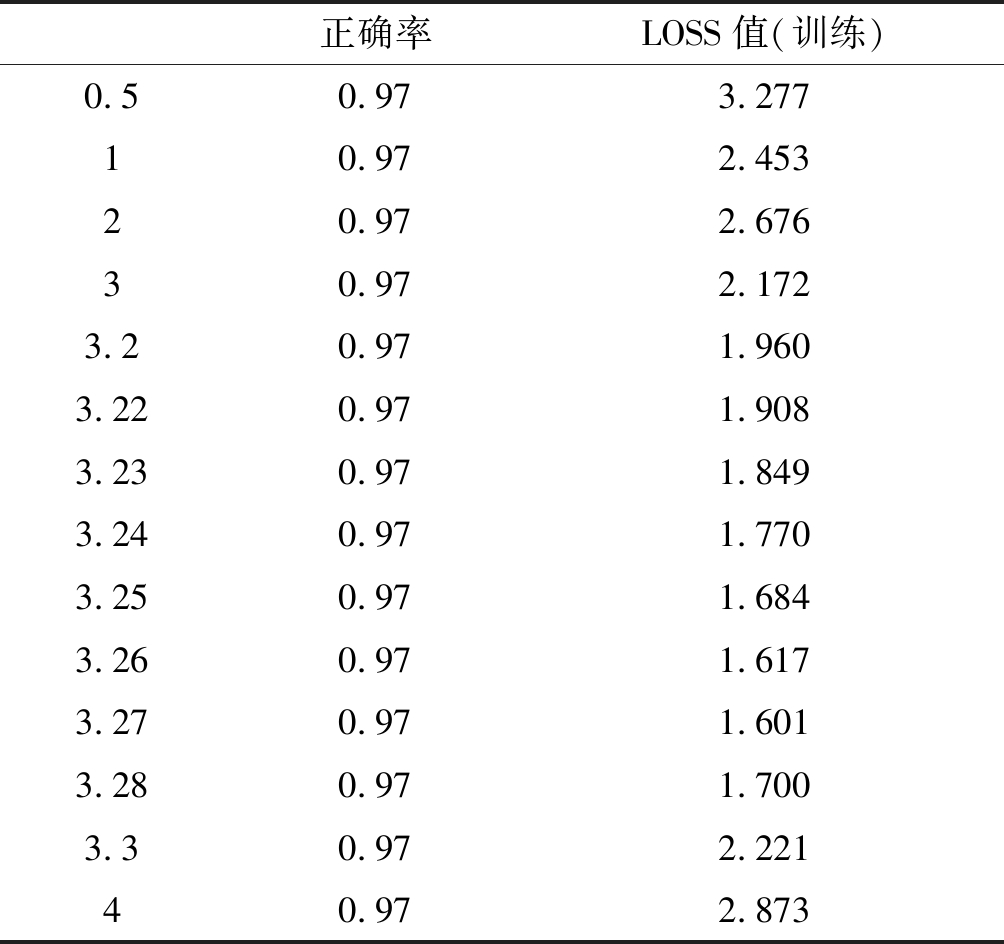
正确率LOSS值(训练)0.50.973.27710.972.45320.972.67630.972.1723.20.971.9603.220.971.9083.230.971.8493.240.971.7703.250.971.6843.260.971.6173.270.971.6013.280.971.7003.30.972.22140.972.873
表2 三种模型在第一组数据集上指标对比表
Tab.2 Comparison of the indicators of the three models on the second set of data sets
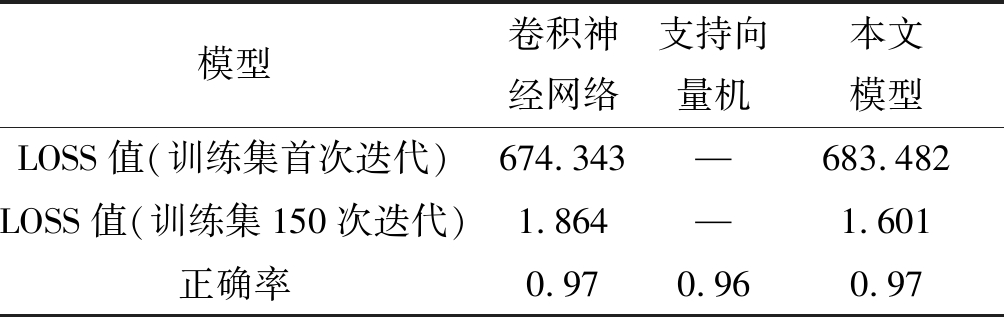
模型卷积神经网络支持向量机本文模型LOSS值(训练集首次迭代)674.343—683.482LOSS值(训练集150次迭代)1.864—1.601正确率0.970.960.97
卷积神经网络和本文模型在第一组数据集训练过程的LOSS值如图3所示。实验表明,两种模型的LOSS值最终都趋于收敛,且收敛效果较好,本文模型在初始迭代与150次迭代后的LOSS值均小于卷积神经网络。
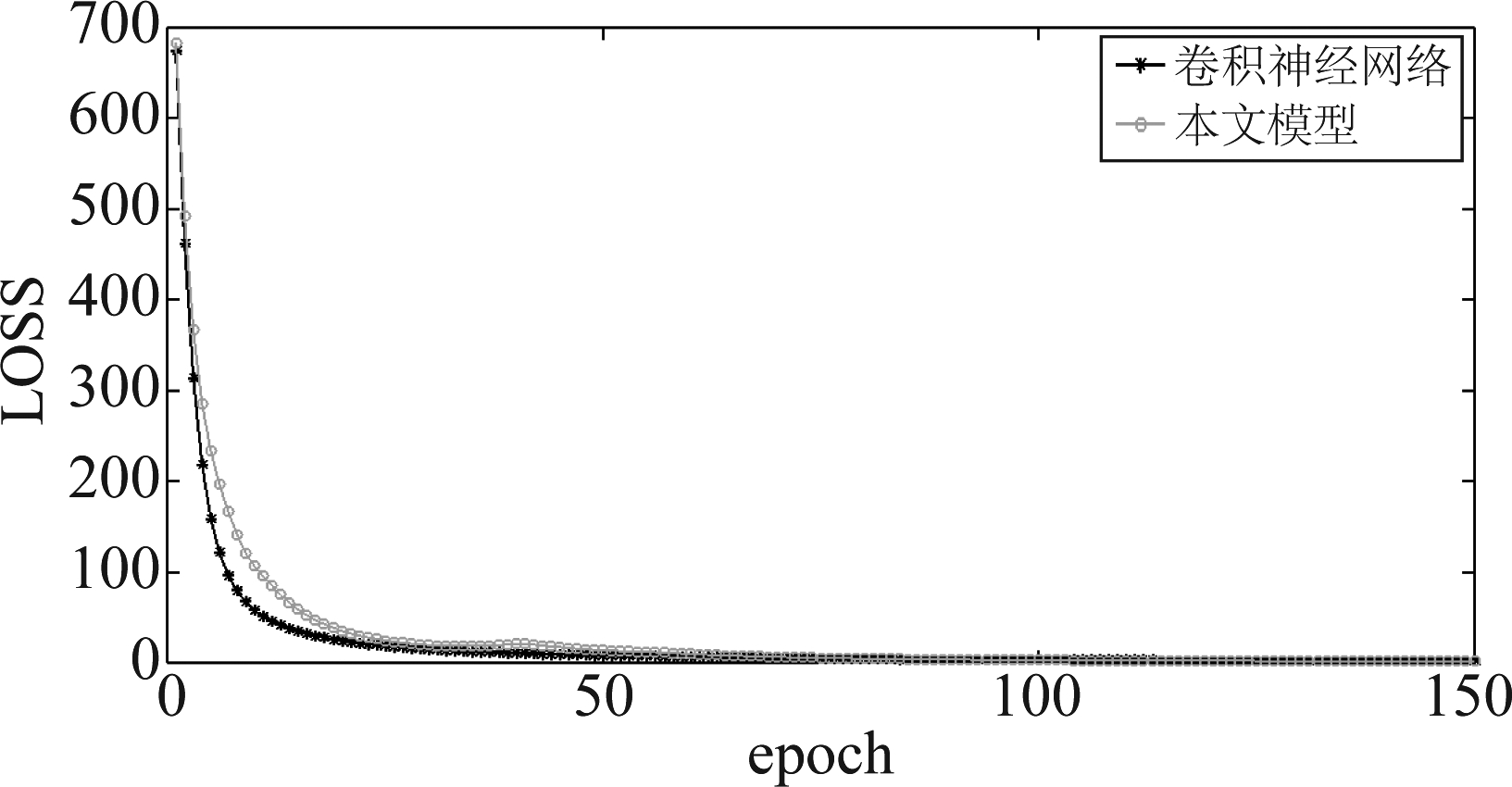
图3 两种模型训练过程LOSS值
Fig.3 LOSS values of two model training processes
两种模型在第一组数据集上训练过程后50次LOSS值如图4所示,由于图3不能清楚观察到两种模型训练后期LOSS值情况,通过绘制两种模型训练过程后50次的LOSS值,可观察到在相同迭代次数时,本文模型LOSS值一直位于卷积神经网络下方,因此本文模型具有较好的效果。
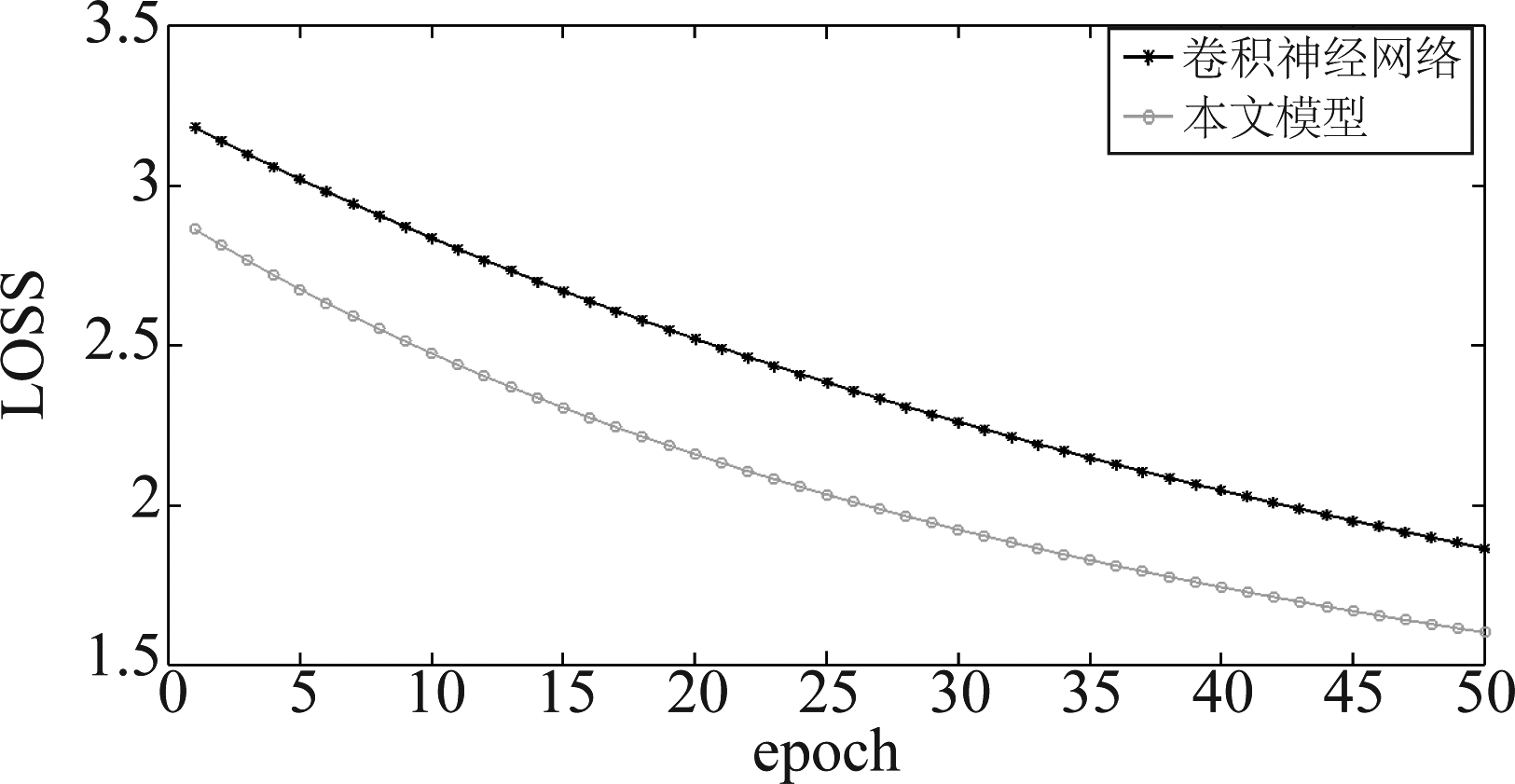
图4 两种模型训练过程后50次LOSS值
Fig.4 The last 50 LOSS values during the training of the two models
(2)第二组数据集实验
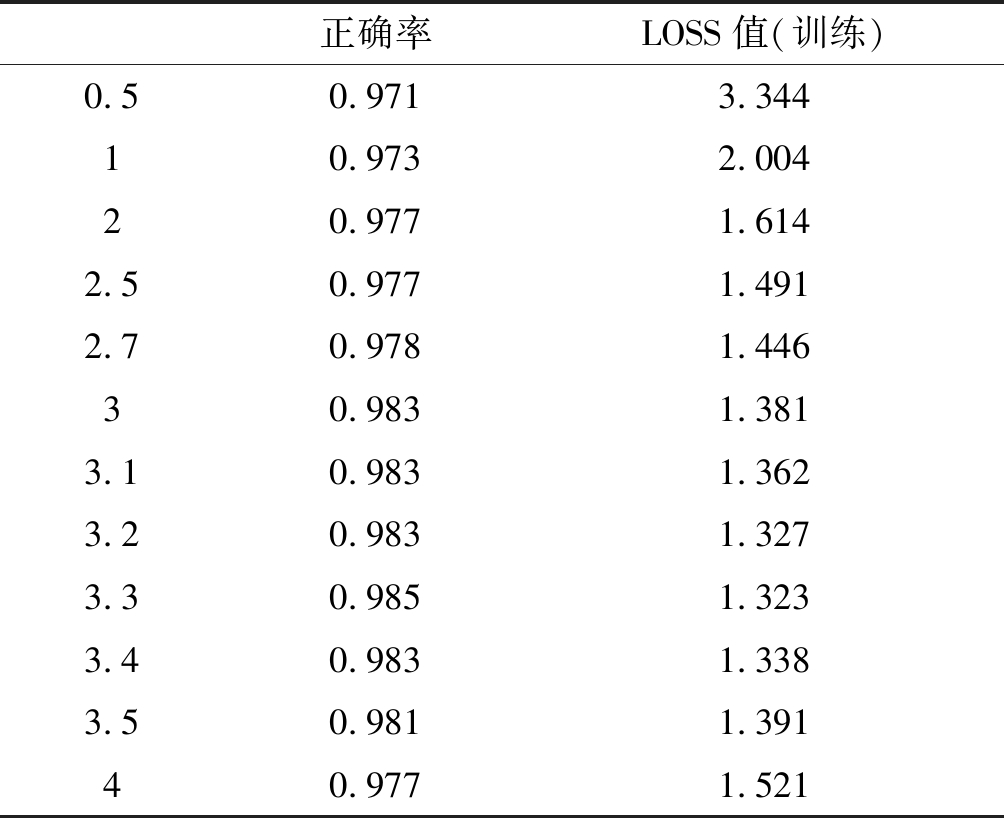
第二组数据集中,图像的像素为28×28,设置卷积核大小为5×5,卷积核个数为20,隐藏层设为每层100个全连接神经元,学习率为0.001。根据实验确定第二组数据集中Kernel-CNN模型中核变换时σ的取值,不同σ值下预测正确率以及150次迭代后的LOSS值如表3所示。
表3 不同参数σ下Kernel-CNN模型预测正确率和LOSS值
Tab.3 Prediction of correct rate and LOSS value of Kernel-CNN model under different parameters σ
正确率LOSS值(训练)0.50.9713.34410.9732.00420.9771.6142.50.9771.4912.70.9781.44630.9831.3813.10.9831.3623.20.9831.3273.30.9851.3233.40.9831.3383.50.9811.39140.9771.521
实验表明,随着σ的增长,正确率和训练集上的LOSS值不断变化,当σ取值为3.3时,正确率达到最大值0.985,此时,训练集上LOSS值最小。因此,第二组数据集在Kernel-CNN中参数σ设置为3.3。
使用卷积神经网络和支持向量机两种模型与本文提出模型Kernel-CNN进行对比,支持向量机使用RBF核函数。则卷积神经网络、支持向量机和Kernel-CNN在第二组数据集上的LOSS值和正确率如表4所示。
表4 三种模型在第二组数据集上指标对比表
Tab.4 Comparison of the indicators of the three models on the second set of data sets
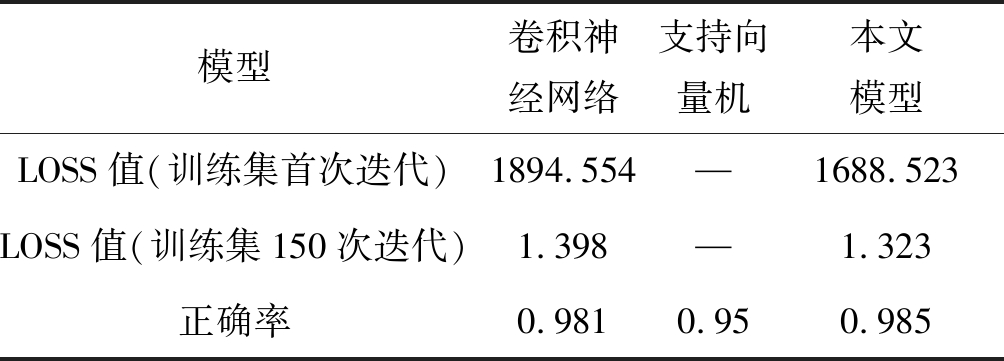
模型卷积神经网络支持向量机本文模型LOSS值(训练集首次迭代)1894.554—1688.523LOSS值(训练集150次迭代)1.398—1.323正确率0.9810.950.985
实验表明,σ为3.3时,经过150次迭代,本文模型相比卷积神经网络和支持向量机具有较好的效果。
卷积神经网络和本文模型在第二组数据集训练过程的LOSS值如图5所示。实验表明,两种模型的LOSS值最终都趋于收敛,本文模型快速收敛阶段较好。
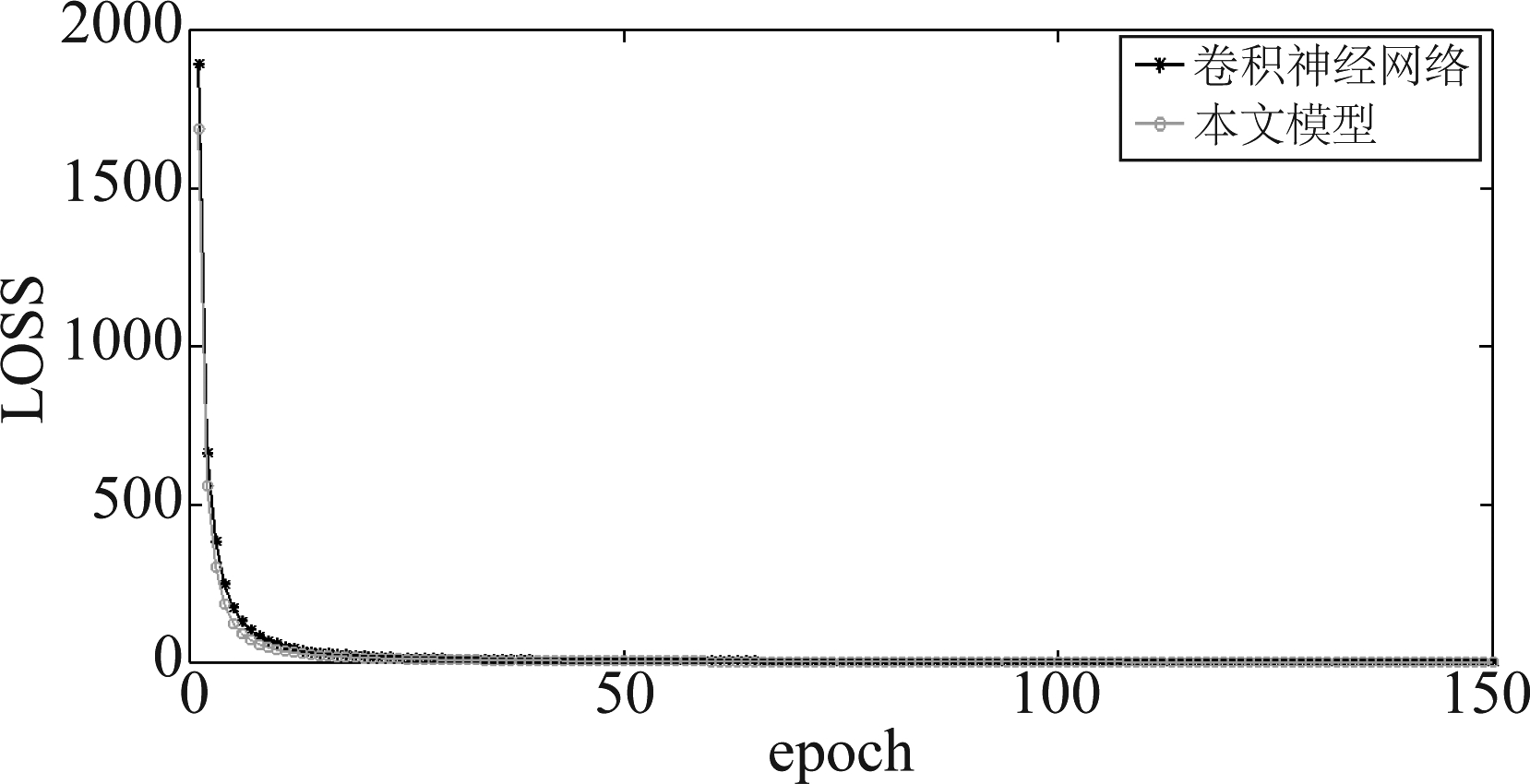
图5 两种模型训练过程LOSS值
Fig.5 LOSS values of two model training processes
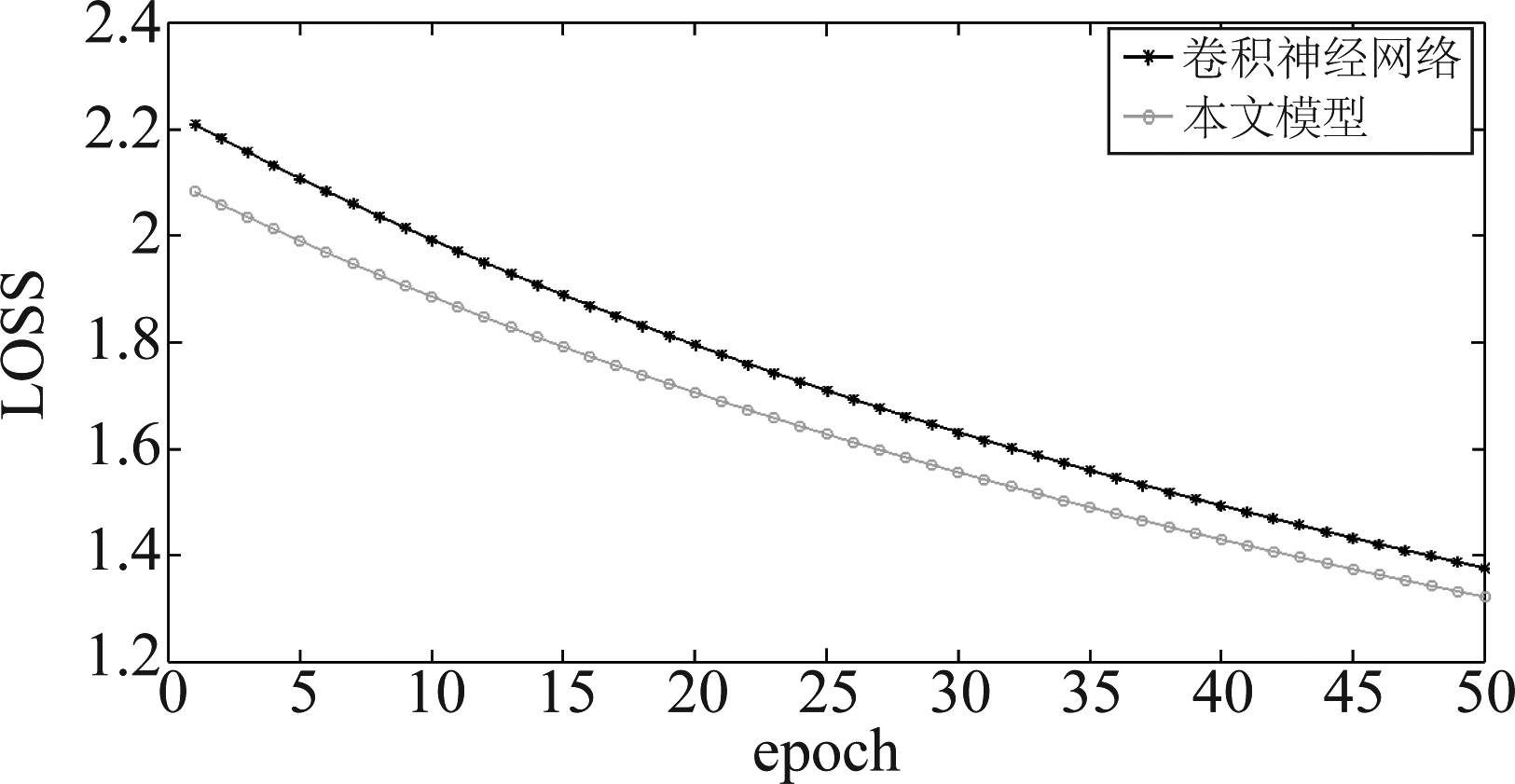
图6 两种模型训练过程后50次LOSS值
Fig.6 The last 50 LOSS values during the training of the two models
两种模型在第二组数据集上训练过程后50次LOSS值如图6所示,鉴于图5不能清晰地观察到两种模型训练后期的LOSS值对比,通过绘制训练过程中后50次的LOSS值,可发现本文模型LOSS值曲线位于卷积神经网络下方,因此本文模型具有较好的效果。
5 结论
本文提出了一种核卷积神经网络模型,该模型在经典卷积神经网络模型的基础上,引入了核函数构成核卷积操作,既保留着经典卷积神经网络出色的特征提取能力,又增加了核变换非线性映射的特点,具有泛化性和鲁棒性。分别采用MIT-BIH心律失常数据库和MNIST手写数字数据库两组官方数据集验证,实验表明,本文模型具有较好的效果。
[1] 董慧妍. 基于机器学习的糖尿病性视网膜病变图像分级研究[D]. 北京: 北京邮电大学, 2019.
Dong Huiyan. Image Classification of Diabetic Retinopathy Based on Machine Learning[D]. Beijing: Beijing University of Posts and Telecommunications, 2019.(in Chinese)
[2] 吴慧华, 苏寒松, 刘高华, 等. 一种基于余弦距离损失函数的人脸表情识别算法[J/OL]. http:∥kns.cnki.net/kcms/detail/31.1690.TN.20190708.1442.008.html.2019-07-08/2019-12-09.
Wu Huihua, Su Hansong, Liu Gaohua, et al. Facial expression recognition algorithm based on cosine distance loss function[J/OL]. http:∥kns.cnki.net/kcms/detail/31.1690.TN.20190708.1442.008.html.2019-07-08/2019-12-09.(in Chinese)
[3] Phillips P J, Yates A N, Hu Y, et al. Face recognition accuracy of forensic examiners, superrecognizers, and face recognition algorithms[J]. Proceedings of the National Academy of Sciences, 2018, 115(24): 6171- 6176.
[4] Cao X, Wang P, Meng C, et al. Region Based CNN for Foreign Object Debris Detection on Airfield Pavement[J]. Sensors, 2018, 18(3): 737-751.
[5] 郭继昌, 吴洁, 郭春乐, 等. 基于残差连接卷积神经网络的图像超分辨率重构[J]. 吉林大学学报:工学版, 2019, 49(5): 1726-1734.
Guo Jichang, Wu Jie, Guo Chunle, et al. Image Super-resolution Reconstruction Based on Residual Connected Convolutional Neural Network[J]. Journal of Jilin University: Engineering & Technology Edition, 2019, 49(5): 1726-1734.(in Chinese)
[6] 杨真真, 匡楠, 范露, 等. 基于卷积神经网络的图像分类算法综述[J]. 信号处理, 2018, 34(12): 1474-1489.
Yang Zhenzhen, Kuang Nan, Fan Lu, et al. Survey of Image Classification Algorithms Based on Convolutional Neural Networks[J]. Journal of Signal Processing, 2018, 34(12): 1474-1489.(in Chinese)
[7] 赵京霞, 钱育蓉, 张猛, 等. 基于改进的卷积神经网络LeNet-5乳腺疾病诊断方法[J]. 东北师大学报: 自然科学版, 2019, 51(2): 65-70.
Zhao Jingxia, Qian Yurong, Zhang Meng, et al. LeNet-5 breast disease diagnosis method based on improved convolutional neural network[J]. Journal of Northeast Normal University: Natural Science Edition, 2019, 51 (2): 65-70.(in Chinese)
[8] 付炜, 杨洋. 基于卷积神经网络和随机森林的音频分类方法[J]. 计算机应用, 2018, 38(S2): 58- 62.
Fu Wei, Yang Yang. Audio classification method based on convolutional neural network and random forest[J]. Computer Applications, 2018, 38(S2): 58- 62.(in Chinese)
[9] 张辉, 王杨, 李昌, 等. 基于深度神经决策森林的体域网数据融合方法[J/OL]. https:∥doi.org/10.19734/j.issn.1001-3695.2019.04.0045.2019-07-09/2019-10-29.
Zhang Hui, Wang Yang, Li Chang, et al. Data fusion method for body area network based on deep neural decision forest[J/OL]. https:∥doi.org/10.19734/j.issn.1001-3695.2019.04.0045.2019-07-09/2019-10-29.(in Chinese)
[10] 胡晓依, 荆云建, 宋志坤, 等. 基于CNN-SVM的深度卷积神经网络轴承故障识别研究[J]. 振动与冲击, 2019, 38(18): 173-178.
Hu Xiaoyi, Jing Yunjian, Song Zhikun, et al. Research on Bearing Fault Identification of Deep Convolution Neural Network Based on CNN-SVM[J]. Journal of Vibration & Shock, 2019, 38(18): 173-178.(in Chinese)
[11] 刘颖, 葛瑜祥. 基于CNN、SVM和迁移学习的轮胎花纹分类[J]. 西安邮电大学学报, 2018, 23(3): 38- 44.
Liu Ying, Ge Yuxiang. Tyre pattern classification based on CNN, SVM and migration learning[J]. Journal of Xi’an University of Posts and Telecommunications, 2018, 23(3): 38- 44.(in Chinese)
[12] Kang J, Park Y J, Lee J, et al. Novel Leakage Detection by Ensemble CNN-SVM and Graph-based Localization in Water Distribution Systems[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4279- 4289.
[13] 汪鸿翔, 柳培忠, 骆炎民, 等. 高斯核函数卷积神经网络跟踪算法[J]. 智能系统学报, 2018, 13(3): 388-394.
Wang Hongxiang, Liu Peizhong, Luo Yanmin, et al. Gaussian kernel function convolutional neural network tracking algorithm[J]. Journal of Intelligent Systems, 2018, 13(3): 388-394.(in Chinese)
[14] 顾晓瑜. 基于支持向量机的声源定位研究[D]. 南京: 南京邮电大学, 2017.
Gu Xiaoyu. Research on Sound Source Localization Based on Support Vector Machine[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2017.(in Chinese)
[15] 李宽. 基于浅层卷积网络的人脸表情识别方法研究[D]. 合肥: 中国科学技术大学, 2019.
Li Kuan. Research on Facial Expression Recognition Method Based on Shallow Convolution Network[D]. Hefei: University of Science and Technology of China, 2019.(in Chinese)
[16] 尹嘉鹏. 支持向量机核函数及关键参数选择研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
Yin Jiapeng. Support vector machine kernel function and key parameter selection research[D]. Harbin: Harbin Institute of Technology, 2016.(in Chinese)



