1 引言
随着深度学习技术的快速发展,人工智能技术与医疗健康领域的融合不断加深,通过卷积神经网络对医学图形进行特征提取,极大地改变了传统医学图像分析[1]。然而深度学习模型的训练通常需要大量数据,由于医学图像的特殊性,很难在实际问题中获取大量医学图像用于提高模型的泛化能力。通过对原始数据采用旋转、平移、缩放、翻转、裁剪等方式做数据增强,从本质上讲,增强后的图像与原始图像并无差别,对模型泛化能力的改善也十分有限[2]。如何产生与真实图像高度逼真但又完全不同的新样本成为了一个挑战和难题。
生成式对抗网络的提出(GAN, Generative Adversarial Networks)[3],为解决这一问题提供了新的思路,通过GAN拟合真实医学图像的分布,从而可以利用生成器输出逼真的新样本。目前,将GAN应用于医疗领域数据增强已经取得了不错的效果。A. Kitchen[4]等人利用DCGAN(Deep Convolutional GAN)[5]用于前列腺病变斑块的新样本生成,实验证明,新样本图像具有与病变斑块相同的粗糙纹理,并通过在隐空间进行线性插值,实现了对两种不同病变形态的平滑过渡;M. Frid-Adar[6]等人利用DCGAN成功地用于肝脏病变组织(囊肿、转移瘤、血管瘤)CT图像的生成,相比于传统仿射变换,通过GAN生成的图像作数据增强在图像分类的准确度上提高7%左右;M. J. M. Chuquicusma[7]在肺结节病变组织生成中,使用DCGAN生成的结节经过图灵测试证实了其生成结节图像的真实性;C. Bermudez等[8]通过具有跳跃连接结构的自编码器对脑部MRI图像首先进行降噪处理,之后通过DCGAN生成的图像无论是病理特征还是图像质量,与真实图像相比都具有较高的相似度。
虽然使用GAN在医学图像地生成上取得了比较好的效果,并且DCGAN相比于原始GAN在生成图像的质量上有明显地提高,但由于DCGAN模型本身存在收敛困难,随着训练的继续进行,极易容易出现模式崩溃等问题,这也在一定程度上阻碍了GAN在医疗领域的应用。因此迫切需要一种新的模型架构可以在相对较少的训练批次内就可以产生质量较高的图像,并兼备稳定性。
针对上述问题,本文对传统的GAN模型进行了如下改进:(1)在判别器模型中使用多尺寸卷积,增加模型的宽度用以提高判别器的特征提取能力;(2)在生成器中添加残差单元[9],增强生成器对真实数据分布的拟合能力;(3)在多尺寸卷积和残差单元中,采用1×1大小的卷积核对输入特征进行降维处理,从而减少巨额参数量引入,降低了模型过拟合的风险;(4)由于在模型训练初始阶段,判别器对真实样本和生成样本的分辨能力较差,无法为生成器提供有效的梯度信息,导致生成器模型训练过程波动较大,通过在训练初期给予判别器更多训练次数的方式,提高判别器早期的辨别能力,增强训练过程;(5)在生成器的卷积层之后添加批量规范层(BN,Batch Normalizaion)[10],判别器采用LReLU(Leaky Rectified Linear Uint)作为激活函数,提升模型的收敛速度以及稳定性。
为验证本文提出算法的有效性,先将模型用于CIFAR-10数据集图像生成,并通过从IS(Inception Score)[11]和FID(Fréchet Inception Distance)[11]两个角度对多种不同类型GAN在训练过程中产生图像的质量与多样性进行定量与定性的分析。最后将模型应用于胸部X射线图像的生成,为客观评判生成图像质量,对两位具有多年从业经验的放射科医师进行视觉图灵测试,测试结果证实,利用本文提出的算法,可以在很短的训练批次内就可以输出较高质量的图像,并且在组织器官的纹理特征上与真实图像相比也有很高的相似度。
2 快速收敛的生成式对抗网络
2.1 生成式对抗网络
GAN的模型结构[12]如图1所示,由生成器模型和判别器模型两部分所组成,其中生成器通过输入的随机噪声输出满足真实数据分布的新样本,而判别器则需要准确的判断样本的来源。当判别器无法正确的分类样本来源时,可以认为生成器和判别器之间达到纳什均衡[13],生成器可以输出满足真实样本分布的新样本。
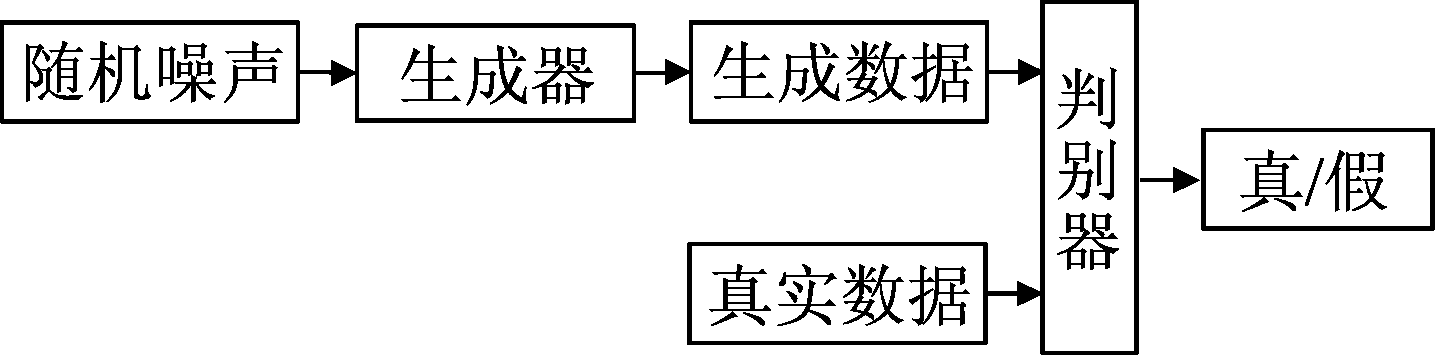
图1 生成式对抗网络的模型
Fig.1 Generative adversarial networks model
GAN设计之初的模型优化函数可以表示为:
![]() Ez~Pz{log[1-D(G(Z))]}
Ez~Pz{log[1-D(G(Z))]}
(1)
其中Pdata为真实数据集的分布,Pz为噪声数据的分布,E(·)为计算的期望值,G(z)表示生成器生成图像。此函数的目的就是在于当真实数据集通过判别模型时可以得到较高的分数,但当噪声形成的图像经过判别模型时,则会有较低的分数。由此区分真实数据和噪声数据,并不断促使生成器输出满足真实数据分布的新样本。
2.2 快速收敛的生成式对抗网络
本文通过增加判别器宽度和生成器深度的方式,提升GAN模型整体的表现力,并在训练的初始阶段,针对判别器无法为生成器提供有效的梯度信息问题,通过预训练判别器,加快生成器对真实数据分布的拟合过程。在增加判别器宽度方面,使用多尺寸卷积的方式,提高对不同尺寸特征的提取能力,记多尺寸卷积模块为Muti-size Conv,在增加生成器深度方面,参考He等人提出的残差网络(ResNet)的思想,在生成器中加入残差单元,减轻模型由神经元网络深度增加所引发的模型退化问题,记残差单元为Residual Unit,并且生成器模型中批量规范化方式的引入,不仅加快了模型收敛速度,还在一定程度上提高了模型训练的稳定性。通过在判别器和生成器中使用不同的激活函数,经过多次实验证明,除判别器和生成器最后一层卷积的激活函数,其余卷积层后判别器使用LReLU,生成器使用ReLU的搭配生成图像的质量最优。
2.2.1 判别器结构
在判别器的网络结构中,通过使用多尺寸卷积增加判别器模型的宽度,用以增强了判别器对特征的提取能力,提高了对真实数据与虚假数据的判别准确率,相比于单尺寸卷积层,多尺寸卷积能够利用不同大小的卷积核,以提取不同尺度的特征,并通过使用1×1大小的卷积核,降低特征图的维度,以及通过两个较小的卷积核叠加代替较大卷积核的方式,减少参数的引入。由于在判别器中使用批量规范化层,会受到每批次数据不同分布带来的影响,会破坏Lipschitz连续性的条件,因此在判别器模型中,不添加规范化处理,以保证判别器Lipschitz连续性的条件。

图2 多尺寸卷积模块
Fig.2 Multi-size convolution module
判别器的多尺寸卷积结构如图2所示。每个多尺寸卷积结构有三个通道,并且每个通道都先经过1×1大小的卷积核降低特征维度,第一个通道在经过降维处理之后,使用两层卷积核大小为3×3的卷积层叠加来获取更大的感受野,第二个通道降维后使用一层卷积核大小为3×3的卷积层,第三个通道仅使用降维处理,而不在添加额外的卷积层。最后,将三个通道的在特征图方向上进行叠加后输出。在判别器的激活函数选择上,选用LReLU作为激活函数,LReLU是ReLU的一种变体,激活函数定义如公式(2)所示,和ReLU不同的是,当神经元没有被激活时也可以获取一定的梯度信息,从而减少了静默神经元的出现。α为负半轴的斜率,在本次实验中α的取值为0.2。
(2)
判别器具体参数设置如表1所示。判别器的输入图像的维度为32×32×3,通过归一化方式,将图像的像素大小由0~255归一化到-1~1之间。输入数据先经过步长为2的卷积层,将输入图像的尺寸下采样至16×16×32,之后通过两个多尺寸卷积模块与两个卷积步长为2的卷积层,将图像的尺寸进一步下采样为4×4×128,最后使用卷积核大小为4×4的卷积层,将特征图的尺寸压缩到1×1×1后输出。
表1 快速收敛GAN判别器参数
Tab.1 Fast convergence GAN discriminator parameters
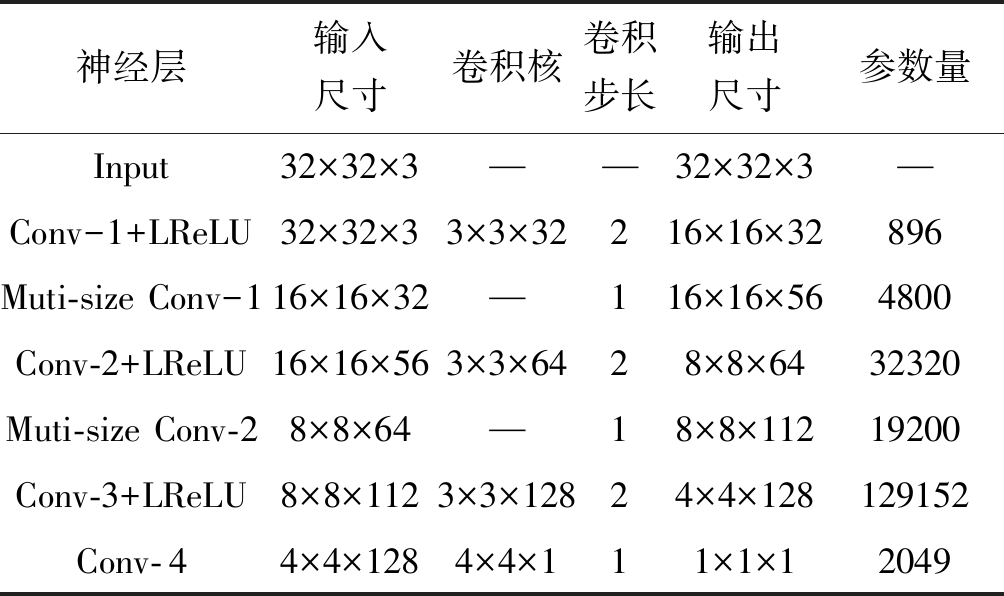
神经层输入尺寸卷积核卷积步长输出尺寸参数量Input32×32×3——32×32×3—Conv-1+LReLU32×32×33×3×32216×16×32896Muti-size Conv-116×16×32—116×16×564800Conv-2+LReLU16×16×563×3×6428×8×6432320Muti-size Conv-28×8×64—18×8×11219200Conv-3+LReLU8×8×1123×3×12824×4×128129152Conv-44×4×1284×4×111×1×12049
2.2.2 生成器结构
生成器中的残差单元结构如图3所示。在生成器的每个残差模块中,一共含有三个反卷积层,第一层卷积使用1×1卷积核对输入特征进行降维处理,用以减少参数量的引入,第二层以及第三层反卷积皆采用3×3卷积核,并且三层反卷积步长全部设置为1,通过对输入图像的边缘进行填充(padding),从而避免因反卷积而引起图像尺寸的改变,同时非线性神经元层数的增加使得生成器可以捕捉到更多图像的细节。最后每经过一个残差单元,通过步长为2的反卷积层进行上采样。
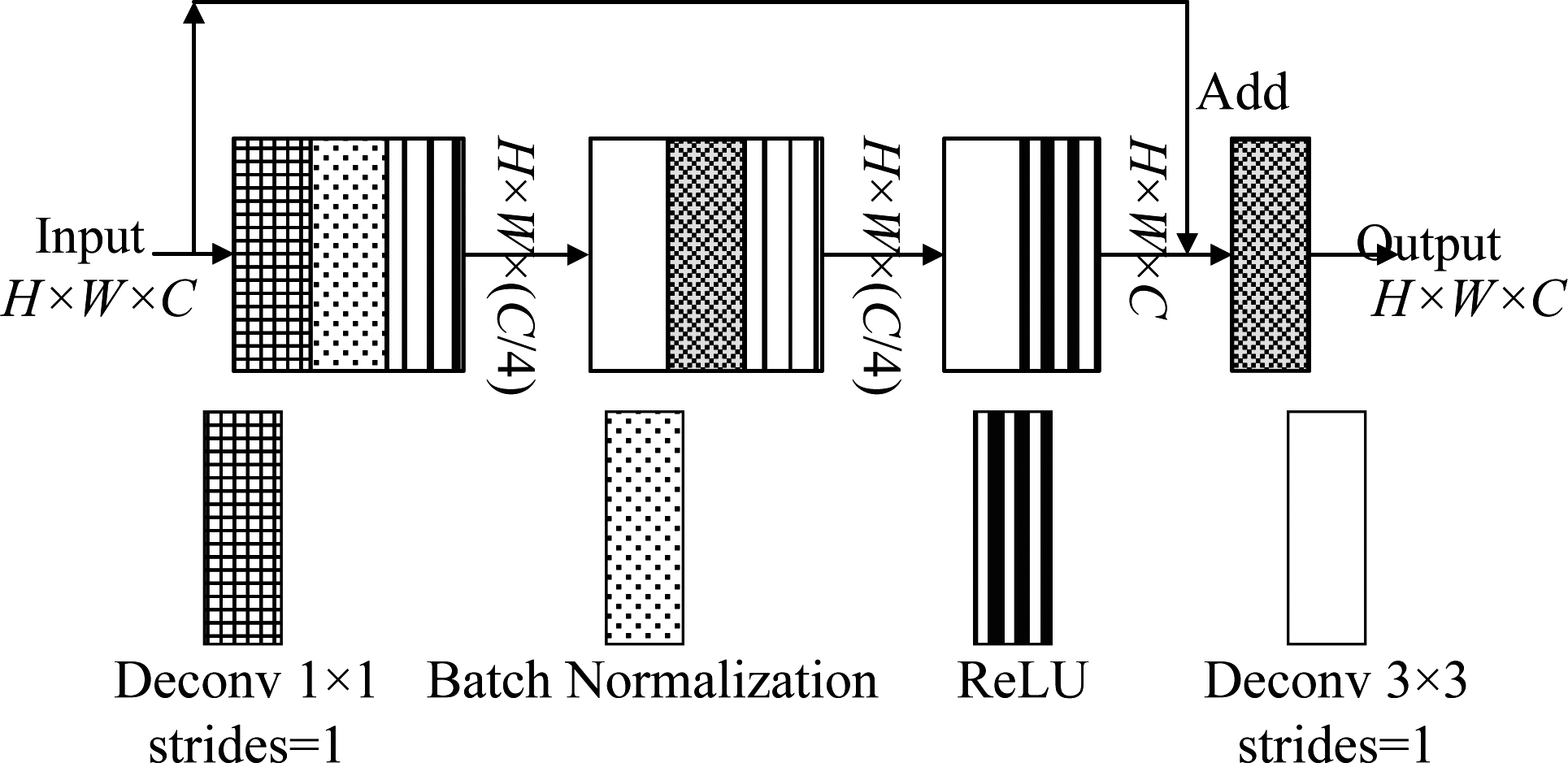
图3 残差单元结构图
Fig.3 Residual unit structure diagram
由于在反卷积层之后添加了批量规范化层确保了模型传播有效的梯度信息,通过对输入数据进行批量规范化处理加速生成器拟合真实数据分布的过程。在生成器的激活函数选用整流线性单元(ReLU,Rectified Linear Uint)[14]作为激活函数,相比于Sigmoid和Tanh激活函数,ReLU由于计算复杂度较低,因此具高效的反向传播速度,而且ReLU作为一种稀疏激活函数也在一定程度上减轻了生成器出现过拟合情况的发生。
生成器具体参数设置如表2所示。通过向生成器输入维度为1×1×128的随机噪声,先通过4×4卷积核的反卷积层将噪声维度上采样至4×4×128,其中4×4表示特征图的尺寸,128表示特征图的维度;随后通过两个残差单元和两个步长为2的反卷积层,将图像的特征维度进一步上采样到16×16×32,最后通过反卷积步长为2的反卷积层,将特征转换为32×32×3大小,并通过Tanh激活函数后输出。
表2 快速收敛GAN生成器参数
Tab.2 Fast convergence GAN generator parameters
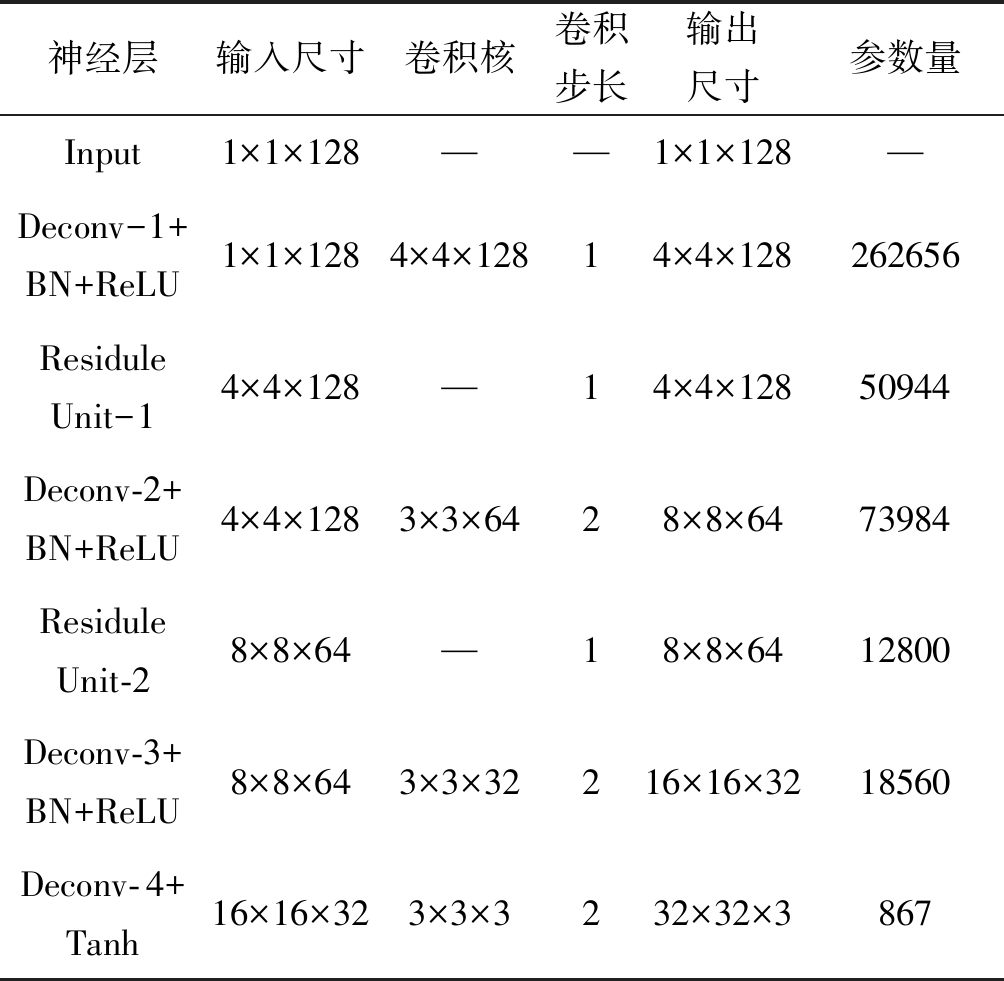
神经层输入尺寸卷积核卷积步长输出尺寸参数量Input1×1×128——1×1×128—Deconv-1+BN+ReLU1×1×1284×4×12814×4×128 262656Residule Unit-14×4×128—14×4×128 50944Deconv-2+BN+ReLU4×4×1283×3×6428×8×64 73984Residule Unit-28×8×64—18×8×64 12800Deconv-3+BN+ReLU8×8×643×3×32216×16×32 18560Deconv-4+Tanh16×16×323×3×3232×32×3867
2.2.3 模型损失函数
原始的损失函数当判别器近似最优的情况下,优化生成器的损失函数,近似等于最小化Pdata和Pz之间JS散度,如果二者的支撑集是在高维空间中的低维度流形时,Pdata和Pz重叠部分的测度几乎为0,因而此时用JS散度衡量二者之间的分布差异时,得到的始终是一个常数,从而生成器损失函数的梯度为0,梯度消失,这也是导致原始GAN训练不稳定的主要原因[15]。
Wasserstein距离相比KL散度、JS散度的优越性就在于,即使两个分布之间没有重叠的部分,但仍然可以度量二者之间差距。但需要判别器的参数权重满足1-Lipschitz function的限制,由于Wasserstein距离没有上下界,如果不加以限制,就会导致D(Pdata)的值越来越大,而D(G(Pz))的值则会越来越小,从而导致判别器永远无法处于收敛状态,因此通过构造公式(3)致使判别器的参数满足1-Lipschitz function的限制。
(3)
判别器的损失函数如公式(4),在判别器的损失函数添加这一梯度惩罚项,当判别器参数梯度的模值不满足小于等于1的时候加以惩罚。当λ取值为10时,模型的表现效果最好。
JD=Ez~Pz[D(G(z))]-Ex~Pdata[D(x)]+ ![]()
(4)
![]() 的计算如公式(5)所示。
的计算如公式(5)所示。![]() 表示从真实数据分布Pdata和生成器输出的分布G(Pz)之间随机插值取样,其中ε取自0~1之间的均匀分布。
表示从真实数据分布Pdata和生成器输出的分布G(Pz)之间随机插值取样,其中ε取自0~1之间的均匀分布。
(5)
生成模型的损失函数如公式(6):
JG=-Ez~Pz{logD[G(z)]}
(6)
因此本次实验采用Wasserstein 距离来衡量真实图像与生成图像分布的差异。在模型训练的学习过程中,需要训练判别器模型最大化的判别输入数据是来自生成器输出的图像还是真实图像,由于生成器与判别器处于相互竞争的状态,可以通过交替优化的方式来训练模型,即先固定判别器,优化生成器,使得判别器的准确率最小化,之后固定生成器,优化判别器,使其判别准确率最大化。当且仅当Pdata=Pz时达到全局最优解。在同一轮的训练过程中,优化判别器多次后仅对生成器进行一次优化。
2.2.4 预训练判别器
在模型的训练的初始阶段,由于判别器不能正确的区分真实数据和虚假数据,因此无法为生成器提供有效的梯度信息“指导”生成器输出逼真的图像。如果判别器在早期就有较强的分辨能力,将会加快模型的训练过程。本文通过在模型初期训练过程中,给予判别器更多的训练次数,以期望判别器更快的具备对真假数据的区分能力,并且为防止判别器过拟合,随着训练的进行逐渐衰减判别器的训练次数。
分别记录预训练模型和不采用预训练模型的生成器在进行1200次训练过程中的损失函数,从图4(a)可以看出,经过预训练判别器的模型生成器损失函数波动幅度明显小于未经预训练的模型,其中生成器损失函数距离横坐标轴的距离代表生成器对真实数据分布的拟合程度。为更便于观察损失函数的变化趋势,通过多元函数对生成器损失函数进行拟合后如图4(b)所示。
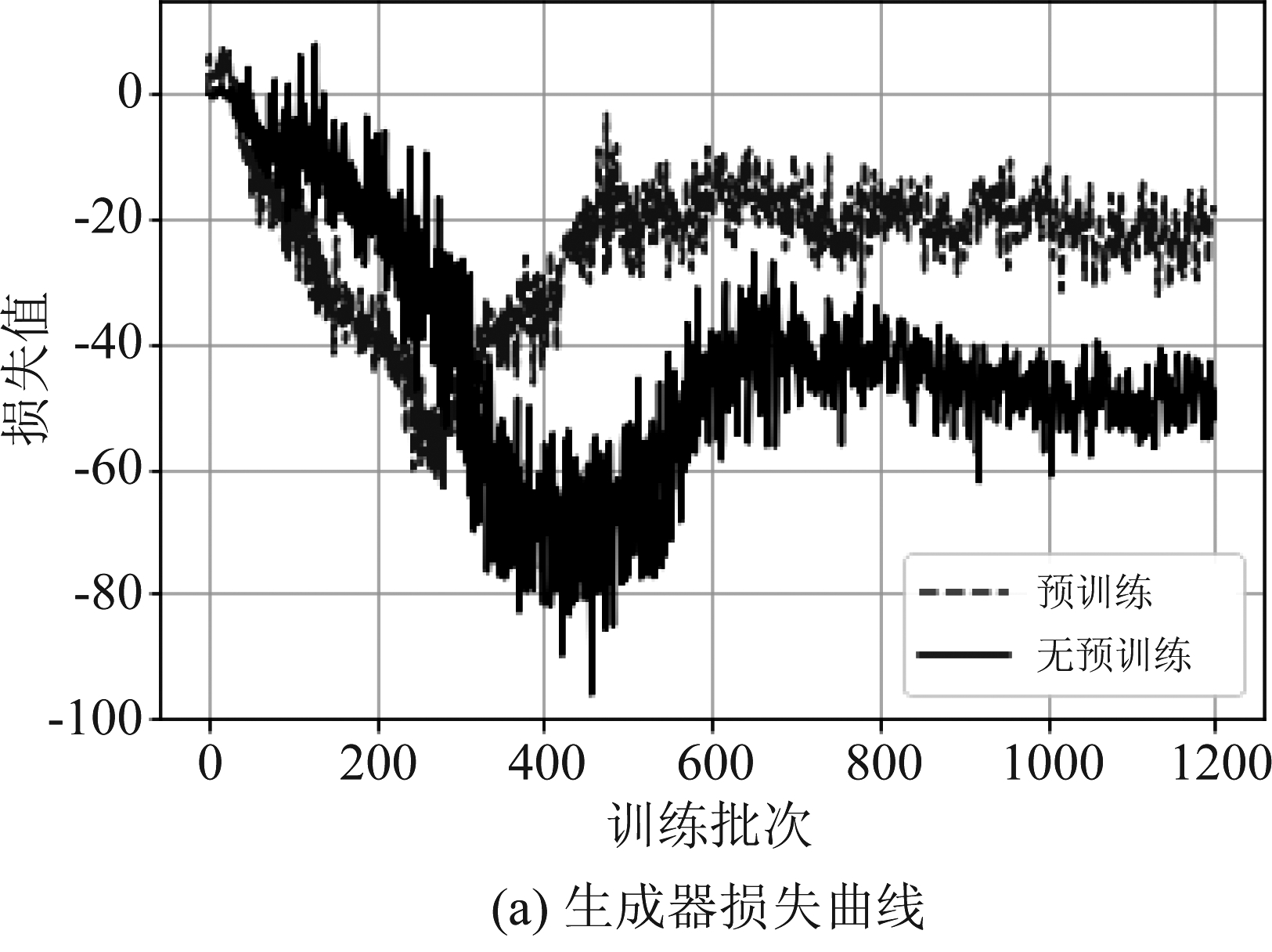
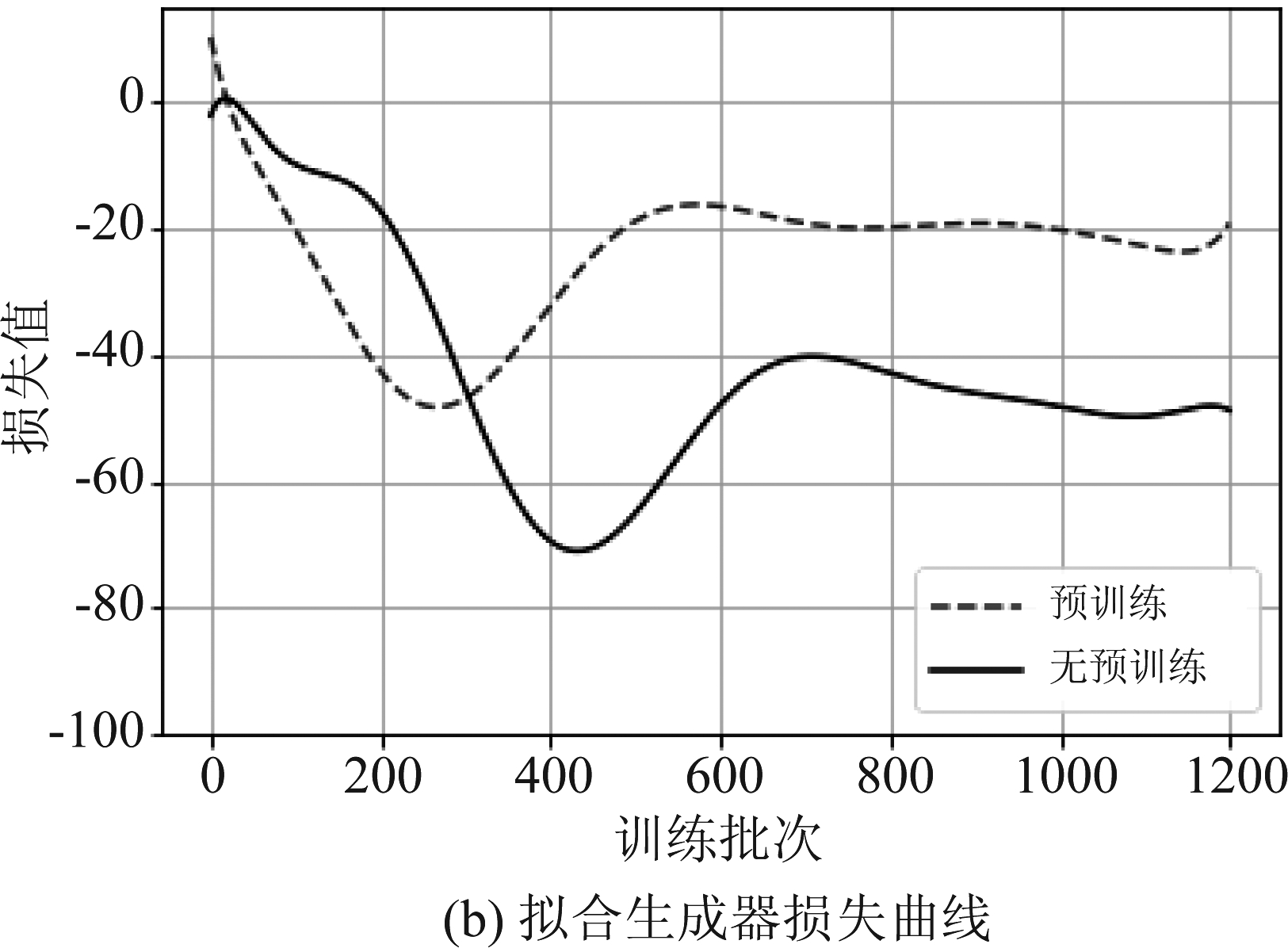
图4 生成器损失曲线对比
Fig.4 Comparision generator loss curve
3 实验
3.1 实验参数和环境
快速收敛GAN的超参数设置如下:生成器模型和判别器模型全部使用Adam[16]优化器,其中参数β1为0.5,参数β2为0.9,学习率统一设置为0.0002,并且在预训练结束后,每更新5次判别器模型参数,更新1次生成器模型参数,每次训练64张样本图像,在CIFAR-10图像生成的实验中对生成器训练7000次。本次实验的计算机配置如表3所示。
表3 实验环境
Tab.3 Experimental environment

实验环境环境配置操作系统Windows 10 64 位CPU/GHzIntel ® CoreTM i7-8750H CPU @ 2.20内存/G32GPUGTX 1070深度学习框架Tensorflow 2.0
3.2 CIFAR-10实验结果
对比实验的不同GAN模型类型有使用全连接网络结构的原始GAN,由于采用全连接神经网络,虽然模型仅仅只有八层,却带来了巨大的参数量;在DCGAN、WGAN-GP[17](Wasserstein GAN-Gradient Penalty)和LSGAN[18](Least Squares GAN)方面,因为仅仅是在模型的损失函数上有不同,模型的网络结构完全一致,全部使用卷积层和反卷积层搭建模型,模型相对于原始GAN,在参数量方面有比较明显的下降,但仅仅是卷积层和反卷积层的简单堆叠,容易发生梯度消失或梯度爆炸等问题;对于本文提出的算法,由于对判别器和生成器的模型结构进行改进,在和其他卷积结构模型神经元网络深度的情况下,不仅参数量最少,而且不易发生梯度问题。各模型具体参数对比如表4。为防止DCGAN、WGAN-GP和LSGAN模型因梯度问题对生成图像产生影响,本文将使用判别器模型和生成器网络结构只有四层的模型。
实验采用的CIFAR-10数据集包含10种类别,图像总数一共为6万张,其中训练数据集5万张,测试数据集1万张,使用训练集中的5万张图像分别在GAN、DCGAN、LSGAN、WGAN-GP和本文提出的快速收敛的生成式网络进行训练,并在训练的不同阶段由生成器输出样本图像。
表4 模型参数对比
Tab.4 Comparison of model parameters
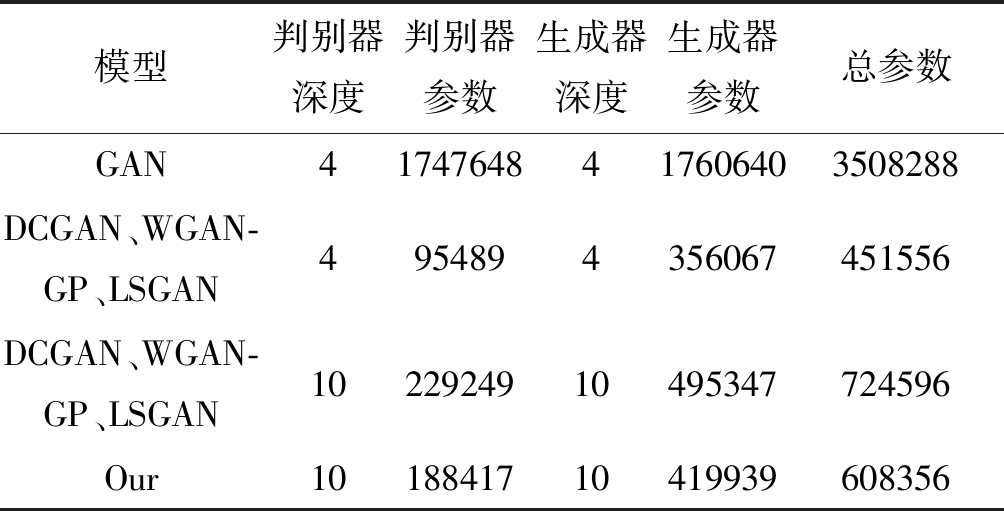
模型判别器深度判别器参数生成器深度生成器参数总参数GAN41747648417606403508288DCGAN、WGAN-GP、LSGAN4954894356067451556DCGAN、WGAN-GP、LSGAN1022924910495347724596Our1018841710419939608356
从各个模型训练的整体情况来看,原始的GAN模型,虽然训练的每一批次都相较于上一批次都有提升,但提升的幅度并不明显,图像的纹理特征模糊,几乎无法分辨;DCGAN由于采用卷积和反卷积的网络模型架构,因而在生成图像的效果好于原始GAN,不过训练的平稳性较差,随着训练的继续进行,出现了模式崩溃的现象;LSGAN采用最小二乘法作为损失函数,在训练的后期可以生成图像纹理清晰的图像,但输出样本的类别单一,并且图像内容扭曲、变形,无法准确判别物体类别;WGAN-GP采用Wasserstein距离作为模型的损失函数,训练过程较为平稳,只是每一批次图像质量提升的幅度较小;采用本文算法的模型可以在较短的训练批次内,就能通过生成器输出图像纹理清晰的新样本,图像的多样性丰富,在训练的同批次内皆好于其他模型,随着训练的继续,生成图像清晰度继续提升,色彩丰富度较高、纹理细腻,较为容易辨认,与原始图像有着较高的相似度。

图5 各类GAN模型生成样本对比图
Fig.5 Comparison of generated samples of various GAN models
对于GAN模型生成的图像,使用人为检验的方式非常耗时,而且由检测者的主观性带来的误差也很难避免,因此为了能够客观评判不同模型生成图像的质量与多样性,本文从IS(Inception Score)和FID(Fréchet Inception Distance)两个角度对不同模型生成的图像做出定性与定量的评价。
3.2.1 Inception Score
事件发生的可能性通常采用熵来衡量,对于GAN生成的新样本,如果其条件概率P(c|G(z))越低,则代表该样本为某一类的概率越高,其中c为样本类别,G(z)为模型生成器输出的新样本。Inception-v1[19]模型通过ImageNet数据集上进行训练,可以分类1000种类别的图像,因此如果输入样本通过Inception-v1模型可以获得较高的置信度,则表示图像的质量较高,通过计算生成样本的边缘分布来衡量生成图像的多样性。一般情况下,IS取值越高,代表着生成图像质量和多样性越好。计算不同GAN模型在训练批次内生成图像的IS值,结果如图6所示。从图6可以看出,本文算法相较于其他GAN模型,可以在较短的训练批次内就达到较高的IS值。由此说明本文算法快速收敛的有效性。
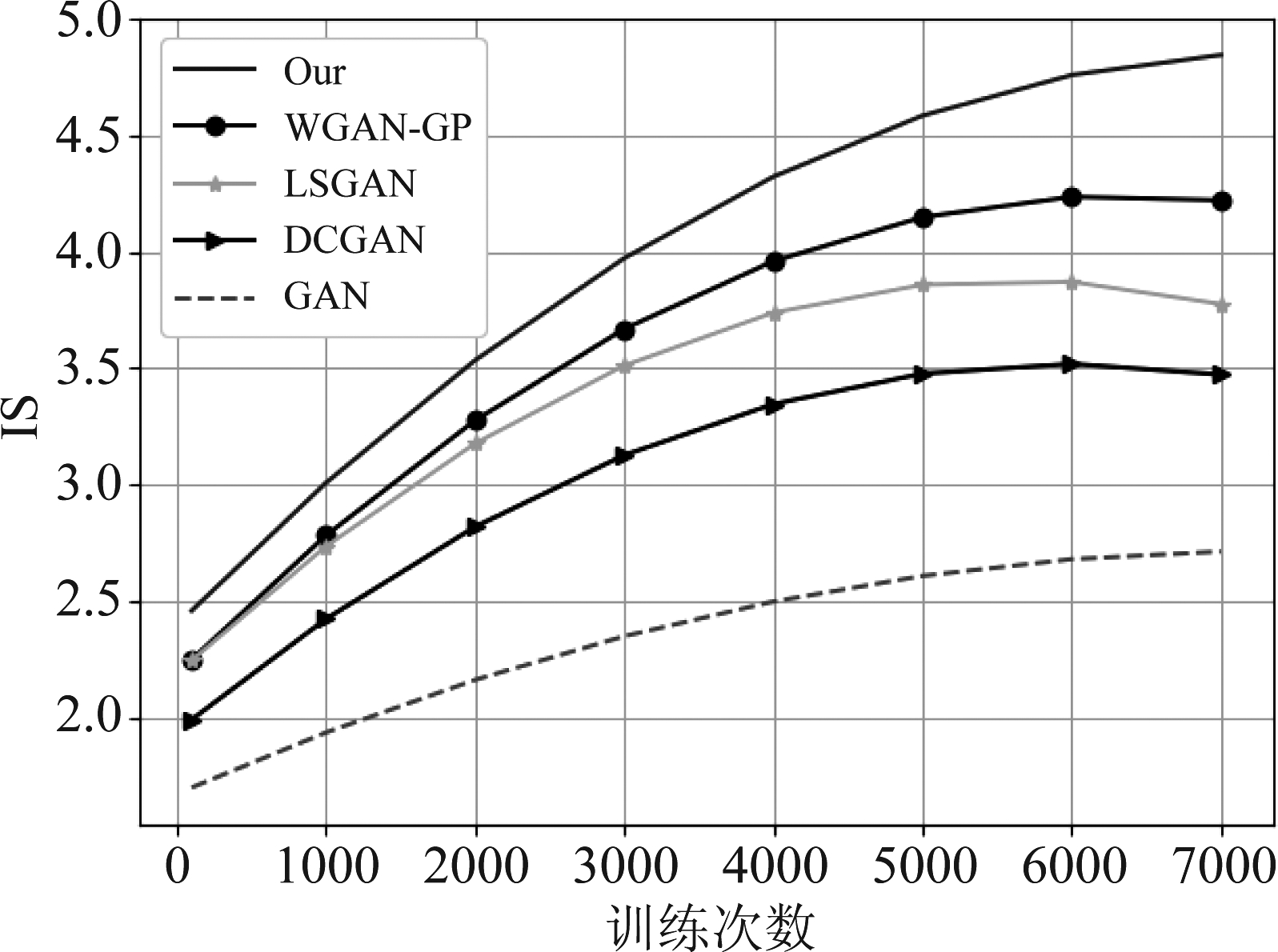
图6 不同GAN模型IS分数
Fig.6 Inception Score of different GAN models
3.2.2 Fréchet Inception Distance
在IS中通过inception模型对新样本的分类置信度评价生成图像的质量与多样性,但是在FID(Fréchet Inception Distance)中,虽然同样使用Inception-v1模型,但是和IS不同的是,FID的通过Inception-v1对图像进行特征提取,之后使用均值为μ方差为σ的正态分布拟合特征分布,FID的计算公式如公式(7)所示,其中μx与∑x,μy与∑y分别表示真实数据和生成数据的方差和协方差。较低的FID值通常意味着生成图像的多样性和质量越高。
FID(x,y)=||μx-μy![]() +
+ 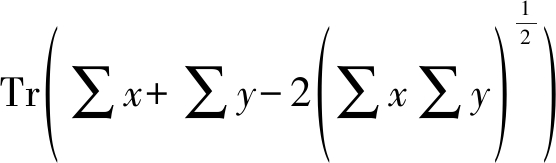
(7)
统计不同模型的FID值,如图7所示,本文算法仍然可以在相对较短的训练批次内达到较低的FID值,并且相比于其他类型的GAN模型,本文算法每经过一个训练FID都有较大幅度的下降。
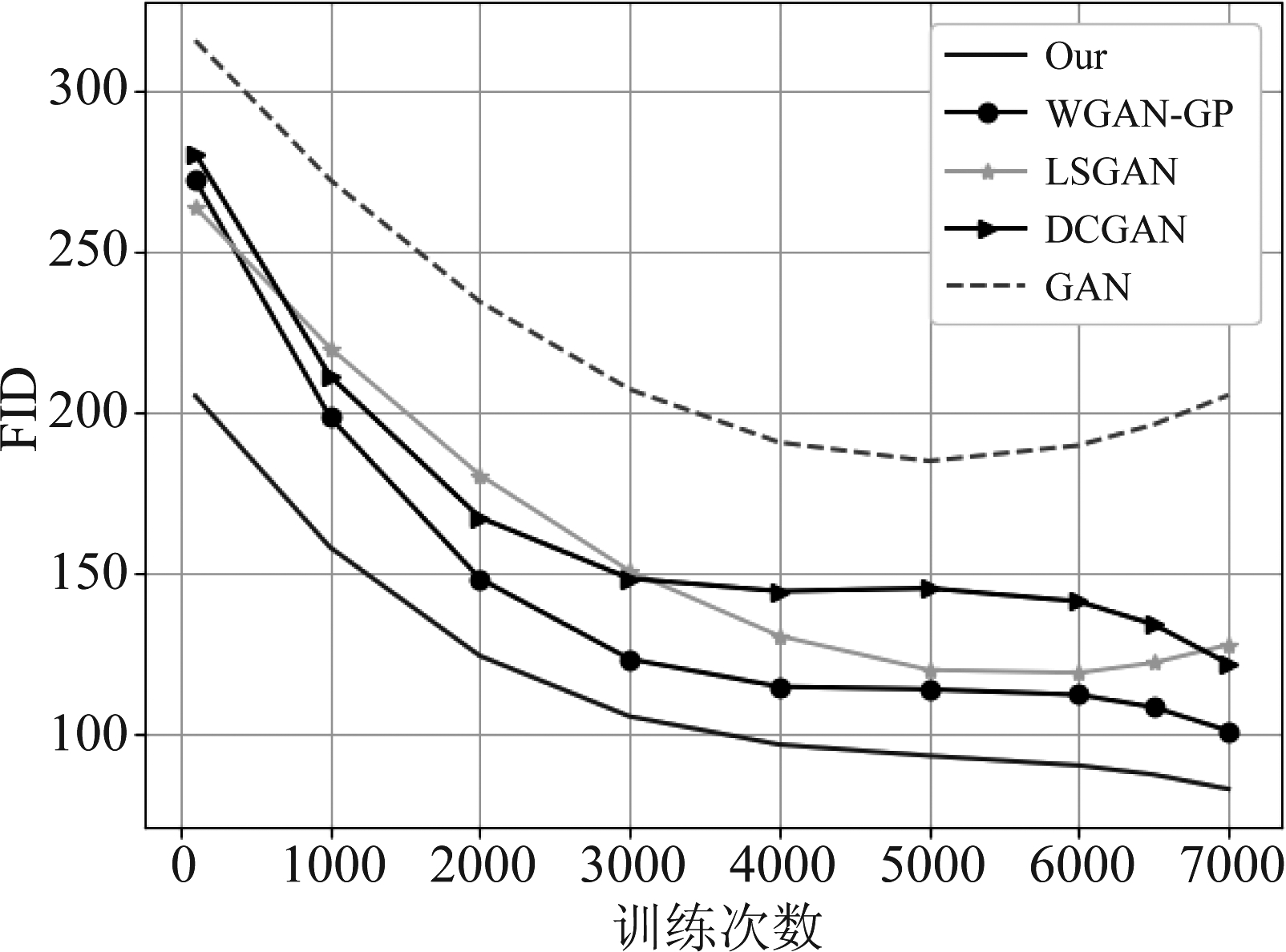
图7 不同GAN模型FID分数
Fig.7 Fréchet Inception Distance of different GAN models
3.3 胸部X射线图像数据增强3.3.1 数据集
本次实验使用美国国立卫生研究院(USA National
表5 判别器与生成器模型参数
Tab.5 Discriminator and generator model parameters
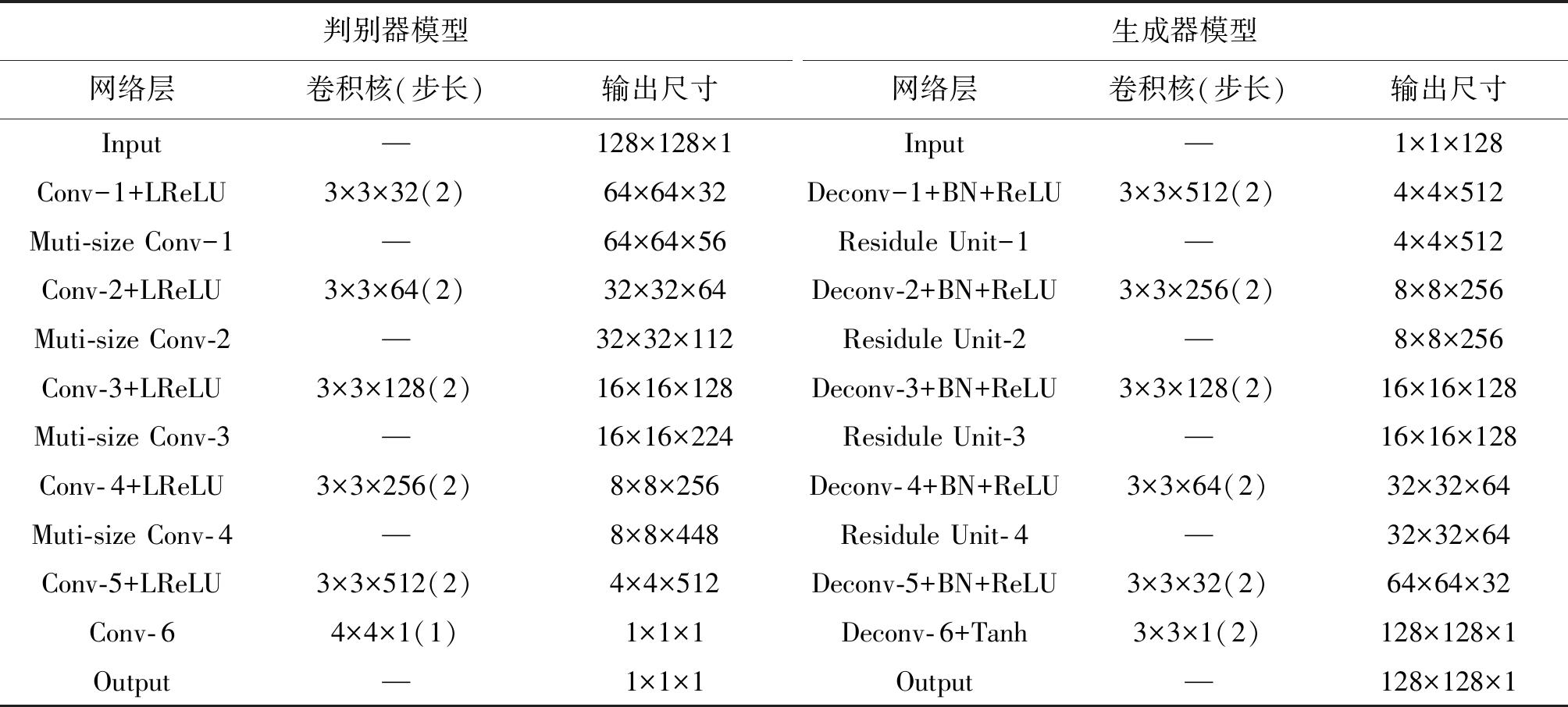
判别器模型网络层卷积核(步长)输出尺寸生成器模型网络层卷积核(步长)输出尺寸Input—128×128×1Input—1×1×128Conv-1+LReLU3×3×32(2)64×64×32Deconv-1+BN+ReLU3×3×512(2)4×4×512Muti-size Conv-1—64×64×56Residule Unit-1—4×4×512Conv-2+LReLU3×3×64(2)32×32×64Deconv-2+BN+ReLU3×3×256(2)8×8×256Muti-size Conv-2—32×32×112Residule Unit-2—8×8×256Conv-3+LReLU3×3×128(2)16×16×128Deconv-3+BN+ReLU3×3×128(2)16×16×128Muti-size Conv-3—16×16×224Residule Unit-3—16×16×128Conv-4+LReLU3×3×256(2)8×8×256Deconv-4+BN+ReLU3×3×64(2)32×32×64Muti-size Conv-4—8×8×448Residule Unit-4—32×32×64Conv-5+LReLU3×3×512(2)4×4×512Deconv-5+BN+ReLU3×3×32(2)64×64×32Conv-64×4×1(1)1×1×1Deconv-6+Tanh3×3×1(2)128×128×1Output—1×1×1Output—128×128×1
Institutes of health,NIH)临床中心PACS数据库中的胸部X 射线数据集。该数据集一共含有112120个前视图胸部X射线图像,由14个常见的肺部病理图像组成,分别为肺不张、肺实变、浸润、气胸、水肿、肺气肿、纤维化、渗出、肺炎、胸膜增厚、心肥大、结节、肿块、疝气,这些图像来自于30805名患者,图像的标注信息正确在90%以上。为满足实际医学图像数据获取困难的现实条件,仅从其中选取7000张用于训练数据集,并将图像由原始尺寸1024×1024像素调整到128×128像素。
3.3.2 模型参数
判别器输入为128×128×1的灰度图像,输入图像通过三层步长为2的卷积层与三个多尺度卷积层,将图像下采样至4×4×512,最后使用卷积核为大小4×4的卷积层输出,输出维度信息为1×1×1,在判别器模型中,除最后一层卷积层,其余层在卷积后采用LReLU作为激活函数。生成器输入为1×1×128的三维均匀分布的噪声,与判别器结构类似,通过三层步长为2的反卷积层与三个残差模块,将噪声上采样至64×64×32,之后再次使用步长为2的反卷积层与激活函数Tanh后输出,最终生成器将通过均匀分布的噪声输出128×128×1像素的灰度图像,在生成器模型中,每次反卷积后都进行批量归一化操作,除了最后一层激活函数为Tanh,其余层激活函数全部为ReLU。判别器与生成器模型具体参数如表5所示。
仅对生成器模型进行一万两千次的训练,生成器模型在训练过程中损失函数的变化如图8所示。从损失函数曲线可以看出,模型训练过程比较平稳,没有发生大幅度的波动,并且在训练过程中,并没有发生模式崩溃等严重问题。
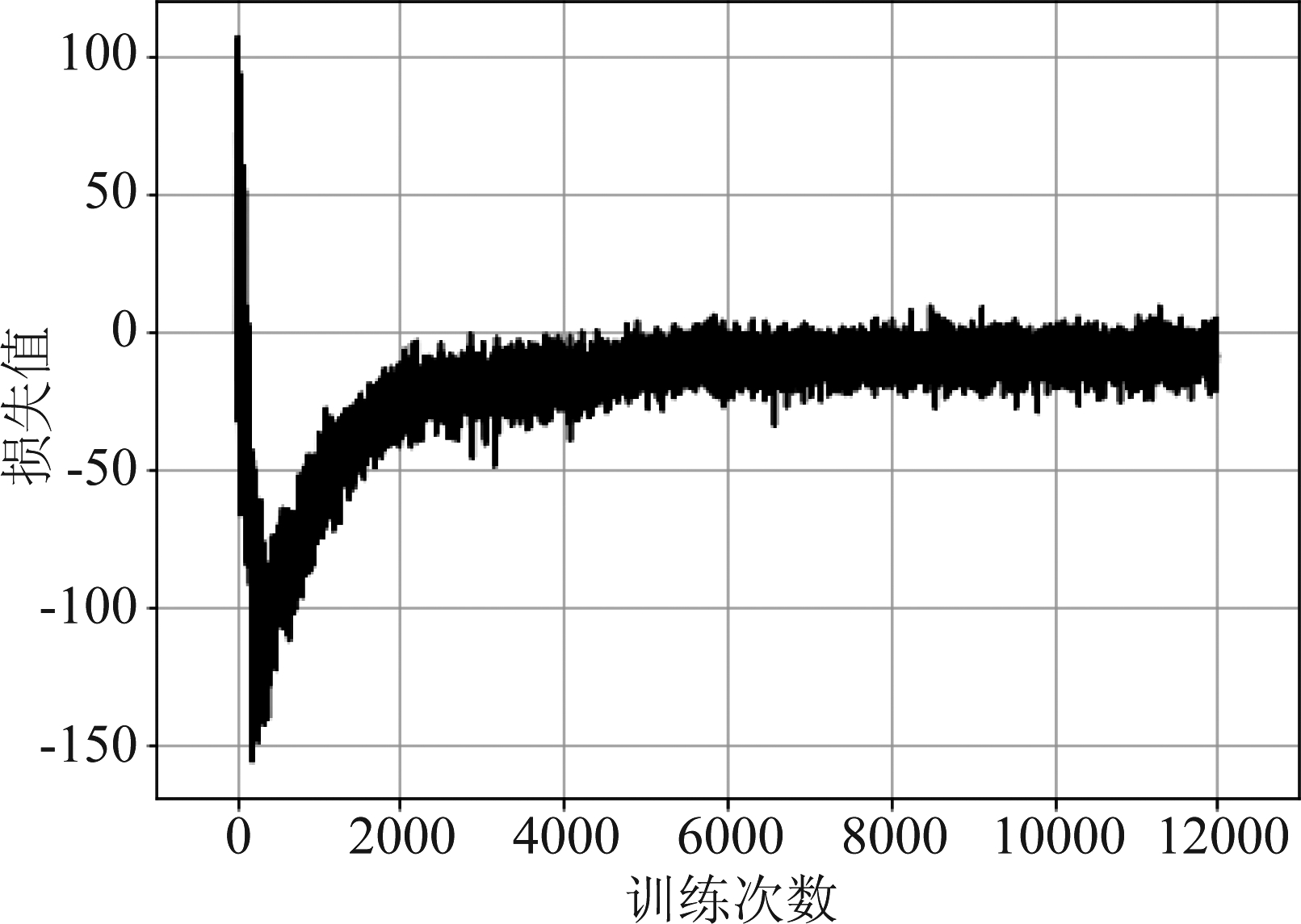
图8 生成器损失曲线
Fig.8 Generator loss curve
3.3.3 图灵测试
生成图像如图9(b)所示,可以看出模型仅经过一万余次的训练就可以输出质量较高的图像,从医学图像的角度看,生成图像噪声小、无伪影、无畸变,具有清晰的组织器官纹理,并且肺部组织与周围组织有着较高的对比度。
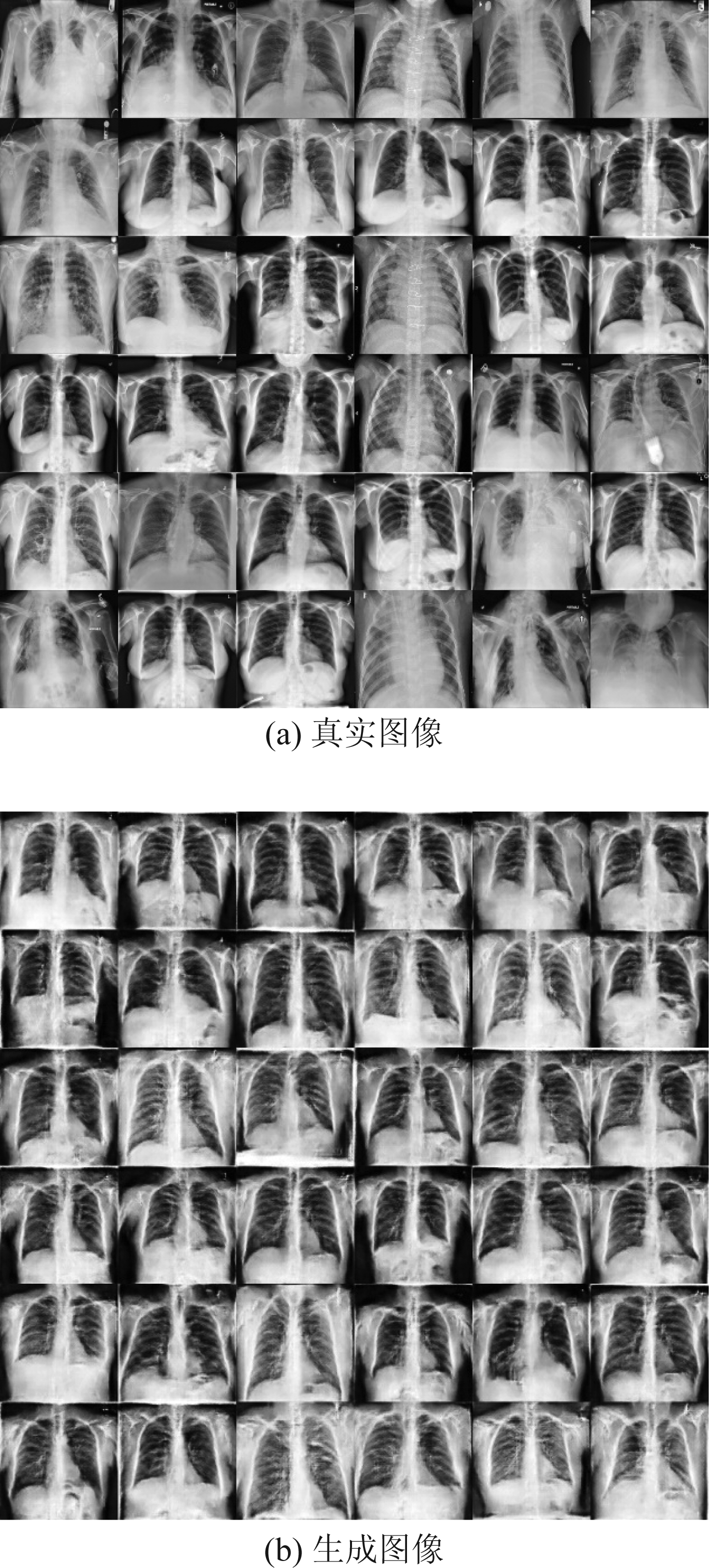
图9 真实图像与生成图像
Fig.9 Real image and generated image
通过训练好的模型随机生成100张图像与100张真实胸部X射线图像进行混合,并由两位专业的放射科医师对成像质量进行评判,其中医师1有五年以上的从业经验,医师2有三年从业经验。评判标准为,图像质量非常差、完全无法辨认为1分,图像质量非常好、器官组织清晰为5分。最后对数据进行统计,结果如图10所示。对于真实图像,医师1评价平均分为3.71分,医师2评价的平均得分为3.85分,对于生成图像,医师1评价平均分为3.31分,医师2评价平均分为3.40分。
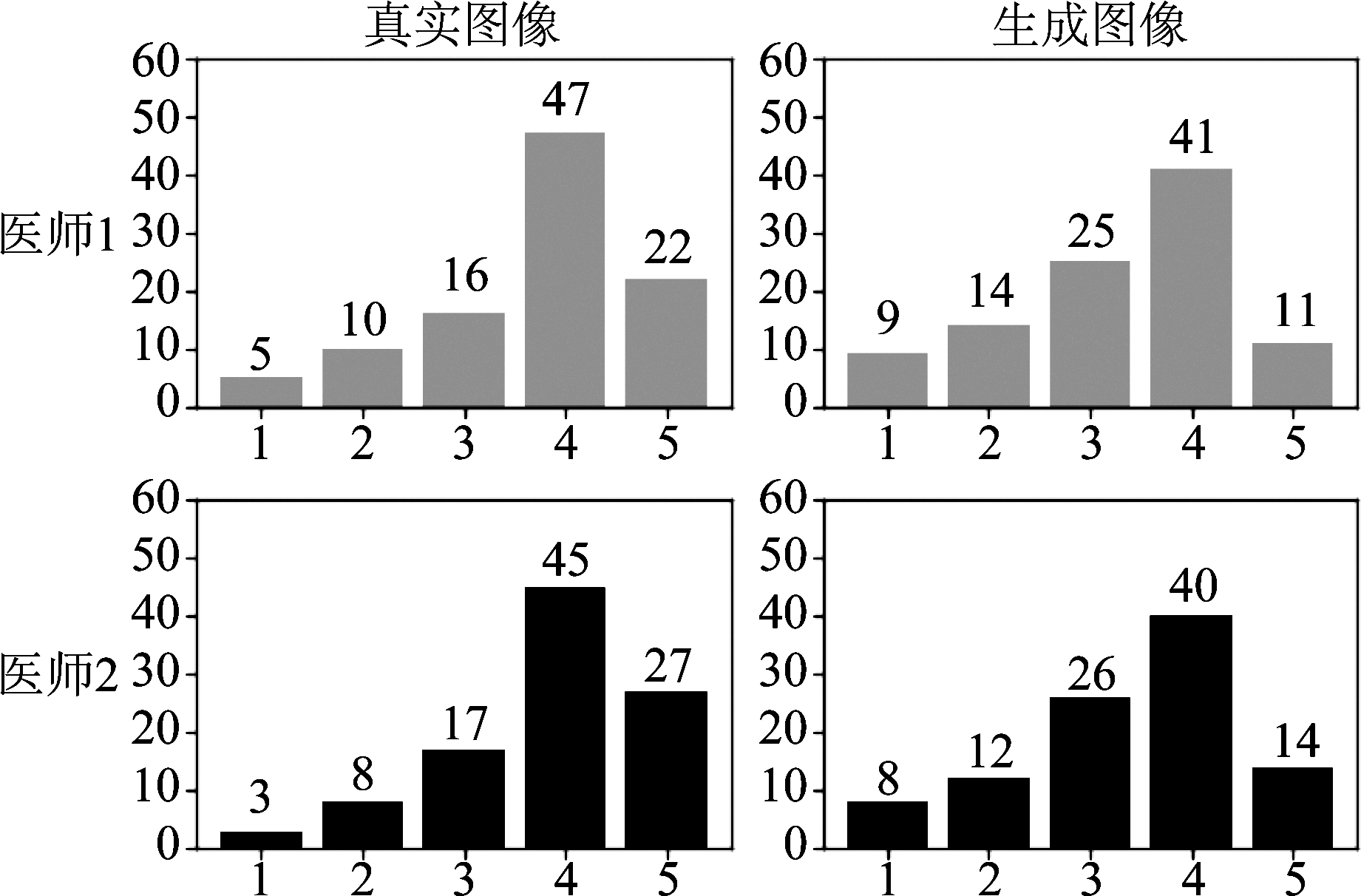
图10 图灵测试结果
Fig.10 Turing test results
通过测试可以看出,虽然生成图像的平均得分略低于真实图像,但对于测试的部分图像即使是专业医师也很难判别出真实图像与生成图像之间的差别,印证了本文提出模型胸部X射线图像的有效性。
4 结论
本文通过在判别器模型中将单一尺寸卷积核替换为多尺寸卷积核,提高判别器对图像特征的提取能力;在生成器模型中添加残差单元,提升生成器对真实数据分布的捕捉能力;并针对判别器模型在训练前期无法为生成器提供有效梯度的问题,提出在训练初始阶段,给予判别器更多的训练次数,从而加强判别器早期特征提取能力,加快训练过程。 通过在CIFAR-10数据集上与其他类型的GAN模型进行对比实验,对生成的图像采用IS和FID两种方式评判模型生成图像的质量与多样性,从实验结果可以看出,相比于其他GAN模型,本文提出的算法可以在短期内就达到比较好的效果,且最终的图像质量和多样性皆优于其他模型。
最后将模型应用于胸部医学图像的生成,并将真实图像与生成图像混合,并由两位专业放射科医师对图像质量进行评判,结果证明,对于部分测试图像,即使是从业多年的专业放射科医师,也很难分清真实图像与生成图像之间的差别,从而印证了算法的有效性。本文的不足之处在于虽然可以用于医学图像的生成,但是只能生成某一种类型的医学图像,下一步,模型结构将应用于条件生成式对抗网络,从而可以根据不同类别生成指定的医学图像,这将对深度学习在医学领域的应用有着重要的意义。
[1] Greenspan H, Van Ginneken B, Summers R M. Guest editorial deep learning in medical imaging: Overview and future promise of an exciting new technique[J]. IEEE Transactions on Medical Imaging, 2016, 35(5): 1153-1159.
[2] Lecun Y, Bengio Y, Hinton G. Deep Learning[J]. Nature, 2015, 521(7553): 436- 444.
[3] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks[J]. Advances in Neural Information Processing Systems, 2014, 3: 2672-2680.
[4] Kitchen A, Seah J. Deep generative adversarial neural networks for realistic prostate lesion MRI synthesis[J]. arXiv preprint arXiv: 1708.00129, 2017.
[5] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. arXiv preprint arXiv: 1511.06434, 2015.
[6] Frid-Adar M, Klang E, Amitai M, et al. Synthetic data augmentation using GAN for improved liver lesion classification[C]∥2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018). IEEE, 2018: 289-293.
[7] Chuquicusma M J M, Hussein S, Burt J, et al. How to fool radiologists with generative adversarial networks? A visual turing test for lung cancer diagnosis[C]∥2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018). IEEE, 2018: 240-244.
[8] Bermudez C, Plassard A J, Davis L T, et al. Learning implicit brain MRI manifolds with deep learning[C]∥Medical Imaging 2018: Image Processing. International Society for Optics and Photonics, 2018, 10574: 105741L.
[9] He Kaming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]∥Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE Press, 2016: 770-778.
[10] Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift [J]. In: Proceedings of the 32nd International Conference on Machine Learning. Lille, France: PMLR, 2015. 448-456.
[11] Karpathy A, Li F. Deep visual-semantic alignments for generating image descriptions[C]∥Computer Vision and Pattern Recognition, 2015: 3128-3137.
[12] Heusel M, Ramsauer H, Unterthiner T, et al. Gans trained by a two timE-scale update rule converge to a local nash equilibrium[C]∥Proc of the Advances in Neural Information Processing Systems. Long Beach CA: Curran Associates, 2017: 6626- 6637.
[13] Ratliff L J, Burden S A, Sastry S S. Characterization and computation of local nash equilibria in continuous games[C]∥2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton). IEEE, 2013: 917-924.
[14] Nair V, Hinton G E.Rectified linear units improve restricted Boltzmann machines[C]∥Proceedings of the 27th International Conference on Machine Learning(ICML), 2010: 807- 814.
[15] Arjovsky M, Chintala S, Bottou L. Wasserstein gan[J]. arXiv preprint arXiv: 1701.07875, 2017.
[16] Duchi J, Hazan E, Singer Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization[J]. Journal of Machine Learning Research, 2011, 12(7): 257-269.
[17] Gulrajani I, Ahmed F, Arjovsky M, et al. Improved trainingof wasserstein gans[J]. arXiv preprint arXiv: 1704.00028, 2017.
[18] Mao Xudong, Li Qing, Xie Haoran, et al. Least squares generative adversarial networks[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2017: 2813-2821.
[19] Szegedy C, Vanhoucke, Ioffe S, et al. Rethinking the inception architecture for computer vision[C]∥The IEEE Conference on Computer Vision and Pattern Recognition, 2016: 2818-2826.

