1 引言
对于航空兵部队来讲,训练方式正在进一步的转变,实战化训练、高原训练和海洋训练等逐渐频繁,航空燃油的消耗也随之增加。燃油作为战机的动力来源,了解其消耗规律,制定合理的加油计划,可以节约军费的开支。对于战机来讲,建立精确的燃油消耗模型显得十分重要。倘若油量过多,则在执行战术动作时会影响战机的机动性能,且在落地时会对战机本身的结构产生冲击,影响飞机服役寿命[1]。此外,由于飞机承载能力有限,载油量的增加会影响弹药以及货物的载重,战机的作战半径以及作战效能会被大幅削弱;倘若油量过少,则不能完成既定的战术要求,严重的会导致飞机无法返航甚至坠毁。
关于飞机燃油模型的建立,民航做了大量研究,军用飞机的研究几乎为空白。建立燃油消耗模型目前有以下几种方法:(1)基于飞机性能进行建模。Collins[2]提出了采用能量守恒的原理,通过分析飞机的动能和势能的变化,建立了飞机的燃油消耗模型,但是此类方法需要通过查阅相关的技术手册得到飞机的性能数据,方式较为繁琐并且准确度不高。(2)基于多元回归的方法。田虎森[3]提出了使用多元线性回归的方式对于军用飞机的非标准动作建立了燃油消耗模型。但燃油消耗过程是非线性的,利用简单的线性回归方法并不能得到较好的效果;T. Baklacioglu[4]创新性地提出了使用遗传算法,通过参数辨识得到了爬升阶段的燃油流率与高度和真空速之间的表达式。(3)基于BADA的方法。BADA是由欧洲航行安全组织(EUROCONTROL)开发的航空器基本性能参数数据库,吴文洁[5]采用了BADA模型仿真,实现了对飞机下降阶段的污染物排放的计算。(4)基于神经网络的方法。刘婧[6]基于QAR数据使用BP神经网络实现了对飞机整个航程的建模;王超[7]使用了回声状态网络(Echo State Network, ESN)的方法,基于轨迹数据实现了对整个航程的燃油消耗的计算。但以上方法对于飞机下降阶段燃油消耗模型的建立,都存在着较大的误差,利用传统的浅层神经网络不能很好地描述下降阶段的燃油消耗规律。
对于飞参数据来讲,最大特点就是时序性[8]。循环神经网络(Recurrent Neural Network, RNN)常被用于解决时间序列数据的分析问题[9],但是随着时间的推移,RNN会忘记之前的状态信息。长短期记忆网络(Long Short-Term Memory, LSTM)作为RNN的变种,其最大特点是具有记忆功能,在处理间隔和延迟较长的事件时具有较大的优势,并广泛应用于股票、气象、交通[10-13]等类的数据处理及预测问题且取得了良好的效果。
为进一步提升LSTM模型精度,本文通过对LSTM的网络结构进行改进,将标准LSTM结构中的输入门优化为与遗忘门耦合的形式,并向遗忘门内引入了窥视孔(Peephole),增加了上一时刻的细胞状态作为门的输入,结合互信息方法筛选了影响燃油流率的关键参数,建立了更加精确的飞机下降阶段燃油消耗模型。通过实际飞参数据检验了模型的有效性,该研究可为军用飞机的燃油消耗预测以及航迹规划提供理论指导。
2 基于互信息的关键参数筛选方法
由于飞参数据中包含大量飞行状态参数,倘若不加筛选直接使用会导致输入向量维度过高,造成模型构建时的维度灾难。互信息是由Shannon提出熵的概念后才随之产生的,广泛应用于对象之间的相关度分析[14]。由于飞参数据记录参数较多,选择了其中部分参数计算与燃油流率的相关度。定义X=[TAS,T4,pitch,N1,N2,az,T,ax,Hp],燃油流率ff定义为Y,所筛选参数含义如表1所示。
表1 参数含义
Tab.1 Parameters meaning
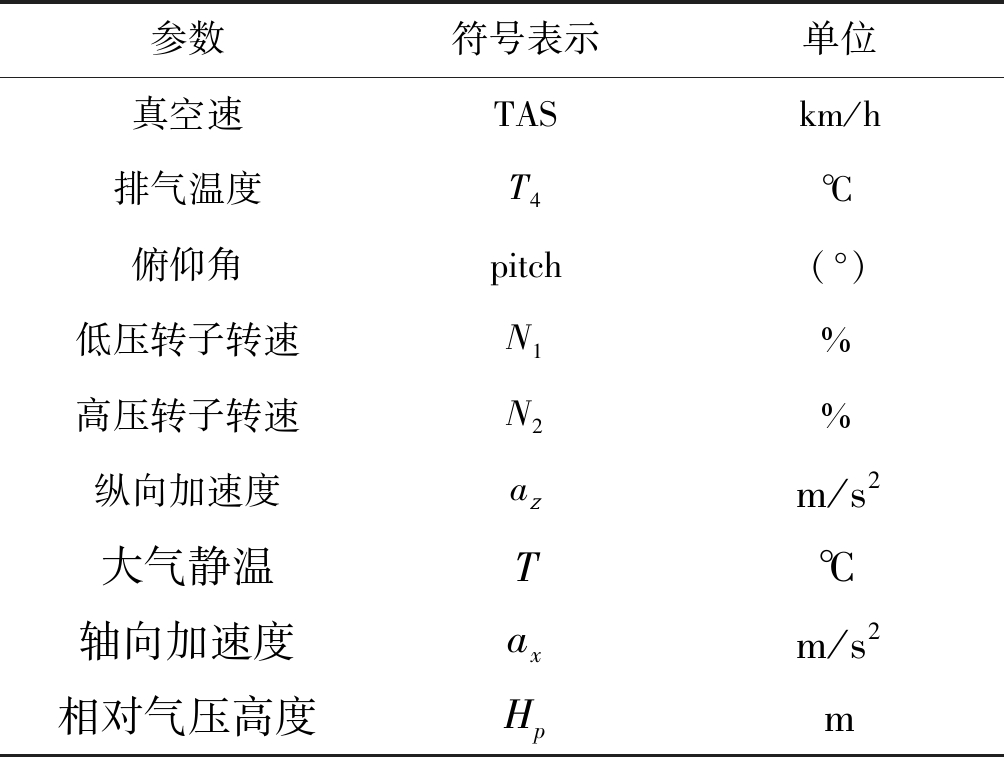
参数符号表示单位真空速TASkm/h排气温度T4℃俯仰角pitch(°)低压转子转速N1%高压转子转速N2%纵向加速度azm/s2大气静温T℃轴向加速度axm/s2相对气压高度Hpm
以真空速为例,各个参数与燃油流率的相关度可以通过式(1)计算:
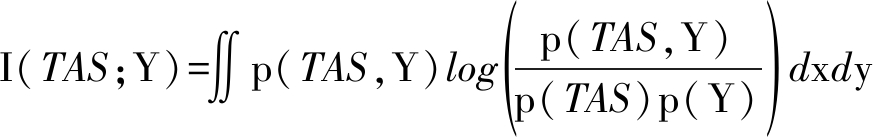
(1)
其中,p(TAS,Y)是TAS和Y的联合概率分布函数,p(TAS)和p(Y)是TAS和Y的边缘概率分布函数。当两个变量之间的互信息值I(X;Y)越大时,则表示两者之间的相关性就越强。其余参数均按照上述方式计算两变量之间的互信息值。
此外,根据信息熵理论,变量X、Y的熵以及联合熵可以表示为如下形式:
(2)
(3)
(4)
两变量之间的互信息值可通过以下方式进行计算:
I(X;Y)=H(X)+H(Y)-H(X,Y)
(5)
3 基于改进LSTM的燃油消耗模型结构
LSTM由Horchreiter和Schmidhuber于1997年提出,有效地解决了RNN梯度消失的问题,对于长时间的记忆能力得到了较大的提升。LSTM主要创新是利用门限思想引入存储单元,除了外部的RNN循环外,还具有内部的“记忆细胞”循环。在“记忆细胞”之中,通过三个门限层来控制通过门的信息量,从而实现对间隔时间较长信息的记忆。图1(a)为标准LSTM单元结构,图1(b)为本文提出的改进LSTM单元结构。相比于标准的LSTM单元结构,做出了以下两点改进:
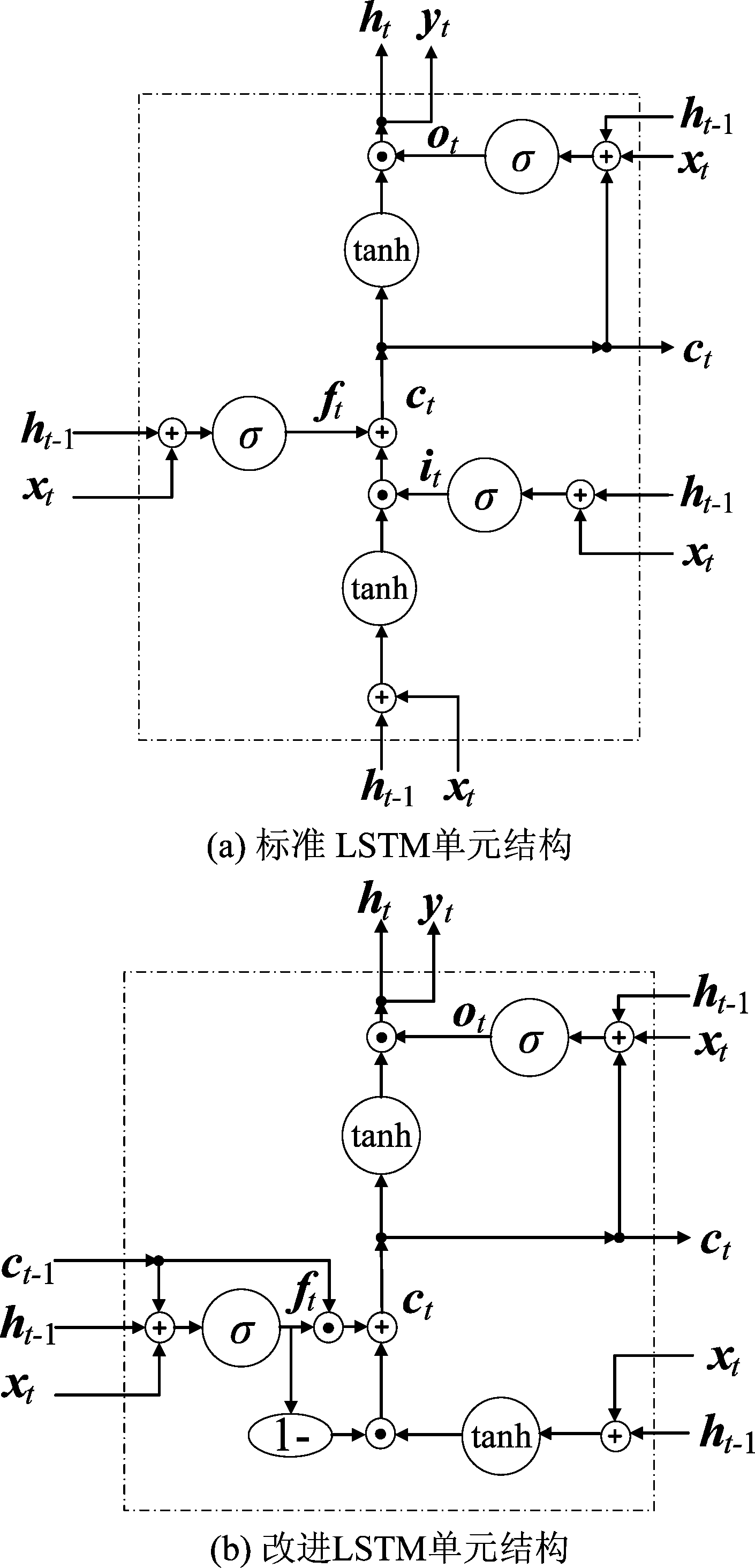
图1 LSTM单元结构 Fig.1 LSTM unit structure
(1)遗忘门的输入中增加了上一时刻的细胞状态ct-1。细胞状态ct-1是LSTM网络结构中的关键所在,它体现了训练过程中的记忆功能,Gers和Schmidhuber[15]提出,为网络结构中的“门”增加窥视孔,即增加细胞状态作为门的输入,能够增强LSTM的抗遗忘性能,具有更强的鲁棒性。
(2)采用了输入门和遗忘门耦合的方式来共同控制细胞状态的更新。相比于标准的输入门只由xt和ht-1组成,使用耦合的方式能够在精简网络结构的同时获得更好的效果。训练过程中的遗忘与保留两种状态是互为依存的,当网络选择保留部分信息时,那么剩余的信息则需要被遗忘,在逻辑上满足“输入门=1-遗忘门”,这相比于标准的LSTM结构更符合逻辑。
图1中,it为输入门限层,用来控制信息的输入;ft为遗忘门限层,用来控制细胞历史状态的保留;ot为输出门限层,用来控制信息的输出。xt为t时刻的输入,ht-1和ht分别为LSTM前一时刻的输出以及当前时刻的输出,ct-1和ct分别是前一时刻和当前时刻的细胞状态。LSTM模型的训练过程可以表示为:
(6)
it=σ(Wi·[ht-1,xt]+bi)
(7)
ft=σ(Wf·[ht-1,xt]+bf)
(8)
(9)
ot=σ(Wo·[ht-1,xt]+bo)
(10)
ht=ot·tanh(ct)
(11)
式中,Wc、Wi、Wf为权值矩阵,bc、bi、bf为偏置,σ(·)为sigmoid函数。得益于三个控制门和存储单元,LSTM可以轻松地保存、读取、重置和更新长时间的信息。由于输入门中引入了上一时刻的细胞状态ct-1,且使用了输入门与遗忘门耦合的方式共同控制细胞状态的更新,所以训练过程中的式(8)和式(9)变为:
ft=σ(Wf·[ht-1,xt,ct-1]+bf)
(12)
(13)
4 实验及结果分析
4.1 实验准备
本文实验基于Keras深度学习工具的Tensorflow框架,它由Python编写而成可以在Tensorflow、Theano以及CNTK框架之间进行切换,并提供深层神经网络的编程接口,从而可以方便快捷的构建模型和实验开发。同时Keras具有模块化的特点,可以进行网络层的自由组合和相互叠加。实验硬件使用惠普主板,配备四核Intel Xeon E5-1603 CPU,搭载AMD FirePro W2100显卡,运行内存为16G。
数据集选用了某型军用飞机一年内110个架次的下降阶段的飞参数据,包含表1中所有的参数以及燃油流率ff,其中100个架次作为训练集,剩下10个架次作为测试集。为了使训练数据能够减少天气等外在因素的影响,所以选取的训练集数据遍布一年的每个月份。
4.2 实验评价指标
为了检验改进的LSTM模型精度,引入均方根误差RMSE,平均绝对误差MAE,平均绝对百分比误差MAPE和决定系数R2来对网络模型进行评价。具体公式如(14)~(17)所示:
(14)
(15)
(16)
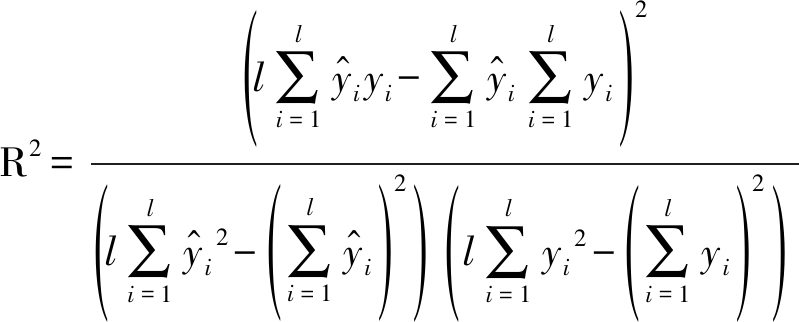
(17)
其中,l为测试集样本个数。![]() 为第i个燃油流率的预测值;yi为第i个燃油流率的真实飞参记录值。RMSE、MAE、MAPE越小,决定系数R2(0
为第i个燃油流率的预测值;yi为第i个燃油流率的真实飞参记录值。RMSE、MAE、MAPE越小,决定系数R2(0
4.3 实验数据的预处理
机载飞参设备中记录了丰富的飞参数据(Flight Data, FD),利用飞参数据可以实现状态监控、飞行事故调查等[16]。由于飞行过程中会受到较多的干扰,传感器对于数据的采集难免会受到影响,导致飞参数据中会产生噪声、野值等。对于此类问题,一般采用中值滤波的方式处理[17],选择合适的参数实现噪声的剔除。本次实验中采用了窗口长度为80的中值滤波器实现了对飞参数据的降噪处理。
由于不同的飞机系统采用了不同的传感器,其采集频率也不尽相同,进而导致所采集的飞参数据长度不一致。笔者采用了拉格朗日插值的方法统一各个参数的数据长度,拉格朗日插值函数如下:
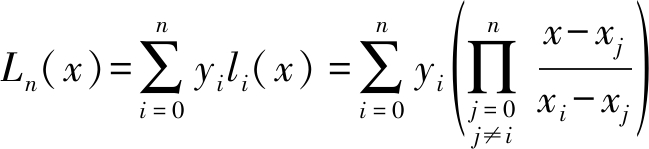
(18)
其中,xi和xj为相异点的横坐标, yi为对应的纵坐标。最终将飞参数据的记录频率统一为2 Hz。飞参数据中的噪声去除并将长度统一之后,对数据归一化处理至[0,1]。
4.4 超参数设置
为模型设置合理的超参数是十分重要的,本文所提出的改进LSTM模型主要涉及的超参数有:输入层节点个数I,输出层节点个数O,隐藏层层数L,隐藏层神经元个数H,学习率α,批尺寸batch和迭代次数epoch。
为降低模型的复杂度,缩短模型训练时间,在LSTM模型训练之前使用互信息的方法筛选输入参数,输入层的节点数需要由筛选后的参数个数来决定。输出只有一个参数,设置输出层节点个数O=1。为了提高模型的训练能力,设置隐藏层层数H=2,隐藏层神经元的个数一般设置为2的次方数,故设置第一层隐藏层神经元H1为128,第二层隐藏层神经元H2为64。学习率α作为最影响模型性能的超参数,其设置是十分重要的,本文中将α设置为0.001。批尺寸batch和迭代次数epoch分别设置为10和200。
Huber损失函数综合了均方误差损失函数和平均绝对误差损失函数的特点,具有更强的鲁棒性[18]。当阈值δ趋近于0时就退化为平均绝对误差损失函数,趋近于无穷时就退化为均方误差损失函数,对于飞参数据这类存在异常值的数据是较为适合的。故本文采用Huber损失函数作为目标损失函数,具体表达如下:
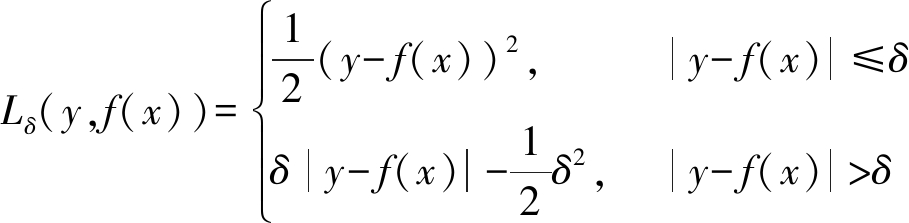
(19)
4.5 影响燃油消耗关键参数的筛选分析
通过观察可知高压转子转速和低压转子转速参数变化趋势相同,考虑到低压压气机用于对进入的空气初步增压,高压压气机用于将空气进一步压缩提供给燃烧室使其与雾化的燃油燃烧[19],为了避免输入向量之间自相关程度过高降低训练精度,选择与燃油消耗更为相关的高压转子转速N2作为输入,所以将俯仰角、纵向加速度、法向加速度、相对气压高度、排气温度、真空速、高压转子转速和大气静温8个参数分别与燃油流率计算MI值。
通常情况下,MI值根据联合概率分布函数和边缘概率分布函数进行计算。在将MI值计算实际应用于本文中的数据集时,笔者采用直方图方法计算两变量之间的MI值,具体步骤如下(以真空速TAS和燃油消耗率ff为例,下面使用X和Y代替,数据长度为n):
Step 1 分别求解TAS和ff中的最大值(maxX、maxY)和最小值(minX、minY),而后按照式(20)、式(21)将两最值之间分为n份,得到区间长度wX和wY;
(20)
(21)
Step 2 统计每个区间内数据的个数,除以数据长度n,即可得到边缘概率密度pX(x)和pY(y);
Step 3 计算两变量对应数据同时落入n×n等分区间的概率,得到联合概率密度pX,Y(x,y);
Step 4 计算X、Y的熵以及联合熵,最终求得两变量之间的互信息值I(X;Y)
H(X)=-∑pX(x)log pX(x)
(22)
H(Y)=-∑pY(y)log pY(y)
(23)
H(X,Y)=-∑pX,Y(x,y)log pX,Y(x,y)
(24)
I(X;Y)=H(X)+H(Y)-H(X,Y)
(25)
其他参数与燃油消耗率ff之间的互信息值计算过程相同,最终得到的结果如图2所示。
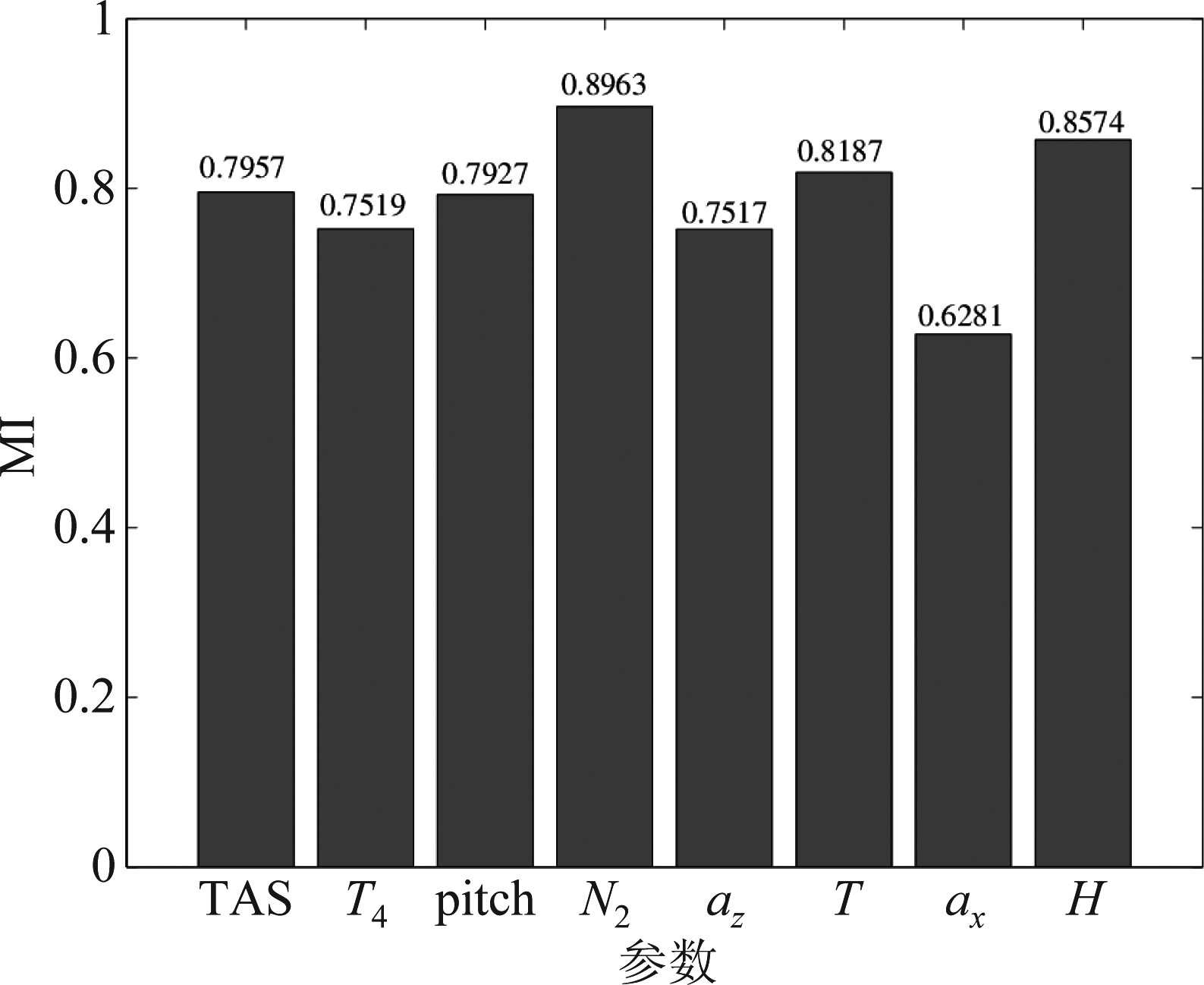
图2 参数与燃油流率之间的MI值
Fig.2 MI Value between parameters and fuel flow rate
由上图可以看出,与燃油流率的相关度从大到小排序为:高压转子转速N2,相对气压高度H,大气静温T,真空速TAS,俯仰角pitch,排气温度T4,纵向加速度az,法向加速度ax。根据相关度的排序,按照相关度从小到大的顺序每次训练后删除一个参数,维度从8维降至3维。为研究输入参数之间的自相关性是否影响实验效果,增加一组实验,其输入中包含低压转子转速N1,各组训练结果如下:
表2 各个输入维度下的模型评价指标
Tab.2 Model evaluation index under each input dimension

输入维度RMSE/(kg·h-1)MAE/(kg·h-1)MAPE/%R2t/s9103.4554.125.61450.9512557898.1250.414.97210.97964807100.4551.435.14250.97244166101.9552.515.47570.96893505102.4453.025.58220.96173014104.6156.125.84210.94622723107.4360.146.32440.9281258
整体上观察可知,随着输入变量维度的增加,精度变高,时间随之增加。输入变量的维度由8变为9时,精度反而降低,原因是该组实验中增加的低压转子转速N1和高压转子转速N2之间高度自相关,使得最终的训练结果变差,这说明通过增加输入的维度并不一定可以增加模型的精度;输入变量的维度由8逐渐减少到5时,时间上得到了较大的缩短,且精度下降并不多;输入变量的维度由5减少到3时,虽然时间上有部分提升,但是精度下降过于明显。在精度允许的范围内,应当选择时间最短的输入变量维度,故最终选择输入变量维度为5,即相关度最高的前5个参数:高压转子转速N2,相对气压高度H,大气静温T,真空速TAS,俯仰角pitch。
4.6 改进LSTM燃油消耗模型实验结果分析
由于最终筛选后的输入参数维度为5,故设置LSTM输入层节点数I为5,其余超参数设置按照4.4节中选定。网络模型训练完毕之后,将测试数据归一化后输入到网络模型之中,得到相应的输出后再进行反归一化,最终将估算的燃油流率结果与实际飞参所记录的数据对比,以其中一个架次的数据为例,仿真结果如图3所示。
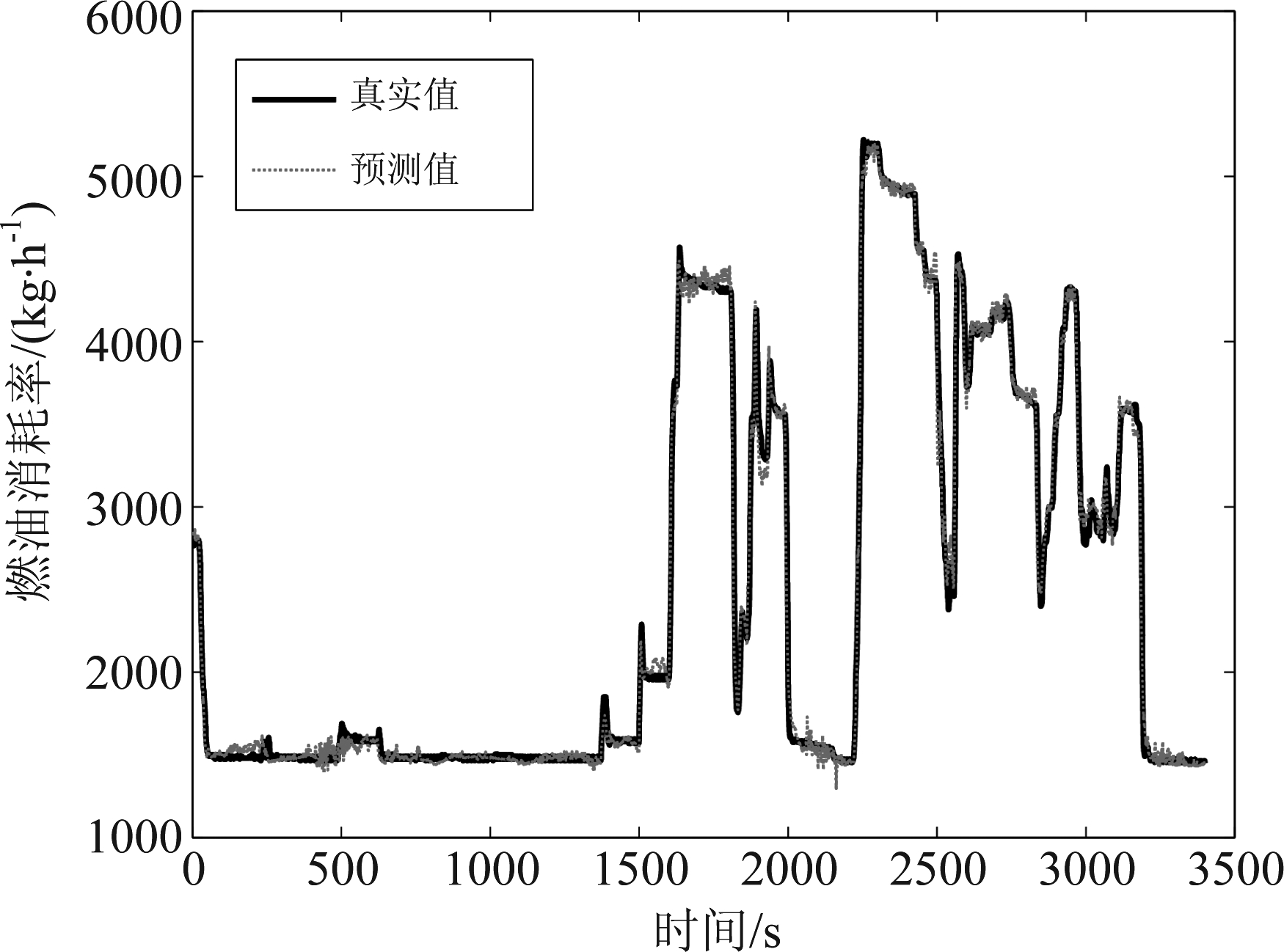
图3 改进LSTM预测结果与实际记录值的对比
Fig.3 Comparison between improved LSTM predicted results and actual recorded values
由图3中可以看出,使用改进LSTM可以较好地描述下降阶段的燃油消耗规律。测试集中各个架次的RMSE,MAE,MAPE,R2如表3所示。
表3中各个架次预测结果与实际记录之间的误差较小,同时各个架次的决定系数在0.96左右,可以表明LSTM方法对于飞机下降阶段的燃油消耗模型的建立是十分精确的。
表3 各个架次的模型评价指标
Tab.3 Model evaluation index of each flight

RMSE/(kg·h-1)MAE/(kg·h-1)MAPE/%R2架次一102.4453.025.58220.9617架次二110.7968.216.99830.9546架次三105.1657.455.91970.9589架次四108.6461.456.43860.9568架次五100.5751.245.24760.9657架次六104.5256.215.86450.9612架次七107.4259.546.12130.9608架次八105.8758.175.98260.9592架次九103.2453.765.75510.9598架次十106.3558.876.02540.9601
4.7 与BP、ESN、标准LSTM的对比实验分析
为了检验LSTM改进后的效果,分别用BP神经网络、ESN、标准LSTM进行训练,而后预测同一个架次飞机的燃油消耗率。由于点数过多,为了显示更加清晰,选取其中100个点的预测结果进行展示。
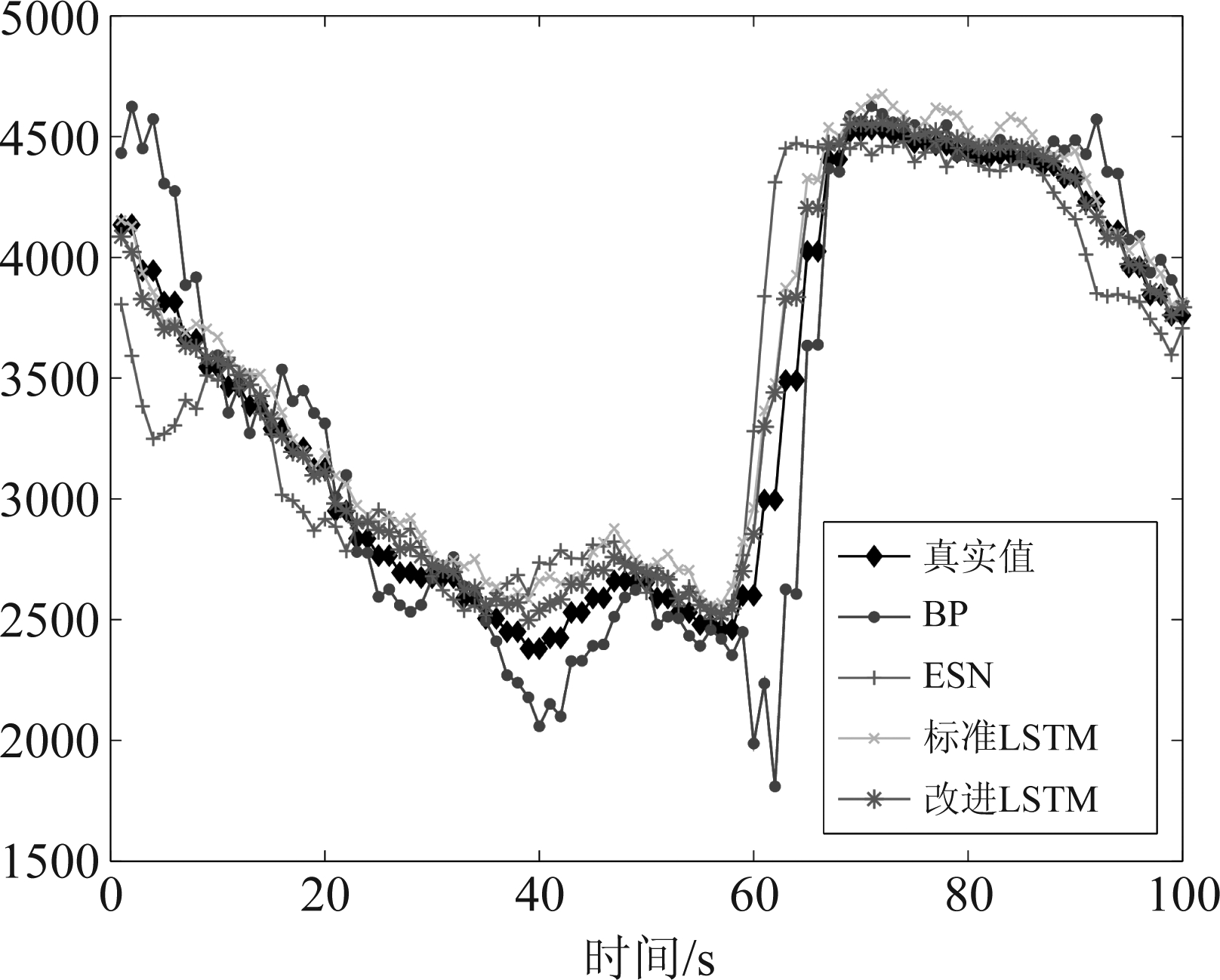
图4 四种方法预测结果与实际记录值的对比
Fig.4 Comparison of the predicted results of four methods with the actual recorded values
各方法均使用MI筛选后相关度最大的五个参数作为输入,燃油流率作为输出。设置BP神经网络输入层节点数5,隐含层节点数10,迭代次数1000次,训练目标精度1×10-3,学习率0.001;设置ESN储备池规模10×10,谱半径0.8,输入放缩系数0.1,稀疏度0.01;标准LSTM与改进LSTM参数设置一致。最终各个方法的训练结果如图4所示,拟合回归效果如图5所示,使用RMSE、MAE、MAPE和R2四个指标来评价以上四种方法的精度,结果如表4所示。

图5 四种方法的拟合回归效果
Fig.5 Regression results of four methods
表4 四种方法的精度对比
Tab.4 Accuracy comparison of four methods
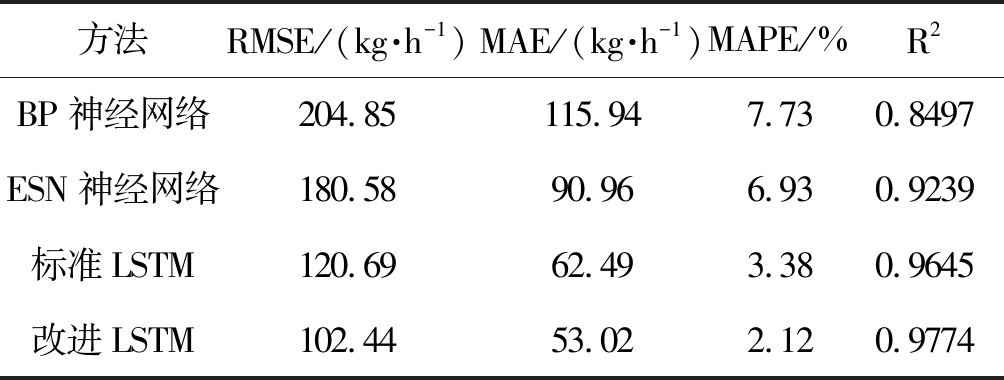
方法RMSE/(kg·h-1)MAE/(kg·h-1)MAPE/%R2BP神经网络204.85115.947.730.8497ESN神经网络180.5890.966.930.9239标准LSTM120.6962.493.380.9645改进LSTM102.4453.022.120.9774
由图4可以明显看出通过对LSTM网络结构的改进,使用改进LSTM方法的预测效果要好于标准的LSTM。ESN神经网络和BP神经网络由于本身的缺陷,对于时间序列数据的处理能力较差,效果相比于LSTM有一定的差距。图5中,横坐标为实际值,纵坐标为预测值,图中的实线斜率为1,若散点越集中于图中的实线,即预测值越接近于实际值,说明模型的拟合回归效果更好。散点图中可以看出BP和ESN有部分点距离实线距离较远,标准LSTM和改进LSTM都集中于实线两侧,以决定系数R2作为拟合程度的评价指标,可以发现改进LSTM效果最好,标准LSTM次之,然后是ESN和BP。由表4中可以看出,改进后的LSTM网络相比于标准LSTM网络有着一定的提升,两种传统的神经网络方法与深度学习方法相比存在较大差距。在RMSE方面,改进LSTM网络相比于标准LSTM网络、ESN神经网络和BP神经网络分别降低了15.1%、43.3%和49.9%;在MAE方面,改进LSTM网络相比于标准LSTM网络、ESN神经网络和BP神经网络分别降低了15.2%、41.7%和54.3%;在MAPE方面,改进LSTM网络相比于标准LSTM网络、ESN神经网络和BP神经网络分别降低了37.2%、69.4%和72.6%。
BP神经网络由于其本身对于非线性特征学习不充分的缺点,导致无法清晰地描述多参数之间的非线性关系。此外还依赖初始参数的设置,若参数设置不理想则得不到令人满意的效果。最重要的是由于BP神经网络缺乏记忆功能,对于时间序列数据处理能力较弱。ESN神经网络中引入了“储备池”,通过这一结构使其拥有了一定的短期记忆功能,但是由于储备池内部神经元之间的连接权值是随机产生的,通过不同方法产生的连接权值会直接影响到网络的效果。飞机下降阶段的燃油消耗问题,涉及到很多参数,且参数之间关系十分复杂,利用传统的机器学习方法很难去表征其间的关系。此外,由于本文中实验数据规模较为庞大,一个架次的飞行时间约为2个小时,其中下降阶段一般持续30分钟左右,每个参数1秒采集2次,100个架次的训练集数据长度即可达到3.6×105。所以深度学习方法由于其强大的学习能力,相比于传统的机器学习方法能够在燃油消耗预测问题上具有更好的表现。LSTM网络对于时间序列数据的处理具有良好的效果,本文通过将标准的LSTM网络结构进行改进,将上一时刻的细胞状态引入到当前时刻,使上一时刻和当前时刻的细胞状态同时决定当前时刻的输出,增强了网络的记忆能力,进而网络能够更加充分地学习数据的特征,故在测试集的表现上相比于标准的LSTM具有更好的表现。
以上分析了四种模型对于燃油消耗率的预测结果,在实际工程运用中,往往应用更多的是对燃油消耗量的预测。此外,对于军用飞机尤其是大型军用飞机来讲,执行任务时间较长,如果建立的燃油消耗率模型不够准确,其误差将会在整个航程中累积,进而导致更大的误差。为了更加明显地体现本文所提LSTM的改进效果,下面将四种方法对该型军用飞机10个架次的下降阶段燃油消耗量的预测值与实际飞参数据记录值进行比较,由于上文已经建立了燃油消耗率模型,所以只需在时间上进行积分即可得到下降阶段的燃油消耗量,结果如表5所示。
表5 燃油消耗量的预测值与真实值的对比
Tab.5 Comparison of predicted and actual fuel consumption
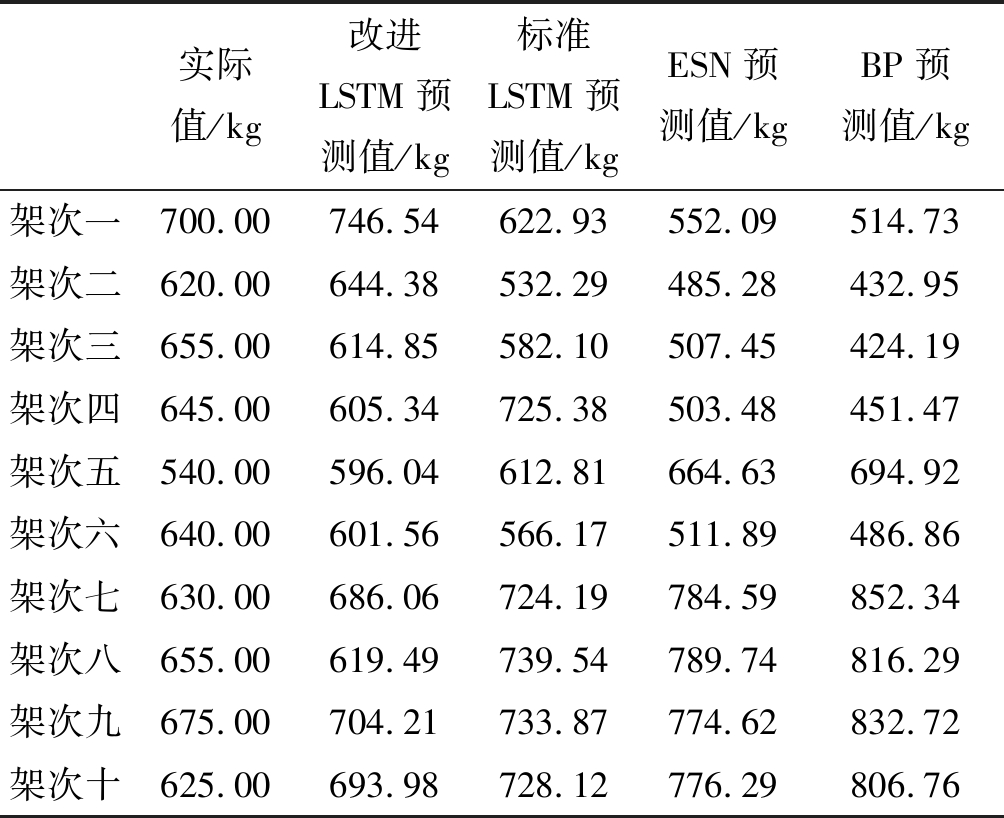
实际值/kg改进LSTM预测值/kg标准LSTM预测值/kgESN预测值/kgBP预测值/kg架次一700.00746.54622.93552.09514.73架次二620.00644.38532.29485.28432.95架次三655.00614.85582.10507.45424.19架次四645.00605.34725.38503.48451.47架次五540.00596.04612.81664.63694.92架次六640.00601.56566.17511.89486.86架次七630.00686.06724.19784.59852.34架次八655.00619.49739.54789.74816.29架次九675.00704.21733.87774.62832.72架次十625.00693.98728.12776.29806.76
由表5中可以看出,使用本文所提的改进LSTM模型的预测值与实际飞参数据的记录值最为接近。通过计算可知,改进LSTM的平均绝对误差为43.49 kg,标准LSTM的平均绝对误差为80.54 kg,ESN神经网络的平均绝对误差为136.47 kg,BP神经网络的平均绝对误差为182.78 kg。由于该类飞机的下降阶段燃油消耗量大约为650 kg,除改进LSTM网络之外,其余三种方法的预测误差均超过了10%,并且预测值相对于真实值忽高忽低,在实际应用于加油时,出于安全考虑,实际加油量一定会多于模型的预测值,那么误差将会进一步增大。故本文所提的改进LSTM模型能够较为准确地估算该型飞机下降阶段的燃油消耗量,克服了燃油消耗率的误差在时间上积累导致的估算不准问题。
5 结论
为了解决目前普遍存在的对于飞机下降阶段油耗模型建立不够精确的问题,以及对于军用飞机燃油消耗模型的建立缺少相关的研究,此外在建模时采用的方法较为陈旧的现状,本文提出了一种改进LSTM方法,基于飞参数据建立了某型军用飞机下降阶段的燃油消耗模型,主要工作及结论如下:
(1)采用了互信息的方法计算输入变量与输出变量之间的相关度,筛选出了相关度较高的变量,降低了后续深度学习模型输入的维度,在保证模型精度的前提大幅度减少了训练时间;
(2)使用改进LSTM与标准LSTM、ESN、BP进行对比,发现深度学习LSTM方法对于时间序列数据处理具有良好的效果,相比于传统的机器学习方法有很大的优势;
(3)通过对LSTM网络结构中的“门”增加窥视孔,并将输入门与遗忘门进行耦合的方式,使其具有了更强的抗遗忘能力和鲁棒性,相比于标准LSTM在精度上有一定的提升。
故本文提出的方法可以很好地描述军用飞机下降阶段的燃油消耗规律,对于领航以及机务保障等工作具有较为重要的意义。但是本文仅仅对于飞机的下降阶段进行了建模分析,后续还需要对飞机的爬升阶段和巡航阶段进行进一步研究,从而实现整个飞行的燃油消耗预测。
[1] Tong Chao, Yin Xiang, Wang Shili, et al. A novel deep learning method for aircraft landing speed prediction based on cloud-based sensor data[J]. Future Generation Computer Systems, 2018, 88: 552-558.
[2] Collins B P. Estimation of aircraft fuel consumption[J]. Journal of Aircraft, 1982, 11: 969-975.
[3] 田虎森, 谢寿生, 任立通, 等. 军用飞机燃油消耗多元线性回归模型[J]. 火力与指挥控制, 2014, 39(10): 104-107.
Tian Husen, Xie Shousheng, Ren Litong, et al. The Fuel Consumption Model of Military Aircraft Based on Multiple Linear Regression[J]. Fire Control & Command Control, 2014, 39(10): 104-107.(in Chinese)
[4] Baklacioglu T. Fuel flow-Rate modeling of transport aircraft for the climb flight using genetic algorithms[J]. Aeronautical Journal, 2015, 119(1212): 173-183.
[5] 吴文洁, 胡荣, 张军峰, 等. 基于BADA模型的飞机持续下降进近节能减排研究[J]. 武汉理工大学学报: 交通科学与工程版, 2017, 41(4): 668- 672.
Wu Wenjie, Hu Rong, Zhang Junfeng, et al. Research on aircraft energy-saving and emission-reduction of continuous descent approach based on BADA model[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2017, 41(4): 668- 672.(in Chinese)
[6] 刘婧. 基于飞行数据分析的飞机燃油估计模型[D]. 南京: 南京航空航天大学, 2010.
Liu Jing. The aircraft fuel estimation model based on flight data analysis[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.(in Chinese)
[7] 王超, 周宣任, 王蕾. 基于轨迹数据的空中交通燃油消耗估算[J]. 空军工程大学学报: 自然科学版, 2018, 19(4): 25-30.
Wang Chao, Zhou Xuanren, Wang Lei. Research on the estimation of air traffic fuel consumption based on trajectory data[J]. Journal of Air Force Engineering University: Natural Science Edition, 2018, 19(4): 25-30.(in Chinese)
[8] 张建业, 张鹏. 飞行数据的时间序列分析方法及其应用[M]. 北京: 国防工业出版社, 2013: 9-12.
Zhang Jianye, Zhang Peng. Time series analysis methods and application for flight data[M]. Beijing: National Defense Industry Press, 2013: 9-12.(in Chinese)
[9] Shi Heng, Xu Minghao, Li Ran. Deep learning for household load forecasting—A novel pooling deep RNN[J]. IEEE Transactions on Smart Grid, 2017, 9(5): 5271-5280.
[10] Cao Jian, Li Zhi, Li Jian. Financial time series forecasting model based on CEEMDAN and LSTM[J]. Physica A: Statistical Mechanics and its Applications, 2019, 519: 127-139.
[11] Qin Dongming, Yu Jian, Zou Guojian, et al. A Novel Combined Prediction Scheme Based on CNN and LSTM for Urban PM 2.5 Concentration[J]. IEEE Access, 2019, 7: 20050-20059.
[12] Petersen N C, Rodrigues F. Multi-output travel time prediction with convolutional LSTM neural network[J]. Expert Systems with Applications, 2019, 120: 426- 435.
[13] 李海峰, 徐聪, 马琳. 基于C-LSTM模型的端到端多粒度运动想象脑电信号分析方法[J]. 信号处理, 2018, 34(8): 883- 890.
Li Haifeng, Xu Cong, Ma Lin. End-to-End Multi-Granular Motor Imagery EEG Signal Analysis Method Based on C-LSTM Model[J]. Journal of Signal Processing, 2018, 34(8): 883- 890.(in Chinese)
[14] 赵超, 陈肇泉, 王斌, 等. 基于互信息和IGSA优化ELM的重整芳烃收率软测量[J]. 仪器仪表学报, 2019, 40(3): 255-263.
Zhao Chao, Chen Zhaoquan, Wang Bin, et al. Soft sensor modeling for reforming aromatic hydrocarbon yield based on MI and IGSA optimized ELM[J]. Chinese Journal of Scientific Instrument, 2019, 40(3): 255-263.(in Chinese)
[15] Gers F A, Schmidbuber J. Recurrent nets that time and count[C]∥IEEE-Inns-Enns International Joint Conference on Neural Networks. IEEE, 2000, 3: 189-194.
[16] 王仲生, 李明, 王翔. 航空发动机突发故障识别与监控方法研究[J]. 西北工业大学学报, 2013, 31(3): 401- 405.
Wang Zhongsheng, Li Ming, Wang Xiang. An effective method of identification and monitoring of sudden fault on aero-engine[J]. Journal of Northwestern Polytechnical University, 2013, 31(3): 401- 405.(in Chinese)
[17] 王小飞, 曲建岭, 高峰, 等. 基于CEMD的燃油消耗率提取方法[J]. 振动. 测试与诊断, 2015, 35(5): 902-907.
Wang Xiaofei, Qu Jianling, Gao Feng, et al. Research of Fuel Consumption Extraction Using Complex Empirical Mode Decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5): 902-907.(in Chinese)
[18] Chen Chuanfa, Yan Changqing, Zhao Na, et al. A robust algorithm of support vector regression with a trimmed Huber loss function in the primal[J]. Soft Computing, 2017, 21(18): 5235-5243.
[19] 孙涛, 秦卫阳, 向欢. 发动机对转双转子系统碰摩非线性相应分析[J]. 机械强度, 2019, 41(2): 255-259.
Sun Tao, Qin Weiyang, Xiang Huan. Analysis on rub impact non-linear response of the counter-rotating dual-rotor system[J]. Journal of Mechanical Strength, 2019, 41(2): 255-259.(in Chinese)


