1 引言
面对现有空中交通管理系统的运行模式在飞行冲突探测、空中交通流量预测管理、空域灵活使用等方面表现不足的问题,欧洲和美国在下一代空中交通管理系统SESAR和NextGen中均采用了基于航迹(Trajectory Based Operation,TBO)的运行理念[1-3]。基于航迹的运行模式通过对飞机飞行时间和飞行轨迹的准确预测,可以有效降低飞行轨迹的不确定性,提高空域资源的利用率,保证航空运行的安全,而基于航空器航迹运行理念的基础技术是精准的航迹预测。航迹预测就是科学准确地预测未来一段时间内飞机的三维位置(经度、纬度、高度),为飞机的运行提供准确的未来运行轨迹和预测过关键航路点的时间[4]。
目前,国内外学者对于航迹预测的研究方法主要有两种:
(1)基于空气动力学或运动学模型的方法。这类方法基于运动学假设构建预测模型,需要飞行计划、大气条件、飞行员动作和飞机意图等诸多参数。文献[5]为了弥补现有的航班轨迹预测方法在冲突探测和解脱方面的不足,提出了一种综合考虑飞行意图信息和风的影响的运动学模型。文献[6]先用基本飞行模型构建速度剖面、高度剖面和水平航迹,然后依据飞机在各个飞行阶段的轨迹特征来拟合生成完整的4D航班飞行轨迹。文献[7]提出了基于运动学的航班飞行轨迹预测方法,该算法基于飞行时间、耗油量等指标从高度剖面和水平运行轨迹面两个角度构建航迹预测模型,并通过仿真实验证明该算法可以提升TBO的鲁棒性。虽然运动学模型对航迹预测做出了重要贡献,但是它们大多是在一些理想的假设下实现的,很少考虑实际约束和人的行为的影响。此外,这些方法需要大量的参数,其中一些参数是商业敏感性的,不容易获取,一旦数据源受到限制,模型的预测精度将大大降低,甚至不适用。
(2)基于无参数估计的方法。与基于空气动力学或运动学模型的方法相比,无参数估计方法是建立在弱假设甚至没有假设的情况下的预测方法。文献[8]从大量航班历史轨迹数据中评估影响航班飞行时间的气象因子和管制因子,首先对下一次航班的全程飞行时间做回归分析预测,再结合历史航迹信息计算每个采样周期点上的飞机位置,从而实现完整的四维航迹预测。文献[9]提出了一种改进卡尔曼滤波(Improved Kalman Filter, IKF)算法,该算法根据上一时刻的预测值和真实值之间的偏差,对当前时刻的航班位置进行调整来提高预测的精度。文献[10]运用高斯混合模型(Gaussian Mixture Model,GMM)算法对相邻时刻飞机的相对位置偏移量进行预测,再结合起飞机场的标高信息和跑道位置来估算航班的运行轨迹。现有的无参数估计预测模型不但需要进行大量的建模分析,工作量较大,而且其内部结构相对简单,无法充分挖掘历史数据中隐藏的依赖关系。简单的结构可能导致模型鲁棒性不足,如果数据中存在着噪声和冗余,预测结果将大大降低[4]。
本文在现有的轨迹数据的基础上,通过特征构建,增加了到目标机场的距离和转向状态两个新的特征,以提高LSTM航迹预测模型的泛化能力。通过对经纬度和高度的平稳性和线性进行分析,结合LSTM网络对非平稳和非线性时间序列有较强的逼近能力,ARIMA对线性时间序列预测性能更优的特点,首先以LSTM神经网络建立主预测模型,对航班的经度、纬度和高度进行初始预测,再以ARIMA模型建立辅预测模型单独对高度进行预测,最后利用CRITIC (Criteria Importance Though Intercrieria Correlation, CRITIC)方法将主模型和辅模型中高度的预测结果进行融合,融合之后的高度值和LSTM预测的经纬度值共同构成了最终的航迹三维位置输出信息,本文中记这种组合模型为LSTM-ARIMA模型。利用实际采集的监视数据对算法性能进行验证,结果表明这种组合模型利用了两种模型的优势,提高了航迹预测的准确性,使得预测结果更贴近真实值,可以为基于航迹的运行模式提供关键技术支持。
2 相关理论
2.1 长短期记忆网络
LSTM作为循环神经网络(Recurrent Neural Network,RNN)的变体,能够改善普通RNN梯度消失和梯度爆炸的问题[11-14],在时间序列处理方面具有优异的表现,已经被广泛应用于自然语言处理、图像识别和时间序列预测问题中,而且取得了巨大的成功。每个LSTM单元由3个控制信息存储和流入的门(gate)和核心信元cell组成,三个门分别是输入门(Input gate)、输出门(Output gate)、遗忘门(Forget gate),具体结构如图1所示。
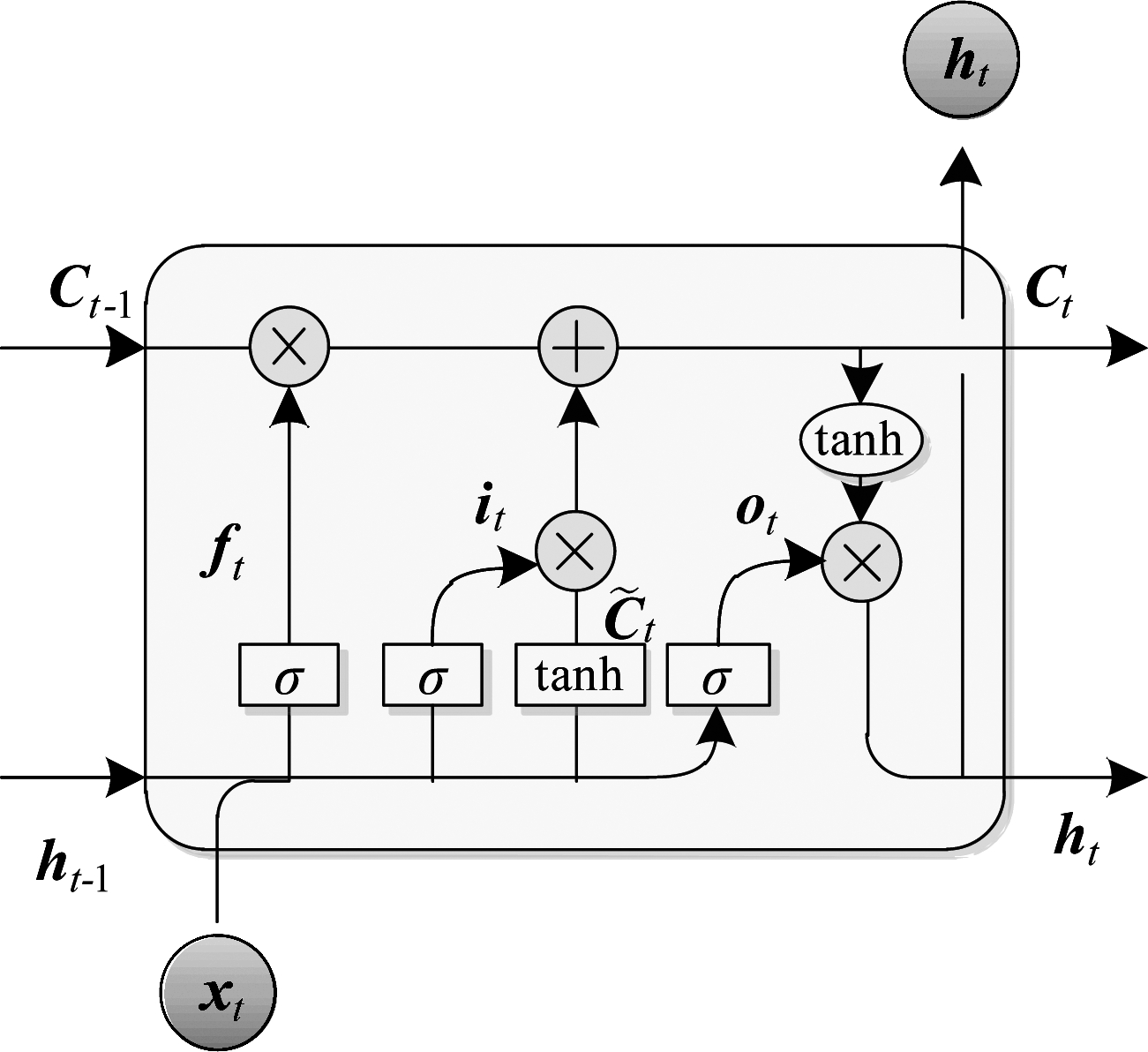
图1 LSTM记忆单元结构
Fig.1 LSTM memory cell structure
如图1中所示,t时刻LSTM有三个输入:当前时刻的输入xt,上一个LSTM单元的输出ht-1,以及上一时刻单元状态Ct-1。LSTM的输出有两个:当前时刻LSTM的单元状态Ct和输出ht。LSTM神经网络的关键是如何控制单元状态C。对于长期状态C,LSTM通过遗忘门和输入门两个门来控制。下面分别对三个门进行数学描述:
(1)遗忘门决定了上一个时刻的单元状态Ct-1有多少会保留进当前时刻Ct中,其计算公式为:
ft=σ(Wf·[ht-1,xt]+bf)
(1)
式中,Wf是遗忘门的权重矩阵,bf为偏置,σ为sigmoid函数。
(2)输入门决定当前输入xt有多少能输入到当前单元状态Ct中,其计算公式为:
it=σ(Wi·[ht-1,xt]+bi)
(2)
式中,Wi表示输入门的权重矩阵,bi为偏置,σ为sigmoid函数。
把记忆单元中的状态从Ct-1更新到Ct时,Ct由两部分组成:第一部分ft⊗Ct-1表示上一个时刻的单元状态有多少可以保留到当前时刻的单元状态中;第二部分![]() 表示当前的临时状态通过输入门之后有多少保留到当前状态单元中。然后将这两部分线性结合,得到更新后的记忆信息Ct,其计算公式为:
表示当前的临时状态通过输入门之后有多少保留到当前状态单元中。然后将这两部分线性结合,得到更新后的记忆信息Ct,其计算公式为:
(3)
式中,⊗表示按位素乘,![]() 是临时状态,
是临时状态,![]() 的计算公式为:
的计算公式为:
(4)
其中,Wc是当前输入单元的状态权重,bc是当前输入单元状态的偏置。
(3)输出门控制当前时刻单元状态Ct中有多少输出到当前时刻的输出状态ht中。输出门的计算公式为:
ot=σ(Wo·[ht-1,xt]+bo)
(5)
式中,Wo表示输出门的权重矩阵,bo为偏置。当前时刻的单元状态Ct经过tanh函数的处理,再经过输出门后,便得到了当前时刻的输出状态ht,其计算公式为:
ht=ot⊗tanh(Ct)
(6)
通过这样的“门”结构,使得LSTM神经网络具有保持长期依赖信息的能力,有效增加了记忆的长度,适用于长时间序列问题的处理。
2.2 ARIMA模型
差分自回归移动平均(Autoregressive Integrated Moving Average,ARIMA)模型是一类有效的时间序列分析和预测的统计模型。其原理是将预测对象视为—个随机时间序列,用一定的数学模型来近似描述这个序列[15]。ARIMA是一个集成的概念,由自回归模型AR、差分模型Difference和移动平均模型MA组成,其构成如式(7)所示:
ARIMA(p,d,q)=AR(p)+Difference(d)+MA(q)
(7)
其中,p是自回归项,d是差分阶数,q是移动平均项数。ARIMA模型的关键是对p、d和q的定阶。平稳序列的ARMA模型的数学形式为:
(8)
其中,μ是常数项,p是自回归模型的阶数,γi是自回归系数,εt是误差值,q是移动平均模型的阶数,φi是移动平均系数。ARIMA的建模步骤如下[16,17]:
Step 1 检验序列的平稳性。通过观察时序图和ADF单根检验来判断时间序列的平稳性。
Step 2 序列平稳化。对于非平稳序列,可以通过差分运算使其平稳,对差分之后的序列进行Step1的平稳性检验;若达到平稳,则进入Step3,否则继续差分,直至平稳,最终达到平稳的差分次数为d。
Step 3 模型的识别和定阶。根据序列的自相关图和偏自相关图选择适当的自相关阶数p和移动平均阶数q,然后对模型进行拟合。
Step 4 模型的参数估计。利用最小二乘法估计序列的回归系数。最小二乘法可以充分利用序列观察值的信息,从而能够提高序列的预测精度。
Step 5 模型检验。通过参数性检验和残差白噪声检验判断选定的参数是否可取,如果不满足要求,则返回Step3,重新进行模型定阶,直到满足残差白噪声检验和参数性检验的要求。
Step 6 模型预测。利用定阶好的ARIMA模型进行序列的短期预测。
2.3 CRITIC权重赋值方法
CRITIC赋值方法是一种客观权重赋权法,其基本思路是以对比度和冲突性为基础来确定指标的客观权数[18]。对比强度以标准差的形式来表现,表示同一指标中不同评价方法取值差距的大小,标准差越大各取值差距越大;指标之间的冲突性是以指标之间的相关性为基础,两个指标之间的正相关越强则冲突性越小。
第j个指标和其他指标的冲突性为:![]() 设Cj为第j个评价指标所包含的信息量,则Cj可表示为:
设Cj为第j个评价指标所包含的信息量,则Cj可表示为:
(9)
其中,σj是第j个指标的标准差,表示指标的对比度;rk, j是评价指标k和j之间的相关系数。Cj越大,表示第j个指标所包含的信息量越大,所以第j个指标的客观权重Wj应为:
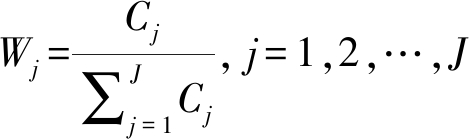
(10)
3 LSTM-ARIMA航迹预测模型
分析历史航班数据,分别用LSTM神经网络和ARIMA两种模型建立航迹预测模型,预测过程主要由数据预处理、模型训练和结果分析三部分组成。在结果分析中将组合预测模型分别与改进卡尔曼滤波模型、LSTM模型进行对比,以验证组合模型的预测性能。
3.1 航迹数据预处理
首先对历史航班轨迹数据按记录的时间尺度、轨迹序列的长度等进行过滤,以确保航迹序列的有效性。又因为航迹数据中可能存在着冗余和缺失,所以还需要对数据进行去冗余、去噪和平滑处理[19-21]。最后对每条有效的轨迹序列以T为间隔进行采样,获得新的轨迹数据集Traj=(X1,X2,…,XI),其中![]() 表示第i条完整的航班轨迹的位置信息序列,I为总的航迹序列条数,m为每条航迹序列中的第m个航迹点。t,lon,lat,h,ν分别是航班在t时刻的5项特征:时间戳、经度、纬度、高度和速度。
表示第i条完整的航班轨迹的位置信息序列,I为总的航迹序列条数,m为每条航迹序列中的第m个航迹点。t,lon,lat,h,ν分别是航班在t时刻的5项特征:时间戳、经度、纬度、高度和速度。
3.1.1 坐标转换
由于飞机导航监视系统中的位置信息是基于地心坐标系(Geocentric Coordinate System,GCS)的,该坐标系是WGS- 84坐标系的一种,坐标系中不同的元素有不同的计量单位,比如高度值一般是几百甚至上千,而纬度和经度的值分别在[0,±90°]和[0,±180°]。将经纬度与高度坐标转化到同一直角坐标系下,可以使得经度、纬度和高度的单位相同,以保证不同维度数值之间的差异较小,也方便后期误差评估时的距离计算。
对于每个航迹点的3D位置坐标(lon,lat,h)经过墨卡托投影[22]转换为直角坐标系下的(x,y,z)。其中,x和y为经纬度转换到同一直角坐标系下的结果,z为原始数据中的飞机高度。
3.1.2 特征维度拓展
若历史航迹数据的信息较少,则网络训练时可能会因约束不足或信息缺乏,对关键信息的保留和扰动信息的丢弃不足,从而导致模型的泛化能力和预测精度不足。因此,通过特征构建将以下维度信息融合到数据集中。
(1)每个航迹点与参考点R的距离d。我们选取降落机场的中心作为参考点R(xref,yref,zref),每个航迹点和R的距离![]() 由下式计算得到:
由下式计算得到:
(11)
(2)每个航迹点和参考点R的角度θ。它显示了相对于参考点的轨迹变化状态(转向状态)。θ由下式计算得到:
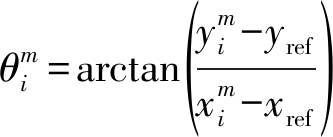
(12)
为了避免在±π处的不连续性和特征缩放,使用θ的正余弦值![]() 和
和![]() 代替
代替![]() 经过坐标转换和维度扩展之后每条完整的轨迹序列为
经过坐标转换和维度扩展之后每条完整的轨迹序列为![]() 在后续的航迹预测过程中,将航迹看成一时间序列,不需要时间戳信息,因此将第i条航迹第m个航迹点的轨迹序列记为
在后续的航迹预测过程中,将航迹看成一时间序列,不需要时间戳信息,因此将第i条航迹第m个航迹点的轨迹序列记为![]() 即用于航迹预测的每个航迹点有7个特征。通过特征构建得到的到参考点距离和角度两个新的特征,很好的区分了一条航迹上不同位置的航迹点,增加了航迹点的约束性。通过实验验证,在网络结构和其他参数相同的情况下,用{x,y,z,ν,d,sin θ,cos θ}7个特征训练的网络模型相比{x,y,z,ν}4个特征训练的模型其在经纬度和高度上的预测误差得以降低。
即用于航迹预测的每个航迹点有7个特征。通过特征构建得到的到参考点距离和角度两个新的特征,很好的区分了一条航迹上不同位置的航迹点,增加了航迹点的约束性。通过实验验证,在网络结构和其他参数相同的情况下,用{x,y,z,ν,d,sin θ,cos θ}7个特征训练的网络模型相比{x,y,z,ν}4个特征训练的模型其在经纬度和高度上的预测误差得以降低。
3.1.3 数据归一化
为了降低量纲和取值范围对网络性能的影响,需要把输入数据归一化到[0,1]区间内。这里采用Min-Max方法进行归一化:
(13)
其中,Xmax为各个数据维度的最大值,Xmin为各个维度的最小值,X*为归一化后的数据。归一化处理可以消除数量级的影响,但不会破坏数据中存在的关系。在使用训练好的LSTM模型预测之后,再利用式(13)对预测值进行反归一化,便可得到符合实际范围和意义的预测航迹。
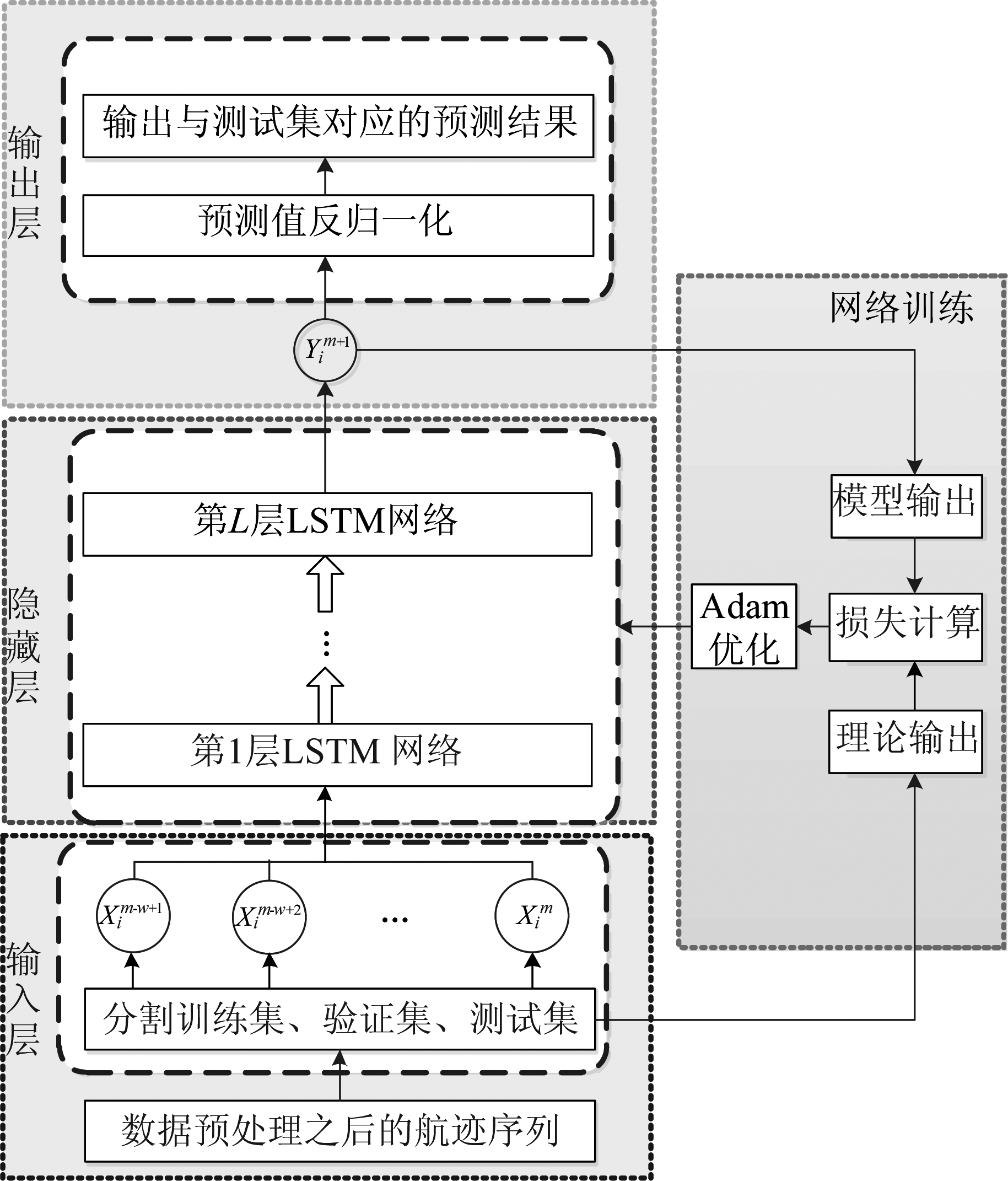
图2 LSTM预测模型
Fig.2 LSTM prediction model
3.2 LSTM模型训练
LSTM预测模型主要分为三层,分别是输入层、隐藏层和输出层。网络结构如图2所示。对经过上一节处理之后的历史航迹数据按照8:2划分为训练集和验证集。将预处理之后的历史数据采用大小为w的滑动窗口进行滑动分割,则网络的输入![]() 将
将![]() 的x, y, z三维位置信息作为标签数据。隐藏层的C和H分别表示LSTM细胞的状态和输出。则模型的预测输出值
的x, y, z三维位置信息作为标签数据。隐藏层的C和H分别表示LSTM细胞的状态和输出。则模型的预测输出值![]() 可表示为:
可表示为:
(14)
经过反复迭代训练直到损失值收敛,即得到LSTM航迹预测模型。将模型的输出值经过反归一化处理就可得到符合实际意义的三维坐标值。
3.2.1 模型参数选择
(1)输入层时间窗口w的选择
LSTM的性能与输入时序的长度紧密相关,其记忆单元在预测某个时刻的输出时会选择忘记或记住积累的信息,所以在本文中加入了时序的概念。在本文的实验中选择前2~6个时刻的航班轨迹特征来预测下一时刻的航班位置,即输入层的时间窗口w选择为2~6,不同的w取值对网络的超参数选择和精度有不同程度的影响。
(2)超参数选择
合理的超参数选取对模型的性能有较大的影响,本文的LSTM模型的超参数主要有:学习率α,LSTM的层数L,每一层隐藏神经元个数S,子训练集样本个数B,网络迭代次数epoch,目标损失函数和优化算法,输入序列长度为I=w×7的1维矩阵,输出序列长度O。本文中的目标损失函数采用平均绝对误差(Mean Absolute Error,MAE),目标损失函数设为10-3,为了防止模型出现过拟合,对输出的全连接层上的权重增加L2范式正则化。
3.2.2 模型参数分析
根据经验,神经网络中神经元的个数一般是2n,仿真实验中把三个隐藏层的神经元节点数分别取为32、64、128、256的三者组合用于模型训练,选取性能最优的一组。同时,为了验证不同w下的参数选择和模型精度,将w从2依次扩充到6个,选取不同时刻下性能最优的网络参数并计算其MAE,结果如图3所示。
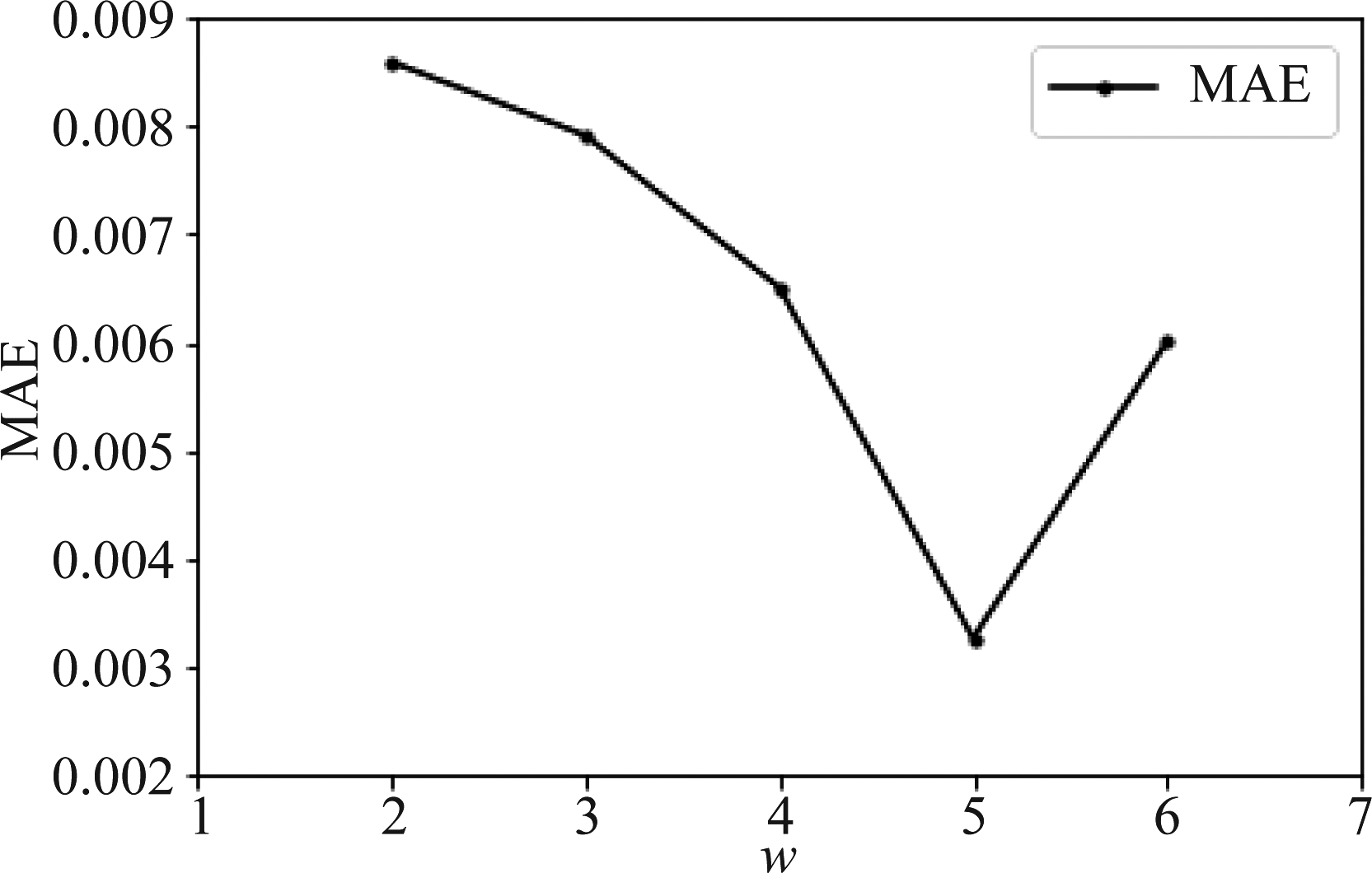
图3 不同w下的平均绝对误差
Fig.3 MAE for different w
由图3可以看出,随着输入层时间窗口w的增加,模型的平均绝对误差逐渐变小,但是当w大于5时,平均绝对误差反而变大了。这是因为随着输入维度的增加,模型变得更加复杂,拟合能力变强,但是拟合程度越高也越可能出现过拟合,所以当w=5时模型的性能最优,此时三个隐藏层的神经元个数分别是128、64、64。其他超参数如表1所示。
3.3 ARIMA模型训练
航班轨迹的经度、纬度和高度序列可以看成一个基于时间的位置序列,根据2.2节的步骤分别构建经度、纬度和高度的ARIMA预测模型,其过程如下:
(1)序列平稳性检测。对历史航迹中的经纬度和高度序列通过散点图和ADF单位根检验进行平稳性测试,结果显示原始的经纬度和高度序列均是非平稳的,所以需要对其差分变化,使之平稳。
(2)序列平稳化。对经度、纬度和高度序列进行二次差分之后,满足平稳性要求。
(3)模型识别和定阶。选取p和q小于等于6中BIC信息量最小时p和q的值,最终确定的经度和纬度模型的参数p=0,d=2,q=1;高度模型的参数p=2,d=2,q=3。
(4)模型检验。对经度、纬度和高度模型进行残差白噪声检验,结果显示符合要求,所以模型的参数选取是合适的。
(5)模型预测。采用循环迭代的方法对LSTM模型预测的同一时间段的经纬度和高度进行预测。
分析飞机从起飞、离场、巡航、进场、进近和着陆的整个飞行过程,可以看出高度数据相对于经纬度具有较好的线性性。因此结合LSTM模型和ARIMA的特点,对经纬度用LSTM建模,对高度用LSTM和ARIMA组合模型建模,最终得出LSTM和ARIMA的组合三维航迹预测模型。
表1 w=5时模型的超参数
Tab.1 Hyper-parameters of the model when w=5
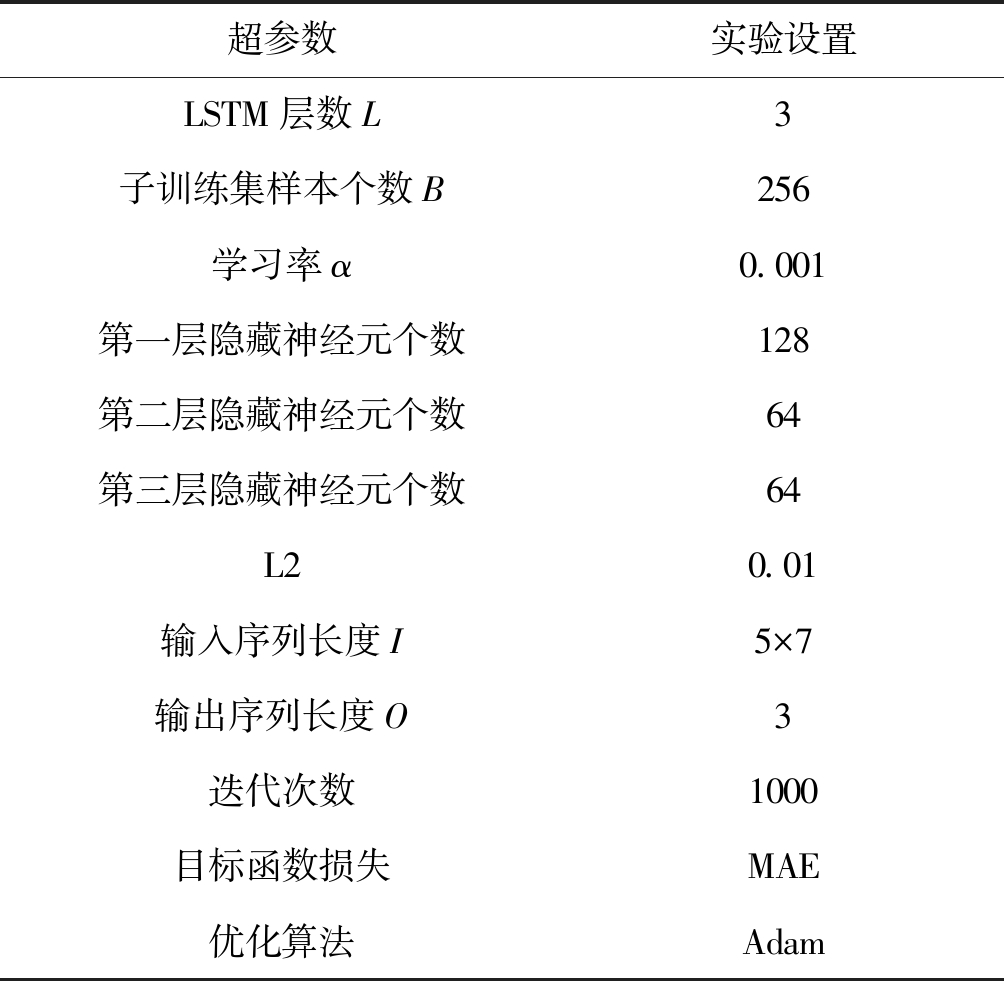
超参数实验设置LSTM层数L3子训练集样本个数B256学习率α0.001第一层隐藏神经元个数128第二层隐藏神经元个数64第三层隐藏神经元个数64L20.01输入序列长度I5×7输出序列长度O3迭代次数1000目标函数损失MAE优化算法Adam
3.4 LSTM与ARIMA组合模型
组合模型采用LSTM模型预测为主,ARIMA模型预测为辅的形式进行预测。首先,用LSTM建立经纬度和高度的预测模型;然后,用ARIMA单独建立高度预测模型;最后,利用CRITIC方法融合LSTM和ARIMA的高度预测值,融合之后的高度预测值和LSTM的经纬度预测值组成最终的预测结果。其预测过程如图4所示。
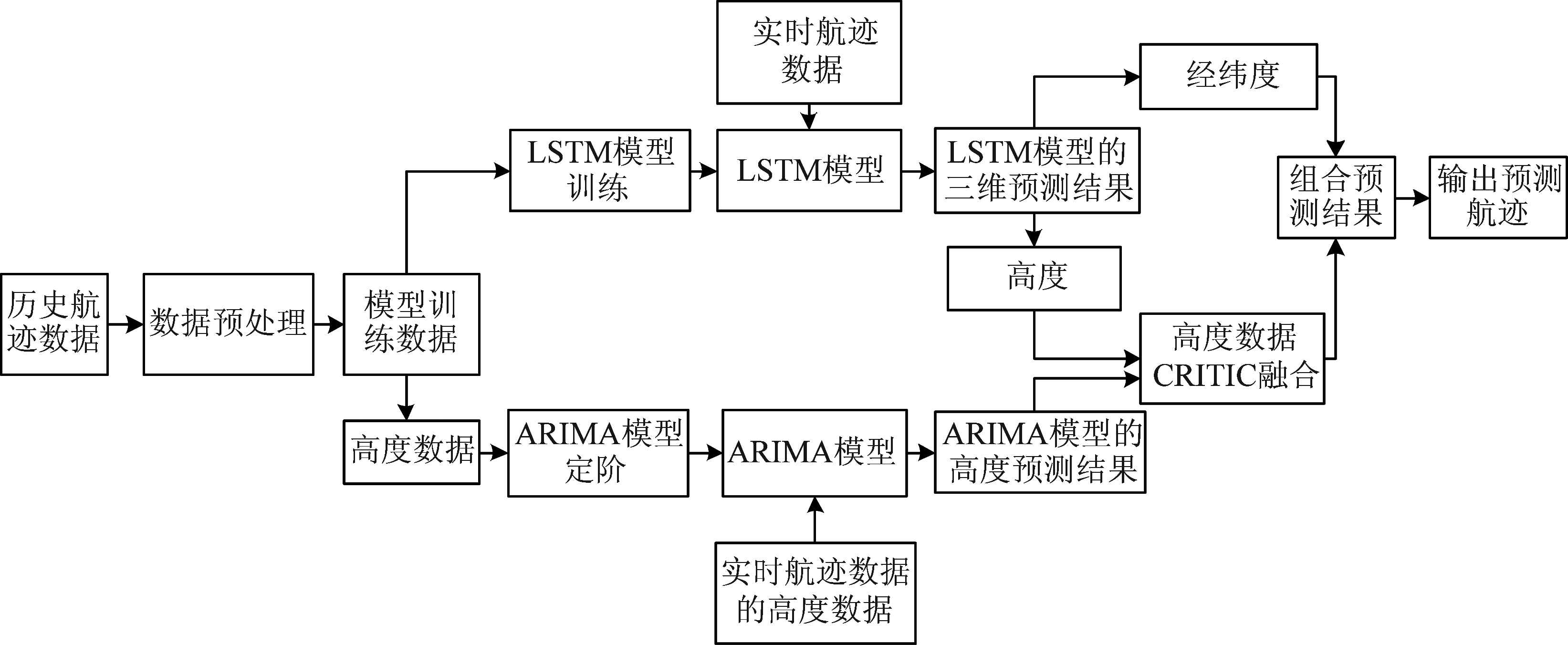
图4 组合模型预测过程 Fig.4 The process of combination model prediction
4 仿真实验及结果分析
4.1 实验数据集和环境
本实验的历史航班轨迹数据是来自某大型空中交通管理系统中某航班在2018年5月15日~2018年7月21日期间从国内机场A到机场B的历史飞行数据。采样时间间隔T为8 s,经过去冗余、采样之后总共有28710条记录。将5月15日~7月20日的航班历史轨迹数据按8:2划分为作为训练集和验证集,用于模型训练调参;7月21日用于模型预测精度的测试和误差分析。
本文的实验环境配置如表2所示。
表2 实验环境配置
Tab.2 Configuration of experimental environment

实验环境环境配置操作系统Windows10-64bitCPUIntel Core i5-4590内存8G编程语言Python 3.5.2深度学习框架Tensorflow 1.10
4.2 实验评价指标
假设预测的航迹点位置是Ppre(xpre, ypre, zpre),实际的观测点位置为Pobs(xobs, yobs, zobs)。用均方根误差(Root Mean Square Error, RMSE)来评价各个维度上的预测精度,用欧式距离Dist来描述预测航迹和真实航迹的相似度,计算如下:
(15)
Disti(upre,uobs)= ![]() i=1,2,…,n
i=1,2,…,n
(16)
其中,uobs表示真实值,upre表示预测值,n表示预测的航迹点个数。
4.3 组合模型CRITIC权重参数
使用CRITIC方法对LSTM和ARIMA预测的高度值进行融合,使其相互补偿的过程中最重要的是确定两组预测值各自的权重。最终,组合预测高度的结果为:
Hfinal=weightLSTM*hLSTM+weightARIMA*hARIMA
(17)
由2.3节CRITIC的计算步骤进行权值计算,最终得出LSTM模型预测的高度值和ARIMA模型预测的高度值的权重分别为:weightLSTM=0.61,weightARIMA=0.39。
4.4 实验及结果分析
为了验证不同大小的训练数据集对预测结果的影响,分别将2018年5月15日~7月20日的航班历史数据按照前12天历史数据、前22天历史数据、前55天历史数据和全部历史数据分割为四组数据集,每个数据集按照8:2划分为训练集和验证集训练LSTM-ARIMA模型,按照第3节所述进行模型训练,并预测其下一次飞行轨迹,计算预测航迹和真实航迹之间的误差,结果如表3所示。
表3 不同大小训练集训练模型的预测误差
Tab.3 Prediction errors of training models with different training sets
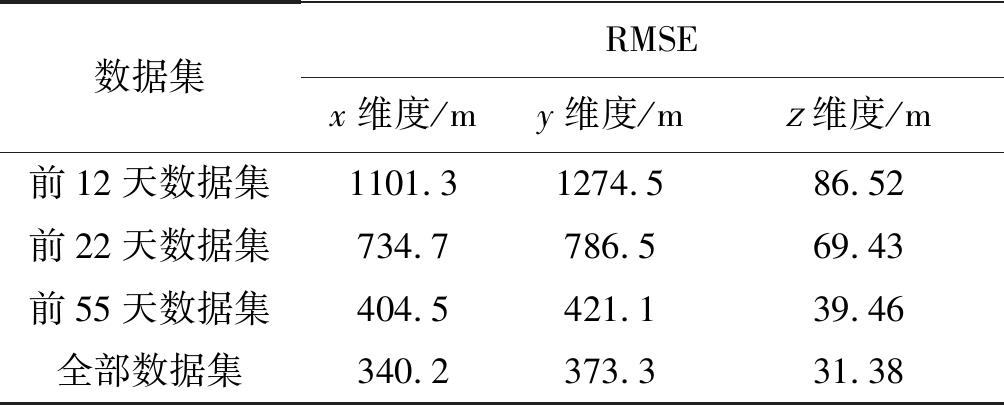
数据集RMSEx维度/my维度/mz维度/m前12天数据集1101.31274.586.52前22天数据集734.7786.569.43前55天数据集404.5421.139.46全部数据集340.2373.331.38
从表3可知,LSTM-ARIMA模型的预测结果和训练集大小密切相关,随着训练集的增大,预测精度逐渐提高,因此在本文中主要用2018年5月15日~7月20日的全部历史数据进行模型训练。在表2所述的实验环境下,用训练好的LSTM-ARIMA组合模型预测下一个航迹点所需要的时间大约是0.0836 s,远远小于相邻航迹点的采样时间间隔8 s,所以组合预测模型具有较好的实时性。
为了验证本文算法的预测性能,分别用IKF算法[9]、LSTM模型与本文的LSTM-ARIMA组合模型(LSTM的w=5)三种算法对2018年7月21日的航迹进行预测,计算各个模型的预测航迹和实际航迹在各个维度分量上的均方根误差和整个航迹的欧式距离分布,结果如表4、图5和图6所示。
表4 不同算法的预测误差
Tab.4 Prediction errors of different algorithms
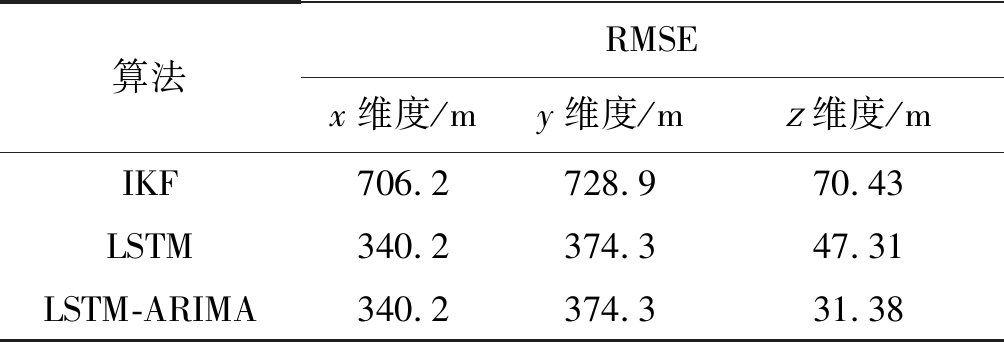
算法RMSEx维度/my维度/mz维度/mIKF706.2728.970.43LSTM340.2374.347.31LSTM-ARIMA340.2374.331.38
从表4和图5可以看出,本文的LSTM-ARIMA组合模型不论是在整个航迹上,还是各个维度分量上的预测性能均优于IKF算法,其高度的预测也有效的补偿了单一LSTM模型在高度预测上表现不足的问题,提高了整个模型的预测准确度;从图6中完整三维航迹可以看出,LSTM和LSTM-ARIMA模型预测的航迹比IKF算法预测的更加平滑稳定,而LSTM-ARIAM组合模型预测的航迹比LSTM模型的更加接近实际航迹,可以更好地描述航班在各个飞行阶段的位置变化。分析以上结果,可能的原因是LSTM对时间序列有良好的记忆能力,可以保持长期的序列特性,对应的在航迹预测中可以通过保持前一段时间的位置变化对当前时刻位置的影响权重及时调整当前的航班位置,而IKF预测算法只是根据前一时刻的位置信息预测当前时刻的位置信息,这样丢失了航班位置的历史变化信息,可能会造成误差累积,所以LSTM和组合模型预测的航迹更加平滑;LSTM-ARIMA组合模型既考虑了时序性也综合考虑了序列的平稳性和线性特征,可以对经度、纬度和高度序列根据其序列特性进行有效建模。

图5 三种算法在不同维度分量上的误差分析
Fig.5 Error analysis of three algorithms on different dimensional components


图6 三种算法预测的三维航迹
Fig.6 Prediction of 3D trajectory by three algorithms
5 结论
本文通过对航班飞行过程的研究,在历史航迹数据的基础上构建了新的特征数据,结合航班轨迹数据的特点,提出了基于LSTM和ARIMA组合模型的短期航迹预测方法。运用实际历史航迹进行实验,分别用LSTM-ARIMA组合模型、LSTM模型、IKF算法进行了航迹预测,对三种算法模型在不同特征维度上的误差进行分析对比,证明了LSTM-ARIMA组合模型算法的有效性。
本文的航迹预测方法仍存在着一些不足。例如,现在只能完成短期航迹预测,时间尺度较小,对于连续多个时刻的航迹点预测还需要通过多次递归实现,这样会存在累积误差,使得预测误差越来越大。因此,下一步将考虑引入天气特征和注意力机制模型继续改进预测模型。此外,LSTM-ARIMA组合模型需要大量的历史数据提前训练模型,模型的训练需要花费较多的时间,下一步也考虑引入在线学习的思想。
[1] Alvin S, John M. Air traffic functions in the NextGen and SESAS airspace[C]∥IEEE/AIAA 28th Digital Avionics Systems Conference. IEEE, 2009: 2.A.6-1-2.A.6-7.
[2] 伊群. 美国新一代空中交通管理系统运行概念[J]. 中国民用航空, 2007, 80(8): 27-31.
Yi Qun. Concepts of US New-generation ATM System[J]. China Civil Aviation, 2007, 80(8): 27-31.(in Chinese)
[3] 吕小平. 中国民航新一代空中交通管理系统发展总体框架[J]. 中国民用航空, 2007, 80(8): 24-26.
Lv Xiaoping. General Framework of China’s New-generation Civil Aviation ATM System[J]. China Civil Aviation, 2007, 80(8): 24-26.(in Chinese)
[4] Wang Z Y, Ling M. A Hybrid Machine Learning Model for Short-term Estimated Time of Arrival Prediction in Terminal Manoeuvring Area[J]. Transportation Research Part C, 2018, 95(2018): 280-294.
[5] Prretta M, Dupuy M D, Schuster W, et al. Performance Evaluation of a Novel 4D Trajectory Prediction Model for Civil Aircraft[J]. The Journal of Navigation, 2008, 61(3): 393- 420.
[6] 王超, 郭九霞, 沈志鹏. 基于基本飞行模型的4D航迹预测方法[J]. 西南交通大学学报, 2009, 44(2): 295-300.
Wang Chao, Guo Jiuxia, Shen Zhipeng. Prediction of 4D Trajectory Based on Basic Flight Models[J]. Journal of South West Jiao Tong University, 2009, 44(2): 295-300.(in Chinese)
[7] Kaneshige J, Benavides J, Sharma S, et al. Implementation of a Trajectory Prediction Function for Trajectory Based Operations[C]∥AIAA Atmospheric Flight Mechanics Conference. AIAA, 2014: 1-12.
[8] 吴鹍, 潘薇. 基于数据挖掘的四维飞行轨迹预测模型[J]. 计算机应用, 2007, 27(11): 2637-2639.
Wu Kun, Pan Wei. 4-D Trajectory Prediction Model Based on Data Mining[J]. Computer Applications, 2007, 27(11): 2637-2639.(in Chinese)
[9] 王涛波, 黄宝军. 基于改进卡尔曼滤波的四维飞行航迹预测模型[J]. 计算机应用, 2014, 34(6): 1812-1815.
Wang Taobo, Huang Baojun. 4D Flight Trajectory Prediction Model Based on Improved Kalman Filter[J]. Computer Applications, 2014, 34(6): 1812-1815.(in Chinese)
[10] 林毅, 张建伟, 武喜萍, 等. 基于GMM的航班轨迹预测算法研究[J]. 工程科学与技术, 2018, 50(4): 104-109.
Lin Yi, Zhang Jianwei, Wu Xiping, et al. Study on Algorithm for Flight Trajectory Prediction Based on GMM[J]. Advanced Engineering Sciences, 2018, 50(4): 104-109.(in Chinese)
[11] 权波, 杨博辰, 胡可奇, 等. 基于LSTM的船舶航迹预测模型[J]. 计算机科学, 2018(11A): 126-131.
Quan Bo, Yang Bochen, Hu Keqi, et al. Prediction Model of Ship Trajectory Based on LSTM[J]. Computer Science, 2018(11A): 126-131.(in Chinese)
[12] 孙致远, 鲁成祥, 史忠植, 等. 深度学习研究与进展[J]. 计算机科学, 2016, 43(2): 1- 8.
Sun Zhiyun, Lu Chengxiang, Shi Zhongzhi, et al. Research and Advances on Deep Learning[J]. Computer Science, 2016, 43(2): 1- 8.(in Chinese)
[13] Graves A. Supervised Sequence Labelling with Recurrent Neural Networks[M]. Springer Berlin Heidelberg, 2012: 31-38.
[14] Hochreiter S, Schmidhuber J. Long Short-term Memory[J]. Neural Computation, 1997: 1735-1780.
[15] 张树京, 齐立心. 时间序列分析简明教程[M]. 北京: 清华大学出版社, 2003: 24-59.
Zhang Shujing, Qi Lixin. Concise Course on Time Series Analysis[M]. Beijing: Tsinghua University Press, 2003: 24-59.(in Chinese)
[16] 刘学文. 基于分数差和分形滤波的网络流量模型[D]. 济南: 山东大学, 2011.
Liu Xuewen. Network Traffic Model Based on Fractional Differencing and Fractal Filter[J]. Jinan: Shandong University, 2011.(in Chinese)
[17] 程俊. 基于ARIMA-LSTM混合模型的机械传动件制造企业销售预测方法研究与应用[D]. 成都: 电子科技大学, 2018.
Cheng Jun. Research and Application of Sales Forecasting Method for Mechanical Transmission Parts Manufacturing Enterprises based on ARIMA-LSTM Hybrid Model[D]. Chengdu: University of Electronic Science and Technology of China, 2018.(in Chinese)
[18] 姜爱萍, 张蓝飞. 基于CRITIC赋权法的我国金融稳定测度体系[J]. 技术与创新管理, 2018, 39(4): 404- 406.
Jiang Aiping, Zhang Lanfei. China’s Financial Stability Measurement System Based on CRITIC Empowerment Method[J]. Technology and Innovation Management, 2018, 39(4): 404- 406.(in Chinese)
[19] Alligier R, Gianazza D, Durand N. Machine Learning and Mass Estimation Methods for Ground-based Aircraft Climb Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3138-3149.
[20] Zheng Yu, Zhou Xiaofang. Computing with Spatial Trajectories[M]. New York: Springer, 2011: 167-171.
[21] 石磊, 吴仁彪. 预测位置空间离散化的多航路中期冲突探测算法[J]. 信号处理, 2012, 28(11): 1522-1528.
Shi Lei, Wu Renbiao. Multi-route Mid-term Conflict Detection Algorithm based on Discretization of Predicted Position Space[J]. Signal Processing, 2012, 28(11): 1522-1528.(in Chinese)
[22] 孙达, 蒲英霞. 地图投影[M]. 南京: 南京大学出版社, 2012: 63-70.
Sun Da, Pu yingxia. Map Projections[M]. Nanjing: Nanjing University Press, 2012: 63-70.(in Chinese)



