1 引言
实际环境中的信号大多数是非平稳的,它们的频率随时间的变化而变化,称为瞬时频率(Instantaneous Frequency,IF)。随着信息化技术的发展和大数据时代的到来,非平稳信号的构成也越来越复杂,通常以多分量的形式存在。而信号IF所包含的信息有利于各个分量的分析与识别,在雷达、声纳、语音分析与识别、通信、生物医学、地震及其他领域中具有重要的实际意义[1-3]。因此,IF估计成为信号处理方向中的一个研究热点,在分类特征提取、信号检测、全球导航卫星系统的干扰消除和故障诊断等实际问题[3-5]中有着广泛的应用前景。
现有的IF估计方法大致可分为参数法与非参数法[6-7]。参数法利用多项式或其他相位模型来估计信号的相位参数[8-10]。尽管这些方法具有统计有效性,但它们通常需要较高的计算复杂度且难以适用于多分量信号。此外,参数法中的信号形式已知,而实际环境中信号的IF变化通常是无法预测的。非参数法能够弥补这一缺陷,它不需要知道信号模型。非参数法主要为相位差分法、瞬时自相关法和时频分布(TimE-Frequency Distribution, TFD)法。由于时频(TimE-Frequency,TF)分析是研究非平稳信号的有效工具,因此基于TFD的IF估计方法吸引了诸多研究者的关注,这也是本文的主要研究对象。
TFD能够沿IF曲线集中信号能量并使噪声散布在TF域上,所以给定时刻点的频率可以通过TF平面上的峰值位置来估计。大多数基于TFD的IF估计方法对于单分量信号的效果令人满意,而针对多分量信号,IF的提取极具挑战性。一些传统方法采用信号频谱分解的方式,将多分量信号转化为单分量信号之和,然后依照单分量信号的处理方法应用到每个分离的分量上。这样的估计方法难以适用于具有交叠IF曲线的信号。另一些方法对检测到的峰值进行分配得到相应的IF曲线,这种分配方式通常利用IF轨迹在连续时间下变化缓慢的特性来完成,例如基于维特比的方法[11-18];或者利用峰值的局部连接性,如基于图像处理的方法[19]。在文献[20]和[21]中,两种盲源分离算法可以从无交叉项的TFD中分离出多分量信号的成分。然而,如果信号分量在TF域相交或相近,该类方法将难以提取出正确的IF曲线。当信号分量的IF轨迹相交时,文献[7]建立马尔可夫随机场连接相同分量的IF线段,但该方法需要对所有的可能路径轨迹进行全面的搜索,产生较高的计算成本。文献[22]提出一种基于路径重组的IF估计方法,尽管该方法计算简单,但它对噪声的鲁棒性不高。大量的研究工作表明TFD分辨率的高低以及交叉项的干扰影响着IF估计的准确度。维格纳分布(Wigner-Ville Distribution,WVD)作为一种经典的TFD,被广泛应用于调频信号的IF估计[11,16,23-24]。WVD在实现信号能量高度集中的同时也引入了交叉项的干扰。因此,许多改进的TFD例如B分布(B Distribution,BD)、S变换等致力于提高分辨率的同时尽可能地抑制交叉项,以更好地反映IF的曲线轨迹[13-15,17, 25-27]。例如文献[17]和[27]利用一种自适应方向分布来减少交叉项的干扰,从而能够准确估计出信号的IF。
从上述研究内容可知,信号的TFD图像与对应的IF轨迹息息相关,基于TFD的IF估计方法受TFD的TF聚集性和交叉项的影响[6, 25]。随着深度学习的不断发展,神经网络的应用深入到各个领域。其中,生成对抗网络(Generative Adversarial Networks,GAN)[28]由于能够学习样本的真实分布,排除干扰,生成多样性的输出样本[29]而被成功应用至图像去噪、增强等领域[30]。考虑对像素较多的图像处理的不可控性,文献[31]对原始GAN增加条件约束,提出条件生成对抗网络(Conditional Generative Adversarial Networks,CGAN)。尽管CGAN在图像风格转换[32]等领域有较为成熟的应用,但如何利用它来克服多分量信号TFD图像的分辨率低与交叉项多等缺点以得到更好的IF估计结果仍然是一个极具挑战性的研究问题。就多分量信号而言,噪声与交叉项的干扰更为明显,现有的TF分析方法也难以达到时域与频域高分辨率的兼顾,这样的训练数据增加了CGAN的训练难度。此外,CGAN损失函数的合理设计也是取得期望TFD图像的重要环节之一,其对于网络训练的结果有较大的影响。受到文献[32]的启发,本文采用CGAN对经过TF分析产生的TFD图像进行处理以获取噪声与交叉项减弱的TFD图像,从而能够更加准确地反映出信号的IF曲线。
综上所述,本文针对多分量信号的IF估计问题提出一种基于条件对抗生成TFD的方法,该方法在信号的IF曲线相交或相近的情况下均能准确有效地估计出相应的IF轨迹。首先本文采用文献[33]提出的掩膜维格纳分布(Masked Wigner-Ville Distribution,MWVD)作为CGAN的输入TFD图像,通过生成模型与判别模型的联合训练,从而实现TFD的对抗生成,得到优化的TFD图像。然后本文通过增加一项惩罚线段梯度的函数提出了一种改进的维特比方法,以提取不同信号分量的IF曲线,实现最终的IF估计。
2 时频分布
一个多分量非平稳信号z(t)可以表示为:
(1)
其中N为分量总数,Ai、 fi(τ)分别表示第i分量的幅值和IF,n(t)为加性噪声。如前所述,TF分析是研究式(1)中信号的强大工具。常见的TFD一般分为两大类:线性TFD与非线性TFD。线性TFD的代表包括短时傅里叶变换(Short-Time Fourier Transform,STFT)、小波变换、S变换以及广义S变换等。这类TFD具有线性叠加特性,尽管没有交叉项的干扰,但其在时间和频率上的分辨率难以同时兼顾。非线性TFD有WVD及其衍生的系列分布、Cohen类TFD等。这类分布在具有良好TF凝聚性的同时引入了交叉项。由于TFD的种类繁多,基于TFD的IF估计方法的性能往往依赖于所选取的具体TF变换[25]。作为最基础的二次(非线性)TFD,信号z(t)的WVD表示为:
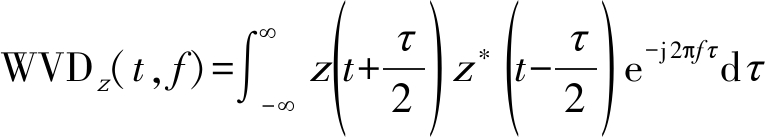
(2)
其中WVDz(t, f)是z(t)的WVD,等式右边的上标*表示共轭操作。WVD实现了信号在TF域上的最大能量集中。但由式(1)可知,它是信号的双线性变换,不可避免地带来交叉项。另一种比较常见的TF分析方法是STFT:
STFTz(t, f)=![]() z(τ)h(τ-t)e-j 2πfτdτ
z(τ)h(τ-t)e-j 2πfτdτ
(3)
其中STFTz(t, f)是z(t)的STFT,h(t)是窗函数。STFT是一种线性TFD,它的二次形式被称为信号谱图(Spectrogram,SPEC):
SPECz(t, f)=|STFTz(t, f)|2
(4)
其中SPECz(t, f)是z(t)的SPEC。根据式(2),STFT没有交叉项,因此SPEC也没有交叉项。与WVD相比,尽管STFT的分辨率较低,但它的计算成本也较低,且无交叉项的干扰。为了使信号的TFD具有较高TF聚集性的同时抑制交叉项的影响,文献[33]提出MWVD:
MWVDz(t, f)=WVDz(t, f)⊙STFTz(t, f)
(5)
其中MWVDz(t, f)是z(t)的MWVD,⊙表示哈达玛积操作。图1的(a)、(b)、(c)、(d)分别展示了信噪比(Signal to Noise Ratio,SNR)为5 dB下的WVD、SPEC、MWVD以及理想TFD。从图1中可看出,MWVD兼顾了上述WVD与SPEC的优点,更加真实地反映了信号的IF轨迹。
3 所提瞬时频率估计方法
3.1 基于条件生成对抗网络的时频分布
尽管MWVD相比WVD而言抑制了交叉项,但这样的抑制效果在信号分量相近或相交的情况下并不明显,且其在TF域的能量聚集性也不及WVD。受到GAN在图像去噪领域成功应用[29]的启发,本文利用GAN的拓展网络CGAN,对MWVD图像进行处理,使生成的TFD在保持高TF聚集性的同时抑制交叉项。文献[28]提出的生成对抗模型GAN是学习将样本z从一个分布映射到另一个分布的样本x。GAN由生成器G和识别器D组成,G的目标是模拟真实的数据分布,而D是一个二进制分类器,负责对模拟的分布进行判断反馈给G来不断提高生成数据的质量。具体来说,通过优化以下目标函数,可以联合训练G和D:

图1 多分量信号的时频分布图像(SNR=5 dB)
Fig.1 Different TFD images of a multicomponent signal (SNR=5 dB)
minGmaxDV(G,D)=Ex~Pdata(x)[logD(x)]+ Ez~Pz(z)[log(1-D(G(z)))]
(6)
其中x是从分布Pdata(x)中采样的真实数据(这里为理想TFD图像),z表示从某已知分布Pz(z)中采样的随机数据(这里为MWVD图像)。D(x)是D对于真实数据x判断是否真实的概率,D(G(z))是D对于生成的数据G(z)(这里为新生成的TFD图像)判断是否真实的概率。足够多的训练数据与迭代次数能够使分布PG收敛到Pdata(本文实验中的训练阶段设为200可达到收敛),从而使新生成的TFD数据与真实的TFD数据分布一致,其证明如下。在GAN的公式中,
V(G,D)=Ex~Pdata(x)[logD(x)]+ Ez~Pz(z)[log(1-D(G(z)))]
(7)
对于判别器D 而言,希望D(x)尽量大(即对于真实数据,D(x)需接近于1),D(G(z))尽量小(即对于生成数据,D(G(z))需接近于0),因此D希望V(G,D)尽量大。而对于生成器G而言,则希望D(G(z))尽量大,而D(x)的值由D决定是不变的,故G希望V(G,D)尽量小。首先固定G来求解最优的D:
V(G,D)=Ex~Pdata(x)[logD(x)]+ Ez~Pz(z)[log(1-D(G(z)))] =
Ex~Pdata(x)[logD(x)]+Ex~PG(x)[log(1-D(x))] =
(8)
将上式积分中的函数Pdata(x)log(D(x))+PG(x)log(1-D(x))对D求导,使其等于0可得![]() 将该表达式代入V(G,D)继续求解使其最小的G的表达式:
将该表达式代入V(G,D)继续求解使其最小的G的表达式:

(9)
其中KL(a||b)≥0代表KL散度,当a=b时等号成立。而根据Jensen-Shannon散度公式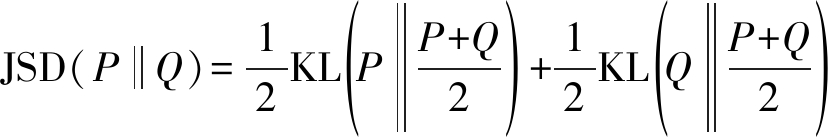 可得:
可得:
maxDV(G,D)=-log4+2JSD(Pdata||PG)
(10)
与KL散度相同,JSD(a||b)≥0且在a=b时等号成立。故要使式(10)达到最小,需使Pdata=PG,即生成数据与真实数据分布一致。
为了获得更多的映射信息,本文采用文献[31]提出的CGAN来增强一些数据的附加信息。假设样本y表示数据的附加信息,则生成器G(z,y)在y的约束下生成数据。而CGAN中判别器D(x,y)的输出也被y所控制,其目标函数变化为:
minGmaxDVCGAN(G,D)=Ex~Pdata(x)[logD(x,y)]+ Ez~Pz(z)[log(1-D(G(z,y),y))]
(11)
研究表明在CGAN中加入传统的损失函数,如l1或l2范数,有利于进一步提升网络的有效性。本文采用l2范数作为附加损失函数,使得最终的生成图像更接近真实图像,则本文网络的总目标函数为:
L*=argminGmaxDVCGAN(G,D)+λVl2(G)
(12)
其中Vl2(G)=Ez,x,y[||x-G(z,y)||2],λ为正则化参数,防止过拟合情况。与文献[29]学习方式相同,本文采取有监督学习方式,将MWVD图像作为CGAN的输入,理想TFD图像作为目标图像,以此来训练网络的生成器G与判别器D。其具体的学习过程如图2所示,第一行过程表示为生成器G接收输入的MWVD图像,将其转换为逼近目标图像的生成图像。该图像将与MWVD图像一起作为判别器D的输入,以此得到负样本。第二行过程表示为目标图像与MWVD图像共同输入至判别器D中,以此得到正样本。本文令基于CGAN新生成的TFD图像的缩写名称是TFDCGAN。需要说明的是,一旦网络的各项参数训练完毕,在实际应用中,对于任何一个随机产生的多分量信号的MWVD图像,该训练好的网络均可得到相应的TFDCGAN,此时不需要理想的TFD作为先验信息。
3.2 基于改进维特比算法的IF估计
如3.1节所示,通过CGAN生成的TFDCGAN图像能够非常准确地反映不同IF曲线的轨迹。对于单分量信号,此时可直接利用TFD的峰值估计出准确的IF信息。但对于多分量信号,一个时间样本点上大概率存在多个TFD峰值。此外,强噪声将干扰TFD峰值的位置分布,这些因素均为多分量信号IF的估计带来一定的挑战。文献[11]所提出的维特比算法是一种经典的多分量信号IF估计算法,在此基础上大量工作(详情见文献[12-18])对此算法提出改进方案,以提高算法在低SNR环境下的稳健性及鲁棒性。考虑到所得TFDCGAN图像更加接近理想的时频分布,在很大程度上已降低了噪声及交叉项对估计算法的不良影响,因此本文提出的改进算法重点解决信号分量的IF在相近或相交情况下所带来的估计误差问题。文献[11]所提出的算法在估计IF曲线相交的区域时会存在如图3(a)所示的错误情况,这是由于维特比算法中的惩罚函数并未考虑到曲线变化的角度信息。因此,本文在原有的惩罚函数上增加了一个惩罚线段梯度的函数,使其在IF曲线交叉的区域仍保持较好的估计准确度(见图3(b))。
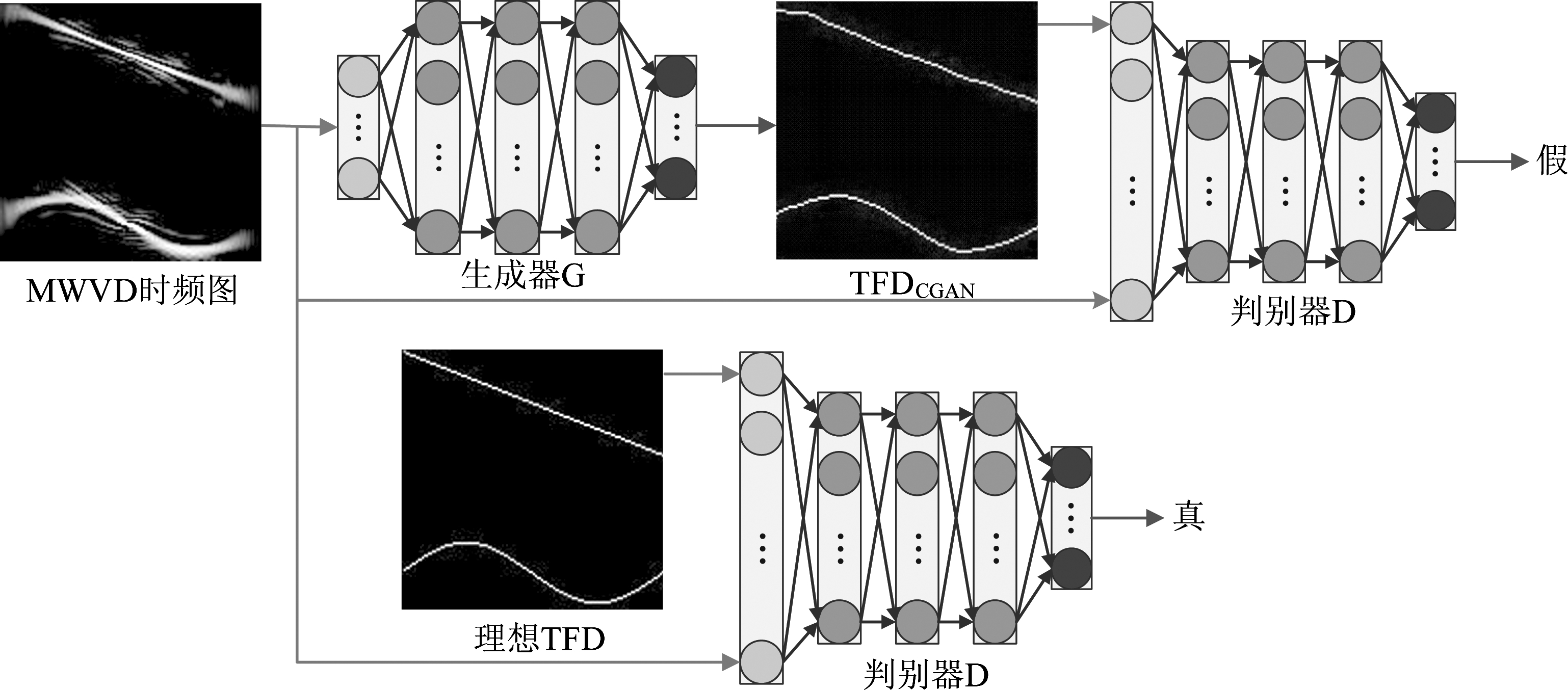
图2 本文用于产生时频分布图像的条件生成对抗网络训练过程
Fig.2 Network training procedure of CGAN for TFD images generation (TFDCGAN) in this paper

图3 二分量信号的IF估计示意图
Fig.3 IF estimation illustration of a two-component signal
假设基于TFD图像得到的所有可能的IF曲线路径为p(t),则本文所期望的IF最优路径可通过下面的惩罚函数获得:
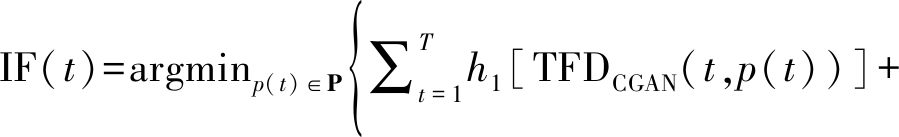

(13)
其中t∈[1,T]表示时间样本点,T为TFD上的时间样本点数。假设每一条路径均能用长度为L(L足够小)的线段来逼近,K是相应线段的数量,则g(k)表示第k线段的梯度。h1是对TFD幅值的惩罚函数;h2是对相邻时间样本点上频率变化的惩罚函数;h3是对相邻时间样本点上IF曲线梯度变化的惩罚函数,它们的数学表达分别为:

(14)
其中fj∈F, j∈[1,F],F是当前时间的频率采样点集合,F是对应的采样点总数。TFDCGAN(t, f)被排序为非递增序列,即:TFDCGAN(t,f1)≥TFDCGAN(t,f2)≥…≥TFDCGAN(t,fj)≥…≥TFDCGAN(t,fF)。参数d1,d2,Δ1,Δ2依据实际情况来确定。对于N个信号分量,基于改进维特比算法的IF估计步骤总结如下:
1)利用式(13)中改进的惩罚函数找到第一条IF最优路径IFi(t),i=0,即代表最强的信号分量;
2)通过对1)中的最优路径区域设置为0产生一个新的TFD;
3)重复1)和2)得到下一个最优路径IFi(t)(i=i+1),直到更新的TFD的能量值小于一个阈值ε,停止迭代。
在上述步骤中,当N个信号分量提取出来后,由于在步骤2)中已提取的信号分量所在的TF区域被设置为0,故最终更新的TFD将不包含分量信息,只留下少数噪声等能量值较小的区域,因此该TFD的能量值将小于所设置的阈值,从而停止迭代。
4 实验仿真
为了验证本文所提方法的有效性,本文选取线性调频(Linear Frequency-Modulated,LFM)分量和正弦调频(Sinusoidal Frequency-Modulated,SFM)分量组成的多分量信号为例进行实验。在TFDCGAN的生成过程中,生成器G与判别器D的具体网络结构参照文献[31]。在IF估计均采用本文改进的维特比算法的前提下,选取经典的WVD、BD以及MWVD三种TFD与TFDCGAN分别进行相应的仿真实验,从而进一步验证所提方法的性能。计算WVD、BD、MWVD、TFDCGAN和实现改进维特比算法的实验运行环境为:Intel(R) Core(TM) i7-7700 CPU,3.60 GHz时钟频率,16.0 GB内存;CGAN在NVIDIA GeForce GTX 1080下进行训练。
4.1 数据集及实验细节
本文的数据集由2000组随机产生的不同SNR环境下的含噪多分量信号的MWVD图像与理想TFD图像组成,所加噪声为高斯白噪声,SNR范围为0~20 dB,分量形式包括LFM与SFM。信号长度T=256,采样率设为1 Hz,则利用式(5)产生的MWVD图像大小均为大小为256×256,对应理想TFD图像的尺寸也与之相同。具体数据集的图像形式与文献[31]相同,MWVD图像与理想TFD图像并列为一幅图像,其大小为512×256。图4展示了本文部分数据集示例,整个数据集涵盖单LFM分量、单SFM分量、二LFM分量、二LFM和SFM分量、三LFM分量、三LFM和SFM分量等多种分量组合形式的信号。数据集中的信号分量数范围是1~3,分量在TF域的位置包括不相交、相近、相交等多种情况。CGAN训练的损失函数如式(12)所示,训练的批量大小为16,并训练200个阶段,初始学习率设置为0.002。
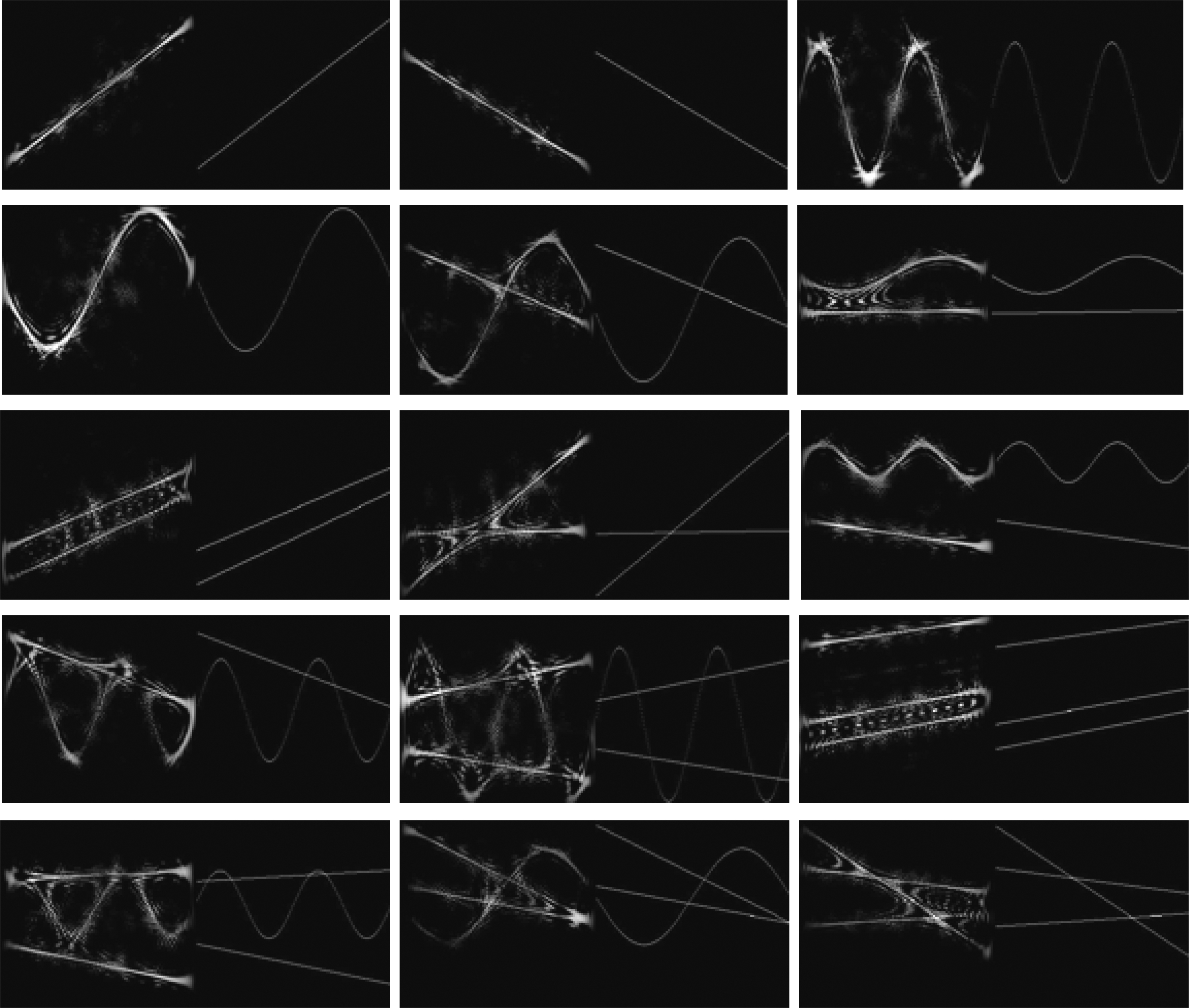
图4 本文部分数据集示例
Fig.4 Examples of dataset in this paper
4.2 实验结果及分析
考虑到文章篇幅问题,本文选择了三种具有代表性的多分量信号进行实验结果的展示,包括二分量信号z1(t):两个LFM分量相交,二分量信号z2(t):两个LFM分量相近和二分量信号z3(t):一个LFM分量与一个SFM分量相交。它们的数学表达式为:
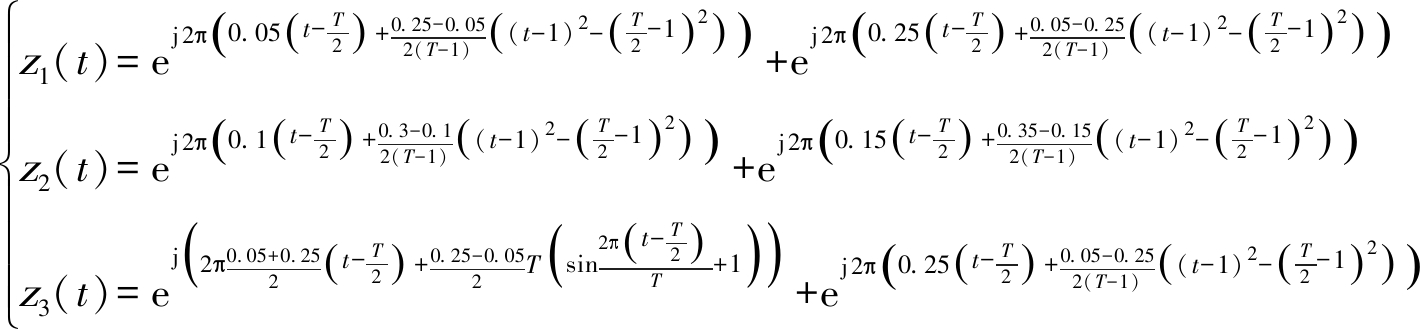
(15)
其中,T为信号的时间样本点数,本文实验中的T=256。分别采用 WVD、BD、MWVD和TFDCGAN图像和本文改进维特比算法进行50次蒙特卡洛实验的IF估计。此外,本文采用文献[33]所给出的标准均方误差(Normalized Mean Square Error,NMSE)作为IF估计的评估指标。
图5(a)、(b)和(c)分别展示了在SNR=4 dB时z1(t)、z2(t)和z3(t)的MWVD图像、理想TFD图像和TFDCGAN图像。如图5所示,z1(t)(见图5第一行)是两个LFM分量相交的信号,它的MWVD在分量相交的区域受到噪声的影响,存在一定的交叉项,而它的TFDCGAN在该区域上的交叉项几乎全被消除,非常接近理想TFD。z2(t)(见图5第二行)是两个LFM分量相近的信号,它的MWVD存在明显的交叉项干扰,而从对应的TFDCGAN图像可看出,这一交叉项问题得到了很好的解决。z3(t)(见图5第三行)是一个LFM分量与一个SFM分量相交的信号,它的MWVD除了在分量相交的区域具有交叉项,其SFM分量在TF域上的能量集中效果不佳,而由CGAN生成的TFDCGAN图像在抑制噪声和交叉项的同时也对SFM分量进行增强,更加准确地反映出IF曲线的轨迹。

图5 网络测试中z1(t)、z2(t)、z3(t)的不同时频分布 图像(z1(t)代表两LFM分量相交的信号; z2(t)代表两LFM分量相近的信号; z3(t)代表LFM分量与SFM分量相交的信号)
Fig.5 TFD images of z1(t), z2(t), z3(t) in CGAN testing (z1(t) denotes a multicomponent signal with 2 LFM components intersecting; z2(t) denotes a multicomponent signal with 2 LFM components closely spaced; z3(t) denotes a multicomponent signal with a LFM component and a SFM component intersecting)
为了进一步验证算法的性能,本文分别在WVD、BD、MWVD与TFDCGAN四种TFD图像下利用改进的维特比算法估计z1(t)、z2(t)和z3(t)的IF,其NMSE结果如图6~图8所示。图6展示了z1(t)信号在不同TFD下的NMSE对比结果。从该结果来看,当两LFM分量在TF域相交时,基于TFDCGAN的IF估计针对不同噪声场景其结果均优于其他三种TFD,而在低SNR情况下,这种优势更加明显。由于WVD对噪声的鲁棒性不高,因此它对应的IF估计效果随SNR增大有显著提高。相比之下,利用其他三种TFD估计IF的结果在高SNR环境下的增长幅度较小。当SNR<16 dB时,BD在一定程度上抑制了由噪声导致的交叉项干扰,因此基于BD的估计结果略优于基于WVD的估计结果。但当SNR >16 dB,噪声对于IF估计的不利影响越来越小,此时WVD集中信号能量的优势突显,其对应的估计结果表现出较大的提升。而当SNR<4 dB时,尽管MWVD抑制了WVD的交叉项,但依然受到强噪声的影响,使得基于MWVD的IF估计结果不如所提方法的结果准确。

图6 z1(t)在不同时频分布下的IF估计性能对比
Fig.6 Performance comparison of IF estimation of z1(t) with different TFDs
图7说明了利用z2(t)信号的四种TFD估计IF的性能对比结果。从图中可看出,TFDCGAN对应的IF估计结果具有非常明显的优势,在SNR=0 dB时其NMSE就已达到-30 dB以下。当两LFM分量在TF域的位置相近时,噪声对于BD图像的分辨率影响较大,因此在SNR<16 dB范围内的相应IF估计效果不佳。而SNR>16 dB,BD的分辨率得到改善而WVD交叉项的影响减少,因此两种TFD得到的NMSE结果相当。此外,尽管MWVD对WVD交叉项进行了抑制,但对于分量位置非常相近的信号,这种抑制效果减弱,使得基于MWVD的IF估计结果相比于WVD对应的估计结果提升幅度不高。
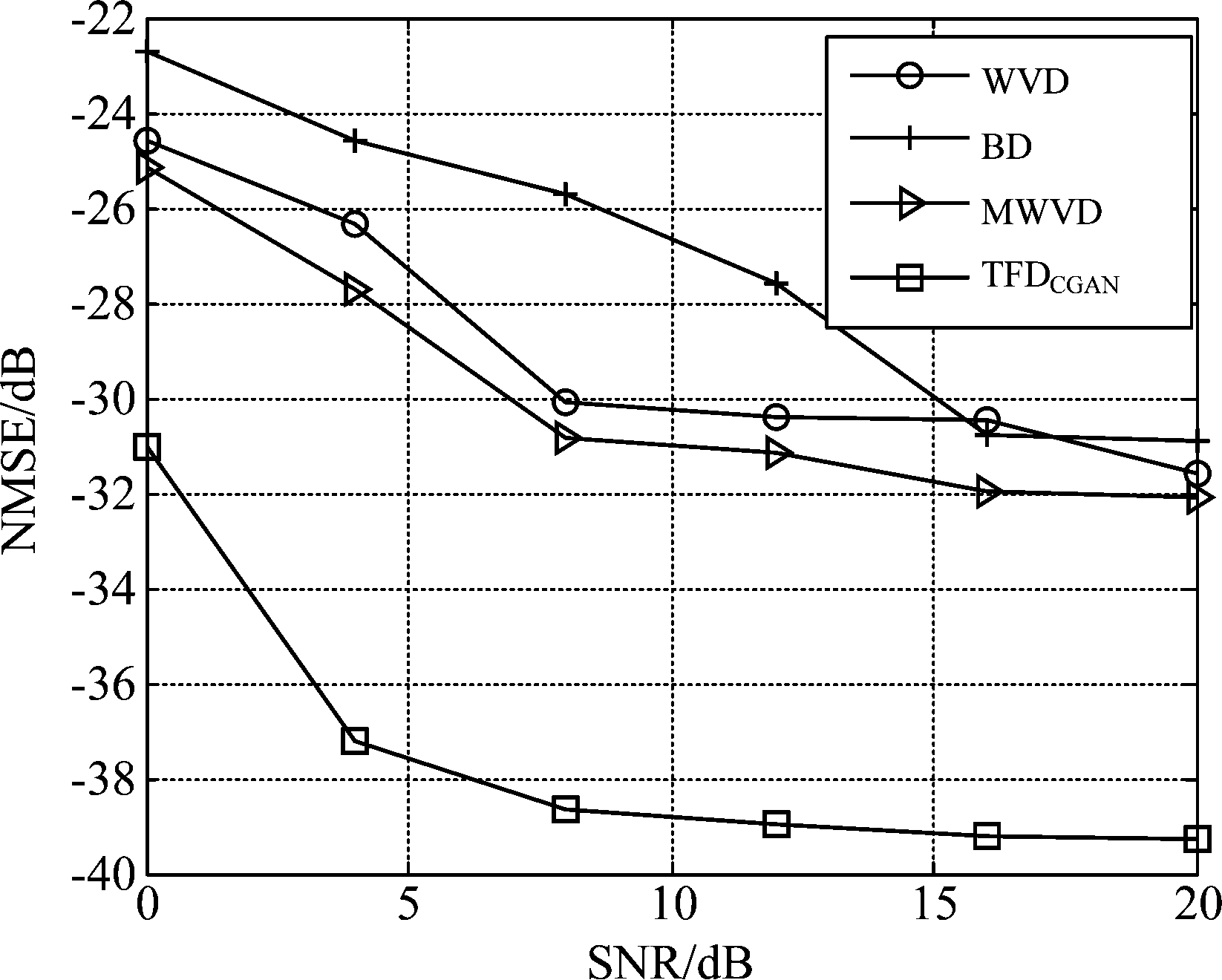
图7 z2(t)在不同时频分布下的IF估计性能对比
Fig.7 Performance comparison of IF estimation of z2(t) with different TFDs
z3(t)信号在不同TFD下的IF估计结果如图8所示,从结果来看,基于TFDCGAN估计的IF在所有TFD中是最准确的。值得注意的是,BD、MWVD和TFDCGAN对应IF估计的NMSE结果随SNR的增大呈下降趋势,而WVD对应IF估计的NMSE结果则保持在-12 dB左右,随SNR的变化缓慢。这是因为当LFM分量与SFM分量相交时,SFM分量的WVD在TF域上的能量集中效果很差,并产生较多的交叉项。这些交叉项对于IF估计的影响已超过噪声对其的影响,因此基于WVD的IF估计效果较为糟糕且基本不随SNR的增大而变化。
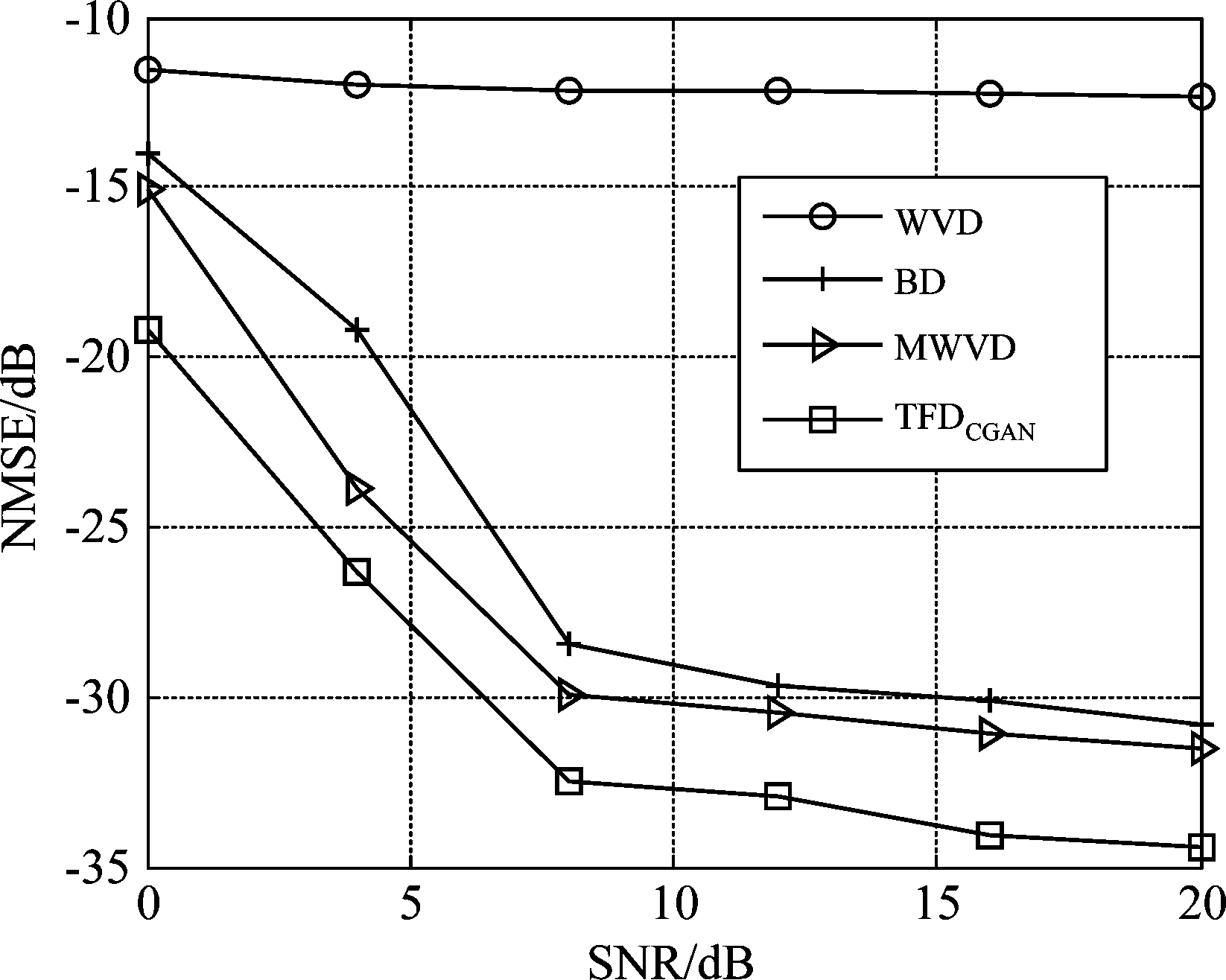
图8 z3(t)在不同时频分布下的IF估计性能对比
Fig.8 Performance comparison of IF estimation of z3(t) with different TFDs
最后,表1展示了当SNR为16 dB时分别在四种TFD下对z1(t)信号(长度为256)进行IF估计的各方法平均运算时间。需要说明的是,CGAN的训练过程花费时间较长。但一旦网络训练完毕,实验表明利用该网络得到TFDCGAN的速度较快。正如表1所示,基于TFDCGAN估计IF的运行时间为7.5749 s,仅比基于MWVD估计IF的运行时间多了0.0076 s。
表1 不同时频分布下z1(t)信号的 IF估计的平均运算时间(SNR=16 dB)
Tab.1 Average time cost of IF estimation ofz1(t) with different TFDs (SNR=16 dB)

TFDWVDBDMWVDTFDCGAN平均时间/s7.53188.02177.56737.5749
5 结论
本文针对信号分量在TF域位置相近或相交的情况,提出一种基于条件对抗生成TFD的多分量非平稳信号的IF估计方法。该方法首先利用MWVD图像训练经典的CGAN,由此得到接近于理想TFD的TFDCGAN图像。然后采用一种改进的维特比算法提取出不同分量的IF曲线。该改进算法增加了一个惩罚线段梯度的函数,从而解决了原始维特比算法在分量相交处的错误估计问题。仿真结果验证了本文提出的IF估计方法在信号分量相交或相近情况下的有效性和优越性。当信号分量在TF域非常接近时,这种优势更加明显。本文提出的IF估计方法具有较强的实用性,能够广泛应用于分类特征提取、信号检测、全球导航卫星系统的干扰消除和故障诊断等多个领域。
[1] ![]()
![]() S, et al. Instantaneous Frequency in TimE-Frequency Analysis: Enhanced Concepts and Performance of Estimation Algorithms[J]. Digital Signal Processing, 2014, 35: 1-13.
S, et al. Instantaneous Frequency in TimE-Frequency Analysis: Enhanced Concepts and Performance of Estimation Algorithms[J]. Digital Signal Processing, 2014, 35: 1-13.
[2] Aoi M, Lepage K, Lim Y, et al. An Approach to TimE-Frequency Analysiswith Ridges of the Continuous Chirplet Transform[J]. IEEE Transactions on Signal Processing, 2015, 63(3): 699-710.
[3] Khan N A, Ali S. Exploiting Temporal Correlation for Detection of Non-stationary Signals Using a DE-chirping Method Based on TimE-Frequency Analysis[J]. Circuits, Systems, and Signal Processing, 2018, 37(8): 3136-3153.
[4] Wang C, Kong F, He Q, et al. Doppler Effect Removal Based on Instantaneous Frequency Estimation and Time Domain RE-sampling for Wayside Acoustic Defective Bearing Detector System[J]. Measurement, 2014, 50: 346-355.
[5] Amin M G, Borio D, Zhang Y D, et al. TimE-Frequency Analysis for GNSSs: From Interference Mitigation to System Monitoring[J]. IEEE Signal Processing Magazine, 2017, 34(5): 85-95.
[6] 白航, 赵拥军, 胡德秀, 等. 基于改进时频分析方法的雷达信号瞬时频率估计[J]. 信号处理, 2012, 28(2): 257-263.
Bai Hang, Zhao Yongjun, Hu Dexiu, et al. Instantaneous Frequency Estimation for Radar Signals Based on Improved TimE-Frequency Distribution[J]. Signal Processing, 2012, 28(2): 257-263.(in Chinese)
[7] Zhang H, Bi G, Yang W, et al. IF Estimation of FM Signals Based on TimE-Frequency Image[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 326-343.
[8] Cirillo L, Zoubir A, Amin M. Parameter Estimation for Locally Linear FM Signals Using a TimE-Frequency Hough Transform[J]. IEEE Transactions on Signal Processing, 2008, 56(9): 4162- 4175.
[9] 刘昌云, 水鹏朗, 李松. 基于频率模型和时频分析的正弦信号频率高精度估计算法[J]. 信号处理, 2012, 28(8): 1077-1082.
Liu Changyun, Shui Penglang, Li Song. Precise Frequency Estimation Algorithm of Sinusoidal Signals Based on Frequency Model and TimE-Frequency Analysis[J]. Signal Processing, 2012, 28(8): 1077-1082.(in Chinese)
[10] 胡鑫磊, 张国毅, 赵立新, 等. 改进多尺度Chirplet路径追踪算法在非线性调频信号估计中的应用[J]. 信号处理, 2015, 31(8): 941-948.
Hu Xinlei, Zhang Guoyi, Zhao Lixin, et al. Improved Muti-scale Chirplet Path Pursuit and its Application in Instantaneous Frequency Estimation of Nonlinear Frequency Modulation Signal[J]. Journal of Signal Processing, 2015, 31(8): 941-948.(in Chinese)
![]() L. An Algorithm for the Wigner Distribution Based Instantaneous Frequency Estimation in a High Noise Environment[J]. Signal Processing, 2004, 84(3): 631- 643.
L. An Algorithm for the Wigner Distribution Based Instantaneous Frequency Estimation in a High Noise Environment[J]. Signal Processing, 2004, 84(3): 631- 643.
[12] Zeng Q, Li Y, Deng X. Adaptive TimE-Frequency Peak Filtering Based on Convex Sets and the Viterbi Algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(6): 1267-1271.
[13] Jiang L, Li L, Zhao G, et al. Instantaneous Frequency Estimation of Nonlinear Frequency-Modulated Signals Under Strong Noise Environment[J]. Circuits, Systems, and Signal Processing, 2016, 35(10): 3734-3744.
[14] 朱明哲, 肖瑞, 苏小凡, 等. 混合噪声下基于Viterbi同步压缩S变换的FM信号分析[J]. 电子与信息学报, 2018, 40(12): 2913-2918.
Zhu Mingzhe, Xiao Rui, Su Xiaofan, et al. Analysis of FM Signals Based on Viterbi Synchrosqueezing S-transform in Mixture Noise[J]. Journal of Electronics & Information Technology, 2018, 40(12): 2913-2918.(in Chinese)
[15] Li P, Zhang Q. An Improved Viterbi Algorithm for IF Extraction of Multicomponent Signals[J]. Signal, Image and Video Processing, 2018, 12(1): 171-179.
[16] 苏小凡, 肖瑞, 朱明哲. 一种多分量调频信号瞬时频率估计方法[J]. 西安电子科技大学学报, 2019, 46(1): 51-56.
Su Xiaofan, Xiao Rui, Zhu Mingzhe. Method for IF Estimation of Multicomponent FM signals[J]. Journal of Xidian University, 2019, 46(1): 51-56.(in Chinese)
[17] Khan N A, Mohammadi M, ![]() I. A Modified Viterbi Algorithm-Based IF Estimation Algorithm for Adaptive Directional TimE-Frequency Distributions[J]. Circuits, Systems, and Signal Processing, 2019, 38(5): 2227-2244.
I. A Modified Viterbi Algorithm-Based IF Estimation Algorithm for Adaptive Directional TimE-Frequency Distributions[J]. Circuits, Systems, and Signal Processing, 2019, 38(5): 2227-2244.
[18] Khan N A, Mohammadi M, ![]() I. Sparse Reconstruction Based on Iterative TF Domain Filtering and Viterbi Based IF Estimation Algorithm[J]. Signal Processing, 2020, 166: 107260.
I. Sparse Reconstruction Based on Iterative TF Domain Filtering and Viterbi Based IF Estimation Algorithm[J]. Signal Processing, 2020, 166: 107260.
[19] Rankine L, Mesbah M, Boashash B. IF Estimation for Multicomponent Signals Using Image Processing Techniques in the TimE-Frequency Domain[J]. Signal Processing, 2007, 87(6): 1234-1250.
[20] Barkat B, Abed-Meraim K. Algorithms for Blind Components Separation and Extraction from the TimE-Frequency Distribution of Their Mixture[J]. EURASIP Journal on Advances in Signal Processing, 2004, 2004(13): 2025-2033.
[21] Khan N A, Boashash B. Instantaneous Frequency Estimation of Multicomponent Nonstationary Signals Using Multiview TimE-Frequency Distributions Based on the Adaptive Fractional Spectrogram[J]. IEEE Signal Processing Letters, 2013, 20(2): 157-160.
[22] Chen S, Dong X, Xing G, et al. Separation of Overlapped Non-Stationary Signals by Ridge Path Regrouping and Intrinsic Chirp Component Decomposition[J]. IEEE Sensors Journal, 2017, 17(18): 5994- 6005.
![]() I, et al. Post-processing of TimE-Frequency Representations in Instantaneous Frequency Estimation Based on Ant Colony Optimization[J]. Signal Processing, 2017, 138: 195-210.
I, et al. Post-processing of TimE-Frequency Representations in Instantaneous Frequency Estimation Based on Ant Colony Optimization[J]. Signal Processing, 2017, 138: 195-210.
![]() S. Efficient Instantaneous Frequency Estimation in High Noise Based on the Wigner Distribution[J]. Signal Processing, 2019, 157: 25-29.
S. Efficient Instantaneous Frequency Estimation in High Noise Based on the Wigner Distribution[J]. Signal Processing, 2019, 157: 25-29.
[25] 朱明哲, 姬红兵, 林琳, 等. 基于方向性S变换的多分量FM信号瞬时频率估计[J]. 系统工程与电子技术, 2013, 35(1): 29-33.
Zhu Mingzhe, Ji Hongbing, Lin Lin, et al. Instantaneous Frequency Estimation of Multicomponent FM Signals Based on Directional S Transform[J]. Systems Engineering and Electronics, 2013, 35(1): 29-33.(in Chinese)
[26] 刘勇, 张国毅, 于岩. 一种非线性调频信号瞬时频率的估计算法[J]. 科学技术与工程, 2013, 13(31): 9390-9395.
Liu Yong, Zhang Guoyi, Yu Yan. An Algorithm for Instantaneous Frequency Estimation of Nonlinear Frequency Modulation Signals[J]. Science Technology and Engineering, 2013, 13(31): 9390-9395.(in Chinese)
[27] Khan N A, Mohammadi M, Ali S. Instantaneous Frequency Estimation of Intersecting and Close Multi-component Signals with Varying Amplitudes[J]. Signal, Image and Video Processing, 2019, 13(3): 517-524.
[28] Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Nets[C]∥NIPS’14 Proceedings of the 27th International Conference on Neural Information Processing Systems. MIT Press Cambridge, 2014, 2: 2672-2680.
[29] 李昆, 朱卫纲. 一种利用生成对抗网络的时频图像去噪和增强处理方法[EB/OL]. 电讯技术, http:∥kns.cnki.net/kcms/detail/51.1267.TN.20190817.1306.002.html, 2019-08-19.
Li Kun, Zhu Weigang. TimE-Frequency Image DE-noising and Enhancement Processing Based on Generative Adversarial Network[EB/OL]. Telecommunication Engineering, http:∥kns.cnki.net/kcms/detail/51.1267.TN.20190817.1306.002.html, 2019-08-19.(in Chinese)
[30] Xia X, Yu F, Liu C, et al. TimE-Frequency Image Enhancement of Frequency Modulation Signals by Using Fully Convolutional Networks[C]∥2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV). IEEE, 2018: 1472-1476.
[31] Mirza M, Osindero S. Conditional Generative Adversarial Nets[J]. arXiv preprint arXiv: 1411.1784, 2014.
[32] Isola P, Zhu J Y, Zhou T, et al. ImagE-to-Image Translation with Conditional Adversarial Networks[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, 2017: 5967-5976.
[33] Aissa-El-Bey A, Linh-Trung N, Abed-Meraim K, et al. Underdetermined Blind Separation of Nondisjoint Sources in the TimE-Frequency Domain[J]. IEEE Transactions on Signal Processing, 2007, 55(3): 897-907.



