1 引言
基于视频的目标跟踪是计算机视觉领域重要课题和研究热点,广泛应用于安防监控、智能交通、人机交互等多个领域[1-2]。但跟踪效果往往受到尺度变化、障碍物遮挡、目标形变、运动出视野、背景杂乱等因素的影响,如何克服诸多困难,实现快速鲁棒的目标跟踪仍值得深入研究。
传统目标跟踪算法大多使用生成式观测模型,例如文献[3]在均值偏移(Mean Shift)跟踪框架上利用颜色直方图对目标建模,将下一帧图像上的目标概率分布沿梯度下降方向迭代,则局部最密集区域为最优位置。文献[4]引入混沌系数非线性作为粒子滤波(Particle Filter)全局运动估计,高阶动力学信息的使用大大减少粒子数,增强了传统粒子滤波跟踪性能。文献[5]采用非自适应随机投影方式建立外观模型,保留物体图像特征空间结构,使用稀疏测量矩阵提取外观模型特征,对前景目标和背景样本进行压缩。由于传统生成式模型跟踪方法没有充分利用背景信息,加之目标外观变化随机多样,因此模板匹配式跟踪方法具有较大局限性。
相关滤波跟踪算法采用判别式观测模型,目标间相似度越大其相关值越大,将跟踪作为区分目标和背景的二分类问题,且兼顾跟踪速度和准确率,是目前应用较多的跟踪算法。Henriques等人[6]提出核化循环结构检测跟踪算法,将图像块循环移位得到大量样本用于分类器训练和检测,将矩阵的时域运算转化为频域点乘运算,算法速度较快,但单通道灰度特征在背景杂乱、目标形变时易跟踪失败。文献[7]将单一灰度特征扩展为灰度、颜色空间(CN)和方向梯度直方图(HOG)特征矢量叠加的多特征,并结合尺度金字塔,提高跟踪准确度。不同于文献[7]中的尺度估计方法,Danelljan等人[8]在平移跟踪之外训练一个具有33个尺度的滤波器,尺度估计更精准。类似于文献[8]的多滤波器协同,Bertinetto等人[9]提出构建孪生网络,其中一条支路保存模板信息作为目标跟踪先验信息,从而取代全连接层在线更新,与另一条特征搜索支路协同定位目标位置。文献[10]将判别相关滤波器加到孪生网络中,充分利用卷积特征的判别优势和相关滤波的效率优势。文献[11]结合递归神经网络和卷积神经网络对目标结构建模,用以区别相似干扰物,减少跟踪漂移。深度方法往往由于网络结构复杂、算法繁琐等因素导致速度较慢,实时性有待提高。Bertinetto等人[12]将基础HOG特征和颜色统计特征在决策层线性加权融合,特征优势互补。文献[13]利用HOG和VGG-19深度特征,实现多线索目标跟踪,并根据峰值旁瓣比等指标进行可靠模型更新。针对跟踪置信度,文献[14]提出最大响应值和平均峰值相关能量两种指标,只在置信度较高时更新模型,在发生遮挡时可有效避免模型污染,但在目标快速形变时无法及时更新模板,易导致跟踪失败。在跟踪失败时,Ma等人[15]利用检测滤波器纠正跟踪误差,对目标重新定位,实现长时稳定跟踪。针对快速运动带来的边界效应,Danelljan等人[16]扩大检测区域,并使用空域正则化惩罚边界区域的滤波器系数,但使用迭代优化方法导致速度较慢。文献[17]在空域正则化的基础上加入时间正则化,在目标外观变化较大时,比文献[16]提供更可靠的外观模型。文献[18]采用相似变换估计框架,并使用块坐标下降算法解决相似变换估计的优化问题,对大位移相似变换目标跟踪更鲁棒。同样采用了块坐标下降算法优化约束目标函数,文献[19]在相关滤波中引入光流信息和Lasso约束,对处理运动模糊目标较为有效。为了解决非线性动态系统估计的不确定性及其测量的非线性问题,文献[20]在卡尔曼滤波中融入观测约束信息,并结合数值优化和遍历全局最优,提出的平滑约束无迹卡尔曼滤波器在跟踪准确性和稳健性方面有所提升。
本文在传统判别相关滤波的基础上,提出位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法,主要有以下几个特点:1)运用由三种基础特征线性组合成的多特征,充分发挥各特征独有的跟踪优势和融合特征的多样性,提高跟踪精度;2)在尺度估计阶段,将目标从笛卡尔坐标空间变换到对数极坐标空间中进行尺度估计,避免使用步长数量有限的尺度金字塔对超出预定范围的大尺度变化估计带来的误差;3)综合参考特征池跟踪结果的鲁棒性和响应图的平均峰值相关能量等指标,设计一种高置信度模型更新策略,缓解遮挡情况下因模型退化导致的跟踪失败问题。
2 位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法
本文跟踪算法总体框架如图1所示。在第一帧提取目标区域的快速方向梯度直方图特征、颜色空间特征和灰度特征,进而构造成特征池分别进行相关滤波跟踪,选择最有效的特征池预测目标位置,然后在对数极坐标中估计目标尺度,在高置信度时更新模型,否则依据置信水平自适应降低模型更新的学习率。
2.1 基于自适应特征选择的相关滤波跟踪
相关滤波目标跟踪将训练得到的模板滤波器作用于目标搜索区域,利用响应图最大值位置预测当前目标的位置,训练一个能有效区分前景和背景的判别性相关滤波器十分关键,其中用于描述目标外观的特征的选取尤为重要,因此本文通过构建特征池以充分提高目标表征能力,提升跟踪精度。
2.1.1 特征池构建
颜色空间(Color Names,CN)特征,就是利用PLSA模型自动从Google图像中学习到的映射矩阵,将图像RGB值映射到11维(黑、蓝、棕、灰、绿、橙、粉、紫、红、白和黄)颜色空间,再映射到10维子空间的正交基中进行归一化得到的特征。这种颜色信息对尺度变化和旋转具有鲁棒性,在目标识别、检测和跟踪方面取得了较好的效果。快速方向梯度直方图(Fast Histogram of Oriented Gradient, FHOG)特征通过统计局部区域离散方向上的梯度信息来描述目标的边缘特征,特征提取过程中的聚合、归一化和求导等操作,使FHOG特征更简洁高效,在图像模糊和光学变化时仍能保持较好的鲁棒性,广泛应用于图像处理中。
每种特征有各自独特的跟踪优势和劣势,而现实目标跟踪场景中干扰因素复杂多样,单一特征无法准确描述目标外观,而直接将多个特征矢量链接进行跟踪,又无法发挥每个特征各自的跟踪优势。有些算法利用多个特征分别进行跟踪后,将各支路响应图以一定的权重进行融合得到最后的响应图,这种方式不可避免地会引入误差较大的跟踪结果,导致预测位置存在偏差。本文分别提取目标区域的10维CN特征、31维FHOG特征和1维像素平均灰度特征,以线性组合的方式构成特征池。为避免表征能力较弱的灰度特征单独跟踪可能带来的较大误差,尽可能丰富特征多样性,本文将灰度特征融合到FHOG特征中,32维融合特征分成16维的HOG1和HOG2,与CN特征线性组合构成含有7种特征的特征池,从而构建判别力强的表观模型。
2.1.2 位置滤波器
提取目标位置矩形图像块f∈RM×N的d维特征图作为训练样本,通过构造最小化代价函数训练一个最佳的位置相关滤波器h
(1)
式中λ>0,l∈{1,···,d},fl表示特征图f的第l维特征图,hl表示第l维特征的相关滤波器,g为峰值在图像块f目标中心的由二维高斯函数产生的理想输出,λ为正则项系数,用以消除由f谱中零频分量带来零除的问题,*表示循环相关操作符,利用帕塞瓦尔定理将式(1)转化到频域计算
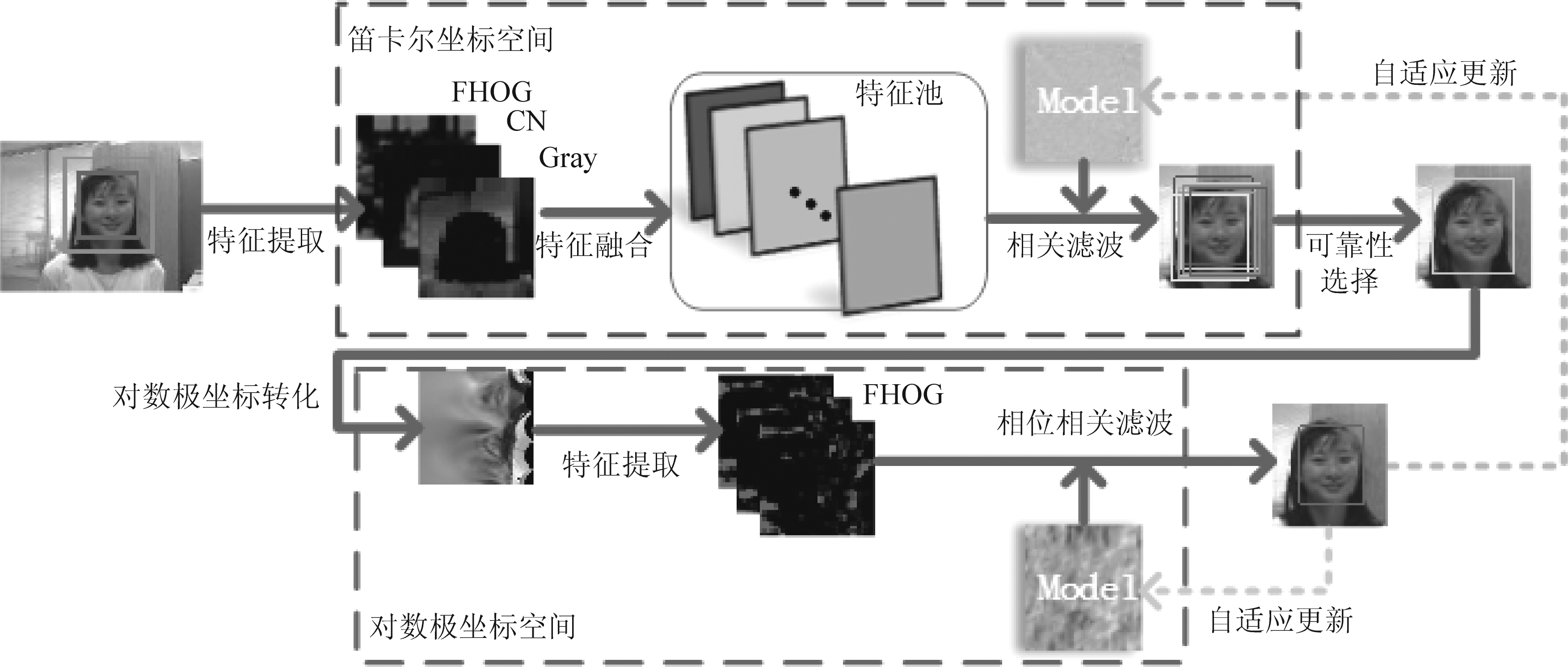
图1 本文跟踪算法示意图
Fig.1 The schematic diagram of proposed tracking algorithm
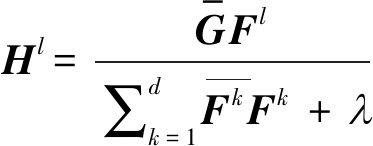
(2)
式中G和Fl分别是g和fl的离散傅里叶变换,![]() 和
和![]() 分别表示G和Fl的复数共轭。式(2)只是计算一个训练样本的相关滤波器,还需要最小化所有训练样本输出误差确定最佳滤波器,求解d×d维线性方程组的复杂计算不适合在线学习。
分别表示G和Fl的复数共轭。式(2)只是计算一个训练样本的相关滤波器,还需要最小化所有训练样本输出误差确定最佳滤波器,求解d×d维线性方程组的复杂计算不适合在线学习。
为了适应多通道特征,减少快速傅里叶变换计算量,本文使用ut=(1-η)ut-1+ηft更新目标模板,并将式(2)中的滤波器Hl在第t帧分别以分子和分母的形式进行更新
(3)
(4)
式中η是样本模型更新时的学习率,提取新一帧图像块z的d维特征图,可以计算出z的相关响应图为
(5)
式中Zl是zl的离散傅里叶变换,为了进一步提升计算的效率和鲁棒近似,采用三角插值法减少FFT运算的尺寸,在Yt的高频位置补零使其尺寸与插值网格大小相同,然后再对补零后的Yt值(记为![]() 进行DFT反变换,得到z的插值响应值
进行DFT反变换,得到z的插值响应值![]()
(6)
式中F-1表示离散傅里叶反变换操作,计算式(5),得到每个特征跟踪的响应值yi,其中i=1,…,K,K为特征池中特征的个数。
2.1.3 自适应特征选择
本文使用特征池中的多个特征并行跟踪目标,由于跟踪目标运动的时空连续性,所以每一条跟踪支路应具有轨迹连续性和平滑性。此外,由于多个特征具有一定的稳定性和关联性,所以大多数跟踪支路结果yi之间也应存在一定程度的一致性。可据此选择鲁棒性高的特征支路预测当前帧的目标位置。一致性评估和连续性评估原理如图2所示,其中![]() 表示第i条特征支路的第t帧。
表示第i条特征支路的第t帧。
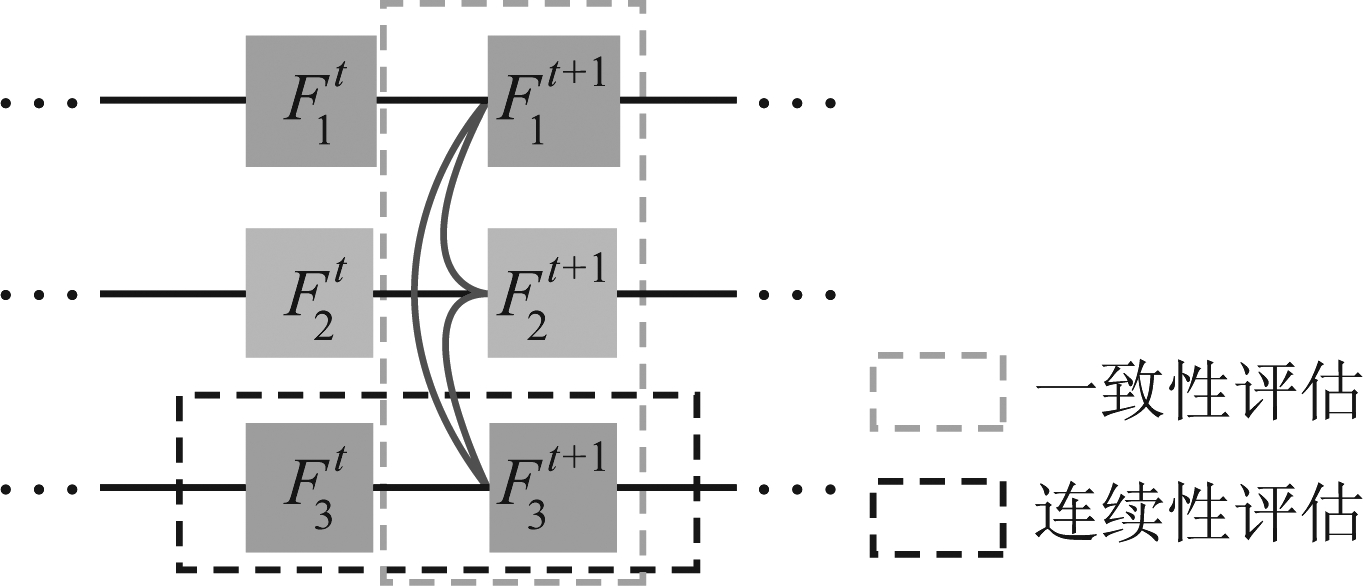
图2 跟踪效果评估标准示意图
Fig.2 The schematic diagram of evaluation criteria for tracking effectiveness
连续性评估:每条特征支路的轨迹连续性和时间连续性在一定程度上反映了该支路跟踪结果的可靠性,轨迹连续情况可由一条支路中相邻两帧跟踪边框的欧几里得距离![]() 计算求得
计算求得
(7)
式中,Fi代表特征池中的第i个特征,i=1,…,K,K为特征池中的特征个数,![]() 表示第i个特征在第t帧跟踪得到的边框,
表示第i个特征在第t帧跟踪得到的边框,![]() 表示
表示![]() 的中心,则Fi的波动程度
的中心,则Fi的波动程度![]() 可以计算为
可以计算为
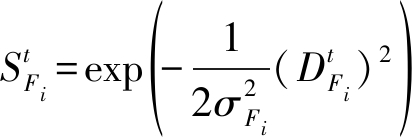
(8)
式中,![]() 和
和![]() 分别是
分别是![]() 的宽和高。
的宽和高。
进一步考虑时间稳定性,引入一个递增序列W={ρ0,ρ1,…,ρΔt-1},(ρ>1)对最近的得分给予更高的权重,则连续性评估得分为
(9)
式中,Wτ表示序列W中的第(τ-t+Δt)个元素,N是定义为N=∑τWτ的归一化因子,![]() 越大表示跟踪轨迹越连续可靠。
越大表示跟踪轨迹越连续可靠。
一致性评估:在同一帧中,可以将各特征支路间的边框重合率用来近似描述各支路的跟踪一致程度。在第t帧,计算Fi和Fj的重合率![]() 为
为
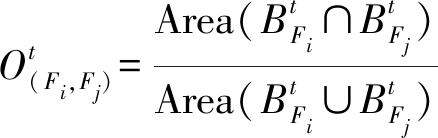
(10)
为了使数据更稳定集中,缩小低重合率和高重合率之间的差距,采用非线性高斯函数统计重合率
(11)
第i个特征Fi与所有其他特征Fj之间的重合率的平均值![]() 就代表了第i个特征与其他特征间的轨迹一致性水平。同理,综合考虑时间稳定性,计算短时间内Fi与Fj的重叠率评估的稳定性
就代表了第i个特征与其他特征间的轨迹一致性水平。同理,综合考虑时间稳定性,计算短时间内Fi与Fj的重叠率评估的稳定性
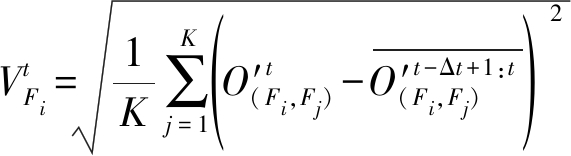
(12)
式中![]() 其中τ∈[t-Δt+1,t],考虑时间背景后,平均权重均值和标准方差可以通过
其中τ∈[t-Δt+1,t],考虑时间背景后,平均权重均值和标准方差可以通过![]() 和
和![]() 分别计算得出。进而得出第i个特征Fi在第t帧的一致性评估得分为
分别计算得出。进而得出第i个特征Fi在第t帧的一致性评估得分为
(13)
式中ξ是一个值较小的常量,用于避免分母为零的情况。![]() 越大,代表Fi与其他Fj的一致性越好,对目标位置预测的稳定性越好。第i个特征Fi在第t帧的鲁棒性得分Rt(Fi)是连续性评估得分
越大,代表Fi与其他Fj的一致性越好,对目标位置预测的稳定性越好。第i个特征Fi在第t帧的鲁棒性得分Rt(Fi)是连续性评估得分![]() 和一致性评估
和一致性评估![]() 的线性组合
的线性组合
(14)
式中μ是自适应权重,在每一帧自适应选择鲁棒性得分Rt(Fi)最高的特征用于当前的跟踪。
2.2 空域变换尺度估计
本文将笛卡尔直角坐标空间域进行转换,在对数极坐标空间域中同时估计尺度和旋转变化,无需对图像进行密集的重采样,节省了计算成本。并且利用坐标变换估计几何尺度变化,可以较好地处理状态空间中超出预定范围的大位移尺度变化。
2.2.1 对数极坐标变换(LPT)
空间域中的一幅图像I(x,y),其对数极坐标I(ρ,θ)可以看作是I(x,y)在原始笛卡尔坐标中的非线性和非均匀变换,选择x轴作为极轴,以(x0,y0)为变换中心,笛卡尔坐标和对数极坐标之间的关系表示为:
(15)
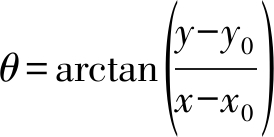
(16)
其中,(ρ,θ)表示对数极坐标系中的极径和极角。假设由先前帧图像获得的图像模板g(x,y)和当前帧图像f(x,y)可以通过缩放s倍和旋转θ0角度进行关联,则在笛卡尔坐标中可以将这种关系表示为:
g(x,y)=f [s-1(xcos θ0+ysin θ0), s-1(-xsin θ0+ycos θ0)]
(17)
对数极坐标的优点就在于上述方程中的关系可在对数极坐标中导出如下公式:
g(lnρ,θ)=f(lnρ-lns,θ-θ0)
(18)
笛卡尔坐标和对数极坐标转换原理如图3所示,由此可知,笛卡尔坐标中的尺度和旋转变化(s,θ0),在对数极坐标中可以看作是沿轴平移(lns,θ0)的运动,该特性自然可用于估计跟踪目标的尺度和旋转变化。
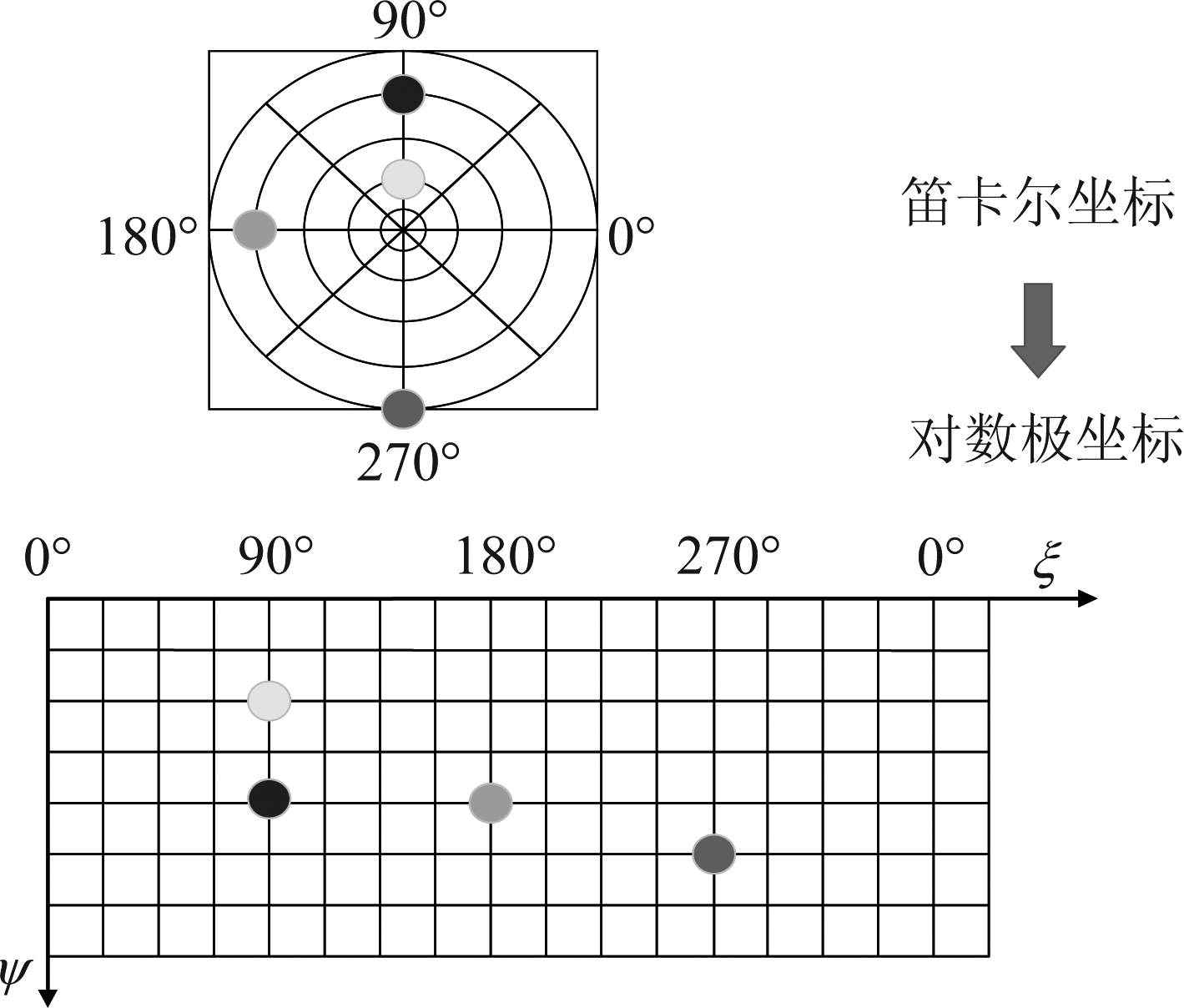
图3 笛卡尔坐标和对数极坐标转换原理示意图
Fig.3 Schematic diagram of the principle of Cartesian and log-polar coordinates transformation
2.2.2 相位相关尺度估计
根据傅里叶变换的性质,信号的平移在频谱中表现为相移,利用相位相关法可以得到平移量。本文将当前帧图像f(x,y)和图像模板g(x,y)从笛卡尔坐标转换至对数极坐标中,利用相位相关法求出当前图像相对于模板发生的尺度和旋转变化。
将对数极坐标中的平移关系等式g(lnρ,θ)=f(lnρ-lns,θ-θ0)转换至频域,其对应的傅里叶变换关系式可表示为G(u,ν)=F(u,ν)e-j(ulns+νθ0),进一步得到g(x,y)和f(x,y)的互功率谱表示形式为
(19)
求式(19)中e-j(ulns+νθ0)的傅里叶反变换,得到一个二维的狄利克雷脉冲函数δ(lnρ-lns,θ-θ0),该脉冲函数只在平移量(lns,θ0)处数值不为零,其余位置均为零,可据脉冲函数的峰值位置确定平移量(lns,θ0)大小,进而求得尺度因子s和旋转因子θ。
2.3 自适应模型更新
跟踪过程中易发生目标遮挡等情况,若不考虑跟踪是否准确的情况下更新每帧的跟踪模型,一旦在当前帧中检测到目标不准确、严重遮挡或完全丢失,这种模板逐帧更新方式易导致模型更新误差累积而退化,最终跟踪失败。本文利用跟踪置信度的反馈信息来自适应调整模型更新的学习率,避免目标模型被污染。
当目标发生严重遮挡时,多个特征跟踪分支面对不可靠样本时会产生分歧,导致平均鲁棒性评估得分![]() 显著降低,据此可以作为结果可靠性评估的标准。
显著降低,据此可以作为结果可靠性评估的标准。
然而,有时当物体被相似物体遮挡时,![]() 可能不会迅速降低,若继续使用原更新率,则模板会错误地学习到相似遮挡物的外观导致模型污染,易发生跟踪漂移。平均峰值相关能量(APCE)近来越来越多地被用于衡量跟踪置信度,定义为
可能不会迅速降低,若继续使用原更新率,则模板会错误地学习到相似遮挡物的外观导致模型污染,易发生跟踪漂移。平均峰值相关能量(APCE)近来越来越多地被用于衡量跟踪置信度,定义为
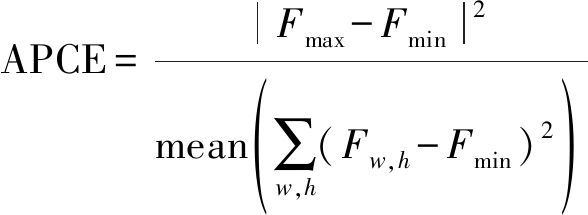
(20)
式中,Fmax,Fmin和Fw,h分别代表响应值的最大值,最小值和第w行、第h列的响应值。APCE反映了响应图的波动情况和目标跟踪的置信水平,对于目标明显出现在检测范围内,除了一个尖锐的峰值之外,响应图将很平滑,APCE将变大,若物体被遮挡或丢失,APCE将显著降低。
综合考虑APCE和平均鲁棒性得分![]() 提出一种综合置信得分
提出一种综合置信得分![]() 用于评估跟踪质量。由于相关滤波器同时学习目标和背景信息,因此简单地丢弃不可靠样本并不合理。当前置信得分St显著低于过去的平均可靠性得分
用于评估跟踪质量。由于相关滤波器同时学习目标和背景信息,因此简单地丢弃不可靠样本并不合理。当前置信得分St显著低于过去的平均可靠性得分![]() 时,公式(4)中的学习率η将以公式(21)的方式更新:
时,公式(4)中的学习率η将以公式(21)的方式更新:
(21)
其中C为标准DCF中的学习率,α为可靠性阈值,β为函数的指数。尺度滤波器学习率也按此方式更新,惩罚置信度低的样本,降低模型学习率,在目标被遮挡时保护模型免受腐败。
此外,为避免弱特征跟踪漂移积累导致跟踪失败,所有跟踪支路均使用上一帧选定的样本模型更新,共享相同的上下文背景,所以多个特征支路跟踪不会带来更多特征提取计算量,保证跟踪效率。
3 实验结果与分析
3.1 实验环境与参数设置
本文实验环境为Intel Core i5-7500 CPU,主频3.4GHz,内存16GB,64位Win7操作系统,实验平台为Matlab R2016b。特征个数K=7,位置滤波器初始学习率C=0.025,正则化权重λ=0.01,可靠性阈值α=0.6,自适应权重μ=0.1,尺度滤波器初始学习率c=0.015。选取OTB-50[21]和OTB-2015[22]作为测试数据集,OTB-50含有50个视频序列,包含光照变化(IV)、尺度变化(SV)、遮挡(OCC)、形变(DEF)、运动模糊(MB)、快速运动(FM)、平面内旋转(IPR)、平面外旋转(OPR)、出视野(OV)、背景杂乱(BC)、低分辨率(LR)共11种挑战属性,OTB-2015数据集共100个视频,跟踪难度更大。每个视频序列具有多种挑战因素,数据更具代表性。
3.2 对比实验分析
采用OTB数据集中的一次性通过评估(OPE)模式,选择跟踪的距离精度(DP)和重叠率精度(OP)作为评价指标。本文设定DP阈值为20像素,OP阈值为0.5。将本文算法与LDES[18],DSST[8],DCFNet[10],Staple[12],LCT[15],SRDCF[16],KCF[23]等几种流行相关滤波算法和深度学习算法进行比较,并做定量和定性分析。
3.2.1 定量分析
在OTB-50和OTB-2015数据集中进行OPE评估,得到8种算法的平均跟踪性能见表1,图4和图5分别为距离精度图和成功率图。测得8种算法在OTB-2015数据集中11种视频属性下的跟踪准确率和成功率,结果见表2和表3,其中加粗数据表示最优结果,下划线数据表示次优结果。
结合表1和图3、图4可知,在OTB-50数据集上,本文算法的平均DP和平均OP分别为73.3%和56.1%,在OTB-2015数据集中分别为79.0%和60.9%,与其他几种算法相比,超越了性能较好相关滤波算法SRDCF和深度算法DCFNet,略低于近期算法中采用相似变换估计框架的LDES算法,获得了较优的跟踪结果。与同样采取判别相关滤波和尺度估计的DSST算法相比,在OTB-2015数据集上的精确度和成功率分别提升了11.0%和9.6%,表明本文算法具有较强的跟踪准确性。
表1 OPE模式下8种算法的平均跟踪性能/%
Tab.1 Average tracking performance comparison of eight tracking algorithm at OPE mode

AlgorithmKCFDSSTLCTDCFNetStapleSRDCFLDESOursOTB-50Mean DP61.160.469.168.368.173.274.973.3Mean OP40.345.249.250.950.953.955.756.1OTB-2015Mean DP69.668.076.275.178.478.979.879.0Mean OP47.751.356.258.058.159.861.660.9
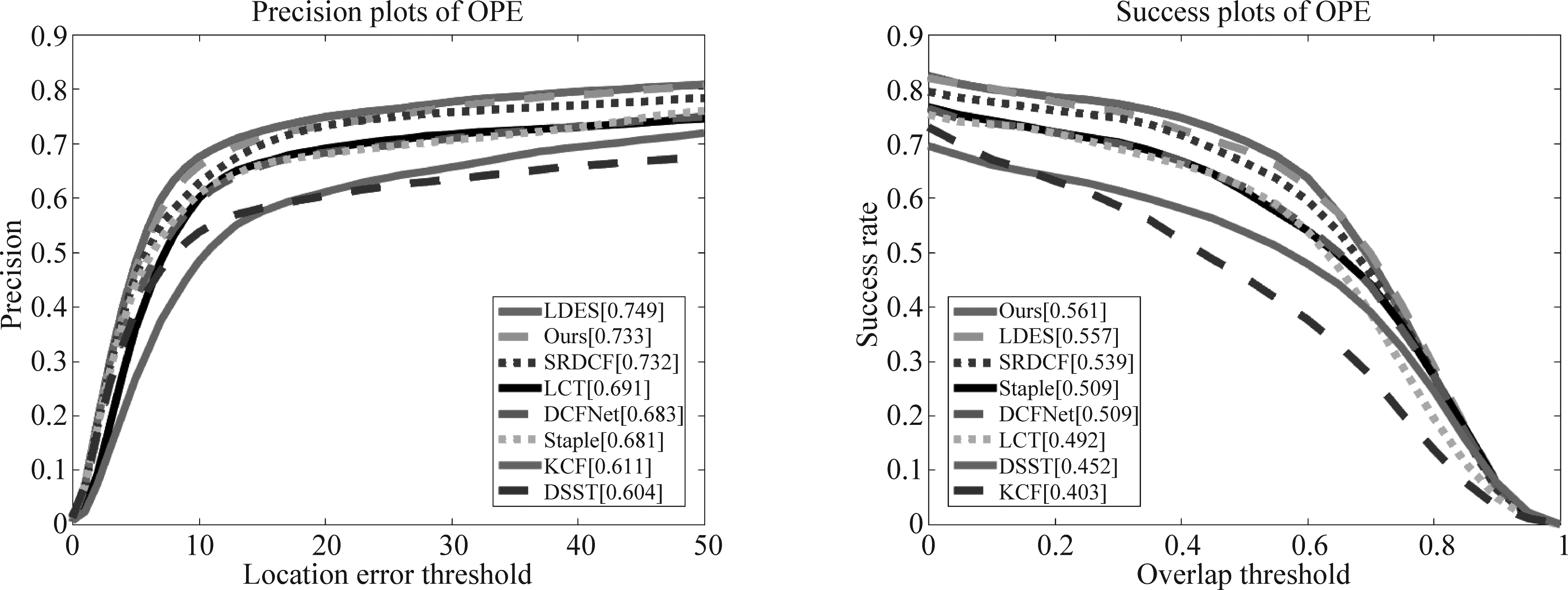
图4 8种算法在OTB-50数据集上跟踪的距离精度图和成功率图
Fig.4 The precision and success plot of eight trackers on OTB-50
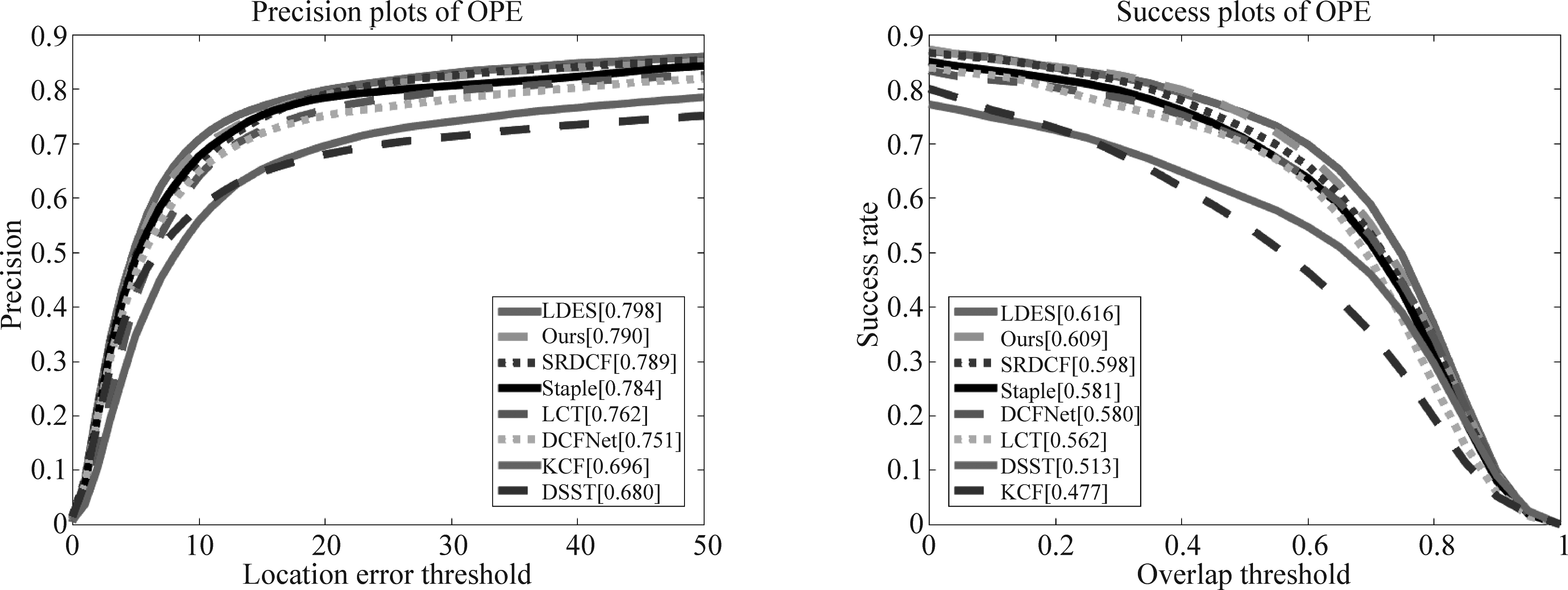
图5 8种算法在OTB-2015数据集上跟踪的距离精度图和成功率图
Fig.5 The precision and success plot of eight trackers on OTB-2015
由表2和表3数据可知,在11种挑战因素中,本文算法的成功率均排在前两名,尤其在遮挡、平面外旋转和背景杂乱3种挑战因素中,本文算法的距离精度和成功率均排在第一名。但在快速形变情况下,本文算法与SRDCF算法跟踪效果接近,与采用颜色直方图和HOG两种互补特征的Staple相比,还具有一定差距,也印证了颜色特征在形变情况下鲁棒性较强的特点。在快速运动和运动模糊两种情况下,由于近期的LDES算法采用块坐标下降算法来解决相似变换估计的优化问题,实现了对大位移相似变换目标的鲁棒跟踪,跟踪效果略胜一筹。综合分析8种算法在两种数据集和分属性视频序列中的跟踪结果,表明本文算法总体性能好,综合跟踪能力强,具有较好的准确性和鲁棒性。
表2 OTB-2015数据集中8种算法对11种不同属性视频序列下的跟踪距离精度/%
Tab.2 Average tracking precision of eight trackers for video sequences with eleven different attributes on OTB-2015 datasets
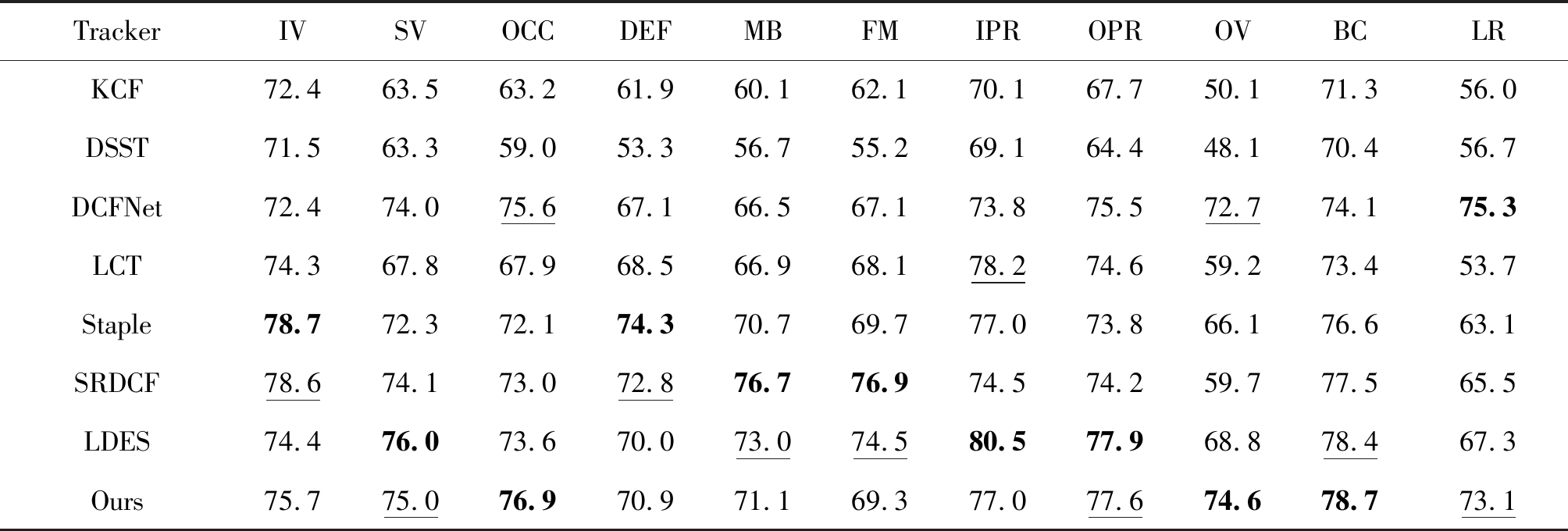
TrackerIVSVOCCDEFMBFMIPROPROVBCLRKCF72.463.563.261.960.162.170.167.750.171.356.0DSST71.563.359.053.356.755.269.164.448.170.456.7DCFNet72.474.075.667.166.567.173.875.572.774.175.3LCT74.367.867.968.566.968.178.274.659.273.453.7Staple78.772.372.174.370.769.777.073.866.176.663.1SRDCF78.674.173.072.876.776.974.574.259.777.565.5LDES74.476.073.670.073.074.580.577.968.878.467.3Ours75.775.076.970.971.169.377.077.674.678.773.1
表3 OTB-2015数据集中8种算法对11种不同属性视频序列下的跟踪成功率/%
Tab.3 Average tracking success of eight trackers for video sequences with eleven different attributes on OTB-2015 datasets
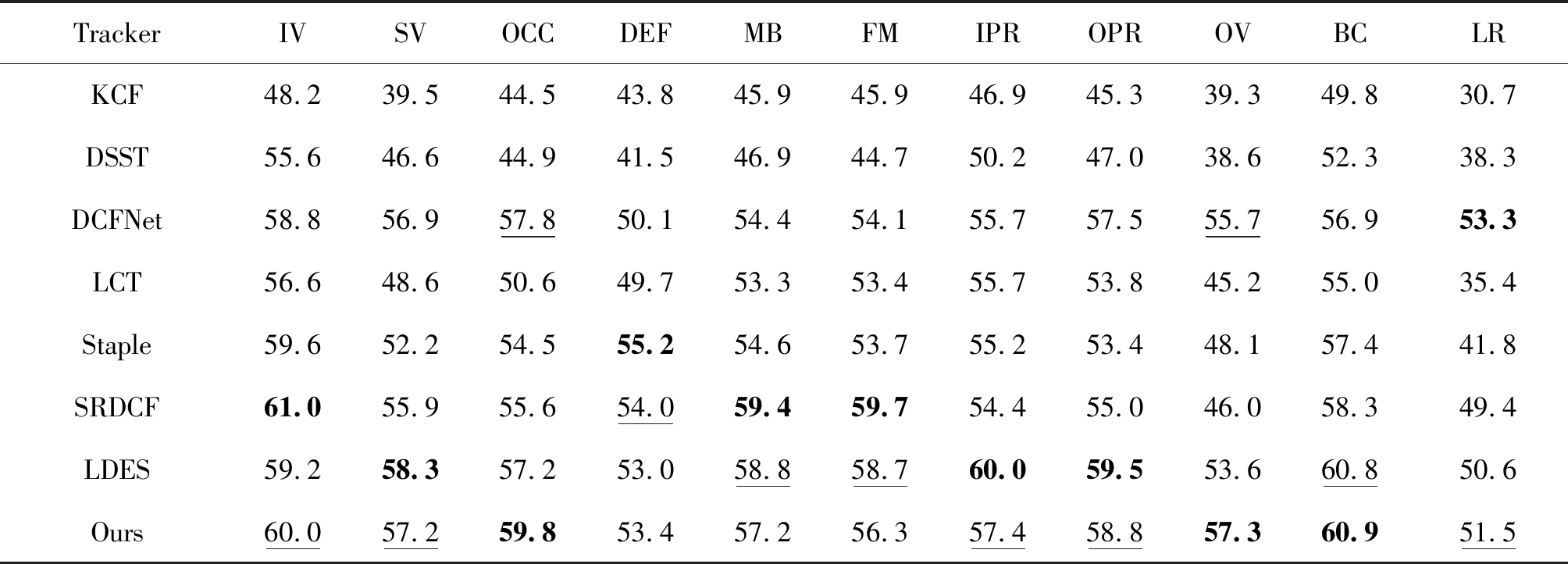
TrackerIVSVOCCDEFMBFMIPROPROVBCLRKCF48.239.544.543.845.945.946.945.339.349.830.7DSST55.646.644.941.546.944.750.247.038.652.338.3DCFNet58.856.957.850.154.454.155.757.555.756.953.3LCT56.648.650.649.753.353.455.753.845.255.035.4Staple59.652.254.555.254.653.755.253.448.157.441.8SRDCF61.055.955.654.059.459.754.455.046.058.349.4LDES59.258.357.253.058.858.760.059.553.660.850.6Ours60.057.259.853.457.256.357.458.857.360.951.5
3.2.2 定性分析
选取6组具有多种挑战因素的视频序列对算法进行分析,各视频包含的视频属性、帧数等信息见表4,图6为8种对比算法在序列中的直观效果。
由图6所示跟踪的直观结果可知,在Girl2序列中,在第129帧发生长时间严重遮挡后,所有算法均跟踪失败,但由于本文算法采用跟踪置信度的反馈信息来自适应调整模型更新的学习率,因此目标模型未被遮挡物污染,只有本文算法以最快速度在第329帧时再次准确跟踪位置和尺度,并且在后续帧中经历形变、遮挡和模糊时,依然能准确跟踪。Box序列背景较杂乱,在目标被相似物体严重遮挡后的第501帧,只有本文算法和LDES能准确预测目标位置,其他算法因学习了错误模板导致跟踪失败,在经历旋转后,本文算法能最准确估计目标出现的位置和尺度,LDES和DCFNet在一定程度上发生延迟(578帧)和漂移(921帧),表明本文算法采取的模型更新策略,对目标旋转和遮挡具有较好的鲁棒性,采用的空域变换尺度估计方法更为有效。
Couple序列背景杂乱且目标发生快速运动,大多数算法一旦跟踪失败无法再次找到目标,本文算法因采取多特征的多条支路分别进行跟踪,虽然也会发生轻微漂移,但能迅速再次定位目标。BlurOwl序列发生快速运动的同时伴随运动模糊,在第161帧以后Staple和DCFNet等算法彻底跟踪失败,SRDCF采用了空域正则化惩罚了大检测区域的边界效应,LCT应用检测机制对跟踪出错的目标进行重新检测,因此跟踪效果较好,本文算法取得了相同的跟踪效果,表明本算法对背景杂乱、快速运动和运动模糊的因素具有一定的适应能力。
表4 8组视频序列的属性及相关信息
Tab.4 Attributes and relevant information of eight video sequences

SequenceAttributesFrameObject size/pixelaGirl2SV,OCC,DEF,MB,OPR1500171×44bBoxIV,SV,OCC,MB,IPR,OPR,OV,BC,LR1161111×80cCoupleSV,DEF,FM,OPR,BC14062×25dBlurOwlSV,MB,FM,IPR631100×56eDragonBabySV,OCC,DEF,FM,OPR,OV11365×56fPandaSV,OCC,DEF,IPR,OPR,OV,LR100023×28

图6 8种跟踪算法在视频序列上的跟踪结果
Fig.6 Comparison of results of the 8 trackers in video sequences
DragonBaby和Panda序列都存在运动出视野和形变等多种干扰因素,在DragonBaby中,在发生多次运动出视野和形变后(27、32帧),本算法能进行及时有效的跟踪(第85帧)。Panda视频像素较低,在第348帧目标发生快速的尺度变化和形变后,DSST和KCF最先停止跟踪,SRDCF因尺度估计不准导致跟踪失败,LCT因无法适应形变而停止更新位置,LDES因无法适应低分辨率和形变而发生跟踪漂移,第608帧经历遮挡后,Staple也彻底丢失目标,本文算法展现出和深度算法DCFNet一样较强的跟踪定位能力,经历过多次干扰后仍能准确进行目标定位和尺度估计。表明本文算法在出视野、形变、低分辨率等情况下的稳定性,能准确跟踪目标。
表5 8种算法在OTB-50和OTB-2015数据集中的跟踪速度比较
Tab.5 Comparison of tracking speed of eight algorithms on OTB-50 and OTB-2015 datasets

TrackerDSSTKCFDCFNetLCTStapleLDESSRDCFOursSpeed/fpsOTB-5023.42116.2440.8622.4942.6811.053.6628.67OTB-201521.99113.4241.2120.7542.8811.753.5526.82
3.2.3 时效性分析
测试本文算法与其他7种算法在OTB-50和OTB-2015数据集中的平均跟踪速度,结果见表5。结合表中数据和算法原理及效果分析可知,DSST采用传统判别相关滤波器进行位置估计,算法计算量较小,尺度滤波器使用33个精细的尺度因子,在每一帧的尺度检测时需要分别对33个图像块采样,所以计算量有所增大。SRDCF由于采用4倍检测区域,加入空域正则化并使用迭代优化方法,导致速度很慢。LDES使用了对尺度和旋转效果更佳的块坐标下降算法,LCT加入了能长时跟踪的检测机制,相应地产生了一定的计算负担。另外几种算法虽然在运行速度上优于本文算法,但整体性能差一些。本文算法为了充分利用各个特征的跟踪优势,并未进行降维,加之置信度判别策略,导致计算量稍大,但位置滤波器的差值运算和尺度估计的高效率使算法速度有所提高。本文算法速度远超过SRDCF和LDES的速度,同时精确度和成功率更高,不仅跟踪速度快于DSST和LCT算法,而且跟踪性能更具优势。
4 结论
本文提出的位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法,利用三种基础特征进行多样性融合构成特征池进行多支路相关滤波跟踪,选择鲁棒性最高的输出响应确定目标位置,提高了对目标的表征能力。通过坐标空域转换,在对数极坐标域中进行高效准确的尺度估计,提出的高置信度模型更新策略有效缓解了遮挡情况下的模型退化的问题。实验结果表明,本文算法在标准数据集OTB-50上的精确度和成功率分别为73.3%和56.1%,在OTB-2015上的精确度和成功率分别为79.0%和60.9%,在目标发生超出视野、遮挡、背景杂乱等情况下,具有较好的跟踪准确性和鲁棒性。
[1] Tsakanikas V, Dagiuklas T. Video surveillance systems-current status and future trends[J]. Computers & Electrical Engineering, 2018, 70: 736-753.
[2] 卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61-76.
Lu Huchuan, Li Peixia, Wang Dong. Visual Object Tracking: A Survey[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(1): 61-76.(in Chinese)
[3] Vojir T, Noskova J, Matas J. Robust scalE-adaptive mean-shift for tracking[J]. Pattern Recognition Letters, 2014, 49: 250-258.
[4] Firouznia M, Faez K, Amindavar H, et al. Chaotic particle filter for visual object tracking[J]. Journal of Visual Communication and Image Representation, 2018, 53: 1-12.
[5] Zhang Kaihua, Zhang Lei, Yang Ming-hsuan. Real-time compressive tracking[C]∥European Conference on Computer Vision, Florence, Italy, 2012, 7574: 864- 877.
[6] Henriques J F, Caseiro R, Martins P, et al. Exploiting the Circulant Structure of Tracking-by-Detection with Kernels[C]∥European Conference on Computer Vision, Florence, Italy, 2012, 7575 (1): 702-715.
[7] Li Yang, Zhu Jianke. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration[C]∥European Conference on Computer Vision, Zurich, Switzerland, 2014: 254-265.
[8] Danelljan M, Hager G, Khan F, et al. Accurate scale estimation for robust visual tracking[C]∥British Machine Vision Conference, 2014: 65.1- 65.11.
[9] Bertinetto L, Valmadre J, Henriques J F, et al. Fully-convolutional siamese networks for object tracking[C]∥European Conference on Computer Vision, Amsterdam, Holland, 2016: 850- 865.
[10] Wang Qiang, Gao Jin, Xing Junliang, et al. DCFNet: discriminant correlation filters network for visual tracking[EB/OL]. [2018-09-03]. http:∥arxiv.org/pdf/1704.04057v1.pdf.
[11] Fan Heng, Ling Haibin, SANet: structurE-aware network for visual tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, 2017: 2217-2224.
[12] Bertinetto L, Valmadre J, Golodetz S, et al. Staple: Complementary Learners for Real-Time Tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, 2016: 1401-1409.
[13] Wang Ning, Zhou Wengang, Tian Qi, et al. Multi-cue Correlation Filters for Robust Visual Tracking[C]∥IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, 2018: 4844- 4853.
[14] Wang Mengmeng, Liu Yong, Huang Zeyi. Large Margin Object Tracking with Circulant Feature Maps[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, 2017: 4800- 4808.
[15] Ma Chao, Huang Jiabin, Yang Xiaokang, et al. Adaptive Correlation Filters with Long-Term and Short-Term Memory for Object Tracking[J]. International Journal of Computer Vision, 2018, 126(8): 771-796.
[16] Danelljan M, Hager G, Khan F S, et al. Learning Spatially Regularized Correlation Filters for Visual Tracking[C]∥IEEE International Conference on Computer Vision, Santiago, 2015: 4310- 4318.
[17] Li Feng, Tian Cheng, Zuo Wangmeng, et al. Learning Spatial-Temporal Regularized Correlation Filters for Visual Tracking[C]∥IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, 2018: 4904- 4913.
[18] Li Yang, Zhu Jianke, Hoi S, et al. Robust Estimation of Similarity Transformation for Visual Object Tracking[C]∥33rd AAAI Conference on Artificial Intelligence, Honolulu, HI, 2019: 8666- 8673. arXiv:1712.05231v2[cs.CV].
[19] 张能波, 苏震斌, 谢维信. Lasso约束下融和光流信息的DCF目标跟踪算法[J]. 信号处理, 2019, 35(5): 911-918.
Zhang Nengbo, Su Zhenbin, Xie Weixin. DCF Visual Object Tracking Algorithm with Lasso Constraints and Fusion Optical Flow[J]. Journal of Signal Processing, 2019, 35(5): 911-918.(in Chinese)
[20] 张宏伟, 谢维信. 平滑约束的无迹卡尔曼滤波器[J]. 信号处理, 2019, 35(3): 466- 471.
Zhang Hongwei, Xie Weixin. Smoothly Constrained Unscented Kalman Filter[J]. Journal of Signal Processing, 2019, 35(3): 466- 471.(in Chinese)
[21] Wu Yi, Lim J, Yang M. Online Object Tracking: A Benchmark[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 2013: 2411-2418.
[22] Wu Yi, Lim J, Yang M. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848.
[23] Henriques J F, Caseiro R, Martins P, et al. High-Speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596.


