1 引言
心电图(Electrocardiogram,ECG)信号能简单地记录由心脏产生的电活动,是一种有效的非侵入性工具,可用于测量心率、检查心律、诊断心脏异常、情绪识别和生物特征识别等多种生物医学应用[1]。由于心电图记录的是心脏在一段时间内通过在人体身上放置电极而产生的微小电活动[2],其波幅较小,一般都是毫伏(mV)级别,其频带范围在0.05~100 Hz,有时噪声可能直接将信号掩盖,所以是一种低幅值、低频率、低信噪比的生理信号[3- 4],这对心电信号检测带来了较大的困难。Wang Y等[5]根据ECG信号性质,将信号进行双斜率处理,最终将QRS波变为一个单峰进行检测定位,算法提高了检测精度,但对于噪声中的小峰值信号其算法性能减弱。Hulya K S[6], 彭自然[7]等利用小波变换对ECG信号处理,Hulya K S等通过小波分析将ECG信号分解为4级,从ECG信号中减去第4级近似系数,以消除基线漂移,新信号再次通过小波包过滤器直到第2级,从该信号中减去第二级的细节系数,以消除高频噪声,其检测算法精确度并不高;而彭自然等只利用小波分解对信号进行了去噪处理。Tang X C等提出一种并行增量调制器架构[8],利用局部最大点和局部最小点算法检测QRS和PT波,并应用于可穿戴式ECG检测系统,其检测精度不高而且抗噪性不强。Tsai Y等提出一种时域多级的检测算法[9],其算法是基于自适应阈值的,具有较低的计算复杂度也不会让原始心电信号有较大的失真,但是精度不高。Satija U等提出了ECG信号处理的一整套方法[10],包括检测与分类,其中R波检测方法是利用信号质量评估(SQA)方法与R峰检测方法结合,使用ECG-SQA算法时降噪的R峰值检测方法的性能有所提高,其精度还有待提升。
本文尝试将单元平均恒虚警率(cell averaging-constant false alarm rate,CA-CFAR)检测方法引入到ECG信号R波的检测中,结合经典的ECG信号预处理办法,改进CA-CFAR以适应ECG信号R波的检测,为ECG信号检测探索一种新的方法。实验证明,该算法能够从噪声和干扰中检测出目标信号,对MIT-BIH数据库的ECG信号R波的检测,其精准率为99.842%,检测误差为0.354%。
2 CA-CFAR检测原理
恒虚警概率是指在判决过程中由于噪声的干扰使得将没有发生的事件错误地判决为发生的概率[11]。雷达信号检测常采用奈曼-皮尔逊(Neyman-Pearson, NP)准则,统计假设检验将充分的统计量与自适应门限进行比较[12],NP准则的目的在于,保证虚警概率一定的情况下,使检测性能达到最优[13],由公式(1)表示,
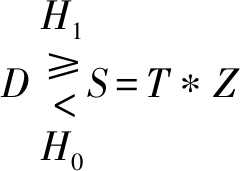
(1)
式中,D为待测单元信号;S为动态判决门限,其中T是选取的乘积因子,T由恒虚警概率Pfa决定,背景功率Z是待测单元周围2N个参考单元的平均值。在CA-CFAR检测中,根据恒虚警概率Pfa的设置选取乘积因子T,再与背景功率Z做乘积得到判决门限S,若待测单元的信号D大于门限S,则说明目标存在,即为假设H1;反之,目标不存在,即为假设H0。
3 改进CA-CFAR对ECG信号R波检测
典型的心电图波形特征如图1所示,一个完整的心电图周期由P波,PR波段,QRS波群,ST波段,T波等组成,有时T波与下一个P波之间可能出现U波。R波是QRS波群乃至整个波群中波形最大也是最重要的一个,是ECG信号中检测的首要问题,只有确定R波位置才能分析ECG信号,以及之后的波形分类。
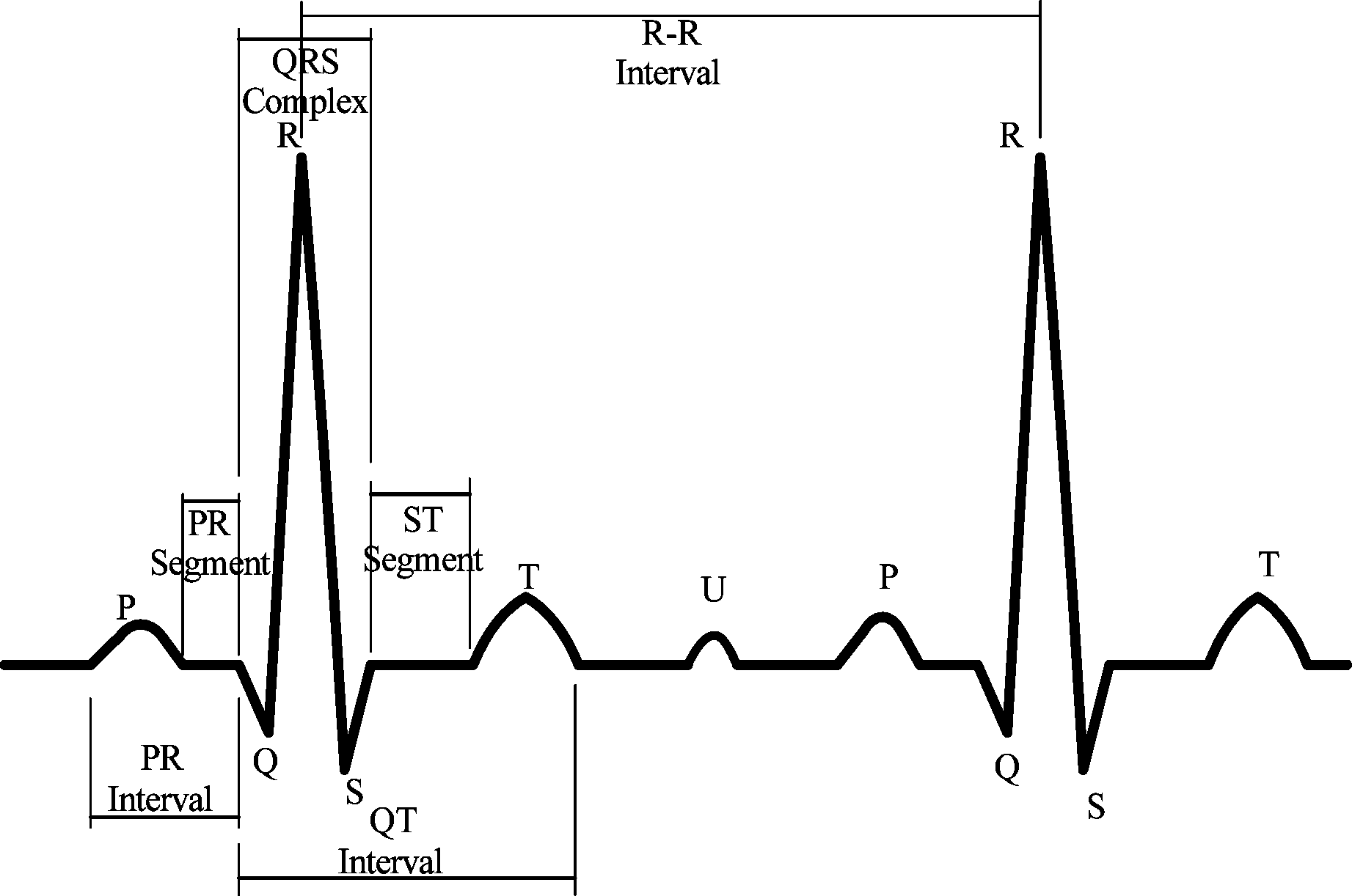
图1 一个完整周期的心电图信号
Fig.1 ECG signal of a complete cycle
一般ECG信号检测算法是利用滤波器组先对ECG信号进行滤波,得到对于检测算法较好的滤波信号,然后进行检测。本文利用滤波器组对ECG信号滤波,消除ECG信号中基线漂移,工频干扰等噪声信号,并自适应选择参考单元以适应ECG信号R波的检测。检测方案如图2所示。
3.1 ECG信号预处理
根据检测方案流程,首先将ECG信号通过带通滤波器滤波处理,带通滤波器是80阶的10~35 Hz滤波器,在这个通带频率内能最大限度保留QRS波群,经过带通滤波器后的信号主要保留了QRS波群,虽然整个输入信号都有所衰减,但QRS波群频率主要集中在通带内,低频噪声和高频噪声得到抑制,相对于其他信号QRS波群得到凸显,相当于“增大”了QRS波群分量,这对R波检测提供了有用信息。然后对信号做绝对值处理,绝对值处理后信号出现多个波峰,所以用低通滤波器对绝对值处理的信号进行平滑。经过滤波后信号能量有所损失,故用两次滑动窗口滤波对信号进行处理,滑动窗口滤波本质是对滑窗内信号求和,经过两次滑窗后增强了信号R波幅值。以MIT-BIH数据库中103和105号病例数据为例,预处理中各阶段信号如图3(a)和(b)所示,103号病例有明显的基线漂移,预处理后信号比较平稳;105号病例有信号质量较差的信号,经过预处理后能得到有波峰的信号,但效果相对较差。所以对于ECG信号本身低幅值、低频率、低信噪比的特点,利用改进的CA-CFAR算法对ECG信号进行检测,有利于在干扰噪声中检测到目标R波。

图2 ECG信号R波检测方案
Fig.2 R-wave detection scheme for ECG signal

图3 ECG信号预处理结果
Fig.3 ECG signal preprocessing results
3.2 改进的CA-CFAR对ECG信号R波检测
预处理后的信号经过平方律检波后送入CA-CFAR检测器进行R波检测定位。在标准的雷达阈值检测中,根据可接受的恒虚警率Pfa,设定一个对应于特定Pfa的阈值[14]。而对于ECG信号,干扰电平通常是来自数据采集设备的工频干扰,人体自身活动或肌肉收缩的肌电噪声干扰,以及呼吸或身体抖动等引起的基线漂移等[15]。这些干扰噪声在经过预处理后已经大部分滤除,使得信号趋于平稳。用单元平均恒虚警率技术处理信号时,其恒虚警率Pfa可以不依赖于干扰噪声,恒虚警率可以精准设定。恒虚警率用来生成乘积因子T,其恒虚警率越大,得到的乘积因子越小,则判决门限越低,误检个数就会越多;恒虚警率越小,得到的乘积因子越大,则判决门限越高,漏检个数就会增多。所以为平衡误检和漏检两者关系,让检测误差降到最低,本文将预期的恒虚警概率Pfa设为10-2,那么初始乘积因子如式(2)所示,
(2)
其中,Rr=2N是参考单元个数。CA-CFAR检测时,选取合适的参考单元需要考虑两个因素:一个是希望参考单元大一些,这样能使恒虚警处理在平稳状态下损失较小;另一个,为使恒虚警处理非平稳状态过渡过程短,就需要参考单元小。由于人体心跳频率一般在0.6~1.2 s[16]之间,选取心跳间隔为0.85 s是符合要求的,初始参考单元与数据采样频率建立函数关系,如式(3)所示,
Rr=0.85fs
(3)
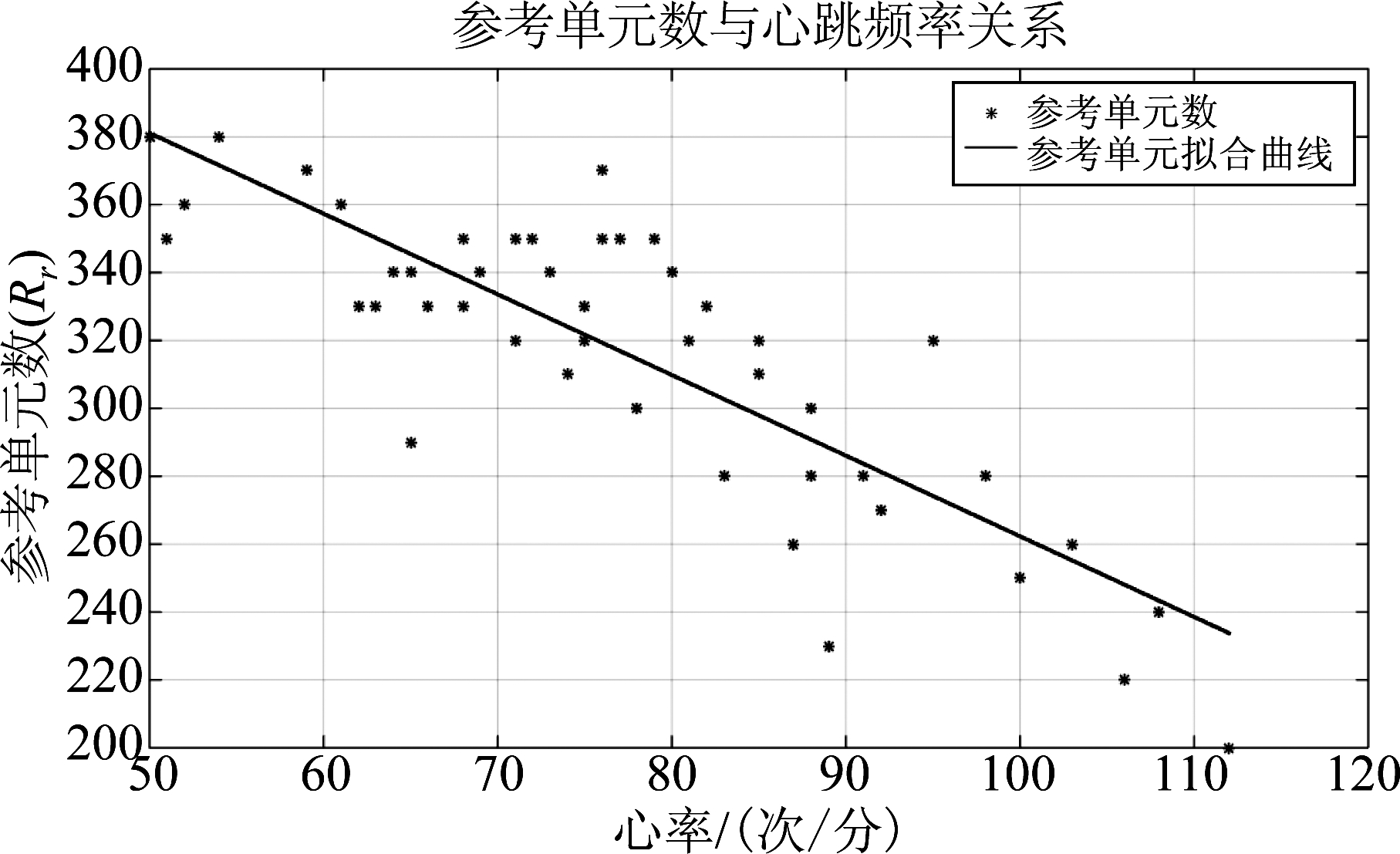
图4 心跳频率与参考单元关系
Fig.4 Relation between Heart Rate and Reference Unit
其中,fs为数据采样频率。MIT-BIH数据库ECG信号的采样频率为360 Hz,所以把初始参考单元选为300左右是合理的。为使得参考单元能适应ECG信号R波的检测,Rr需要更新。根据实验仿真,得到MIT-BIH数据库48例病例各自的最佳参考单元,并拟合参考单元Rr与心跳频率的关系,由如图4所示。
根据拟合曲线,设心跳频率为xr,参考单元Rr与xr的函数关系式如式(4)所示,
Rr=-2.376xr+499.911
(4)
由拟合关系式,进行拟合误差分析,根据式(5)计算其均方差(Mean squared error, MSE)。
(5)
其中,yi为原始的参考单元值,![]() 为拟合的参考单元值。以MIT-BIH数据库为例,求得MSE为534.57,均方差相对较大,对每个参考单元求拟合的误差,结果如图5所示。其中200号、210号、214号以及201号病例误差相对较大,可看作是异常值,整体误差是在0左右震荡,所以拟合函数是合理的,而在拟合参考单元下,仍然能较好的检测到其R波。因为参考单元在一定范围内是能较好检测到R波,如210号病例,在参考单元为180~230时漏检数最小,在210~260时,误检数最小,综合选取230作为其最佳参考单元。心率与参考单元存在一定的关系,一般情况心率越快,参考单元应适当调小,而心率越慢参考单元要适当调大,其关系不是强相关,有时应考虑ECG信号波形。一般人体心跳在0.6 s~1.2 s之间,即每分钟心跳50~100次,极端情况下考虑到40~120次/分钟,根据拟合关系式参考单元范围在215~405之间,是可控范围。所以根据拟合函数调整参考单元能让整体的检测误差平衡在较小的范围,检测误差越小,检测效果越佳,所以对参考单元做自适应调整是必要的。
为拟合的参考单元值。以MIT-BIH数据库为例,求得MSE为534.57,均方差相对较大,对每个参考单元求拟合的误差,结果如图5所示。其中200号、210号、214号以及201号病例误差相对较大,可看作是异常值,整体误差是在0左右震荡,所以拟合函数是合理的,而在拟合参考单元下,仍然能较好的检测到其R波。因为参考单元在一定范围内是能较好检测到R波,如210号病例,在参考单元为180~230时漏检数最小,在210~260时,误检数最小,综合选取230作为其最佳参考单元。心率与参考单元存在一定的关系,一般情况心率越快,参考单元应适当调小,而心率越慢参考单元要适当调大,其关系不是强相关,有时应考虑ECG信号波形。一般人体心跳在0.6 s~1.2 s之间,即每分钟心跳50~100次,极端情况下考虑到40~120次/分钟,根据拟合关系式参考单元范围在215~405之间,是可控范围。所以根据拟合函数调整参考单元能让整体的检测误差平衡在较小的范围,检测误差越小,检测效果越佳,所以对参考单元做自适应调整是必要的。
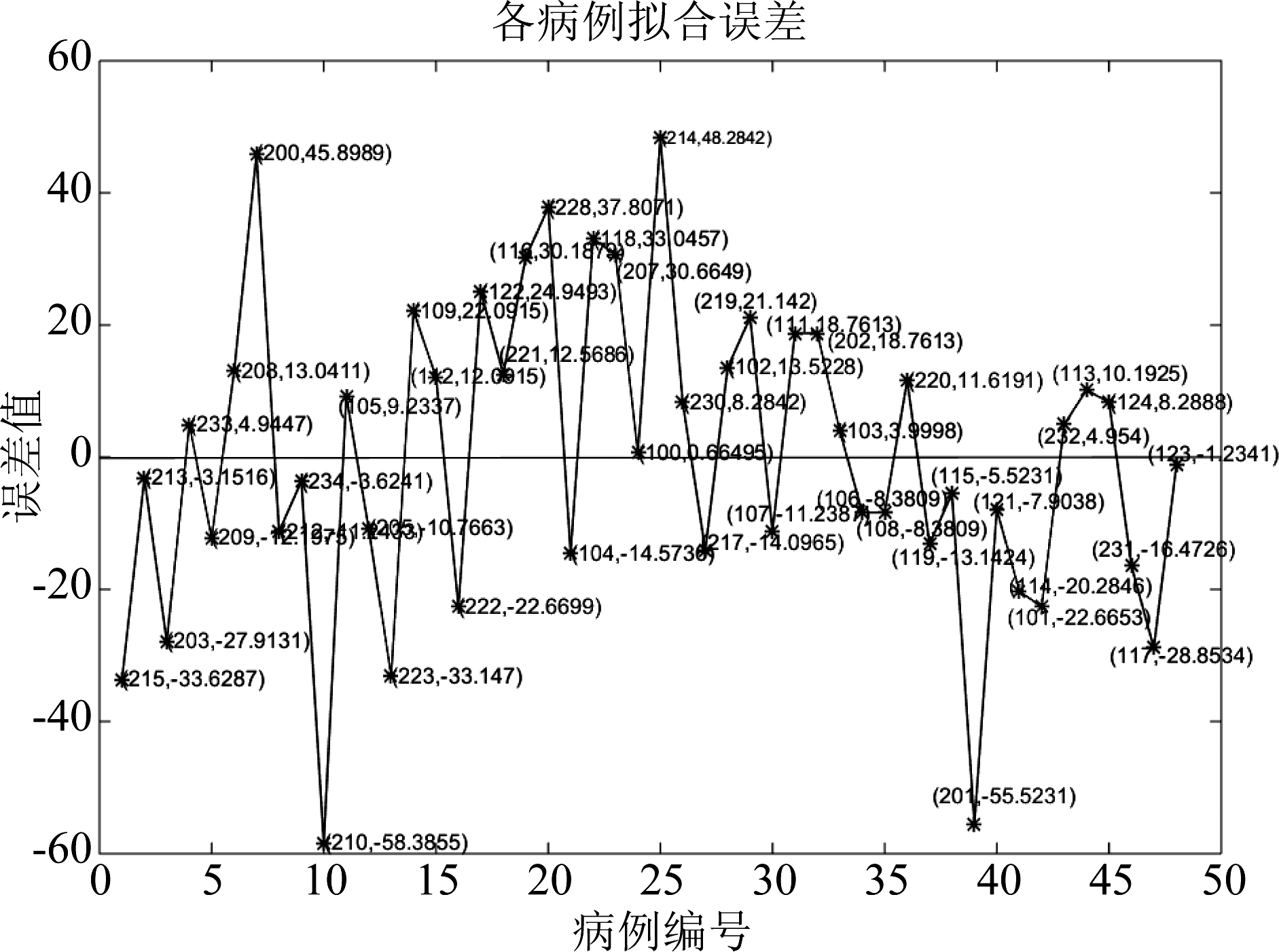
图5 各病例的拟合误差
Fig.5 Fitting error of each case
以103号病例为例,平均心率约为每分钟70次,那么由式(4)计算得其参考单元应更新为Rr=-2.376×70+499.911=333.591,近似为334,而实际103号病例的参考单元为340时有最佳检测率,拟合函数关系式符合CA-CFAR参考单元的设置。实际上,ECG信号除R波比较高大外,其他波形相对较小,再经过预处理后,理想情况下只剩近似一个脉冲的特征R波存在,两个R波间期之间为趋近于0的信号,所以在心率较快的情况下,RR间期较短,而参考单元在做平均时如果参考单元数大于RR间期,会使单元平均值加大,那么整个门限将会增加,很有可能检测不到感兴趣的信号,所以应该根据心率快慢适当调整参考单元大小。
设置好参考单元Rr后,信号经过Rr+1的参考窗,参考单元的平均功率如式(6)所求得,
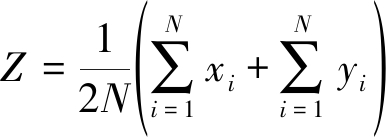
(6)
其中,xi和yi分别是待测信号前后的参考单元内元素。由设定的初始乘积因子T与平均功率Z相乘得到CA-CFAR门限S,对待测信号D和门限S进行归一化并取其对数,如式(7)和(8)所示,
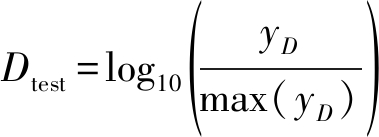
(7)
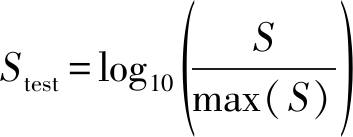
(8)
其中,yD为平方律检波后的待测信号。文献[14]证明,对数据进行对数变换后数值动态范围变小,且参考窗内的孤立干扰目标对干扰功率的估计平均值大小影响较小,从而减弱目标遮蔽效应。文献[17]也证明对数累积量的参数估计方法具有更低的估计方差,所以引用对数方法,对待测信号和门限进行对数处理,能提升检测的准确性。这样使待测信号最大限度准确的判决在假设H1下,即目标存在,然后对H1下信号进行不应期剔除,由ECG信号R波间隔的特性,即本次心跳与下一次心跳之间的间隔至少应该大于0.2 s[18],由于试验中降低了门限,故将间隔扩大到0.225 s,即每个心跳间隔应满足:
(dRi+1-dRi)>0.225×fs i=1,2,3...
(9)
其中,dRi为本次检测定位到的R波位置,dRi+1为下一次定位到的R波。这样满足式(9)保证能剔除不需要的定位,MIT-BIH数据库ECG信号的采样频率为360 Hz,故每次检测定位的距离至少是大等于81的,若检测定位到的本次R波与上一个R波的距离小于81,则删除本次定位到的R波。由此得到最初检测到的R波,根据RR间期计算出平均心率,再根据平均心率更新参考单元数做检测,直到检测效果不变,最后得到最佳R波检测,并根据检测结果由式(10)、(11)和(12)计算精准率、召回率和检测误差。
(10)
(11)
(12)
其中,TP、FP、FN分别为检测R波的正确个数、误报个数、漏报个数;Total R表示每个病例的R波总个数,即为正样本,不存在负样本;Precision为精准率,表示正确检测到R波个数占总的检测到R波个数之比;Recall为召回率,表示正确检测到R波个数占总的R波个数之比(不存在负样本);DER为检测误差,表示未检测到R波个数与检测到但不符合R波的个数和占总R波的个数,其检测误差越小,检测越好。
完整的检测步骤为:
步骤1 预处理:先将ECG信号x送入一个带通滤波器得到信号e;然后经过双斜率处理得到信号Smax,再将信号Smax通过一个低通滤波器,处理得到检波信号m,最后将信号m经过两次滑动窗口滤波得到预处理后的信号l;
步骤2 将预处理后的信号l经过平方律检波后得到信号yn,yn作平方律检波提高了待测信号分量,yn为CA-CFAR检测器的输入信号;
步骤3 由设定的乘积因子T和平均功率Z得到门限S,相应的降低门限S,对待测信号D和门限S进行归一化并取其对数,经CA-CFAR检测最大限度得到目标信号,判决为假设H0下的是不需要的信号,对于判决为假设H1下的目标信号,根据ECG信号的R波间隔的特殊性,做其一个不应期剔除规则的处理;
步骤4 利用剔除后检测所得R波位置计算心率,根据心率快慢更新参考单元数得到ECG信号R波检测;
步骤5 重复步骤3、4,直到检测稳定。然后得到预处理信号R波的位置,最终在实际信号上定位R波位置。
4 实验
对ECG信号做预处理后,根据CA-CFAR参数的设定,对待测信号检测判决。选取MIT-BIH数据库中具有代表性的病例103、107、111、116、118、119等进行实验仿真。以103号病例为例,103号病例有明显的基线漂移,如图6(a)所示,由CA-CFAR检测算法得到R波位置,第一栏“对数处理后R波定位”是预处理后的信号经过对数处理后对R波的定位,第二栏“原始信号R波定位”是在原始ECG信号波形上R波的定位,第三栏“去除基线漂移后R波定位”是在去除基线漂移后的信号上根据原始的定位进行峰值搜寻的定位。


图6 CA-CFAR R波检测定位
Fig.6 CA-CFAR R Wave Detection and Location
107号病例是起博心跳波形伴有明显的ST段抬高,且有高大的T波存在,利用CA-CFAR算法检测判决,再经过不应期剔除能有效的定位到R波,如图6(b)所示;116号病例存在J点抬高,所提算法能有效检测到R波,如图6(c)所示;119号病例有明显的室性早搏,包括偶发早搏、二联律和三联律等典型心律失常波形,利用CA-CFAR算法也能有效检测得到R波,如图6(d)所示;111号是左束支传导阻滞的波形,其出现了两个波峰,所提CA-CFAR算法能避开非R波定位到真正的波峰,如图6(e)所示;118号是右束支传导阻滞的波形,如图6( f )所示,也能有效检测到R波。
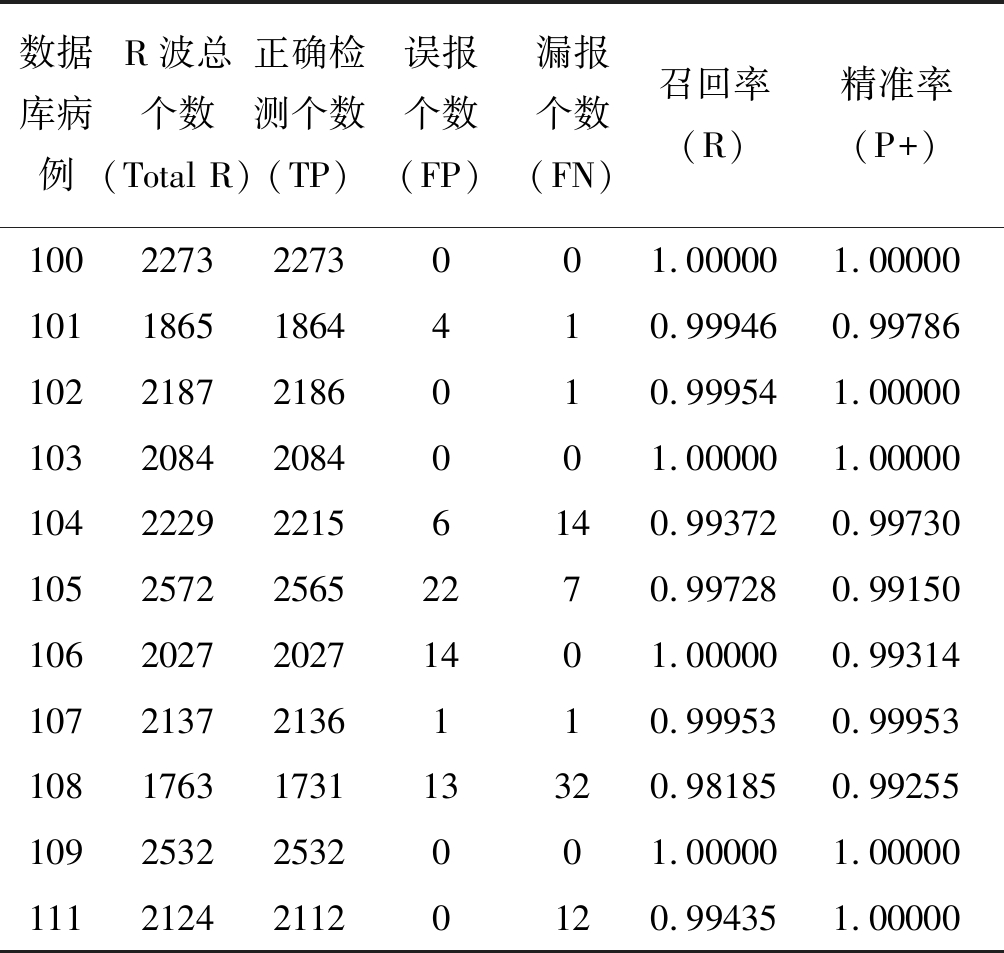
用MIT-BIH数据库中48例病例数据对算法进行验证,剔除其中“节奏变化”、“信号质量发生变化”等非R波所在位置的标记,剩余109966个R波,另外111, 213病例最后一个波形不全,不计在检测总数中。实验结果如表1所示。
表1 MIT-BIH心律失常数据库48例病例统计结果
Tab.1 Statistical results of 48 cases in MIT-BIH arrhythmia database
数据库病例R波总个数(Total R)正确检测个数(TP)误报个数(FP)漏报个数(FN)召回率(R)精准率(P+)10022732273001.000001.0000010118651864410.999460.9978610221872186010.999541.0000010320842084001.000001.00000104222922156140.993720.99730105257225652270.997280.99150106202720271401.000000.9931410721372136110.999530.999531081763173113320.981850.9925510925322532001.000001.00000111212421120120.994351.00000
续表1
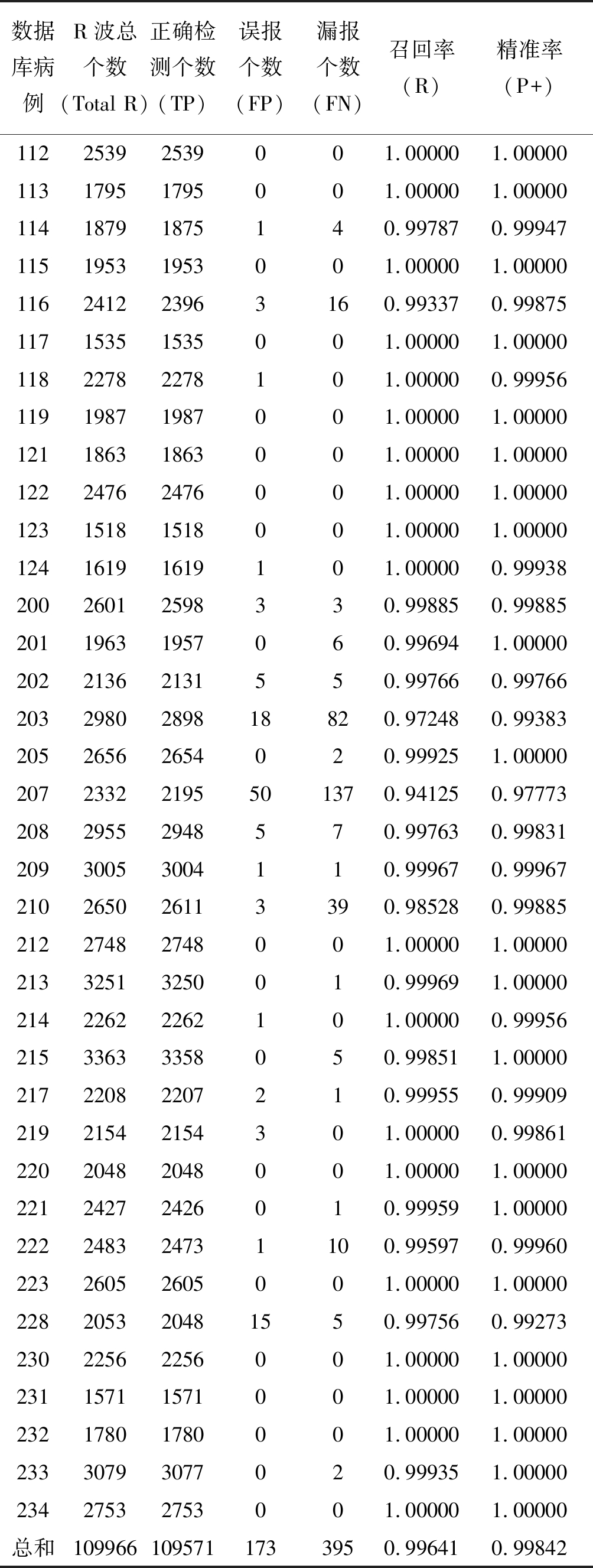
数据库病例R波总个数(Total R)正确检测个数(TP)误报个数(FP)漏报个数(FN)召回率(R)精准率(P+)11225392539001.000001.0000011317951795001.000001.0000011418791875140.997870.9994711519531953001.000001.00000116241223963160.993370.9987511715351535001.000001.0000011822782278101.000000.9995611919871987001.000001.0000012118631863001.000001.0000012224762476001.000001.0000012315181518001.000001.0000012416191619101.000000.9993820026012598330.998850.9988520119631957060.996941.0000020221362131550.997660.997662032980289818820.972480.9938320526562654020.999251.0000020723322195501370.941250.9777320829552948570.997630.9983120930053004110.999670.99967210265026113390.985280.9988521227482748001.000001.0000021332513250010.999691.0000021422622262101.000000.9995621533633358050.998511.0000021722082207210.999550.9990921921542154301.000000.9986122020482048001.000001.0000022124272426010.999591.00000222248324731100.995970.9996022326052605001.000001.00000228205320481550.997560.9927323022562256001.000001.0000023115711571001.000001.0000023217801780001.000001.0000023330793077020.999351.0000023427532753001.000001.00000总和1099661095711733950.996410.99842
对207号病例的检测效果不佳,因为207号病例有心室扑动/颤动波形存在,没有明显的波峰,给检测算法带来了困难。如图7所示,是利用CA-CFAR检测算法对207号病例心室颤动的检测,其检测的精准率是97.361%,召回率是76.240%。主要原因是当人体心脏发生心室颤动引起心律失常时,其波形变换较快而不整齐,又无明显QRS波群,甚至为近似正弦波一样的波形,算法对心室颤动检测不敏感。
文献[5]、[6]、[9]、[10]、[18]等都没有对207号病例的心室扑动/颤动波进行检测,所以除去207号病例对算法进行对比验证,如表2所示。
本文算法与文献[5]、[6]、[8]、[9]、[10]、[18]对比,其中文献[5]、[8]、[9]、[10]、[18]等所用MIT-BIH的数据较全,整体对比下本文算法效果更佳,文献[6]数据不全,可从召回率看出本文算法也优于文献[6]。在同等数据下与文献[6]进行对比,如表3所示,在同等数据条件下本文提出算法召回率与检测误差优于文献[6],精准率略低于文献[6]。

图7 CA-CFAR算法对207号室颤波形检测
Fig.7 CA-CFAR algorithm for 207 ventricular fibrillation waveform detection
表2 除去207号病例算法对比
Tab.2 Comparisons of algorithms for removing 207 cases
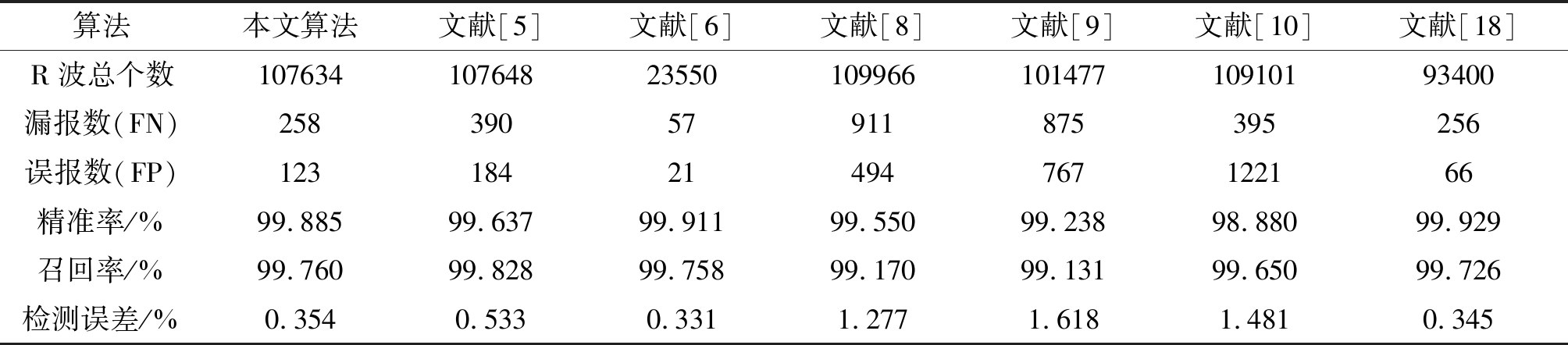
算法本文算法文献[5]文献[6]文献[8]文献[9]文献[10]文献[18]R波总个数1076341076482355010996610147710910193400漏报数(FN)25839057911875395256误报数(FP)12318421494767122166精准率/%99.88599.63799.91199.55099.23898.88099.929召回率/%99.76099.82899.75899.17099.13199.65099.726检测误差/%0.3540.5330.3311.2771.6181.4810.345
表3 文献[6]同等数据条件下对比
Tab.3 Comparison of literature [6] under the same data conditions

算法R波总数正确检测个数(TP)误报个数(FP)漏报个数(FN)精准率(P+)召回率(R)检测误差(DER)本文算法235502353127190.99885 0.99919 0.00195 文献[6]算法235502349321570.99911 0.99758 0.00331
表4 CA-CFAR检测算法对MIT-BIH其他数据库验证结果
Tab.4 Validation results of CA-CFAR detection algorithm for other databases of MIT-BIH
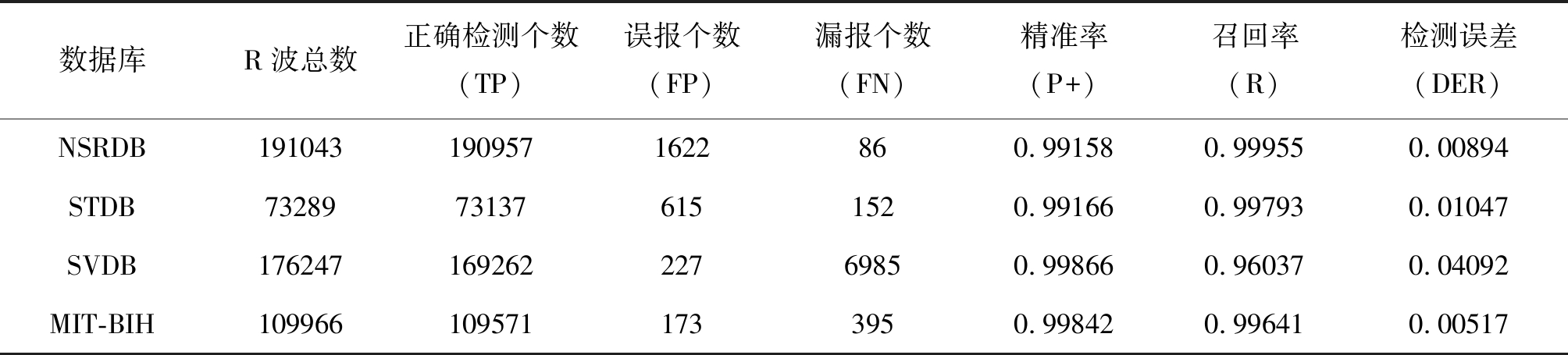
数据库R波总数正确检测个数(TP)误报个数(FP)漏报个数(FN)精准率(P+)召回率(R)检测误差(DER)NSRDB1910431909571622860.991580.999550.00894STDB73289731376151520.991660.997930.01047SVDB17624716926222769850.998660.960370.04092MIT-BIH1099661095711733950.998420.996410.00517
对MIT-BIH的窦性心律数据库(NSRDB)的18个记录,每个记录取1000000个数据,MIT-BIH的ST段改变数据库(STDB)的28个记录所有数据,以及MIT-BIH的室上性心律失常数据库(SVDB)的75个记录所有数据进行仿真验证算法的有效性,结果如表4所示,用CA-CFAR检测的平均精准率为99.508%,平均召回率为98.857%,平均检测误差为1.638%。
5 结论
本文将CA-CFAR检测方法引入到ECG信号R波的检测中,并根据ECG信号特有的性质,在信号检测判决后加入不应期判别规则剔除多余检测,拟合出ECG信号的平均心率与参考单元的函数关系,自适应调整CA-CFAR的参考单元,以最大限度适应ECG信号的检测,最终定位ECG信号中R波的所在位置。实测数据实验表明了算法的有效性和适用性。
[1] Vincent A E, Sreekumar K. A survey on approaches for ECG signal analysis with focus to feature extraction and classification[C]∥International Conference on Inventive Communication & Computational Technologies. IEEE, 2017.
[2] Sayantan G, Kien P T, Kadambari K V. Classification of ECG beats using deep belief network and active learning[J]. Medical & Biological Engineering & Computing, 2018, 56(10): 1-12.
[3] Haberman Z C, Jahn R T, Bose R, et al. Wireless Smartphone ECG Enables LargE-Scale Screening in Diverse Populations[J]. Journal of Cardiovascular Electrophysiology, 2015, 26(5): 520-526.
[4] Varon C, Caicedo A, Testelmans D, et al. A novel algorithm for the automatic detection of sleep apnea from singlE-lead ECG[J]. IEEE Transactions on Biomedical Engineering, 2015, 62(9): 1-1.
[5] Wang Y, Deepu C J, Lian Y. A computationally efficient QRS detection algorithm for wearable ECG sensors[C]∥International Conference of the IEEE Engineering in Medicine & Biology Society. Boston, MA, USA: IEEE, 2011: 5641-5644.
[6] Hulya K S, Suleyman C, Omer S. Wavelet transform based noise removal from ECG signal for accurate heart rate detection using ECG[C]∥Medical Technologies National Conference. Bodrum, Turkey: IEEE, 2016: 1- 4.
[7] 彭自然, 王国军. 用小波变换对ECG信号进行去噪研究[J]. 信号处理, 2017, 33(8): 1122-1131.
Peng Ziran, Wang Guojun. Study on denoising ECG signal with wavelet transform[J]. Journal of Signal processing, 2017, 33(8): 1122-1131.(in Chinese)
[8] Tang X C, Hu Q S, Tang W. A Real-Time QRS Detection System With PR/RT Interval and ST Segment Measurements for Wearable ECG Sensors Using Parallel Delta Modulators[J]. IEEE Transactions on Biomedical Circuits and Systems, 2018, 12(4): 751-761.
[9] Tsai Y, Chang Z Y, Huang C W. TimE-Domain Multi-Level R-Peak Detection Algorithm for ECG Signal Processing[C]∥Eurasia Conference on Biomedical Engineering, Healthcare and Sustainability (ECBIOS), Okinawa, Japan: IEEE, 2019: 35-38.
[10] Satija U, Ramkumar B, Manikandan M S. A New Automated Signal Quality-Aware ECG Beat Classification Method for Unsupervised ECG Diagnosis Environments[J]. IEEE Sensors Journal, 2019, 19(1): 277-286.
[11] Tao L, Zheng L, Rong X, et al. An Improved Superpixel-Level CFAR Detection Method for Ship Targets in High-Resolution SAR Images[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2018, PP(99): 1-11.
[12] Zhang L, Ding G, Wu Q, et al. Spectrum Sensing Under Spectrum Misuse Behaviors: A Multi-Hypothesis Test Perspective[J]. IEEE Transactions on Information Forensics & Security, 2017, 13(4): 993-1007.
[13] 张晓伟, 杨咚咚. 基于压缩感知测量值的宽带雷达回波信号NP检测[J]. 火控雷达技术, 2017, 46(4): 1- 6.
Zhang Xiaowei, Yang Dongdong. Broadband radar echo signal NP detection based on compressed sensing measurement[J]. Fire Control Radar Technology, 2017, 46(4): 1- 6.(in Chinese)
[14] Mark A. Richards. 雷达信号处理基础[M]. 邢孟道, 王彤, 李真芳, 等, 译. 第二版. 北京: 电子工业出版社, 2008: 266-290.
Mark A. Richards. Fundamentals of radar signal processing[M]. Xing Mengdao, Wang Tong, Li Zhenfang, et al. translate. 2nd Ed. Beijing: Electronic Industry Press, 2008: 266-290.(in Chinese)
[15] 赵静, 韦海成. ECG信号自适应贝叶斯小波去噪算法研究[J]. 现代电子技术, 2019, 42(5): 61- 65.
Zhao Jing, Wei Haicheng. Research on adaptive Bayesian wavelet denoising algorithm for ECG signals[J]. Modern Electronic Technology, 2019, 42(5): 61- 65.(in Chinese)
[16] 项延德. 基于卷积神经网络的心电信号检测和分类研究[D]. 杭州: 浙江大学, 2018.
Xiang Yande. Study on detection and classification of ecg signals based on convolutional neural network[D]. Hangzhou: Zhejiang University, 2018.(in Chinese)
[17] 王亢, 贡毅, 徐志江, 等. 基于对数累积量的重尾分布脉冲干扰参数估计及性能分析[J]. 中国科学: 信息科学, 2017, 47(2): 221-234.
Wang Kang, Gong Yi, Xu Zhijiang, et al. Parameter estimation and performance analysis of heavy-tail distributed pulse interference based on logarithmic cumulations[J]. Science in China: Information Science, 2017, 47(2): 221-234.(in Chinese)
[18] 夏翀. 心电信号实时检测算法研究[D]. 武汉: 湖北工业大学, 2017.
Xia Chong. Research on real-time ecg signal detection algorithm[D]. Wuhan: Hubei University of Technology, 2017.(in Chinese)



