1 引言
2017年中国民用航空局等部门共发布60余条通用航空相关政策和文件,使通航产业迎来了新一轮快速增长机遇,但期间发生的安全事故却为通航发展的美好前景增添了几份阴霾,通用航空运行不安全的问题愈加突出[1],区别于运输航空,大部分通用航空企业更加重视飞行前的监管,对于飞行中和飞行后的监管不够重视,在技术层面,目前我国通用航空的运行缺乏对航空器的动态预测,特别是对无法提供航迹数据的通用航空器进行动态预测,导致通用航空飞行中和飞行后的监管缺乏合理有效的机制。航空器的动态预测对于飞行中辅助掌握航空器的飞行动态,飞行后辅助预测坠机区域及缩小搜救范围将发挥重要作用。
当对航空器进行目标跟踪时,利用雷达获取目标的位置和运动参数,将所有数据组合成航空器的飞行航迹,常用的目标跟踪方法包括卡尔曼滤波、粒子滤波、检测前跟踪等方法[2]。通用航空器的动态预测问题是在目标跟踪的基础上利用航空器的位置和运动参数,根据航空器当前的飞行状态、气象环境等因素对通用航空器的未来运动状态做出预测。当存在监视数据时,可通过航迹预测实现航空器的动态预测;当不存在持续稳定的监视数据时,可通过在预设报告点进行话音报告的方式对航空器进行动态预测。
近年来部分学者陆续开展研究通用航空器动态预测的方法。文献[3]根据现有空管自动化系统航迹估算的方法,以爬升、巡航、下降三阶段的飞行模型为基础,利用通用航空器的性能参数,给出了通用航空飞行计划航迹估算的具体实现方法。文献[4]在对无人机航迹进行分析的基础上,基于粒子滤波原理,通过对航迹敏感的姿态角的预测来间接实现无人机航迹的预测。文献[5]建立了爬升避让4D 航迹预测模型,在爬升阶段大大缩短了爬升时间,同时在避让时简化转弯程序。文献[6]针对物理特性一致的多无人机协同任务分配问题,提出一种多阶段航迹预测分布式任务规划方法。文献[7]针对无人机编队内躲避碰撞的问题,提出一种可实时躲避碰撞以及多碰撞冲突管理的多无人机协同航迹规划方案。文献[8]提出一种基于运行状态识别的无人机高斯过程—无味卡尔曼滤波的混合估计方法。
对于有人驾驶的作业飞行通用航空器,当执行航空摄影、航空喷洒、护林消防等作业任务时,由于无法提供监视数据,在执行较为危险的作业任务时,无法及时掌握作业飞行通用航空器的飞行动态,为安全飞行带来隐患。文献[3]算法的正常运行需依赖于航迹数据的稳定支持,且三阶段飞行模型较为简单,估算误差较大;文献[4]至文献[8]的算法均根据无人机的飞行特性进行设计,无法适用于有人驾驶的作业飞行通用航空器,现有方法已无法满足需求。本文提出一种基于动态扩展蚁巢的估算方法,在没有监视数据情况下对有人驾驶的作业飞行通用航空器的报告点位置进行预测,为保障航空器安全飞行提供技术参考。
2 算法研究
2.1 经典蚁群算法
蚁群算法是由意大利学者Dorigo.M等人提出的一种基于模拟自然界蚂蚁种群觅食行为特征的智能优化并行算法[9]。蚁群算法的基本思想:蚂蚁爬行时会在经过的路径上释放一种分泌物,称为信息素。信息素仅会留存一段时间,信息素浓度越高的路径被同一蚁巢的其他蚂蚁选择的概率越大[10]。蚁群算法的优点:具有很强的并行性及鲁棒性,在很多领域得到广泛应用[11]。蚁群算法的缺点:蚂蚁待爬行的路径点选择范围较大时会增加算法的迭代次数及收敛于局部最优解的概率,降低算法的搜索效率[12]。在算法处理数据中,每只蚂蚁将按照一定的规则从没有访问过的路径点中选择下一个路径节点,同时蚂蚁每爬行一步或爬行到终点后更新所有路径点上的信息素浓度[12]。
2.2 动态扩展蚁巢模型的通航报告位置预测算法
针对没有监视数据情况下对有人驾驶的作业飞行通用航空器报告点位置的预测问题,本文以护林消防作业飞行为例进行阐述。假设森林有多处地点发生火灾,将每一处火灾地点设置为一个飞行报告点。执行护林消防任务的通用航空器接到任务委派指令后从停机坪起飞,为了防止火势进一步蔓延,飞行员会尽可能选择一条用时最短且每处火灾地点只到达一次的飞行路径,由于没有监视数据,飞行员每到达一处火灾地点,均需向地面指挥部门报告,便于地面指挥部门对通用航空器进行动态预测,保障航空器安全飞行。飞行员在护林消防作业过程中,由于某几个较远的火灾地点火势加剧需尽快实施救援,飞行员需改变飞行路径优先保障火势加剧的地点,导致预测报告点出现错误。
本文根据经典蚁群算法,将航空器起飞点设置为全部蚂蚁的出发点,将航空器预计飞行的报告点设置为蚂蚁预计爬行的路径点,构建飞行路径表、路径禁忌表及信息素表,使用公式(1)计算未飞行报告点间的转移概率,经过多次迭代根据转移概率基于轮盘赌方法获取各代全部蚂蚁中用时最短蚂蚁的路径点及时间。
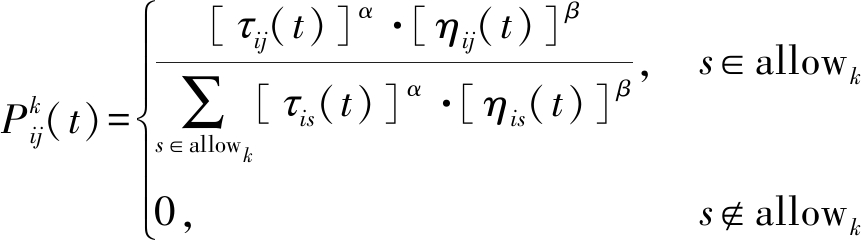
(1)
其中
表示t时刻第k只蚂蚁从点i转移到点j的概率,τij(t)表示t时刻点i与点j连接路径上的信息素浓度,ηij(t)表示t时刻从点i转移到点j的期望程度,α表示信息素重要程度因子,β表示启发函数重要程度因子,allowk表示为第k只蚂蚁待爬行点的集合。
使用公式(2)计算式(1)中的τij(t)与ηij(t)。其中ρ表示信息素的挥发程度,dij表示点i与点j之间的距离,Δτij表示全部蚂蚁在点i与点j连接路径上释放总信息素浓度。
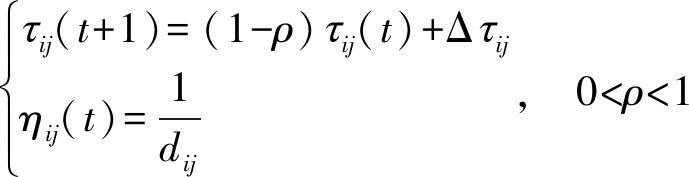
(2)
使用公式(3)计算式(2)中的Δτij。其中Q表示蚂蚁循环一次释放的总信息素,Lk表示第k只蚂蚁爬行的总距离,
表示第k只蚂蚁在点i与点j连接路径上释放的信息素浓度。
(3)
自然界中的蚂蚁种群为了适应外界环境的变化往往会进行蚁巢的搬迁,其对蚂蚁种群的繁衍及扩散具有十分重要的意义[13]。多蚁后型种群婚飞后扩张形成新蚁巢,新入侵地不同环境中蚁巢的分布存在差异[14]。在运用算法处理数据中,当使用公式(4)计算蚂蚁最短用时满足最快爬行偏差阈值要求时,新蚁巢将根据错误报告点信息进行动态扩展。
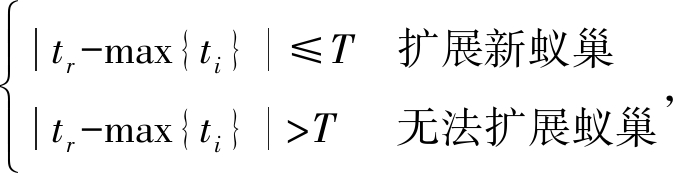r∈[1,n] i∈[1,r-1]
(4)
其中tr表示第r次扩展蚁巢爬行全部路径点最短用时,max{ti}表示前r-1次扩展蚁巢中爬行最短用时的最大值,T表示最快爬行偏差阈值。
根据用时最短蚂蚁的全部路径点及当前最新蚁巢位置预测未飞行报告点的位置。当航空器报告点位置与预测位置不相同时,将当前航空器错误报告点设置为扩展的新蚁巢,由于种群间的相互排斥,新建蚁巢的蚂蚁很少会在临近蚁巢的蚂蚁覆盖范围内觅食,将扩展的新蚁巢与临近蚁巢间的路径点添加到路径禁忌表;由于新入侵地不同环境中蚁巢的分布存在差异,重置飞行路径表及信息素表,记录扩展蚁巢数量及位置,基于扩展的新蚁巢重新估算未飞行报告点的位置。
2.3 预测算法实施步骤
动态扩展蚁巢模型的通航报告位置预测算法流程如图1所示,具体步骤如下:
步骤1 初始化地图位置参数及航空器报告点估算参数,其中关键参数包含:蚂蚁数量、信息素重要程度因子、启发函数重要程度因子、信息素挥发因子、最大迭代次数、最快爬行偏差阈值等;
步骤2 将航空器起飞点设置为全部蚂蚁的出发点,将航空器预计飞行的报告点设置为蚂蚁预计爬行的路径点,构建飞行路径表、路径禁忌表及信息素表;
步骤3 根据路径禁忌表获取航空器未飞行的报告点位置;根据信息素表计算未飞行报告点间的转移概率;根据转移概率基于轮盘赌方法获取下一个预测报告点位置,更新飞行路径表及路径禁忌表;
步骤4 更新估算报告点数量及蚂蚁数量,判断全部蚂蚁是否均已到达终点,若判断结果为“否”,则进入步骤3;若判断结果为“是”,则进入下一步处理;
步骤5 根据飞行路径表计算全部蚂蚁到达终点的时间,获取用时最短蚂蚁的全部路径点及时间;重置飞行路径表,更新路径禁忌表及信息素表;
步骤6 更新迭代次数,判断迭代次数是否满足参数要求,若判断结果为“否”,则进入步骤3;若判断结果为“是”,则进入下一步处理;
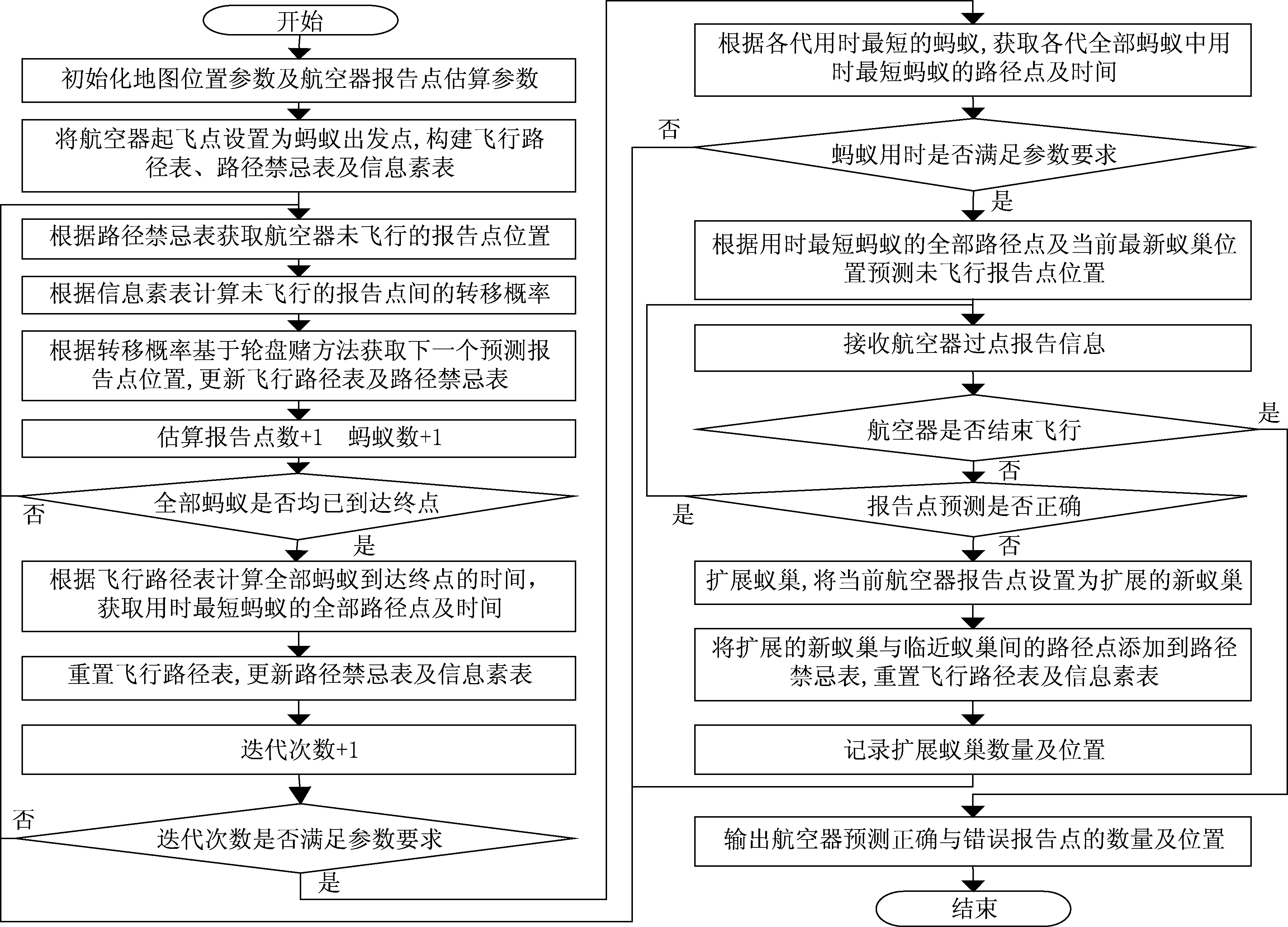
图1 动态扩展蚁巢模型的通航报告位置预测算法流程图
Fig.1 Flow chart of general aviation report location prediction algorithm based on dynamic extended ant nest model
步骤7 根据各代用时最短的蚂蚁数据,获取各代全部蚂蚁中用时最短蚂蚁的路径点及时间;判断蚂蚁最短用时是否满足最快爬行偏差阈值的要求,若判断结果为“否”,则进入步骤3;若判断结果为“是”,则进入下一步处理;
步骤8 根据用时最短蚂蚁的全部路径点及当前最新蚁巢位置预测未飞行报告点位置;
步骤9 接收航空器过点报告信息,判断航空器是否结束飞行,若判断结果为“否”,则进入下一步处理;若判断结果为“是”,则输出航空器预测正确与错误报告点的数量及位置,退出处理流程;
步骤10 判断当前报告点位置与预测位置是否一致,若判断结果为“否”,则进入下一步处理;若判断结果为“是”,则进入步骤9;
步骤11 扩展蚁巢,将当前航空器错误报告点设置为扩展的新蚁巢,将扩展的新蚁巢与临近蚁巢间的路径点添加到路径禁忌表,重置飞行路径表及信息素表;
步骤12 记录扩展蚁巢数量及位置,进入步骤3。
3 实验仿真
3.1 仿真条件
实验仿真前需设置预测算法参数及实际飞行参数。预测算法参数包括:蚂蚁数量、信息素重要程度因子、启发函数重要程度因子、信息素挥发因子、蚂蚁循环一次释放总信息素、最大迭代次数、最快爬行偏差阈值等参数,预测算法参数如表1所示。实际飞行参数包括:实际飞行路径、实际飞行速度等参数,实际飞行参数如表2所示。
表1 预测算法参数
Tab.1 Prediction algorithm parameters
参数参数值蚂蚁数量35信息素重要程度因子1启发函数重要程度因子5信息素挥发因子0.1蚂蚁循环一次释放总信息素1最大迭代次数200最快爬行偏差阈值0.1
3.2 仿真场景
仿真实验中实际飞行路径如图2所示。图2(a)的飞行场景为原始飞行路径;图2(b)的飞行场景为变更一次飞行路径点,由于点16火势加剧等原因,飞行路径由点2飞行到点13变更为由点2飞行到点16;图2(c)的飞行场景为变更二次飞行路径点,由于点18火势加剧等原因,在图2(b)飞行路径的基础上由点14飞行到点17变更为由点14飞行到点18;图2(d)的飞行场景为变更三次飞行路径点,由于点20火势加剧等原因,在图2(c)飞行路径的基础上由点19飞到点21变更为由点19飞到点20。
表2 实际飞行参数
Tab.2 Actual flight parameters Simulation parameters
参数参数值实际飞行路径111 9 10 8 3 4 5 6 7 2 13 16 15 14 17 18 19 21 20 23 24 22 1 12实际飞行路径211 9 10 8 3 4 5 6 7 2 16 15 13 14 17 18 19 21 20 23 24 22 1 12实际飞行路径311 9 10 8 3 4 5 6 7 2 16 15 13 14 18 17 19 21 20 23 24 22 1 12实际飞行路径411 9 10 8 3 4 5 6 7 2 16 15 13 14 18 17 19 20 21 23 24 22 1 12实际飞行速度50(m/s)
图2 实际飞行路径图
Fig.2 Actual flight path map
3.3 基于一种实际飞行路径条件下的算法功能仿真分析
为了比较实际飞行中多次变更路径点位置对两种方法报告点预测正确率的影响,选取四种实际飞行路径中变更点数量最多的路径4进行功能仿真。基于实际飞行路径4条件下的算法仿真如图3所示。
图3 基于实际飞行路径4条件下的算法仿真
Fig.3 Algorithmic simulation based on actual flight path 4
图3(a)为实际飞行路径4,变更三次飞行路径点;图3(b)为经典蚁群算法报告点预测结果,由于实际飞行中变更三次飞行路径点,导致经典蚁群算法报告点预测结果正确率较低;图3(c)为动态扩展蚁巢算法第一次扩展蚁巢结果,根据错误报告点位置,将点16扩展为新蚁巢,将点11与点16间的路径点添加到路径禁忌表,重置飞行路径表及信息素表,重新进行报告点估算;图3(d)为动态扩展蚁巢算法第二次扩展蚁巢结果,根据错误报告点位置,将点18扩展为新蚁巢,将点16与点18间的路径点添加到路径禁忌表,重置飞行路径表及信息素表,重新进行报告点估算;图3(e)为动态扩展蚁巢算法第三次扩展蚁巢结果,根据错误报告点位置,将点20扩展为新蚁巢,将点18与点20间的路径点添加到路径禁忌表,重置飞行路径表及信息素表,重新进行报告点估算;图3( f )为动态扩展蚁巢算法报告点预测结果,经过多次扩展蚁巢,报告点位置预测结果与实际飞行结果一致。经数据分析,此次实验共扩展蚁巢3次,经典蚁群算法报告点预测正确率为62.5%,动态扩展蚁巢算法报告点预测正确率为87.5%,动态扩展蚁巢算法报告点预测正确率优于经典蚁群算法。
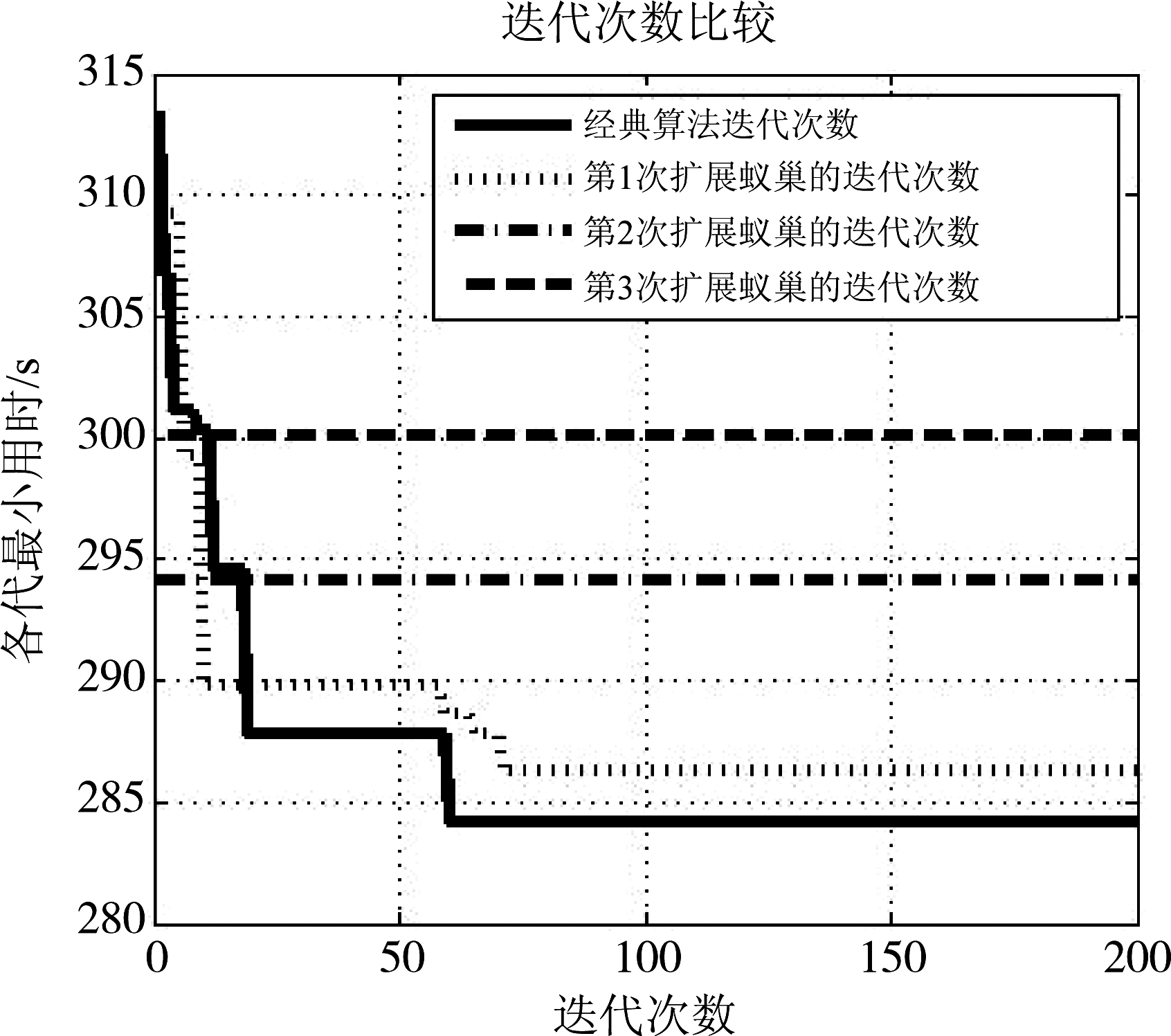
图4 基于实际飞行路径4条件下迭代次数比较
Fig.4 Iteration number comparison based on actual flight path 4
基于实际飞行路径4条件下迭代次数比较如图4所示。第1次扩展蚁巢达到最小用时的迭代次数略高于经典蚁巢算法,但第2次及第3次扩展蚁巢达到最小用时的迭代次数很少。经数据分析,经典蚁巢算法迭代次数为61次,扩展蚁巢算法迭代次数累计为74次,扩展蚁巢算法在较高正确率的前提下未增加过多的迭代次数。
基于实际飞行路径4条件下的信息素分布如图5所示。信息素分布坐标(i, j)表示从点i到点j路径间的信息素浓度,因为实际飞行路径由24个报告点构成,所以估算报告点位置本质上是在信息素分布中找到信息素浓度最大的24个坐标点。图5(a)为经典蚁群算法信息素分布三维图,图5(b)为经典蚁群算法信息素分布二维图,发现经典蚁群算法信息素分布中有24个信息素浓度较大的坐标点,8个信息素浓度较小的坐标点;图5(c)为动态扩展蚁巢算法信息素分布三维图,图5(d)为动态扩展蚁巢算法信息素分布二维图,发现动态扩展蚁巢算法只有24个信息素浓度较大的坐标点,不存在其他坐标点信息素干扰的影响。
3.4 基于四种实际飞行路径条件下蒙特卡洛实验的算法性能仿真分析
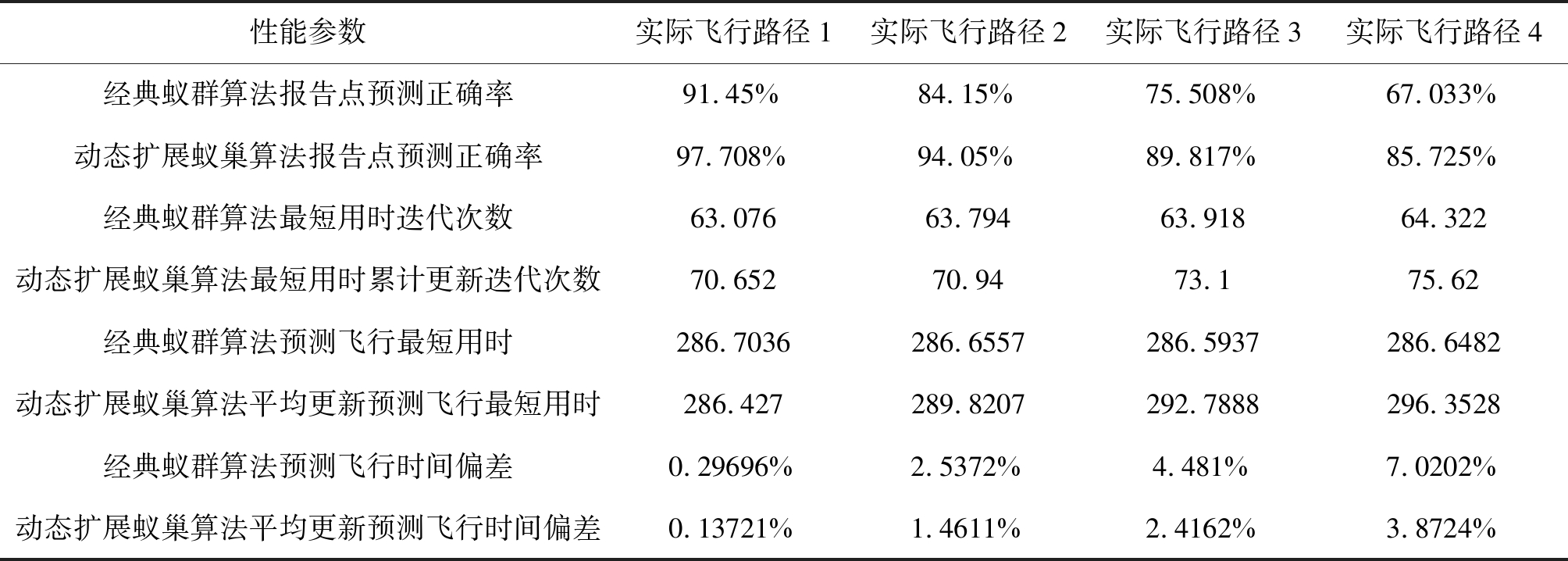
蒙特卡洛实验500次后经典蚁群算法与动态扩展蚁巢算法报告点预测性能比较如表3所示。本文基于以下四个方面进行分析:
(1)报告点预测正确率方面:在四种实际飞行路径条件下,动态扩展蚁巢算法报告点预测正确率均高于经典蚁群算法,且随着实际飞行路径点变更次数的增多,经典蚁群算法报告点预测正确率由91.45%下降到67.033%,动态扩展蚁巢算法报告点预测正确率由97.708%下降到85.725%,经典蚁群算法预测正确率急剧恶化较为明显,动态扩展蚁巢算法预测正确率均在85%以上,报告点预测正确率较好。
(2)预测最短用时迭代次数方面:在四种实际飞行路径条件下,动态扩展蚁巢算法最短用时累计更新迭代次数仅约高于经典蚁群算法10次左右,且随着实际飞行路径点变更次数的增多,两种方法迭代次数均涨幅较小。
(3)预测飞行最短用时方面:在四种实际飞行路径条件下,随着实际飞行路径点变更次数的增多,经典蚁群算法预测飞行最短用时基本没有太大变化,动态扩展蚁巢算法在实际飞行路径点变更次数增多的条件下,由于实际飞行用时增加,动态扩展蚁巢算法平均更新预测飞行最短用时也逐渐增加。
图5 基于实际飞行路径4条件下的信息素分布
Fig.5 Pheromone distribution based on actual flight path 4
表3 报告点预测性能比较
Tab.3 Performance comparison of report point prediction
性能参数实际飞行路径1实际飞行路径2实际飞行路径3实际飞行路径4经典蚁群算法报告点预测正确率91.45%84.15%75.508%67.033%动态扩展蚁巢算法报告点预测正确率97.708%94.05%89.817%85.725%经典蚁群算法最短用时迭代次数63.07663.79463.91864.322动态扩展蚁巢算法最短用时累计更新迭代次数70.65270.9473.175.62经典蚁群算法预测飞行最短用时286.7036286.6557286.5937286.6482动态扩展蚁巢算法平均更新预测飞行最短用时286.427289.8207292.7888296.3528经典蚁群算法预测飞行时间偏差0.29696%2.5372%4.481%7.0202%动态扩展蚁巢算法平均更新预测飞行时间偏差0.13721%1.4611%2.4162%3.8724%
(4)预测飞行最短用时偏差方面:在四种实际飞行路径条件下,动态扩展蚁巢算法平均更新预测飞行最短用时偏差均低于经典蚁群算法,且随着实际飞行路径点变更次数的增多,两种方法预测飞行最短用时偏差也逐渐增加。
算法性能仿真结果表明:动态扩展蚁巢方法在提高算法正确率的同时可以兼顾搜索效率。由于动态扩展蚁巢算法根据错误报告点预测信息动态扩展新蚁巢,根据蚁巢间的相互排斥性将扩展的新蚁巢与临近蚁巢间的路径点添加到路径禁忌区,从而减少路径点选择范围,降低迭代次数及收敛于局部最优解的概率。
4 结论
(1)本文针对通用航空特点,根据业务需求对基于动态扩展蚁巢模型的通航报告位置预测算法进行了阐述,并给出了预测算法的详细实施步骤;
(2)本文结合实验仿真条件以及通用航空器的仿真飞行场景,分别给出了基于一种实际飞行路径条件下的算法功能仿真以及基于四种飞行路径条件下蒙特卡洛实验的算法性能仿真;
(3)仿真结果表明通过动态扩展蚁巢算法可降低迭代次数及收敛于局部最优解的概率,在提高算法正确率的同时可以兼顾搜索效率;
(4)本文基于动态扩展蚁巢算法的各项参数为蚁群算法的常规设置,调整参数的影响分析将在接下来的工作中做进一步研究;
(5)本文算法可为我国通用航空发展和通用航空器动态预测提供技术参考。
[1] 吴仁彪, 何理, 王晓亮, 等. 通用航空飞行计划评估方法综述[J]. 信号处理, 2019, 35(3): 426- 434.
Wu Renbiao, He Li, Wang Xiaoliang, et al. Review of General Aviation Flight Plan Evaluation Method[J]. Journal of Signal Processing, 2019, 35(3): 426- 434.(in Chinese)
[2] 王雪君, 孙进平, 张旭旺. 基于压缩感知的PD雷达序贯扩展卡尔曼滤波跟踪方法[J]. 信号处理, 2017, 33(4): 601- 606.
Wang Xuejun, Sun Jinping, Zhang Xuwang. Progressive Extended Kalman Filter Tracking Method Based on Compressive Sensing for PD Radar[J]. Journal of Signal Processing, 2017, 33(4): 601- 606.(in Chinese)
[3] 吴仁彪, 刘燕彬, 王晓亮. 通用航空飞行计划航迹估算实现方法[J]. 中国民航大学学报, 2014, 32(1): 1-9.
Wu Renbiao, Liu Yanbin, Wang Xiaoliang. Implementation of track estimation based on flight plan for general aviation[J]. Journal of Civil Aviation University of China, 2014, 32(1): 1-9.(in Chinese)
[4] 刘志花, 李淑芬, 李宝安. 基于粒子滤波的无人机航迹预测方法研究[J]. 电子测量与仪器学报, 2010, 24(7): 643- 649.
Liu Zhihua, Li Shufen, Li Baoan. Research of UAV track forecast based on particle filter[J]. Journal of Electronic Measurement and Instrument, 2010, 24(7): 643- 649.(in Chinese)
[5] 王坤, 王莉莉. 无人机爬升转弯航迹预测[J]. 航空计算技术, 2014, 44(1): 83- 85.
Wang Kun, Wang Lili. Prediction of UAV Climbing and Turning Track[J]. Aeronautical Computing Technique, 2014, 44(1): 83- 85.(in Chinese)
[6] 齐骥, 王宇鹏, 钟志. 无人机多阶段航迹预测协同任务规划[J]. 计算机测量与控制, 2016, 24(6): 189-191.
Qi Ji, Wang Yupeng, Zhong Zhi. Multi-stage Path Prediction Mission Planning Algorithm for Multiple Unmanned Aerial Vehicles[J]. Computer Measurement & Control, 2016, 24(6): 189-191.(in Chinese)
[7] 李相民, 薄宁, 代进进. 基于模型预测控制的多无人机避碰航迹规划研究[J]. 西北工业大学学报, 2017, 35(3): 513-522.
Li Xiangmin, Bo Ning, Dai Jinjin. Study on Collision Avoidance Path Planning for Multi-UAVs Based on Model Predictive Control[J]. Journal of Northwestern Polytechnical University, 2017, 35(3): 513-522.(in Chinese)
[8] 赵嶷飞, 杨明泽. 基于运行状态识别的无人机航迹预测[J]. 科学技术与工程, 2019, 19(23): 304-309.
Zhao Yifei, Yang Mingze. Unmanned Aerial Vehicle Trajectory Prediction Based on Operating State Recognition[J]. Science Technology and Engineering, 2019, 19(23): 304-309.(in Chinese)
[9] 江明, 王飞, 葛愿, 等. 基于改进蚁群算法的移动机器人路径规划研究[J]. 仪器仪表学报, 2019, 40(2): 113-121.
Jiang Ming, Wang Fei, Ge Yuan, et al. Research on path planning of mobile robot based on improved ant colony algorithm[J]. Chinese Journal of Scientific Instrument, 2019, 40(2): 113-121.(in Chinese)
[10] 王晓燕, 杨乐, 张宇, 等. 基于改进势场蚁群算法的机器人路径规划[J]. 控制与决策, 2018, 33(10): 1775-1781.
Wang Xiaoyan, Yang Le, Zhang Yu, et al. Robot path planning based on improved ant colony algorithm with potential field heuristic[J]. Control and Decision, 2018, 33(10): 1775-1781.(in Chinese)
[11] 黄辰, 费继友, 刘洋, 等. 基于动态反馈A*蚁群算法的平滑路径规划方法[J]. 农业机械学报, 2017, 48(4): 34- 40.
Huang Chen, Fei Jiyou, Liu Yang, et al. Smooth Path Planning Method Based on Dynamic Feedback A* Ant Colony Algorithm[J]. Journal of Agricultural Machinery, 2017, 48(4): 34- 40.(in Chinese)
[12] 马学森, 宫帅, 朱建, 等. 动态凸包引导的偏优规划蚁群算法求解TSP问题[J]. 通信学报, 2018, 39(10): 59-71.
Ma Xuesen, Gong Shuai, Zhu Jian, et al. Ant colony algorithm of partially optimal programming based on dynamic convex hull guidance for solving TSP problem[J]. Journal on Communications, 2018, 39(10): 59-71.(in Chinese)
[13] 齐国君, 刘杰, 陈婷, 等. 药剂灌巢剂量对红火蚁蚁巢迁移的影响[J]. 环境昆虫学报, 2017, 39(4): 848- 853.
Qi Guojun, Liu Jie, Chen Ting, et al. Effect of drench insecticide dose on the nest movement of Solenopsis invicta Buren[J]. Journal of Environmental Entomology, 2017, 39(4): 848- 853.(in Chinese)
[14] 王磊, 陆永跃, 曾玲, 等. 草坪生境中红火蚁蚁巢空间关系和蚁群迁移动态规律研究[J]. 华南农业大学学报, 2012, 33(2): 149-153.
Wang Lei, Lu Yongyue, Zeng Ling, et al. Nest Distribution and Dynamics of Colony Movement of Red Imported Fire Ant in Lawn[J]. Nest Distribution and Dynamics of Colony Movement of Red Imported Fire Ant in Lawn, 2012, 33(2): 149-153.(in Chinese)
