1 引言
与单载波信号相比,OFDM 作为多载波调制信号,由多路子载波通过串并变换构成,结构上则更为复杂。目前对OFDM信号与单载波信号的识别方法主要有高阶累积量法、小波分解以及谱相关法等。
文献[1]利用OFDM调制具有渐近高斯性的特点,采用高阶统计量法对OFDM信号和单载波信号进行识别,取得较好的识别效果,但采用高阶累积量必然会提高运算复杂度。文献[2]通过比较多次小波变换的变换系数,根据小波变换的系数分析法,完成OFDM信号和单载波信号在多径信道下的识别,在低信噪比条件下可以获得较高的识别率,但此方法需要的先验条件比较多,对于协作通信双方比较适用,对于信息对抗侦察接收方来说,这些先验条件均是无法获知的,因此其应用范围有限。文献[3]通过分析了OFDM信号循环前缀的结构特点,提出一种基于循环前缀的OFDM信号盲识别方法,但需要知道载波频率以及循环前缀的长度,受信噪比值的影响较大,并且只适合在高斯白噪声信道条件下的分析,没有考虑多径效应的影响。文献[4]通过对特定时延相关函数进行分析,实现对OFDM信号的识别,但为了在频域相关函数上提取极大值作为特征值,需要在不同的延时条件下进行搜索,增加了运算的复杂性,并且整体识别率不高。文献[5]通过将高阶累积量和三角矩相结合,来识别 OFDM 信号和单载波信号,但该方法计算复杂度高,而且瞬时相位提取时存在相位混叠问题,存在识别精度不高、应用范围受限的问题。
本文通过对分形理论的分析发现分形特性能够有效的反应出信号几何尺度的特点,把分形盒维数应用到数字化离散信号中,通过数据分析和仿真说明分形盒维数可以作为一种有效的特征值完成OFDM信号和单载波信号的识别。
2 OFDM信号与单载波分形盒维数
2.1 分形盒维数
在分形理论中,分形维数简称分维[6- 8],能够刻画非线性系统行为的数字特征。本文对通信信号的分形维数进行研究。
定义(F,D)表示一个度量几何空间的数学模型,设R是F的非空紧集族,ε表示一个非负实数,令B(f,ε)表示一个中心点在f,半径是ε的封闭圆球,也可形象的称作是一个半径为ε的小盒子[9-11]。再设A⊂R2是一个非空集合,对于每个正整数ε,令N(A,ε)表示覆盖A的最小盒子数,即:
(1)
其中f1, f2,…, fM是F中的不同中心点。在二维空间中,进一步对非空集合A进行定义[6]:
A={(x,y)|x∈T⊂R,y=g(x)⊂R}
(2)
其中g(x)表示y对于X关系函数,也就是说g(x)表示在R的一个封闭子集T中X到y的映射[12],它是一个连续函数,对此分形盒维数的定义可表示为:

(3)
针对数字化采样后的离散空间信号,为了便于计算,文献[12]结合数字采样信号对公式(3)进行整理,给出了分形盒维数的简化形式。对接收到的通信信号进行离散化采样后得s(t1),s(t2),…,s(tN+1),为了对其进行分组,N取偶数,令:
(4)
式(4)表示N组相邻的两个采样点之间幅度绝对值之差的和,采样点跳变程度越大,d(Δ)的值也越大。
smax(t2i)=max[s(t2i-1),s(t2i),s(t2i+1)]
(5)
smin(t2i)=min[s(t2i-1),s(t2i),s(t2i+1)]
(6)
(7)
对于相邻的三个采样点,式(5)和(6)分别表示三个采样点中的最大值和最小值,式(7)表示从N/2组相邻三个采样点之间,计算最大值与最小值之差的和,结合式(3)可知,简化后的分形盒维数的定义可表示如下:
(8)
由公式(8)可知分形盒维数反映了多组相邻离散化采样点之间幅度跳变程度的相互关系,对于采用一定约束条件的固定调制,其采样点在几何空间的变化有着一定的规律,也就是说分形盒维数能够有效的表示信号幅度的变化特征。所以理论上可以作为一种特征量,用以完成不同调制信号的识别。此外,通过公式(8)也可以看出,采样点越多,分形盒维数相对越稳定,但当采样点到达一定数量时,分形盒维数便不再变化。
2.2 OFDM信号的分形盒维数
对于接收端的OFDM信号,把同一时刻第i路的OFDM信号记为s(ti),为了便于分析,记为si。因为在OFDM信号中各路子载波之间是相互独立的,由中心极限定理可知,大量的独立随机变量之和具有近似正态分布的特点,对于具有n路子载波的OFDM信号,令它们的和s=s1+s2+…sn的分布密度为fs(s),对S进行适当的归一化处理,则具有n路子载波调制的OFDM信号,随着n→∞而趋于正态曲线分布,即:
(9)
其中σ和η表示OFDM信号归一化处理后的均方差和均值,则其分布函数为Fs(s)。下面结合2.1节分形理论,对归一化处理后具有高斯分布特性的OFDM信号进行分析,公式(4)可进一步表示为:
(10)
在公式(7)中,令U=smax(t2i),V=smin(t2i),则U、V的分布函数分别为![]() 利用极限公式对其求导,其概率密度分布函数分别可以表示为:
利用极限公式对其求导,其概率密度分布函数分别可以表示为:
(11)
(12)
那么由(11)和(12)的概率密度分布函数公式,可以进一步推导出U和V的期望为:
(13)
E(V)=![]() νfV(ν)dν=
νfV(ν)dν=![]() ν[3fs(ν)
ν[3fs(ν)
(14)
其中![]() 3νfs(ν)dν=3E(si),为了表示
3νfs(ν)dν=3E(si),为了表示![]() 6νFS(ν)fs(ν)dν的值,参照式(13)的结构形式,此时定义两个采样点的最大值:
6νFS(ν)fs(ν)dν的值,参照式(13)的结构形式,此时定义两个采样点的最大值:
pi=max(si,si-1)
(15)
则P的分布函数分别为![]() 同样利用极限公式对其求导,其概率密度分布函数可以表示为:
同样利用极限公式对其求导,其概率密度分布函数可以表示为:
fP(p)=2Fs(p)fs(p)
(16)
那么由(16)的概率密度分布函数公式,进一步推导出P的期望为:
E(P)=![]() pfp(p)dp=
pfp(p)dp=![]() 2pFs(p)fs(p)dp
2pFs(p)fs(p)dp
(17)
由式(17)知,可以用所定义的变量P的期望,表示要求公式![]() 6νFS(ν)fs(ν)dν的值,即
6νFS(ν)fs(ν)dν的值,即![]() 6νFS(ν)
6νFS(ν)
fs(ν)dν=3E(P),而对于P的期望又可以表示为:
E(P)=E(max(si,si-1))=[E(si)+E(si-1)-
E|si-si-1|]
(18)
则U和V期望的差值可以进一步表示为:
E(U)-E(V)=3E(max(si,si-1))-3E(si)=
(19)
所以公式(7)的值可以进一步表示为:
(20)
把式(10)和(20)带入(8),得OFDM信号的分形盒维数为:
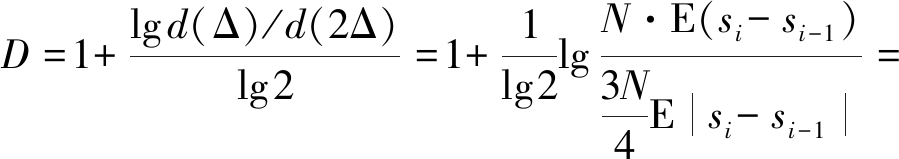
(21)
经以上计算分析得知OFDM信号的分形盒维数近似为1.415,通过公式(21)可以看出,OFDM信号的分形盒维数与调制无关,高斯分布的条件只与子载波的总路数有关。
对此,本文随机选取OFDM信号中的一段数据(为多路子载波数的叠加值),子载波采用不同的调制方式,进行50组模拟仿真,实验结果如图1所示。
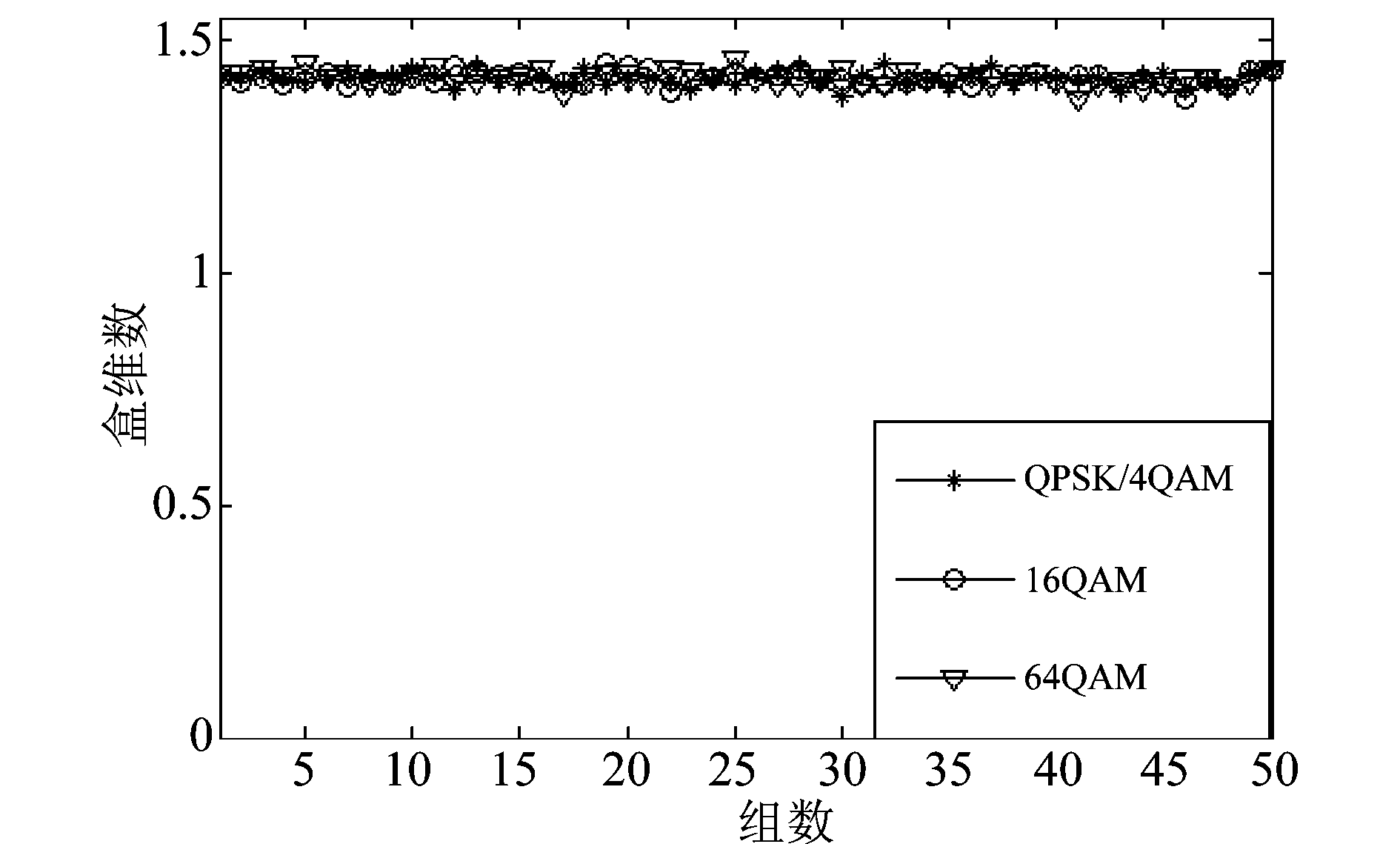
图1 OFDM中采用不同调制子载波的分形盒维数
Fig.1 The fractal dimension box of OFDM signal modulated by different modulation types
图1可以看出,OFDM中分形盒维数与子载波的调制样式无关,子载波无论采用哪种调制方式,分形盒维数都相对固定不变,近似为1.415,验证了上述分析的正确性。此外,由于高斯分布的条件与子载波的总路数有关,针对不同子载波个数的OFDM信号进行模拟仿真,实验结果如图2所示。
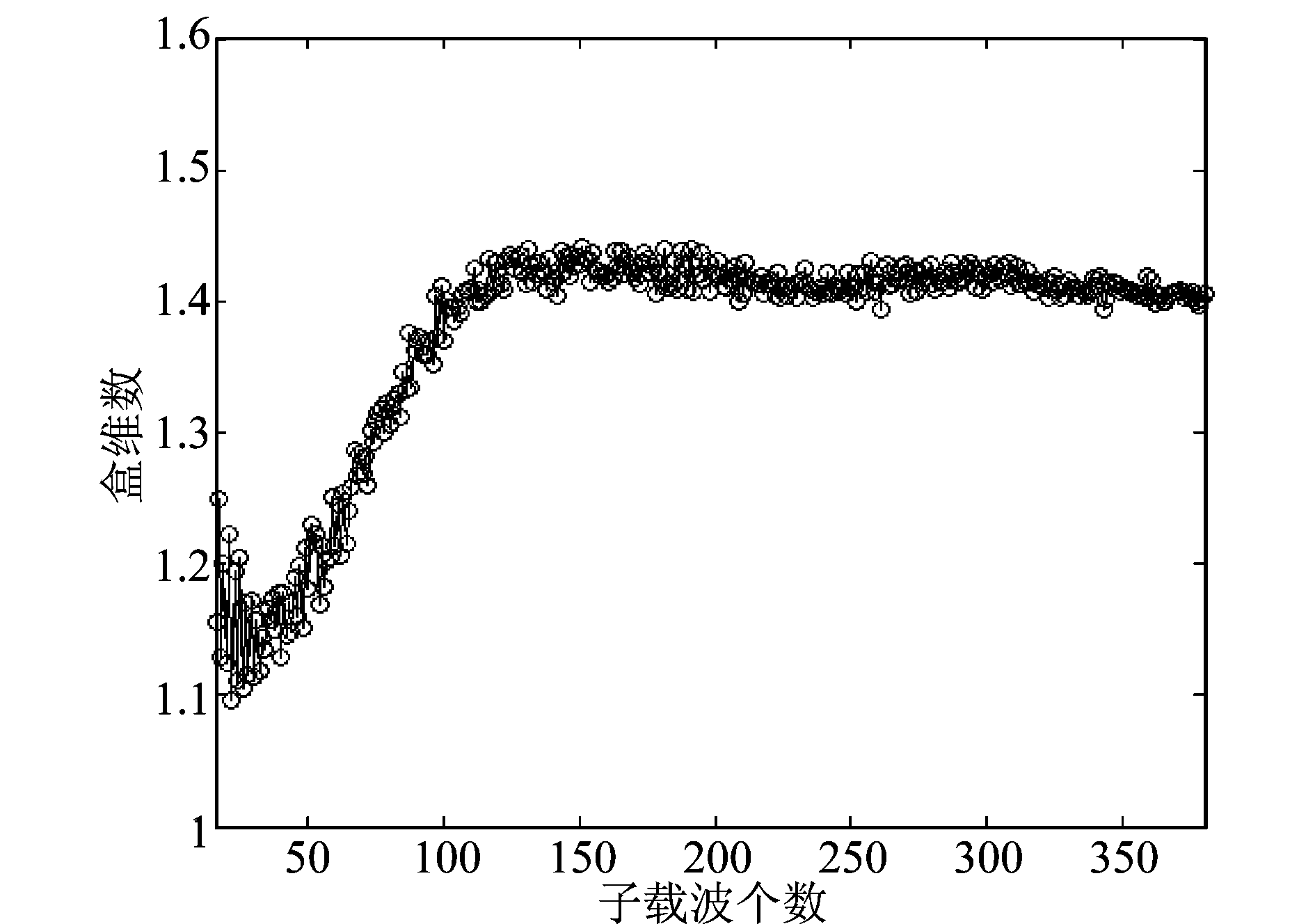
图2 分形盒维数与子载波个数的关系
Fig.2 The relation between fractal dimension box and the number of carriers
由图2可见分形盒维数与子载波个数有关,子载波个数较少时分形盒维数随子载波个数的增多而增大,符合中心极限定理,即大量的独立随机变量之和具有近似正态的分布的特点。图中显示当子载波数大于100时已经基本趋近于理论值,并且不再随子载波路数的增加而变化。目前常见的OFDM系统,子载波数一般在100以上,所以可以近似的认为OFDM信号的分形盒维数为1.415。
2.3 单载波信号的分形盒维数
单载波通信中由于每个码元经过的成型滤波器相同,对于正弦波调制信号,在理想条件下,瞬时幅度的样点之间具有一定的约束关系,不会像OFDM信号那样由于子载波数的叠加具有近似高斯分布的特点。所以在分形盒维数中,与OFDM信号相比,单载波调制信号相似度更强,理论上分形盒维数应小于OFDM信号的分形盒维数。
由于单载波信号的瞬时幅度是由载波幅度、码元幅度和脉冲成形函数三部分的乘积构成,而对于同一种调制方式,载波幅度与码元幅度相对固定为常数,所以瞬时幅度随脉冲成形函数的变化而变化。对于最常见的升余弦成形脉冲函数,由于整个瞬时幅度是连续的,则只有在码元顶点处或者相邻码元跳变点处才会出现极值点。下面讨论瞬时幅度中三个相邻采样点与分形盒维数的关系,为了便于分析,同样令U=smax(t2i),V=smin(t2i)。
i)当s(t2i-1)、s(t2i)、s(t2i+1)具有单调性时, 也就是说采样点的最大值和最小值分别位于两个端点,|s(t2i-1)-s(t2i)|+|s(t2i)-s(t2i+1)|与U-V=|s(t2i-1)-s(t2i+1)|相等,若仅考虑到满足上述单调性条件的三个点,此时d(Δ)=2d(2Δ),分形盒维数D=1;
ii)当s(t2i-1)、s(t2i)、s(t2i+1)不具有单调性时,根据在同一平面上三个点的位置关系,不难看出U-V<|s(t2i-1)-s(t2i)|+|s(t2i)-s(t2i+1)|≤2(U-V),在极端情况下,s(t2i-1)=s(t2i+1)时,上述等号才能够成立,同样,符合要求的上述三个点有d(2Δ)≤d(Δ)<2d(2Δ),分形盒维数1<D≤2。
为了对包含瞬时幅度采样点序列进行进一步量化分析,将公式(4)和(7)带入(8),得:
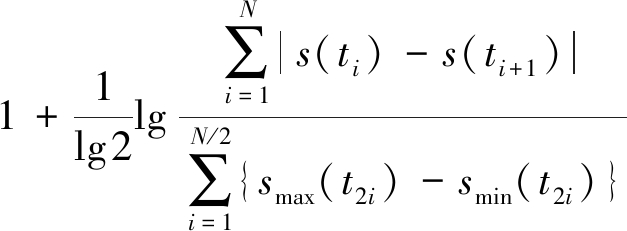
(22)
由公式(22)知,对于一串瞬时幅度采样点序列,其每三个相邻采样点均满足上述两种条件,两种条件的采样点所占总采样点的比例,将对公式(22)的后半部分值产生影响,从而与所求分形盒维数的值密切相关。通常来说,当采样的倍数较大时,满足关系ii)的相邻采样点要远小于满足关系i)的相邻采样点,所以单载波信号的分形盒维数D稍大于1,在没有噪声干扰的条件下,本文把单载波的分形盒维数D定为1,具体仿真如实验1。
3 基于分形盒维数的OFDM信号识别方法
3.1 OFDM信号与单载波信号的识别
通过分析OFDM信号与单载波信号分形盒维数,OFDM信号的瞬时幅度分形盒维数近似为1.415,而单载波信号的瞬时幅度分形盒维数近似为1,两者有较为明显的不同,可以把分形盒维数作为识别这两类信号的特征值。在设定判决门限时,考虑到分形盒维数的计算误差,经第4节实验1的仿真分析,判决门限要比OFDM信号的理论分形盒维数略小,取Dth=1.4。如果接收信号采样序列的分形盒维数大于判决门限值则判为OFDM信号,否则判为单载波信号。
采用分形盒维数进行识别的框图如图3所示,接收到的信号经过带通滤波器后,对其进行A/D转换,求出分形盒维数,根据分形盒维数与设定的判决门限值进行比较,完成判决识别任务。该识别方法的关键步骤是对接收信号分形盒维数的计算,可以根据2.2节和2.3节分析的相关公式计算出分形盒维数。
![]()
图3 基于盒维数识别框图
Fig.3 The identification method flow chart based fractal dimension box
本节中OFDM信号与单载波信号的盲识别问题,可以看成是一个二元假设检验问题。设H0表示待测样本信号为OFDM信号,则H1表示待测样本信号为单载波信号,判决模型可表示为:
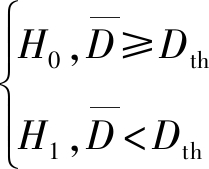
(23)
为了克服噪声带来的影响和减小计算中所带来的误差,![]() 表示多个样本分形盒维数D的平均值。
表示多个样本分形盒维数D的平均值。
3.2 识别步骤
采用分形盒维数完成对OFDM信号和常见单载波调制信号的识别流程如图4所示。首先对接收到的数据进行多次离散化采样处理,计算相应采样数据的分形盒维数,然后取多组分形盒维数的平均值,最后与设定的判决门限值作比较,完成识别任务。
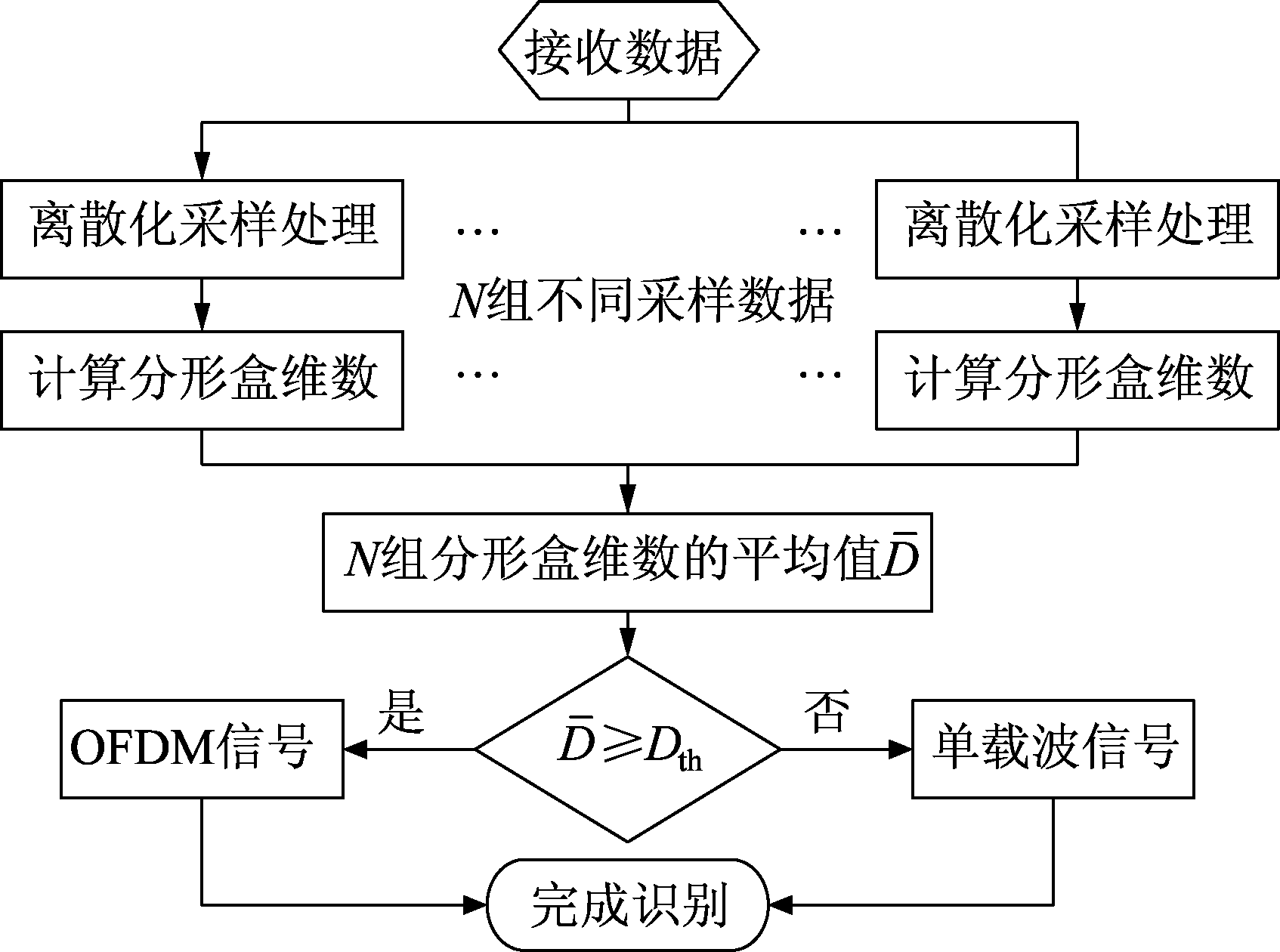
图4 OFDM与单载波信号的识别流程
Fig.4 The identification flow chart of OFDM signal and single carrier signal
具体步骤归纳如下:
1)首先对接收的数据进行离散化采样处理,为了使所得到的采样值能够准确的表示原信号的特点,一般要按照奈奎斯特采样定理进行采样[13-14],本文为了满足OFDM信号的过采样率的要求,选择4倍的采样率对模拟信号进行采样;
2)将采样后的数据代入公式(4)和(7),进一步再由公式(8)求出一组采样数据的分形盒维数;
3)计算多组不同数据的分形盒维数,求出平均值;
4)设定判决门限值,结合公式(23)进行判决。如果接收信号采样序列的分形盒维数大于判决门限值说明信号为OFDM信号,否则判断为单载波信号,从而完成识别。
4 仿真实验及分析
在MATLAB软件平台上建立仿真实验模型。为了方便对算法性能进行对比评估,本文采用与文献[4]相同的外部仿真条件:OFDM信号中子载波的调制方式为QPSK,单载波的调制方式为BPSK、QPSK、16QAM。在单载波信号中,符号周期长度是5 us,对其基带信号进行载波调制的载波频率是400 kHz,选择的采样频率是800 kHz。在OFDM信号中,子载波数目是512,子信道之间的频率间隔是3.125 kHz,根据文献[1]中介绍的数字电视传输标准,选择OFDM信号循环前缀的长度与有效数据的长度之比为1/4,也就是说占总符号长度的1/5,符号周期长度是0.4 ms,调制载波频率是100 kHz。同样,采样频率是800 kHz(为了反映连续OFDM符号的变化特性,实施4倍的过采样),仿真中采用5径衰落信道[14],各路径的归一化延时为[0 25 50 75 100](μs),各路径的幅度衰落为[0 -2 -4 -7 -10](dB)。
实验1 不同信噪比条件下的分形盒维数
图5表示几种常见的单载波调制信号和OFDM信号在不同的信噪比条件下的分形盒维数。由图可知,在较高信噪比条件下,几种调制方式的分形盒维数均基本趋于稳定,完全符合3.2节中对OFDM信号和单载波调制信号分形盒维数的数学分析结果,即OFDM信号的瞬时幅度分形盒维数近似为1.415,而单载波信号的瞬时幅度分形盒维数近似为1。此外,在较低信噪比条件下,分形盒维数受噪声影响比较大,无法完成两类信号的区别。但在信噪比为0 dB以上时,把判决门限定为1.4,可以基本实现两类信号的识别。
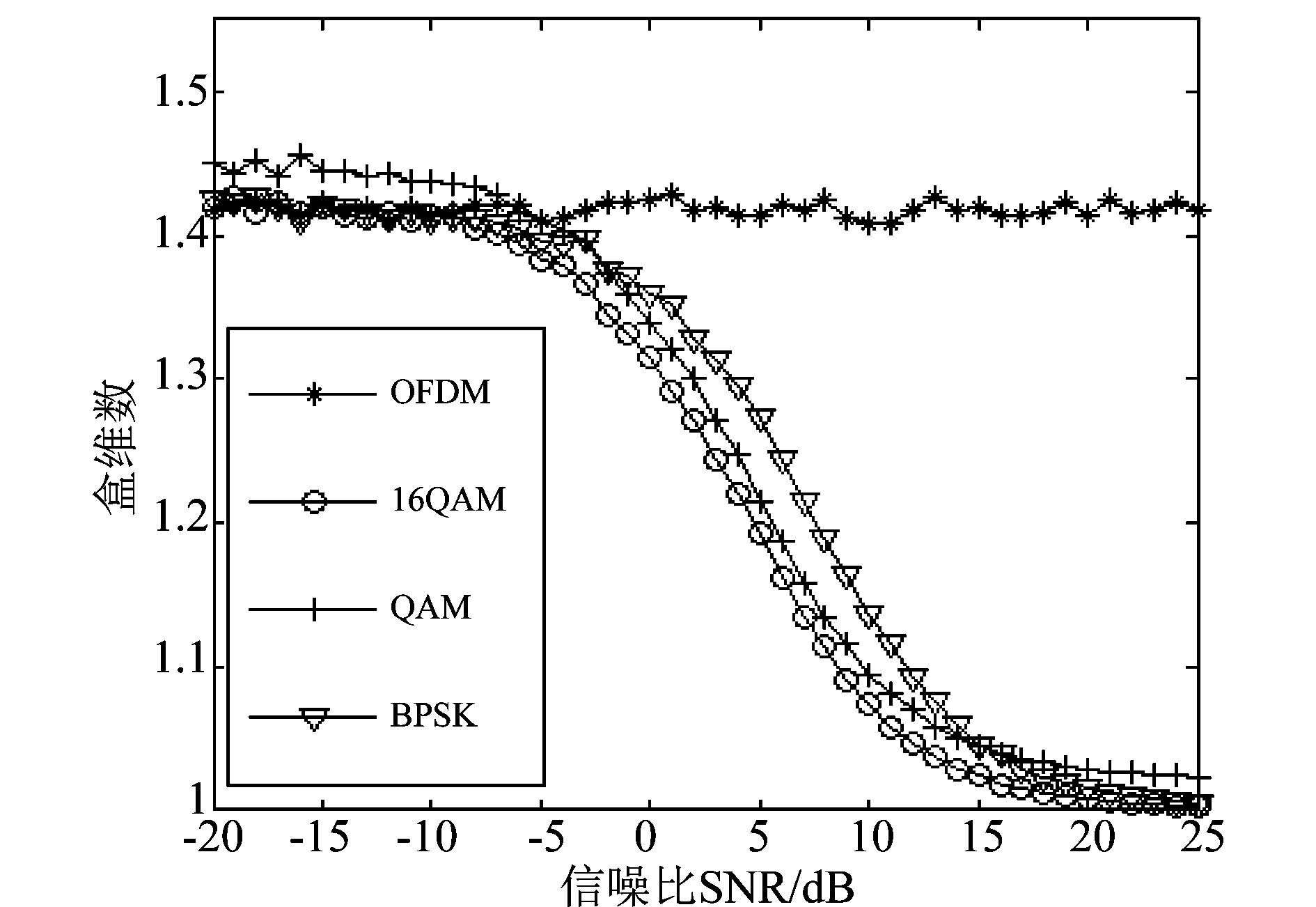
图5 不同信噪比条件下的分形盒维数
Fig.5 The fractal dimension box under different SNR
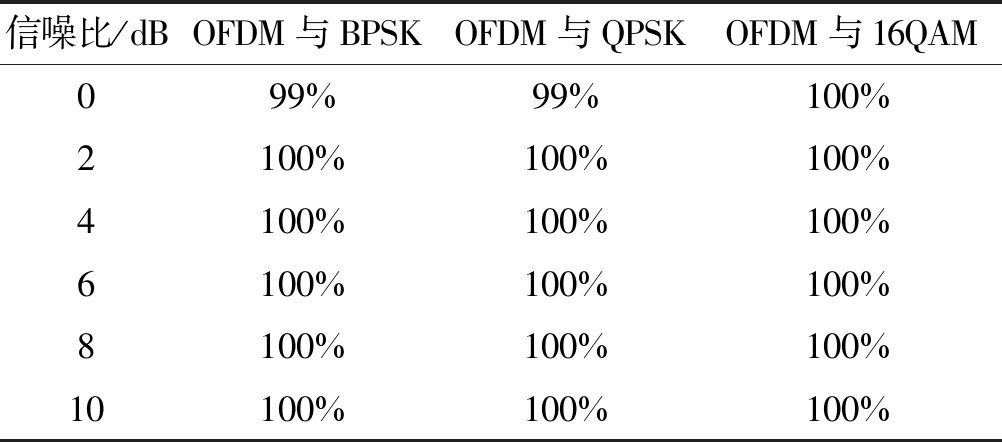
实验2 不同信噪比条件下的识别率
采用上文分析的判决门限,即Dth=1.4,在信噪比每隔2 dB的步长做1000次蒙特卡洛仿真,识别结果如表1所示。
表1 OFDM与单载波信号的识别率
Tab.1 The correct identification rate of OFDM and single carrier
信噪比/dBOFDM与BPSKOFDM与QPSKOFDM与16QAM099%99%100%2100%100%100%4100%100%100%6100%100%100%8100%100%100%10100%100%100%
通过上表可以看出本文提出的基于分形盒维数的OFDM信号识别方法,在表中所给出的信噪比条件下,均能够有效的对几种不同调制的单载波信号与OFDM信号加以区分,在信噪比为2 dB以上时已经达到近100%的识别率,可见在一定的信噪比条件下具有较好的识别性能。
实验3 几种算法的计算复杂度比较
为了有效的分析分形盒维数在计算复杂度上的优势,对于具有N个采样点的数据信号,表2给出了计算过程中实数乘法和实数加法的复杂度比较。
表2 几种算法的计算复杂度比较
Tab.2 The computation complexity of different algorithms

乘法加法本文算法13N-2文献[13]21N+312N+6文献[4]>N(N-1)/4>N(N-1)/4
文献[13]中,郭黎利通过不同高阶累积量之间的特点,构造了多个特征值,从而完成OFDM信号与单载波信号的识别,在分析过程中,最高采用了八阶累积量进行计算,所以计算量复杂。文献[4]中,张路平通过对循环谱进行分析,提出了一种基于信号循环自相关的调制识别算法,在相差有效个数据长度位时,OFDM信号会产生一个次峰值,据此识别出OFDM信号,算法复杂度与循环前缀的长度有关,也就是说它必须遍历搜索超过循环前缀长度的数据量才会发现相应的波峰,其计算量则更为复杂。通过表2可以发现,基于分形盒维数的OFDM信号与单载波信号识别方法,具有计算复杂度低的特点。
5 结论
本文通过对分形理论中的分形盒维数进行详细分析,提出把分形盒维数作为特征值用以完成OFDM信号与单载波信号的识别。经数学分析和理论推导,计算出OFDM信号的瞬时幅度分形盒维数近似为1.415,而单载波信号的瞬时幅度分形盒维数近似为1,从而利用分形盒维数的不同,实现单载波信号与OFDM信号识别。最后通过仿真实验和结果分析可知,本文提出的识别方法,在信噪比为2 dB以上时,对几种不同调制的单载波信号与OFDM信号达到了100%的识别率,具有较高的识别精度。在计算复杂度上,与现有的两种识别方法相比,具有计算复杂度低的特点。因此,本文提出的OFDM信号与单载波信号的识别算法具有一定的实用价值。
[1] 刘献玲. 基于累计量的OFDM信号调制识别[D]. 西安电子科技大学硕士学位论文, 2006.
Liu Xianling. Modulation identification based on cumulants for OFDM signal[D]. Master's Degree Thesis of Xi'an Electronic and Science University, 2006.(in Chinese)
[2] Zhang Jingjing, Li Bingbing. A new modulation identification scheme for OFDM in Multipath Rayleigh Fading Channel[C]∥ISCSCT'08. International Symposium on Computer Science and Computational Technology, 2008.
[3] 曹鹏, 彭华, 董延坤. 一种基于循环前缀的OFDM盲检测及参数估计算法[J]. 信息工程大学学报, 2010, 11(2): 196-200.
Cao Peng, Peng Hua, Dong Yankun. Blind detection and parameter estimation algorithm for OFDM signals based on cyclic prefix[J]. Journal of Information University, 2010,11(2):196-200.(in Chinese)
[4] 张路平, 王建新, 马宁. 多径信道下OFDM信号和单载波信号的盲识别[J]. 宇航学报, 2012, 33(9): 1289-1294.
Zhang Luping, Wang Jianxin, Ma Ning. Blind recognition of OFDM signal and single carrier signals in Multipath channel[J]. Journal of Astronautics, 2012, 33(9): 1289-1294.(in Chinese)
[5] 于志明, 郭黎利, 陆满君. 基于高阶累积量和三角矩的联合多参数特征OFDM信号盲识别[J]. 电子技术应用, 2009, 35(8): 127-131.
Yu Zhiming, Guo Lili, Lu Manjun. Blind recognition of joint multi-parameter OFDM signals based on high order cumulants and trigonometric moments characteristics[J]. Communication and Network, 2009, 35(8): 127-131.(in Chinese)
[6] 朱波华. 基于分形理论的信号处理与分形的研究[D]. 武汉理工大学硕士学位论文, 2008.
Zhu Bohua. The Research of signal processing and analysis[D]. Master's Degree Thesis of Wuhan University of Technology, 2008.(in Chinese)
[7] 郝研, 王太勇, 万剑. 分形盒维数抗噪研究及其在故障诊断中的应用[J]. 仪器与仪表学报, 2011, 32(3): 540-545.
Hao Yan, Wang Taiyong, Wan Jian. Research on fractal box dimension anti-noise performance and its application in fault diagnosis[J]. Chinese Journal of Scientific Instrument, 2011, 32(3): 540-545.(in Chinese)
[8] 赵春晖, 马爽, 杨伟超. 基于分形盒维数的频谱感知技术研究[J]. 电子与信息学报, 2011, 33(2): 475- 478.
Zhao Chunhui, Ma Shuang, Yang Weichao. Spectrum sensing in cognitive radios based on fractal box dimension[J]. Journal of Electronics & Information Technology, 2011, 33(2): 475- 478.(in Chinese)
[9] 李一兵, 李靖超, 林云. 基于分形盒维数的线性调频信号参数估计[J]. 系统工程与电子技术, 2012, 34(1): 24-27.
Li Yibing, Li Jingchao, Lin Yun. Parameter estimation of LFM signals based on fractal box dimension[J]. Systems Engineering and Electronics, 2012, 34(1): 24-27.(in Chinese)
[10] 王青红, 彭华, 王彬. 改进的基于分形盒维数的共信道多信号存在性检测算法[J]. 信号处理, 2012, 28(7): 1044-1055.
Wang Qinghong, Peng Hua, Wang Bin. Improved algorithms for detecting the presence of Co-channel multi-signal based on fractal box dimension[J]. Signal Processing, 2012, 28(7): 1044-1055.(in Chinese)
[11] 党月芳, 徐启建, 张杰. 高阶累积量和分形理论在信号调制识别中的应用研究[J]. 信号处理, 2013, 29(6): 761-765.
Dang Yuefang, Xu Qijian, Zhang Jie. Research on modulation classification based on high-order cumulants and fractal theory[J]. Journal of Signal Processing, 2013, 29(6): 761-765.(in Chinese)
[12] 吕铁军, 郭双冰,肖先赐. 调制信号的分形特征研究[J]. 中国科学,2001, 31(6): 508-513.
Lv Tiejun, Guo Shuangbing, Xiao Xianci. The fractal characteristic research on modulated signal[J]. Chinese Science, 2001, 31(6): 508-513.(in Chinese)
[13] 郭黎利, 于志明. 基于多参数特征的OFDM信号盲识别[J]. 西南交通大学学报, 2010, 35(5): 732-738.
Guo Lili, Yu Zhiming. Blind Recognition of OFDM signals based on multi-parameter characteristic[J]. Journal of Southwest Jiaotong University, 2010, 35(5): 732-738.(in Chinese)
[14] 金国平, 钟华, 郑林华. FMT——正交多载波滤波多音调制技术研究现状分析[J]. 信号处理, 2008, 24(3): 444- 449.
Jin Guoping, Zhong Hua, Zheng Linhua. Analysis of the research on filtered multitone modulation[J]. Signal Processing, 2008, 24(3): 444- 449.(in Chinese)

