1 引言
目标检测自从雷达诞生以来就一直是一个重要的研究内容,其中最关键的就是提升检测的信噪比,它直接影响检测性能。频控阵(FDA)因为在每个阵元上附加了一个远小于载频的频偏,使阵列方向图角度-距离二维相关,大大提高了雷达的检测性能,与相控阵相比,FDA的距离维指向为抑制距离维干扰甚至是主瓣干扰提供了可能性[1-2]。而多输入多输出(MIMO)阵列由于它拥有和相控阵一样的空间自由度,将FDA和MIMO结合,即FDA-MIMO,是最能够实际应用的阵列模型。
近年来,关于FDA和FDA-MIMO在目标检测以及雷达性能提升方面已经做了相关研究。由于FDA发射波束存在角度-距离耦合,所以文献[3]提出了一种差分阵列,每个子阵采用不同的频偏来进行解耦,文献[4]提出了一种采用对数频偏的发射阵列解耦。而FDA-MIMO可以实现自然解耦,没有设计复杂度,同时又很好地利用了FDA和MIMO各自的优势。文献[5]采用空间多重信号分类算法(MUSIC)进行了波达方向(DOA)的准确估计,并对估计性能进行了分析。文献[6]针对FDA-MIMO模型提出一种空距频三维聚焦的信号处理方法,利用多维积累提高信噪比,提升低可观测运动目标的信噪比。文献[7]提出了一种相干FDA接收机模型,采用多通道处理技术,解决了单通道接收处理抵消距离信息的问题,并做了估计性能分析。文献[8]提出了一种快速运动目标的鲁棒自适应波束形成方法,解决了快速运动造成角度-多普勒散焦的问题,然而是基于目标运动没有跨距离单元的前提。
以上研究对运动目标检测涉及不多,并且没有涉及目标运动造成跨距离单元走动的问题。针对以上研究的不足,本文考虑运动目标距离徙动情况,提出一种利用FDA-MIMO与keystone算法相结合的技术,处理该问题,其中正交波形设计采用脉内线性调频,脉间相位调制。所提出的方案带来以下优点:(1)FDA-MIMO实现角度距离自然解耦可以二维波束形成对目标角度距离准确定位;(2)该模型可以处理传统单通道接收机匹配滤波后FDA信号由于时变性抵消距离信息的问题;(3)对距离徙动进行校正处理,便于脉冲积累提高检测信噪比。
本文接下来内容安排如下:第2节给出了LFM正交波形设计方法,建立FDA-MIMO模型并分析了其可行的原因,并分析了距离徙动带来的影响。第3节提出了采用keystone变换与FDA-MIMO相结合的方法解决距离走动问题,提升检测性能。第4节给出了相应的仿真结果,包括传统单通道处理和FDA-MIMO的发射接收波束形成图,距离徙动校正前后的效果图,距离徙动校正前后进行脉冲积累的效果图和信噪比检测曲线图。第5节进行了总结。
2 信号模型
考虑窄带信号,远场点目标假设,传统单天线接收处理:去载频,匹配滤波后的信号可以表示为[7]:
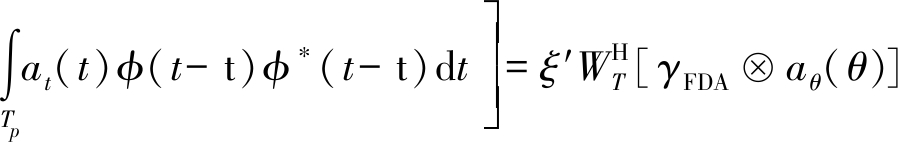
(1)
式中ξ表示反射系数, f0是参考载频,r为双程距离,c是光速,φ(t)是信号波形。
和at(t)分别是发射权矢量、角度、距离和时间导向矢量,(·)H是共轭转置算子。其中WT,m=wT,m,aθ,m(θ)=ej2πmdf0sin θ/c,ar,m(r)=e-j2πmΔ fr/c,at,m(t)=ej2πmΔ ft,γFDA,m=Α(0,mΔ f ),
表示阵元间距,Δ f为频偏,m=1,2,…,M-1。从式(1)可以看出:与距离相关的导向矢量已经完全被抵消了,其波束方向图函数更像是相控阵的波束方向图函数。而单天线收多通道处理后的第n通道输出信号为:
(2)
从式(2)中可以看出A函数与波束方向图函数
存在耦合,因此不能准确测距,因为式(2)峰值不一定出现在A函数的原点。FDA-MIMO可以很好地处理这个问题,不难发现,FDA-MIMO满足:
Α(tb,[m-n]Δ f )=0→Α(0,[m-n]Δ f )=0
→Α(tb,0)Α(0,[m-n]Δ f )=0
→Α(tb,[m-n]Δ f )=Α(tb,0)Α(0,[m-n]Δ f )
(3)
所以,式(2)可以写为:
Α(0,[m-n]Δ f ),此式峰值在Α(tb,0)的原点处,因此FDA-MIMO可以准确测量回波时延并且有效地检测目标。
FDA-MIMO的发射接收示意图如图1所示,其振源间距为d,发射接收阵列各有M和N阵元,波达方向角为θ。
对于均匀线阵(ULA):
fm=f0+mΔ f,m=0,1,…,M-1
(4)
f0为参考载频,Δ f为频偏。FDA-MIMO雷达第m个阵元发射信号可以表示为:
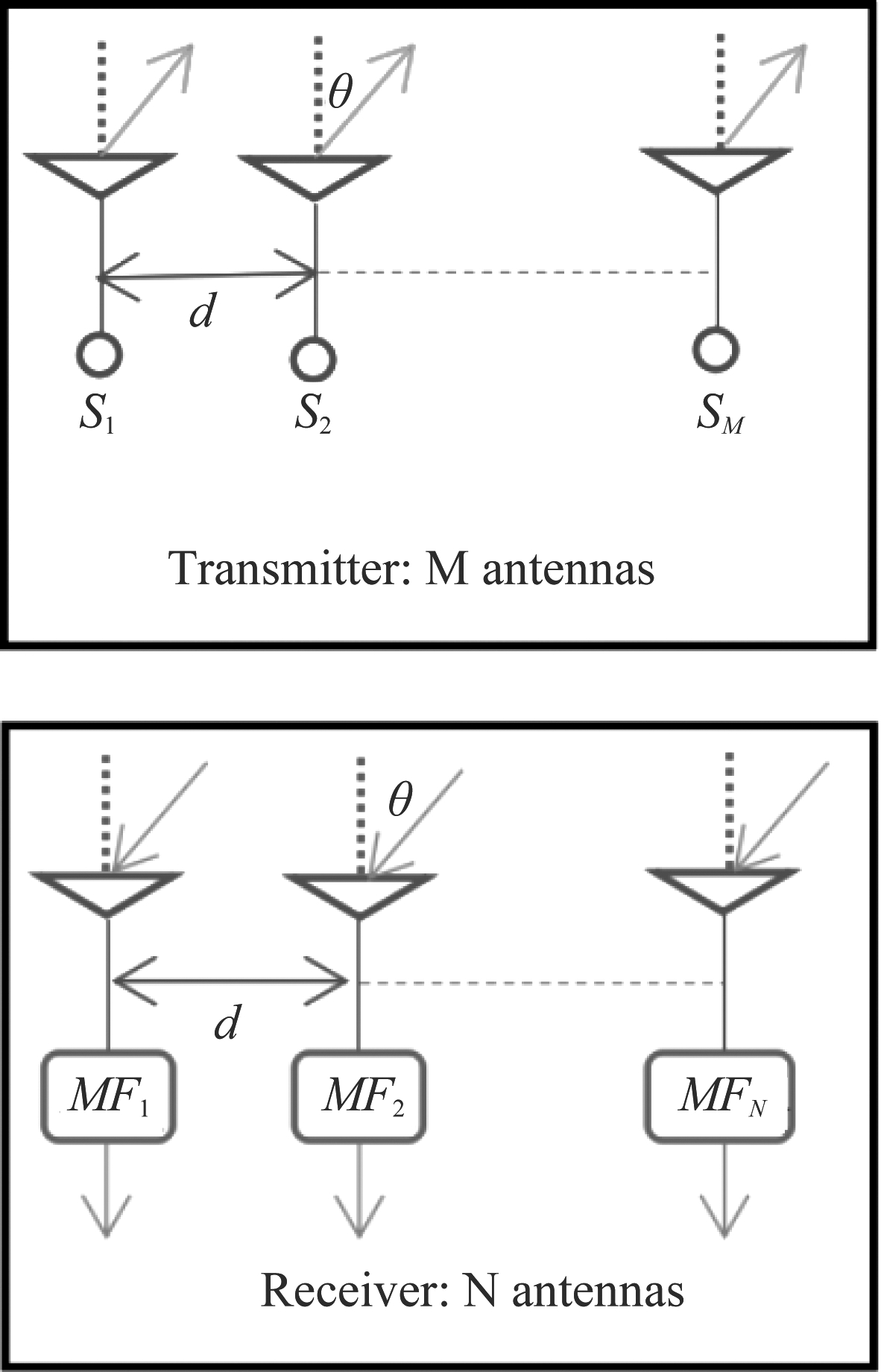
图1 FDA-MIMO雷达示意图
Fig.1 FDA-MIMO radar diagram
(5)
其中T是脉冲宽度,φm(t)是满足正交条件的信号波形,采用脉内线性调频,脉间相位调制,
代表卷积运算,其设计方法[9]如下:
(6)
其中
为矩形子脉冲,δ(·)为冲击函数,Tp为子脉冲宽度。理想的正交波形集应具备两个特征:一是每个波形具有类似冲激函数形的自相关函数;二是任意两个不同波形的互相关函数为零。根据这两个特征可以构造如下优化问题:
(7)
其中A(·)是自相关函数,C(·,·)是互相关函数。
假定信号具有归一化能量,即:
从第m个阵元发射到第n个阵元接收的时延为:τmn=2r/c-md sin θ/c+nd sin θ/c,所以,第n个阵元接收到的信号:
(8)
ζ是复反射系数,接着进行去载频,如图1所示,第m个匹配滤波器的参考函数为φm(t)ej2πΔ fmt,由于正交波形满足: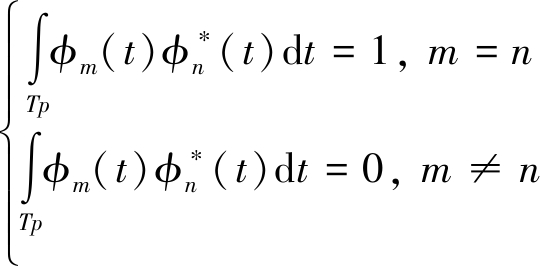
所以第n个接收阵元输出的第m个发射阵元的信号为:
ymn≈ζ′exp(-j2πmΔ fr/c)exp(j2πf0md sin θ/c)
exp(j2πf0nd sin θ/c)
(9)
考虑目标运动,发射多脉冲对目标进行探测。为了分析简便,假定目标为径向运动,即:r=r0+νηT,其中r0为初始距离,ν是运动速度,T是脉冲重复周期,η为脉冲个数。所以,重写式(9)如下:
ymn(η)≈ζ′exp(-j2πmΔ fr(η)/c)
exp(j2πf0md sin θ/c)exp(j2πf0nd sin θ/c)
(10)
对于微弱低可观测运动目标探测,我们希望提高检测的信噪比,所以接下来还要进行脉冲积累,常用的方法是将匹配后的信号再做脉冲维的FFT运算,这样操作后的峰值功率理论上可以达到单个脉冲匹配后的η倍。但是有一个前提,积累脉冲必须在一个分辨单元里面,对于线性调频信号来说,即满足:
为光速,B为信号带宽。不妨做如下简要分析:信号带宽为150 M,目标运动速度为1000 m/s,脉冲重复周期为100 μs,在这样的参数条件下,不难得到最多可以积累10个脉冲,显然,对于微弱低可观测目标来说,这是远远不够的,需要把跨距离单元的脉冲校正到同一分辨单元进行积累,提高检测信噪比。
3 徙动校正
运动目标的距离徙动校正,采用的是keystone变换,如图2所示,简要示意了变换的原理。对于运动目标的回波数据,可以存储为一个二维的矩阵,一维代表快时间,一维代表慢时间,也就是脉内时间和脉间时间。然后将快时间进行傅里叶变换就可以变换到f-tk数据域,如图2左所示。keystone变换进行的是变量代换:tk=τ f0/(f+ f0),此变换可以将图2左图的矩形数据域变为右图的倒梯形数据域,可见,这种变换是对tk轴的伸缩变换,伸缩幅度取决于多普勒频率f,频率越大,伸缩幅度也就越大。
图2 keystone变换示意图
Fig.2 Keystone transformation diagram
前面的分析是基于信号能量归一化,这里为了清楚展示距离徙动校正的推导过程,基于远场窄带假设,对子脉冲进行分析可以改写式(10)如下:
ymn(t,η)≈ζ′exp(-j2πmΔ fr(η)/c)
exp(j2πf0md sin θ/c)exp(j2πf0nd sin θ/c)
(11)
其
是卷积算子,
是线性调频信号:
exp(jπb(t-τ11(η))2)
(12)
其中η为脉冲数,T0为脉冲宽度,b为调频率,式(11)的频域信号为[10]:
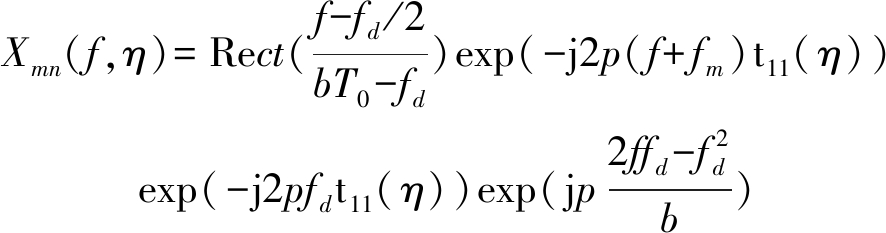
(13)
式(13)相应的时域信号为:
xmn(t,η)≈B sin c[B(t-τ11(η)+ fd/b)]
exp(jπfd(t-τ11(η)+ fd/b))exp(-j2π(fm+ fd)τ11(η))
(14)
如式(14)所示,信号峰值位置应在辛克函数自变量等于0的位置,即:t=τ11(η)-fd/b处,所以峰值位置由脉冲数、目标速度还有调频率决定,如前面分析一样,目标速度越大,时间越长就越容易发生距离走动。
Keystone消除距离徙动:对式(13)进行伸缩变换:Ymn(f,ς)=X(f, f0/(f0+ f )η),将变换后的表达式转换为时域表达式:
ymn(t,ς)≈B sin c(B(t-τ11(0)+ fd/b))
exp(-jπfd(t-τ11(0)+ fd/b))exp(-j2πfdςT)
exp(-j2π(fm+ fd)τ11(0))
(15)
由式(15)可以看出,信号峰值位置始终在t=τ11(0)-fd/b处,可以近似认为所有脉冲经变换后都在初始距离位置,也就是说消除了距离走动,此时进行FFT积累,可以积累所有的脉冲。
值得注意的是,本文分析过程是针对于单目标情况,而对于多目标情况,距离向是没有影响的,只要目标的运动速度偏差不大,也就是具有相似的多普勒特性,本文的方法都是普遍适用的。
4 仿真结果
本节给出相应的仿真结果,分别包括传统单通道接收波束形成和FDA-MIMO接收波束形成,距离徙动对脉冲积累带来的影响和利用keystone变换消除距离走动的结果,最后进行蒙特卡罗实验给出检测性能曲线。
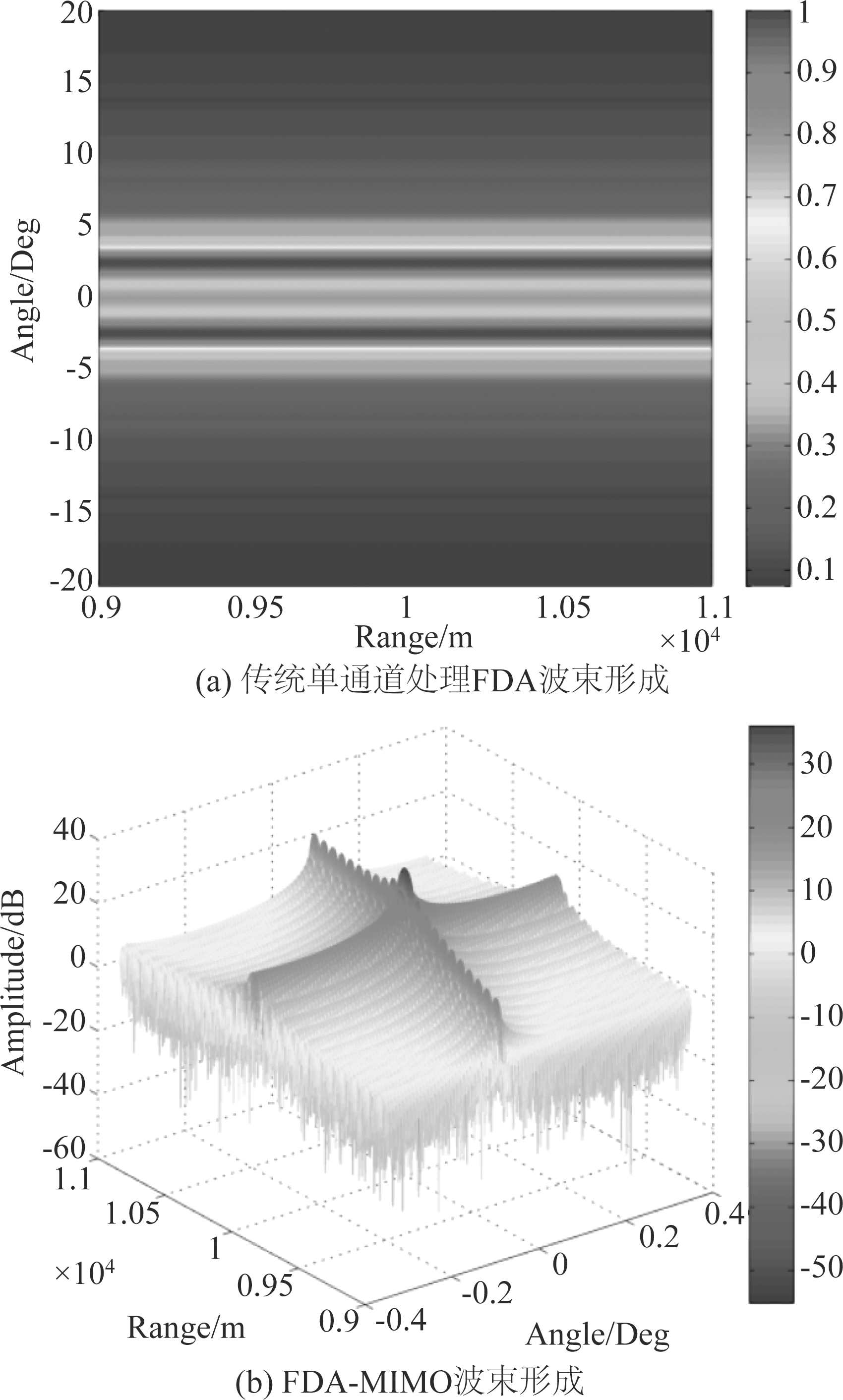
图3 传统单通道处理波束形成和FDA-MIMO波束形成
Fig.3 Conventional single-channel processing beamforming and FDA-MIMO beamforming
如图3所示,仿真参数:M=N=64, f0=10e9,Δ f=1e5,r0=1e4,θ0=0°。图3(a)是传统单通道处理后FDA接收波束形成,可见它只与角度维相关,只能定位目标角度,距离维的信息已经完全被抵消,与前面式(1)的理论分析结果一致,并且波束方向图在0°附近略有展宽,这类似于相控阵的波束主瓣宽度。图3(b)是FDA-MIMO的接收波束形成,它是距离角度二维相关的,可以准确定位目标的二维信息。两图对比可以证明FDA-MIMO可以很好地处理传统单通道匹配滤波处理后抵消距离维信息的问题。
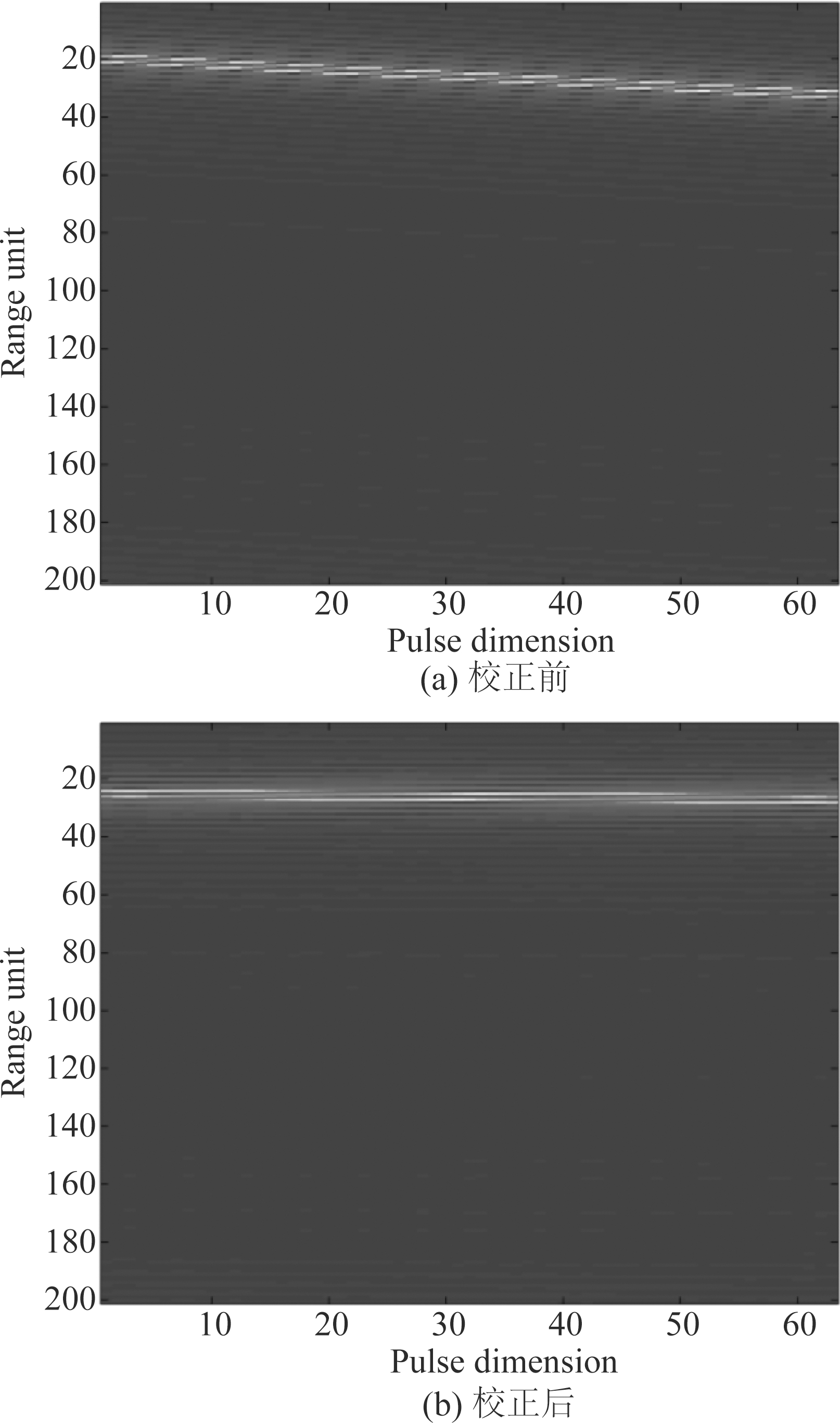
图4 校正前后脉压信号俯视图
Fig.4 Diffraction pattern of pulse pressure signal before and after correction
图4仿真参数:f0=10e9,r0=1e4,Δ f=8e3,ν=1000 m/s,η=63。图4(a)显示的是未经校正的脉压信号图,横坐标代表脉冲维,纵坐标代表距离单元维,从图中可以看到,脉压后各个脉冲的位置都不一样,在图中显示为一条斜线,这就是出现了距离走动。对于设计好的雷达系统来说,走动的程度取决于目标速度和所要积累脉冲的数量,速度越大所要积累的脉冲数越多,走动越剧烈。图4(b)显示的是经过距离徙动校正后脉压信号的结果,可以看到,每个脉压后的脉冲都已经校正到初始位置,在图中显示为一条直线,这和前面式(15)的理论分析结果一致。
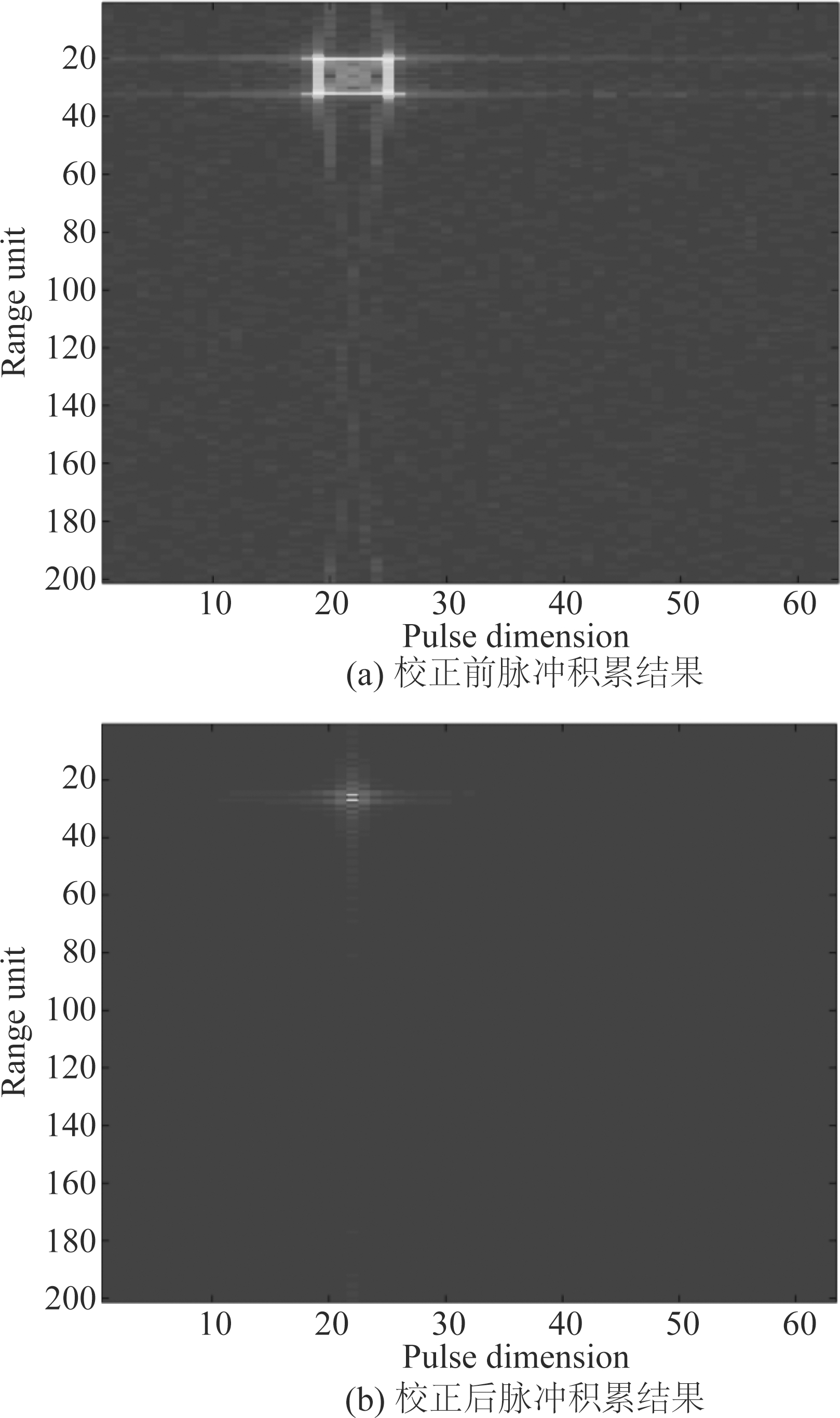
图5 校正前后脉冲积累结果图
Fig.5 Pulse accumulation results before and after correction
图5是距离校正前后对所有脉冲进行FFT积累的结果,图5(a)是有距离走动情况下积累的结果,图5(b)是校正后积累的结果。对比两图不难发现,(b)图聚焦效果远比(a)图好,这是因为在没进行距离徙动校正之前,直接进行脉冲积累,其积累的脉冲数小于校正后的积累脉冲数,其能量分散较大,且峰值能量也远比校正后的小。而且,当脉冲数增加,该对比会更加明显,因为根据前面分析结果可以知道,校正后的所有脉冲都在初始位置处,而未校正的脉冲一直在走动,对于固定分辨单元的雷达系统而言,进行脉冲积累,校正后的能量越来越强,而未校正的能量峰值固定且远小于前者。所以,该方法可以很好地处理目标运动带来的距离徙动问题,提高检测性能。
图6给出的是检测性能曲线,参数:时宽Tp=0.5e-6,带宽B=150e6,积累脉冲数n=63,虚警概率Pfa=1e-3,其他参数如前图所示。仿真方法说明:图6(a)中红色曲线是直接MTD处理,即对脉压后信号直接多脉冲积累,而蓝色曲线是在校正之后,在方位向对齐后进行多脉冲积累,积累过程在MATLAB中使用的FFT函数。在第2节做过简要分析,直接MTD只能积累到10个脉冲,而keystone变换后可以积累63个脉冲,所以在图上表现为检测性能优于直接MTD。图6(b)是keystone变换后积累的检测曲线图,可以知道,当虚警概率增大,同信噪比条件下,因为虚警率增大意味着检测门限减小,检测概率增大,但是对比上下两图可以发现keystone变换后积累的检测性能在Pfa=1e-4时比直接相参积累在Pfa=1e-3时的检测性能还要好。
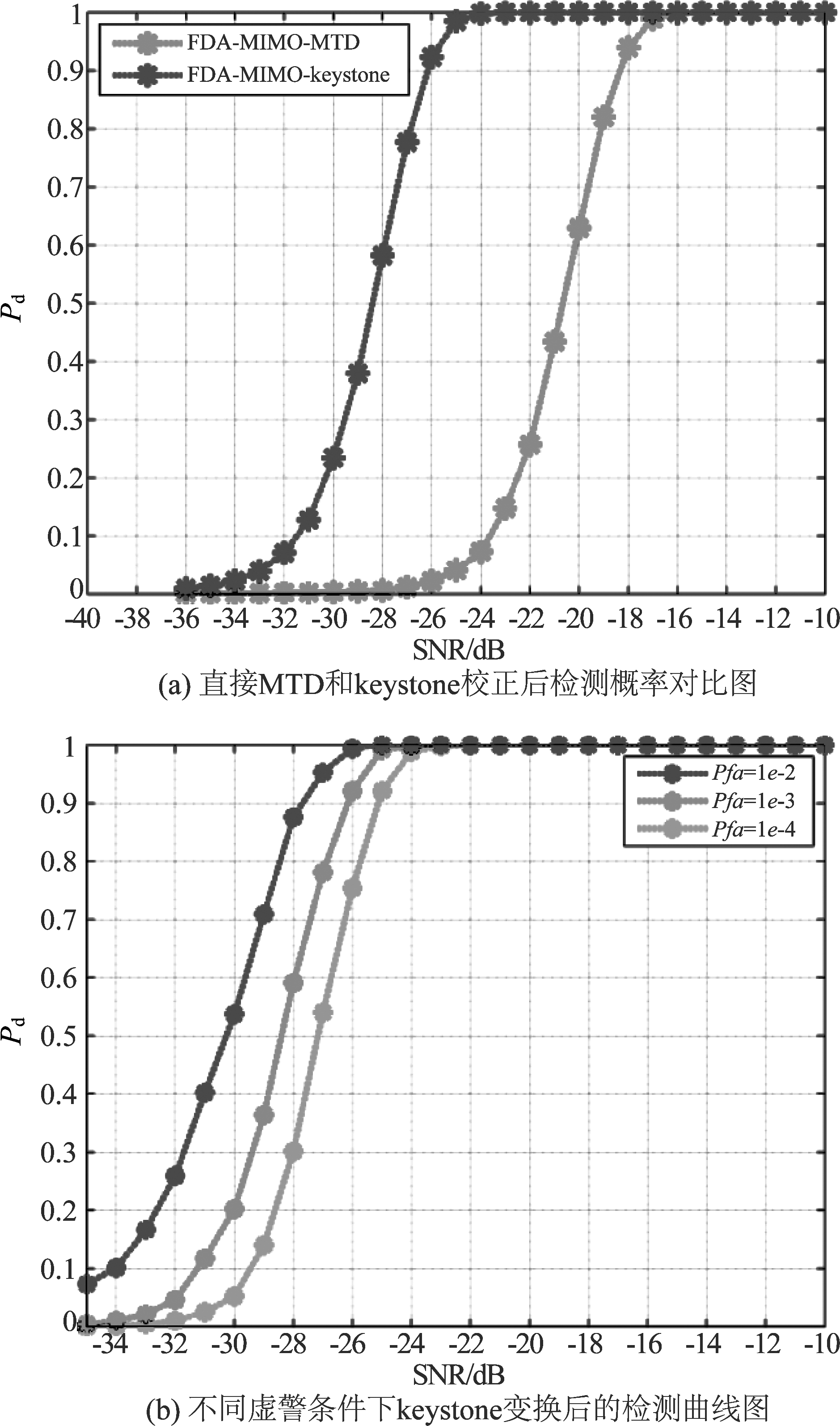
图6 FDA-MIMO检测性能曲线
Fig.6 Detection performance curve of FDA-MIMO
5 结论
本文针对频控阵目标检测研究未考虑运动目标跨距离单元走动问题,以及频控阵存在波束时变造成脉压峰值错位等问题,提出利用FDA-MIMO与keystone算法相结合进行处理,理论及仿真结果显示:FDA-MIMO实现角度距离自然解耦,可以二维波束形成准确定位目标;解决了传统单通道匹配滤波处理抵消距离信息的问题;keystone变换结合可以很好地应用在FDA-MIMO雷达模型上处理运动目标跨距离单元走动问题,提高检测信噪比,有利于微弱低可观测运动目标的探测。
[1] Wang W Q, Shao H Z, Chen H. Frequency diverse array radar: Concept, principle and application[J]. Journal of Electronics & Information Technology, 2016, 38(4): 1000-1011. DOI: 10.11999/JEIT151235.
[2] 王文钦, 陈慧, 郑植, 等. 频控阵雷达技术及其应用研究进展[J]. 雷达学报, 2018, 7(2): 153-166.
Wang W Q, Chen H, Zheng Z, et al. Advances on Frequency Diverse Array Radar and Its Applications[J]. Journal of Radars, 2018, 7(2): 153-166.(in Chinese)
[3] 黄玲, 贺知明, 李想, 等. 基于差分阵列的频控阵雷达距离-角度联合估计[J]. 系统仿真学报, 2017(4): 886- 893.
Huang L, He Z M, Li X, et al. Frequency Diverse Array Radar for Range-Angle Estimation Based on Difference Co-array[J]. Journal of System Simulation, 2017(4): 886- 893.(in Chinese)
[4] 蒋燕妮, 陈泽宗, 赵晨. 基于固定与对数频偏的频率分集阵列雷达波束特性研究[J]. 现代雷达, 2017(39): 29.
Jiang Y N, Chen Z Z, Zhao C. A Study on Beampattern of Frequency Diverse Array Radar of Uniform and Logarithmically Increasing Frequency Offset[J]. Modern Radar, 2017(39): 29.(in Chinese)
[5] Xiong J, Wang W Q, Gao K. FDA-MIMO Radar Range-Angle Estimation: CRLB, MSE and Resolution Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017: 1-1.
[6] Chen X L, Chen B X, Guan J, et al. Space-Range-Doppler Focus-Based Low-observable Moving Target Detection Using Frequency Diverse Array MIMO Radar[J]. IEEE Access, 2018(6): 43892- 43904.
[7] Gui R, Wang W Q, Cui C, et al. Coherent Pulsed-FDA Radar Receiver Design With Time-Variance Consideration: SINR and CRB Analysis[J]. IEEE Transactions on Signal Processing, 2017, 66(1): 200-214.
[8] Xu J, Liao G, Huang L, et al. Robust adaptive beamforming for fast-moving target detection with FDA-STAP radar[J]. IEEE Transactions on Signal Processing, 2016, 65(4): 973-984.
[9] 牛朝阳, 张剑云. MIMO雷达正交波形集设计——线性调频-相位编码混合波形[J]. 计算机工程与应用, 2012, 48(13): 133-137.
Niu Z Y, Zhang J Y. Orthogonal waveform set of hybrid LFM and phase code for mimo radar[J]. Computer Engineering and Applications, 2012, 48(13): 133-137.(in Chinese)
[10] 张顺生, 曾涛. 基于keystone变换的微弱目标检测[J]. 电子学报, 2005, 33(9): 1675-1678.
Zhang S S, Zeng T. Weak Target Detection Based on Keystone Transform[J]. Acta Electronica Sinica, 2005, 33(9): 1675-1678.(in Chinese)
[11] 王娟, 赵永波. Keystone变换实现方法研究[J]. 火控雷达技术, 2011(1): 45-51.
Wang J, Zhao Y B. Research on Implementation of Keystone Transform[J]. Fire Control Radar Technology,2011(1): 45-51.(in Chinese)
[12] Chen B X, Chen X L, Guan J, et al. Transmit Beampattern Synthesis for the FDA Radar[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(1): 98-101.
[13] 关键, 陈小龙, 于晓涵. 雷达高速高机动目标长时间相参积累检测方法[J]. 信号处理, 2017, 33(3A): 1-8.
Guan J, Chen X L, Yu X H. Long-time Coherent Integration-based Detection Method for High-speed and Highly Maneuvering Radar Target[J]. Journal of Signal Processing, 2017, 33(3A): 1-8.(in Chinese)
[14] 肖慧, 胡卫东, 郁文贤. LFMCW雷达高速运动目标检测与估计[J]. 信号处理, 2007, 23(6): 829- 832.
Xiao H, Hu W D, Yu W X. High-speed Target Detection and Estimation in LFMCW Radar[J]. Signal Processing, 2007, 23(6): 829- 832.(in Chinese)
[15] 李军, 刘红明, 苗江宏. 正交信号MIMO雷达动态范围与弱目标检测性能分析[J]. 信号处理, 2010, 26(4): 512-516.
Li J, Liu H M, Miao J H. Analysis of the Dynamic Range and the Detection Performance of Weak Target for Orthogonal Waveform MIMO Radar[J]. Signal Processing, 2010, 26(4): 512-516.(in Chinese)
